Theoretical Economics Letters
Vol. 2 No. 2 (2012) , Article ID: 19274 , 3 pages DOI:10.4236/tel.2012.22024
Impact of Sex on Worker’s Effort within Efficiency Wage Setting
1Department of Economics, University of Brasilia, Brasília, Brazil
2Department of Economics, Catholic University of Brasilia, Brasília, Brazil
Email: pauloloureiro@unb.br, {orrillo, tito}@pos.ucb.br
Received October 13, 2011; revised December 20, 2011; accepted January 2, 2012
Keywords: Sexual Frequency; Efficiency Wages; Nash Equilibrium
ABSTRACT
We provided a simple equilibrium model where both the wage paid by firms and the sexual frequency of their workers are determined in equilibrium. The analysis is carried out within an efficiency wage model where the worker’s effort is influenced, in addition to wage, by the willingness to work. The concept of equilibrium used in this paper is that of Nash.
1. Introduction
One of the basic assumptions of the efficiency wage model is that the worker’s effort depends, in an increasing way, on the wage. In the classical efficiency wage model the wage is the only determinant of the effort [1]. It well known that this theory (see [2,3]) has been created to explain unemployment in ways, which are consistent with the individual agent’s optimization behavior.
In this paper we assume that there are only two things that affect the representative worker’s effort. On one hand we have the wage offered by firms, and on the other, the willingness to work. This willingness to work could be affected by many factors (see, for instance [4]) but for the shake of simplicity we only consider the conjugal relationships. Notice, however, that these relationships are difficult to measure. To make things even simpler, we take the sexual frequency as a measure for a good or bad conjugal relationship. The greater the sexual frequency, the better the conjugal relationships will be.
The main goal of this paper is to determine the equilibrium in a labor market considering an augmented efficiency wage setting. The rest of the paper is arranged as follows: Section 2 describes the model; Section 3 establishes both firm and worker’s problems and determines the equilibrium. Finally, in Section 4 we offer some concluding remarks.
2. The Model
The economy consists of a large number of workers and a large number of firms. Workers are assumed to be identical and firms as well. Workers maximize their utility function and firms maximize their profits.
2.1. Workers
The representative worker’s utility is assumed to be
 . (1)
. (1)
As already said, unlike Solow’s model [1], where the wage is the only determinant of effort, we believe that the effort depends on both the wage,  , and willingness to work,
, and willingness to work, . The latter is assumed to depend on the sexual frequency. Thus,
. The latter is assumed to depend on the sexual frequency. Thus,
 (2)
(2)
and
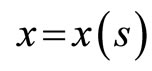 with
with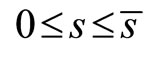 . (3)
. (3)
As is already traditional in efficiency—wage models it is assumed that
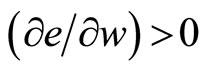 (4)
(4)
In this paper we postulate that
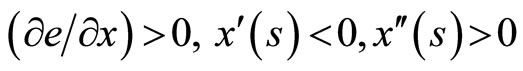 (5)
(5)
The first condition in Equation (5) implies that the greater the willingness to work, the greater the worker’s effort will be. Notice that the effort made by the worker represents a disutility by him or her. The second condition in Equation (5) implies that the willingness to work decrease with the sexual frequency. As a result the worker’s disutility represented by the effort decrease with sexual frequency. Finally the last condition in Equation (5) implies that the function  is strictly convex, meaning that it decrease at increasing rates.
is strictly convex, meaning that it decrease at increasing rates.
2.2. Firms
There is a large number,  , of identical competitive firms. The representative firm seeks to maximize its real profits, which are given by
, of identical competitive firms. The representative firm seeks to maximize its real profits, which are given by
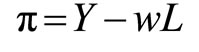 (6)
(6)
where 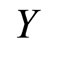 is the firm’s output,
is the firm’s output,  is the real wage that is pays, and
is the real wage that is pays, and 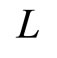 is the amount of labor it hires.
is the amount of labor it hires.
A firm’s output depends on both the number of workers it employs and on their effort, which in turn depends on sexually stimulated willingness to work. For simplicity, we once again neglect other inputs, and assume that labor and effort enter the production function in a multiplicative way.
 (7)
(7)
3. Equilibrium
Due to the hypotheses assumed above, we must remark that workers will want to increase the frequency since this would lead to a decrease in the disutility (effort), and therefore workers will become happier. On the other hand the firm will pay a higher wage to workers to increase their effort which in turn will lead to an increase in the firm’s output. The conflict created between workers and firms will allow us to determine the equilibrium wage and sexual frequency. The notion of equilibrium used is that of Nash Equilibrium.
Before formulating and solving both the representative worker and firm’s problems we will state and discuss our hypothesis that supports our result, namely the existence of Nash equilibrium.
H1 
H2 
H3 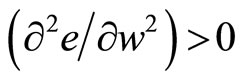
H1 and H2 state that both marginal disutility in relation to wage and marginal disutility in relation to work decrease as the willingness to work increases. Noticing that disutility is represented by the effort exercised by work. Hence, although the effort increases, this increase occurs ever less. This hypothesis may be reasonable due to the fact that the incentive to raise his or her effort comes from him or herself, namely from his or her willingness to work, which is influenced by sexual activity. However, the last assumption, H3, states the contrary. That is, marginal disutility of wage is strictly increasing. Again, one reason could be that the incentive comes from outside, namely from the firm, and therefore the disutility that the firm produces, by means of wages, is ever more. It is as if the worker will be making an effort by obligetion. However, since the incentive is because by sex, workers will be make effort because they want to do.
3.1. The Representative Firm’s Decision Problem
The problem facing the representative firm is to choose the wage and labor, given the level of frequency of sexual activity s of the representative work, in order to maximize its benefit. Mathematically, one has

L, w Thus, the first order conditions are
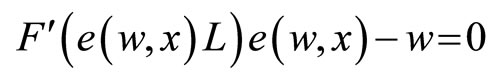 (8)
(8)
 (9)
(9)
Equation (8) is equivalent to
 (10)
(10)
Substituting (10) into (9) and dividing by L yields
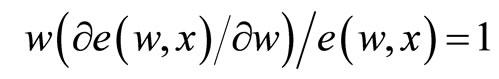 (11)
(11)
This last condition (known as Solow’s condition) states that at the optimum, the elasticity of effort with respect to wage is 1. And the wage w satisfying Equation (11) is known as the efficiency wage (see [1]).
To find the firm’s reaction function, we assume that the function e is sufficiently well-behaved so that there is a unique optimal w* for a given s*. Thus the determination of the firm’s reaction function follows from the application of the Implicit Function Theorem.
Taking the functional form of x and defining the function G from Equation (11), we have
 (12)
(12)
The function G satisfies G(w*,s*) = 0 and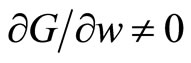 . Thus, by applying the implicit Function Theorem (see [5]) to G, w can be locally solved as a function of the frequency of sexual activity. More precisely, there are two neighborhoods U and V of s* and w* respectively, and a function
. Thus, by applying the implicit Function Theorem (see [5]) to G, w can be locally solved as a function of the frequency of sexual activity. More precisely, there are two neighborhoods U and V of s* and w* respectively, and a function  such that w(s*) = w* and
such that w(s*) = w* and
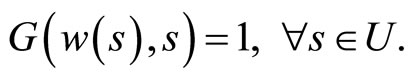 (13)
(13)
Moreover,
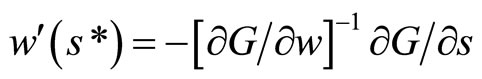 (14)
(14)
By computing the derivatives above, on has
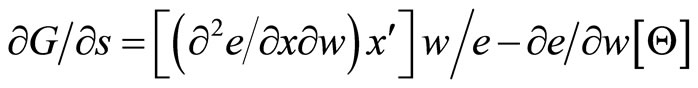 (15)
(15)
where  and
and
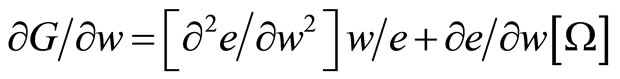 (16)
(16)
where 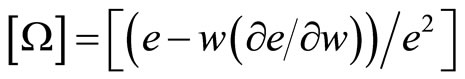
Simplifying and substituting these derivates into (14), we have (17)

H1, H3 and the second condition in Equation (5) imply that 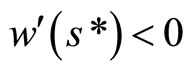 meaning that the firm will offer a lower wage provided the worker wants to increase his or her sexual frequency.
meaning that the firm will offer a lower wage provided the worker wants to increase his or her sexual frequency.
3.2. The Representative Worker’s Decision Problem
Next, we examine the decision problem of the representtative worker, who is assumed to be risk-neutral, in the representative firm. As in the case of the firm, we assume that there are M identical workers who seek to maximize their utility which is assumed to be
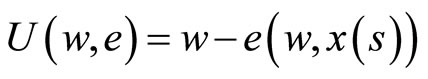 (18)
(18)
More precisely, each worker will have to choose the level of frequency of sexual activity s, given the wage w offered by the representative firm, in order to maximize U(s). That is,
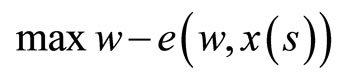 (19)
(19)
where 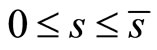
The Lagrangean associated to this problem is
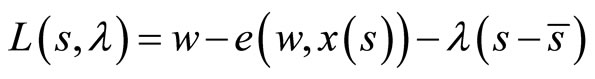 . (20)
. (20)
First-order conditions for this problem are the following Kuhn-Tucker conditions:
 (21)
(21)
and
 (22)
(22)
where 
To solve these conditions, we first assume that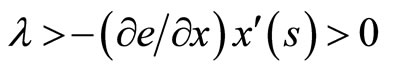 , and then from the first set of conditions we have
, and then from the first set of conditions we have  Thus, using the second set of conditions one has
Thus, using the second set of conditions one has 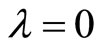 which is a contradiction. Hence
which is a contradiction. Hence 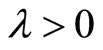 and thus
and thus 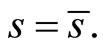 Therefore the only solution of Kuhn-Tucker conditions will be
Therefore the only solution of Kuhn-Tucker conditions will be
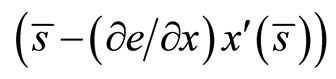 (23)
(23)
Since the objective function is strictly concave, due to Equation (5) and H2, this will be a solution for the worker’s problem decision. The representative worker’s reaction function is  Therefore the Nash equilibrium is
Therefore the Nash equilibrium is
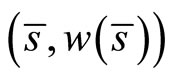 (24)
(24)
4. Concluding Remarks
We have developed a simple equilibrium model where firms, besides hiring workers, decide what wage to pay. In this model workers decide the frequency sexual level in order to maximize their utility that consists of the difference between the wages received and the effort made. The letter was assumed to depend on the both wage and willingness to work.
Notice that the willingness to work has been considered to depend only on conjugal relationships, although actually it depends on many other factors. Notice also that our analysis has been developed within the setting of symmetric information leading to a asymmetric information setting for future researches.
REFERENCES
- R. Solow, “Another Possible Source of Wage Stickiness,” Journal of Macroeconomics, Vol. 1, No. 1, 1979, pp. 79- 82. doi:10.1016/0164-0704(79)90022-3
- G. Akerlof and J. Yellen, “Efficiency Wage Models of the Labor Markets,” Cambridge University Press, Cambridge, 1984.
- L. Weiss, “Efficiency Wages: Models of Unemployment, Layoffs and Wage Dispersion,” Clarendon Press, Oxford, 1990.
- D. Romer, “Advanced Macroeconomics,” McGraw-Hill, Boston, 1996.
- A. Mas-Colell, “The Theory of General Economic Equilibrium: A Differentiable Approach,” Cambridge University Press, Cambridge, 1985.

