Received 30 September 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT

Leveraged Exchange Traded Funds (LETFs) are constructed to provide the indicated leverage multiple of the daily total return on an underlying index. LETFs may perform as expected on a daily basis; however, fund issuers state that there is no guarantee of achieving the multiple of the index return over longer time horizons. LETF returns are extremely volatile and funds frequently underperform their target for horizons greater than one month. In this paper, we contribute two nonparametric simulation methods for analyzing LETF return volatility and how this is related to the underlying index. First, to overcome the limited history of LETF returns data, we propose a method for simulating implied LETF tracking errors while still accounting for their dependence on underlying index returns. This allows for the incorporation of the complete history of index returns in an LETF returns model. Second, to isolate the effects of daily, leveraged compounding on LETF volatility, we propose an innovative method for simulating daily index returns with a chosen constraint on the multi-day period return. By controlling for the performance of the underlying index, the range of volatilities observed in a simulated sample can be attributed to compounding with leverage and the presence of tracking errors. Our nonparametric methods are flexible-easily incorporating any chosen number of days, leverage ratios, or period return constraints, and can be used in combination or separately to model any quantity of interest derived from daily LETF returns.

Keywords:

Nonparametric Density Estimation, Exchange Traded Fund, Realized Volatility

1. Introduction

The class of securities commonly known as LETFs, or Leveraged Exchange Traded Funds, began trading on the New York Stock Exchange in 2006. LETFs are managed by their issuers with a mandate to provide a multiple of the daily return of the underlying asset, and are developed to provide professional investors a convenient means for the short term hedging of market risk. Since their issuance, their popularity in the investment world has risen steadily and now there are investors promoting buy and hold strategies that feature long term positions in LETFs [1] [2] . The lack of understanding of the risks associated with these strategies and more generally LETF return dynamics was a primary motivation for our work. In this paper, our objective is to offer improved tools for analyzing the risks involved with investing in LETFs.

The first Exchange Traded Fund (ETF) began trading in 1993. By 2015, there are over 1400 ETFs from over 15 different issuers, with over $1 trillion invested in ETFs globally [3] . The existing universe of ETFs covers all major asset classes such as equities, debt, commodities, and real estate. Many ETFs are referenced as the underlying asset of actively traded options. We will focus on a specific subset of ETFs called Leveraged ETFs (LETFs) which feature a leverage ratio different than 1:1 as part of their fund structure.

The mandate for LETFs is to provide the daily return of an underlying asset, most often an equity index, at the multiple indicated by the leverage ratio. As of 2015 there are fund offerings featuring leverage ratios of 2:1, −2:1, 3:1, and −3:1. Going forward, we will simply refer to leverage by its multiple (i.e. 2, −2, 3, −3). For example, if the underlying index returned 1% on the day, then LETFs with leverage multiples of 2, −2, 3, and −3 would have a mandate to return 2%, −2%, 3%, and −3% on the day, respectively. Positive values indicate long market exposure, while negative multiples indicate short exposure, or betting that the market will decline. Funds that feature negative leverage multiples are often times referred to as Inverse ETFs, but we will not make this distinction because the returns dynamics are the same except for the obvious negative sign on the leverage term.

In addition to the included leverage, providing investors with the ability to easily acquire short exposure is an important selling point for LETF issuers. Before these LETFs started trading in 2006, leveraging one’s assets or betting against the market required utilizing expensive margin and collateral accounts or navigating the challenges involved with trading options [4] . Investors have since grown to appreciate the conveniences offered by the LETF structure and as in 2015 there are over 100 funds with a total notional value over $20 billion listed on exchanges worldwide, with Direxion, ProShares, Credit Suisse, and Barclays issuing the majority of them [5] .

Not long after LETFs started trading, researchers began to examine the leveraged returns they provide and the associated daily compounding. Jarrow [6] and Avellaneda and Zhang [7] were some of the first to do so. The work by both sets of authors is very similar. They clearly prove that the multi-day return on an LETF is not the same as the return on an (unleveraged) ETF with the same underlying index and relate the difference to the ETF’s volatility and borrowing costs. Avellaneda and Zhang also provide a strong collection of empirical results to reinforce their proof. In a similar fashion, Lu, Wang, and Zhang [8] provide empirical results that extensively quantify the underperformance of LETFs with respect to their benchmark over multi-day periods. They claim generally that with a leverage multiple of 2, or we say “2x leverage”, one can expect an LETF to deliver its targeted return for periods up to a month, and then they quantify expected deviations for longer horizons.

The work by Dobi and Avellaneda [9] takes the discussion of LETFs a step further. They highlight the total return swap exposures that are rebalanced daily by LETF issuers to provide the leveraged return target as a cause of LETF underperformance. We strongly agree with their comment that LETF underperformance “… is especially true for longer holding periods and for periods of high volatility”. Tuzun [10] expands on the ramifications of the swap exposures that are held by the LETF issuers. He notes the similarities between daily rebalancing necessitated by LETFs and portfolio insurance strategies from the 1980s. This work is written from the perspective of market regulators, but we found it helpful because it emphasized the effects of consecutive gains or consecutive losses on LETF performance. With LETFs a period of consecutive gains produces lever- aged gains on leveraged gains, resulting in a compound return that is much greater than would be experienced without leverage. This scenario should not be difficult to understand, but in the case of consecutive losses with leverage, the authors demonstrate that this also results in improved performance (relatively). In other words, relative to the same index exposure without leverage, the magnitude of the cumulative loss experienced with leverage is less. This is because with every consecutive negative return, exposure is decreased before the next loss, and with leverage the decrease of exposure is greater.

Cooper [11] provides a detailed review of volatility drag and LETF dynamics in an attempt to prove that there exists a leverage ratio greater than one that is optimal for buy and hold investing in any equity index. We are doubtful of his claims because of the assumption of no tracking errors. We show later this would be poor judgment with the LETFs that we analyze. Also, Bouchey and Nemtchinov [12] show that underperformance of high volatility stocks compared to low volatility stocks is mostly the result of volatility drag. There is a parallel that could be considered between their thesis and the performance of LETFs with high volatility underlying indexes compared to LETFs with low volatility underlying indexes, but we do not investigate it here.

Qualitatively speaking, we agree with the above mentioned authors that LETFs frequently underperform over time horizons greater than one month, underperformance is greater in times of high volatility, and that under- peformance is intrinsically related to volatility drag. But, we view our contributions as an empirical framework that complements their analytical models and we do not attempt to reproduce the results on which their conclusions are based. Instead, our intention is to provide methods that can help LETF investors better account for these dynamics. The remainder of this paper is organized as follows.

In Section 2 we review the LETF returns dataset used throughout this paper, present a visual motivation for our contributions, and describe two statistics for measuring the realized volatility of LETF returns-sample standard deviation and Shortfall from Maximum Convexity (SMC). SMC is a variant of volatility drag that specifically accounts for the effects of leverage. We defined SMC and documented the advantages of using it to measure realized volatility in a separate publication [13] , which is summarized in Section 2.

In Section 3 we propose a method for simulating LETF tracking errors. The proposed method allows us to produce simulated LETF returns derived from index returns and LETF tracking errors that are simulated separately. In turn, we can make use of the entirety of their respective datasets, greatly improving the robustness of our density estimates used in simulation.

In Section 4 we exploit this separation by proposing a method for simulating index returns with a constrained total period return. Constraining the underlying index performance allows for greater nuance with modeling LETF volatility. With this method, a practitioner can formulate more customized LETF volatility summaries by including a specific returns forecast for the underlying index.

Finally, we demonstrate how to combine the two simulation methods with a brief case study in Section 5.

2. Visualizing LETF Returns and Measuring Realized Volatility

We have selected a wide ranging set of 10 equity indexes referenced as the underlying asset by 10 pairs of long and short LETFs for demonstrating our work (10 funds with a +3 leverage multiple and 10 with a −3 multiple). All of the included pairs of ±3x levered ETFs are issued by Direxion and ProShares. Our set includes established U.S. market indexes (S&P 500, Dow Jones Industrial Average, Russell 2000, NASDAQ 100), sector specific indexes (NYSE ARCA Gold Miners, Dow Jones U.S. Financials, S&P Technology Select), and international equity indexes (MSCI Developed Markets, MSCI Emerging Markets, and Market Vectors Russia). The specific instruments included in the demonstration set are listed in the Appendix in Chart 1 and Chart 2.

Throughout this paper, we assume that daily LETF returns (for a generic ticker LEFT) and their matching daily index returns (generic ticker Index) are related through the following decomposition:

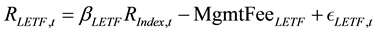(1)

where 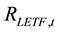is the daily return on day t for fund ticker LETF, is the daily return on day t for the underlying ticker Index, 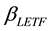is the indicated leverage multiple for LE T F (constant), 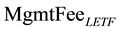is the indicated rate of daily management expenses for LETF (constant), and 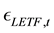is the tracking error on day t for LETF (random variable).

The leverage multiple and annualized management expenses are indicated in a given LETF’s fund prospectus. As mentioned, since 2015 there are commercially available LETFs with leverage multiples of 2, −2, 3, and −3. All of the management fees indicated on the LETFs in our demonstration set were listed as 0.95% annually, or a daily rate of approximately 0.375 basis points [14] -[17] . Fees for other LETFs from Direxion and ProShares or other fund issuers are the same or comparable [5] .

All the daily returns data for the 10 indexes and 20 LETFs in the demonstration set are sourced from Bloomberg and the LETF leverage and fees constants are sourced in their fund prospectuses provided by their respective issuers [16] -[18] . No other sources of data are referenced in this paper.

2.1. Visualizing LETF Returns

Our contributions can best be motivated through visualization, and so we begin with Figure 1. There are two

scatter plots of 252 day compound LETF returns (y axis) against the matching 252 day compound index returns (x axis) from the same periods. The right plot is for +3x LETF Ticker SPXL, the left plot is for the hypothetical LETF “+3x SPX” created by daily, leveraged compounding of S&P 500 returns, and then for both the underlying index is the S&P 500. The diagonal blue line in each plot corresponds to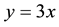, and is provided to indicate what return would be achieved by a leveraged investment in the index without daily compounding. It has been said time and again that “a picture is worth 1000 words,” but in our case we could say 10,000 words, the approximate length of this paper.

Three extraordinarily important observations need to be made. First, there are many more points representing a much wider range of outcomes in the left plot, which is derived from the entire daily returns series of the S&P 500 (21,591 intervals of 252 days), compared to the right plot that includes only the SPXL returns series (1288 intervals of 252 days). Second, there is an interesting crescent shape with a hard upper bound apparent in the left plot, where the overwhelming majority of points are clustered near the upper bound. Third, again in the left plot, points seem to disperse from the upper bound in a way that maintains some degree of curvature such that the range of dispersion is not constant. These characteristics were readily observable when the same plot was generated using other LETF and index pairs.

Figure 1 illustrates the advantages of having more data. The right plot was limited to the returns data available for SPXL, which extends back to 2008. On the other hand, the left plot used all the data available for the S&P 500, which extends back to the 1920s. Except for the Market Vectors Russia Index (MVRSX) there are at least 16 years of data for every index that we consider in this paper. Given the dependence of an LETF’s daily returns on the matching returns of the underlying index, it follows naturally that we should develop schemes for modeling LETF returns that can incorporate and control for the variation in the complete history of index returns data. Our methods presented in Sections 3 and 4 address these two motivations, respectively.

The potential enhancements offered by our methods are especially significant given the fact that North American equity indexes have generally been in an upward trend since March 2009. In other words, the majority of available LETF returns were observed when the index returns that they are derived from were positive or compound to a positive value over periods of months or years. This can be seen in Figure 1, where the right plot has no points with an x value less than 0 (the underlying index return), but there are many points that satisfy this condition in the left plot. Obviously, any quantitative LETF analysis would benefit from the ability to include data from downward trending markets and isolate the resulting effects.

2.2. Measuring Realized Volatility

Modeling the volatility of asset returns as the standard deviation of the returns distribution has been commonly accepted since the publication of Markowitz’ benchmark paper on portfolio theory [19] . Accordingly, sample standard deviation would be the usual measure of realized volatility of a p dimensional vector of daily log LETF returns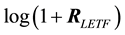. We denote this statistic as PSD, or Periodized Standard Deviation.

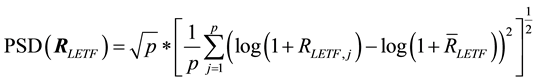(2)

(3)

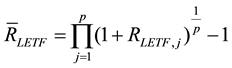(4)

where 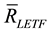is the geometric mean of the elements of the geometric returns vector.

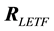Alternatively, we will measure realized volatility with Shortfall from Maximum Convexity (SMC), a novel statistic that was designed specifically for application to LETF returns [13] .

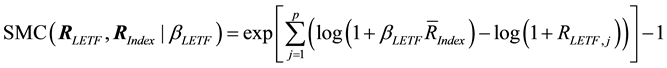(5)

(6)

where is the indicated leverage multiple for LETF (constant), is the matching p dimensional vector of daily returns for Index, and is the geometric mean of the elements of. What differentiates SMC from PSD is subtle―a mean return of is used instead of, and the sum of daily differences is exponentiated instead of taking the square root of the sum of squared, daily differences.

These changes were inspired by the geometric details of the plotting arrangements used in Figure 1. SMC is simply the vertical distance between a data point and the point on the convex upper bound that is located at the same x value (calculating the exact form of points on the upper bound is trivial). The interpretation of this measure is the geometric excess return of a hypothetical, maximum return derived from the index return, with respect to the LETF return. We use SMC because the interpretation of PSD becomes problematic with non- normal, dependent data, and when applied to LETF returns SMC provides more information, statistically speaking. These arguments are covered in much greater detail within the original proposal for SMC, and we refer interested readers there for more information.

3. Simulation of Tracking Errors Using Nonparametric Density Estimation

A naive approach for modeling LETF returns would be to simply assume no tracking errors and approximate daily returns as the underlying daily index return with leverage and net of management fees. These ap- proximated returns, after compounding, could be used in the denominator when calculating SMC in place of a true LETF return. This naive approach is simple and allows for the incorporation of the entire history of index returns data; however, it ignores the impact of LETF tracking errors on returns and realized volatilities.

This impact becomes significant over time, as demonstrated in Figure 2 and Figure 3 for two LETFs. First, density curves of 252 day returns of LETF Ticker RUSS (top) and LETF Ticker TECL (bottom) are plotted against 252 day returns of their respective underlying indexes, but compounded daily with a leverage multiple of −3. Note the separation between the density curves, which is due to the cumulative effect of tracking errors because the index returns were calculated with daily compounding and leverage. Second, density curves of 252 day SMC are plotted using the same data and plotting arrangements. Again, note the separation between the density curves, and that the separation is much greater when visualizing realized volatility compared to visualizing returns.

In light of this evidence, it is our opinion that approximating LETF returns by assuming no tracking errors would provide for inaccurate analyses, and in response we propose the nonparametric method for simulating LETF tracking errors described in this section. Our method estimates filtering and smoothing densities using only data from the days when LETFs were trading. The proposed method effectively allows for simulating LETF returns derived from index returns and LETF tracking errors that are simulated separately, thus incorporating the entire history of index returns and LETF returns data in an extremely efficient manner.

3.1. Framing Tracking Error Simulation as Filtering

When discussing any statistical analysis of daily LETF returns, over a period of k days, the following length 2k random vector of daily asset returns is observed:

(7)

where is the daily index return on day t for the underlying index ticker Index, and is the daily LETF return on day t for the specified LETF ticker LETF. We assume that daily LETF returns and their matching daily index returns are related through the following decomposition:

(8)

where is the indicated leverage multiple for LETF (constant), is the indicated rate of daily management expenses for LETF (constant), and is the tracking error on day t for LETF (random variable). Implicitly, then, we are assuming that the following random vector captures the same information as the vector that was stated originally:

. (9)

From this view of the LETF and index returns processes we develop a simulation method that is based on the following factorization of the joint density for these variables:

. (10)

The density is a filter as used in state space modeling, where (by necessity) the index returns process is designated as the observation process and the LETF returns process is designated as the state process. This runs counter to a more intuitive arrangement of designating LETF returns as functions of the state (index returns) with observation noise (tracking error).

To handle any dependence that may exist within a sequence of index return variables, we do not factorize the density. Modeling all of the index return variables jointly captures their complete k day dependence structure. To account for dependence of LETF tracking error data and inter-dependence of tracking errors and index returns, in our filtering density we will additionally include lagged index returns and lagged tracking errors as given, where is an integer valued parameter that will be selected in a later subsection. This arrangement reflects our view that LETF tracking errors have a simpler dependence structure compared to index returns (in practice), and that LETF tracking errors are dependent on the underlying index returns. We do not consider index returns to be dependent on the respective LETF returns or tracking errors; therefore, nowhere in our approach do we attempt to model the statistical relationship of.

To include the additional lagged variables, the joint density factorization is revised as follows:

. (11)

There are three important changes to highlight. First, the filtering density is now con-

ditioned on lagged index return variables and lagged LETF return variables (in addition to). Second, the joint density of index returns and LETF tracking errors (left-hand side), and unconditional joint density of index returns (final term of right-hand side), both include the additional lagged variables such that the random vector being modeled is now of length. Third, we have introduced a conditional density for

smoothing the tracking error variables,. This additional term

is necessary to initiate, or “burn-in”, the sequence of tracking error variables, providing the first set of lags that are required by the first iteration of the filtering density.

Also, the decision to smooth the first variables instead of the first variables and then starting filtering at deserves further comment. Our reasoning is implementation related, so the dataset needs to be transformed only once. As written, the conditional densities differ only by which variables are considered as given. Otherwise both densities model the same variables―a sequence of index returns and the matching sequence of tracking errors. Having both densities model the same variables allows for the same observation matrix being used for both of the resulting kernel density estimates, as shown in the next subsection of derivations. If only the first variables were smoothed, and iterations of the filtering density began with day, the dataset would need to be transformed twice. One transform would be required to implement an estimate of the density with variables used for smoothing the initial lagged errors and another to implement an estimate of the density with variables used for filtering the remaining errors. There is one exception, when, a case which results in smoothing and filtering densities that are identical and the joint density factorization reverts to the initially stated form with only two terms,

.

However, to avoid the additional bias introduced by smoothing the first tracking errors (conditioning on index returns forward in time relative to the tracking errors constitutes look-ahead bias), we will discard the first terms when using our simulation method, making any samples generated have an effective length of k. The st term is not discarded because the associated look-ahead bias is the same as filtering (relative to this tracking error only index returns at the same time step or backward, but not forward, are given). We ac- knowledge that the filtering density also constitutes the look-ahead bias. In real time we observe the daily closing index price and the daily closing LETF price (which imply daily returns) simultaneously, so the information provided by should not be available for filtering. But we accept this bias for the increased precision of our estimate of the filtering density that it allows, thus improving our modeling of the realized volatility of LETF returns. Our method is not intended for a live setting and we do not calculate the expectation of any random variables (e.g.) for the purposes of predicting tracking errors or LETF returns.

3.2. Derivation of Kernel Density Estimates

Given a random process generating daily LETF returns, a random process generating the daily

underlying index returns, the target leverage multiple of the LETF, the rate of daily

management expenses incurred by the LETF, and a chosen number of lags indicating the degree of dependence, we construct kernel density estimates of the smoothing density

and filtering density as follows.

Note, in this subsection we use slightly different notation so that the implementation details of the kernel density estimates can be documented more clearly. The selection of will be discussed in the following subsection that outlines the tracking error simulation routine.

1) Calculate the implied tracking errors from the observed data, and transform the data to allow for fitting the desired density estimates.

Assume the following relationship for decomposing daily LETF returns (as stated previously):

. (12)

Using the decomposition, observed LETF returns, and observed index returns, calculate the implied tracking error observations. All of the observation vectors are length T.

Take the log transform of observed index returns and arrange them into a observation matrix of rolling day periods. Denote this matrix as. In the same way, take the log transform of observed tracking errors and arrange them into a observation matrix of rolling day periods. Denote this matrix as.

To form the final observation matrix used for fitting the kernel density estimate, combine and in column-wise fashion. Denote this as, a matrix. For notational convenience in the follow- ing steps, let and, so that observation matrix is.

(13)

. (14)

Using log returns and log tracking errors is extremely important because of the fact that log values do not suffer from asymmetry or a hard left bound at 0 (now transformed to), making the transformed data less challenging to model.

2) Fit a kernel density estimate for, using a jointly independent multivariate normal kernel and ob- servation matrix.

(15)

where is the p dimensional multivariate normal density function evaluated at using mean vector and covariance matrix, is the ith row vector of observation matrix, and is the diagonal matrix formed from element-wise squaring of the p dimensional vector of bandwidths. Elements indexed correspond to bandwidths for index returns, and elements correspond to band- widths for tracking errors.

The selection of is dependent on the LETFs (and underlying indexes) being analyzed. Our selections for the demonstration set of LETFs will be detailed later in this section.

Note that in using a diagonal matrix based on the vector of s, the selected bandwidths for single dimensions, we are not ignoring the dependence structure that exists between the variables. The dependence structure will be estimated through the addition of the n multivariate kernels centered on the observation data points. This point might be easier to understand algebraically, because although the kernel in the density estimate can be decomposed as the product of univariate kernels, it is not the same as an estimate that is the product of independent univariate density estimates.

(16)

where is the jth element of observation vector.

By capturing the dependence structure of the data through the addition of multivariate kernels that use a diagonal covariance matrix, we are achieving an effective compromise between modeling power and complexity. Selecting bandwidths for dimensions individually incorporates some information about the respective variable, yet making p separate selections separately is not difficult. The alternative choices of using a single bandwidth for all dimensions or selecting an entire covariance matrix are generally considered too simple or too difficult, respectively [20] .

3) Factor and rearrange terms of the density estimate for to produce an estimate of the conditional

density.

(17)

where is the subvector of elements indexed from vector, or the elements that represent index returns whose observations were sourced from the matrix, and is the subvector of elements indexed from vector, or the elements that represent tracking errors whose observations were sourced from the matrix. Equation (17) could be restated as; however, the following notation will be used for the sake of brevity and consistency with Step 4.

(18)

In this way, when x and y are written as subscripts, let and, and by extension and.

Continue by inserting the appropriate density estimates.

(19)

(20)

Because of our choice of a jointly independent multivariate normal kernel, can be factored as follows:

. (21)

Insert this factorization and rearrange terms to produce the final density estimate.

(22)

(23)

. (24)

is the estimate of the smoothing density that will be used to simulate the first tracking errors of a new sample.

4) Factor and rearrange terms of the density estimate for to produce an estimate of the conditional density.

(25)

where is the vector without the last element. Equation (25) could be restated as

; however, the original notation will be maintained for the sake of

brevity.

Continue by inserting the appropriate density estimates.

(26)

(27)

As in Step 3, factor, but adjusting for the desired elements of.

(28)

Insert this factorization and rearrange terms to produce the final density estimate.

(29)

(30)

(31)

is the estimate of the filtering density that will be used to simulate tracking errors through k of a new sample.

3.3. Simulation Routine

With the final density estimates ready, LETF tracking errors can be simulated using the following routine. Given: length input vector of log index returns, length p bandwidth vector, number of daily lags, and

length p observation vectors

1) Sample an index value from a multinomial distribution with weight vector, where

.

2. Use index value i from step 1 to select the ith observation vector and sample, an

length vector from the multivariate normal distribution with density.

Perform steps 3 and 4 for

3) Sample an index value from a multinomial distribution with weight vector, where

, and

is the length vector formed by concatenating the indicated elements of and.

4) Use index value i from step 3 to select the ith observation vector and sample from the multivariate normal distribution with density.

5) Combine the simulated tracking errors with the input index returns according to our

LETF returns decomposition.

(32)

where is the final, length k output vector of simulated LETF returns. Elements indexed in vectors, , and are discarded.

When simulating data for the intended application, the sampled index returns to be used as inputs are first arranged as a matrix of rolling periods of days (and transformed to log returns). Regular choices of k are 21 or 252. The simulation routine can be executed in parallel because there is no dependence on the input data across rows. Each row of the matrix is input as vector separately and the density sampling steps can execute on each row simultaneously. Step 5 can obviously execute in parallel with basic matrix algebra. The simulation routine is also put to use for estimating the lag parameter, but the input data is not arranged into rolling periods initially. With lag estimation this step occurs after sampling using the simulated data in order to avoid simulating multiple tracking errors based on the same index returns.

3.4. Lag and Bandwidth Selection for Simulation of LETF Tracking Errors

Estimating the lag parameter proceeds as a brute force sweep of possible selections 0 to N (for some reasonable N), using the simulation routine and a Kolmogorov-Smirnov test for evaluation of fit. For each LETF and index combination and choice of to be considered, K iterations of tracking error simulation are performed (for some large K). The entire observation vector of daily index returns (log transformed) for the days which LETF returns are available is supplied as the input vector. The routine is executed without the use of rolling periods, but this transformation is made after Step 5 has completed, such that the simulated LETF returns are arranged into a matrix of rolling periods of k returns. The compound return is calculated for each row producing a final simulated sample of k day LETF returns. These two steps are repeated with the actual LETF returns to produce the reference sample of k day LETF returns, and then the samples are compared using a two-tailed Kolmogorov-Smirnov test. Final lag selection is based on the resulting p-values collected from K iterations of the simulation routine and Kolmogorov-Smirnov test.

The K-S test is comparing a sample of k day LETF returns derived from observed index returns and simulated LETF tracking errors against a sample of k day LETF returns derived from observed index returns and observed LETF tracking errors (i.e. the observed LETF returns). Each iteration uses only the index returns observed on days when the paired LETF was trading to ensure that the two samples are derived from the same sequence of data. The null hypothesis in a K-S test states that the two samples being compared are drawn from the same distribution [21] . Our goal is to simulate tracking errors in a way that the K-S test of the LETF returns samples cannot reject the null hypothesis at sufficiently high confidence levels. Based on the results of the K-S tests, our goal translates to selecting the value of that produces greater p-values compared to other selections. This generic mandate could be interpreted in many different ways, and we settled on selecting the value of with the greatest proportion of p-values that were. For some LETFs there were multiple possible selec- tions where all resulting p-values were. In these cases ties were broken by selecting the least value of to avoid any possible overfitting. A p-value that is indicates that iteration of simulation produced a sample that could not be rejected at a confidence level, the threshold of confidence we are in effect selecting to delineate as sufficiently high.

In Table 1, we present our final lag selections for the demonstration set of LETFs. Column headers prefixed with “21D” or “252D” refer to results produced when using day or day periods, respectively, and the notation refers to the proportion of p-values that were. We used 10,000 iterations for testing each LETF. We feel that our selection criteria resulted in satisfactory lag parameter selections for all LETFs when using 21 day periods (except for FINZ), but the results are mixed when using 252 day periods, with 9 of 20 LETFs (FINZ, DUST, TECL, TECS, RUSL, RUSS, DZK, EDC, EDZ) failing to offer values of greater than 0.9. There were many lag selections for each LETF that performed well when using 21 day periods, so we simplified the estimation task and present only the lag selection that provided the best results with 252 day periods (the values shown in columns with a “21D” prefix may not actually be the best). The minimum and median p-values were not incorporated into any decision making, but are included here for reference.

Our selections for the kernel bandwidth vector are based on the multivariate “Scott Rule” [20] , defined as:

(33)

where is the bandwidth for jth dimension of density estimate, is the estimated standard deviation of jth dimension, n is the number of p dimensional observations used for fitting density estimate, and p is the number of dimensions of the sample space.

We use, the traditional unbiased estimator of, and scale down our final selections of. After extensive testing of our tracking error simulation routine with the demonstration set of 20 LETFs, we concluded that the elements of corresponding to index returns (elements) needed to be scaled down by a factor of 100, and the elements of corresponding to LETF tracking errors (elements) needed to be scaled down by a factor of 100,000. We provide visual justification for this heuristic in Figure 4. For the final bandwidth selections, we have:

(34)

(35)

(36)

. (37)

Figure 4 shows the lag testing results from 10,000 iterations of LETF Ticker SPXL using 252 day periods for each lag parameter value 0 through 8. In all simulations, the bandwidths were scaled down as indicated above, producing in our opinion a reasonable increase in K-S p-values (using any of the statistics shown) as the lag value increases from 0 to 8. These results are somewhat representative of the results experienced when testing the other LETFs. Alternatively, when using larger factors to scale the bandwidths, the simulation routine would fail on some iterations because the estimates for the smoothing and filtering densities did not have sufficient support. We experienced this type of result when testing FINZ, TECS, RUSL, and RUSS with the factors indicated above, forcing us to create an exception for these LETFs where we decrease the factor used to scale the tracking error portion of the bandwidth vector to 10,000. When using smaller factors to scale the bandwidths, significant increases in p-values were generally not observed at any lag, or not observed until 8 or more lags were included. In the latter cases, these results appeared to us as overfitting.

4. Constrained Simulation Using Nonparametric Density Estimation

The nonparametric method for constrained simulation we propose in this section was devised as part of the larger body of work on LETF volatility documented throughout this paper, but the method is truly general in nature. It could be helpful in any setting where the practitioner would like to simulate multivariate data with a constrained sample sum (or average). For this reason the second and third subsections are presented in the context of using generic multivariate data, without references to financial data or financial constructs.

4.1. Extending the LETF Returns Model with an Index Return Constraint

In order to constrain the compound underlying index return for the period, the joint density of our LETF returns model from Section 3 must be revised as follows:

(38)

where, the total k day compounded return of the underlying index for days

through, and the density function is the joint density of a sequence of unconstrained index return variables (the lags) and a sequence of index return variables constrained to compound to. This form of the full joint density for index returns and LETF tracking errors (left-hand side) can be used to simulate sequences of LETF returns constrained such that the sampled sequence of index returns compounds to the given total period return.

It needs to be emphasized that this modification is implemented using the log form of index returns as was the case with all estimators and simulation work featured in Section 3. When index return variables are modeled as

, the density being estimated becomes, the joint density of

a sequence of unconstrained variables (the lags) and a sequence of variables constrained to sum to. The estimate for this form of the constrained joint density is much easier to derive and more generally useful in applications outside of finance.

4.2. Derivation of Kernel Density Estimate

Given any p dimensional random vector with unconstrained dimensions (lags) and n observations of arranged as an observation matrix, our nonparametric density estimate is constructed as follows:

1) Fit a kernel density estimate for using a jointly independent multivariate normal kernel and observation matrix.

(39)

where is the p dimensional multivariate normal density function evaluated at using mean vector and covariance matrix, is the ith row vector of observation matrix, and is the diagonal matrix formed from element-wise squaring of the p dimensional vector of bandwidths.

Note that the selection of is ultimately application dependent, so we cannot provide advice for any kind of general case other than recommending what has already been published about using the multivariate normal density as a kernel [20] . The selections for our applications will be detailed later in a later subsection.

2) Perform a change of variables and derive the corresponding kernel density estimate.

Let, , , ,. Or using matrix notation, define random vector as

follows:

(40)

(41)

where the first elements of the bottom row of are 0 to allow for the unconstrained dimensions of.

To derive the kernel density estimate for the transformed variables, invoke the following theorem for trans- forming multivariate normal random vectors [22] :

(42)

where is a constant matrix, is the transpose of that matrix, and is a constant vector. Apply the theorem to the kernel from the result of Step 1 to produce the estimate of the joint density for.

(43)

3) Factor the kernel within into the product of an unconditional univariate kernel for and a multivariate kernel for conditional on.

(44)

where is the vector without the pth element.

For the kernel factor corresponding to the univariate density for, re-apply the theorem cited in Step 2 to construct the following univariate density kernel:

. (45)

To construct invoke another theorem for transforming multivariate normal random vectors

[22] :

(46)

(47)

where, , , and taken together constitute a partition of. Apply this theorem to the conditional kernel.

(48)

(49)

(50)

where is the ith observation vector without the pth element, and is the bandwidth vector,

without the pth element, squared element-wise, and transposed.

4) Factor and rearrange terms of the density estimate for to produce an estimate for the conditional density Start by factoring the density for and inserting the appropriate density estimates.

(51)

(52)

. (53)

Continue by inserting the factors of that were derived in Step 3 and rearranging terms to produce the final density estimate.

(54)

(55)

. (56)

Because there was no effective change in the to transformations, define

to denote the given value for the sum of the random vector and the density estimate can be

written entirely in terms of. The final form of the density estimate:

(57)

(58)

4.3. Simulation Routine

With the final density estimates ready, constrained data can be simulated using the following routine.

Given: length p bandwidth vector, vector sum constraint, and length p observation vectors

1) Sample an index value from a multinomial distribution with weight vector, where

.

2) Use index value i from step 1 to select the ith observation and sample, a dimensional

vector, from the multivariate normal distribution with density, where

, and.

3) Use elements through of the the sampled dimensional vector from Step 2

to arrive at the pth (implied) sample value.

Because Steps 1 and 3 are computationally trivial, the computational complexity of the simulation routine is no worse than that of the chosen implementation for the sampled multivariate normal distribution. Our testing and development was performed using the mvrnorm() implementation available in the R package MASS. Package version 7.3 - 27, R version 3.0.1.

Table 2 is presented to better illustrate what real time performance a user can expect with the routine (based on our choice of mvrnorm()). The routine was executed 100 times each using various sizes of the observation matrix, and for the sake of completeness included various values for number of iterations k. For all simulations the returns data for the S&P 500 index were used with a constrained return of 0 and our final bandwidth selection (described in the next subsection). As the iterations of the routine can be executed in parallel, theoretically, the number of iterations k should have no impact on the final runtime. The tests were performed on a Dell server with 2 Intel Xeon 2.5 GHz processors (6 cores each, 64 GB memory total) running a virtualized instance of Red Hat Enterprise Linux Server 6.5 (Kernel 2.6, 64 bit).

As expected there are significant increases in execution time at the largest selections for n and p, while k does not have much of an impact. With an average execution time near 3 minutes when using a

observation matrix we hope that interested readers will not consider runtime as a drawback against using our routine in practice.

4.4. Bandwidth Selection for Constrained Simulation of Index Returns

Our selection here is similar to the final rule presented in Section 3. Again we begin with the multivariate “Scott Rule” [20] , defined as it was previously.

In the case of simulating only index returns, we simplify the initial rule because the p dimensional row vectors of the observation matrix used to fit the density estimate are rolling p day intervals of the same series of daily data. Therefore, a single value from the average of the terms will be used because individually they will be nearly identical. Also, we use, the traditional unbiased estimator of.

(59)

(60)

(61)

where is a p dimensional vector of s. After extensive testing of our simulation routine with the 10 indexes included in the demonstration set, we concluded that our choice of needed to be scaled down by a factor of 10. We provide visual justification for this heuristic in Figure 5 and Figure 6.

In the top half of Figure 5, the density for the sample distribution of SMC (colored blue) is plotted using rolling 21 day intervals from the observed history of the S&P 500 restricted to where the compound return for the period was between 1% and 2%. In the bottom half, the densities for the sample distribution of SMC are plotted using simulated data with (Adjustment Factor = 10, colored red) and without (Adjustment Factor = 1, colored green) scaling down the bandwidth. For the simulations, the period return constraint was set to 1.5%, the midpoint of the data interval used to generate the density

in the top half of the plot. Figure 6 follows the same layout and color scheme as Figure 5, but this time using rolling 252 day intervals and different target returns. Only periods where the compound return on the S&P 500 was between 10% and 15% were used in the top half, and the return constraint for simulated data in the lower half was 12.5%. For all SMC calculations (using observed or simulated data), a leverage multiple of +3 is included as if we were approximating LETF Ticker SPXL, where

is the series of daily returns used for testing. Shortfall from Maximum Con-

vexity was used as the test statistic to stay consistent with the rest of our work, but an adjustment factor of 10 appeared equally appropriate when standard deviation was used.

In the figures shown (and including many other cases not shown), it was obvious to us that the bandwidths derived from our simplified Scott Rule were producing simulated data that looked exaggerated when plotted against the comparable subset of observed data. We decided on a final scaling factor of 10 through trial and error, but we think the results shown in Figure 5 and Figure 6 speak for themselves. Our final bandwidth

selection used in the following application examples is then.

5. Case Study: Simulating LETF Returns with Underlying Index Return Constraints and Calculating Nonparametric p-values for Volatility Statistics

We conclude with a demonstration of our three contributions in one example. Our intention is to capture the significance, or rarity, of the volatility experienced during the chosen period as measured by Shortfall from Maximum Convexity. A p-value for the observed SMC value will be calculated with respect to a SMC sample distribution generated by our LETF return model. In the experimental setting described here a p-value of 1 means the lowest possible volatility was observed (if the period in question was repeated, greater volatility would be experienced 100% of the time), and 0 means the highest possible volatility was observed (if the period in question was repeated, greater volatility would be experienced 0% of the time).

The absolute low point of the U.S. equity markets during the 2008-2009 recession occurred in early March 2009, so we will analyze the realized volatility for that month (22 days) as experienced by LETF Ticker TNA. The underlying index, the Russell 2000, returned 8.92% for the month (the market low point was early in the month, and the rebound was underway by month end). The log form of this value is used as the input total period return of our constrained simulation routine from Section 4 to sample 100,000 sequences of 22 days of Russell 2000 returns. For each of the 100,000 index return samples, our tracking error simulation routine is executed to sample sequences of TNA tracking errors. The data are combined with a +3 leverage multiple (and daily management fee) to produce a final sample of 22 day TNA returns sequences.

As displayed by the row for Ticker TNA in Table 1, the lag parameter for the simulations was set to 3. The history of daily returns for the Russell 2000 index dating back to 1/2/1979 was arranged into a data matrix of 9151 observations of rolling 25 day intervals (22 days plus 3 lags) to derive the kernel density estimate for constrained simulation. The history of daily returns for the LETF Ticker TNA dating back to 11/11/2008 was combined with the matching Russell 2000 daily returns into a data matrix of 1536 observations of 8 dimensions (4 day sequence of index returns, 4 day sequence of LETF tracking errors) to derive the kernel density estimate for tracking error simulation. All observed values were log transformed before simulation, and our bandwidth selections described in Sections 3 and 4 were applied accordingly.

Our realized volatility statistic SMC was calculated for each 22 day sample and the density of the final SMC sampling distribution is plotted below in Figure 7. The red line marks the actual SMC value of 0.1527 that was observed for March 2009. The resulting p-value for this observation with respect to the simulated sample is 0.0053, which indicates that the proportion of simulated SMC values that were less than or equal to the observed value is 0.9947.

Our constrained simulation routine for index returns guarantees all the 22 day index return samples compound to the observed index return of 8.92%. Given this fact, the range of outcomes represented by the SMC sample is entirely the result of index return volatility and tracking error. Based on the output of our simulation methods we conclude that the realized volatility for TNA in March 2009 was greater than the overwhelming majority of outcomes that may be observed while the Russell 2000 experiences an 8.92% increase over the same period.

6. Conclusions

Leveraged ETF returns are unique due to the dynamics produced by daily compounding, and we hope to have illuminated some of the challenges involved with modeling these returns over time horizons longer than one day. We have presented a nonparametric framework for modeling daily LETF returns that feature a simulation method for LETF tracking errors and a method for simulating index returns with a constrained period return.

The two methods allow for incorporating additional index returns data and controlling for index performance, respectively. We feel that these contributions can improve the public understanding of the relationship between LETF return volatility and index returns.

Our methods can model almost any dependence structure that may exist in LETF returns data and each can be used separately if desired. When used together, the two methods complement each other nicely, enabling powerfully customized risk summaries of LETF investing strategies. Finally, the constrained simulation method is not limited to our particular index returns dataset. It can be used to sample any generic multivariate data with a constraint on the sum of the random vector elements.

Acknowledgements

We thank Dan Cohen, the Editor, and an anonymous reviewer for their helpful comments.

Cite this paper

MatthewGinley,David W.Scott,Katherine E.Ensor, (2015) Simulation of Leveraged ETF Volatility Using Nonparametric Density Estimation. Journal of Mathematical Finance,05,457-479. doi: 10.4236/jmf.2015.55039

References

Appendix