Open Journal of Antennas and Propagation
Vol.1 No.2(2013), Article ID:37173,12 pages DOI:10.4236/ojapr.2013.12006
Non-Linear Synthesis Problems for Plane Radiating Systems According to the Prescribed Power Directivity Pattern
![]()
Pidstryhach Institute for Applied Problems in Mechanics and Mathematics, NASU, Lviv, Ukraine.
Email: *andr@iapmm.lviv.ua, spo@iapmm.lviv.ua, tmd@iapmm.lviv.ua
Copyright © 2013 Mykhaylo Andriychuk et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 1st, 2013; revised September 1st, 2013; accepted September 10th, 2013
Keywords: Power Radiation Pattern; Synthesis Problem; Non-Linear Equation; Bifurcation of Solutions; Numerical Modeling
ABSTRACT
A variational formulation of the synthesis problem for plane radiating systems according to the prescribed power directivity pattern (DP) is considered. The function representing the mean-square deviation of the prescribed and synthesized power DPs and containing the additional term with squared norm of the current or field in the antenna aperture is considered as the criterion of optimization. Freedom to choose the phase DP is used to improve the proximity of the prescribed and synthesized DPs. In such formulation, the classes of non-linear problems, for which the non-uniqueness of solutions, their branching and bifurcation are characteristic, arise. The properties of solutions depend on the electric size of radiating system and prescribed power DP. From a practical point of view, the existence of different solutions creating the same or similar DPs, gives the opportunity to choose the solution that has a simpler implementation. The synthesis problems for plane radiating systems and plane arrays are considered.
1. Introduction
Increasing requirements to the modern radiating systems promote to further evolution of classical antenna synthesis theory [1-6] and development of new methods [7-11] in order to take into account a series of stringent requirements to control of the antenna directivity characteristics [12-14], consideration of the mutual coupling of radiators [15], noise-immunity [16] etc.
In many practical applications at the design stage of antennas and arrays the requirements are imposed only to the power DP [17,18]. At that, the freedom of choice among the phase DPs is used for improvement of the approximation quality of the synthesized DP’s squared module to the prescribed power DP. Appearing at that a necessity to approximate the real positive function (prescribed power DP) by square of module of the complex valued function generates the classes of the non-linear synthesis problems. Non-uniqueness and bifurcation of solutions are the characteristic feature of such problems. From the practical point of view, the existence of several types of solutions, which create the same or close power DPs, gives a possibility to choose that solution, which has simpler realization.
The problems of quantity and properties of the existing solutions using the methods of non-linear analysis [19] were investigated partially for the synthesis problems of linear antenna arrays in [10,11,15,18,20,21]. It was shown that the non-uniqueness and branching of solutions are the characteristics for these problems in the both cases if the mutual coupling of separate radiators of array is not being taken into account, and by being taken into account of such coupling. The properties of existing solutions depend on the value of physical parameters of array and properties of the prescribed power DP.
Investigation of solutions of the nonlinear synthesis problems for plane radiating systems substantively differs from such investigation of the synthesis problems for linear antennas and arrays. In particular, unlike the existing the branching points for the synthesis problems of linear antenna and arrays, the lines of branching of the solutions appear in the synthesis problems for the plane antenna systems. The problem to search these lines is insufficiently investigated two-parameter non-linear spectral problem [22].
In the proposed work, the variational statement of the synthesis problems for the plane radiating systems according to the prescribed power DP is examined. These problems are reduced to the investigation and numerical solution of the non-linear integral equations of Hammerstein’s type. The kernel of these equations contains two physical parameters, which describe the geometry of radiating aperture and region where the prescribed power DP is given.
The method for search of the bifurcation lines of the optimal solutions is developed; the justified algorithms to determine the optimal solutions of the synthesis problems and to search the existing solutions of various types for the synthesis equations are elaborated. It is shown that freedom in choosing the obtained optimal phase DP improves the quality of approximation of the synthesized DP to the prescribed one considerably, as compared with the synthesis in the class of the cophased DPs. In particular, this allows in some cases to decrease the dimensions of radiating system up to 30%, as compared with the synthesis in the class of cophased DPs, remaining the effectiveness of the synthesis the same.
2. Statement of Problem
The statement of the synthesis problem according to the prescribed power DP is used in many practical applications [1,5,8]. In spite of fact that the power DP N can be easy obtained from the amplitude DP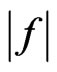 : (
: (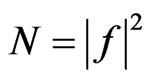 ), and vice versa, the synthesis problems of the given amplitude DP F0 and the given power DP
), and vice versa, the synthesis problems of the given amplitude DP F0 and the given power DP 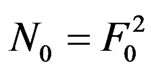 are the different problems. For example, if
are the different problems. For example, if 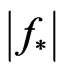 is optimal solution for some variational synthesis problem according to the amplitude DP F then
is optimal solution for some variational synthesis problem according to the amplitude DP F then 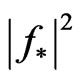 will not be optimal solution of the analogous problem according to the prescribed power DP N0.
will not be optimal solution of the analogous problem according to the prescribed power DP N0.
In general case the calculation of the DP f of antenna by the currents (fields) I in the antenna aperture is realized by action of some linear bounded operator A [11]
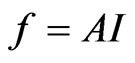 . (1)
. (1)
The functions f and I can be either the vectors if the vector character of electromagnetic field is taking into account in the process of statement and solving the synthesis problem, or scalar functions if some simplifications for antenna are applicable.
The specific forms of operator A, functions f and I will be presented below in the process of solving the synthesis problems for the investigated radiating systems. We demonstrate here the peculiarities of the synthesis problem according to the prescribed power DP N0 on example of a plane continuous aperture.
Introducing the specific generalized coordinate system [6] we pass from the vectorial statement of the synthesis problem to two scalar problems. Separation of the qand j-components of the DP and current’s (field’s) components in the antenna elements is assumed too. We consider below the scalar synthesis problems for plane radiating apertures and arrays.
The geometry of synthesis problem for plane rectangular aperture is shown in Figure 1. The DP of plane aperture is determined by formula [3]
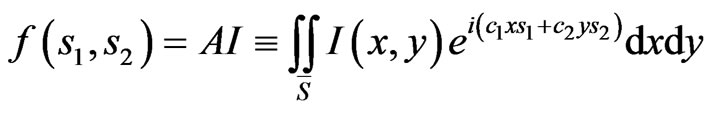 , (2)
, (2)
where
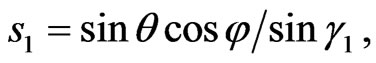 (3)
(3)
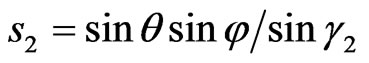 (4)
(4)
are the generalized dimensionless coordinates that allows to consider the synthesis problem in two relatively-perpendicular planes independently [1,6]. The parameters
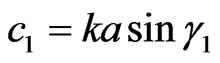 , (5)
, (5)
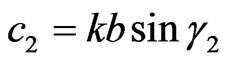 (6)
(6)
describe electrical size of antenna; a, b are the geometrical parameters of aperture;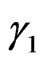 ,
, 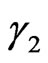 are the angles characterizing the domain where DP N0 is prescribed (N0 = 0 outside
are the angles characterizing the domain where DP N0 is prescribed (N0 = 0 outside 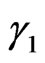 and
and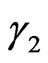 );
); 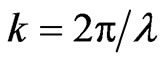 is wave number.
is wave number.
Use of generalized parameters c1 and c2 allows to consider the synthesis problem in wide region of frequencies, including the submm, mm, cm and longer lengths of the EM field’s waves.
The variational formulation of the synthesis problem consists in minimization of functional
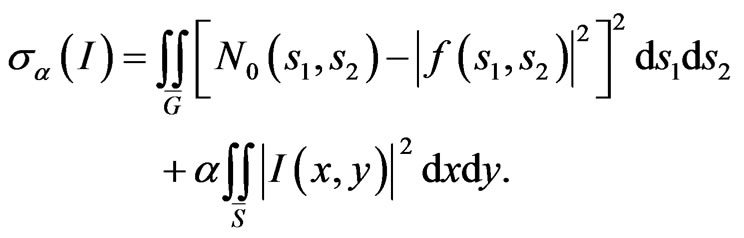 (7)
(7)
The respective Euler’s equation relative to optimal current distribution I is given by
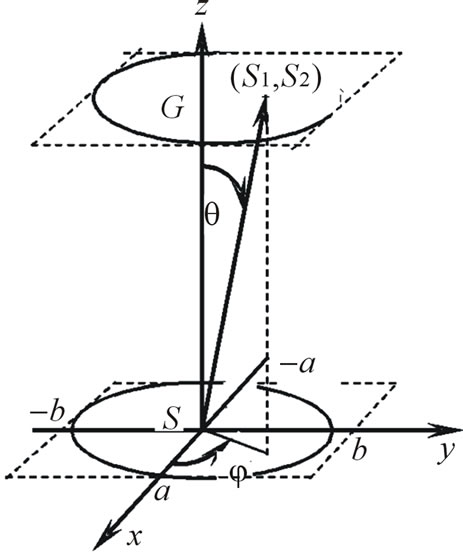
Figure 1. Geometry of synthesis problem for plane aperture.
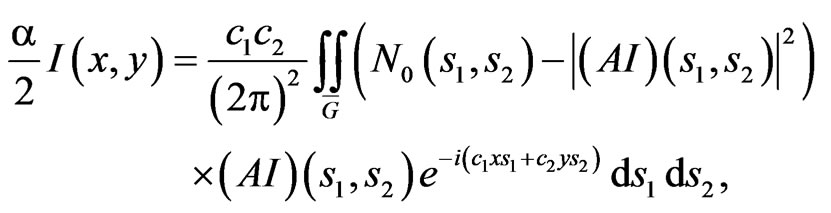 (8)
(8)
and respective equation for the DP f has form
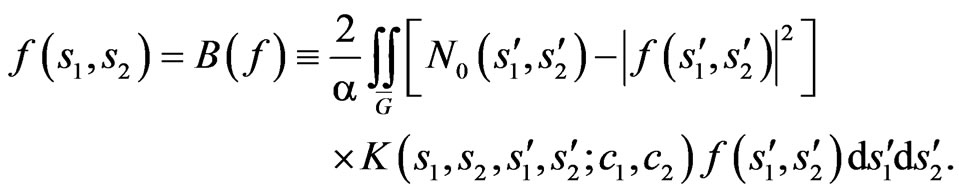 (9)
(9)
The kernel 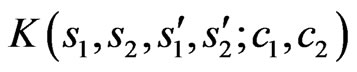 in the general case is expressed as
in the general case is expressed as
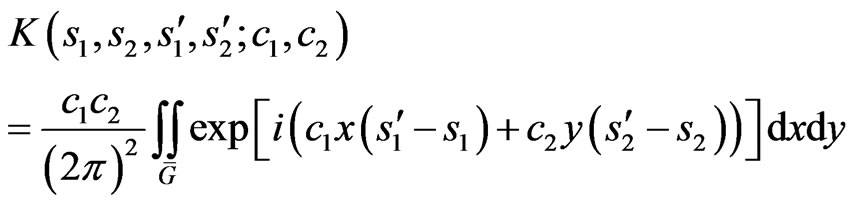 (10)
(10)
and depends essentially on the form of aperture. For the rectangular aperture (10) has form
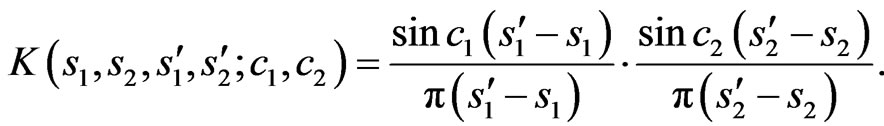 (11)
(11)
If the optimal solution  to (9) is found, then optimal distribution of current is determined by formula
to (9) is found, then optimal distribution of current is determined by formula
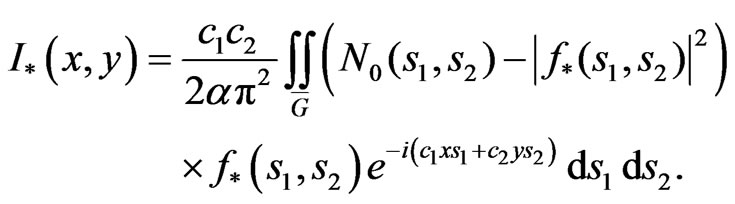 (12)
(12)
Numerical solving Equation (9) is simpler than solving Equation (8), therefore we use below in the process of solving the specific synthesis problems solution to Equation (9) and determine the optimal current distribution 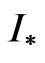 by formula (12).
by formula (12).
3. Determination of Bifurcation Lines: Case of the Plane Rectangular Aperture
The non-linear Equation (9) has only zero solution at small values of parameters c1 and c2 which contain in the kernel (11). The non-zero solutions appear, namely the bifurcation of solutions occurs, if c1 and c2 increase. The bifurcated solutions have the different properties depending on the form of the prescribed power DP N0, values c1 and c2. For one’s turn, these solutions correspond to the different optimal current distributions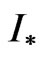 , calculated by (12). Of course, the different sets of functions
, calculated by (12). Of course, the different sets of functions  and
and 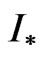 give the different values of functional
give the different values of functional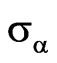 . In this connection, investigation of the branching process, search of different solutions, and determination of those provide the minimal value of
. In this connection, investigation of the branching process, search of different solutions, and determination of those provide the minimal value of 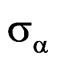 is of practical interest.
is of practical interest.
Accordingly to the theory of branching the solutions [23], the bifurcation points of solutions to (9) are determined using the next linear equation
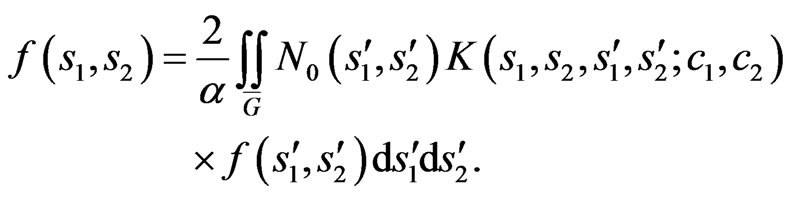 (13)
(13)
On the other hand, this equation can be considered as the non-linear two-parameter spectral problem. We use the method of implicit function proposed in [22] for determination of values of the parameters c1 and c2 at which (13) has non-zero solutions. The non-zero solutions originate at the values c1 and c2, for which except the evident eigen value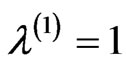 , the other eigen values
, the other eigen values 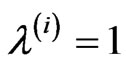 of Equation (13) appear.
of Equation (13) appear.
Using the cubature formulas we obtain on the basis of (13) the homogeneous linear algebraic system (LAS) of P-th order for determination of eigenfunctions and corresponding eigenvalues
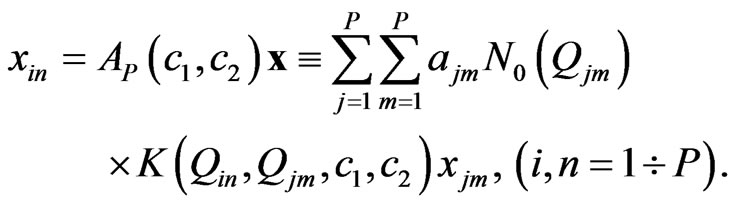 (14)
(14)
Here the number P corresponds to quantity of discretization points. In Equation (14)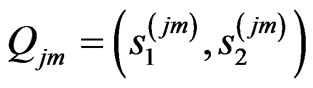 ,
,  is vector of unknowns eigenfunctions,
is vector of unknowns eigenfunctions, 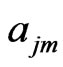 are the coefficients of cubature formula.
are the coefficients of cubature formula.
In order LAS (14) has different from zero solutions, it is necessary that parameters c1 and c2 be the solutions of equation
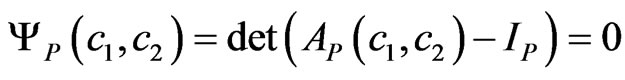 , (15)
, (15)
where 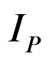 is unit matrix.
is unit matrix.
According to the method of implicit functions, search of solutions to (15) is reduced to the next Cauchy problem
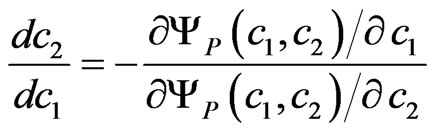 , (16)
, (16)
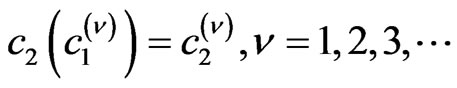 (17)
(17)
Initial conditions (17) are determined by solving the auxiliary non-linear one-parameter spectral problem on the beam 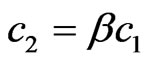 in (15). As result, we receive the next equation for finding the zeros of determinant
in (15). As result, we receive the next equation for finding the zeros of determinant
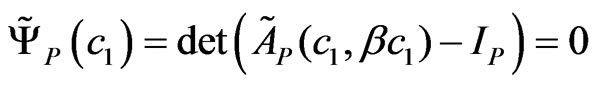 , (18)
, (18)
which are determined by some known method, for example, by the bisection method.
Consequently, solving the Cauchy problem, we obtain a set of bifurcation points of the solution to (9). As the matrix of (15) is analytical function of parameters c1 and c2, the respective curves, which describe the spectrum’s connected components of (14), are the continuous solutions of Cauchy problem (16)-(17).
Note that eigenfunctions of the problem (14), which correspond to bifurcation points, describe the properties of solutions of the initial Equation (9) in the first approximation.
We consider the results related to determination of the bifurcation lines for the synthesis problem of plane aperture at the prescribed power DP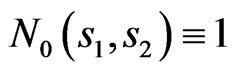 . The bifurcation points, obtained as the result of solving the auxiliary one-dimensional spectral problem (18) on the beams
. The bifurcation points, obtained as the result of solving the auxiliary one-dimensional spectral problem (18) on the beams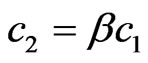 , are shown in Figure 2. The obtained sets of values (
, are shown in Figure 2. The obtained sets of values (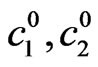 ) are the initial conditions (17) for the Cauchy problem (16). The first four curves, obtained in the process of solving the problem (16)-(17), are presented in Figure 3. The both Runge-Kutta and Adams methods were used to obtain the numerical solution. The initial values (
) are the initial conditions (17) for the Cauchy problem (16). The first four curves, obtained in the process of solving the problem (16)-(17), are presented in Figure 3. The both Runge-Kutta and Adams methods were used to obtain the numerical solution. The initial values (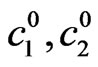 ), which were chosen on the beam
), which were chosen on the beam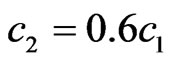 , are indicated by small circles.
, are indicated by small circles.
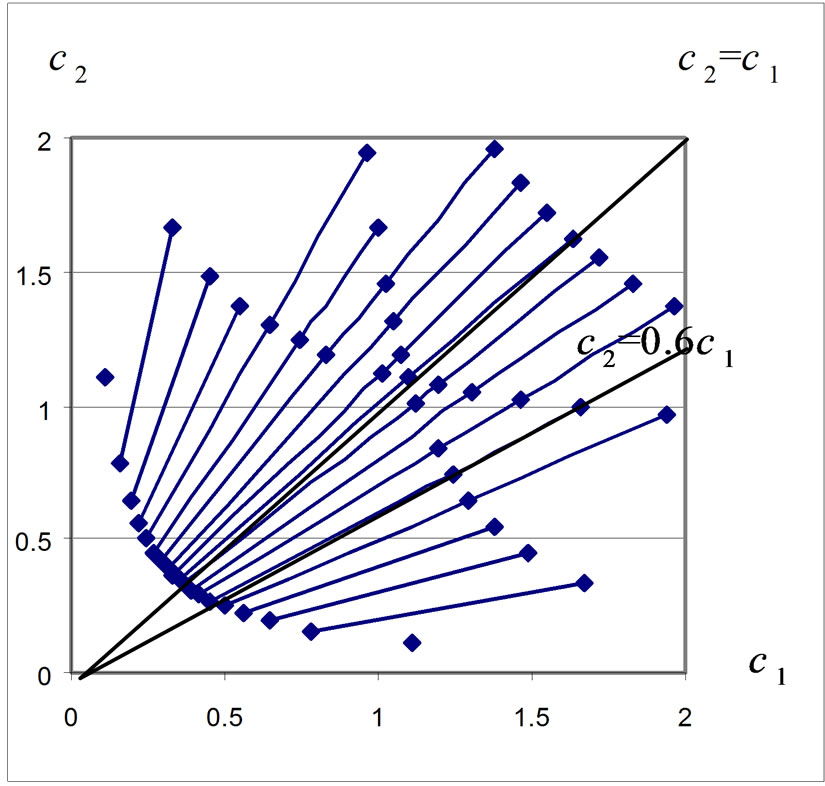
Figure 2. The bifurcation points on the beams 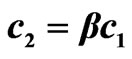 for plane aperture.
for plane aperture.
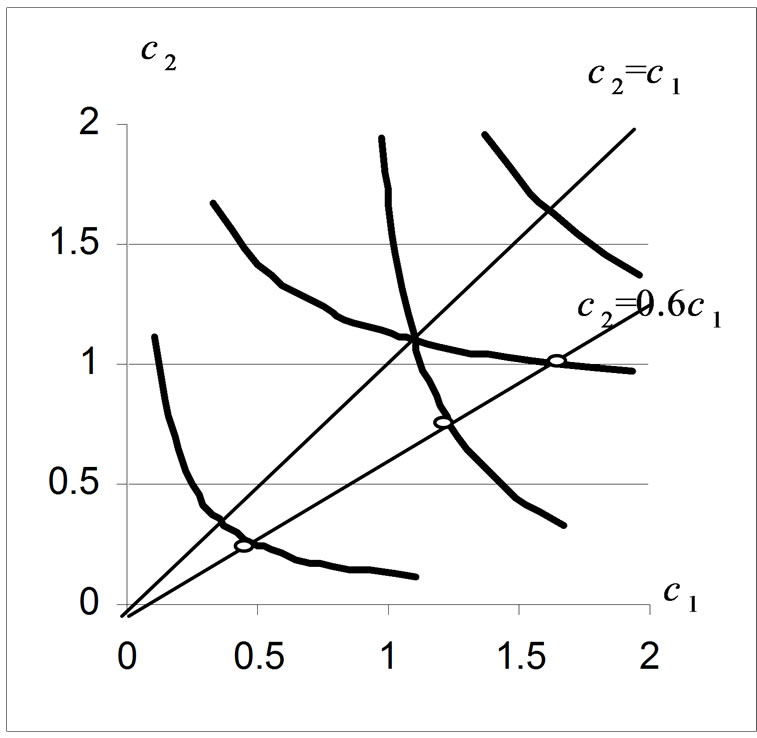
Figure 3. The bifurcation lines in the plane (c1,c2) for plane aperture.
The eigenfunctions of LAS (14) are used in the process of construction of the bifurcated solutions of the nonlinear Equation (9), which branch off the zero solution. The properties of bifurcated solutions depend on the properties of symmetry (parity) of the prescribed DP N0 and on the properties of eigenfunctions. In the process of construction of the bifurcated solutions one should take into account that the properties of the eigenfunctions differ for the various set of parameters c1 and c2 in the plane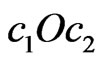 .
.
4. Features of Statement for Specific Radiating Systems
4.1. Elliptic Aperture
The synthesis problem for an elliptic aperture is reduced to minimization of functional (7), and the respective Euler’s equation for determination of optimal current in the aperture is determined by formula similar to (8). By this, integration is carried out over the elliptic domain of the antenna aperture.
The aperture DP is determined by formula similar to (2). The kernel (10) for elliptic aperture is given by
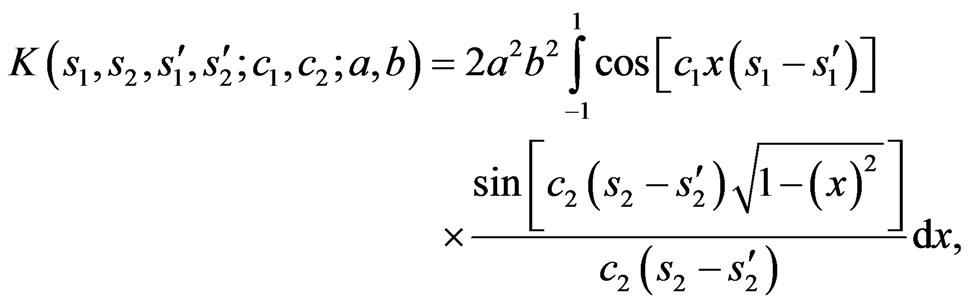 (19)
(19)
where a and b are semiaxes of ellipse. The optimal current is determined by the DP 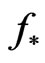 found from (9) as follows
found from (9) as follows
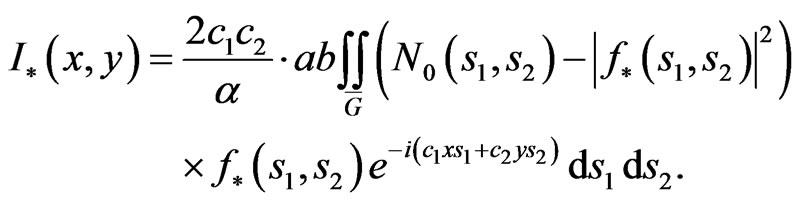 (20)
(20)
The numerical results of synthesis for specific prescribed power DPs N0 will be given in Subsection 5.2.
4.2. Plane Equidistant Rectangular Array, Bifurcation of Solutions
In the case of scalar consideration of the synthesis problem one can restrict by the following representation for DP (array multiplier)
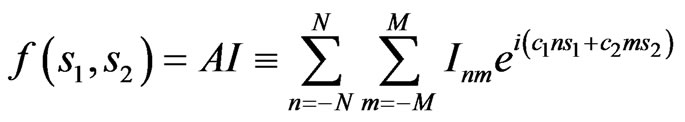 , (21)
, (21)
where 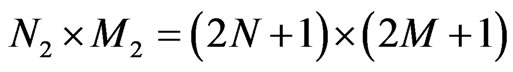 is number of radiators;
is number of radiators;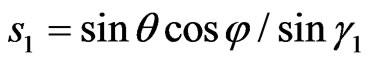 ,
, 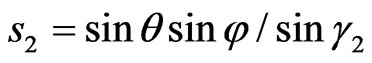 are the generalized angular coordinates;
are the generalized angular coordinates;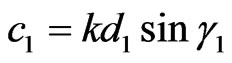 ,
,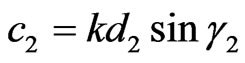 ;
; 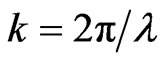 is wavenumber;
is wavenumber; 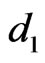 and
and 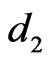 are the distances between radiators along the
are the distances between radiators along the 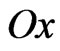 and
and 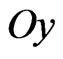 axes, respectively;
axes, respectively; 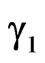 and
and 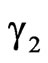 are the angles where the DP
are the angles where the DP 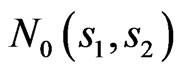 is given (
is given (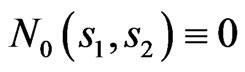 outside these angles).
outside these angles).
Function 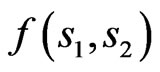 is
is 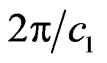 -periodical relative to
-periodical relative to 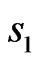 and
and 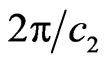 -periodical relative to
-periodical relative to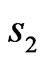 . In this connection, one can consider the synthesis problem for such array within the limits of one period.
. In this connection, one can consider the synthesis problem for such array within the limits of one period.
The minimizing functional has form similar to (7), the Euler’s equation for the optimal currents I and DP f are determined by formulas similar to (8) and (9), respectively.
The kernel K is degenerated and it is presented as the product of two independent functions
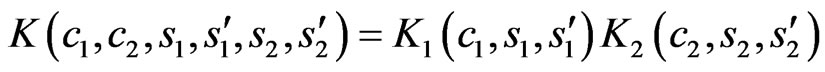 , (22)
, (22)
where
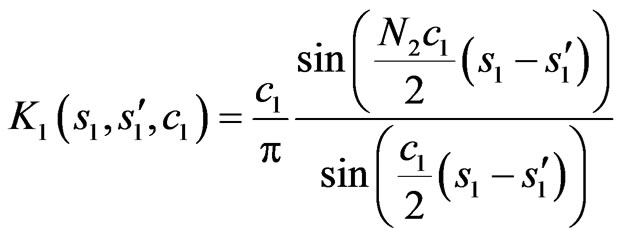 , (23)
, (23)
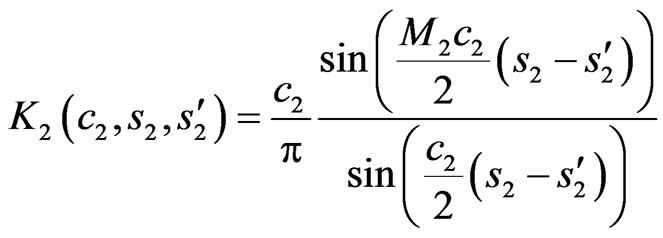 . (24)
. (24)
The investigation of solution to respective Euler’s equations is carried out in the manner similar to the case of plane aperture. If the optimal DP  by solving equation type of (9) is found, the optimal current distribution
by solving equation type of (9) is found, the optimal current distribution 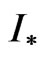 is given by
is given by
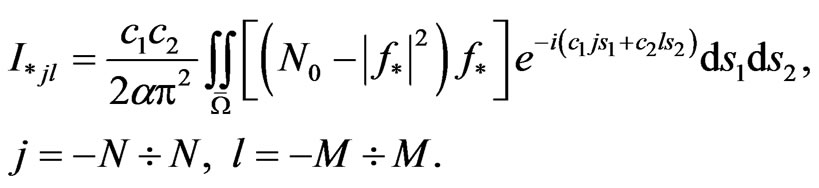 (25)
(25)
The numerical results for rectangular array are presented for the problems of determination of the bifurcation lines for the array consisting of N2 × M2 = 11 × 11 radiators for the prescribed power DP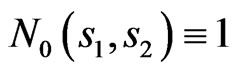 ,
,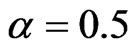 . In Figure 4 the bifurcation points on the beams
. In Figure 4 the bifurcation points on the beams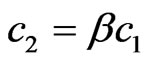 , received by solving the series of auxiliary one-parameter problems, are shown. The bifurcation
, received by solving the series of auxiliary one-parameter problems, are shown. The bifurcation
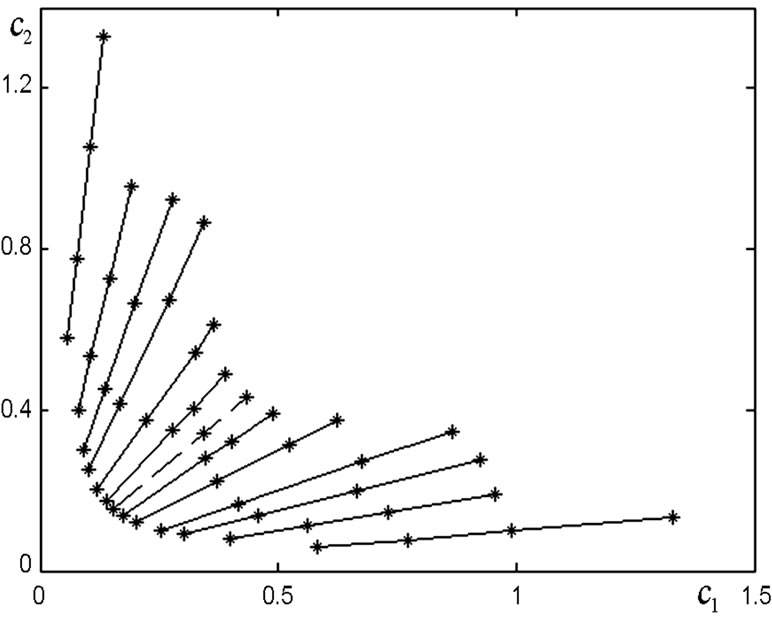
Figure 4. The bifurcation points in the plane  for rectangular array.
for rectangular array.
lines obtained by solving the Cauchy problem (16) with the initial values (17) are presented in Figure 5. Similarly to the case of rectangular plane aperture, the bifurcation lines are symmetrical relatively the axes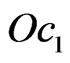 ,
, 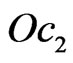 , and intersection of the curves corresponding to the second and third eigenvalues is observed.
, and intersection of the curves corresponding to the second and third eigenvalues is observed.
4.3. Plane Hexagonal Array, Bifurcation of Solutions
The DP of hexagonal array has the form similar to (21):
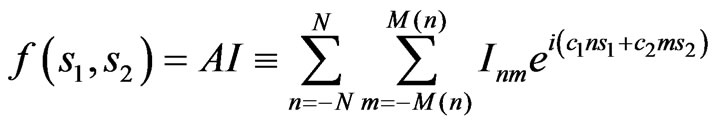 . (26)
. (26)
The number of linear subarrays along the  axes (coordinate
axes (coordinate ) is odd, and number of radiators in the central linear subarray along the
) is odd, and number of radiators in the central linear subarray along the  axes (coordinate
axes (coordinate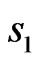 ) is odd too. For such array’s geometry, the kernel of integral Equation (9) can be written in form (27).
) is odd too. For such array’s geometry, the kernel of integral Equation (9) can be written in form (27).
In the case when the above assumption regarding the number of radiators in the subarrays does not satisfied, (27) has more complicate form.
Search of bifurcation lines for the solutions to nonlinear Equation (9) is carried out for array consisting of 61 radiators for the prescribed power DP 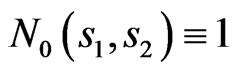 in the region
in the region 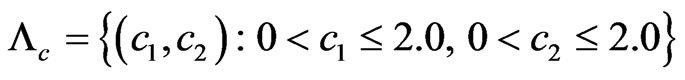 at the various values of parameter
at the various values of parameter  in functional (7). In the first stage, the one-dimensional auxiliary problems is solved on the beams
in functional (7). In the first stage, the one-dimensional auxiliary problems is solved on the beams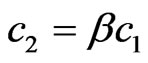 . The bifurcation points in
. The bifurcation points in
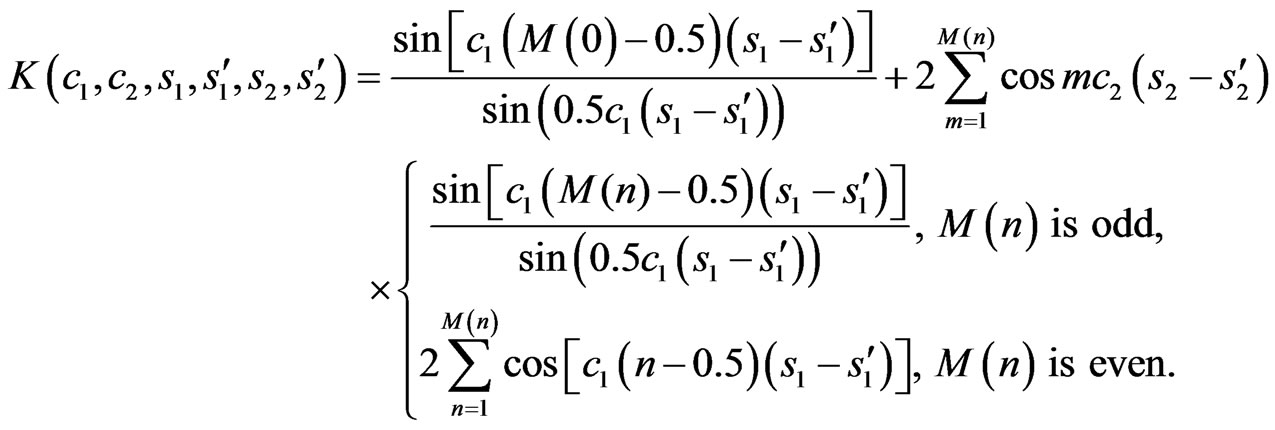 (27)
(27)
the respective beams are presented in Figure 6. The points (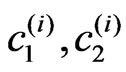 ), for which eigen values
), for which eigen values 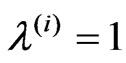 determined approximately from plot data in this stage.
determined approximately from plot data in this stage.
In the second stage, the specification of the values (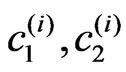 ) by solving the transcendental equation type of (18) is carried out. The points (
) by solving the transcendental equation type of (18) is carried out. The points (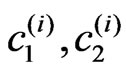 ) considered as initial approximations in this procedure. The bijection method is used for this goal. In the third finish stage after the specifications of the values (
) considered as initial approximations in this procedure. The bijection method is used for this goal. In the third finish stage after the specifications of the values (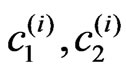 ), the bifurcation lines in the plane (
), the bifurcation lines in the plane (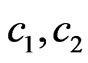 ) are determined by solving Chauchy problem (16)-(17). In Figure 7, the curves corresponding to the first four eigenvalues
) are determined by solving Chauchy problem (16)-(17). In Figure 7, the curves corresponding to the first four eigenvalues 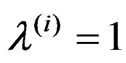 are shown. Similarly to previous investigations, the cross section of curves corresponding to the second and third eigenvalues is observed.
are shown. Similarly to previous investigations, the cross section of curves corresponding to the second and third eigenvalues is observed.
Note that the problem of specification of the roots of Equation (18), as well as correct solving the Cauchy problem (16)-(17) are quite complicate computational problems, because they require for their solving a series of computational experiments with the various initial approximations.
Figure 5. The bifurcation lines in the plane 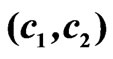 for rectangular array.
for rectangular array.
Figure 6. The bifurcation points in the plane 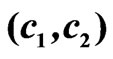 for hexagonal array.
for hexagonal array.
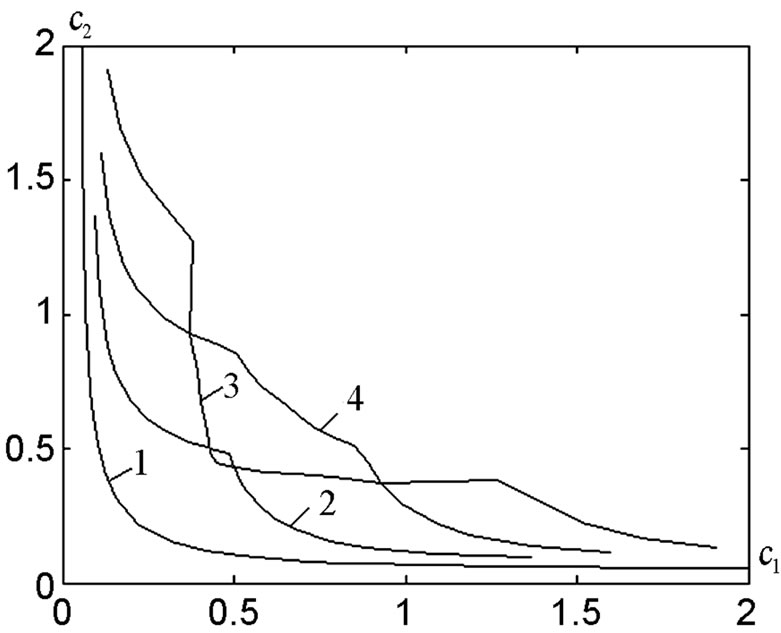
Figure 7. The bifurcation lines in the plane 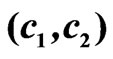 for hexagonal array.
for hexagonal array.
5. Computational Results of Synthesis
The results of numerical calculations are presented for the synthesis problems of several prescribed power DPs. We use the iterative process [24]
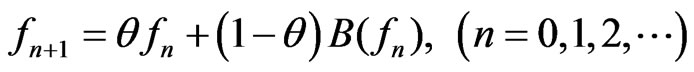 (28)
(28)
for numerical solution of (9). Parameter 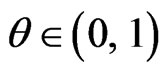 is used for convergence acceleration of (28).
is used for convergence acceleration of (28).
The numerical results demonstrate that for the certain ranges of the physical parameters of antennas there exist different types of solutions to (9). These solutions provide different degree of approximation of the synthesized power DP to the prescribed one. The investigations which show the dependence of the mean square deviation of the DP on the type of parity of the prescribed initial approximations are carried out for the various types of the considered antennas.
In the process of numerical calculations one substantiated that for the prescribed power DP 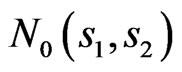 with two axes of symmetry, there exist the solutions of different types of parity relative to the coordinates
with two axes of symmetry, there exist the solutions of different types of parity relative to the coordinates 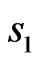 and
and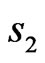 . It is ascertained that for this case there exist various types of solutions to (9) with the next properties of the phase of synthesized DP, namely function
. It is ascertained that for this case there exist various types of solutions to (9) with the next properties of the phase of synthesized DP, namely function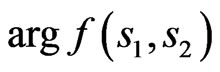 :
:
1) even relatively 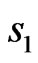 and
and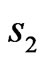 ;
;
2) even relatively 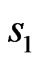 and odd relatively
and odd relatively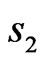 ;
;
3) odd relatively 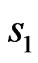 and even relatively
and even relatively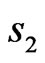 ;
;
4) odd relatively 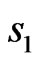 and
and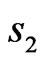 .
.
In order to obtain these solutions, one should to give initial approximation of the respective type for (28).
5.1. Plane Rectangular Aperture
The computational results related to solving the synthesis problem of plane rectangular aperture are shown at the prescribed power DP 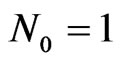 (Figure 8). The problem is reduced to solving the non-linear Equation (11) by the successive approximation method (28). In order to obtain the different types of solutions, the initial approximations of type 1) - 4) were chosen for the iterative process (28). The synthesized power DP
(Figure 8). The problem is reduced to solving the non-linear Equation (11) by the successive approximation method (28). In order to obtain the different types of solutions, the initial approximations of type 1) - 4) were chosen for the iterative process (28). The synthesized power DP  and phase DP arg f are shown in Figures 9 and 10 at
and phase DP arg f are shown in Figures 9 and 10 at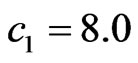 ,
,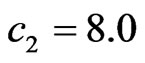 .
.
One can see that the phase DP arg f presented in Figure 10 is even relative to 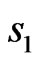 and odd relative to
and odd relative to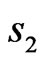 . This indicates that phase DP arg f has the same parity properties that the eigenfunction which corresponds to the eigenvalue
. This indicates that phase DP arg f has the same parity properties that the eigenfunction which corresponds to the eigenvalue 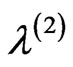 in Figure 3 (curve corresponds to this value of
in Figure 3 (curve corresponds to this value of 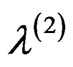 crosses the beam
crosses the beam 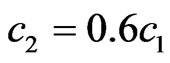 in the point
in the point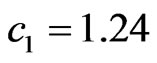 ,
,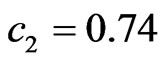 ). Optimal current distribution
). Optimal current distribution 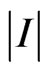 (see Figure 11) creating the synthesized power DP is symmetrical relative to
(see Figure 11) creating the synthesized power DP is symmetrical relative to 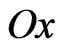 axis and non-symmetrical relative to
axis and non-symmetrical relative to 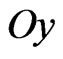 axis. This optimal current distribution corresponds to solution of Equation (9) with initial approximation of type 2). The mean-square deviation of the prescribed DP N0 and synthesized DP
axis. This optimal current distribution corresponds to solution of Equation (9) with initial approximation of type 2). The mean-square deviation of the prescribed DP N0 and synthesized DP 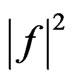 (the first summand in functional (7)) for this type of so-
(the first summand in functional (7)) for this type of so-
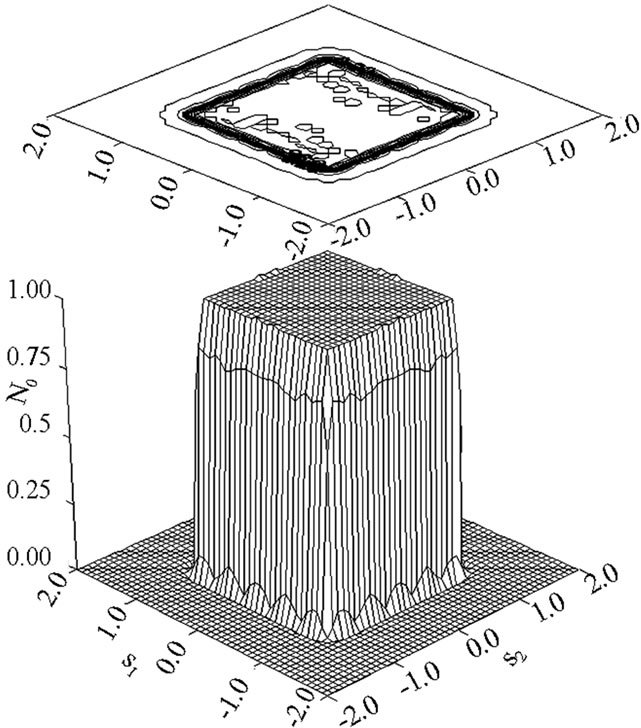
Figure 8. The prescribed power DP 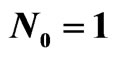 for rectangular aperture.
for rectangular aperture.
Figure 9. The synthesized DP 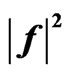 for the rectangular aperture.
for the rectangular aperture.
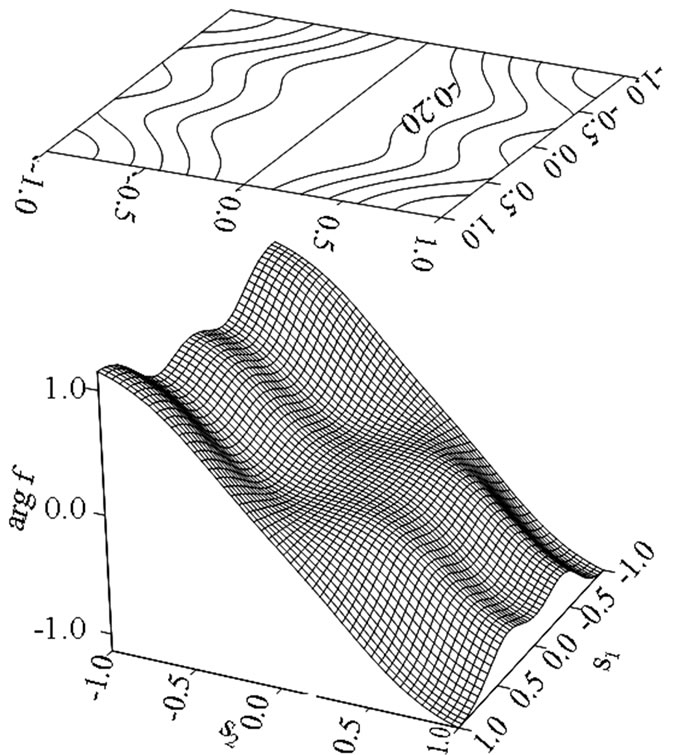
Figure 10. The phase DP arg f for the rectangular aperture.
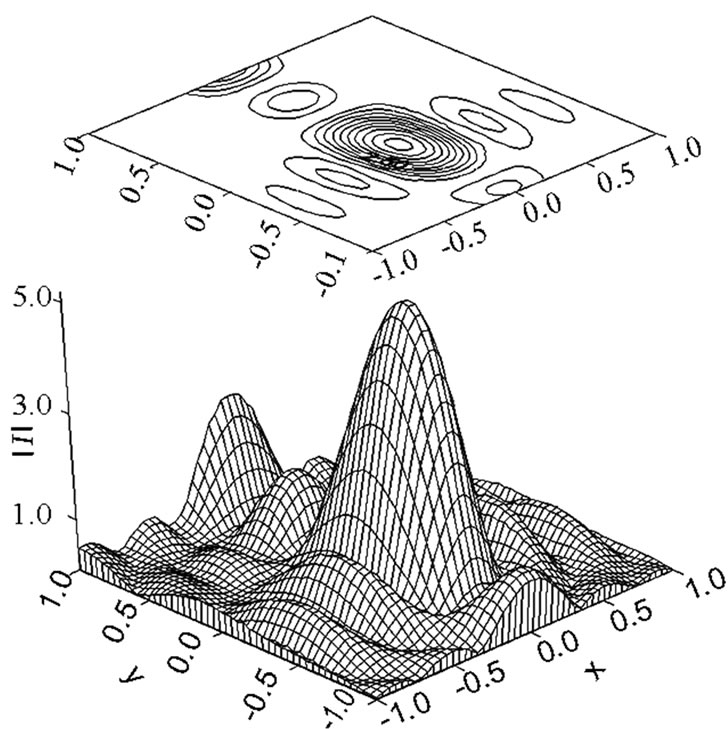
Figure 11. The optimal non-symmetrical distribution of current.
lution is approximately three times smaller than the mean-square deviation for symmetrical solution of type 1).
In that way, the optimal symmetrical power DP can be created by the non-symmetric current’s distribution in the antenna aperture.
As the numerical calculations show, the effectiveness of synthesis essentially depends on the form of the prescribed power DP N0, on the parameters 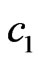 and
and 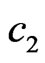 describing size of aperture, and on the type of obtained optimal solution.
describing size of aperture, and on the type of obtained optimal solution.
5.2. Plane Circular Aperture
The numerical results for circular aperture (particular case of elliptic aperture considered in Subsection 4.1) are shown for the synthesis of the prescribed power DP in the form of the figure of revolution with zero value in the centre (Figure 12), which is even on 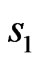 and
and 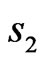
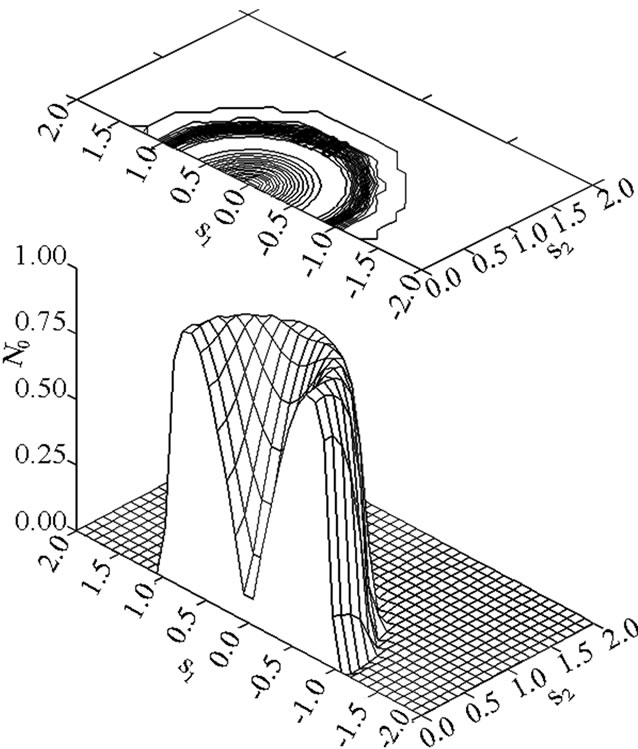
Figure 12. The prescribed power DP (29) in form of the figure of revolution.
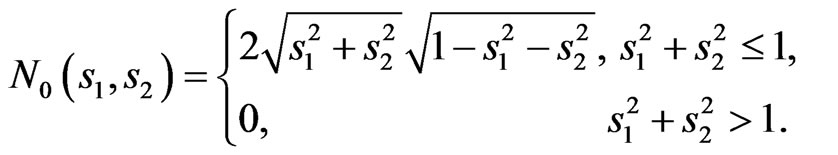 (29)
(29)
The synthesized DP 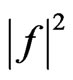 (Figure 13) and optimal amplitude current distributions
(Figure 13) and optimal amplitude current distributions 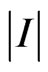 (Figures 14-16) at
(Figures 14-16) at 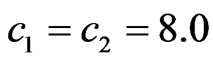 are presented. The optimal current distributions correspond to various types of bifurcated solutions, namely function
are presented. The optimal current distributions correspond to various types of bifurcated solutions, namely function  which has different parity properties relative to arguments
which has different parity properties relative to arguments  and
and .
.
In particular, the phase DP 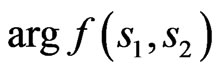 even respect to
even respect to 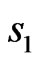 and
and 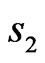 corresponds to amplitude distribution
corresponds to amplitude distribution 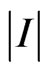 of current presented in Figure 14. As a result this distribution is symmetric relatively two coordinate axes. Even relative to
of current presented in Figure 14. As a result this distribution is symmetric relatively two coordinate axes. Even relative to 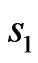 and odd respect to
and odd respect to 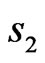 phase DP
phase DP 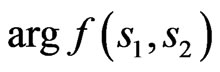 correspond to non-symmetrical relative to
correspond to non-symmetrical relative to  axis amplitude distribution of current in aperture, presented in Figure 15.
axis amplitude distribution of current in aperture, presented in Figure 15.
In Figure 16, the amplitude distribution 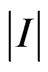 of current, which correspond to odd relative to
of current, which correspond to odd relative to 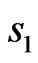 and
and 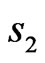 phase DP
phase DP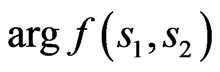 , is shown. The synthesized power DP
, is shown. The synthesized power DP 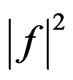 presented in Figure 13 is created by this current distribution. This current distribution essentially differs on those presented in Figures 14 and 15.
presented in Figure 13 is created by this current distribution. This current distribution essentially differs on those presented in Figures 14 and 15.
The cross sections of the synthesized power DPs in the plane 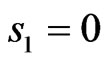 demonstrate effectiveness of the synthesis for the obtained optimal current distributions (see Figure 17). Curve 1 corresponds to prescribed power DP N0, curves 2, 3, and 4 correspond to amplitude distributions of current presented in Figure 16, Figures 14 and 15, respectively. One can see that the current distribution presented in Figure 16 is more effective, because the synthesized power DP created by it approximate the prescribed DP in the best way; this properties the most evidently is observed in the neighborhood of central zero point.
demonstrate effectiveness of the synthesis for the obtained optimal current distributions (see Figure 17). Curve 1 corresponds to prescribed power DP N0, curves 2, 3, and 4 correspond to amplitude distributions of current presented in Figure 16, Figures 14 and 15, respectively. One can see that the current distribution presented in Figure 16 is more effective, because the synthesized power DP created by it approximate the prescribed DP in the best way; this properties the most evidently is observed in the neighborhood of central zero point.
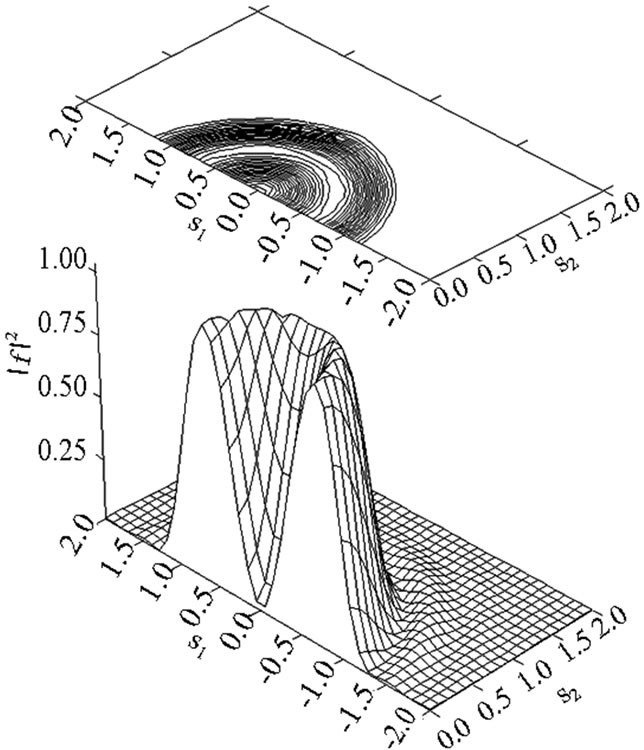
Figure 13. The synthesized power DP 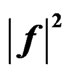 of the plane aperture for prescribed DP (29).
of the plane aperture for prescribed DP (29).
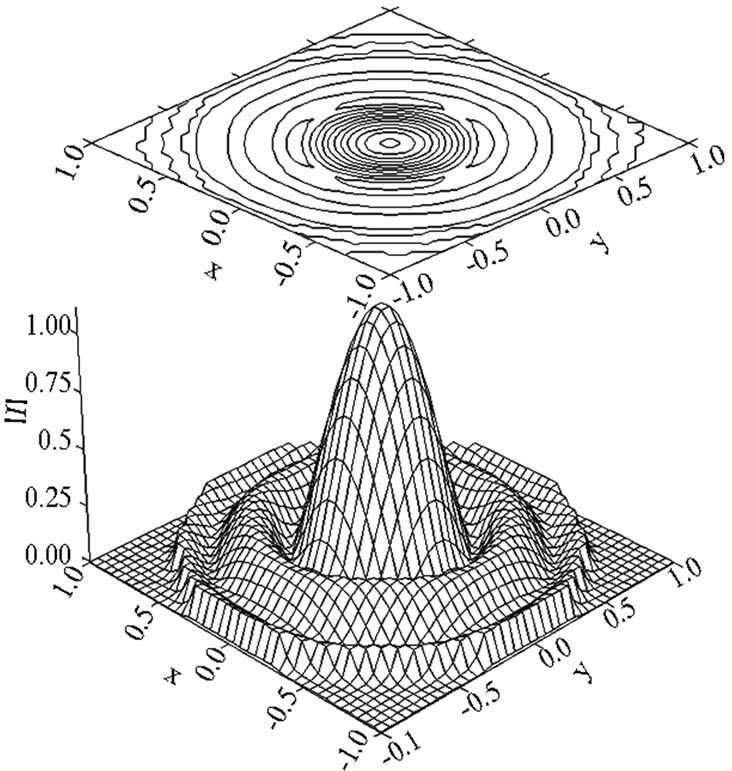
Figure 14. The symmetric optimal current distribution.
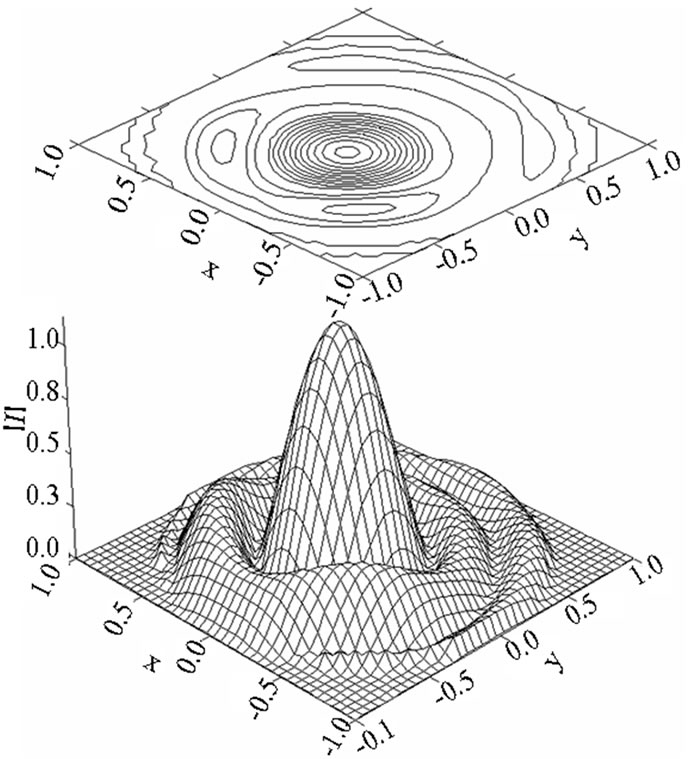
Figure 15. The optimal current distribution non-symmetric relative to  axis.
axis.
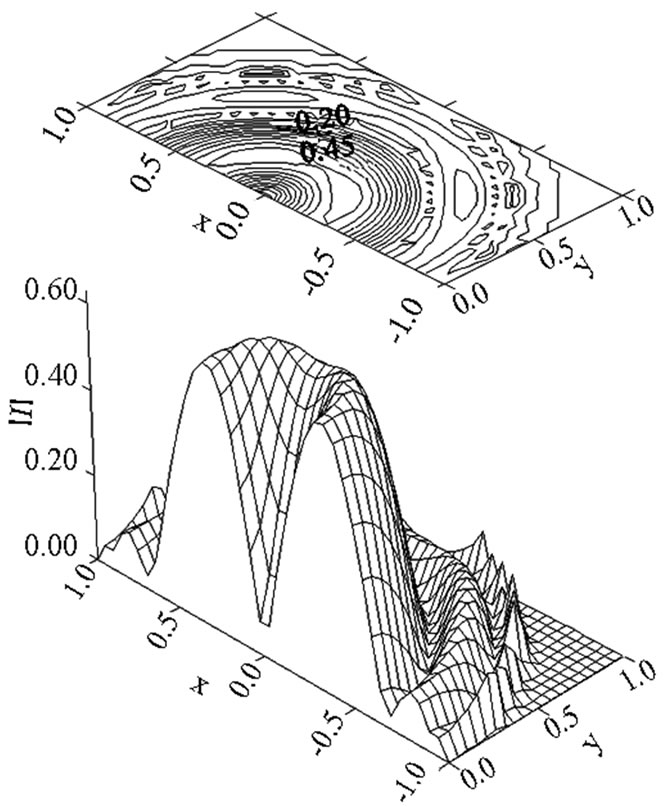
Figure 16. The optimal current distribution non-symmetric relative to both axes.
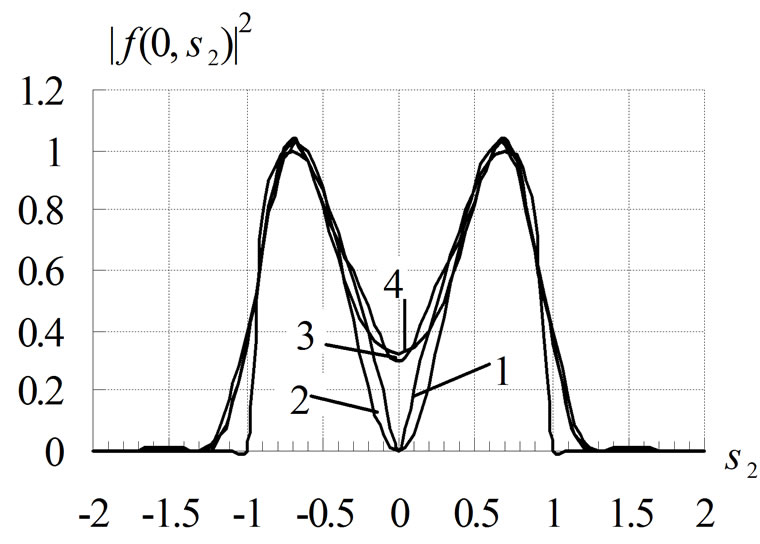
Figure 17. The cross sections of the synthesized DP in the plane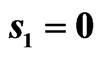 .
.
5.3. Plane Rectangular Equidistant Array
The results of synthesis for the prescribed power DP 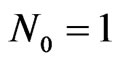 are shown for the solutions with properties 1) (Figure 18) and properties 2) (Figure 19); the equidistant plane array consisting of
are shown for the solutions with properties 1) (Figure 18) and properties 2) (Figure 19); the equidistant plane array consisting of 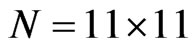 radiators is examined. In spite of the fact that phase DP
radiators is examined. In spite of the fact that phase DP 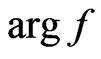 for the latter solution is odd respect to the coordinate
for the latter solution is odd respect to the coordinate 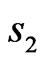 the synthesized power DP
the synthesized power DP 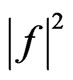 is even relative to
is even relative to 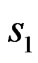 and
and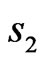 , but the value of mean-square deviation of the prescribed and synthesized power DPs for the latter solution is equal to 0.0562 against 0.0897 for the solution of type 1).
, but the value of mean-square deviation of the prescribed and synthesized power DPs for the latter solution is equal to 0.0562 against 0.0897 for the solution of type 1).
In order to demonstrate the effectiveness of synthesis for the different type of solutions, the value of functional 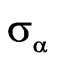 are shown for the solutions of type 1) - 4) at
are shown for the solutions of type 1) - 4) at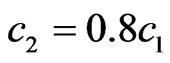 ,
, 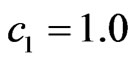 ,
, 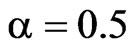 (see Figure 20). The numbers of lines corresponds to types of solutions. One can see that the solution of type 4) provides the worst approximation of the prescribed power DP. The even relative to
(see Figure 20). The numbers of lines corresponds to types of solutions. One can see that the solution of type 4) provides the worst approximation of the prescribed power DP. The even relative to 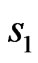 and
and 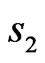 solution is more optimal for such
solution is more optimal for such
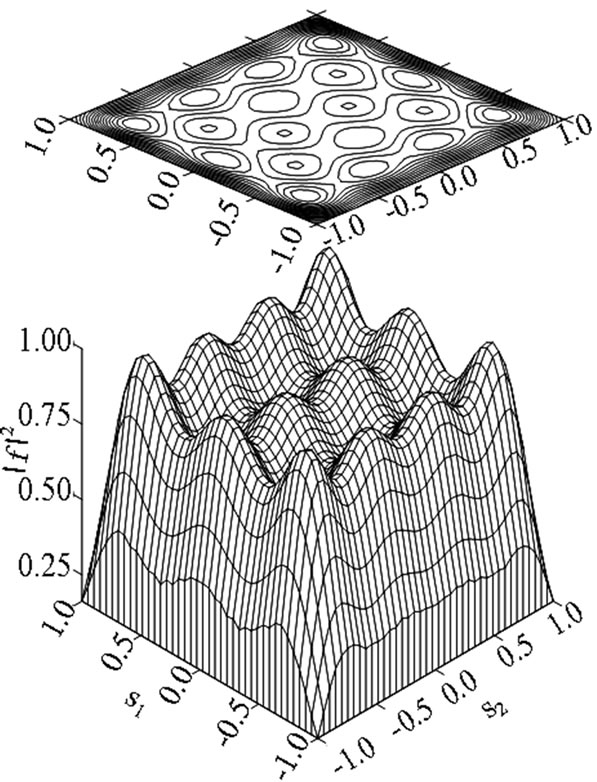
Figure 18. The synthesized power DP 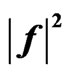 corresponding to solution of type 1).
corresponding to solution of type 1).
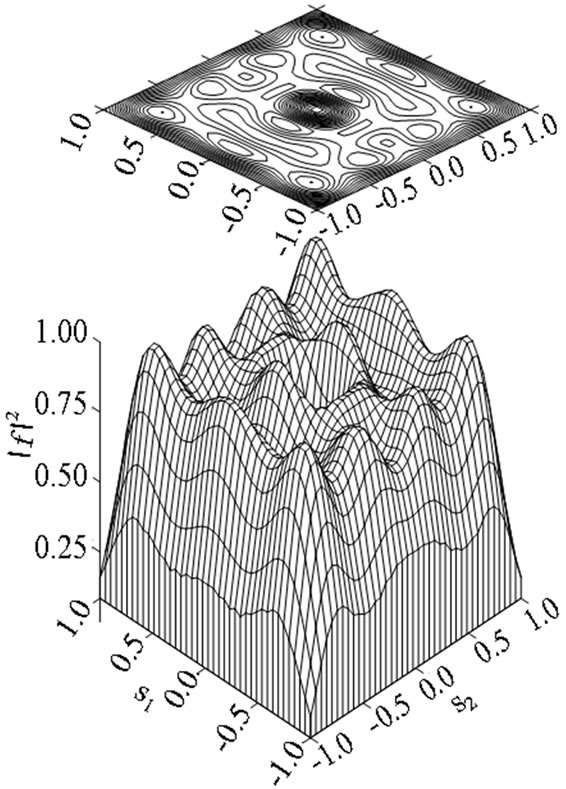
Figure 19. The synthesized power DP 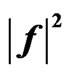 corresponding to solution of type 2).
corresponding to solution of type 2).
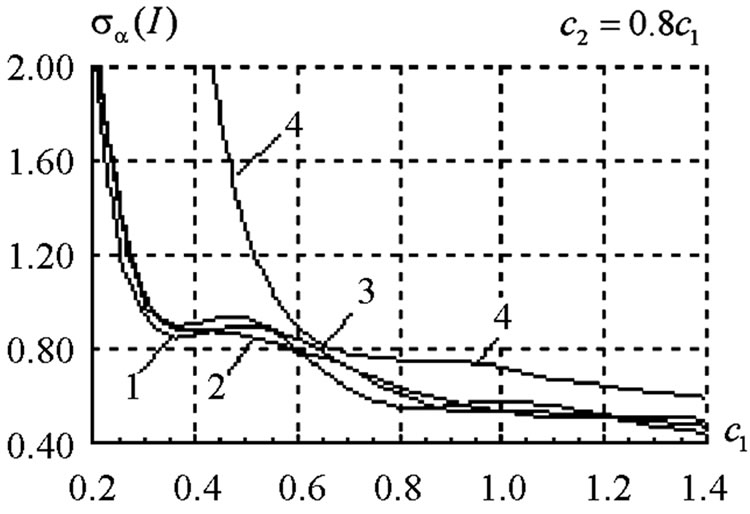
Figure 20. The value of functional 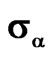 for different types of solution to Equation (11),
for different types of solution to Equation (11),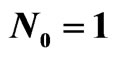 .
.
prescribed DP in the considered range of 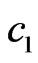 and
and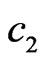 .
.
The effectiveness of synthesis also depends on the form of the prescribed power DP considerably. The synthesis results for the prescribed power DP
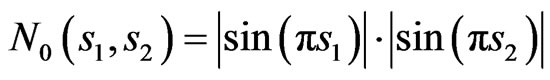 (30)
(30)
are presented in Figures 21 and 22. The synthesized power DP for the same values N, 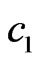 ,
, 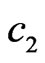 , and
, and 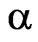 as in the previous example is shown in Figure 21. The initial approximation odd relative to
as in the previous example is shown in Figure 21. The initial approximation odd relative to 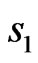 and
and 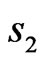 was given for iterative process (28). Such type of approximation provides the smallest value of
was given for iterative process (28). Such type of approximation provides the smallest value of 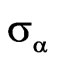 among the solutions with properties 1) - 4). In Figure 22, the values of functional
among the solutions with properties 1) - 4). In Figure 22, the values of functional 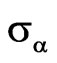 are shown for the solutions of type 1) - 4). One can see that solution of type 4) provides the worst value of
are shown for the solutions of type 1) - 4). One can see that solution of type 4) provides the worst value of 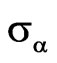 at
at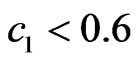 , at
, at 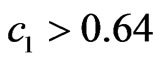 this solution is the best among the considered ones. The solution with the phase DP arg f even respective to
this solution is the best among the considered ones. The solution with the phase DP arg f even respective to  and
and 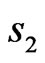 is the better for
is the better for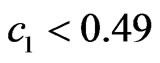 , but is the worst for the values
, but is the worst for the values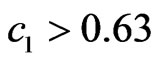 .
.
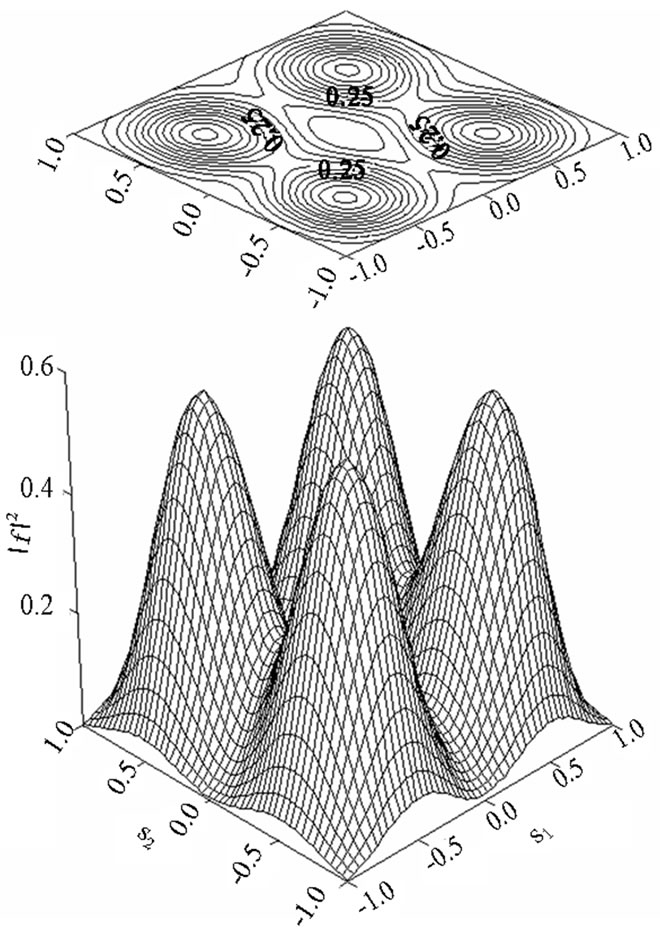
Figure 21. The synthesized power DP 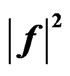 corresponding to solution of type 4).
corresponding to solution of type 4).
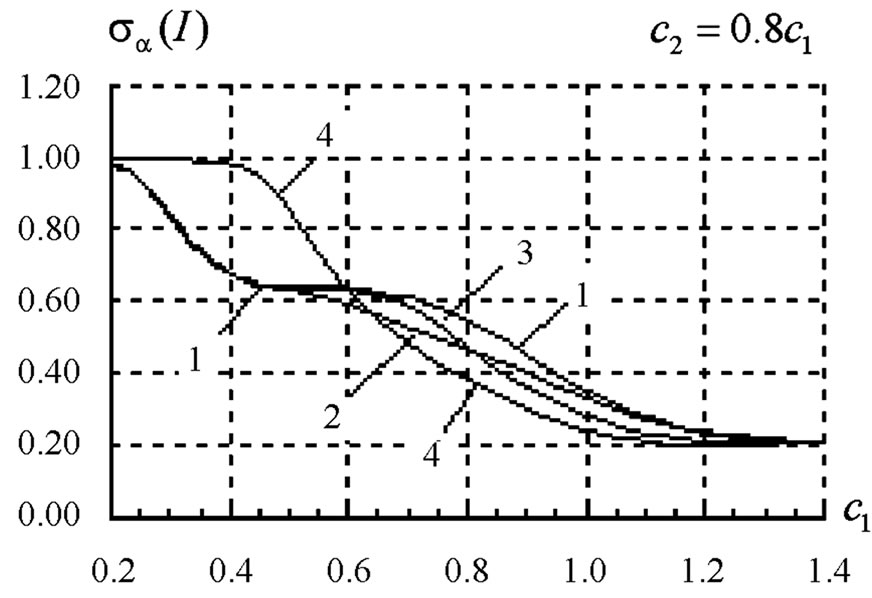
Figure 22. The value of functional 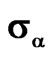 for different types of solution to Equation (11) for prescribed power DP (30).
for different types of solution to Equation (11) for prescribed power DP (30).
5.4. Plane Hexagonal Array
The synthesis results are presented for prescribed power DP 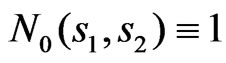 and DP (29). The array consisting of 127 radiators is considered, parameter
and DP (29). The array consisting of 127 radiators is considered, parameter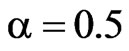 . The synthesis problem is reduced to solving Equation (11) by the method of successive approximations (28). The main lobe of synthesized power DP
. The synthesis problem is reduced to solving Equation (11) by the method of successive approximations (28). The main lobe of synthesized power DP 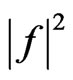 for the prescribed N0 is narrower than the main lobe of prescribed DP. The maximal deviation of the both DPs does not exceed −10 dB in the main lobe; the level of the first side lobe does not exceed −45 dB. The mean-square deviations (values of the first summand in (9)) are equal to 0.3774 and 0.2218 for the first and second prescribed DPs, respectively. The level of the first side lobe for the prescribed DP (29) does not exceed −35 dB. The plots of synthesized power DPs
for the prescribed N0 is narrower than the main lobe of prescribed DP. The maximal deviation of the both DPs does not exceed −10 dB in the main lobe; the level of the first side lobe does not exceed −45 dB. The mean-square deviations (values of the first summand in (9)) are equal to 0.3774 and 0.2218 for the first and second prescribed DPs, respectively. The level of the first side lobe for the prescribed DP (29) does not exceed −35 dB. The plots of synthesized power DPs 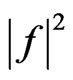 are shown in Figures 23 and 24. In Figures 25 and 26, the cross-sections of both the prescribed and synthesized DPs in the planes
are shown in Figures 23 and 24. In Figures 25 and 26, the cross-sections of both the prescribed and synthesized DPs in the planes 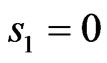 and
and 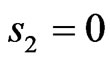 are shown.
are shown.
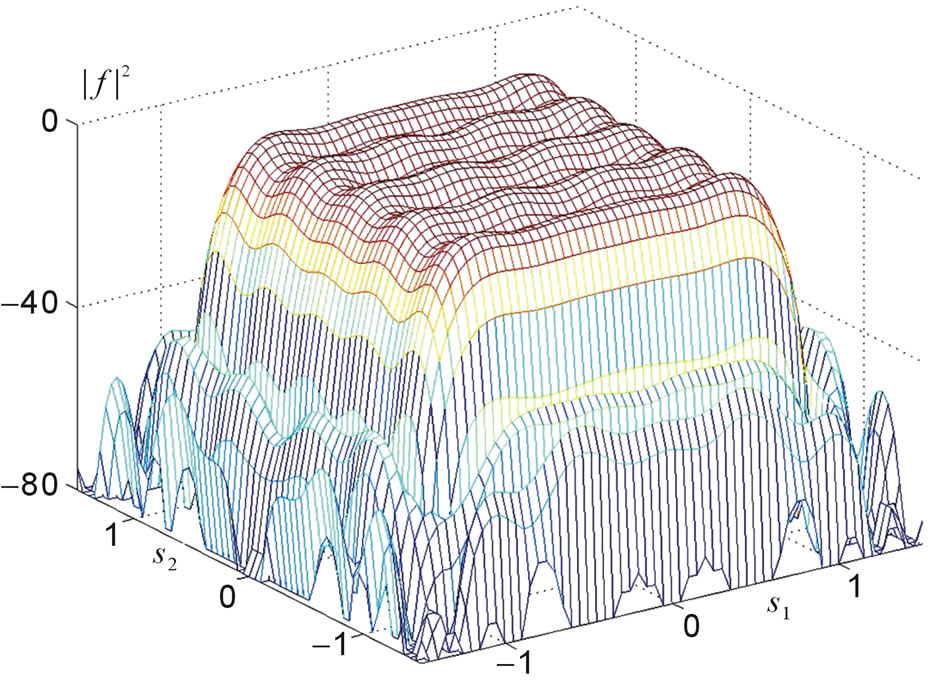
Figure 23. The synthesized power DP 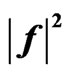 for
for 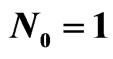 at
at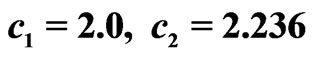 .
.
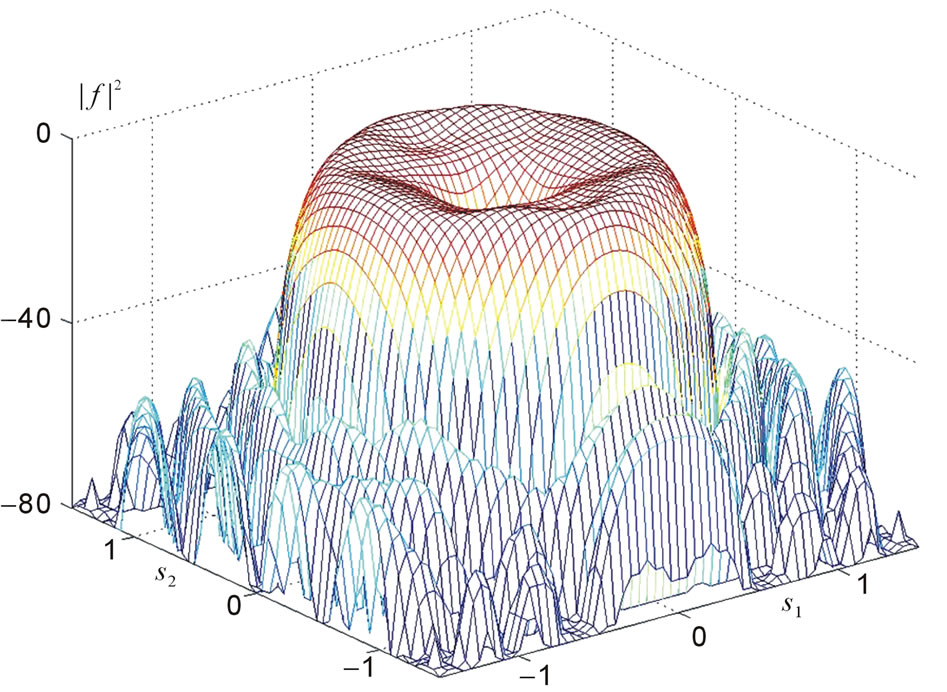
Figure 24. The synthesized power DP 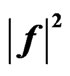 for the prescribed DP (29) at
for the prescribed DP (29) at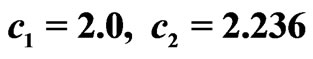 .
.
Figure 25. Cross-section of the synthesized DP 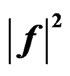 in the planes
in the planes 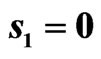 and
and 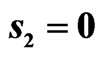 for
for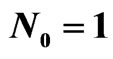 .
.
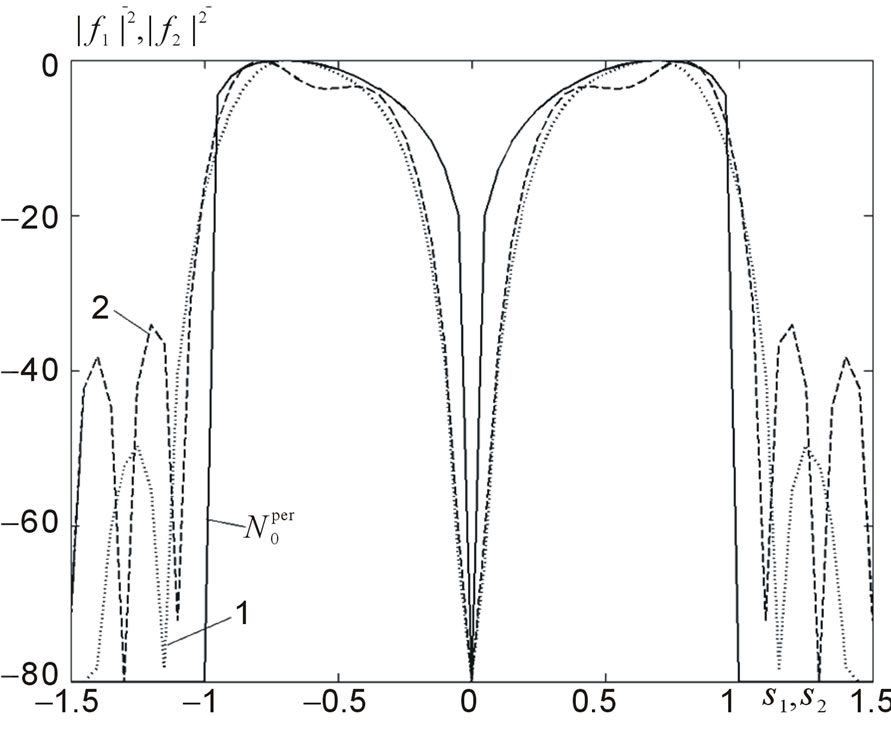
Figure 26. Cross-section of the synthesized DP 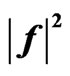 in the planes
in the planes 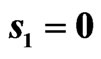 and
and 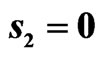 for the prescribed DP (29).
for the prescribed DP (29).
The solid line 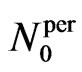 presents the cross-section of the prescribed power DPs N0, the dashed lines 1 and 2 corresponds to the synthesized DPs in the cross-sections
presents the cross-section of the prescribed power DPs N0, the dashed lines 1 and 2 corresponds to the synthesized DPs in the cross-sections 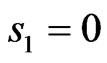 and
and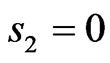 , respectively. The level of the first side lobe for the synthesized power DP
, respectively. The level of the first side lobe for the synthesized power DP 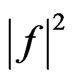 does not exceed −50 dB in the plane
does not exceed −50 dB in the plane 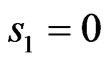 and −36 dB in the plane
and −36 dB in the plane 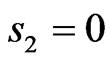 for case if DP
for case if DP 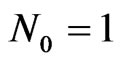 is synthesized. For the case of DP (29), these values are −52 dB and −35 dB, respectively. The level of side lobes grows considerably if either the values
is synthesized. For the case of DP (29), these values are −52 dB and −35 dB, respectively. The level of side lobes grows considerably if either the values 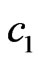 and
and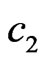 , or number of radiators in array decrease.
, or number of radiators in array decrease.
The quality of approximation to the prescribed power DP depends also on the parameter 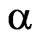 in functional (7). The dependence of mean-square deviation (msd) of the prescribed and synthesized power DPs on the parameter
in functional (7). The dependence of mean-square deviation (msd) of the prescribed and synthesized power DPs on the parameter 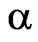 at the various
at the various 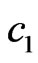 on the beam
on the beam 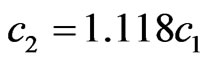 is shown in Figures 27 and 28. Such ratio of
is shown in Figures 27 and 28. Such ratio of 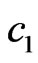 and
and 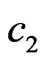 provide the regularity of the array geometry, and, as the
provide the regularity of the array geometry, and, as the
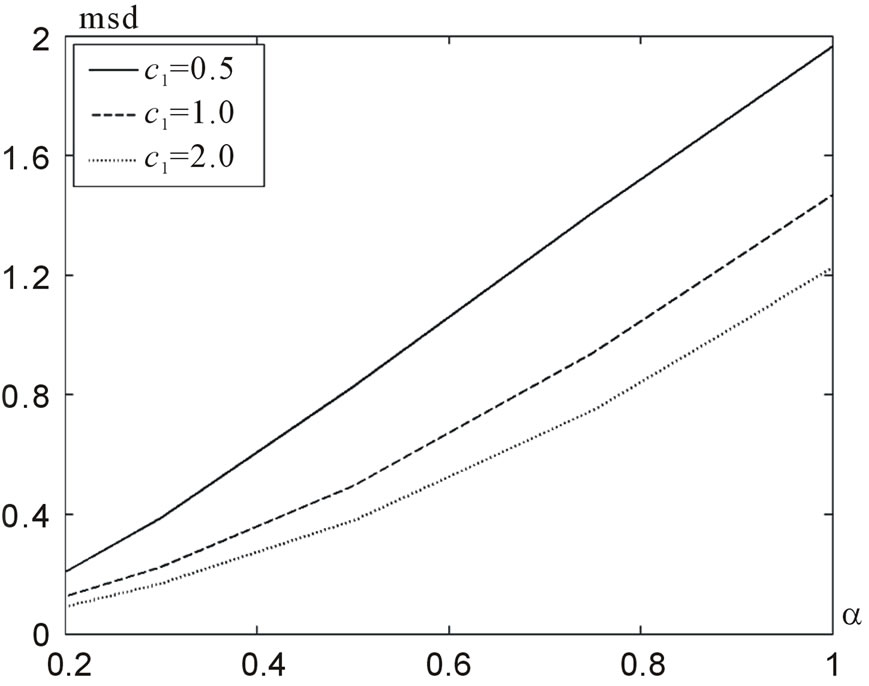
Figure 27. The msd value versus parameter a for the prescribed DP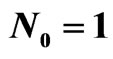 .
.
Figure 28. The msd value versus parameter a for the prescribed DP (29).
numerical calculations showed, gives possibility to obtain close DPs in the planes 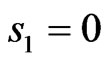 and
and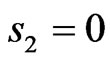 .
.
The maximal value of msd for the prescribed DP 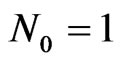 is attained at
is attained at 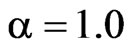 for
for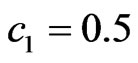 , and it is equal to 1.96443. The value of msd diminishes as
, and it is equal to 1.96443. The value of msd diminishes as 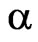 decreases almost linearly. The maximal value of msd for DP (29) is equal to 1.43685. As is easy to see that in the general the value of msd diminishes as
decreases almost linearly. The maximal value of msd for DP (29) is equal to 1.43685. As is easy to see that in the general the value of msd diminishes as 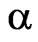 decreases, but the value of the second term in functional (7) (containning terms with the current’s norm) grows considerably that yields in total increase of
decreases, but the value of the second term in functional (7) (containning terms with the current’s norm) grows considerably that yields in total increase of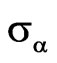 .
.
6. Conclusions
The generalized technique for the synthesis of plane radiating systems according to the prescribed power DP is proposed on the basic of the variational approach. The non-linear synthesis equation is received, the investigation of their solutions is carried out, and it is shown that bifurcation of solutions is a characteristic feature of obtained solutions. The numerical results of synthesis, demonstrated for several prescribed power DPs, testify about existence of the various types of solutions which differ by the parity of phase DP. It is shown that the same value of msd in functional 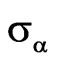 is attained at the various values of
is attained at the various values of  and
and 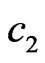 depending on the type of initial approximation. This gives the possibility to choose the solution corresponding to smaller values of
depending on the type of initial approximation. This gives the possibility to choose the solution corresponding to smaller values of 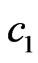 and
and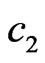 , and as result, to reduce the antenna size on 10% - 20%.
, and as result, to reduce the antenna size on 10% - 20%.
The use of the generalized parameters 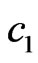 and
and 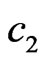 describing the electrical size of antenna and region of the prescribed power DP N0 allows examining the directivity properties of the investigated radiation systems in the wide range of frequencies and geometrical parameters of antennas.
describing the electrical size of antenna and region of the prescribed power DP N0 allows examining the directivity properties of the investigated radiation systems in the wide range of frequencies and geometrical parameters of antennas.
REFERENCES
- C. A. Balanis, “Antenna Theory: Analysis and Design,” 3rd Edition, Wiley-Interscience, New York, 2005.
- L. D. Bakhrakh and S. D. Kremenetskyi, “Synthesis of Radiating Systems (Theory and Methods of Design),” Sov. Radio, Moscow, 1974.
- B. M. Minkovich and V. P. Yakovlev, “Theory of Antenna Synthesis,” Sov. Radio, Moscow, 1969.
- Ya. S. Shifrin, “Problems of Statistical Theory of Antennas,” Sov. Radio, Moscow, 1970.
- W. L Stutzman and G. A. Thiele, “Antenna Theory and Design,” 3rd Edition, Wiley, London, 2013.
- E. G. Zelkin and V. G. Sokolov, “Methods of Antenna Synthesis. Phased Arrays and Antennas with Continuous Aperture,” Sov. Radio, Moscow, 1980.
- J. N. Sahalos, “Orthogonal Methods for Array Synthesis,” Wiley, New York, 2006, doi:10.1002/0470028548
- E. G. Zelkin, V. F. Kravchenko and V. I. Gusevskyi, “Constructive Methods of Approximation in Antenna Theory,” Science Press, Moscow, 2005.
- V. F. Kravchenko, “Atomic and R-Functions in Radiophysical Applications (Review),” Proceedings of 7th International Conference on Antenna Theory and Techniques (ICATT-2009), Lviv, 6-9 October 2009, pp. 3-12.
- M. I. Andriychuk, N. N. Voitovich, P. A. Savenko and V. P. Tkachuk, “Antenna Synthesis according to Amplitude Radiation Pattern: Numerical Methods and Algorithms,” Nauk. Dumka, Kiev, 1993.
- P. O. Savenko, “Nonlinear Problems of Radiating Systems,” Publ. IAPMM of NASU, Lviv, 2002.
- W. F. Crosswell, T. Durham, M. Jones, D. Shaubert, P. Friederich and J. Maloney, “Wideband Arrays,” In: Modern Antenna Handbook, Wiley, Interscience, New York, 2008, pp. 581-607.
- S. P. Skobelev, “Phased Array Antennas with Optimized Element Pattern,” Artech House, London, 2011.
- R. G. Ayestarana, J. Laviadab and F. Las-Herasc, “Realistic Antenna Array Synthesis in Complex Environments Using a MOM-SVR Approach,” Journal of Electromagnetic Waves and Applications, Vol. 23, No. 1, 2009, pp. 97-108. doi:10.1002/0470028548
- P. A. Savenko and L. M. Pasnak, “Numerical-Analytical Method of Synthesis for Linear Array of Vibrators with due to Mutual Coupling according to Prescribed Amplitude Radiation Pattern,” Izvestiya Vuzov. Radioelectronics, Vol. 40, No. 12, 1997, pp. 11-25.
- D. A. Morgan, “Handbook for EMC Testing and Measurement,” IET Press, London, 2007.
- V. I. Dmitriev and N. I. Berezina, “Numerical Methods of Solution of Synthesis Problems for Radiating Systems,” Publ. MSU, Moscow, 1986.
- P. A. Savenko and M. D. Tkach, “Structure of Solutions of the Synthesis Problem for Linear Microstrip Array Using the Power Criterion,” Izvestiya Vuzov. Radioelectronics, Vol. 46, No. 1, 2004, pp. 38-49.
- M. A. Krasnoselskyi, G. M. Vainikko and P. P. Zabreyko, “Approximate Solution of Operator Equations,” Nauka, Moscow, 1969.
- P. A. Savenko, “Synthesis of Linear Arrays according to Prescribed Amplitude Radiation Pattern,” Izvestiya Vuzov. Radioelectronics, Vol. 22, No. 12, 1979, pp. 1498-1504.
- V. F. Kravchenko, L. P. Protsakh, P. A. Savenko and M. D. Tkach, “Mathematical Features of Synthesis of Plane Equidistant Arrays according to Prescribed Amplitude Radiation Pattern,” Antennas, Vol. 3, No. 154, 2010, pp. 34-48.
- P. A. Savenko and L. P. Protsakh, “Method of Implicit Function Applying to Solution of Two-Dimensional Nonlinear Spectral Problem,” Izvestiya Vuzov. Radioelectronics, Vol. 11, No. 546, 2007, pp. 41-44.
- M. M. Veinberg and V. A. Trenogin, “Theory of Branching of Solutions to Nonlinear Equations,” Nauka, Moscow, 1969.
- P. O. Savenko and M. D. Tkach, “Antenna Synthesis with Flat Radiating Aperture according to the Prescribed Directivity Pattern by Power,” Proceedings of 17th International Seminar/Workshop DIPED-2012, Tbilisi, 24-27 September 2012, pp. 75-80.
NOTES
*Corresponding author.

