Open Journal of Statistics
Vol.04 No.02(2014), Article ID:43294,9 pages
10.4236/ojs.2014.42014
Numerical Procedures for Calculating the Probabilities of Recurrent Runs
M. P. Silverman
Department of Physics, Trinity College, Hartford, USA
Email: mark.silverman@trincoll.edu
Copyright © 2014 M. P. Silverman. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property M. P. Silverman. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.



ABSTRACT
Received October 22, 2013; revised November 22, 2013; accepted November 30, 2013
Run count statistics serve a central role in tests of non-randomness of stochastic processes of interest to a wide range of disciplines within the physical sciences, social sciences, business and finance, and other endeavors involving intrinsic uncertainty. To carry out such tests, it is often necessary to calculate two kinds of run count probabilities: 1) the probability that a certain number of trials results in a specified multiple occurrence of an event, or 2) the probability that a specified number of occurrences of an event take place within a fixed number of trials. The use of appropriate generating functions provides a systematic procedure for obtaining the distribution functions of these probabilities. This paper examines relationships among the generating functions applicable to recurrent runs and discusses methods, employing symbolic mathematical software, for implementing numerical extraction of probabilities. In addition, the asymptotic form of the cumulative distribution function is derived, which allows accurate runs statistics to be obtained for sequences of trials so large that computation times for extraction of this information from the generating functions could be impractically long.
Keywords:
Recurrent Events; Theory of Runs; Time Series Analysis; Generating Functions; Probability Distributions
1. Introduction
1.1. Runs Tests for Non-Randomness
A stochastic process generates random outcomes in time or space. Such processes occur widely in the physical and social sciences, as well as in purely practical human activities such as finance, manufacturing, and commerce. Despite their random occurrence―indeed, precisely because of it―the outcomes of a stochastic process will display ordered patterns which a statistically naïve observer may mistakenly interpret as predictively useful information. In recent years, controversial issues over the information content of time series have arisen in a variety of disciplines such as nuclear physics [1] and econophysics (i.e. dynamics of the stock market) [2]. Although it is not possible to prove with certainty that a particular process is random, there are various statistical tests to demonstrate within specified confidence limits that it is not random. Among these, nonparametric runs tests are especially useful, in part because of their ease of implementation and statistical power [3].
1.2. Exclusive Runs
An exclusive run is an unbroken sequence of similar events, ordinarily of a binary nature. For example, a sequence of symbols aabbbaa comprises 2 runs of a’s of length 2 and 1 run of b’s of length 3. If the events a and b occur with fixed probabilities throughout the sequence, the stochastic process is of the Bernoulli kind, and the distribution theory of binary runs [4] can be used to test for non-randomness in permutational ordering of any such empirical sequence of outcomes.
It is not necessary for a stochastic process to generate binary events in order to be analyzed for runs. For example, a sequence of n different observations
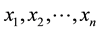 of a continuous random variable will yield
of a continuous random variable will yield
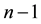 sequential differences that are either positive (+) or negative (?) and therefore again subject to binary runs analysis. The binary elements, however, are not Bernoulli variates since the probability of obtaining an element decreases with its position in the unbroken sequence. Nevertheless, one can test for non-randomness in permutational ordering with a different distribution theory [5].
sequential differences that are either positive (+) or negative (?) and therefore again subject to binary runs analysis. The binary elements, however, are not Bernoulli variates since the probability of obtaining an element decreases with its position in the unbroken sequence. Nevertheless, one can test for non-randomness in permutational ordering with a different distribution theory [5].
Although developed initially for testing quality control in manufacturing, exclusive runs and up-down runs have been employed in analysis of a variety of experiments to test the fundamental prediction of quantum mechanics that transitions between quantum states occur randomly [6,7]. A problematic issue in the counting of exclusive or up-down runs is that the length of a run can be changed by future events. Thus, in the succession aabbbaa, the second run of 2 a could change to a run of 3 a or 4 a if the next two trials resulted in ab or aa respectively.
1.3. Runs of Recurrent Events
A third kind of runs analysis, based on Feller’s theory of recurrent events [8], was recently employed to examine certain quantum optical processes for evidence of non-random behavior [9]. A recurrent run of length t, as defined by Feller, is a sequence of non-overlapping, uninterrupted successions of exactly t elements of the same kind. It is distinguished from the other two kinds of runs in that the concept of run length is so defined as to be independent of subsequent trials. For example, in the sequence aaaabaaaaaa, there are two runs of length 4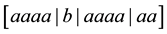 , three runs of length 3
, three runs of length 3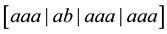 , and five runs of length 2
, and five runs of length 2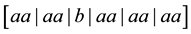 . (Analyzed in terms of exclusive runs, there would have been 1 run of a of length 4 and 1 run of a of length 6, provided the sequence ended at the 11th trial). In a sequence of Bernoulli trials, a recurrent run of length t occurs at the
. (Analyzed in terms of exclusive runs, there would have been 1 run of a of length 4 and 1 run of a of length 6, provided the sequence ended at the 11th trial). In a sequence of Bernoulli trials, a recurrent run of length t occurs at the
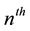 trial if the
trial if the
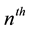 trial adds a new run to the sequence. Thus, the recurrent runs of length 4 occur at positions 4, 9, and the recurrent runs of length 3 occur at positions 3, 8, 11.
trial adds a new run to the sequence. Thus, the recurrent runs of length 4 occur at positions 4, 9, and the recurrent runs of length 3 occur at positions 3, 8, 11.
The advantage of Feller’s definition is that runs of a fixed length become recurrent events, and the statistical theory of recurrent events can then be applied to testing empirical data sequences for permutational invariance over a much wider variety of patterns than just those of unbroken sequences of identical binary elements. For example, one may be interested in testing the recurrence of a pattern abab, which, in a quantum optics experiment, might correspond to a sequence of alternate detections of left and right circularly polarized photons, or, in a series of stock price variations, might correspond to a sequence of alternative observations of rising and falling closing prices. Besides the application to runs, the same theoretical foundation may be applied to recurrent events in other forms such as return-to-origin problems, ladder-point problems (instances where a sum of random variables exceeds all preceding sums), and waiting-time problems.
The theory of recurrent runs, the relevant parts of which are examined in the following section, leads to generating functions from which the probability of a run of defined events of specified length can in principle be calculated exactly. As a practical matter, the extraction of these probabilities requires geometrically longer computation times with increasing sequence length. The availability of fast lap-top computers with large random access memory and of symbolic mathematical software of hitherto unparalleled ability to execute series expansions and perform differentiation and integration provides the analyst with computational power unimaginable to the creators of the statistical theory of runs. I report here mathematical strategies for reducing significantly the computation time for the probability of the widely applicable case of k occurrences of runs of length t in a Bernoulli sequence of length n.
2. Theory and Implementation of Recurrent Runs
2.1. Probability Generating Functions
Following Feller, I define the recurrent event E to be a run of successes of length t in a sequence of Bermoulli trials with p the probability of a single successful outcome and
 the probability of failure. Consider the following random variables:
the probability of failure. Consider the following random variables:
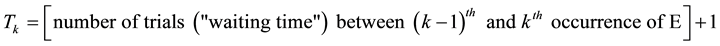 (1)
(1)
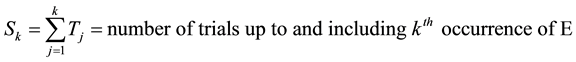 (2)
(2)
 . (3)
. (3)
The distribution of the variable T is defined by
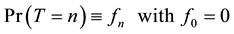 (4)
(4)
where
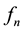 is the probability that E occurs for the first time at the
is the probability that E occurs for the first time at the
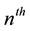 trial. The generating function of the probabilities of first occurrence is expressed by
trial. The generating function of the probabilities of first occurrence is expressed by
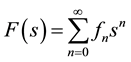 . (5)
. (5)
The number of trials to the
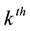 occurrence of E is then characterized by the random variable
occurrence of E is then characterized by the random variable
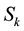 in (2), which is a sum of the waiting times of k independent trials, from which it is follows that the associated generating function takes the form
in (2), which is a sum of the waiting times of k independent trials, from which it is follows that the associated generating function takes the form
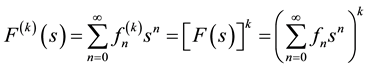 (6)
(6)
where
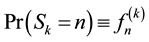 (7)
(7)
is the probability that the
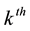 occurrence of E first takes place at the
occurrence of E first takes place at the
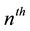 trial.
trial.
I leave to the cited literature the proof that the generating function (5) for runs of length t with individual probability of success p is given by
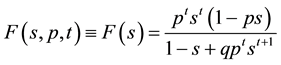 (8)
(8)
from which the mean and standard deviation of the recurrence times follow by differentiation
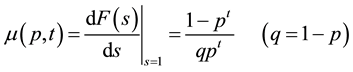 (9)
(9)
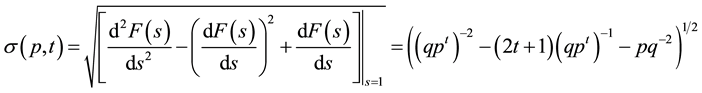 . (10)
. (10)
For economy of expression, the parameters p, t will be suppressed in the arguments of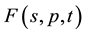 ,
,
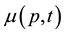 , and
, and
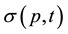 unless needed to avoid ambiguity. In general, these parameters will be chosen and fixed at the outset of any illustrative applications. Note, too, that to obtain a statistical moment from a probability generating function (pgf), the derivatives are evaluated at
unless needed to avoid ambiguity. In general, these parameters will be chosen and fixed at the outset of any illustrative applications. Note, too, that to obtain a statistical moment from a probability generating function (pgf), the derivatives are evaluated at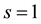 , which leads to a sum of terms, whereas to obtain a probability the derivatives are evaluated at
, which leads to a sum of terms, whereas to obtain a probability the derivatives are evaluated at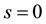 , which leads to a single term.
, which leads to a single term.
For many applications the analyst’s interest is not necessarily in the recurrence time (i.e. number of trials) to the
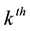 occurrence of E, but in the probability that E occurs k times in a fixed number n of trials. The relation connecting the two variates is
occurrence of E, but in the probability that E occurs k times in a fixed number n of trials. The relation connecting the two variates is
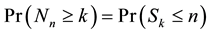 . (11)
. (11)
The probability
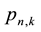 that k events E occur in n trials is then expressible as
that k events E occur in n trials is then expressible as
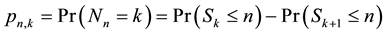 (12)
(12)
and serves in the construction of two pgf’s
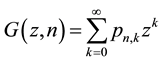 (13)
(13)
and
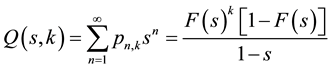 . (14)
. (14)
Note that the summation in (13) is over the number of occurrences, whereas the summation in (14) is over the number of trials. The second equality in (14) follows directly from Equation (11). Multiplying both sides of (13) by
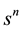 and summing over n leads to the bivariate generating function
and summing over n leads to the bivariate generating function
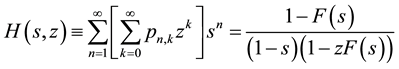 (15)
(15)
from which the probabilities
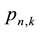 are calculable by series expansion of both sides of the equality.
are calculable by series expansion of both sides of the equality.
A sense of the structure of the formalism can be obtained by considering the case of recurrent runs of length
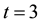 for a stochastic process with
for a stochastic process with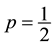 . Substitution of these conditions into Equation (8) for
. Substitution of these conditions into Equation (8) for
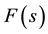 yields
yields
the following rational expression for the right side of Equation (15) and its corresponding Taylor-series expansion
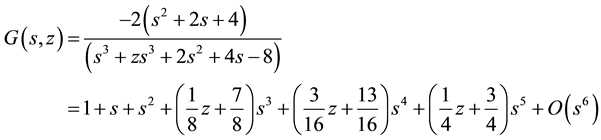 (16)
(16)
to order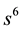 . Recall that the powers of s designate the number of trials, and the powers of z designate the number of recurrences of runs of length 3. For a fixed power of s, the sum of the coefficients of the powers of z within each bracketed expression equal unity, as they must by the completeness relation for the probability of mutually exclusive outcomes. Note that the first three terms
. Recall that the powers of s designate the number of trials, and the powers of z designate the number of recurrences of runs of length 3. For a fixed power of s, the sum of the coefficients of the powers of z within each bracketed expression equal unity, as they must by the completeness relation for the probability of mutually exclusive outcomes. Note that the first three terms
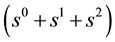 are independent of z―i.e. contain only powers
are independent of z―i.e. contain only powers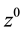 ―since there cannot be runs of length 3 in a sequence of no more than 2 trials. For 3 trials, the probability of 0 runs of length 3 is 7/8 and the probability of 1 run of length 3 is 1/8. For 5 trials, however, the probability of 0 runs is 1/4 and the probability of 1 run is 3/4. This pattern persists: (a) to obtain a run of length t, the sequence of trials must be of length
―since there cannot be runs of length 3 in a sequence of no more than 2 trials. For 3 trials, the probability of 0 runs of length 3 is 7/8 and the probability of 1 run of length 3 is 1/8. For 5 trials, however, the probability of 0 runs is 1/4 and the probability of 1 run is 3/4. This pattern persists: (a) to obtain a run of length t, the sequence of trials must be of length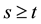 , and (b) the greater the number of trials, the higher is the probability of obtaining longer runs.
, and (b) the greater the number of trials, the higher is the probability of obtaining longer runs.
2.2. Moment Generating Functions
It is not necessary to know the individual
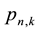 to determine the mean number of recurrent runs
to determine the mean number of recurrent runs
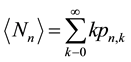 (17)
(17)
which, for many applications in the physical sciences and elsewhere, is the experimentally observed quantity of interest. Multiplying both sides of Equation (17) by
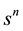 and summing n over the range
and summing n over the range
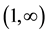 leads to the generating function for the distribution of
leads to the generating function for the distribution of
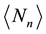
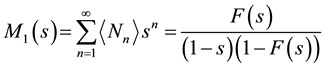 . (18)
. (18)
Starting from the relation
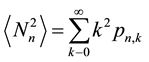 (19)
(19)
and following the same procedure that led to (18) yields the generating function for the distribution
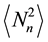
 . (20)
. (20)
From the generating functions (18) and (20) one can deduce the asymptotic relations for mean and variance
 (21)
(21)
and
 . (22)
. (22)
2.3. Numerical Procedures
The statistics (probabilities and expectation values) for any physically meaningful choice of probability of success p, run length t, and number of trials n are deducible exactly from expressions (15) and (18) in the manner previously illustrated. For many applications, however, particularly where it is possible to accumulate long sequences of data as is often the case in atomic, nuclear and elementary particle physics experiments or investigations of stock market time series, the tests for evidence of non-random behavior are best made by examining long runs. Suppose, for example, one wanted the probability of obtaining the number of occurrences of runs of length 50 in a sequence of 100 trials. One approach, leading directly to all non-vanishing probabilities, would be to extract the 100th term
from the series expansion of the bivariate generating function (15). Powerful symbolic mathematical software such as Maple or Mathematica permits one to do this up to a certain order limited by the speed and memory of one’s computer, but these calculational tools may become insufficient when one is seeking exact probabilities of runs in data sequences of thousands to millions of bits.
Using complex variable theory, one can extract expressions for
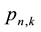 and
and
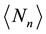 by evaluation of contour integrals
by evaluation of contour integrals
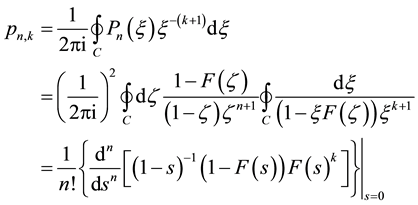 (23)
(23)
and similarly
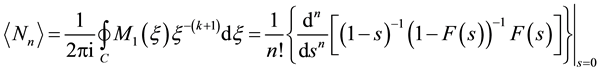 (24)
(24)
where C is the unit circle and the generating function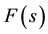 , given by Equation (8), specifies the single-event probability p and run length t. Contrary to first impression, however, the execution of expressions (23) or (24) for
, given by Equation (8), specifies the single-event probability p and run length t. Contrary to first impression, however, the execution of expressions (23) or (24) for
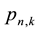 or
or
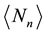 directly by differentiation, instead of by a series expansion of the corresponding generators up to the order that yields the desired
directly by differentiation, instead of by a series expansion of the corresponding generators up to the order that yields the desired
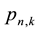 or
or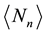 , is not computationally economic. The computer, in fact, executes the series expansion of the generator much more rapidly than it performs symbolic differentiation.
, is not computationally economic. The computer, in fact, executes the series expansion of the generator much more rapidly than it performs symbolic differentiation.
Because the generator
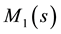 [Equation (18)] is univariate, one can take advantage of the rapidity with which symbolic mathematical software executes a series expansion to obtain exact values
[Equation (18)] is univariate, one can take advantage of the rapidity with which symbolic mathematical software executes a series expansion to obtain exact values
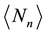 for very long sequence lengths by the following simple procedure:
for very long sequence lengths by the following simple procedure:
1) For given p and t, express
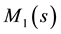 as a rational function
as a rational function
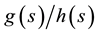 of s.
of s.
2) Convert
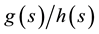 to a power series
to a power series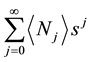 . In Maple this can be done by the command
. In Maple this can be done by the command
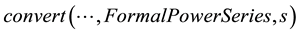 where the ellipsis
where the ellipsis
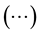 represents either the expression to be converted or the Maple equation number of that expression.
represents either the expression to be converted or the Maple equation number of that expression.
3) Extract the single desired term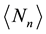 . In Maple this can be done by filtering the sum:
. In Maple this can be done by filtering the sum: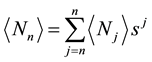 .
.
Alternatively, one can convert the series generated to order
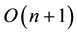 to a polynomial of degree n, and use the command lcoeff to extract the leading coefficient of the polynomial.
to a polynomial of degree n, and use the command lcoeff to extract the leading coefficient of the polynomial.
As an illustration, consider the calculation (by means of Maple) of the exact mean number of runs of length
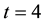 in a sequence of 1 million trials with probability of success
in a sequence of 1 million trials with probability of success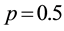 . Following the foregoing steps, we have
. Following the foregoing steps, we have
1)
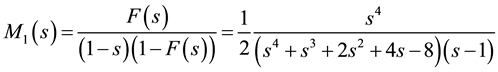
2)
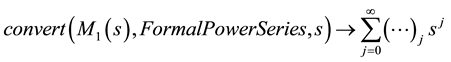
3)
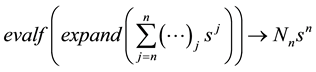
where
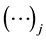 is to be replaced by the actual
is to be replaced by the actual
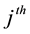 numerical element in the sum obtained in step (2). The arrow, inserted by the author, symbolically points to the form of the output. Extraction of this element for the specified conditions led to
numerical element in the sum obtained in step (2). The arrow, inserted by the author, symbolically points to the form of the output. Extraction of this element for the specified conditions led to
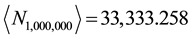 in a fraction of a second. In Maple, the command evalf calls for numerical evaluation of expressions; omitting this command results in an exact fraction, which for a sequence length of 1 million is too unwieldy to be useful. Use of the command lcoeff yields the same result, but executes more slowly for large n.
in a fraction of a second. In Maple, the command evalf calls for numerical evaluation of expressions; omitting this command results in an exact fraction, which for a sequence length of 1 million is too unwieldy to be useful. Use of the command lcoeff yields the same result, but executes more slowly for large n.
The procedure described above for converting the rational expression of s into a formal power series in s did not work with the bivariate generator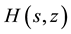 , which involved a product of z with a power of s (depending on run length t) in the denominator, and required, for the conversion, solution of the roots of a high-order (>2) algebraic equation. Maple did return, however, the recursion relation for the coefficients of the formal power series. An alternative procedure to isolate the values
, which involved a product of z with a power of s (depending on run length t) in the denominator, and required, for the conversion, solution of the roots of a high-order (>2) algebraic equation. Maple did return, however, the recursion relation for the coefficients of the formal power series. An alternative procedure to isolate the values
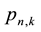 for fixed n, which still relied on the computational speed of series expansion and worked well for sequence lengths in the thousands, is the following:
for fixed n, which still relied on the computational speed of series expansion and worked well for sequence lengths in the thousands, is the following:
1) For given p and t, express
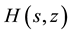 as a rational function of s and z.
as a rational function of s and z.
2) Generate a series expansion of
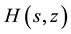 to order n and
to order n and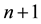 .
.
3) Convert the series expansions into polynomials
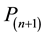 and
and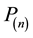 .
.
4) Subtract one polynomial from the other to obtain an expression of the form
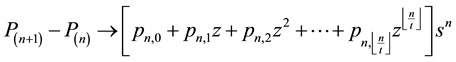
where
 is the largest integer k such that
is the largest integer k such that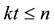 . The coefficients
. The coefficients
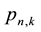 are given as exact fractions.
are given as exact fractions.
5) Evaluate the set
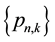 as floating-point numbers, if desired.
as floating-point numbers, if desired.
As an example, the procedure led in under 10 seconds to the full set
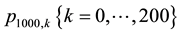 for the probability of k occurrences of runs of length 4 in a sequence of 1000 trials. The calculations described in this section were performed with a laptop computer (Intel-based Mac Powerbook) running Maple 16.
for the probability of k occurrences of runs of length 4 in a sequence of 1000 trials. The calculations described in this section were performed with a laptop computer (Intel-based Mac Powerbook) running Maple 16.
One final procedure, particularly suitable when only selected probabilities of the full set
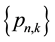 are desired, is to obtain these probabilities directly from the generating function
are desired, is to obtain these probabilities directly from the generating function
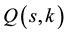 in (14). As in the previous examples, this can be accomplished in either of two ways: (1) by evaluating the leading coefficient of the polynomial in the desired degree n, or (2) by filtering the power series for the
in (14). As in the previous examples, this can be accomplished in either of two ways: (1) by evaluating the leading coefficient of the polynomial in the desired degree n, or (2) by filtering the power series for the
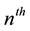 term. As an example, consider the probability
term. As an example, consider the probability
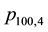 for obtaining 4 runs of length
for obtaining 4 runs of length
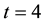 in a series of 100 trials with probability of success
in a series of 100 trials with probability of success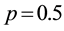 . The generating function then takes the form
. The generating function then takes the form
In Maple, method (1) proceeds as follows:
1)
2)
where the ellipsis is to be replaced by the



Note that the series must be expanded to


3. Generating Function of Cumulative Probability
For many applications in the physical sciences and elsewhere, the full set of probabilities



introduced in Equation (11). Experimental situations calling for preferential usage of a cumulative probability distribution over a probability function abound in the physical sciences, as, for example, in the analysis of fragmentation [10] and other stochastic processes leading to a power-law distribution.
The generating function for the ccp is derivable from


(It is understood that



4. Asymptotic Distributions
One can show by application of the Central Limit Theorem (CLT) to relation (11) that for sufficiently large number of trials n and number of occurrences k, the number





The Gaussian approximation, however, does not work well in estimating the cumulative probability




in which the constant




Recall that







which is a sum of k independent exponential random variables


Table 1. Comparison of exact and Gaussian mean numbers of runs for n = 100 trials with p = 0.5.
Table 2. Asymptotic mean and SD of
where


By virtue of equivalence (11), Equation (28) also yields a closed-form asymptotic relation for the sought-for cumulative probability distribution
Consider, for example, the probability of 1 or more runs of length 20 in 2000 trials with individual probability of success 0.5. A comparison of the results of (a) Equation (28), (b) the cumulative Gaussian distribution with mean and variance given by relations (21) and (22), and (c) the exact calculation obtained from the generating function (26)
supports the distribution (28). If the number of trials is increased to 106, the Gamma and Gaussian asymptotic distributions lead to comparable results
but the former is still superior to the latter when compared to the probability calculated from the exact generating function.
The relation (28), by which one can calculate the cumulative probability



5. Conclusions
The theory of recurrent runs provides a statistical basis for rejecting the hypothesis that a series of observations (in time or space) are random. This is a matter that often arises in experimental investigations in atomic, optical, nuclear, and elementary particle physics, as well as in other sciences, finance, and commerce, which may entail a very large number―perhaps in the thousands to millions―of trials or observations.
In this paper theoretical and numerical methods based on different generating functions were derived and investigated to determine (a) the probability



The methods reported here can be implemented on modern laptop computers running commercially available symbolic mathematical software, such as Maple (which was the application used by the author). Computation times for application of these methods to data sequences up to millions of trials could range from seconds to minutes.
To compute runs statistics for sequences of intermediate to very long trial numbers, the asymptotic distribution for the number of trials up to and including the





References
- 1. M. P. Silverman and W. Strange, “Search for Correlated Fluctuations in the β+ Decay of Na-22,” Europhysics Letters, Vol. 87, No. 3, 2009, pp. 32001-32006. http://dx.doi.org/10.1209/0295-5075/87/32001
- 2. D. Sornette, “Critical Market Crashes,” Physics Reports, Vol. 378, No. 1, 2003, pp. 1-98.
http://dx.doi.org/10.1016/S0370-1573(02)00634-8 - 3. J. Wolfowitz, “On the Theory of Runs with Some Applications to Quality Control,” The Annals of Mathematical Statistics, Vol. 14, No. 3, 1943, pp. 380-288.
http://dx.doi.org/10.1214/aoms/1177731421 - 4. A. M. Mood, “The Distribution Theory of Runs,” The Annals of Mathematical Statistics, Vol. 11, No. 4, 1940, pp. 367-392.
http://dx.doi.org/10.1214/aoms/1177731825 - 5. H. Levene and J. Wolfowitz, “The Covariance Matrix of Runs Up and Down,” The Annals of Mathematical Statistics, Vol. 15, No. 1, 1944, pp. 58-69. http://dx.doi.org/10.1214/aoms/1177731314
- 6. M. P. Silverman, W. Strange, C. Silverman and T. C. Lipscombe, “Tests for Randomness of Spontaneous Quantum Decay,” Physical Review A, Vol. 61, No. 4, 2000, Article ID: 042106.
http://dx.doi.org/10.1103/PhysRevA.61.042106 - 7. M. P. Silverman and W. Strange, “Experimental Tests for Randomness of Quantum Decay Examined as a Markov Process,” Physics Letters A, Vol. 272, No. 1-2, 2000, pp. 1-9.
http://dx.doi.org/10.1016/S0375-9601(00)00374-1 - 8. W. Feller, “Fluctuation Theory of Recurrent Events,” Transactions of the American Mathematical Society, Vol. 67, 1949, pp. 98-119. http://dx.doi.org/10.1090/S0002-9947-1949-0032114-7
- 9. D. Branning, A. Katcher, W. Strange and M. P. Silverman, “Search for Patterns in Sequences of Single-Photon Polarization Measurements,” Journal of the Optical Society of America B, Vol. 28, No. 6, 2011, pp. 1423-1430.
http://dx.doi.org/10.1364/JOSAB.28.001423 - 10. M. P. Silverman, W. Strange, J. Bower and L. Ikejimba, “Fragmentation of Explosively Metastable Glass,” Physica Scripta, Vol. 85, 2012, Article ID: 065403. http://dx.doi.org/10.1088/0031-8949/85/06/065403
- 11. A. M. Mood, F. A. Graybill and D. C. Boes, “Introduction to the Theory of Statistics,” 3rd Edition, McGraw-Hill, New York, 1974, pp. 540-541.







