Intelligent Information Management
Vol.2 No.11(2010), Article ID:3238,10 pages DOI:10.4236/iim.2010.211073
Nonsmooth Optimization Algorithms in Some Problems of Fracture Dynamics
Centro de Investigacion Cientifica de Yucatan A.C, Colonia Chuburná de Hidalgo,
Yucatán, México
E-mail: zozulya@cicy.mx
Received October 16, 2009; revised July 10, 2010; accepted September 15, 2010
Keywords: Unilateral Contact, Friction, Crack, Variational Principles, Boundary Variational Functional, Nonsmooth Optimization Algorithm
Abstract
Mathematical statement of elastodynamic contact problem for cracked body with considering unilateral restrictions and friction of the crack faces is done in classical and weak forms. Different variational formulations of unilateral contact problems with friction based on boundary variational principle are considered. Nonsmooth optimization algorithms of Udzawa’s type for solution of unilateral contact problem with friction have been developed. Convergence of the proposed algorithms has been studied numerically.
1. Introduction
The mathematical formulation of the elastodynamic problem for a cracked body, that takes into account the possibility of crack edge contact interaction and the formation of areas with close contact, adhesion and sliding, was presented first in [1]. The algorithm for the solution of this problem was elaborated in [2] and is based on a theory of subdifferentional functionals and the finding of their saddle points. Many examples of the crack faces contact interaction and friction influence on the fracture mechanics criterions have been considered in the book by Guz and Zozulya [3] and review papers [4-6]. In these cases the contact area is “a priori” unknown and the unilateral conditions have to be imposed on the relative displacements and the mutual tractions. The unilateral contact restriction with friction can be written as an inequality for the displacement and traction vectors. As a result a complete set of boundary conditions at crack faces is written as a system of equations and inequalities. The presence of inequality type boundary conditions implies the boundary problems to be nonlinear, which requires the investigation of corresponding boundary value problems.
Mathematical formulation of the problem of crack faces contact interaction in the dynamic case has bee done in [3-5,7]. Since the constraints concern boundary variables only, it is natural to look for a numerical solution by means of boundary integral equation (BIE) method. Approach is based on use of fundamental solutions. In [8] BIE formulation via energy method is based on boundary min-max principle, i.e., a principle expressed in terms of the boundary unknowns. First time boundary variational formulation of elastodynamic contact a problem with frication was proposed in [2] and then was extended and applied to elastodynamic problems for bodies with cracks with considering unilateral frictional contact of the crack faces in Guz and Zozulya [3,5].
There are many algorithms for unilateral contact problems with friction. Because of nonlinearity of the problem most of them include discretization and iterative procedure to satisfy unilateral constrains. Iterative algorithms of such type in [9,10] are named Uzawa’s type algorithms. For the first time Uzawa’s type algorithm was proposed in for solution elastodynamic frictional contact problem for body with crack in [1]. Then the approach was developed and more algorithms were proposed in [2,11-13]. The algorithms are based on saddle point finding and projection on the set of unilateral restrictions and friction respectively. In [14] it was shown that proposed algorithms are convergent and was studies rate of convergence. Some mathematical problems related existence and uniqueness of the problem of unilateral contact problem with friction were studied in [7,15,16]. More information related to mathematical formulation and numerical solution of the unilateral contact problems can found in [17,18].
The aim of this paper is to present variational formulation of the elastodynamic problem for body with crack with considering possibility for unilateral crack faces contact interaction with friction. Variational formulation of the problem, which is based boundary variational principle is presented. Nonsmooth functionals that correspond to unilareral frictional contact conditions are constructed. The case of the crack in infinite elastic media is considered in more details. In order to study convergence of the proposed algorithms, two problems related to the crack faces contact interaction under action of the harmonic tension-compression and shear waves have been solved numerically using BIE method.
2. Classical Formulation of the Problem
Let us consider dynamical loading of crack in an infinite homogeneous, lineally elastic body. The crack is described by a corresponding oriented middle surface 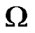 since we suppose that only small deformations occur. We assume that displacements of body points and their gradients are small.
since we suppose that only small deformations occur. We assume that displacements of body points and their gradients are small.
In this case in 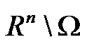
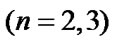 the differential equations of equilibrium in displacement may be presented in the form
the differential equations of equilibrium in displacement may be presented in the form

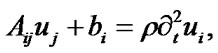 ,
,
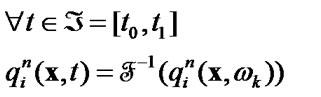 (1)
(1)
The operator Aij for an isotropic body has the form
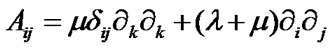 , (2)
, (2)
where l and m are Lame constants, 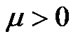 and
and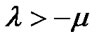 ,
,  is a Kronecker’s symbol,
is a Kronecker’s symbol, 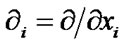 denotes the partial derivatives with respect to space,
denotes the partial derivatives with respect to space, 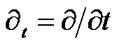 denotes the partial derivatives with respect to time. Throughout this paper we use the Einstein summation convention.
denotes the partial derivatives with respect to time. Throughout this paper we use the Einstein summation convention.
If the problem is defined on an infinite region, then the solution of Equation (1) is uniquely determined by assigning displacements and velocity vectors in the initial instant of time. Then the initial conditions are
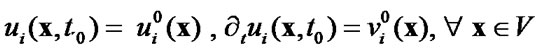 (3)
(3)
Additional conditions at the infinity must be satisfied
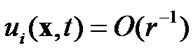 ,
,  for
for 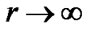 in 3-D case (4)
in 3-D case (4)
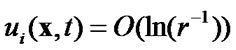 ,
,  for
for 
in 2-D case (5)
Here 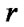 is the distance in the 3-D and 2-D Euclidian spaces respectively.
is the distance in the 3-D and 2-D Euclidian spaces respectively.
The differential operator 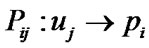 is called stress operator. It transforms the displacements into the tractions. For homogeneous isotropic elastic medium it has the forms
is called stress operator. It transforms the displacements into the tractions. For homogeneous isotropic elastic medium it has the forms
 (6)
(6)
Here 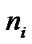 are components of the outward unit normal vector,
are components of the outward unit normal vector,  is a derivative in direction of the vector
is a derivative in direction of the vector  normal to the surface
normal to the surface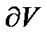 .
.
The contact forces 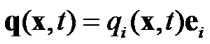 which arise on the cracks edges during the interaction are denoted by
which arise on the cracks edges during the interaction are denoted by
 (7)
(7)
where 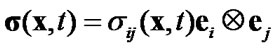 is the strain tensor;
is the strain tensor;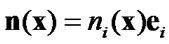 ,
,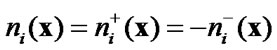 ;
; 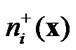 and
and  are the normal unit vectors directed to the positive side of the opposite cracks edges.
are the normal unit vectors directed to the positive side of the opposite cracks edges.
The displacement discontinuity vector characterizes mutual displacements of the cracks edges
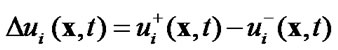 , (8)
, (8)
where  and
and  are displacements of opposite cracks edges.
are displacements of opposite cracks edges.
Furthermore, we impose the following Signorini constraints

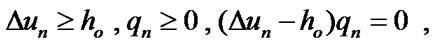 (9)
(9)
and Coulomb’s friction law:
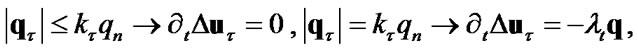
 (10)
(10)
with  for
for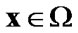 ; the Coulomb’s friction coefficient
; the Coulomb’s friction coefficient 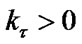 is here assumed to be constant.
is here assumed to be constant.
Here the normal and tangential components of the displacement discontinuity on 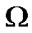 are denoted by
are denoted by
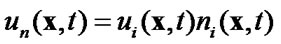 ,
,
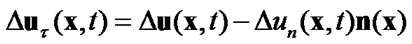 , (11)
, (11)
and the normal and tangential components of the contact forces on 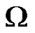 are denoted by
are denoted by
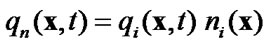 ,
,
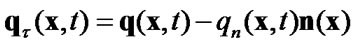 . (12)
. (12)
Classical formulation of the elastodynamic problem for body with crack with considering opposite crack sides interaction consists in solution of the initial boundary value problem (1)-(5) with considering Signorini contact conditions (9) with friction (10).
In classical elastodynamics the equations of motion (1) and initial conditions (2) must be satisfied exactly (see [19]). This means that the components of the displacement vector should be functions of the class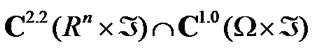 . Here
. Here 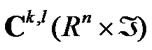 is a functional space of functions, with k smooth derivatives with respect to the space coordinates and
is a functional space of functions, with k smooth derivatives with respect to the space coordinates and  smooth derivatives with respect to the time. In order to satisfy all the equations of elastodynamics in the classical sense, the components of the stress-strain state should belong to the following functional spaces
smooth derivatives with respect to the time. In order to satisfy all the equations of elastodynamics in the classical sense, the components of the stress-strain state should belong to the following functional spaces
 (13)
(13)
These requirements of classical elastodynamics are very stringent. Therefore many important physics and engineering problems, in particular problems with unilateral restrictions and friction, have no classical solution. For this reason it is necessary to consider “weakened” formulations to elastodynamic problems. With such an approach it is not necessary to fulfill all the elastodynamics equations in the classical sense.
3. Variational Formulation of the Problem without Contact Conditions
In order to formulate an elastostatic contact problem for body with crack in week form we will consider the boundary variational principle introduced in [2,5,11,12].
In [2,5] it have been shown that in the case if body with crack occupied infinite region the boundary variational functional may be presented in the form
 (14)
(14)
where ,
, 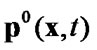 is a vector of given loading applied to the crack edges,
is a vector of given loading applied to the crack edges, 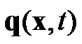 is a vector of contact forces,.
is a vector of contact forces,.
The boundary variational functional (14) is smooth and Gateaux-differentiable, therefore the following condition of functional minima take place
 (15)
(15)
and the problem of finding minima is equivalent to the following integral equation
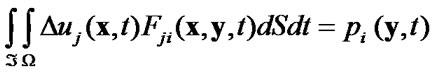 (16)
(16)
We can represent boundary variational functional (14) in the form
 (17)
(17)
where  is matrix integral operator defined in (16).
is matrix integral operator defined in (16).
Then variational formulation of an elastodynamic problem for cracked body without unilateral constraints (7) and friction (8) is as follows:
 (18)
(18)
where
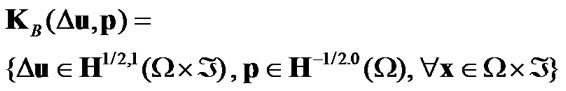 (19)
(19)
4. Nonsmooth Functionals for Unilateral Contact Conditions with Friction
In order to formulate boundary conditions in form of inequalities (9) and (10) in week form let us consider a maximal monotone operators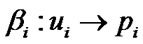 . For each maximal monotone operator
. For each maximal monotone operator  may be defined with accuracy up to a constant component convex semi-continuous from below functional
may be defined with accuracy up to a constant component convex semi-continuous from below functional 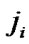 such, that
such, that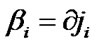 . Here ¶ is denoted the subdifferential of the nonsmooth functional (see [18] for details).
. Here ¶ is denoted the subdifferential of the nonsmooth functional (see [18] for details).
4.1. Signorini Boundary Conditions in Functional Space
Let  and
and  satisfy following conditions
satisfy following conditions 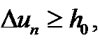
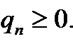
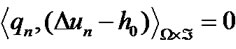 , Here
, Here  denotes the duality pairing between the functional spaces
denotes the duality pairing between the functional spaces 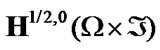 and
and . Then corresponding functional has the form
. Then corresponding functional has the form
 (20)
(20)
The conjugate functional has the form
 (21)
(21)
4.2. Boundary Conditions with Coulomb Friction
Lets  and
and  satisfy following conditions if
satisfy following conditions if 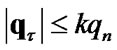 then
then , if
, if 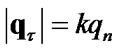 then
then 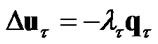 and also
and also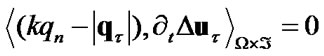 . Here
. Here  denotes the duality pairing between the functional spaces
denotes the duality pairing between the functional spaces  and
and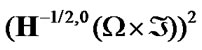 . Then corresponding functional has the form
. Then corresponding functional has the form
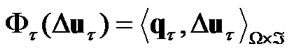 (22)
(22)
The conjugate functional has the form
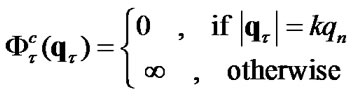 (23)
(23)
4.3. Signorini Boundary Conditions with Friction
These boundary conditions may be considered as combination of the previously considered boundary conditions. Really lets  and
and 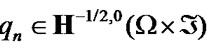 satisfy following conditions
satisfy following conditions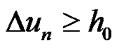 ,
,  ,
, 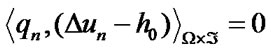 and also
and also  and
and  satisfy following conditions if
satisfy following conditions if 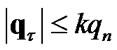 then
then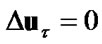 , if
, if 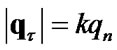 then
then  and also
and also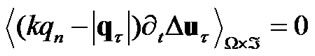 . We consider functionals such that
. We consider functionals such that
 and
and
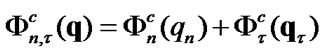 (24)
(24)
These functionals have the form
 (25)
(25)
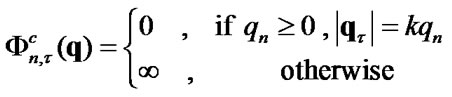 (26)
(26)
4.4. Sets of Admissible Displacements and Traction for Signorini Boundary Conditions with Friction
For variational formulation of the unilateral contact problems with friction also are used sets of admissible displacements
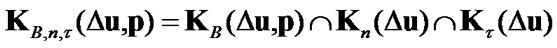 ,
,
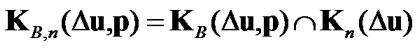 ,
, 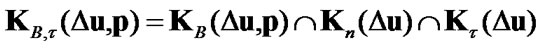 ,
,
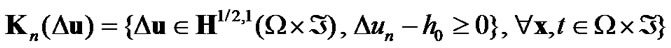
(27)
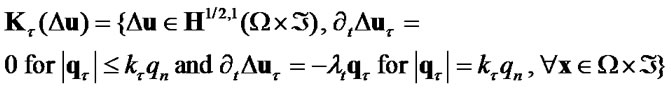
and traction
 ,
,
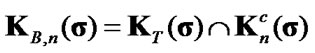 ,
, 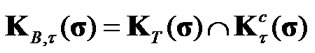
 (28)
(28)
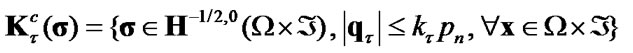
5. Variational Formulation of the Problem with Contact and Friction
In order to formulate an elastodynamic contact problem for body with crack in variational form we consider functional (17) on the set of admissible displacements (27) or admissible traction (28).
In the first case the problem is formulated in the form
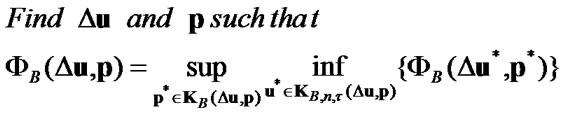 (29)
(29)
In the second case the problem is formulated in the form
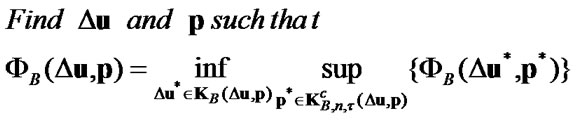 (30)
(30)
In order to formulate an elastodynamic contact problem for body with crack in week form using nonsmooth functionals (23) and (24) we will consider the boundary variational principle in the form
 (31)
(31)
where
 (32)
(32)
In the same way we can consider the complementary functional
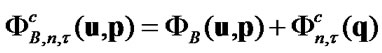 . (33)
. (33)
In this case the problem well be
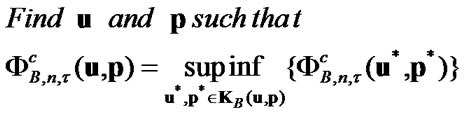 (34)
(34)
Functional in (29) and (30) has a simple form, but the sets of restrictions (27) and (28) are complicate, they contains unilateral constraints (9) and (10). Functionals (30) and (31) are more complicate and nonsmooth, but the set of restrictions (19) is simple, it does not contain unilateral constraints (9) and (10). Which for is more is preferable depend on algorithm used for numerical solution of the problem. It is necessary to mention that the boundary variational principles are usually used with BEM.
6. Dual Variational Formulation and Uzawa’s Optimization Algorithm
We can reformulate above variational problems using duality feature. On these dual formulations are based Uzawa’s nonsmooth optimization algorithms. Let us consider dual formulations and corresponding Uzawa’s algorithms for the problems under consideration.
6.1. Bounadry Variational Principles I
Let us introduce functional
 (35)
(35)
which is considered on the following sets of restrictions
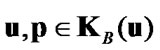 ,
, (36)
(36)
Dual to (31) variational formulation of the contact problem with friction for elastic body with crack has the form
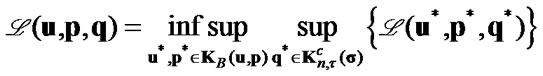 (37)
(37)
The Uzawa’s algorithm includes the following steps:
1) specify an initial value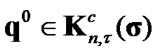 2) solve the minimization problem for known
2) solve the minimization problem for known 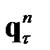 and determine the unknown quantity
and determine the unknown quantity 
 (38)
(38)
3) correct the quantity 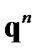 to satisfy the constraints
to satisfy the constraints
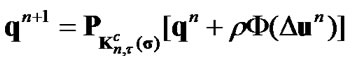 (39)
(39)
where 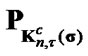 is the operator of projection in
is the operator of projection in  on
on 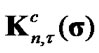 and coefficient
and coefficient  is selected so as to provide the best convergence of the algorithm4) proceed to the next step of iteration.
is selected so as to provide the best convergence of the algorithm4) proceed to the next step of iteration.
6.2. Bounadry Variational Principles II. Let us Introduce Functional
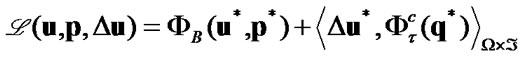 (40)
(40)
Which is considered on the following sets of restrictions
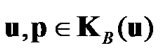 ,
,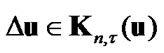 (41)
(41)
Dual to (34) variational formulation of the contact problem with friction for elastic body with crack has the form
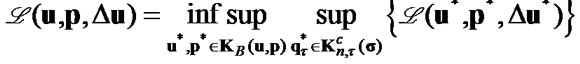 (42)
(42)
The Uzawa’s algorithm includes the following steps:
1) specify an initial value 2) solve the minimization problem for known
2) solve the minimization problem for known 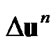
and determine the unknown quantity 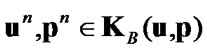
 (43)
(43)
3) correct the quantity 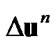 to satisfy the constraints
to satisfy the constraints
 (44)
(44)
where 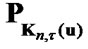 is the operator of projection in
is the operator of projection in 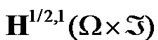 on
on  and coefficient
and coefficient  is selected so as to provide the best convergence of the algorithm4) proceed to the next step of iteration.
is selected so as to provide the best convergence of the algorithm4) proceed to the next step of iteration.
Next we will show how these algorithm applied to some problems of fracture dynamics. More application one can find in the book [3] and review papers [4-6].
7. Harmonic Loading of the Crack in Infinite Elastic Region
Let a load, which changes harmonically in time 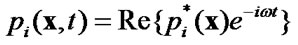 be applied to crack edges. Moreover, we suppose that on the crack edges the unilateral restrictions (9) and friction (10) should be satisfied. In [4,5] it was shown that in this case the contact interaction vector is not harmonic and can not be presented in the form
be applied to crack edges. Moreover, we suppose that on the crack edges the unilateral restrictions (9) and friction (10) should be satisfied. In [4,5] it was shown that in this case the contact interaction vector is not harmonic and can not be presented in the form . Therefore components of the contact forces and displacements discontinuity vectors have to be expanded into Fourier series, which depend on the loading parameter w,
. Therefore components of the contact forces and displacements discontinuity vectors have to be expanded into Fourier series, which depend on the loading parameter w,
 (45)
(45)
where
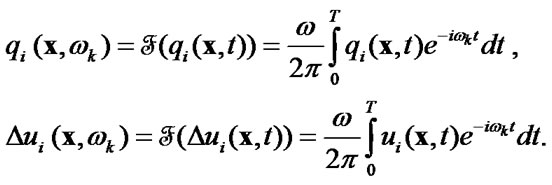 (46)
(46)
Here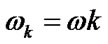 ,
, 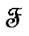 and
and 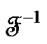 are direct and inverse discrete Fouirer transforms.
are direct and inverse discrete Fouirer transforms.
Fourier coefficients of the components of the contact forces and displacements discontinuity are related by the following integral equations
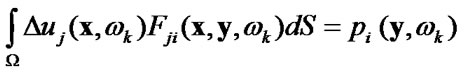 (47)
(47)
Because of the unilateral restrictions (9) and friction (10) the problem becomes a “constructively” nonlinear one. This means that the functionals (20) - (26) define unilateral contact conditions with friction point by point and in fuctional spaces can not be rewritten in frequency domain because of their nonlinearity. As result of all above variational formulation of the problem can not be formulated in frequency domain. Therefore we will use vatiational formulations (32) and (33) in space-time domain and adapt algorithms 1-4 for solution of the problem in the case of harmonic loading with considering unilateral restrictions (9) and friction (10).
Algorithm 1 includes the following steps:
1) specify an initial value 2) calculate Fourier coefficients
2) calculate Fourier coefficients
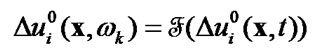 (48)
(48)
3) calculate  substituting known
substituting known 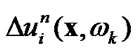 in the internals equation
in the internals equation
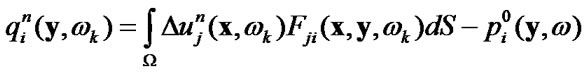 (49)
(49)
4) calculate  using known
using known 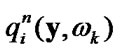
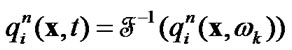 (50)
(50)
5) correct the quantity  to satisfy the constraints
to satisfy the constraints
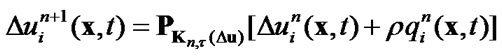 (51)
(51)
where 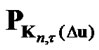 is the operator of projection on the sets
is the operator of projection on the sets 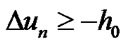 and
and 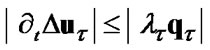 and coefficient
and coefficient  is selected so as to provide the best convergence of the algorithm6) proceed to the next step of iteration.
is selected so as to provide the best convergence of the algorithm6) proceed to the next step of iteration.
Algorithm 2 includes the following steps:
1) specify an initial value 2) calculate Fourier coefficients
2) calculate Fourier coefficients
 (52)
(52)
3) calculate  solving internals equation for known
solving internals equation for known 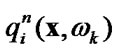
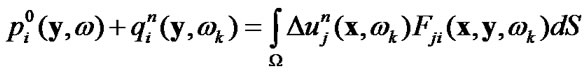 (53)
(53)
4) calculate  using known
using known 
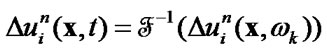 (54)
(54)
5) correct the quantity  to satisfy the constraints
to satisfy the constraints
 (55)
(55)
where 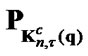 is the operator of projection on the sets
is the operator of projection on the sets 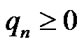 and
and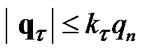 , and coefficient
, and coefficient 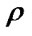 is selected so as to provide the best convergence of the algorithm6) proceed to the next step of iteration.
is selected so as to provide the best convergence of the algorithm6) proceed to the next step of iteration.
Algorithm 3 includes the following steps:
1) specify an initial value 2) calculate Fourier coefficients
2) calculate Fourier coefficients
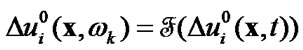 (56)
(56)
3) calculate substituting known
substituting known 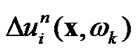 in the internals equation
in the internals equation
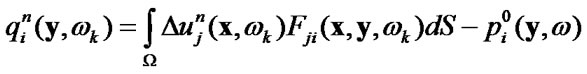 (57)
(57)
4) calculate  using known
using known 
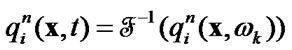 (58)
(58)
5) correct the quantity 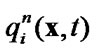 to satisfy the constraints
to satisfy the constraints
 (59)
(59)
where  is the operator of projection on the sets
is the operator of projection on the sets 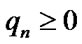 and
and 6) calculate Fourier coefficients
6) calculate Fourier coefficients
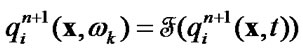 (60)
(60)
7) calculate 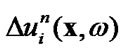 solving internals equation for known
solving internals equation for known 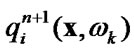
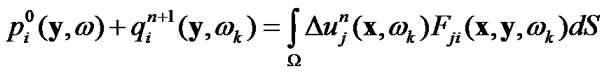 (61)
(61)
8) calculate 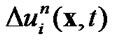 using known
using known 
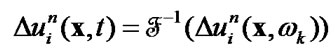 (62)
(62)
9) correct the quantity 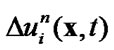 to satisfy the constraints
to satisfy the constraints
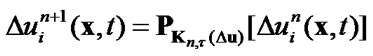 (63)
(63)
where 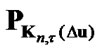 is the operator of projection on the sets
is the operator of projection on the sets 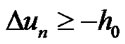 and
and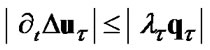 10) proceed to the next step of iteration.
10) proceed to the next step of iteration.
Algorithm 4 includes the following steps:
1) specify an initial value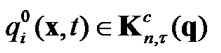 2) calculate Fourier coefficients
2) calculate Fourier coefficients
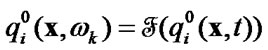 (64)
(64)
3) calculate 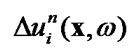 solving internals equation for known
solving internals equation for known 
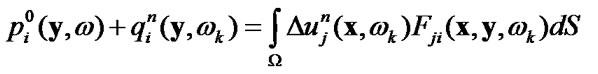 (65)
(65)
4) calculate 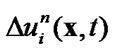 using known
using known 
 (66)
(66)
1) correct the quantity 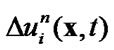 to satisfy the constraints
to satisfy the constraints
 (67)
(67)
where 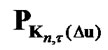 is the operator of projection on the sets
is the operator of projection on the sets  and
and 2) calculate Fourier coefficients
2) calculate Fourier coefficients
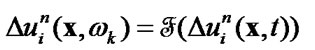 (68)
(68)
3) calculate 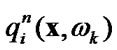 substituting known
substituting known 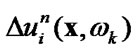 in the internals equation
in the internals equation
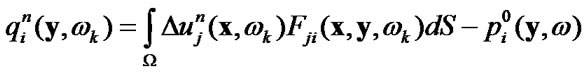 (69)
(69)
4) calculate 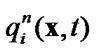 using known
using known 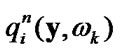
 (70)
(70)
5) correct the quantity 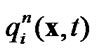 to satisfy the constraints
to satisfy the constraints
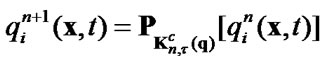 (71)
(71)
where 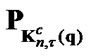 is the operator of projection on the sets
is the operator of projection on the sets  and
and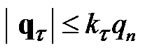 6) proceed to the next step of iteration.
6) proceed to the next step of iteration.
8. Numerical Study of the Algorithms Convergence
Convergence and comparison analyses of the above four algorithms were done for two test problems with the following parameters. The cracked material has the following mechanical characteristics: elastic modulus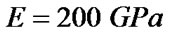 , Poisson’s ratio
, Poisson’s ratio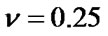 , specific density
, specific density . The finite crack is located in the plane
. The finite crack is located in the plane 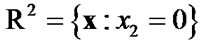 and its surface is described by the Cartesian coordinates
and its surface is described by the Cartesian coordinates
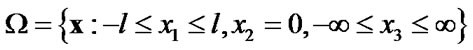 (72)
(72)
8.1. Tension-Compression Wave
Let harmonic tension-compression P-wave with multiple frequencies 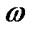 propagates normally to the crack surface. The incident wave is defined by the potential function
propagates normally to the crack surface. The incident wave is defined by the potential function
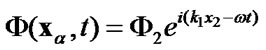 (73)
(73)
where  is the amplitude of the incident wave,
is the amplitude of the incident wave, 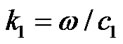 is the wave number,
is the wave number, 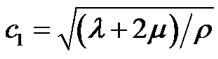 is the velocity of the P-wave,
is the velocity of the P-wave, 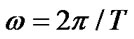 is the frequency,
is the frequency,  is the period of wave propagation,
is the period of wave propagation,  and
and 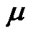 are the Lame constant, and
are the Lame constant, and 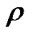 is the density of the material.
is the density of the material.
Following [3-5] we consider two separate problems: the problem for incident waves and the problem for reflection waves. Obviously, in the case under consideration the problem for incident wave is trivial. Therefore we will pay attention to solution of the problem for the reflected waves.
The load on the crack’s edges caused by the incident waves has the form
 ,
, 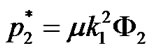 (74)
(74)
In this case the crack surfaces are subjected to the boundary conditions
 for
for 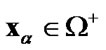 (75)
(75)
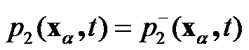 for
for , as it is shown in the Figure 1.
, as it is shown in the Figure 1.
With considering contact interaction at the crack edges, the load vector on the crack edges has the form
 (76)
(76)
where  is a region of close contact, which is varied during time.
is a region of close contact, which is varied during time.
The force of contact interaction at the crack edges
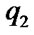 and displacement discontinuity (crack opening)
and displacement discontinuity (crack opening)

Figure 1. Rectangular crack under normal loading.
 should satisfy the contact constrains in the form
should satisfy the contact constrains in the form
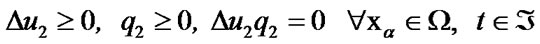 (77)
(77)
Loading  on the crack edges and their opening
on the crack edges and their opening 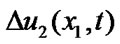 may be expanded into Fourier series
may be expanded into Fourier series
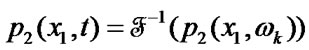 ,
,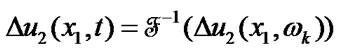
(78)
where
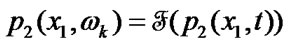 ,
,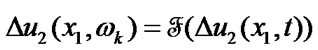
(79)
Fourier series expansions of the displacement discontinuity 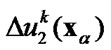 and the traction
and the traction 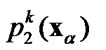 are related by the BIE of the form
are related by the BIE of the form
 ,
,
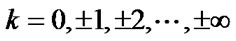 ,
,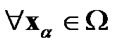 (80)
(80)
The kernels  may be obtained from fundamental solutions for the 2-D steady-state wave equations of elastodynamics, which is well known and may be find in [3,4,20].
may be obtained from fundamental solutions for the 2-D steady-state wave equations of elastodynamics, which is well known and may be find in [3,4,20].
This problem was solved using above four algorithms. Dependence of the algorithms convergence rate on wave number is presented in Figure 2. Analysis of these data shows that all algorithms are convergent and obtained results coincide for all algorithms, but convergence rate is different.
An analysis of results in Figure 2 reveals that Algorithm 3 and Algorithm 4 have significantly faster convergence for all wave numbers.
8.2. Shear H-Wave
Let harmonic shear H-wave with multiple frequencies 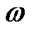 propagates normally to the crack surface. The incident wave is defined by the potential function
propagates normally to the crack surface. The incident wave is defined by the potential function
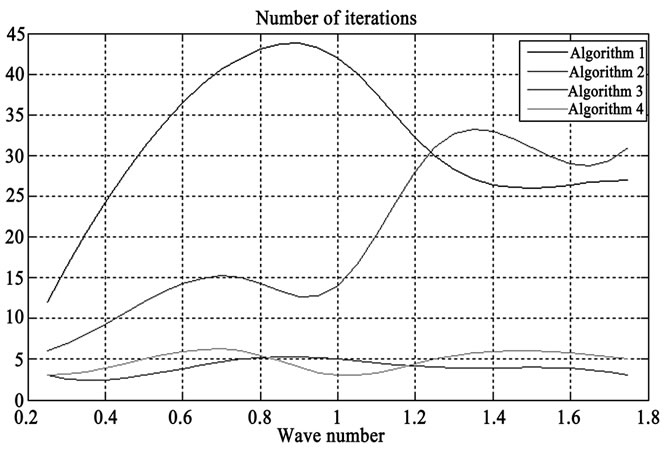
Figure 2. Convergence of the algorithms for different wave numbers.
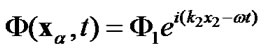 , (81)
, (81)
where  is the amplitude of the incident wave,
is the amplitude of the incident wave, 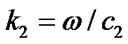 is the wave number,
is the wave number, 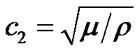 is the velocity of the H-wave,
is the velocity of the H-wave, 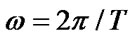 is the frequency.
is the frequency.
Following [3,4] we consider two separate problems: the problem for incident waves and the problem for reflection waves. Obviously, in the case under consideration the problem for incident wave is trivial. Therefore we will pay attention to solution of the problem for the reflected waves.
The load on the crack’s edges caused by the incident waves has the form
 ,
, (82)
(82)
In this case the crack surfaces are subjected to the boundary conditions
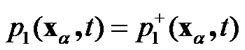 for
for , (83)
, (83)
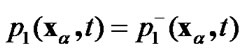 for
for , as it is shown in the Figure 3.
, as it is shown in the Figure 3.
With considering contact interaction at the crack edges, the load vector on the crack edges has the form
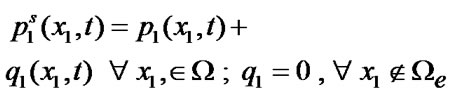 (84)
(84)
where 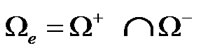 is a region of close contact, which is varied during time.
is a region of close contact, which is varied during time.
The force of contact interaction at the crack edges 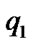 and displacement discontinuity (crack opening)
and displacement discontinuity (crack opening) 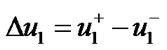 should satisfy the contact constrains in the form
should satisfy the contact constrains in the form
 (85)
(85)
where 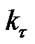 is a friction ration;
is a friction ration; 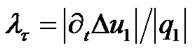 is a coefficient that depend on quality if contact faces,
is a coefficient that depend on quality if contact faces,  is
is

Figure 3. Rectangular crack under shear loading.
a normal contact force, in the problem under consideration it is known before.
Loading  on the crack edges and their opening
on the crack edges and their opening 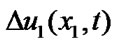 may be expanded into Fourier series
may be expanded into Fourier series


(86)
where
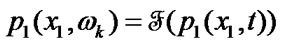 ,
, 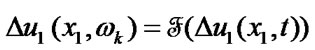
(87)
In Guz and Zozulya 2001, 2002 it was shown that Fourier series expansions of the displacement discontinuity 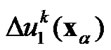 and the traction
and the traction 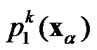 are related by the BIE of the form
are related by the BIE of the form
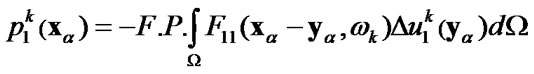 ,
,
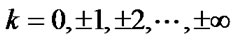 ,
,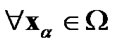 (88)
(88)
The kernels 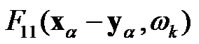 may be obtained from fundamental solutions for the 2-D steady-state wave equations of elastodynamics, which is well known and may be find in [3,4,20].
may be obtained from fundamental solutions for the 2-D steady-state wave equations of elastodynamics, which is well known and may be find in [3,4,20].
This problem was solved using above four algorithms. Dependence of the algorithms convergence rate on wave number is presented in Figure 4.
Analysis of these data shows that all algorithms are convergent and obtained results coincide for all algorithms and convergence rate is not differing significantly. Our calculations show that all four above algorithms are convergent in elastodynamic problems with contact and with friction for infinite cracked body. It is important to mention that Algorithm 3 and Algorithm 4 have significantly faster convergence in both cases frictionless contact problem and problem with friction.
9. Conclusions
This paper present various variational formulations of elastodynamic problem for body with crack with considering possibility for unilateral crack faces contact interaction and friction. Variational formutations is based on boundary variational principle and on fundamental solu-
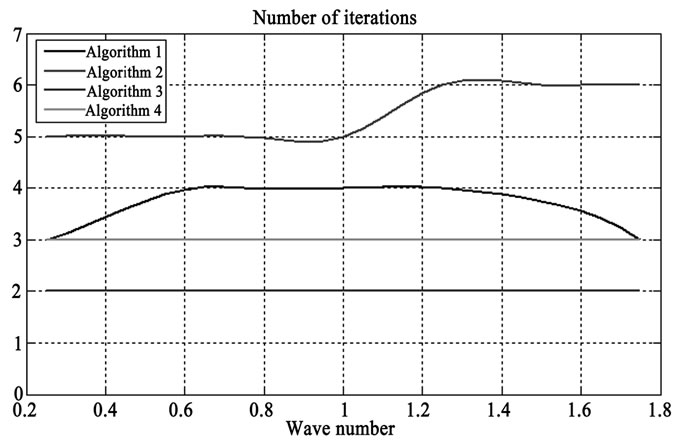
Figure 4. Convergence of the algorithms for different wave numbers.
tions. Nonsmooth functionals that correspond to unilareral frictional contact conditions are constructed. Iterative algorithms of the Uzawa’s type that are based on projection on the set of unilateral restrictions and friction are proposed. It was shown that in the case if varational formulation is based on principles formulated only for boundary the BIE method may be used. The case of the crack in infinite elastic media is considered in more details and four new algorithms are proposed. To study convergence of the proposed algorithms two problems related to the crack faces contact interaction under action of the harmonic tension-compression and shear waves have been solved numerically using BIE method.
10. References
[1] V. V. Zozulya, “On Solvability of the Dynamic Problems in Theory of Cracks with Contact, Friction and Sliding Domains,” Doklady Akademii Nauk Ukrainskoy SSR, Vol. 3, 1990, pp. 53-55, in Russian.
[2] V. V. Zozulya, “Method of Boundary Functionals in Contact Problems of Dynamics of Bodies with Cracks,” Doklady Akademii Nauk Ukraine, Vol. 2, 1992, pp. 38-44, in Russian.
[3] A. N. Guz and V. V. Zozulya, “Brittle Fracture of Constructive Materials under Dynamic Loading,” Naukova Dumka, Kiev, 1993, in Russian.
[4] A. N. Guz and V. V. Zozulya, “Fracture Dynamics with Allowance for a Crack Edges Contact Interaction,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 2, No. 3, 2001, pp. 173-233.
[5] A. N. Guz and V. V. Zozulya, “Elastodynamic Unilateral Contact Problems with Friction for Bodies with Cracks,” International Applied Mechanics, Vol. 38, No. 8, 2002, pp. 895-932.
[6] V. V. Zozulya and P. I. Gonzalez-Chi, “Dynamic Fracture Mechanics with Crack Edges Contact Interaction,” Engineering Analysis with Boundary Elements, Vol. 24, No. 9, 2000, pp. 643-659.
[7] V. V. Zozulya, “Mathematical Investigation of Nonsmooth Optimization Algorithm in Elastodynamic Contact Problems with Friction for Bodies with Cracks,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 4, No. 4, 2003, pp. 405-422.
[8] C. Polizzotto, “A Boundary Min – Max Principle as a Tool for Boundary Element Formulations,” Engineering Analysis with Boundary Elements, Vol. 8, No. 2, 1991, pp. 89-93.
[9] J. Cea, “Optimization,” Teorie et Algorithms, Dunod, Paris, 1971, in French.
[10] I. Ekeland and R. Temam, “Convex Analysis and Variational Problems,” North-Holland, 1975.
[11] V. V. Zozulya, “Variational Principles and Algorithms in Contact Problem with Friction,” In: N. Mastorakis, V. Mladenov, B. Suter and L. J. Wang, Eds., Advances in Scientific Computing, Computational Intelligence and Applications, WSES Press, Danvers, 2001(a), pp. 181- 186.
[12]V. V. Zozulya, “Variational Principles and Algorithms in Elastodynamic Contact Problem with Friction,” In: S. N. Atluri, M. Nishioka and M. Kikuchi, Eds., Advances in Computational and Engineering Sciences, Technology Science Press, Puerto Vallarta, Mexico, 2001(b).
[13] V. V. Zozulya and O. V. Menshykov, “Use of the Constrained Optimization Algorithms in Some Problems of Fracture Mechanics,” Optimization and Engineering, Vol. 4, No. 4, 2003, pp. 365-384.
[14] V. V. Zozulya and M. V. Menshykova, “Study of Iterative Algorithms for Solution of Dynamic Contact Problems for Elastic Cracked Bodies,” International Applied Mechanics, Vol. 38, No. 5, 2002, pp. 573-577.
[15] V. V. Zozulya, “Fracture Dynamics with Allowance for Crack Edge Contact Interaction,” In: C. Constanda, P. Schiavone and A. Mioduchowski, Integral Methods in Science and Engineering, Birkhauser, Boston, 2002, pp. 257-262.
[16] V. V. Zozulya and P. Rivera, “Boundary Integral Equations and Problem of Existence in Contact Problems with Friction,” Journal of the Chinese Institute of Engineers, Vol. 3, No. 3, 2000, pp. 313-320.
[17] N. Kikuchi and J. T. Oden, “Contact Problems in Elasticity,” SIAM Publications, Philadephia, 1987.
[18] P. D. Panagiotopoulos, “Inequality Problems in Mechanics and Applications, Convex and Non Convex Energy Functions,” Birkhauser, Stuttgart, 1985.
[19] A. C. Eringen and E. S. Suhubi, “Elastodynamics, Vol. 2. Linear Theory,” Academic Press, New York, 1975.
[20] J. Dominguez, “Boundary Elements in Dynamics,” Computational and Mechanical Publishing, Southempton, 1993.

