Energy and Power Engineering, 2013, 5, 902-905
doi:10.4236/epe.2013.54B173 Published Online July 2013 (http://www.scirp.org/journal/epe)
The Research of Transmission Network Planning Based
on System’s Self-organized Criticality
Zheng-yu Shu, Chang-hong Deng, Wen-tao Huang, Yi-xuan Weng
Wuhan University, Hubei, Wuhan, China
Received March, 2013
ABSTRACT
This paper presents a new line importance degree evaluation index for the propagation of cascading failures, which is
used to quantify transmission lines for cascade spread. And propose an improved capital matching model, according to
the results of the evaluation, to enhanced robustness of the power system. The simulation results proved that in the case
of the same system, the new model can inhibit cascade spread, reduce the probability of large-scale blackouts.
Keywords: Transmission Line Assessment, Self-organized Criticality, Cascade, Load Di stribut i on
1. Introduction
The power system is a typical extended dissipative
system, such a system will evolve to reach self-organized
criticality[1], its important feature is the scale of the fault
occurs in the system and the corresponding probability
distribution follows the power law characteristic. This
phenomenon also been verified in many domestic and
international large-scale grid statistics [2-5].
In response to this phenomenon, the researchers analyzed,
according to the cascading failures model, the self-
organized critical characteristics in the power grid. The
results show, for the power system, in addition to the
network topology, the load rate factor of the system for
grid characteristics of self-organized criticality is
particularly important. Reference [6, 7], respectively, for
the system average load rate and load rate heterogeneity
characteristics analysis, where in [6] proposed the
concept of a uniform load distribution, assuming that the
active power flow of each line of the system and the
corresponding transmission limit into a uniform rate.
And pointed out that the higher the rate of the average
load of the system, the closer to self-organized criticality,
the higher the chance of large-scale cascade. In contrast,
if the load rate is lower, the s ystem occurs cascade chance
also lower. Reference [7], which based on entropy theory,
analysis the relationship between load rate heterogeneity
and the self-organized criticality of the power grid. The
simulation results prove, the distribution of the entropy
has an important impact on the scale of the cumulative
probability of blackouts, with the trend of an increase in
entropy, the power grid from non-self- organized critical
state transition to self-organized criticality.
The above studies have indicated that the system load
rate will directly affect the power system cascade
probability and its scale. However, in reality, the capital
of transmission lines as well as transmission limit of lines,
can not raise unlimited. Therefore, how to plan the grid
investment makes the system’s load rate distribution
optimal are the main issues that need to be addressed. In
view of this, we propose a new evaluation index to
quantify the importance of transmission lines, and based
on the assessment results to optimize investment, In
order to improve the robustness of grids, reduce the
probability of large-scale failure.
2. SOC-PF Model of Self-organized
Criticality
In this paper, we use SOC-PF model for system’s self-
organized criticality simulation [7]. Its Concrete steps as
described below:
1) Loading the parameters for flow calculatio n and the
transmission limit of each line.
2) Increase the load of a node randomly and recalcu-
late the power flow of the grid.
3) Checking whether there is flow of lines over the
transmission limit (the capital of the line), and if so, go to
step 4; otherwise return to step 2.
4) Cut off the line which is beyond transmission li mit,
and determine whether there is disconnected from the
neighboring lines of hidden faults caused.
5) If the system has been cut into two or more silos,
first processing Islands problem. If no silos problem,
judged whether the load is cut, if there is go to step 6,
and if not, to modify the network topology, the process

Z.-Y. SHU ET AL. 903
returns to step 2.
6) Statistics the loss load of blackouts, the end.
3. Match Model Based on Spread
Betweenness
3.1. Spread Betweenness
Evaluate the importance of the transmission lines from
the direction of the network topology is complex network
theory’s application hot spots in the power system.
Mainly from a static perspective of the components for
the overall performance of the system, recognize the
weak links in the grid. This identification results similar
to the static N-1 calibration of the power system.
However, the cascading failure of the power network is a
dynamic process. When the flow of the grid has changed,
such static assessments can not be fully reactive the de-
gree of importance of a bus or line[8-11]. So we propose
a new assessment index to quantify transmission line’s
impor- tance from cascade spread angle. The formula of
cascade spread betweenness (hereinafter referred to as
spread be- tweenness) is as follow:
()( )
mn
Gijij mn
eG
Le Le



 (4)
In formula (4), is spread betweenness of
transmission line ij , its value equal the sum of the
generated-load in the other branches when ij has been
cut from the system. n is the generated-load on
transmission line mn , when ij has been cut from the
system, its formula as below equation(5):
()
Gij
Le
(
ij m
Le
e
e
e
)
e
() (T
ijmnmnmn ijij
Ley XZX ) (5)
In this formula, mn is the admittance of transmission
line mn, ij
y
e
Z
is impedance matrix of the system after
mn has been cut off. ij
e
X
is a N-dimensional column
vector, that the I-th Element equals 1 and the J-th
Element equals -1. ij
X
could be described as follow:


01 1
ij
X 0
(6)
The physical meaning of ()
ij mn
Le

is the electric
current generated by ij ’s fault, when unit current
injected from node i and flow out from node j.
is sum of all the generated-current caused by ’s fault.
e()
Gij
Le
ij
e
3.2. Improved Match Model
Seen by the physical meaning of the spre ad betweenness,
the more disturbances transfer to the grid as if the higher
spread betweenness line failed. So, in the fault spread
process, we should try to avoid higher spread between-
ness transmission lines arise overload fault[12-15].
Therefore, in this paper, we propose a new capital match
model in order to optimize the redundancy capacity
expressed as:
max ,0
()
(1 )
()
Gij
ij ij
G
avg ij
Le
F
F
Le

 (7)
max
ij
F

and ,0ij
F
,
ady respectively, are the transmission limit as well as ste-state flow of transmission line ij e.

is the tolerate coefficient for the system, that re
the capital redundancy of the transmission lines in the
system. ()
G
avg ij
Le is the average value of spread be-
tweennessmission lines in the system :
present
s of tran
1
GG
() ()
ij
avg ij ij
eG
Le Le
m
 (8)
4. Simulation
ed Criticality of Electric Power
This using
experimental result of above chart we can find
th
rge scale of fault is big. The fault
si
ng model had a better effect in inhibiting
fa
distribution.
4.1. Self-organiz
Network in Improved Matching Model
paper sets up load factor of transmission line
traditional load-capacity model and improved matching
model under the example of IEEE118, IEEE145 and
IEEE300 nodes. It did repeated test for 500 times to
observe fault spreading action of power grid based on the
SOC-PF model introduced in the quarter 1. The purpose
of this test is to research the relationship between the
probability of fault and the size of fault under different
conditions of power grid. The vertical axis of the chart
represents size of fault and horizontal axis represents
probability of fault. The frame of axes uses logarithmic
scale.
From
at the method of matching load rate of each line using
the traditional load-capacity model can do nothing to
prevent the happening of large scale fault of grid. When
the redundant capacity of the power system is limited,
the power system is easy to becoming self-organized
criticality. The ML curve is as shown in Figure 1, when
the tolerance coefficient of the three examples is smaller
than 1.5, 1.3 and 1.2.
The probability of la
ze and the fault probability are obeying the power
distribution. The slope in the 3 examples is -0.82, -1.12
and -0.96.
The matchi
ult diffusion comparing with the traditional model. As
shown in the PM curve of Figure 1, we let tolerance
coefficient of the three examples remain unchanged. We
adjusted the load factor of each line using improved
model that it can be found huge change in the above
curve. The probability of large scale fau lt drops when the
system redundancy of three examples is the same. When
the tolerance coefficient is 1.5 1.3 1.2, the curve in the
logarithmic coordinate system is not straight line. The
fault size and fault probability is obeying logarithmic
configuration. Improved capital match model can be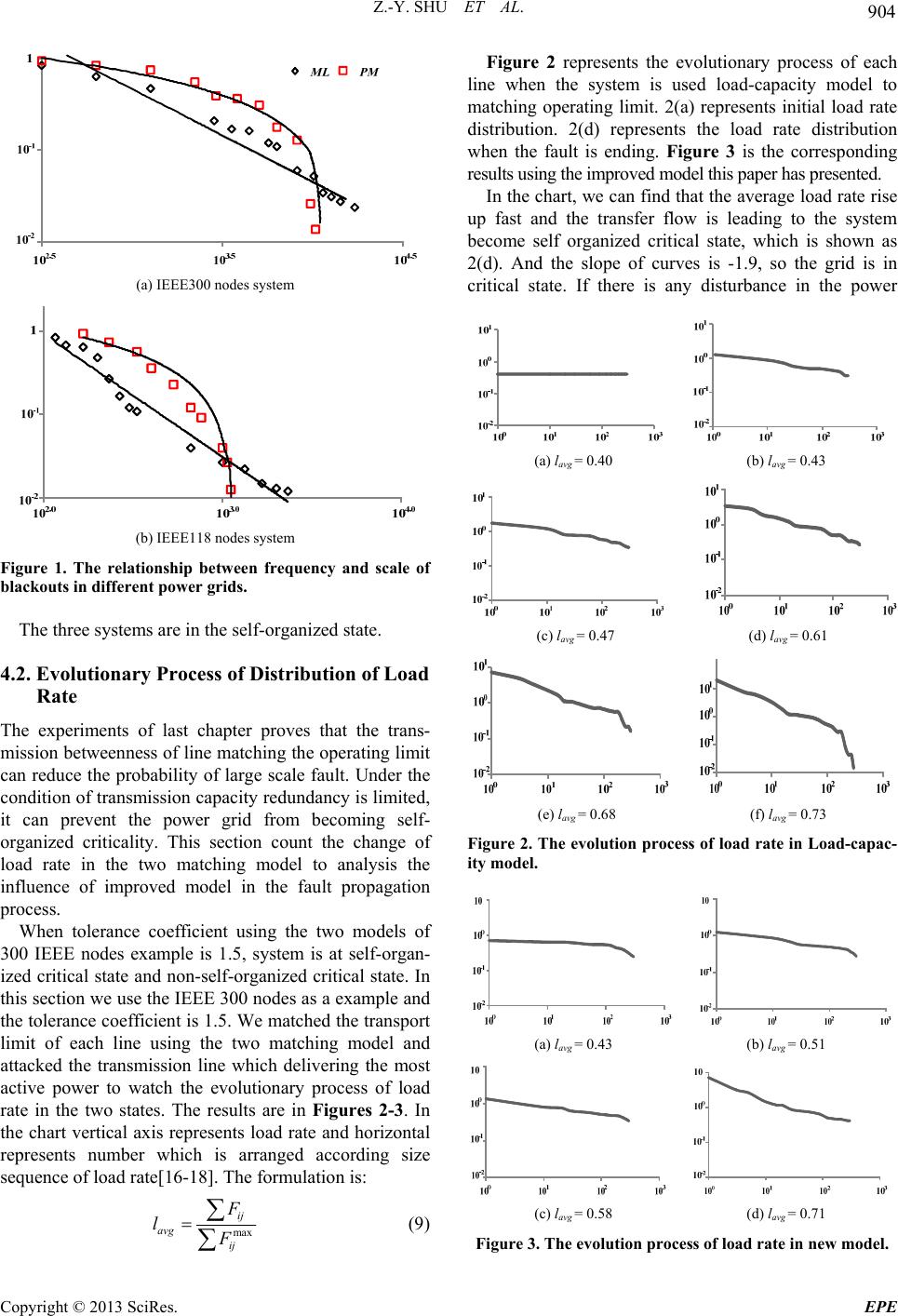

Z.-Y. SHU ET AL. 904
(a) IEEE300 nodes system
(b) IEEE118 nodes system
Figure 1. The relationship between frequency and scale of
blackouts in differ
-organized state.
4.oad
Rate
missiweenness of line matching the operating limit
nodes example is 1.5, system is at self-organ-
iz
ent power grids.
The three systems are in the self
2. Evolutionary Process of Distribution of L
The experiments of last chapter proves that the trans-
on bet
can reduce the probability of large scale fault. Under the
condition of transmission capacity red undancy is limited,
it can prevent the power grid from becoming self-
organized criticality. This section count the change of
load rate in the two matching model to analysis the
influence of improved model in the fault propagation
process.
When tolerance coefficient using the two models of
300 IEEE
ed critical state and non-self-organized critical state. In
this section we use the IEEE 300 nodes as a example and
the tolerance coefficient is 1.5. We matched the transp ort
limit of each line using the two matching model and
attacked the transmission line which delivering the most
active power to watch the evolutionary process of load
rate in the two states. The results are in Figures 2-3. In
the chart vertical axis represents load rate and horizontal
represents number which is arranged according size
sequence of load rate[ 16-18]. The formulation is:
max
ij
avg
ij
F
l
F
 (9)
Figure 2 represents the evolutionary process of each
line when the system is used l
matching operating limit. 2(a) represents initial load rate
di
2(
oad-capacity model to
stribution. 2(d) represents the load rate distribution
when the fault is ending. Figure 3 is the corresponding
results using the improved model this paper has presented.
In the chart, we can find that the average load rate rise
up fast and the transfer flow is leading to the system
become self organized critical state, which is shown as
d). And the slope of curves is -1.9, so the grid is in
critical state. If there is any disturbance in the power
(a) lavg = 0.40 (b) lavg = 0.43
(c) lavg = 0.47 (d) lavg = 0.61
(e) lavg = 0.68 (f) lavg = 0.73
Figure 2. The evolution proces of load rate in Load-capac-
ity model.
s
(a) lavg = 0.43 (b) lavg = 0.51
(c) lavg = 0.58 (d) lavg = 0.71
Figure 3. The evolution process of load rate in new model.

Z.-Y. SHU ET AL.
905
system, it can leads to large scale of fault in the power
system and the loss of load is rising which is shown as (e)
and (f). If it used the improved model in this paper has
presented we can find that it has a better effect
suppress the fluctuation of load. The rising extent of
average load rate is small. The load distribution has a
rising te0.7,
I
planning process, the distribution of load
rate of the system has been optimized. SOC-PF m
sults has proved that this new model
omplex Power System,” Power
System Technology, Vol. 5, No. 10, 2006, pp. 18-22.
[3] Q. Y. Xie, C.et al., “Evalua
Method for No Grid Based on the
lnerability Assessment Based on Complex
ode
uence of
G. Z. Wang, L. H. Cao and L. J. Ding, “An
Zhao, “Discussion on Several
ng and B.-J. Kim, “A High-robustness and
in
Identification Model for Self-oganized Criticality of
Power Grids Based on Power Flow Entropy,” Automation
of Electric Power Systems, Vol. 7, No. 35, 2011, pp. 1-8.
[8] H. Q. Deng, X. Ai and L.
ndency and the slope is in the range of [- 0.1].
Problems of Self-Organized Criticality of Blackout,”
Power System Technology, Vol. 31, No. 8, 2007, pp.
42-48.
[9] H. J. Sun, H. Zhao and J. J. Wu. “A Robust Matching
t can prevent the system from becoming self-organized
critical state.
5. Conclusions
The load rate of power system has a direct impact on the
self-organized criticality. For this reason this paper,
based on the evaluation result (spread betweenness),
propose a new capital match model. In this proved model,
through the rational allocation of transmission capacity
of the grid in
Low
odel-
based simulation re
could prevent the system involved to the self-organized
critical state, reduce the probability of occurrence of
large-scale power outages.
REFERENCES
[1] J. Yi, X. X. Zhou and Y. N. Xiao, “Analysis on Power
System Self-Organized Criticality and Its Simulation
Model,” Power System Technology, Vol. 32, No. 3, 2008,
pp. 7-12.
[2] R.-R. Li, Y. Zhang and Q. Y. Jiang, “Risk Assessment for
Cascading Failures of C
H. Deng, H. S. Zhao,
de Importance of Powertion
Weighted Network Model,” Automation of Electric
Power Systems, Vol. 33, No. 4, 2009, pp. 21-24.
[4] X. P. Ni, S. W. Mei and X. M. Zhang, “Transmission
Lines’ Vu
Network Theory,” Automation of Electric Power Systems,
Vol. 32, No. 4, 2008, pp. 1-4.
[5] M. Ding and P. P. Han, “Small World Topological Ml
Based Vulnerability Assessment to Large Scale Power
Grid,” Proceedings of the CSEE, Vol. 25, 2005, pp.
118-122.
[6] Q. Yu, N. Cao and J. B. Guo, “Analysis on Infl
Load Rate on Power System Self-organized Criticality,”
Automation of Electric Power Systems, Vol. 36, No. 1,
2012, pp. 24-30.
[7] Y. J. Cao,
Model of Capacity to Defense Cascading Failure on
Complex Networks,” Physical Review A, Vol. 20, 2008,
pp. 6431-6435.
[10] B. Wa
-cost Model for Cascading
Failures, Europhysics Letters, Vol. 78, 2007, 48001.
doi:10.1209/0295-5075/78/48001
[11] X. P. Ni, X. M. Zhang and S. W. Mei, “Generator
entrality Measure for
le Lines in Power Grid Based on Complex
ontrol and Defense in Complex
Proceedings of the
x
erability Assessment of
1.
Tripping Strategy Based on Complex Network Theory,”
Power System Technology, Vol. 9, No. 34, 2010, pp.
33-38．
[12] P. Hines and S. Blumsack, “A C
Electrical Networks,” Hawaii International Conference on
System Sciences, 2008.
[13] Y. J. Cao, X. G. Chen and K. Sun, “Identincation of
Vulnerab
Network Theory,” Automation of Electric Power Systems,
Vol. 26, No. 12, 2006, pp. 27-31.
[14] A. E. Motter, “Cascade C
Networks,” Physical Review E, Vol. 93, 2008, 098701.
[15] L. Xu, X. L. Wang and X. F. Wang, “Cascading Failure
Mechanism in Power Grid Based on Electric
Betweenness and Active Defense,”
CSEE, Vol. 13, 2010, pp. 61-65.
[16] Ae Motter, “Cascade-based Attacks on Comple
Networks,” Physical Review E, Vol. 66, 2002, pp.
065102.
[17] W. Kai, B.-H. Zhang and Z. Zhang, et al., “An Electrical
Betweenness Approach for Vuln
Power Grids Considering the Capacity of Generators and
Load,” Science Direct Physica A, Vol. 390, 2011, pp.
4692-470
[18] J.-F. Zheng, Z.-Y. Gao, X.-M. Zhao, “Modeling
Cascading Failures in Congested Complex Networks,”
Science Direct Physica A., Vol. 385, 2007, pp. 700-706.