Paper Menu >>
Journal Menu >>
 Journal of Information Security, 2011, 2, 8-27 doi:10.4236/jis.2011.21002 Published Online January 2011 (http://www.SciRP.org/journal/jis) Copyright © 2011 SciRes. JIS A Novel Attack Graph Posterior Inference Model Based on Bayesian Network Shaojun Zhang1, Shanshan Song2 1School of Information Security Engineering, Shanghai Jiao Tong University, Shanghai, China 2Information Technology Department, Guotai Junan Futures Co., Ltd, Shanghai, China E-mail: {leony7888, songss1985 }@hotmail.com Received January 5, 2011; revised January 17, 2011; accepted January 18, 2011 Abstract Network attack graphs are originally used to evaluate what the worst security state is when a concerned net- work is under attack. Combined with intrusion evidence such like IDS alerts, attack graphs can be further used to perform security state posterior inference (i.e. inference based on observation experience). In this area, Bayesian network is an ideal mathematic tool, however it can not be directly applied for the following three reasons: 1) in a network attack graph, there may exist directed cycles which are never permitted in a Bayesian network, 2) there may exist temporal partial ordering relations among intrusion evidence that can- not be easily modeled in a Bayesian network, and 3) just one Bayesian network cannot be used to infer both the current and the future security state of a network. In this work, we improve an approximate Bayesian posterior inference algorithm–the likelihood-weighting algorithm to resolve the above obstacles. We give out all the pseudocodes of the algorithm and use several examples to demonstrate its benefit. Based on this, we further propose a network security assessment and enhancement method along with a small network scenario to exemplify its usage. Keywords: Network Security, Attack Graph, Posterior Inference, Bayesian Network, Likelihood-Weighting 1. Introduction Network attack graphs [1-5] are widely used as a good tool to analyze network security state in comprehensive consideration of exploits, vulnerabilities, privileges, net- work connectivity, etc. Originally, they are built to tell what the worst scenarios are when a network is under attack. But later, it is found that security alerts can be mapped to them [6-8] and along with these observed intrusion evidence, attack graphs can also be used to as- sess the security state of a concerned network dynami- cally. In this area, probabilistic approaches have been pro- posed to perform such analysis. In [9], a method which reasons about complementary intrusion evidence is pre- sented. According to the method, security alerts gener- ated by intrusion detection systems (IDSs) as well as reports generated by system monitoring tools can be in- tegrated into Bayesian networks. And prior conditional probability values which denote the success rate of the corresponding attacks can be assigned to each of the evi- dence nodes. By doing this, uncertain or unknown intru- sion evidence can be reasoned about based on verified evidence. Although quite useful in reasoning observed intrusion evidence, this method cannot tell people what attack will be executed next and with what probability. In [10], HCPN (Hidden Colored Petri-Net) is used to depict the relationship among different steps carried out by an intruder and model intrusion actions and intrusion evidence together. The initial state of HCPN attack graph is determined by an initial probability distribution. And empirical formulas are defined to reevaluate its state af- ter receiving each alert from the sensors (most com- monly are IDSs). This method runs quite well in predict- ing what the next intrusion actions are. However, at re- evaluating the probabilities of the graph nodes according to the alerts, the method only updates probabilities of the successor nodes of an assumed action node, which obvi- ously contravenes our intuition that in most inference algorithms there must be backward belief propagation (i.e. probabilities of the predecessor nodes should also be updated). To overcome these flaws, we firstly thought about ex- tending the Bayesian network into a general attack graph  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 9 definition to integrally model intrusion resources, actions and evidence. By exploiting Bayesian network’s embed- ded posterior inference capability, it can not be plainer to perform attack graph-based posterior inference [11]. However, soon we found that things were not so easy. There are at least three main differences between an at- tack graph and a Bayesian network which obstruct this way: In a Bayesian network, no directed cycles are al- lowed. However, in a network attack graph, this re- striction is not appropriate since people always want to depict potential intrusion paths succinctly. In a Bayesian network, there can not be any partial ordering relations among evidence nodes. However, we can often observe temporal partial ordering re- lations among intrusion evidence (e.g. when an ips- weep is observed before a portscan), which may in- dicate that some exploits happen before some oth- ers. At performing attack graph-based posterior infer- ence, two questions are most often raised: 1) what is the current state of a network, and 2) what is the future state of it. Essentially this means one set of observed intrusion evidence should be used to infer two temporally different states. In Bayesian infer- ence, this demands two prior conditional probabi- listic distribution, one for current state inference and one for future state inference. Although we think it feasible to define the later one (For exam- ple we say an exploit will happen in probability 0.8 if an attacker was given enough time), it is really a disaster to define the former one (how to assess the exploit probability when the attacker has got two hours). These obstacles almost made us give up Bayesian po- sterior inference. But fortunately we find a good way to overcome them—we manage to improve the likelihood- weighting algorithm (an approximate Bayesian inference algorithm) into a novel attack graph-based posterior in- ference algorithm. And based on this, we find a method to quantitively assess the overall security level of a con- cerned network and identify the most cost-effective se- curity measures to enhance it. The rest of this paper is organized as follows. Section 2 depicts the aforementioned posterior inference prob- lems in details. Section 3 introduces the underlying for- malized attack graph definition. Section 4 describes our improved likelihood-weighting algorithm and Section 5 gives out several examples for benefit testification. Sec- tion 6 presents our security assessment and enhancement method and Section 7 gives out an example to exemplify it. The last section concludes the paper. 2. The Primal Motives 2.1. Directed Cycles Various models and methods have been proposed to re- present multi-step network attacks and generate network attack graphs automatically. These models and methods can be roughly divided into two categories: security state enumeration and vulnerability/exploit dependency. Com- paratively, the later one is more popular since it exhaus- tively and succinctly depicts the interdependency of se- curity elements such as privilege, trust, vulnerability, ex- ploit, network connectivity, etc. Representatives of this category include the approaches proposed in [2-5]. In this category, although some approaches promise that they only generate attack graphs without directed cycles, we cannot assume that all of them are generating DAG (Di- rected Acyclic Graph). Here is an example to demonstrate that directed cycles sometime are useful since we want to depict the intrusion paths succinctly. Assume there are three hosts on a small network which is illustrated in Figure 1. Host Master has a certain vulnerability that can be exploited by the other two hosts to gain its USER privilege. On the other hand, the USER accounts on Master are mapped to a ROOT account on the other two hosts. We can imagine that a succinct network attack graph for this network is like the one shown in Figure 2. In Figure 2 we adopt a graph notation widely used in Petri-Net. Circle s1, s2 and s3 respectively denote that the attacker has got ROOT privilege on Slave1, ROOT privilege on Slave2 and USER privilege on Master. Line a1 and a2 denote the attacker exploits the vulnerability of Master respectively from Slave1 and Slave2. Obviously, in this attack graph, there exist directed cycles. 2.2. Evidence Partial Ordering Relations In a Bayesian network, there cannot be any partial or- dering relations among observed evidence. However, at performing security posterior inference, temporal partial ordering relations among evidence nodes often provide us important cues. Figure 3 illustrates an example which demonstrates the benefit of analyzing temporal partial ordering relations among intrusion evidence. In Figure 3, we assume that the attacker initially oc- cupies resource s1 and her goal is to occupy s6. The at- tacker can use exploit a1~a6 to perform intrusion. How- ever, exploit a1 and a4 will trigger alert o1, exploit a2 and a3 will trigger alert o2 and a5 and a6 will trigger alert o3. Finally, during the intrusion, an evidence sequence o2→ o1→o3 is observed. Analysis: To achieve her goal, the attacker can choose  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 10 Figure 1. A small network environment. a 2 a 1 s 1 s 3 s 2 Figure 2. Attack graph for the network. s 4 s 1 s 2 s 3 a 1 o 1 o 2 s 5 a 2 a 3 a 4 s 6 a 5 a 6 o 3 Figure 3. A simple network attack graph. two intrusion paths: α. s1→a1→s2→a3→s4→a5→s6 β. s1→a2→s3→a4→s5→a6→s6 If we neglect all temporal partial ordering relations, then the three evidence nodes are set to True. And since the attack graph is symmetrical (notice there is no ordering relations between evidence nodes), using Bayesian pos- terior inference we can find that both intrusion paths can be chosen by the attacker. However, if we do consider temporal partial ordering relations, we can infer that only intrusion path β is chosen by the attacker, since execut- ing intrusion path α will violate the temporal partial or- dering relation o2→o1. 2.3. Posterior Inference for Multi-State As we mentioned before, two questions are most often raised at performing attack graph-based posterior infer- ence: 1) what is the current state of a network, and 2) what is the future state of it. In Bayesian inference, this means two different prior conditional probabilistic dis- tribution should be assigned—one for current state in- ference and one for future state inference. If we say the assignment for the later one is tough but still practical, then it is almost infeasible to define the former one. People may argue that Hidden Markov Model [12] or Generalized Hidden Semi-Markov Models [13] can be used to resolve this problem. But in HMM or GHSMMs, a key concept is the time instants associated with state changes. This concept is quite natural in technique areas such as speech signal processing. However in security analysis we cannot just fix a time slot for an attacker to perform actions. And even we do constrainedly figure out this slot, we still face the problem of how to define the probability of an action when the attacker is given one time slot. Under this understanding, we decide to stick to Baye- sian inference and seek if we can use one prior condi- tional probabilistic distribution with one set of observed intrusion evidence to infer two temporally different secu- rity states. Eventually we successfully resolve this chal- lenge by inventing a sample reprocessing method called transientization which will be introduced in Section 4. 3. The Underlying Model In this section, we propose a formalized network attack graph definition as the basis for attack graph-based secu- rity posterior inference. In the early days of Internet, network attacks are often performed to demonstrate the personal skills of the at- tacker. They were limited to a small number of known methods such as cracking the password and exploiting the operating system vulnerabilities. But lately attacks have evolved into complex procedures which may com- prise several interrelated intrusion actions. Execution of these actions incrementally changes the security state of the network, making the attacker take over more and more resources (and most commonly during the intrusion procedure the attacker will not give up resources she has already got [3]) and eventually achieve her goal. Fortu- nately, security devices such as IDSs will send alerts if there is an attack. Then administrators can use them to assess the real state of the network and take proper measures to compensate. A network attack graph depicts the above three com- ponents (network resource, intrusion action and intrusion evidence) and their causal relationship. In most cases, it can exhaustively and succinctly comprises all of the po- tential intrusion paths. Based on the above analysis, an attack graph can formally be defined as: Definition 1. An attack graph is a 10-tuple directed graph 0 ,,,,,,,,,AGSSGA OE , where: 1, , is Ssi N is a finite set of resource state nodes. The value of each node variable i s can be either True or False, denoting if a resource has been taken over by the attacker; 0 SS is a subset of S representing resources the attacker may initially occupy. Graphically it is the root nodes of AG;  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 11 GS is a subset of S representing attack goals; 1, , ia A ai N is a finite set of intrusion ac- tion nodes. The value of each node variable i a can be either True or False, denoting whether an intrusion action has been conducted by the at- tacker; 1, , io Ooi N is a finite set of intrusion evidence nodes. The value of each node variable i o can be either True or False, denoting whether the evidence has been observed. Considering that in most occasions intrusion evidence will be pre- processed (e.g. fused) by the low-layer sensors so that their observation numbers are often distorted, here we only consider whether a kind of evidence has been observed, discarding its concrete observa- tion number; 123 EEEE is a finite set of edges which link nodes together. 1 ESA is a set of edges which denote actions can only be conducted given that all the prerequisite resources are taken over by the attacker; 2 EAS is a set of edges which denote actions may consequently let the attacker take over some other resources and 3 EAO is a set of edges which denote actions may trigger cer- tain intrusion evidence. Generally we use nPre and nCon to respectively denote the prerequi- site nodes and consequent nodes of node n; :,0,1 ii aa Pre is the prior condi- tional probability distribution that an action will be conducted if its prerequisite is satisfied. In this pa- per, we assume that all elements of i aPre are in a conjunctive normal form. In other words, an action can be conducted only if all its prerequisite resources are occupied by the attacker; :, 0,1 ii aa Con is the probability distribution that an action will succeed if it is con- ducted. Since an action changes its consequent re- source state only when it succeeds, is also the probability that an action set its consequent node variables to True. Here we assume that for any re- source node i s if there are more than one suc- cessful actions in i s Pre , then each of them can set i s to True independently; :, 0,1 ij ao is the probability distri- bution that a type of intrusion evidence will be ob- served if one of its prerequisite actions is con- ducted. Here we also assume that for any evidence node j o if there are more than one successful ac- tions in j oPre , each of them can set j o to True independently; :0,1SAO is the node belief distribution of AG. Here i s denotes the prob- ability that the attacker has taken over resource i s ; i a denotes the probability that action i a has been conducted by the attacker and i o de- notes the probability that evidence i o has been observed. Specially, 0 is the initial node belief distribution of AG, denoting what resources are occupied by the attacker at the very beginning. So, we can expect: 00 00 0, 0, ii ii nnS nnS . Graphically, a network attack graph follows Definition 1 is like the one illustrated in Figure 4. In Figure 4, the attacker initially occupies resource s1, s2 and s3 (with probabilities defined in 0 ). Then intru- sion actions a1, a2 and a3 will be conducted (with prob- abilities defined in ), and further make the attacker take over resource s4~s7 (with probabilities defined in ). As actions being conducted, intrusion evidence o1~o4 will be triggered and observed (with probabilities defined in ). As mentioned before, in this paper, we are only inter- ested in whether a type of evidence has been observed, discarding its concrete observation number. However, we can still utilize the temporal partial ordering relations among attack evidence to assist posterior inference. Definition 2. There are two categories of evidence temporal partial ordering relations. We say: There is a type I temporal partial ordering relation om↗on if om is observed before on is observed. In other words, the first observation timepoint of om is earlier than the first observation timepoint of on. There is a type II temporal partial ordering relation om↘on if om is never observed after on is firstly observed. In other words, all the observation time- points of om are earlier than any of the ones of on. With the above definition, the problem of network at- tack graph-based posterior inference can be defined as: Given an attack graph AG, when an evidence sequence 12ii ik oo o which conforms to a partial s 1 o 1 s 2 s 3 s 4 s 5 s 7 a 1 a 2 a 3 o 2 o 3 o 4 s 6 Figure 4. A typical network attack graph.  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 12 ordering relation set Ω = {om↗on}{om↘on} is ob- served, how to compute the corresponding graph node belief distribution sequence 01 k ? 4. The Posterior Inference Algorithm In this section, we propose an algorithm for resolving the above posterior inference problem. Our algorithm is mai- nly based on the approximate Bayesian inference algo- rithm—the likelihood-weighting algorithm. A Bayesian network (or a belief network, a causal net- work) is a probabilistic graphical model that represents a set of variables and their probabilistic independencies. Essentially, a network attack graph following Definition 1 is a mimetic Bayesian network. However, since a Baye- sian network cannot contain any directed cycle or partial ordering relation of evidence nodes, traditional Bayesian inference should not be used to perform this attack graph-based posterior inference. To support these additional features, we manage to im- prove one of the approximate Bayesian network inference algorithms–the likelihood weighting algorithm [14,15] to a novel one. Likelihood weighting enhances logic sam- pling algorithm in that it never discards samples. It is the most commonly used simulation method for Bayesian network inference. Pseudocode of our improved algo- rithm is as follow: The 2nd line of the pseudocode is an outside loop con- trol statement which drives the algorithm to generate n effective samples in one run. In the loop, effective sam- ples are generated and added into a sample set Ξ which will eventually be returned. Pseudocode 3~35 is to generate an effective sample, which could be regarded as one potential attack scenario. This procedure can be further divided into five stages: 1) Initialization (3~6). In this stage, firstly two vari- ables wi and C are initialized. Here wi will be used to hold the weight of the sample and C will be used to hold the node pairs that temporally cannot be updated for their causation relationship. Then each node X in the attack graph is set to False and two assistant set variable FX and BX are initialized to empty. FX will be used to hold the nodes whose value are set to True by X. BX will be used to hold the nodes who set X to True. From another point of view, FX and BX respectively hold the forward and backward causation pointers of X. 2) Nodes sampling (7~23). In this stage, all the nodes in AG (except those nodes in OD) will be sampled. Firstly, in line 7~10, root nodes are sampled according to the initial node belief distribution Π0. Then, in line 11~23, AG is circularly updated until no more changes occur. In each cycle, every True value node X is checked out and a subfunction UpdateAttackGraph (for space limitation, pseudocodes of all the subfunctions are given out in An- ImprovedLikelihoodWeighting (AG, n, OD, OF, Ω, m) Input: AG — a network attack graph; n — effective sample number to generate; O D — a set of observed evidence nodes; O F — a set of not observed evidence nodes; Ω — a temporal partial ordering relation set on OD∪OF; m —inference mode, 0 for future state, 1 for current state. Output: Ξ — a set of effective samples. Algorithm: 01: Ξ←Ø; i←0; 02: while (i<n) 03: wi←1; C←Ø; 04: for (each node variable X in AG) 05: X←False; FX←Ø; BX←Ø; 06: end for (04) 07: for (each node variable X∈S0) 08: X←the sampling result according to Π0; 09: Mark X as sampled; 10: end for (07) 11: converged←False; 12: while (!converged) 13: converged←True; 14: for (each node variable X=True in AG) 15: for (each node variable Y∈Con(X)) 16: if (edge X→Y is not sampled) then 17: if (UpdateAttackGraph(AG,X,Y)) then 18: converged←False; 19: end if (17) 20: end if (16) 21: end for (15) 22: end for (14) 23: end while (12) 24: for (each node variable X∈OD) 25: X←True; 26: wX←SelectEvidenceCausation(AG,X); 27: wi←wi*wX; 28: end for (24) 29: if (m=1) then 30: b←Transientize(AG,OD,OF); 31: end if (29) 32: if (b∧PartialRelationSatisfied(AG,OD∪OF,Ω)) then 33: ξi.AG←AG; ξi.w←wi; 34: Ξ←Ξ∪{ξi}; i←i+1; 35: end if (32); 36: end while (02) 37: return Ξ;  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 13 nex A of this paper) is called on each pair of X and its descendant node Y iff the edge X→Y is not sampled. 3) Observed evidence causation selection (24~28). In this stage, for each observed evidence node X in OD, a subfunction SelectEvidenceCausation is called on X to randomly select a causation set from Pre(X) to denote what set X to True. At the same time, the occurrence probability of this chosen causation set will affect the weight of the sample. 4) Transientization (29~31). If what we need to infer is the current state of the network, then the sample should be reshaped to represent a budding (not fully developed) attack scenario. The processing transientization is based on the idea that although some evidence nodes in OF may equal to True in the sample, they actually represent evi- dence that will be observed only in the future (currently only the ones in OD are observed). So, correspondingly, the actions that trigger the evidence also have not oc- curred yet. This means, in order to reshape the sample to represent current state, all these nodes should be set to False. In our algorithm, this processing will be perfor- med through a subfunction Transientize. 5) Sample effectiveness verification (32~35). In this stage, a subfunction PartialRelationSatisfied is called to check whether the temporal partial ordering relations among the evidence nodes conform to the causation rela- tions among the action nodes. By running the algorithm, we can get a set of samples which not only have node values generated under the gi- ven probability distribution, but also definitely conform to the temporal partial ordering relations among evidence. Then, to use this sample set, a node belief computation function is defined as follow: By running this function, a set M will be returned which contains all the node belief values for later queries. By inputting different intrusion evidence sequences which correspond to different observation timepoints, we can get an attack graph node belief distribution sequence 01 k to represent security state evolvement. 5. Node Belief Computation Examples In order to exemplify the improved likelihood-weighting algorithm, we design and implement a Java program to perform following experiments: 5.1. Comparison with Bayesian Inference Firstly, we use the variable elimination algorithm (a tra- ditional Bayesian inference algorithm) to compute the posterior node belief values of the attack graph illustra- ted in Figure 3. The result is listed in Table 1. In Table 1, different number i denotes different infer- ence layer. In this example, i = 0 denotes the inference is performed before any evidence is observed, i = 1 denotes the inference is performed after o2 is observed, i = 2 de- notes the inference is performed after sequence o2→o1 is observed and i = 3 denotes the inference is performed after o2→o1→o3 is observed. Then we use our improved likelihood weighting algo- rithm to perform the same inference. The result is listed in Table 2 (10000 effective samples without transienti- zation) and Table 3 (10000 samples with transientiza- tion). Since traditional Bayesian network inference methods does not support intrusion evidence ordering, we are not surprised to see that in Table 1, when i > 1, the node belief values of intrusion path α and β are mirror sym- metrical. This makes it difficult for us to judge which path has been chosen by the attacker. However, by using improved likelihood weighting algorithm, we can ob- serve no matter in Table 2 or Table 3, the node belief values of path β are all higher than path α, indicating it is more likely to have been chosen by the attacker. NodeBeliefComputing(AG,n,OD,OF,Ω,m) Input: AG — a network attack graph; n — effective sample number to generate; O D — a set of observed evidence nodes; O F — a set of not yet observed evidence nodes; Ω — a temporal partial ordering relation set on OD∪OF; m —inference mode, 0 for future state, 1 for current state. Output: M — a node belief metric set Algorithm: 01: M←Ø; W←0; 02: Ξ←ImprovedLikelihoodWeighting(AG,n, OD,OF,Ω,m); 03: for (each node variable X in AG) 04: NX←0; 05: end for (03) 06: for (each sample ξ in Ξ) 07: for (each node variable X in ξ.AG) 08: if (X=1) then 09: NX←NX+ξ.w; 10: end if (08) 11: end for (07) 12: W←W+ξ.w; 13: end for (06) 14: for (each node variable X in AG) 15: M←M∪{PX=NX/W}; 16: end for (14) 17: return M; 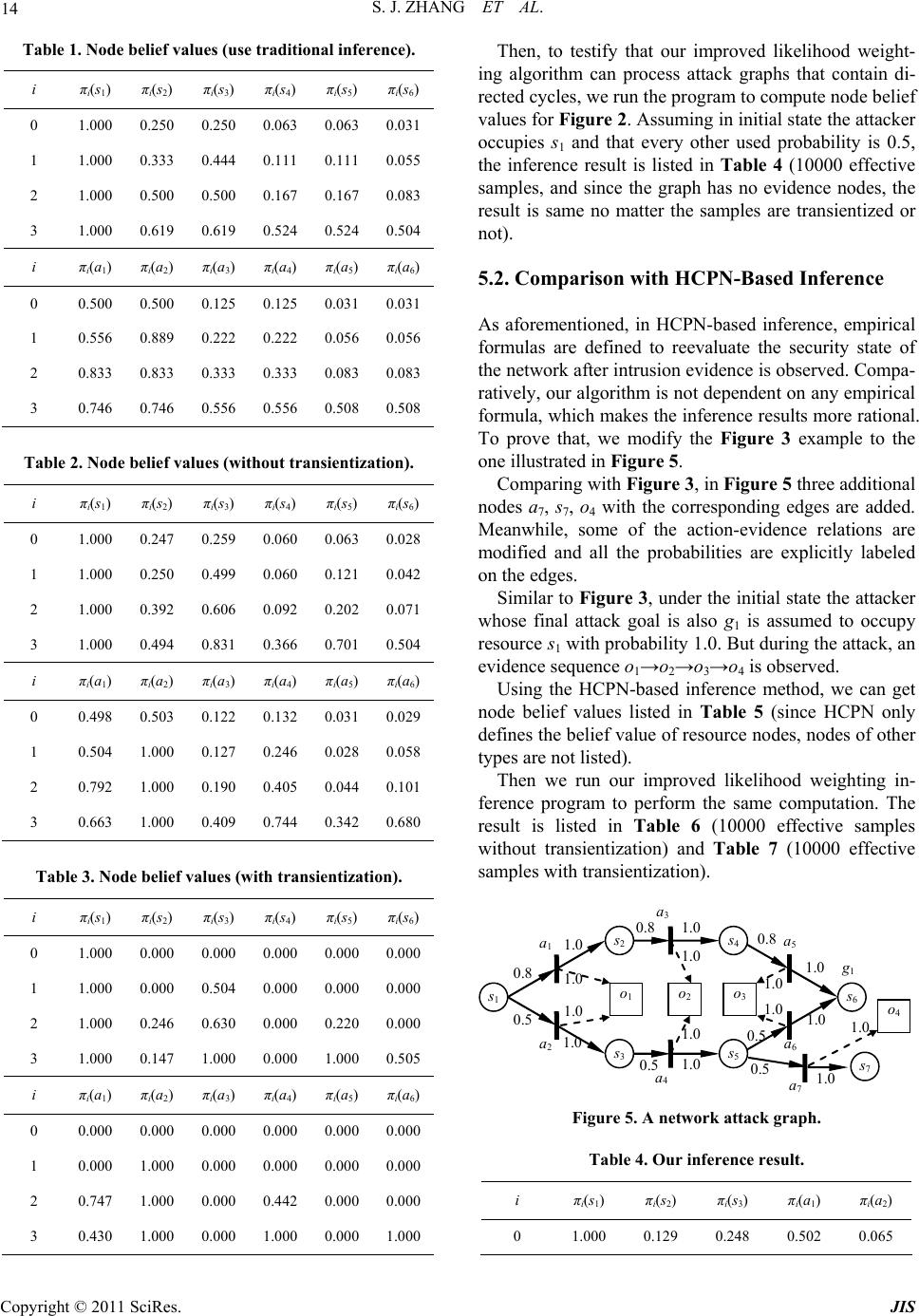 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 14 Table 1. Node belief values (use traditional inference). i πi(s1) πi(s2) πi(s3) πi(s4) πi(s5) πi(s6) 0 1.000 0.250 0.250 0.063 0.063 0.031 1 1.000 0.333 0.444 0.111 0.111 0.055 2 1.000 0.500 0.500 0.167 0.167 0.083 3 1.000 0.619 0.619 0.524 0.524 0.504 i πi(a1) πi(a2) πi(a3)πi(a4) πi(a5) πi(a6) 0 0.500 0.500 0.125 0.125 0.031 0.031 1 0.556 0.889 0.222 0.222 0.056 0.056 2 0.833 0.833 0.333 0.333 0.083 0.083 3 0.746 0.746 0.556 0.556 0.508 0.508 Table 2. Node belief values (without transientization). i πi(s1) πi(s2) πi(s3) πi(s4) πi(s5) πi(s6) 0 1.000 0.247 0.259 0.060 0.063 0.028 1 1.000 0.250 0.499 0.060 0.121 0.042 2 1.000 0.392 0.606 0.092 0.202 0.071 3 1.000 0.494 0.831 0.366 0.701 0.504 i πi(a1) πi(a2) πi(a3)πi(a4) πi(a5) πi(a6) 0 0.498 0.503 0.122 0.132 0.031 0.029 1 0.504 1.000 0.127 0.246 0.028 0.058 2 0.792 1.000 0.190 0.405 0.044 0.101 3 0.663 1.000 0.409 0.744 0.342 0.680 Table 3. Node belief values (with transientization). i πi(s1) πi(s2) πi(s3) πi(s4) πi(s5) πi(s6) 0 1.000 0.000 0.000 0.000 0.000 0.000 1 1.000 0.000 0.504 0.000 0.000 0.000 2 1.000 0.246 0.630 0.000 0.220 0.000 3 1.000 0.147 1.000 0.000 1.000 0.505 i πi(a1) πi(a2) πi(a3)πi(a4) πi(a5) πi(a6) 0 0.000 0.000 0.000 0.000 0.000 0.000 1 0.000 1.000 0.000 0.000 0.000 0.000 2 0.747 1.000 0.000 0.442 0.000 0.000 3 0.430 1.000 0.000 1.000 0.000 1.000 Then, to testify that our improved likelihood weight- ing algorithm can process attack graphs that contain di- rected cycles, we run the program to compute node belief values for Figure 2. Assuming in initial state the attacker occupies s1 and that every other used probability is 0.5, the inference result is listed in Table 4 (10000 effective samples, and since the graph has no evidence nodes, the result is same no matter the samples are transientized or not). 5.2. Comparison with HCPN-Based Inference As aforementioned, in HCPN-based inference, empirical formulas are defined to reevaluate the security state of the network after intrusion evidence is observed. Compa- ratively, our algorithm is not dependent on any empirical formula, which makes the inference results more rational. To prove that, we modify the Figure 3 example to the one illustrated in Figure 5. Comparing with Figure 3, in Figure 5 three additional nodes a7, s7, o4 with the corresponding edges are added. Meanwhile, some of the action-evidence relations are modified and all the probabilities are explicitly labeled on the edges. Similar to Figure 3, under the initial state the attacker whose final attack goal is also g1 is assumed to occupy resource s1 with probability 1.0. But during the attack, an evidence sequence o1→o2→o3→o4 is observed. Using the HCPN-based inference method, we can get node belief values listed in Table 5 (since HCPN only defines the belief value of resource nodes, nodes of other types are not listed). Then we run our improved likelihood weighting in- ference program to perform the same computation. The result is listed in Table 6 (10000 effective samples without transientization) and Table 7 (10000 effective samples with transientization). s 4 s 1 s 2 s 3 a 1 o 1 o 2 s 5 a 2 a 4 s 6 a 5 a 6 o 3 g 1 s 7 o 4 0.8 0.5 1.0 1.0 0.81.0 a 3 0.8 1.0 0.5 1.0 0.5 0.5 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 a 7 Figure 5. A network attack graph. Table 4. Our inference result. i πi(s1) πi(s2) πi(s3) πi(a1) πi(a2) 0 1.000 0.129 0.248 0.502 0.065 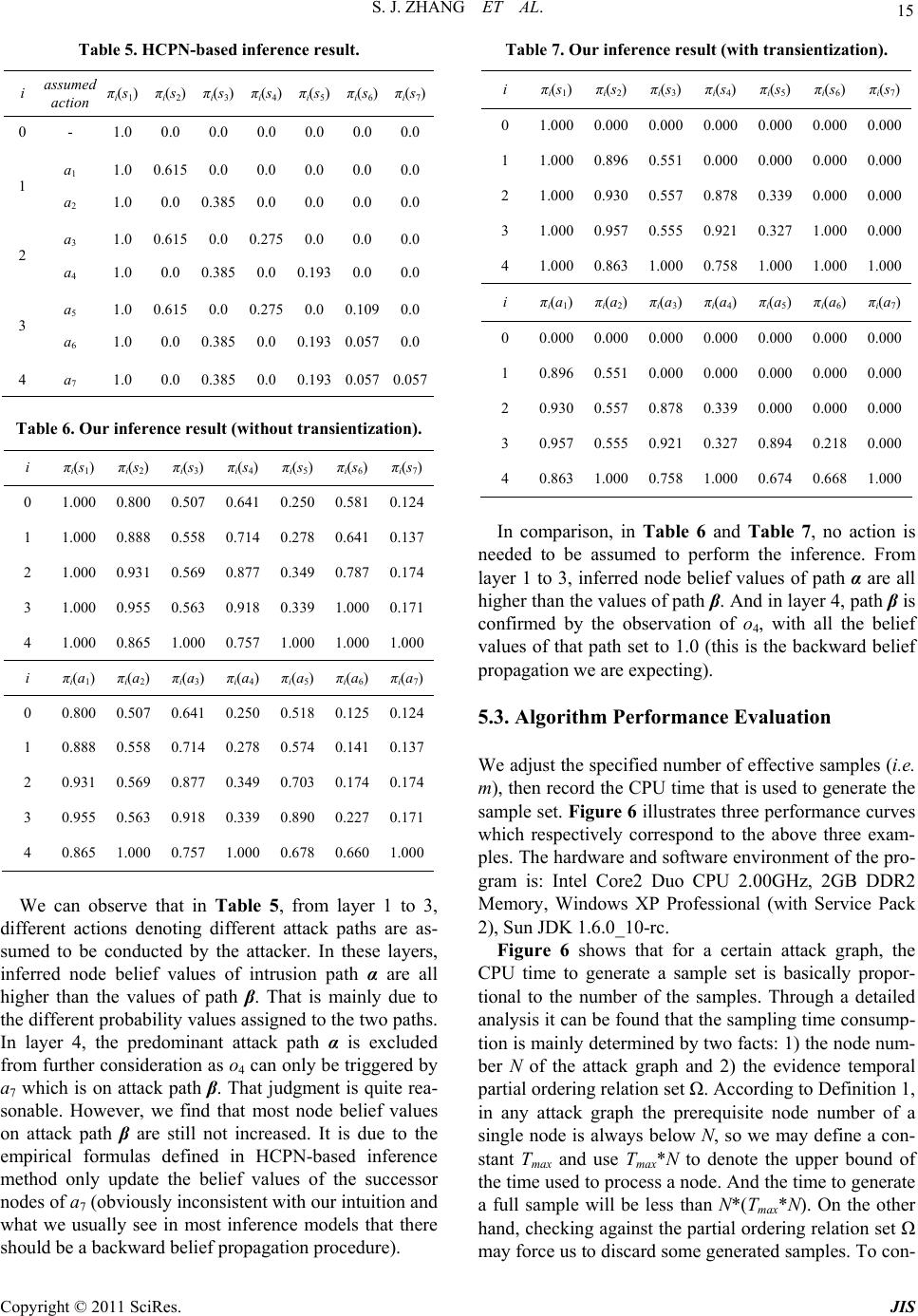 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 15 Table 5. HCPN-based inference result. i assumed action πi(s1) πi(s2) πi(s3)πi(s4) πi(s5) πi(s6)πi(s7) 0 - 1.0 0.0 0.0 0.0 0.0 0.0 0.0 a1 1.0 0.615 0.00.0 0.0 0.00.0 1 a2 1.0 0.0 0.3850.0 0.0 0.0 0.0 a3 1.0 0.615 0.0 0.275 0.0 0.00.0 2 a4 1.0 0.0 0.385 0.0 0.193 0.00.0 a5 1.0 0.615 0.0 0.275 0.0 0.109 0.0 3 a6 1.0 0.0 0.385 0.0 0.193 0.057 0.0 4 a7 1.0 0.0 0.385 0.0 0.193 0.0570.057 Table 6. Our inference result (without transientization). i πi(s1) πi(s2) πi(s3) πi(s4) πi(s5) πi(s6)πi(s7) 0 1.000 0.800 0.507 0.641 0.250 0.581 0.124 1 1.000 0.888 0.558 0.714 0.278 0.641 0.137 2 1.000 0.931 0.569 0.877 0.349 0.787 0.174 3 1.000 0.955 0.563 0.918 0.339 1.000 0.171 4 1.000 0.865 1.000 0.757 1.000 1.000 1.000 i πi(a1) πi(a2) πi(a3) πi(a4) πi(a5) πi(a6)πi(a7) 0 0.800 0.507 0.641 0.250 0.518 0.125 0.124 1 0.888 0.558 0.714 0.278 0.574 0.141 0.137 2 0.931 0.569 0.877 0.349 0.703 0.174 0.174 3 0.955 0.563 0.918 0.339 0.890 0.227 0.171 4 0.865 1.000 0.757 1.000 0.678 0.660 1.000 We can observe that in Table 5, from layer 1 to 3, different actions denoting different attack paths are as- sumed to be conducted by the attacker. In these layers, inferred node belief values of intrusion path α are all higher than the values of path β. That is mainly due to the different probability values assigned to the two paths. In layer 4, the predominant attack path α is excluded from further consideration as o4 can only be triggered by a7 which is on attack path β. That judgment is quite rea- sonable. However, we find that most node belief values on attack path β are still not increased. It is due to the empirical formulas defined in HCPN-based inference method only update the belief values of the successor nodes of a7 (obviously inconsistent with our intuition and what we usually see in most inference models that there should be a backward belief propagation procedure). Table 7. Our inference result (with transientization). i πi(s1)πi(s2)πi(s3)πi(s4) πi(s5) πi(s6)πi(s7) 0 1.000 0.000 0.000 0.000 0.000 0.000 0.000 1 1.000 0.896 0.551 0.000 0.000 0.000 0.000 2 1.000 0.930 0.557 0.878 0.339 0.000 0.000 3 1.000 0.957 0.555 0.921 0.327 1.000 0.000 4 1.000 0.863 1.000 0.758 1.000 1.000 1.000 i πi(a1)πi(a2)πi(a3)πi(a4) πi(a5) πi(a6)πi(a7) 0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 1 0.896 0.551 0.000 0.000 0.000 0.000 0.000 2 0.930 0.557 0.878 0.339 0.000 0.000 0.000 3 0.957 0.555 0.921 0.327 0.894 0.218 0.000 4 0.863 1.000 0.758 1.000 0.674 0.668 1.000 In comparison, in Table 6 and Table 7, no action is needed to be assumed to perform the inference. From layer 1 to 3, inferred node belief values of path α are all higher than the values of path β. And in layer 4, path β is confirmed by the observation of o4, with all the belief values of that path set to 1.0 (this is the backward belief propagation we are expecting). 5.3. Algorithm Performance Evaluation We adjust the specified number of effective samples (i.e. m), then record the CPU time that is used to generate the sample set. Figure 6 illustrates three performance curves which respectively correspond to the above three exam- ples. The hardware and software environment of the pro- gram is: Intel Core2 Duo CPU 2.00GHz, 2GB DDR2 Memory, Windows XP Professional (with Service Pack 2), Sun JDK 1.6.0_10-rc. Figure 6 shows that for a certain attack graph, the CPU time to generate a sample set is basically propor- tional to the number of the samples. Through a detailed analysis it can be found that the sampling time consump- tion is mainly determined by two facts: 1) the node num- ber N of the attack graph and 2) the evidence temporal partial ordering relation set Ω. According to Definition 1, in any attack graph the prerequisite node number of a single node is always below N, so we may define a con- stant Tmax and use Tmax*N to denote the upper bound of the time used to process a node. And the time to generate a full sample will be less than N*(Tmax*N). On the other hand, checking against the partial ordering relation set Ω may force us to discard some generated samples. To con-  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 16 Figure 6. CPU time curves of sampling. trol this fact, we may specify a maximal try number M. Once M samples have been generated (no matter how many effective samples are there), the program will cease sampling. In conclusion, for any attack graph, the sampling procedure can always finish in Tmax*M*N2. In other words, the algorithm has quadratic computational complexity. 6. Security Assessment & Enhancement In this section, based on the above node belief computa- tion algorithm, we propose a model for assessing net- work security level and performing security enhance- ment. 6.1. Security Assessment Generally, the overall security level of a concerned net- work is mainly determined by three factors: 1) threat of the network, 2) vulnerability of the network and 3) in- fluence of the potential attacks. In the previously pro- posed model, the former two factors have been dealt with (by IDS alerts indicating threats and network attack graph itself indicating vulnerabilities). However, we still have a problem with how to model the influence of po- tential attacks. In this section, we introduce a concept of asset value breakage rate to quantify it. Asset value breakage rate is the ratio of the lost asset value to the overall asset value, illustrated in Figure 7. Since we often use asset CIA (confidentiality, integrity and availability) value to achieve more particular quanti- fication, we introduce asset CIA breakage nodes into Figure 7. Components of asset value. network attack graph and extend Definition 1 into Defi- nition 3. Definition 3. An extended attack graph is a 12-tuple directed graph 0 ,,,,,,,,,,,AGSSAGOE where 0 ,,,,,,,,SS AGO are the same elements as defined in Definition 1 and: CIA is a set of asset breakage nodes where C is a set of asset confidentiality breakage nodes, I is a set of asset integrity breakage nodes and A is a set of asset availabil- ity breakage nodes. Values of each node variable Xi (X = C, I, A; i = 1, , N. where N is the total asset number) all lie in [0, 1], denoting the breakage percentage of every asset in particular aspect. Apart from that, we define a function :0,+ to map each asset to its overall value in confidential- ity, integrity and availability. So we can use ii to denote the absolute loss value of an asset in CIA. 12345 EEEEEE is a finite set of edges which link graph nodes together. Here E1, E2 and E3 share the same definition as in Definition 1, while 4 ES denotes that if the attacker gains certain resources, she will do damage to cer- tain assets, and 5 EA denotes that if the at- tacker executes certain actions, she will do damage to certain assets. 12 :, 0,1,:, 0,1 ij ij sa is the asset breakage conductivity rate distribution where 1 denotes when the attacker gains a re- source, how much damage will she do to an asset and 2 denotes when the attacker executes an ac- tion, how much damage will she do to an asset. Just like the other prior conditional probability dis- tributions, values of also lies in [0, 1] where a larger value denotes a greater potential damage. Based on Definition 3, we can use a function to quantify the network security level: 111 1 CCI IAA CCII AA CCI IAA CI A  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 17 In the above equation, is the function to com- pute the normalized asset residual value. The right ex- pression uses asset residual value as the numerator and asset overall value as the denominator. Just like other network attack graph node variables, all the belief values of asset breakage nodes also can be computed by the inference algorithm in Section 4. So, by inputting different evidence sequences corresponding to different observation timepoints, eventually we can get a sequence 01k indicating the security evolvement. 6.2. Security Enhanceme nt Broadly speaking, as long as a measure can help en- hacing network security, it is referred to as a network security enhancement measure. In most cases, the im- plementation of a security enhancement measure may affect a network attack graph in two ways: 1) it changes the structure of the attack graph, or 2) it changes the conditional probability distributions of the attack graph including 0 ,,,, . However, since commonly the implementation of a security enhancement measure will cut off certain intru- sion paths, the resulting (enhanced) attack graph is often the sub-graph of the original attack graph. Based on this, we can always convert the above situation 1 into situa- tion 2 by adjusting certain conditional probability. For example, in the previous example illustrated in Figure 2, if the vulnerability on Master is patched, we need not generate a new attack graph, but set the con- ducting probability of a1 and a2 to 0.0. On this basis, we introduce a security enhancement measure tuple ,,M : 1,, K M mm is a candidate measure set. :22 M is a function which maps a combina- tion of measures to a rectified attack graph prob- ability distribution 0 ,,,, . :2 MR is a function which maps a combina- tion of measures to its implementation cost. With the above security measure tuple, we can per- form the following analysis: 1) Static Security Enhancement. This analysis is to find the best combination of security measures to be im- plemented before any potential intrusion happens. A ty- pical usage of this analysis is to enhance a network sys- tem before it is placed online. To achieve this, all candi- date measure combinations need to be iterated. For each measure combination 2 M C M, we set the probability distribution to C M and recompute the network normalized asset residual value 0 . Then the net profit of C M is: 00CC uMOverallAsset ValueM , where 0 is the normalized asset residual value when no security measure is implemented (C M). Finally, by sorting these measure combinations according to their net profits, we can easily choose the greatest one as the optimal enhancement solution. 2) Dynamic Security Enhancement. This analysis is to find the best measure combination when intrusion is happening (or has happened). To achieve this, we firstly need to use the previous inference algorithm to generate a set ΞT of transientized attack samples. Then we iterate all of the candidate measure combinations. For each combination 2 M C M, we rectify the graph probability distribution to C M . After doing this, we re- sample (a process same to line 11~23 of the Improved LikelihoodWeighting algorithm) ΞT according to the new distribution and get a new set ΞS which will be actu- ally used to compute the network normalized asset re- sidual value S . Then the net profit of C M is: CSS C uMOverallAsset ValueM , where S is a normalized asset residual value when no measure is implemented (C M). Finally, by sorting these measure combinations according to their net profits, we can easily choose the greatest one as the optimal en- hancement solution. 7. Assessment & Enhancement Examples To exemplify the above security assessment and enhan- cement method, in one experiment we generated an at- tack graph for a two tier network system. Based on it, we performed corresponding security assessment and used our enhancement method to find out optimal security en- hancement measure combinations for static and dynamic security enhancement respectively. 7.1. Basic Posterior Inference Figure 8 illustrates the topology of the two tier network. In this network, four intranet servers were connected to a switch which was further connected to the Internet by a router. A firewall was placed between the two devices to perform package filtering, besides an IDS was connected to a mirror port of the switch to monitor the outflow and inflow of the servers. We assumed a scenario that an attacker on the Internet intends to use her personal computer to attack this net- work. The final goal of the attacker was to get the ROOT privilege on server3 and steal its business data. For further analysis, we firstly need to generate a net- work attack graph to find out all the potential intrusion paths. So we scanned the online devices and servers and found out six vulnerabilities (listed in Table 8). Addi-  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 18 Figure 8. A two tier network system. Table 8. Host vulnerabilities. device OS application vulnerabilities server1 windows nt 4.0 serv-u ftp 3.0 cve-2004-0330 cve-2004-1992 server2 windows 2000 - cve-2003-0533 server3 redhat linux 7.3 oracle 9i cvs 1.11 cve-2004-0417 cve-2004-0415 server4 redhat linux 7.3 apache 1.3.23 cve-2002-0392 tionally, we found that the firewall is configured to per- mit and only permit the Internet user to access intranet servers through HTTP protocol. By importing these information into a network attack graph building system developed by us (design concept of this system mainly follows the framework proposed in [16]), we get a network attack graph shown in Figure 9. In Figure 9, resource state nodes are represented in circles while action nodes are represented in rectangles. The top row in the figure (11 resource state nodes) inclu- des the 6 vulnerabilities on the servers and the 5 low lev- el privileges which can be used by anyone to access the servers. However, owes to the firewall, initially the atta- cker can only access server4’s HTTP service and exploit the apache vulnerability (this exploitation is represented in the figure with the action node right below the top re- source state node row). After that, the attacker may get the USER privilege of server4 and use this server as a stepping stone to perform further intrusion (mainly by exploiting the rest vulnerabilities listed in Table 8). Ac- cording to Figure 9, to the maximum extent, the attacker can get the USER privilege of server1, server3 and serv- er4 as well as the ROOT privilege of server2 and server3 (represented by the other 5 circles in the figure exclude the top row). Then we should assigned conditional probability dis- tributions to the generated graph. In this stage, we mainly used data sources such as CVSS [17] and OSVBD [18] complemented with expertise knowledge. For example, in CVSS, a score metric named Exploitability are defined to indicate the difficulty for an attacker to exploit vul- nerability. So we decide to use this metric to evaluate the success rate of an action by the following transformation: of 1.0 E xploitability a ae With all prior conditional probability distributions as- signed, we were able to perform posterior inference ac- cording to observed intrusion evidence. As an example for exemplification, we assumed that an IDS alert se- quence is observed as in Table 9: By running the improved likelihood weighting algo- rithm, we computed node belief values for each inference layer. Due to space limitation, detailed result is not given out here. But in Annex B this security evolvement proce- dure is illustrated graphically. In each figure of the annex, a darker node is used to represent a greater node belief value. We see that with more evidence observed, belief values of some graph nodes increase rapidly, indicating intrution paths that are most probably chosen. 7.2. Security Assessment Since our aim is to assess security level of the network and find out an optimal enhancement solution, we sele- cted 5 important service assets from the network system whose CIA values are listed in Table 10 (in thousands $US). Correspondingly, we introduced into the attack graph 15 corresponding asset breakage nodes. Meanwhile, we quantified the asset breakage conduc- tivity rate between these 15 nodes and the aforemen- tioned 5 resource state nodes which represent the esca- lated privileges that may be gained by the attacker. The conductivity rates between them are listed in Table 11. Table 9. Observed alerts. id exploited vulnerability source target 1 cve-2002-0392 pc server4 2 cve-2003-0533 server4 server2 3 cve-2004-0417 server3 server3 Table 10. Important assets and their CIA values. id asset host λ(ρC) λ(ρI) λ(ρA) 1 ftp server1 1 1 1 2 file server2 50 50 50 3 database server3 100 100 50 4 cvs server4 10 10 10 5 apache server4 0 10 10 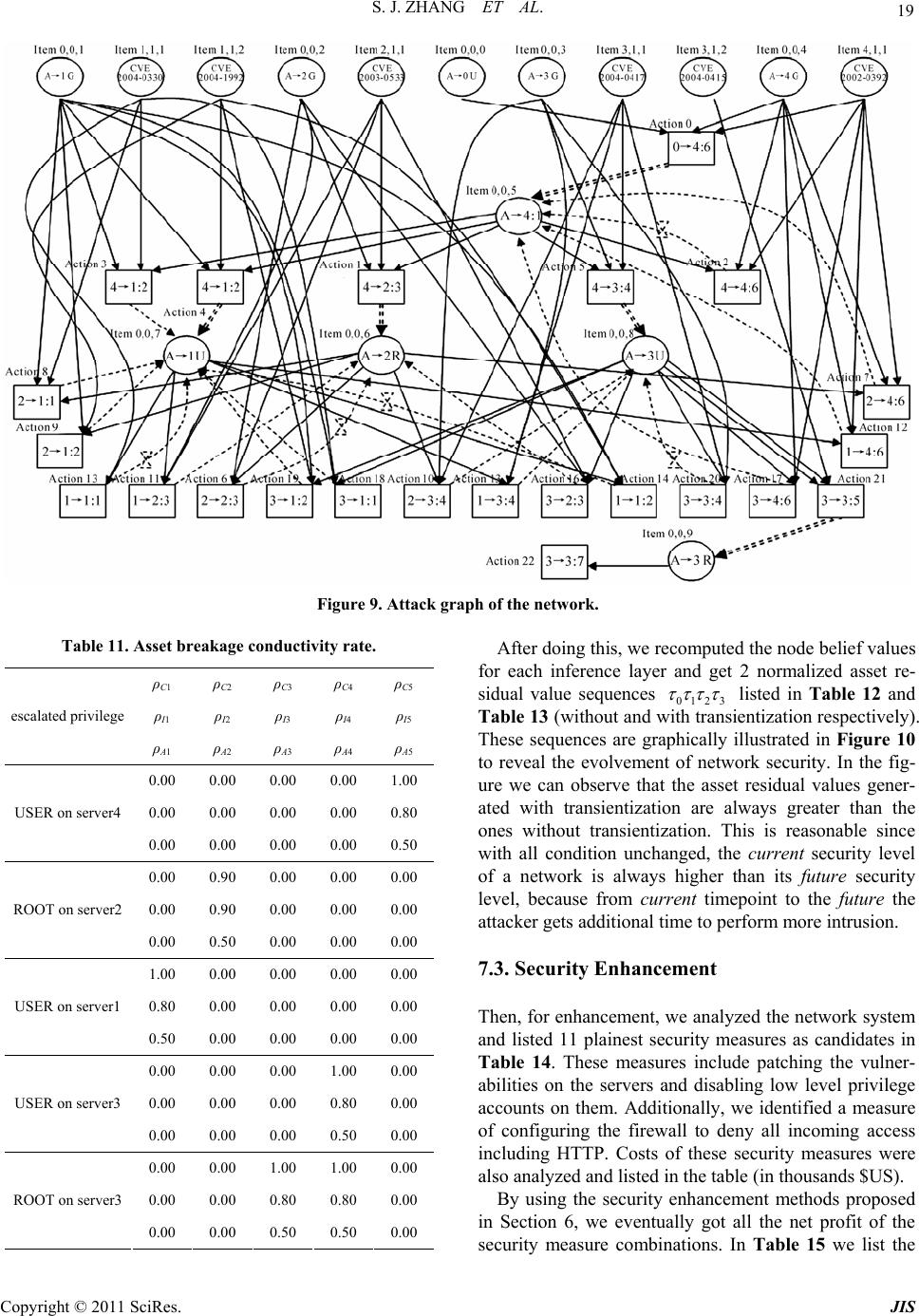 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 19 Figure 9. Attack graph of the network. Table 11. Asset breakage conductivity r a te . ρC1 ρC2 ρC3 ρC4 ρC5 ρI1 ρI2 ρI3 ρI4 ρI5 escalated privilege ρA1 ρA2 ρA3 ρA4 ρA5 0.00 0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.80 USER on server4 0.00 0.00 0.00 0.00 0.50 0.00 0.90 0.00 0.00 0.00 0.00 0.90 0.00 0.00 0.00 ROOT on server2 0.00 0.50 0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.80 0.00 0.00 0.00 0.00 USER on server1 0.50 0.00 0.00 0.00 0.00 0.00 0.00 0.00 1.00 0.00 0.00 0.00 0.00 0.80 0.00 USER on server3 0.00 0.00 0.00 0.50 0.00 0.00 0.00 1.00 1.00 0.00 0.00 0.00 0.80 0.80 0.00 ROOT on server3 0.00 0.00 0.50 0.50 0.00 After doing this, we recomputed the node belief values for each inference layer and get 2 normalized asset re- sidual value sequences 0123 listed in Table 12 and Table 13 (without and with transientization respectively). These sequences are graphically illustrated in Figure 10 to reveal the evolvement of network security. In the fig- ure we can observe that the asset residual values gener- ated with transientization are always greater than the ones without transientization. This is reasonable since with all condition unchanged, the current security level of a network is always higher than its futu re security level, because from current timepoint to the future the attacker gets additional time to perform more intrusion. 7.3. Security Enhanceme nt Then, for enhancement, we analyzed the network system and listed 11 plainest security measures as candidates in Table 14. These measures include patching the vulner- abilities on the servers and disabling low level privilege accounts on them. Additionally, we identified a measure of configuring the firewall to deny all incoming access including HTTP. Costs of these security measures were also analyzed and listed in the table (in thousands $US). By using the security enhancement methods proposed in Section 6, we eventually got all the net profit of the security measure combinations. In Table 15 we list the 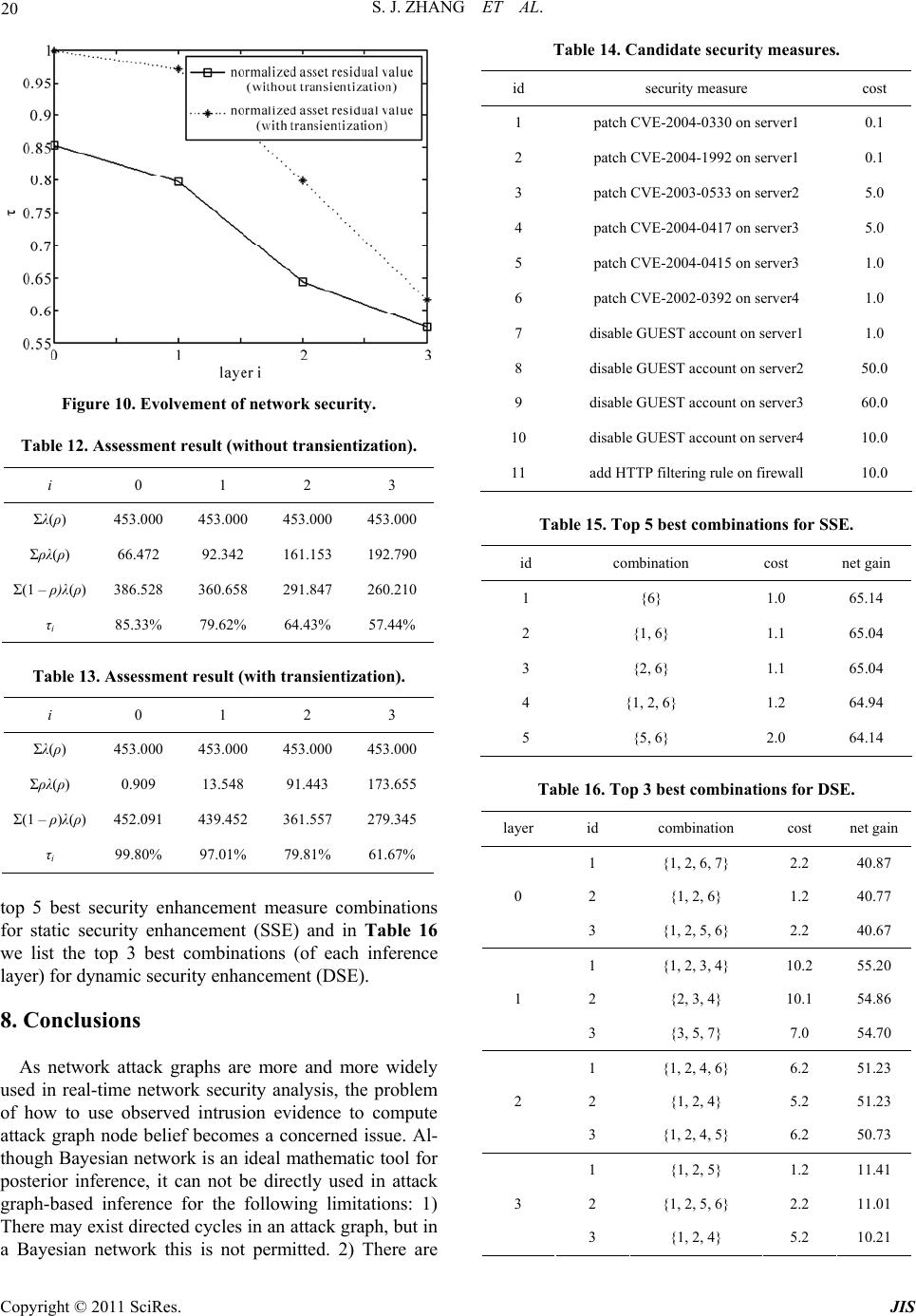 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 20 Figure 10. Evolvement of network security. Table 12. Assessment result (without transientization). i 0 1 2 3 Σλ(ρ) 453.000 453.000 453.000 453.000 Σρλ(ρ) 66.472 92.342 161.153 192.790 Σ(1 – ρ)λ(ρ) 386.528 360.658 291.847 260.210 τi 85.33% 79.62% 64.43% 57.44% Table 13. Assessment result (with transientization). i 0 1 2 3 Σλ(ρ) 453.000 453.000 453.000 453.000 Σρλ(ρ) 0.909 13.548 91.443 173.655 Σ(1 – ρ)λ(ρ) 452.091 439.452 361.557 279.345 τi 99.80% 97.01% 79.81% 61.67% top 5 best security enhancement measure combinations for static security enhancement (SSE) and in Table 16 we list the top 3 best combinations (of each inference layer) for dynamic security enhancement (DSE). 8. Conclusions As network attack graphs are more and more widely used in real-time network security analysis, the problem of how to use observed intrusion evidence to compute attack graph node belief becomes a concerned issue. Al- though Bayesian network is an ideal mathematic tool for posterior inference, it can not be directly used in attack graph-based inference for the following limitations: 1) There may exist directed cycles in an attack graph, but in a Bayesian network this is not permitted. 2) There are Table 14. Candidate security measures. id security measure cost 1 patch CVE-2004-0330 on server1 0.1 2 patch CVE-2004-1992 on server1 0.1 3 patch CVE-2003-0533 on server2 5.0 4 patch CVE-2004-0417 on server3 5.0 5 patch CVE-2004-0415 on server3 1.0 6 patch CVE-2002-0392 on server4 1.0 7 disable GUEST account on server1 1.0 8 disable GUEST account on server2 50.0 9 disable GUEST account on server3 60.0 10 disable GUEST account on server4 10.0 11 add HTTP filtering rule on firewall 10.0 Table 15. Top 5 best combinations for SSE. id combination cost net gain 1 {6} 1.0 65.14 2 {1, 6} 1.1 65.04 3 {2, 6} 1.1 65.04 4 {1, 2, 6} 1.2 64.94 5 {5, 6} 2.0 64.14 Table 16. Top 3 best combinations for DSE. layer id combination cost net gain 1 {1, 2, 6, 7} 2.2 40.87 2 {1, 2, 6} 1.2 40.77 0 3 {1, 2, 5, 6} 2.2 40.67 1 {1, 2, 3, 4} 10.2 55.20 2 {2, 3, 4} 10.1 54.86 1 3 {3, 5, 7} 7.0 54.70 1 {1, 2, 4, 6} 6.2 51.23 2 {1, 2, 4} 5.2 51.23 2 3 {1, 2, 4, 5} 6.2 50.73 1 {1, 2, 5} 1.2 11.41 2 {1, 2, 5, 6} 2.2 11.01 3 3 {1, 2, 4} 5.2 10.21  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 21 temporal partial ordering relations among intrusion evi- dence, but we can not use a Bayesian network to model this information. 3) A Bayesian network cannot be direc- tly used to infer both the current and the future security state of a network. In this work, we resolve these critical problems by developing an approximate Bayesian infer- ence algorithm—the likelihood weighting algorithm. We give out all the pseudocodes of the algorithm and use se- veral examples to show its advantage. Essentially, we be- lieve this algorithm is not only limited in attack graph- based analysis, but also can be applied in other techni- ques employing traditional Bayesian posterior inference. Based on the algorithm and its underlying model, we further propose a novel network security assessment and enhancement method. In this paper, we use a small net- work system to exemplify how to use this method to quantify the overall network security level and make de- cisions about what security measures are most cost- ef- fective for network security enhancement. 9. Acknowledgements This work was supported in part by the National Natural Science Foundation of China under Grant Nos.60605019; the National High-Tech Research and Development Plan under Grant Nos.2007AA01Z473; the National Research Foundation for the Doctoral Program of Higher Educa- tion of China under Grant No.20070248002. The authors would also like to thank all the members of Shanghai Key Laboratory for Information Security Integrated Management Technology Research. If anyone is interested in the algorithms of this article, please feel free to contact leony7888@hotmail to get the java source codes. 10. References [1] O. Sheyner, J. Haines, S. Jha, et al., “Automated Genera- tion and Analysis of Attack Graphs,” Proceedings of the 2002 IEEE Symposium on Security and Privacy, Oakland, 12-15 May 2002, pp. 273-284. doi:10.1109/SECPRI.2002. 1004377 [2] S. Jajodia, S. Noel and B. O’Berry, “Topological Analy- sis of Network Attack Vulnerability,” Managing Cyber Threats: Issues, Approaches and Challenges, Kluwer Academic Publisher, 2004. [3] P. Ammann, D. Wijesekera and S. Kaushik, “Scalable, Graph-Based Network Vulnerability Analysis,” Procee- dings of the 9th ACM Conference on Computer & Com- munications Security, Washington DC, 2002, pp. 217-224. [4] X. Ou, S. Govindavajhala and A. Appel, “MulVAL: A Logic-Based Network Security Analyzer,” Proceedings of the 14th conference on USENIX Security Symposium, Baltimore, 31 July-5 August 2005, pp. 8-23. [5] R. Lippmann, K. Ingols, C. Scott, et al., “Validating and Restoring Defense in Depth Using Attack Graphs,” Pro- ceedings of the 2007 IEEE Military Communications Conference, Washington DC, 2006. [6] P. Ning and D. Xu, “Learning Attack Strategies from Intrusion Alerts,” Proceedings of the 10th ACM Confer- ence on Computer and Communications Security, Wash- ington DC, October 2003. [7] S. Noel, E. Robertson and S. Jajodia, “Correlating Intru- sion Events and Building Attack Scenarios through At- tack Graph Distances,” Proceedings of the 20th Annual Computer Security Applications Conference, Tucson, December 2004, pp. 350-359. doi:10.1109/SECPRI.2002. 1004377 [8] L. Wang, A. Liu and S. Jajodia, “Using Attack Graphs for Correlating, Hypothesizing, and Predicting Intrusion Alerts,” Computer Communications, Vol. 29, No. 15, 2006, pp. 2917-2933. doi:10.1016/j.comcom.2006.04.001 [9] Y. Zhai, P. Ning, P. Iyer, et al., “Reasoning about Com- plementary Intrusion Evidence,” Proceedings of the 20th Annual Computer Security Applications Conference, Tucson, 6-10 December 2004, pp. 39-48. doi:10.1109/ CSAC.2004.29 [10] D. Yu and D. Frincke, “Improving the Quality of Alerts and Predicting Intruder’s Next Goal with Hidden Colored Petri-Net,” Computer Networks, Vol. 51, No. 3, 2007, p. 632. doi:10.1016/j.comnet.2006.05.008 [11] S. Zhang, L. Li, J. Li, et al., “Using Attack Graphs and Intrusion Evidences to Extrapolate Network Security State,” Proceedings of the 4th International Conference on Communications and Networking in China, Guang Zhou, 2009. doi:10.1109/CHINACOM.2009.5339841 [12] Z. Bhahramani, “An Introduction to Hidden Markov Models and Bayesian Networks,” International Journal of Pattern Recognition and Artificial Intelligence, Vol. 15, No. 1, 2001, pp. 9-42. doi:10.1142/S0218001401000836 [13] F. Salfner, “Modeling Event-driven Time Series with Generalized Hidden Semi-Markov Models,” Technical Report 208, Department of Computer Science, Humboldt University, Berlin, Germany, 2006. [14] F. Jensen, “Bayesian Networks and Decision Graphs,” Statistics for Engineering and Information Science, Springer, 2001. [15] K. Korb and A. Nicholson, “Bayesian Artificial Intelli- gence,” CRC Press, 2003. doi:10.1201/9780203491294 [16] S. Zhang, J. Li and X. Chen, “Building Network Attack Graph for Aalert Causal Correlation,” Computers & Se- curity, Vol. 27, No. 5-6, 2008, pp. 188-196. doi:10.1016/ j.cose.2008.05.005 [17] “National Institute of Standards and Technology,” 2010. Common Vulnerability Scoring System. http://nvd.nist.gov/cvss.cfm [18] “Open Security Foundation,” 2010. OSVDB: The Open Source Vulnerability Database. http://osvdb.org/  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 22 Annex A: Pseudocode of Subfunctions SF1. UpdateAttackGraph—called in ImprovedLike- lihood Weighting SF2. IsCriticalCausation—called in UpdateAttack- Graph and later SFs SF3. SelectEvidenceCausation—called in Improved- LikelihoodWeighting UpdateAttackGraph(AG,X,Y) Input: AG—an attack sample X—an ancestor node Y—a descendant node Output: a boolean variable indicating if AG is updated Alg: 01: updated←False; 02: if (Y cand not sampled) then 03: if (for each node X’ in Pre(Y) variable X’=True) then 04: if (for each node X’ in Pre(Y) IsCriticalCausation(AG,Y,X’,Ø)=False) then 05: Y←the sampling result according to 1()Y ; 07: if (Y=True) then 08: for (each node X’ in Pre(Y)) 09: FX←FX∪{Y}; 10: BY←BY∪{X}; 11: end for (08) 12: updated←True; 13: for (each node Z in Con(Y)) 14: if (edge Y→Z is not sampled) then 15: UpdateAttackGraph (AG,Y,Z); 16: end if (14) 17: end for (13) 18: end if (07) 19: mark Y as sampled; 20: for (each node X’ in Pre(Y)) 21: mark edge X’→Y as sampled; 22: end for (20) 23: end if (04) 24: end if (03) 25: end if (02) 26: if (Y is other type node) then 27: if (!IsCriticalCausation(AG,Y,X,Ø)) then 28: Yold←Y; 29: y←sampling result by (,) X Y or (,) X Y ; 30: if (y=True) then 31: Y←True; 32: FX←FX∪{Y}; 33: BY←BY∪{X}; 34: updated←True; 35: if (Yold=False) then 36: for (each node Z in Con(Y)) 37: if (edge Y→Z is not sampled) then 38: UpdateAttackGraph(AG,Y,Z); 39: end if (37) 40: end for (36) 41: end if (35) 42: end if (30) 43: mark edge X→Y as sampled; 44: end if (27) 45: end if (26) 46: return updated; IsCriticalCausation(AG,X,Y,H) Input: AG—an attack sample X—a candidate causation node Y—a candidate affection node H—a set to hold historically processed nodes Output: a boolean variable indicating if X is a critical causation of Y Alg: 01: if (Y is an action node) then 02: if (Y∈H ∨BY=Ø) then 03: r←False; 04: end if (02) 05: if (X∈BY (∨for each node Z in BY, IsCriticalCausation(AG,X,Z, H∪{Y})=True)) then 06: r←True; 07: else (05) 08: r←False; 09: end if (05) 10: end if (01) 11: if (Y is other type node) then 12: if (Y∈H或BY=Ø) then 13: r←False; 14: end if (12) 15: if ({X}=BY (∨for each node Z in BY, IsCriticalCausation(AG,X,Z, H∪{Y})=True)) then 16: r←True; 17: else (15) 18: r←False; 19: end if (15) 20: end if (11) 21: return r; SelectEvidenceCausation(AG,X) Input: AG — a network attack graph X — an observed evidence node (whose value is True) Output: the occurrence probability of the chosen causation set Alg: 01: pΣ←0; 02: Φ←Ø; Ψ←{Y|Y∈Pre(X)∧Y=True}; 03: for (each non-emtpy subset ψ of Ψ) 04: pψ←∏Y∈ψθ(Y,X) * ∏Y(∈Ψ-ψ)(1-θ(Y,X)); 05: Φ←Φ{(∪ψ, pψ)};  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 23 SF4. Transientize—called in ImprovedLikelihood- Weighting SF5. PartialRelationSatisfied—called in Improved- LikelihoodWeighting 06: pΣ←pΣ+pψ; 07: end for (03) 08: for (each pair (ψ, pψ) in Φ) 09: pψ←pψ / pΣ; 10: end for (08) 11: (ψr, pψr)←chose a pair in Φ according to pψ of the pair; 12: for (each node Z in ψ) 13: FZ←FZ∪{X}; 14: BX←BX∪{Z}; 15: end for (12) 16: return pψr*pΣ; Transientize(AG,OD,OF) Input: AG—an attack sample OD—a set of observed evidence nodes OF—a set of not yet observed evidence nodes Output: a boolean indicating AG’s effectiveness after transientization Alg: 01: for (each node X in OF) 02: for (each action node Y in BX) 03: Y←False; 04: mark edge Y→X as not sampled; 05: BX←BX -{Y}; FY←FY -{X}; 06: if (Y is an action node) then 07: mark Y as not sampled; 08: end if (06) 09: for (each node Z in BY) 10: mark edge Z→Y as not sampled; 11: BY←BY -{Z}; FZ←FZ -{Y}; 12: end for (09) 13: end for (02) 14: end for (01) 15: converged←False; 16: while (!converged) 17: converged←True; 18: for (each non-root node in AG) 19: if (X is an action node) then 20: if (X is sampled(some node in ∧BX is False∨ X is the critical causation of some node in BX)) the n 21: X←False; 22: mark X as not sampled; 23: for (each node Y in BX) 24: mark edge Y→X as not sampled; 25: BX←BX -{Y}; FY←FY -{X}; 26: end for (23) 27: converged←False; 28: end if (20) 29: else (19) 30: for (each node Y in BX) 31: if (Y=False∨IsCriticalCausa tion(AG,X,Y,Ø)) then 32: mark edge Y→X as not sampled; 33: BX←BX -{Y}; FY←FY -{X}; PartialRelationSatisfied (AG,O,Ω) Input: AG—an attack sample O—the evidence set of AG Ω—a temporal partial ordering relation set on O Output: a boolean indicating if AG conforms to Ω (and is effective) Alg: 01: typeI_satisfied←True; typeII_satisfied←True; 02: for (each type I partial ordering relation Om↗On in Ω) 03: pairSatisfied←False; 04: for (each node Ai in BOm) 05: existJCoversI←False; 06: for (each node Aj in BOn) 07: if (IsCriticalCausation(AG,Aj,Ai,Ø)) then 08: existJCoversI←True; 09: end if (07) 10: end for (06) 11: if (!existJCoversI) then 12: pairSatisfied←True; 13: end if (11) 14: end for (04) 15: if (!pairSatisfied) then 16: typeI_satisfied←False; 17: end if (15) 18: end for (02) 19: for (each type II partial ordering relation Om↘On in Ω) 20: for (each node Ai in BOm) 21: for (each node Aj in BOn) 22: if (IsCriticalCausation(AG,Aj,Ai,Ø)) 23: typeII_satisfied←False; 24: end if (22) 25: end for (21) 26: end for (20) 27: end for (19) 28: return typeI_satisfied ∧ typeII_satisfied; 34: end if (31) 35: end for (30) 36: if (BX = Ø) then 37: if (X∈OD) then 38: return False; 39: else (37) 40: X←False; 41: converged←False; 42: end if (37) 43: end if (36) 44: end if (19) 45: end for (18) 46: end while (16) 47: return True; 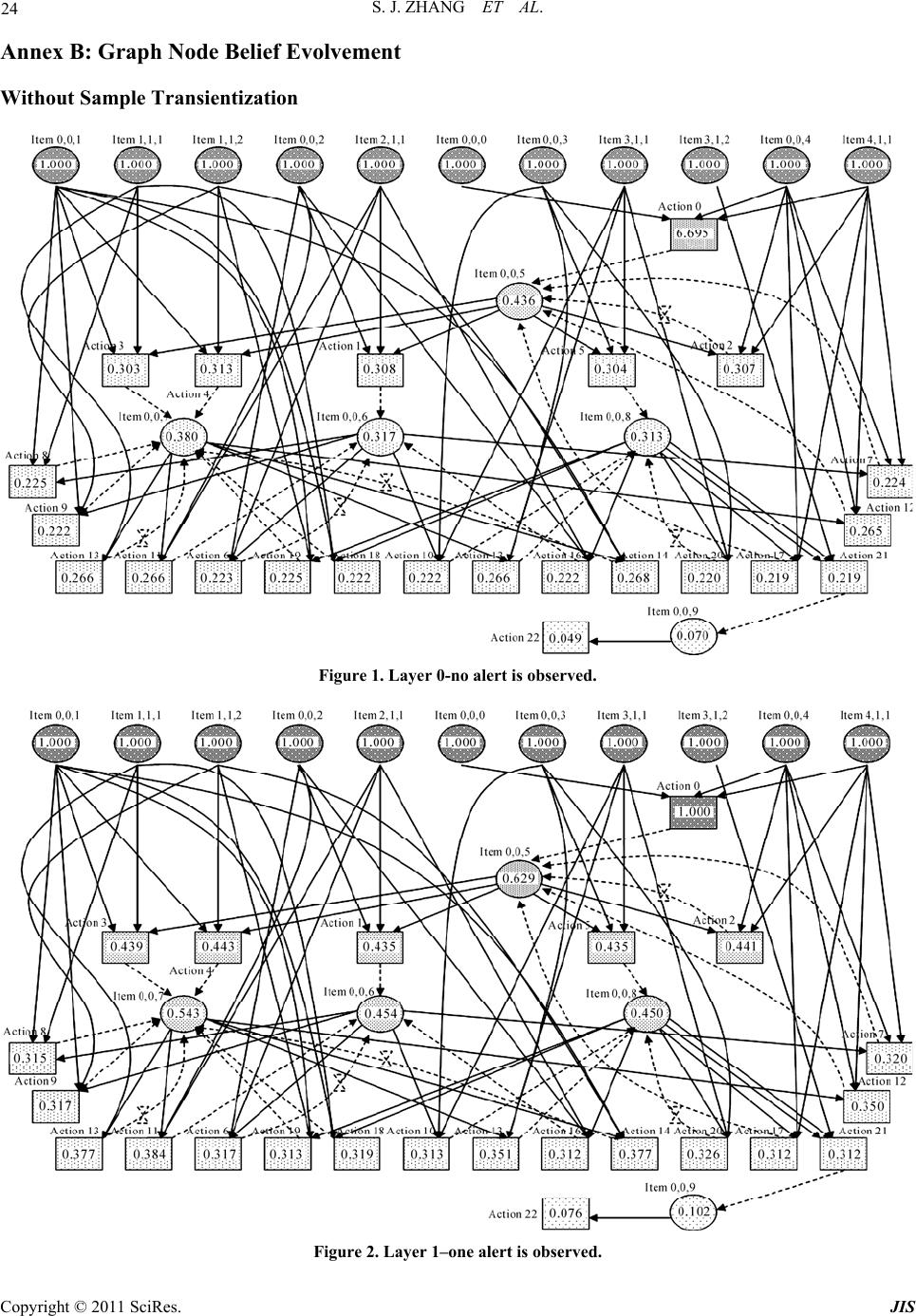 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 24 Annex B: Graph Node Belief Evolvement Without Sample Transientization Figure 1. Layer 0-no alert is observed. Figure 2. Layer 1–one alert is observed. 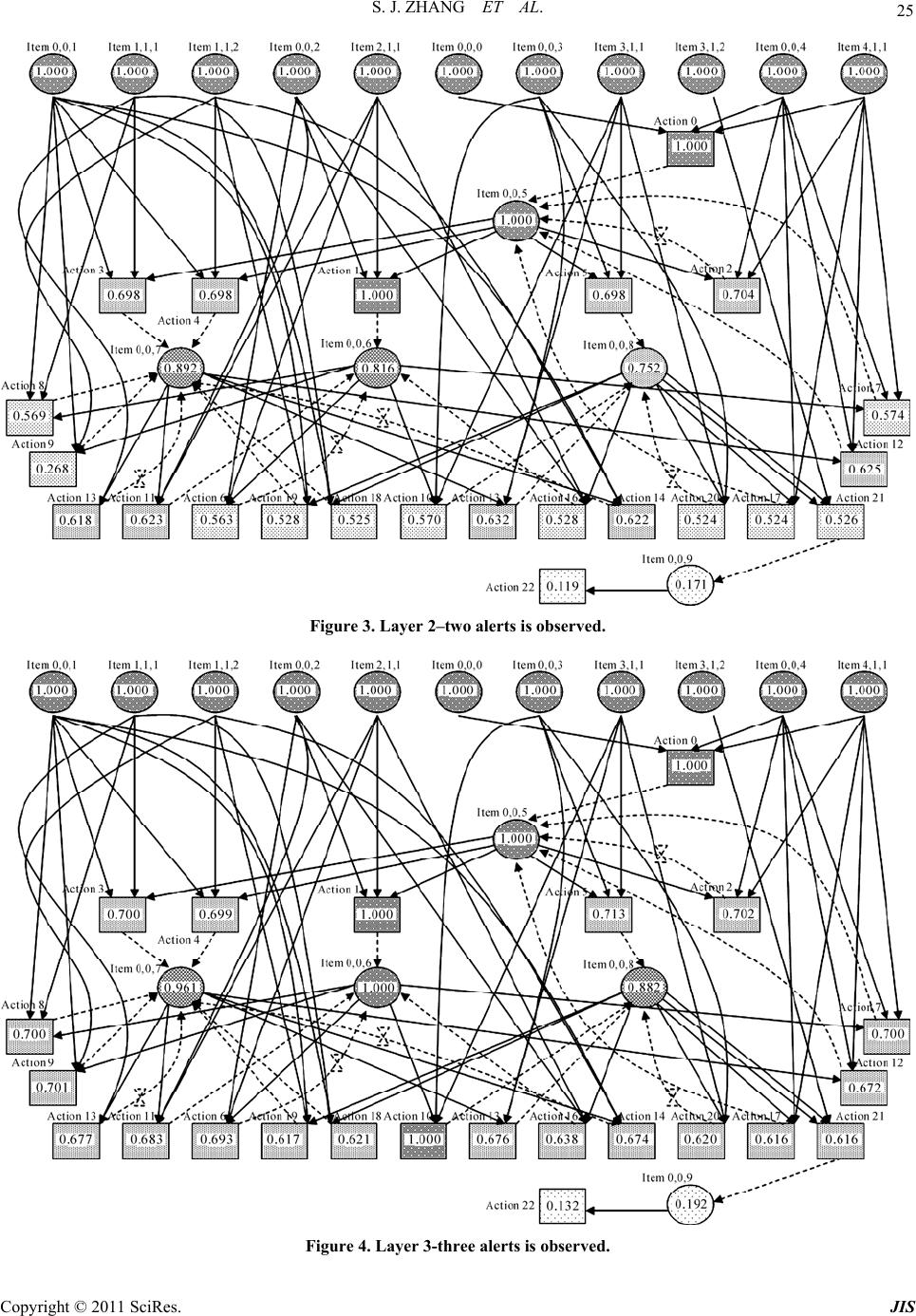 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 25 Figure 3. Layer 2–two alerts is observed. Figure 4. Layer 3-three alerts is observed.  S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 26 With Sample Transientization Figure 1. Layer 0-no alert is observed. Figure 2. Layer 1–one alert is observed. 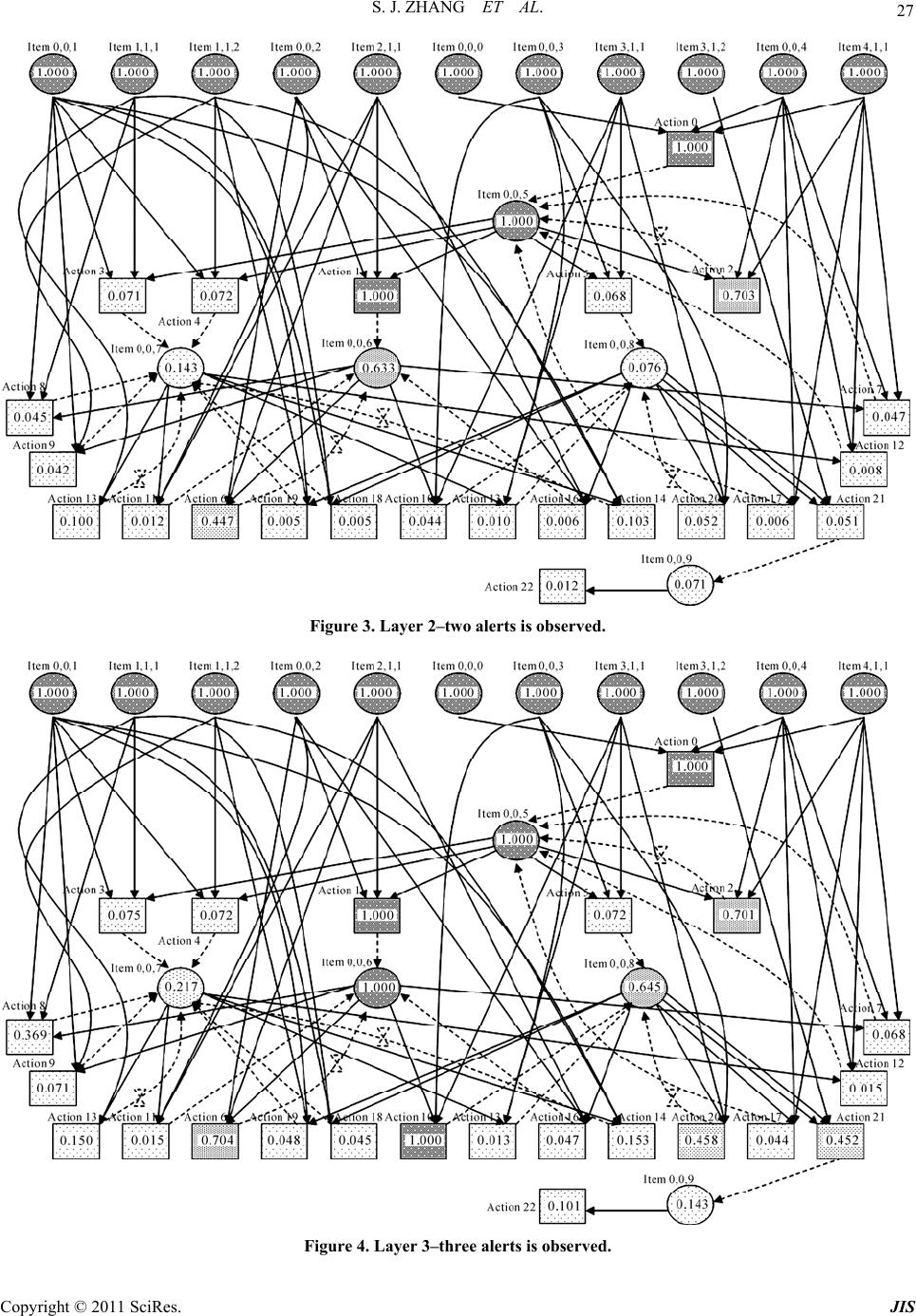 S. J. ZHANG ET AL. Copyright © 2011 SciRes. JIS 27 Figure 3. Layer 2–two alerts is observed. Figure 4. Layer 3–three alerts is observed. |

