Circuits and Systems, 2011, 2, 38-44
doi:10.4236/cs.2011.21007 Published Online January 2011 (http://www.SciRP.org/journal/cs)
Investigation of the Mechanism of Tangent Bifurcation in
Current Mode Controlled Boost Converter
Ling-ling Xie1, Ren-xi Gong1, Kuang Wang2, Hao-ze Zhuo1
1College of Electrical Engineering, Guangxi University, Nanning, China
2Airline Mechanical Company Ltd., Shenzhen, China
Received November 23, 2010; revised November 29, 2010; accepted December 25, 2010
Abstract
Tangent bifurcation is a special bifurcation in nonlinear dynamic systems. The investigation of the mechan-
ism of the tangent bifurcation in current mode controlled boost converters operating in continuous conduc-
tion mode (CCM) is performed. The one-dimensional discrete iterative map of the boost converter is derived.
Based on the tangent bifurcation theorem, the conditions of producing the tangent bifurcation in CCM boost
converters are deduced mathematically. The mechanism of the tangent bifurcation in CCM boost is exposed
from the viewpoint of nonlinear dynamic systems. The tangent bifurcation in the boost converter is verified
by numerical simulations such as discrete iterative maps, bifurcation map and Lyapunov exponent. The si-
mulation results are in agreement with the theoretical analysis, thus validating the correctness of the theory.
Keywords: Tangent Bifurcation, Discrete Iterative Map, Boost Converter, Continuous Current Mode (CCM)
1. Introduction
In recent years, ones are quite interested in chaos exhi-
bited in the field of power electronics. They are becom-
ing the hot spots of the study in the field. DC-DC con-
verters are a kind of strong nonlinear system. They exhi-
bit various bifurcation and chaos behavior under some
operating conditions, such as period-doubling bifurcation
[1-5], Hopf bifurcation [6-8], border collision bifurcation
[9-11], tangent bifurcation [12,13] and chaos behavior
[14-20]. Bifurcation is a complex structure in nonlinear
system. The chaos is characteristic of non-repeat, uncer-
tainty and is extreme sensitive to initial conditions. These
nonlinear phenomena make the nonlinear dynamic cha-
racteristics of DC-DC converter more complex. Deep
investigation of these nonlinear phenomena is of great
benefit to understanding the nonlinear behavior and
practical design.
Up to now, most published papers are mainly about
the period-doubling bifurcation in DC-DC converters.
The tangent bifurcation, which is a special bifurcation,
has been less investigated. The most studies of tangent
bifurcation mainly focus on the numerical simulation
modeling. The main approaches used for simulation in-
clude bifurcation diagram, Lyapunov exponent. The two
methods are characteristics of simpleness and intuition,
but the main shortcoming of that is large computing
quantity, time consuming and blindness. The essential
mechanism causing tangent bifurcation was not analyzed
in these simulation methods. However, no rigorous at-
tempts have been made to analyze formally the essential
mechanism leading to the tangent bifurcation in DC-DC
converters.
Boost converters are a kind of important converters
with wide applications. Current mode control, being one
of the most commonly used control schemes in DC-DC
converters, has received much attention to power elec-
tronics engineers. Although the work in [12] gives no
theoretical insights into the underlying cause of tangent
bifurcation in such system, it does prompt the important
question of what mechanism may give rise to tangent
bifurcation behavior. This paper attempts to answer to
this question in the light of the theories of nonlinear dy-
namic systems. The investigation of the mechanism of
the tangent bifurcation in current mode controlled boost
converters operating in continuous conduction mode
(CCM) is deeply studied. In fact, there are strict stability
criteria and the conditions leading to the tangent bifurca-
tion in mathematics based on the theories of nonlinear
dynamic systems [13,14]. Based on the tangent bifurca-
tion theorem, the conditions leading to the tangent bifur-
cation in the discrete iterative model of the boost con-

L.-L. XIE ET AL.
39
verter are demonstrated mathematically. Discrete itera-
tive maps, bifurcation diagram, Lyapunov exponent are
done to analyze the mechanism and evolution of leading
to the tangent bifurcation. The simulation results are in
agreement with the theoretical analysis, thus validating
the correctness of the theory. The methods proposed in
the paper can also be suitable to analysis of the tangent
bifurcation and chaos of other kinds of converter circuits.
2. Discrete Iterative Map of a Boost
Converter
In Figure 1, the circuit model of a boost converter is
shown, which consists of a switch S, a diode D, a capa-
citor C, an inductor L and the load resistor R connected
in parallel with the capacitor. The assumptions are made
as follows:
1) The boost converter operates in continuous conduc-
tion mode.
2) All the components in the boost converter circuit
are ideal, no parasitic effects are considered.
Hence, there are two circuit states depending on
whether S is closed or open. Assume that the circuit is at
the switch state 1 when the switch S is off and diode D is
on, and at the switch state 2 when S is on and D is off.
The two switch states toggle periodically.
The boost converter is controlled under the current
mode. Switch S is controlled by a feedback path that
consists of a flip-flop and a comparator. The comparator
compares the inductor current iL with a reference current
Iref. The switch is triggered to ON when the clock pulse
is received and is triggered to OFF when the inductor
current reaches the reference current Iref. Specifically,
switch S is turned on at the beginning of each cycle, i.e.
at t=nT, where n is an integer, T is the switching period.
The inductor current iL increases linearly while switch S
is on. As iL approaches to the value of Iref, switch S is
turned off, and remains off until the next cycle begins.
Figure 1. Circuit configuration of current-mode boost con-
verter.
When the switch S closed, diode D is reverse biased.
Figure 2 shows the inductor current waveform. The
circuit parameters of the boost converter are listed in
Table 1.
Let x denote the state vector of the circuit, i.e.,
c
L
v
xi






 (1)
where vC is the voltage across the capacitor and iL is the
current through the inductor.
The state equation for the circuit in any switch state
can be written in the form of
.
iiin
x
Ax BV (2)
where Ai and Bi are the system matrices in switch state i,
and Vin is the input voltage. In switch state 1, we have
1
10
00
ARC











, 1
0
1
B
L




And in switch state 2, we have
2
11
10
RC C
A
L















, 2
0
1
B
L




The switch S is turned off when the inductor current
iL reaches reference current Iref. The closed-state time tn
can be obtained from (2) by integration, therefore the
closed-state time tn is calculated by the Equation (3).
Figure 2. Inductor current waveform.
Table 1. Circuit parameter s.
Circuit Components Values
Switching period T 100 μs
Input Voltage Vin 10 V
Load Resistor R 20 Ω
Inductor L 1 mH
Capacitor C 12 μF
Reference Current Iref 0.5~5.5 A
I
re
f
iL
I
ref
iL
t
t
R
C
L
Vin Vo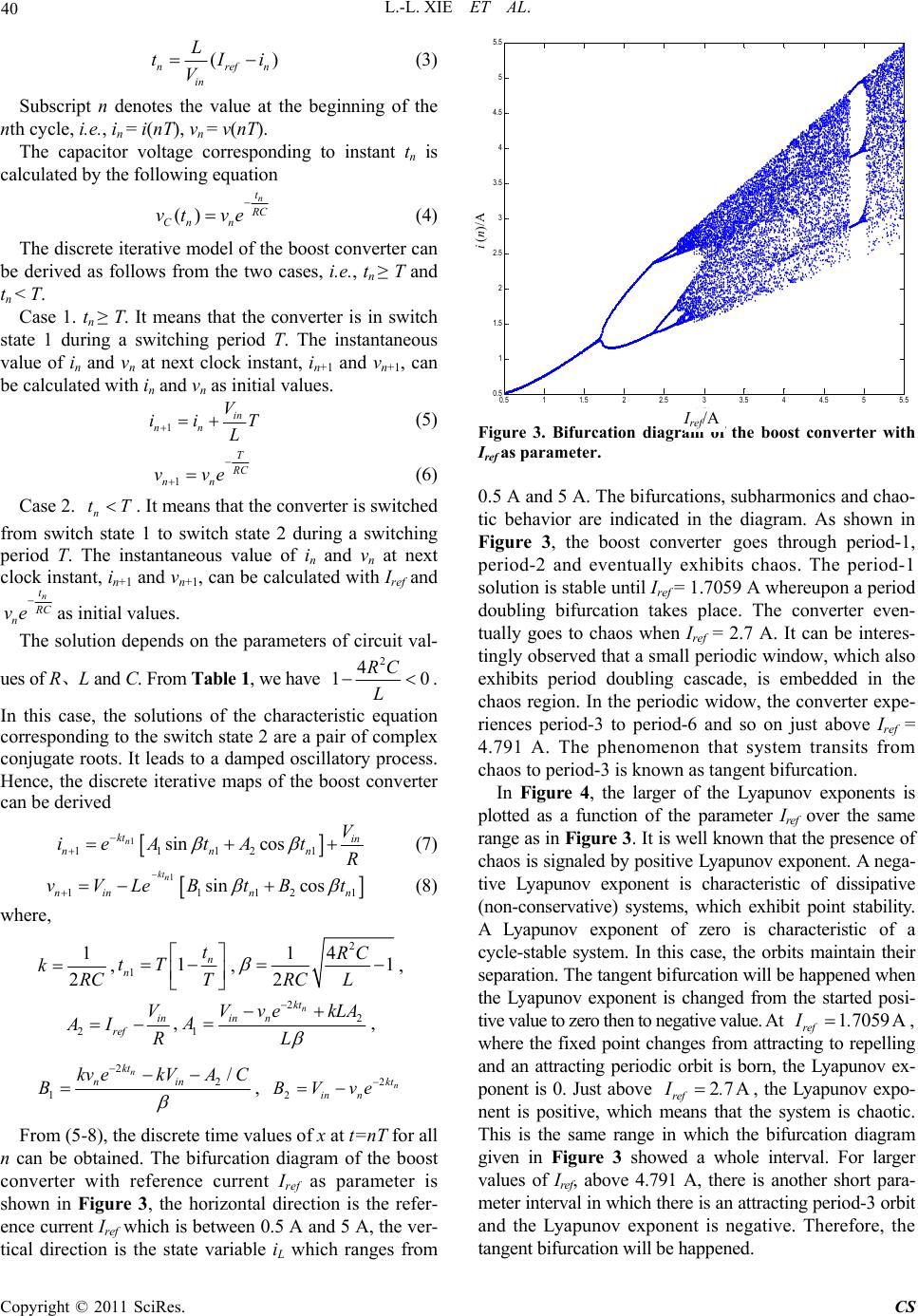

L.-L. XIE ET AL.
40
()
nrefn
in
L
tIi
V
 (3)
Subscript n denotes the value at the beginning of the
nth cycle, i.e., in = i(nT), vn = v(nT).
The capacitor voltage corresponding to instant tn is
calculated by the following equation
()
n
t
R
C
Cn n
vt ve

 (4)
The discrete iterative model of the boost converter can
be derived as follows from the two cases, i.e., tn ≥ T and
tn < T.
Case 1. tn ≥ T. It means that the converter is in switch
state 1 during a switching period T. The instantaneous
value of in and vn at next clock instant, in+1 and vn+1, can
be calculated with in and vn as initial values.
1
in
nn
V
ii T
L
 (5)
1
T
R
C
nn
vve

 (6)
Case 2. n tT. It means that the converter is switched
from switch state 1 to switch state 2 during a switching
period T. The instantaneous value of in and vn at next
clock instant, in+1 and vn+1, can be calculated with Iref and
n
t
R
C
n
ve
as initial values.
The solution depends on the parameters of circuit val-
ues of R、L and C. From Table 1, we have
2
4
10
RC
L

.
In this case, the solutions of the characteristic equation
corresponding to the switch state 2 are a pair of complex
conjugate roots. It leads to a damped oscillatory process.
Hence, the discrete iterative maps of the boost converter
can be derived

1
11121
sin cos
n
kt in
nnn
V
ieAtAt R



(7)

1
11121
sin cos
ktn
ninn n
vVLeBtBt 

 (8)
where,
1
2
kRC ,11n
n
t
tT T




,
2
14 1
2
RC
RC L
 
,
2
in
ref
V
AI R 
,
2
2
1
n
kt
in n
Vve kLA
AL



,
2
2
1
/
n
kt
nin
kv ekVAC
B


, 2
2
n
kt
in n
BVve


From (5-8), the discrete time values of x at t=nT for all
n can be obtained. The bifurcation diagram of the boost
converter with reference current Iref as parameter is
shown in Figure 3, the horizontal direction is the refer-
ence current Iref which is between 0.5 A and 5 A, the ver-
tical direction is the state variable iL which ranges from
0.5 11.5 22.5 33.5 44.5 55. 5
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
Iref/A
i(n)/A
Figure 3. Bifurcation diagram of the boost converter with
Iref as parameter.
0.5 A and 5 A. The bifurcations, subharmonics and chao-
tic behavior are indicated in the diagram. As shown in
Figure 3, the boost converter goes through period-1,
period-2 and eventually exhibits chaos. The period-1
solution is stable until Iref = 1.7059 A whereupon a period
doubling bifurcation takes place. The converter even-
tually goes to chaos when Iref = 2.7 A. It can be interes-
tingly observed that a small periodic window, which also
exhibits period doubling cascade, is embedded in the
chaos region. In the periodic widow, the converter expe-
riences period-3 to period-6 and so on just above Iref =
4.791 A. The phenomenon that system transits from
chaos to period-3 is known as tangent bifurcation.
In Figure 4, the larger of the Lyapunov exponents is
plotted as a function of the parameter Iref over the same
range as in Figure 3. It is well known that the presence of
chaos is signaled by positive Lyapunov exponent. A nega-
tive Lyapunov exponent is characteristic of dissipative
(non-conservative) systems, which exhibit point stability.
A Lyapunov exponent of zero is characteristic of a
cycle-stable system. In this case, the orbits maintain their
separation. The tangent bifurcation will be happened when
the Lyapunov exponent is changed from the started posi-
tive value to zero then to negative value. At 17059 A
ref
I.,
where the fixed point changes from attracting to repelling
and an attracting periodic orbit is born, the Lyapunov ex-
ponent is 0. Just above 27A
ref
I., the Lyapunov expo-
nent is positive, which means that the system is chaotic.
This is the same range in which the bifurcation diagram
given in Figure 3 showed a whole interval. For larger
values of Iref , above 4.791 A, there is another short para-
meter interval in which there is an attracting period-3 orbit
and the Lyapunov exponent is negative. Therefore, the
tangent bifurcation will be happened.
i (n)/A
I
ref/A

L.-L. XIE ET AL.
41
Figure 4. Larger Lyapunov exponent diagram.
3. The Conditions Leading to Tangent
Bifurcation
3.1. A Theorem of Tangent Bifurcation
The theorem of tangent bifurcation is briefly reviewed in
this section.
Consider the discrete-time nonlinear system


,xfx

 (9)
where x is the system variable and μ is a parameter.
A point *
x
is called a fixed point or a stationary
point if

***
,xfx

.
It is convenient to have a notation for these functions.
We write


0
f
xx for the 0th iterate that is the iden-
tity,

1
f
xfor


f
x, and


2
f
x for the composition
of f with f, that is
  
2
f
xffx. Continuing by
induction, we obtain
 

() 1
,
nn
f
xff x 

, is the
composition of f with itself n times. Using this nota-
tion, for the initial condition0
x
,

10
x
fx,


2
20
x
fx,
and


0
n
n
x
fx.
Theorem 1 [13,14] (Tangent Bifurcation). Assume that
f is a C2 function from R2 to R. We write
 
f
x,fx .

  Assume that there is a bifurcation
value *

that has a fixed point *
x
with derivative
equal to one
1).

** *
f
x, x  
2).


*
'*
1fx


3). The second derivative


*
'' *0fx

, so the graph of
*
f

lies on one side of the diagonal for x near *
x
.
4). The graph of
f

is moving up or down as the pa-
rameter

varies, or more specifically,

**
,0
fx




The tangent bifurcation takes place in the nonlinear
system at the fixed point


**
,x

,
3.2. Derivation of One-Dimensional Discrete
Iterative Map
The research of tangent bifurcation should be start from
one-dimensional discrete iterative map [12,13]. With one
state vector be fixed, reduction of dimension can be done
in the boost converter so that the boost converter is
transformed into one-dimensional dynamic system. In
this study, the capacitor voltage is taken as the state va-
riable needing to be fixed, and the inductor current is
chosen as the state variable. The capacitor voltage vc is
assumed to be a constant CO V, then, the inductor current
increases and decreases linearly during any period. The
following one-dimensional discrete iterative map can be
derived by substituting of cCO vV into (5-8),
Case 3. n tT.

1
in
nnn
V
ifiiT
L
 (10)
Case 4. .
n
tT




1
1
312 1
sin cos
n
nn
kt in
nn
ifi
V
eAtAt R





(11)
where
2
2
3
n
kt
in co
VVe kLA
AL





From (10) and (11),


2
n
f
i is obtained
Case 5. ’
2n
tT.
 
2
21 2in nn nn
V
ifi fiiT
L


(12)
Case 6. ’
2n
tT

.





2
(2)
21
422 2
sin cos
n
nn n
kt in
nn
ifi fi
V
eAtAt R





(13)
where,
'
2
21n
n
t
tT T






,

'
21 nrefn
in
L
tIi
V
 ,
'2
2
2
4
n
kt
in co
VVe kLA
AL




Similarly, 3()
n
f
i is obtained
Case 7. t’
n3 ≥ T.
 
3
32 3in nn nn
V
ifi fiiT
L


(14)
Case 8. ’
3n
tT

.





3
(3)
32
532 3
sin cos
n
nn n
kt in
nn
ifi fi
V
eAtAt R





(15)
where,
'
3
31n
n
t
tT T






,

'
32 nrefn
in
L
tIi
V



,
I
re
f
/A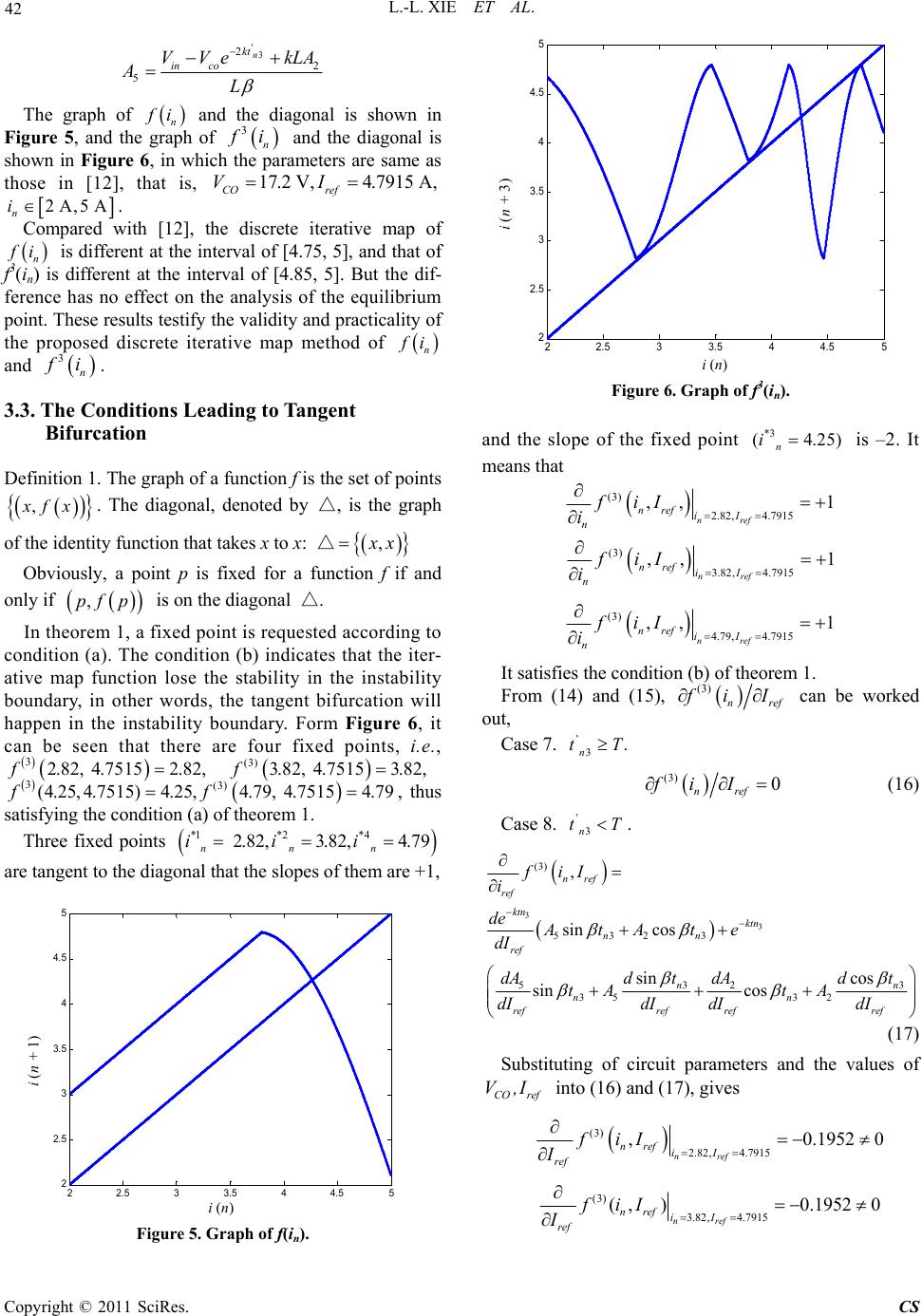

L.-L. XIE ET AL.
42
'3
2
2
5
n
kt
in co
VVe kLA
AL




The graph of

n
f
i and the diagonal is shown in
Figure 5, and the graph of 

3
n
f
i and the diagonal is
shown in Figure 6, in which the parameters are same as
those in [12], that is, 17.2 V,4.7915 A,
CO ref
VI




2 A,5 A
n
i.
Compared with [12], the discrete iterative map of

n
f
i is different at the interval of [4.75, 5], and that of
f3(in) is different at the interval of [4.85, 5]. But the dif-
ference has no effect on the analysis of the equilibrium
point. These results testify the validity and practicality of
the proposed discrete iterative map method of


n
f
i
and


3
n
f
i.
3.3. The Conditions Leading to Tangent
Bifurcation
Definition 1. The graph of a function f is the set of points
 



,
x
fx . The diagonal, denoted by △, is the graph
of the identity function that takes x to x: △




,
x
x
Obviously, a point p is fixed for a function f if and
only if




,
p
fp is on the diagonal △.
In theorem 1, a fixed point is requested according to
condition (a). The condition (b) indicates that the iter-
ative map function lose the stability in the instability
boundary, in other words, the tangent bifurcation will
happen in the instability boundary. Form Figure 6, it
can be seen that there are four fixed points, i.e.,

 
3(3)
2.82, 4.75152.82,3.82, 4.75153.82,ff


3(3)
(4.25,4.7515)4.25,4.79, 4.75154.79ff , thus
satisfying the condition (a) of theorem 1.
Three fixed points

*1*2 *4
2.82, 3.82,4.79
nnn
iii
are tangent to the diagonal that the slopes of them are +1,
22.5 33.5 44.5 5
2
2. 5
3
3. 5
4
4. 5
5
in
i(n+1)
Figure 5. Graph of f(in).
22.5 33.5 44.5 5
2
2.5
3
3.5
4
4.5
5
in
i(n+3)
Figure 6. Graph of f3(in).
and the slope of the fixed point *3 (4.25)
n
i is –2. It
means that

(3)
2.82, 4.7915
,, 1
nref
nref iI
n
fiI
i



(3)
3.82, 4.7915
,, 1
nref
nref iI
n
fiI
i



(3)
4.79, 4.7915
,, 1
nref
nref iI
n
fiI
i


It satisfies the condition (b) of theorem 1.
From (14) and (15), 

(3)
nref
f
iI can be worked
out,
Case 7. ’
3. n
tT


(3) 0
nref
fi I


(16)
Case 8. ’
3n
tT

.


3
3
(3)
532 3
53 3
2
35 32
,
sin cos
sin cos
sin cos
nref
ref
ktn
ktn
nn
ref
nn
nn
refref refref
fiI
i
de AtAte
dI
dAd tdt
dA
tA tA
dIdI dIdI








 



(17)
Substituting of circuit parameters and the values of
CO ref
V,I into (16) and (17), gives

(3)
2.82, 4.7915
,0.1952 0
nref
nref
iI
ref
fiI
I
 

(3)
3.82, 4.7915
( ,)0.19520
nref
nref
iI
ref
fiI
I
 

i (n)
i (n + 1)
i (n)
i (n + 3)

L.-L. XIE ET AL.
43

(3)
4.7915, 4.79
,0.16390
ref n
ref ii
ref
fix
i


There is no question that it satisfies condition (c) of
theorem 1.
The secondary partial derivative

2
(3)
2,
nref
n
f
iI
i


can be also obtained according to (14) and (15), which is
as follows
Case 7. 3
’
n
tT.

2
(3)
2,0
nref
n
fiI
i

 (18)
Case 8. 3
’
n
tT.



3
3
22
(3)
5323
22
2
532 3
2
,,sin cos
sin cos
n
n
kt
nrefn n
nn
kt
nn
n
e
f
iIAt At
ii
eAtAt
i










(19)
Similarly, substituting of the parameters values into
(18) and (19), gives

2
(3)
22.82, 4.7915
,14.4706 0
nref
nref
iI
n
fiI
i



2
(3)
23.82, 4.7915
,14.4706 0
nref
nref
iI
n
fiI
i



2
(3)
24.79, 4.7915
,47.7344 0
nref
nref
iI
n
fiI
i
 

Without question, it satisfies condition (d) of theorem 1.
In summary, the current mode controlled boost con-
verter operating in CCM satisfies the hypothesis of theo-
rem 1. Therefore, the discrete iterative map of f3(in) un-
dergoes the tangent bifurcation at the fixed point, and the
tangent bifurcation behavior occurs in this system.
4. Conclusions
The mechanism of tangent bifurcation in the current
mode controlled boost converter operating in CCM is
explored in this paper. Based on the discrete iterative
map of the boost converter, by taking the capacitor vol-
tage as a constant, and choosing the inductor current as
the state variable, the one-dimensional discrete iterative
maps of

n
f
i and


3
n
f
i have been derived. It is
demonstrated in mechanism that the tangent bifurcation
will happen inevitably in the boost converter according
to the tangent bifurcation theorem. The computer simula-
tions, such as discrete iterative maps, bifurcation diagram
with reference current ref
I as parameter, Lyapunov
exponent are used to verify the phenomenon. It has been
shown that tangent bifurcation does exist for this system.
The method presented in the paper provides the theoreti-
cal basics for analyzing the tangent bifurcation and chaos.
It has generality and can be also used to analyze the tan-
gent bifurcation of other kinds of DC-DC converters.
5. References
[1] F. Angulo, G. Olivar and M. di Bernardo, “Two-Pa-
rameter Discontinuity-Induced Bifurcation Curves in a
ZAD-Strategy-Controlled DC–DC Buck Converter,” IEEE
Transactions on Circuits and Systems I: Regular Papers,
Vol. 55, No. 8, 2008, pp. 2393-2401. doi:10.1109/TCSI.
2008.918226
[2] X. Q. Wu, S.-C. Wong, C. K. Tse and J. Lu, “Bifurcation
Behavior of SPICE Simulation of Switching Converters:
A Systematic Analysis of ErroneousResults,” IEEE Trans-
actions on Power Electronics, Vol. 22, No. 5, 2007, pp.
1743-1752. doi:10.1109/TPEL.2007.904207
[3] A. El Aroudi and R. Lewa, “Quasi-Periodic Route to
Chaos in a PWM Voltage-Controlled DC-DC Boost
Converter,” IEEE Transactions on Circuits and Systems I:
Fundamental Theory and Applications, Vol. 48, No. 8,
2001, pp. 967-978. doi:10.1109/81.940187
[4] Ch. Bi, J. M. Wang, Z. W. Lan, K. L. Jia and T. Hu, “In-
vestigation of Bifurcation and Chaos in Forward Conver-
ter,” Proceedings International Conference on Mecha-
tronics and Automation, Harbin, 5-8 August 2007, pp.
663-668. doi:10.1109/ICMA.2007.4303622
[5] X.-M. Wang, B. Zhang and D.-Y. Qiu, “Mechanism of
Period-Doubling Bifurcation in DCM DC-DC Conver-
ter,” Acta Physica Sinice, Vol. 57, No. 6, 2008, pp.
2728-2736.
[6] A. Kavitha and G. Uma, “ Experimental Verification of
Hopf Bifurcation in DC-DC Luo Converter,” IEEE
Transactions on Power Electronics, Vol. 23, No. 6, 2008,
pp. 2878-2883. doi:10.1109/TPEL.2008.2004703
[7] M. B. D’Amico, J. L. Moiola and E. E. Paolini, “Hopf
Bifurcation for Maps: A Frequency-Domain Approach,”
IEEE Transactions on Circuits and Systems I: Funda-
mental Theory and Applications, Vol. 49, No. 3, 2002, pp.
281-288. doi:10.1109/81.989161
[8] M. Debbat, A. El Aroud, R. Giral and L. Marti-
nez-Salamero, “Hopf Bifurcation in PWM Controlled
Asymmetrical Interleaved Dual Boost DC-DC Converter,”
Proceedings IEEE International Conference on Industrial
Technology, Vol. 2, Maribor, 10-12 December 2003, pp.
860-865.
[9] Z. T. Zhusubaliyev, E. A. Soukhoterin and E. Mosekilde,
“Quasi-Periodicity and Border-Collision Bifurcations in a
DC-DC Converter with Pulsewidth Modulation,” IEEE
Transactions on Circuits and Systems I: Fundamental
Theory and Applications, Vol. 50, No. 8, 2003, pp. 1047-
1057. doi:10.1109/TCSI.2003.815196

L.-L. XIE ET AL.
44
[10] M. Yue, C. K. Tse, T. Kousaka and H. Kawakami,
“Connecting Border Collision with Saddle-Node in
Switched Dynamical Systems,” IEEE Transactions on
Circuits and Systems II: Express Briefs, Vol. 52, No. 9,
2005, pp. 581-585. doi:10.1109/TCSII.2005.850488
[11] H. Khammari and M. Benrejeb, “Tangent Bifurcation in
Doubling Period Process of a Resonant Circuit’s Res-
ponses,” Proceedings IEEE International Conference on
Industrial Technology, Vol. 3, Hammamet, 8-10 Decem-
ber 2004, pp. 1281-1286.
[12] Y. F. Zhou and J. N. Chen, “Tangent Bifurcation and
Intermittent Chaos in Current-Mode Controlled Boost
Converter,” Proceedings of the Chinese Society for Elec-
trical Engineering, Vol.25, No.1, 2005, pp. 23-26.
[13] B. L. Hao, “Starting with Parabolas, an Introduction to
Chaotic Dynamics,” Shanghai Scientific and Technolo-
gical Education Publishing House, Shanghai, 1993.
[14] R. C. Robinson, “An Introduction to Dynamical Systems:
Continuous and Discrete,” Pearson Prentice Hall, New
Jersey, 2004.
[15] C. K. Tse, “Flip Bifimcation and Chaos in the Three-
State Boost Switching Regulars,” IEEE Transactions on
Circuits Systems I: Fundamental Theory and Applications,
Vol. 41, No. 1, 1994, pp. 16-23. doi:10.1109/81.260215
[16] C. K. Tse and M. di Bernardo, “Complex Behavior in
Switching Power Converters,” Proceedings of the IEEE,
Vol. 90, No. 5, 2002, pp. 768-781. doi:10.1109/JPROC.
2002.1015006
[17] B. Basak and S. Parui, “Exploration of Bifurcation and
Chaos in Buck Converter Supplied from a Rectifier,”
IEEE Transactions on Power Electronics, Vol. 25, No. 6,
2010, pp. 1556-1564. doi:10.1109/TPEL.2009.2035500
[18] F.-H. Hsieh, K.-M. Lin and J.-H. Su, “Chaos Phenome-
non in UC3842 Current-Programmed Flyback Conver-
ters,” Proceedings IEEE Conference on Industrial Elec-
tronics and Applications, Xi’an, 25-27 May 2009, pp.
166-171.
[19] J. H. Chen, K. T. Chau and C. C. Chan, “Analysis of
Chaos in Current-Mode-Controlled DC Drive Systems,”
IEEE Transactions on Industrial Electronics, Vol. 47, No.
1, 2000, pp. 67-76. doi:10.1109/41.824127
[20] K. W. E. Cheng, M. J. Liu and Y. L. Ho, “Experimental
Confirmation of Frequency Correlation for Bifurcation in
Current-Mode Controlled Buck-Boost Converters,” IEEE
Power Electronics Letters, Vol. 1, No. 4, 2003, pp.
101-103. doi:10.1109/LPEL.2004.825548