J. Software Engineering & Applications, 2010, 3, 1141-1147
doi:10.4236/jsea.2010.312133 Published Online December 2010 (http://www.scirp.org/journal/jsea)
1141
An Efficient PRBG Based on Chaotic Map and
Engel Continued Fractions
Atef Masmoudi1,2, William Puech2, Mohamed Salim Bouhlel1
1Research Unit: Sciences and Technologies of Image and Telecommunications, Higher Institute of Biotechnology, University of Sfax,
Sfax, Tunisia; 2Laboratory LIRMM, University of Montpellier II, Montpellier, France
Received March 3rd, 2010; revised April 12th, 2010; accepted April 16th, 2010.
ABSTRACT
In recent years, a variety of chaos-based cryptosystems have been proposed. Some of these systems are used in design-
ing a pseudo random bit genera tor (PRBG) for stream cipher application s. Most of the chaotic systems used in crypto-
graphy have good chaotic properties like ergodicity, sensitivity to initial values and sensitivity to control parameters.
However, some of them are not very suitable for use in cryptography because of their non-uniform density function, and
their relatively small key space. To be used in cryptography, a PRBG may need to meet stronger requirements than for
other applications. In particular, various statistical tests can be applied to the outputs of such generators to conclude
whether the generator produ ces a truly random sequen ce or not. In this pap er, we propose a PRBG based on the use of
the standard chaotic map with large key space and the Engle Continued Fractions (ECF) map. The outputs of the stan-
dard map are used as the inputs of ECF-map. The chaotic nature of the standard map and the good statistical proper-
ties of the ECF map motivate us to design a new PRBG for stream cipher applications. The numerical simulation anal-
ysis indicates that our PRBG produces bit sequences possessing excellent statistical and cryptographic properties.
Keywords: Cry ptography , Continued Fraction, Statistical Tests, PRBG, Chaotic Map
1. Introduction
Recently, a variety of crypto-systems have been pro-
po sed. Many of them are based on chaotic systems [1-5]
which possess good cryptographic characteristics. Chaos
systems have many important features like ergodicity,
sensitivity to initial condition, sensitivity to control pa-
rameters and randomness. These features are very im-
portant in cryptography as they form the basis of some
new and efficient ways to develop encryption algorithms
for secure digital image transmission over the Internet
and through public networks. In addition, most of the
chaos-based image cryptosystems are based on a single
chaotic system. And it is possible according to the chaos
theory to extract some useful information about the
chaotic system from its orbit, which makes chaotic sys-
tems in sec ur e [6-8 ]. To over co me th ese dr awb ack s, some
techniques such as multiple chaotic systems [9-12],
high-dimensional chaotic systems [13-15], multiple ite-
rations of chaotic systems, and many other techniques
have been proposed to improve chaos-based ciphers
[6,16]. To be used in cryptographic applications, a cha-
otic system must sat isfy two important characteristics;
its large key space, to resist bruit force attacks, and its
ability to generate a sequence that has a uniform inva-
riant density function to make it resistant to statistical
attacks. The problem is that not all chaotic systems sa-
tisfy these characteristics. For example, the chaotic logi-
stic map is widely used to design cryptosystems. The
known one-Dimensional logistic map is defined as


11 nnn
x
xx 
 where


0,4  , 0, 1,2,nand

 1,0

n
x. Mi et al. [17] proposed a chaotic encryption
scheme based on randomized arithmetic coding using the
logistic map as the PRBG. In [18], Kanso and Smaoui
proposed two Pseudo Random Bit Gener ator (PRBG) for
stream cipher applications. The first is based on a single
1-D logistic map and the second is based on a combina-
tion of two logistic maps. The logistic map is weak in
security because it neither satisfies the uniform distribu-
tion proper ty nor d o es its k ey space [1 9,20]. Fo r this map,
the key size is determined by the initial value 0 x and
the control parameter

; 50 bits with a precision of 10-14.
In [11], Patidar and Sud proposed a PRBG for stream
cipher applications based on two chaotic standard maps
running side-by-side and starting from randomly inde

An Efficient PRBG Based on Chaotic Map and Engel Continued Fractions 1142
pendent initial conditions. The pseudo random bit se-
quence is generated by comparing the outputs of both the
chaotic standard maps. They presented the detailed re-
sults of the statistical testing on generated bit sequences,
using two statistical test suites: the NIST [21] and the
DIEHARD [22]. Thus, the need to find a secure and effi-
cient chaotic-based cryptosystem motivates us to propose
a new scheme which consists of using the standard chao-
tic map and the Engle Continued Fractions (ECF) map.
The use of ECF-map increases the complexity of a cryp-
tosystem based only on standard chaotic system and thus
makes difficulties in extraction of information about it.
In addition, ECF-map conserves the cryptography prop-
erties of the chaotic system; like sensitivity to initial
values/control parameters, non periodicity and random-
ness; and adds interesting statistical properties such uni-
form distribution density function and zero co-corre-
lation.
The rest of this paper is organized as follows. In Sec-
tion 2, we discuss the CF theory and we present a brief
description of the ECF-map along with some important
features. Section 3 details our proposed PRBG for stream
cipher applications. In Section 4, we analyze the security
of the proposed PRBG and discuss experimental results
based on statistical testing. The concluding remarks are
given in Section 5.
2. Continued Fraction
Continued fractions (CF) [23-26] refer to all expressions
of the form:
1
0
1
2
2
3
4
3...
a
xb a
ba
ba
b




(1)
Where i a(i > 0) are the partial numerators, i b are the
partial denominators, 0 b is the integer part of the con-
tinued fraction and
x
is a real numb er.
Hartono et al. [27] introduce a new contin ued fraction
expansion, called Engel continued fraction (ECF) expan-
sion.
The Engel continued fraction (ECF) map


:[0,1)0,1
E
T is given by :

11 10
1
00
if x
xx
Tx
Ex
if x





 






(2)
For any
 
1,0x, the ECF-map generates a new and
unique continued fraction expansion of
x
of the form:
1
1
12
21
3
1,,
nnn
n
n
x
bINbb
b
bb
bb
bb





 
(3)
Let

 1,0

x, and define:

11 1
bbx
x











11
1,2, 0,
nn
nn EE
bbxbT xnT x



(4)
Where

 xxTE
0and
   xTTxTn
EE
n
E1
for 1n.
From definition of E
Tit follows that:


11
1
12
21
3
1
1,
E
nn
nnE
xbbTx
b
bb
bb
bbbTx







(5)
We describe the method for generating the ECF-con-
tinued fraction expansion of x as follows.
Algorithm 1 ECF expansion
Initialize 0,
0


ixx
while 0
1

x do

































11
1
1
11
1
1
1
1
ii
i
i
i
i
xx
x
x
x
b
ii
end while
From the theorem presented in [27], if we let


1,0

x,
then
x
has a finite ECF-expansion (i.e.,


0xT n
E for
some 1n) if and only if
x
Q. In this paper, we pay
most attention to the following sequence:




,1.
n
nnE
Zx bxTxn

 (6)
The sequence
 
1
n
ii
Zx

is in
 
0,1 and uniformly
distributed for almost all points
x
(for a proof see [27]).
So, the ECF-map generates a random and unpredictable
sequence
 
1
n
ii
Zx

with a uniform distribution. These

An Efficient PRBG Based on Chaotic Map and Engel Continued Fractions 1143
properties, which are very useful in cryptography, moti-
vate us to propose a new PRBG for stream cipher appli-
cations based on ECF-ma p.
3. The Proposed Pseudo Random Bit
Generator Algorithm
In this section, we describe the process of the proposed
PRBG. The first step in designing the proposed PRBG is
to choose an n-Dimensional chaotic map [10,28]. Choo-
sing maps for encryption algorithms is the most impor-
tant task. The use of chaotic maps can make the output
very sensitive to the input and in our PRBG, the outputs
of the chosen chaotic map are used as the input to the
ECF-map for generating sequences with desirable chao-
tic and statistical properties. In the proposed PRBG, we
suggest to use the standard map due to their good chaotic
properties like sensitivity to the initial values, sensitivity
to the control parameter and its large key space. The 2-D
map function known as the standard map is defined by:

10 1
1
sin ,
jj j
jj j
xx py
yy x







(7)
Where j x and
j
y are taken modulo 2

. The secret
key in the proposed PRBG is a set of three floating point
numbers and one integer

000 0
,,,
x
ypN , where

00
,[0,2)xy

 is the initial values, 0 p is the control
parameter value which can have any real value greater
than 0.18 and 0
N is the number of initial iterations of
the standard chaotic map. The standard map has a good
chaotic properties and a large key space of the order 157
bits [10] with an accuracy of 14 10. This key space is
sufficient enough to resist the brute-force attack. In the
following paragraph, we give the detailed procedure to
generate pseudo random binary sequences using the
standard and ECF maps.
We define a funct i on


:[0,1)0,1G such that:
 
,
ijiji
jj
Gx ZxZx








(8)
Where


j
Z
is the set calculated according to (6) using
ECF-map. In addition, assuming that we have defined a
function
  1,01,0:F that converts the real number
i
x to a discrete bit symbol as follows:

00.5
,
1
i
i
ifx
Fx otherwise



 (9)
We propose to use the 2-D standard map, with parame-
ters  )2,0[, 00

yx are the initial values and 0 p is the
control parameter of the chaotic map. Firstly, we propose
to iterate the chaotic map0
ptimes. And the operation
procedures of the proposed PRBG are described as fol-
lows:
1) Step 1: The standard map is iterated continuously.
For the jth iteration, the output of the standard map is a
new 2-tuplet




,0,2
jj
xy

.
2) Step 2: Now, we propose to calculate the set


1
N
j
j
a

using the relation:

 
jjj jj
axyxy

 

(10)
3) Step 3: Finally, the sequence

1
N
Njj
Kk

 repre-
sents the random binary sequence and it is generated by:
 
jj
kFGa (11)
The standard and ECF maps are iterated until the gen-
eration of a key stream with length N. In order to gener-
ate the random binary sequence

1
N
j
j
k, an initial se-
quence


1
N
j
j
a

has to be created using the standard map.
From a cryptographic point of view, the sequence


1
N
j
j
a

is not good enough for designing a PRBG be-
cause it is not random. Therefore, we propose to use the
ECF-map to convert the gener ated sequence


1
N
j
j
a

to a
binary sequence


1
N
j
j
k

of the same length by applying
(11).
4. Statistical Tests
In this section, we apply the statistical test suite d esigned
by NIST [21] to verify the randomness of the binary se-
quences generated by our PRBG. The NIST test suite
includes 16 independent and computationally intensive
statistical tests. These tests are useful in detecting devia-
tions of a binary sequence from randomness. The 16 tests
can be classified into two categories:
1) Non-parameterized tests: Frequency (monobit)
test (FT), Runs test (RT), Test for longest run of ones in
a block (LROT), Lempel-Ziv compression test (LZT),
Binary matrix rank test (MRT), Cumulative sums test
(CST), Discrete Fourier transform (spectral) test (SPT),
Random excursions test (RET) and Random excursions
variant test (REVT).
2) Parameterized tests: Frequency test within a block
(BFT), Approximate entropy test (AET), Linear com-
plexity test (LCT), Maurer’s universal statistical test
(MUST), Serial test (ST), Overlapping template match-
ing test (OTMT) and Non-overlapping template match-
ing test (NOTMT). The detailed description of all 16
tests of NIST suite can be found in [21].
4.1. Statistical Analysis of the Proposed PRBG
First, the generator should produce a binary sequence of
0s and 1s of a given length N. Next, we invoke the NIST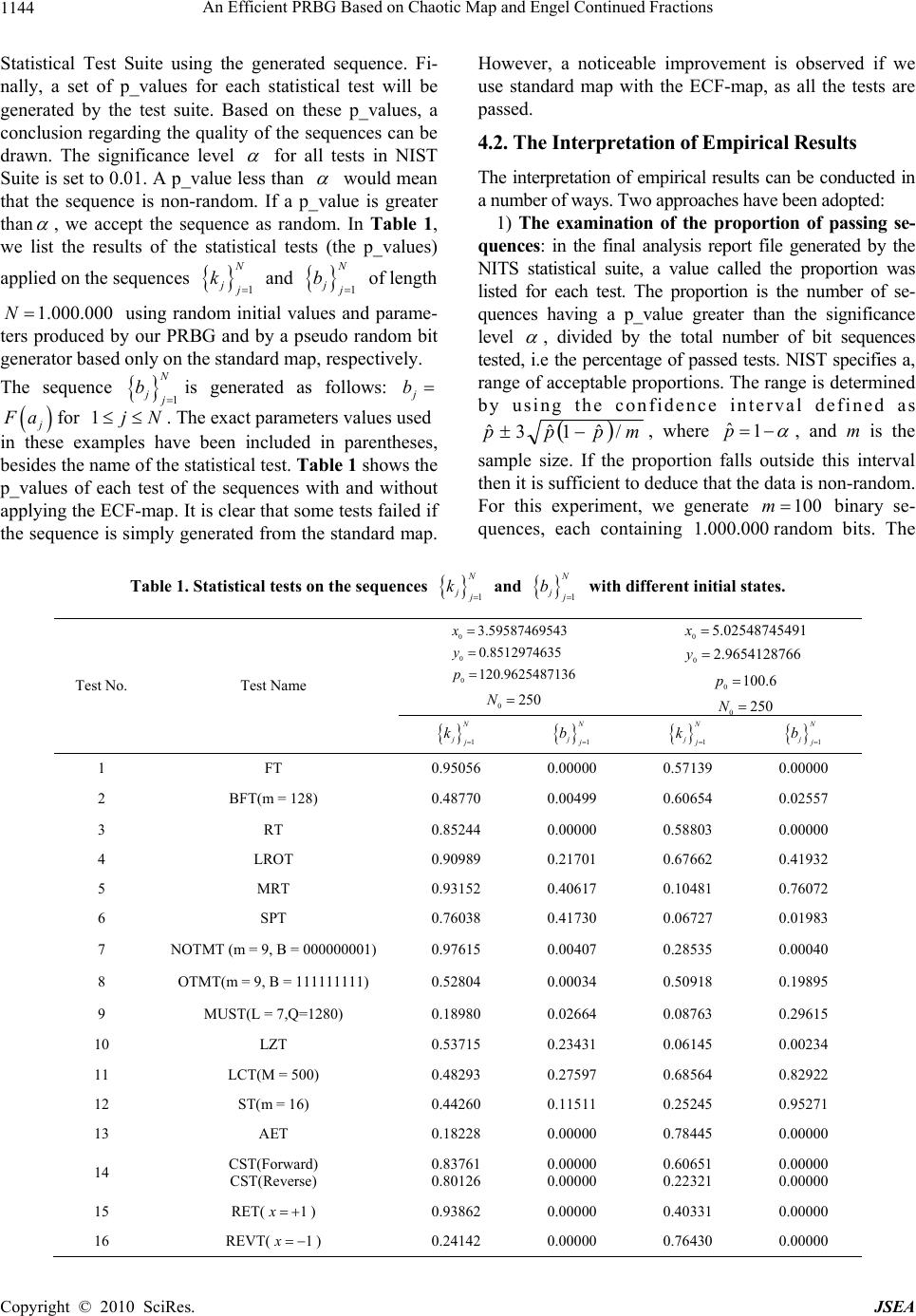

An Efficient PRBG Based on Chaotic Map and Engel Continued Fractions 1144
Statistical Test Suite using the generated sequence. Fi-
nally, a set of p_values for each statistical test will be
generated by the test suite. Based on these p_values, a
conclusion regarding the quality of the sequences can be
drawn. The significance level

for all tests in NIST
Suite is set to 0.01. A p_value less than

would mean
that the sequence is non-random. If a p_value is greater
than

, we accept the sequence as random. In Table 1,
we list the results of the statistical tests (the p_values)
applied on the sequences

1
N
j
j
k

and

1
N
j
j
b of length
1.000.000N using random initial values and parame-
ters produced by our PRBG and by a pseudo random bit
generator based only on the standard map, respectively.
The sequence

1
N
j
j
bis generated as follows: j b


j
F
afor 1jN . The exact parameters values used
in these examples have been included in parentheses,
besides the name of th e statistical test. Table 1 sh ow s th e
p_values of each test of the sequences with and without
applying the ECF-map. It is clear that some tests failed if
the sequence is simply generated from the standard map.
However, a noticeable improvement is observed if we
use standard map with the ECF-map, as all the tests are
passed.
4.2. The Interpretation of Empirical Results
The interpretation of empirical results can be conducted in
a number of ways. Two approaches have been adopted:
1) The examination of the proportion of passing se-
quences: in the final analysis report file generated by the
NITS statistical suite, a value called the proportion was
listed for each test. The proportion is the number of se-
quences having a p_value greater than the significance
level

, divided by the total number of bit sequences
tested, i.e the p ercentage of passed tests. NIST specifies a,
range of acceptable proportions. The range is determined
by using the confidence interval defined as

 mppp /
ˆ
1
ˆ
3
ˆ, where ˆ1p

 , and m is the
sample size. If the proportion falls outside this interval
then it is sufficient to deduce that the data is non-random.
For this experiment, we generate 100m binary se-
quences, each containing 000.000.1 random bits. The
Table 1. Statistical tests on the sequences


1
N
j
j
k

and


1
N
j
j
b

with different initial states.
Test No. Test Name
0
0
0
3.59587469543
0.8512974635
120.9625487136
x
y
p



0250N
0
0
5.02548745491
2.9654128766
x
y


0100.6p
0
250N


1
N
jj
k



1
N
jj
b



1
N
jj
k


1
N
jj
b
1 FT 0.95056 0.00000 0.57139 0.00000
2 BFT(m = 128) 0.48770 0.00499 0.60654 0.02557
3 RT 0.85244 0.00000 0.58803 0.00000
4 LROT 0.90989 0.21701 0.67662 0.41932
5 MRT 0.93152 0.40617 0.10481 0.76072
6 SPT 0.76038 0.41730 0.06727 0.01983
7 NOTMT (m = 9, B = 000000001) 0.97615 0.00407 0.28535 0.00040
8 OTMT(m = 9, B = 111 111111) 0.52804 0.00034 0.50918 0.19895
9 MUST(L = 7,Q=128 0 ) 0.18980 0.02664 0.08763 0.29615
10 LZT 0.53715 0.23431 0.06145 0.00234
11 LCT(M = 500) 0.48293 0.27597 0.68564 0.82922
12 ST(m = 16) 0.44260 0.11511 0.25245 0. 952 71
13 AET 0.18228 0.00000 0.78445 0.00000
14 CST(Forward)
CST(Reverse) 0.83761 0.80126 0.00000 0.00000 0.60651 0.22321 0.00000 0.00000
15 RET( 1x ) 0.93862 0.00000 0.40331 0.00000
16 REVT( 1x ) 0.24142 0.00000 0.76430 0.00000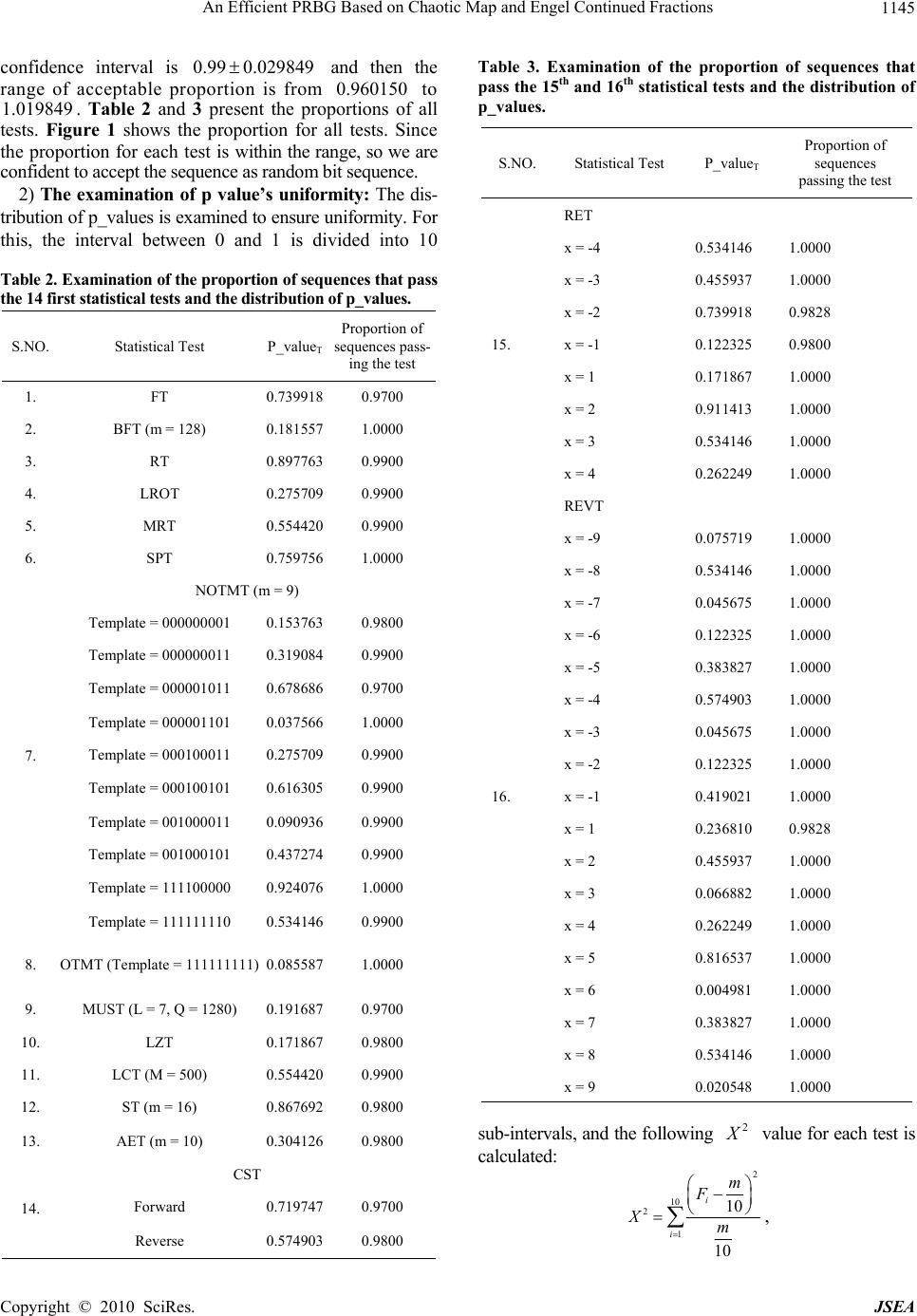

An Efficient PRBG Based on Chaotic Map and Engel Continued Fractions 1145
confidence interval is 0.99 0.029849

and then the
range of acceptable proportion is from 960150.0 to
019849.1 . Table 2 and 3 present the proportions of all
tests. Figure 1 shows the proportion for all tests. Since
the proportion for each test is within the range, so we are
confident to accept the sequence as random bit sequence.
2) The examination of p value’s uniformity: The dis-
tribution of p_values is examined to ensure uniformity. For
this, the interval between 0 and 1 is divided into 10
Table 2. Examination of the proportion of sequences that pass
the 14 first statistical tests and the distribution of p_values.
S.NO. Statistical Test P_valueT
Proportion of
sequences pass-
ing the test
1. FT 0.739918 0.9700
2. BFT (m = 128) 0.181557 1.0000
3. RT 0.897763 0.9900
4. LROT 0.275709 0.9900
5. MRT 0.554420 0.9900
6. SPT 0.759756 1.0000
7.
NOTMT (m = 9)
Template = 00000 0 0 0 1 0.153763 0.9800
Template = 00000 0 0 1 1 0.319084 0.9900
Template = 00000 1 0 1 1 0.678686 0.9700
Template = 00000 1 1 0 1 0.037566 1.0000
Template = 00010 0 0 1 1 0.275709 0.9900
Template = 00010 0 1 0 1 0.616305 0.9900
Template = 00100 0 0 1 1 0.090936 0.9900
Template = 00100 0 1 0 1 0.437274 0.9900
Template = 11110 0 0 0 0 0.924076 1.0000
Template = 11111 1 1 1 0 0.534146 0.9900
8. OTMT (Template = 111111111) 0.085587 1.0000
9. MUST (L = 7, Q = 1280) 0.191687 0.9700
10. LZT 0.171867 0.9800
11. LCT (M = 500) 0.554420 0.9900
12. ST (m = 16) 0.867692 0.9800
13. AET (m = 10) 0.304126 0.9800
14.
CST
Forward 0.719747 0.9700
Reverse 0.574903 0.9800
Table 3. Examination of the proportion of sequences that
pass the 15th and 16th statistical tests and the distribution of
p_values.
S.NO. Statistical Test P_valueT Proportio n of sequences
passing the test
15.
RET
x = -4 0.534146 1.0000
x = -3 0.455937 1.0000
x = -2 0.739918 0.9828
x = -1 0.122325 0.9800
x = 1 0.171867 1.0000
x = 2 0.911413 1.0000
x = 3 0.534146 1.0000
x = 4 0.262249 1.0000
16.
REVT
x = -9 0.075719 1.0000
x = -8 0.534146 1.0000
x = -7 0.045675 1.0000
x = -6 0.122325 1.0000
x = -5 0.383827 1.0000
x = -4 0.574903 1.0000
x = -3 0.045675 1.0000
x = -2 0.122325 1.0000
x = -1 0.419021 1.0000
x = 1 0.236810 0.9828
x = 2 0.455937 1.0000
x = 3 0.066882 1.0000
x = 4 0.262249 1.0000
x = 5 0.816537 1.0000
x = 6 0.004981 1.0000
x = 7 0.383827 1.0000
x = 8 0.534146 1.0000
x = 9 0.020548 1.0000
sub-interva ls, and the fo llowing 2
X
value for each test is
calculated:
2
10
2
1
10
10
i
i
m
F
Xm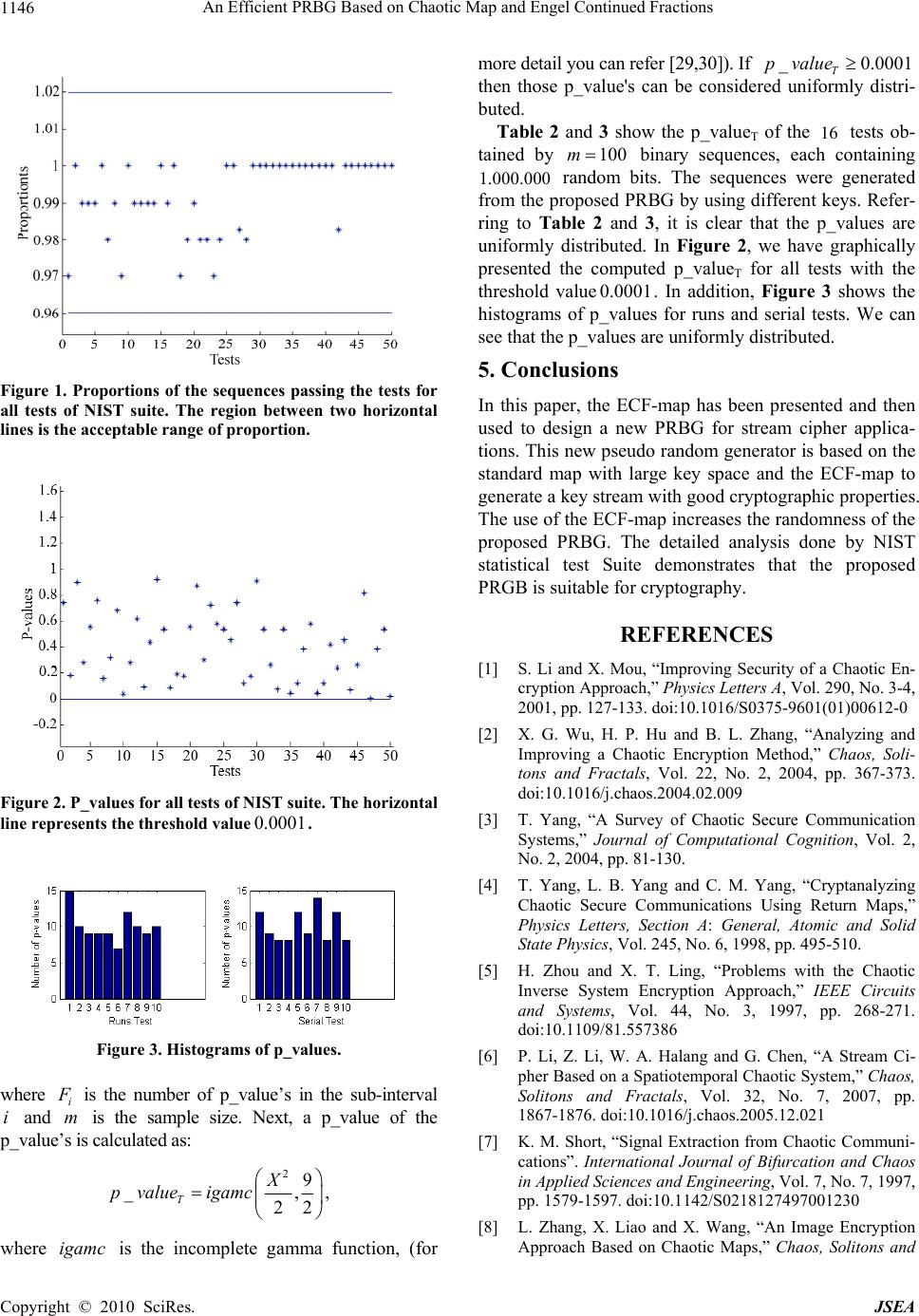





,

An Efficient PRBG Based on Chaotic Map and Engel Continued Fractions 1146
Figure 1. Proportions of the sequences passing the tests for
all tests of NIST suite. The region between two horizontal
lines is the acceptable range of proportion.
Figure 2. P_values for all tests of NIST suite. The horizontal
line represe nts the threshold value0001.0 .
Figure 3. Histograms of p_values.
where i
F
is the number of p_value’s in the sub-interval
i and m is the sample size. Next, a p_value of the
p_value’s is calculated as:
29
_
,,
22
TX
p valueigamc 

where igamc is the incomplete gamma function, (for
more detail you can refer [29,30]). If
_
0.0001
T
pvalue
then those p_value's can be considered uniformly distri-
buted.
Table 2 and 3 show the p_valueT of the 16 tests ob-
tained by 100m

binary sequences, each containing
000.000.1 random bits. The sequences were generated
from the proposed PRBG by using different keys. Refer-
ring to Table 2 and 3, it is clear that the p_values are
uniformly distributed. In Figure 2, we have graphically
presented the computed p_valueT for all tests with the
threshold value0.0001. In addition, Figure 3 shows the
histograms of p_values for runs and serial tests. We can
see that the p_values are uniformly distributed.
5. Conclusions
In this paper, the ECF-map has been presented and then
used to design a new PRBG for stream cipher applica-
tions. This new pseudo random generator is based on the
standard map with large key space and the ECF-map to
generate a key stream with good cryptographic properties.
The use of the ECF-map increases the randomness of the
proposed PRBG. The detailed analysis done by NIST
statistical test Suite demonstrates that the proposed
PRGB is suitable for cryptography.
REFERENCES
[1] S. Li and X. Mou, “Improving Security of a Chaotic En-
cryption Approach,” Physics Letters A, Vol. 290, No. 3-4,
2001, pp. 127-133. doi:10.1016/S0375-9601(01)00612-0
[2] X. G. Wu, H. P. Hu and B. L. Zhang, “Analyzing and
Improving a Chaotic Encryption Method,” Chaos, Soli-
tons and Fractals, Vol. 22, No. 2, 2004, pp. 367-373.
doi:10.1016/j.chaos.2004.02.009
[3] T. Yang, “A Survey of Chaotic Secure Communication
Systems,” Journal of Computational Cognition, Vol. 2,
No. 2, 2004, pp. 81-130.
[4] T. Yang, L. B. Yang and C. M. Yang, “Cryptanalyzing
Chaotic Secure Communications Using Return Maps,”
Physics Letters, Section A: General, Atomic and Solid
State Physics, Vol. 245, No. 6, 1998, pp. 495-510.
[5] H. Zhou and X. T. Ling, “Problems with the Chaotic
Inverse System Encryption Approach,” IEEE Circuits
and Systems, Vol. 44, No. 3, 1997, pp. 268-271.
doi:10.1109/81.557386
[6] P. Li, Z. Li, W. A. Halang and G. Chen, “A Stream Ci-
pher Based on a Spatiotemporal Chaotic System,” Chaos,
Solitons and Fractals, Vol. 32, No. 7, 2007, pp.
1867-1876. doi:10.1016/j.chaos.2005.12.021
[7] K. M. Short, “Signal Extraction from Chaotic Communi-
cations”. International Journal of Bifurcation and Chaos
in Applied Sciences and Engineering, Vol. 7, No. 7, 1997,
pp. 1579-1597. doi:10.1142/S0218127497001230
[8] L. Zhang, X. Liao and X. Wang, “An Image Encryption
Approach Based on Chaotic Maps,” Chaos, Solitons and

An Efficient PRBG Based on Chaotic Map and Engel Continued Fractions 1147
Fractals, Vol. 24, No.3, 2005, pp. 759-765. doi:10.1016/
j.chaos.2004.09.035
[9] S. J. Li, X. Q. Mou and Y. L. Cai, “Pseudo-Random Bit
generator Based on Couple Chaotic Systems and its Ap-
plication in Stream-Ciphers Cryptography,” Progress in
Cryptology-INDOCRYPT, Lecture Notes in Computer
Science, Vol. 2247, 2001, pp. 316-329.
[10] V. Patidar, N. K. Parekk and K. K. Sud, “A New Substi-
tution-Diffusion Based Image Cipher Using Chaotic
Standard and Logistic Maps,” Communications in Nonli-
near Science and Numerical Simulation, Vol. 14, No. 7,
2009, pp. 3056-3075. doi:10.1016/j.cnsns.2008.11.005
[11] V. Patidar and K. K. Sud, “A Novel Pseudo Random Bit
Generator Based on Chaotic Standard Map and its Test-
ing,” Electronic Journal of Theoretical Physics, Vol. 6,
No. 20, 2009, pp. 327-344.
[12] X. Y. Wanga and Q. Yu, “A Block Encryption Algorithm
Based on Dynamic Sequences of Multiple Chaotic Sys-
tems,” Communications in Nonlinear Science and Nu-
merical Simulation, Vol. 14, No. 2, 2009, pp. 574-581.
doi:10.1016/j.cnsns.2007.10.011
[13] G. Chen, Y. Mao and C. K. Chui, “A Symmetric Image
Encryption Scheme Based on 3D Chaotic Cat Maps,”
Chaos, Solitons and Fractals, Vol. 21, No. 3, 2004, pp.
749-761. doi:10.1016/j.chaos.2003.12.022
[14] P. Garcia, A. Parravano, M. G. Cosenza, J. Jiménez and
A. Marcano, “Coupled Map Networks as Communication
Schemes,” Physical Review E, Vol. 65, No. 4, 2002, pp.
045201.1-045201.4.
[15] H. Li and J. Zhang, “A Secure and Efficient Entropy Coding
Based on Arithmetic Coding,” Communications in Nonlinear
Science and Numerical Simulation, Vol. 14 No. 12, 2009, pp.
4304-4318. doi:10.1016/j.cnsns.20 09.03.003
[16] K. Fallahi, R. Raoufi and H. Khoshbin, “An Application
of Chen System for Secure Chaotic Communication
Based on Extended Kalman Filter and Multi-Shift Cipher
Algorithm,” Communications in Nonlinear Science and
Numerical Simulation, Vol. 13, No. 4, 2008, pp. 763-781.
doi:10.1016/j.cnsns.2006.07.006
[17] B. Mi, X. Liao and Y. Chen, “A Novel Chaotic Encryp-
tion Scheme Based on Arithmetic Coding,” Chaos, Soli-
tons and Fractals, Vol. 38, No. 5, 2008, pp. 1523-1531,
2008.
[18] A. Kanso and N. Smaoui, “Logistic Chaotic Maps for
Binary Numbers Generations,” Chaos, Solitons and
Fractals, Vol. 40, No. 5, 2009, pp. 2557-2568. doi:
10.1016/j.chaos.2007.10.049
[19] G. Alvarez, F. Montoya, M. Romera and G. Pastor,
“Cryptanalysis of a Discrete Chaotic Cryptosystem Using
External Key,” Physics Letters A, Vol. 319, No. 3-4, 2003,
pp. 334-339. doi:10.1016/j.physleta.2003.10.044
[20] G. A. Alvarez and L. B. Shujun, “Cryptanalyzing a Non-
linear Chaotic Algorithm (NCA) for Image Encryption,”
Communications in Nonlinear Science and Numerical
Simulation, Vol. 14, No. 11, 2009, pp. 3743-3749.
doi:10.1016/j.cnsns.2009.02.033
[21] A. Rukhin, J. Soto, J. Nechvatal, M. Smid, E. Barker, S.
Leigh, M. Levenson, M. Vangel, D. Banks, A. Heckert, J.
Dray and S. Vo, “A Statistical Test Suite for Random and
Pseudo Random Number Generators for Cryptographic
Applications,” National Institute of Standards and Tech-
nology Special Publication 800-22, 2001.
[22] G. Marsaglia, “DIEHARD: A Battery of Tests of Random-
ness,” 1997. http://stat.fsu.edu/geo/diehard.html.
[23] L. Lorentzen and H. Waadeland, “Continued Fractions
with Applications,” North Holland, Amsterdam, 1992.
[24] R. B. Seidensticker, “Continued Fractions for High-Speed
and High-Accuracy Computer Arithmetic,” Proceedings
of the 6th IEEE Symposium on Computer Arithmetic,
1983, pp. 184-193.
[25] J. Vuillemin, “Exact Real Computer Arithmetic with
Continued Fractions,” INRIA Report 760, Le Chesnay,
1987.
[26] H. S. Wall. “Analytic Theory of Continued Fractions”.
Chelsea, 1973.
[27] Y. Hartono, C. Kraaikamp and F. Schweiger, “Algebraic
and Ergodic Properties of a New Continued Fraction Al-
gorithm with Non-Decreasing Partial Quotients,” Journal
de théorie des nombres de 9 Bordeaux, Vol. 14, No. 2,
2002, pp. 497-516.
[28] X. Di, X. Liao and P. Wei, “Analysis and Improvement
of a Chaos-Based Image Encryption Algorithm,” Chaos,
Solitions and Fractals, Vol. 40, No. 5, 2009, pp.
2191-2199. doi:10.1016/j.chaos.2007.10.009
[29] W. H. Press. “Numerical Recipes in C: The Art of Scien-
tific Computing,” Cambridge University Press, Cam-
bridge, 1992, pp. 169-173.
[30] M. Abramowitz and I. Stegun, “Handbook of Mathemat-
ical Functions,” Applied Mathematics Series, Vol. 55,
1968, pp. 2286-2293.