 Advances in Nanoparticles, 2013, 2, 266-279 http://dx.doi.org/10.4236/anp.2013.23037 Published Online August 2013 (http://www.scirp.org/journal/anp) Viscosity of Nanofluids—Why It Is Not Described by the Classical Theories* Valery Ya. Rudyak Department of Theoretical Mechanics, Novosibirsk State University of Architecture and Civil Engineering, Novosibirsk, Russian Federation Email: valery.rudyak@mail.ru Received May 8, 2013; revised June 8, 2013; accepted June 15, 2013 Copyright © 2013 Valery Ya. Rudyak. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Transport properties of nanofluids are extensively studied last decade. This has been motivated by the use of nanosized systems in various applications. The viscosity of nanofluids is of great significance as the application of nanofluids is always associated with their flow. However, despite the fairly large amount of available experimental information, there is a lack of systematic data on this issue and experimental results are often contradictory. The purpose of this review is to identify the typical parameters determining the viscosity of nanofluids. The dependence of the nanofluid viscosity on the particles concentration, their size and temperature is analyzed. It is explained why the viscosity of nanofluid does not described by the classical theories. It was shown that size of nanoparticles is the key characteristics of nanofluids. In addition the nanofluid is more structural liquid than the base one. Keywords: Nanofluids; Gas Nanosuspensions; Nanoparticles; Viscosity; Kinetic Theory; Molecular Dynamics; Rheology of Nanofluids; Effect of Nanoparticles Size 1. Introduction Nanofluid is a two-phase system consisting of a carrier medium (liquid or gas) and nanoparticles. The term nan- ofluid was first used by Choi [1] to describe a suspension consisting of carrier liquid and solid nanoparticles. In our papers [2-5], nanoparticle suspensions in gases (gas nano- suspensions) are also called nanofluids. This is done for several reasons: 1) both gas and liquid nanosuspensions have extensive practical applications; 2) many properties of nanofluids and gas nanosuspensions are very similar, especially if the carrier gas is dense; 3) in some cases, transport processes in gas and liquid suspensions of nanoparticles are studied using the same methods or models. For example, the procedure of molecular dy- namics simulation is the same in both cases. Typical carrier fluids are water, organic liquids (eth- ylene glycol, oil, biological liquids, etc.), and polymer solutions. The dispersed solid phase is usually nanoparti- cles of chemically stable metals and their oxides. Fullere- nes with a diameter of about 1 nm can be considered the smallest nanoparticles. Viruses are intermediate in size: their sizes are of the order of tens of nanometers. On the other hand, nanofluids based on carbon nanotubes have also been widely studied, but these liquids will not be considered in this paper. Investigation of the physics of nanofluids and their transport properties began relatively recently. This has been motivated by the use of nanosized systems in vari- ous applications. The special properties of nanoparticles are due to their small size. Nanofluids have peculiar transport properties. In contrast to large dispersed parti- cles, nanoparticles do not sediment and erode the chan- nels in which they move. For these and some other rea- sons, nanofluids have already been successfully used, or are proposed for use, in chemical processes, including catalysis, for cooling devices, in various bio-, MEMS-, and nanotechnologies, in the development of thermal en- rgy production and transport systems, in pharmaceutical and cosmetic products, for pollution detection and air and water purification systems, as lubrication materials and drug delivery systems. This list can be extended, but the transport properties and flow patterns of nanofluids play a key role in these applications. The wide potential application of nanofluids has stimu- lated the development of their production processes and extensive research activity. In particular, numerous ex- *This work was supported in part by the Russian Foundation for Basic Research (grant No. 13-01-00052-а). C opyright © 2013 SciRes. ANP  V. Ya. RUDYAK 267 perimental and theoretical studies have focused on the thermal conductivity and viscosity of nanofluids. The vis- cosity of nanofluids is of great significance as the appli- cation of nanofluids is always associated with their flow. However, despite the fairly large amount of available experimental information, there is a lack of systematic data on this issue and experimental results are often con- tradictory. Two good reviews published recently [6,7] have not improved the situation. The importance of ob- taining adequate data on the viscosity coefficients has motivated a series of special measurements simultane- ously in more than thirty laboratories around the world. However, the results of these measurements have not clarified the situation [8]. This is due to the fact that the measurements were carried out without adequate tem- perature control, in a narrow range of volume concentra- tions of nanoparticles, with a wide spread of nanoparticle sizes, and for different carrier liquids. Therefore, a fur- ther critical review of the results is needed to make pro- gress in the understanding of what nanofluid viscosity is. Such a review should not be limited to listing available data, but should identify the methodological shortcom- ings of the procedures used to obtain these data and indi- cate ways to overcome them. The present paper is written with exactly this goal in mind. The purpose of the review is to identify the typical parameters determining the vis- cosity of nanofluids. Below methods for producing nan- ofluids will not be discussed. We note only that in almost all studies, nanofluids are prepared using the so-called two-step method [9,10], in which a nanopowder contain- ing particles of a given size is added in a certain ratio to the carrier (base) fluid. 2. Viscosity of Molecular Mixtures and Gas Nanosuspensions Nanoparticle size varies within two orders of magnitude. At the lower limit are nanoparticles with characteristic sizes of one to a few nanometers. These particles are only a few times larger than conventional inorganic molecules and are similar in size to some organic molecules. At the upper limit are nanoparticles with sizes of 80 - 100 nm. In fact, they are close in size to usual Brownian particles (in Perrin’s experiments [11], the size of Brownian parti- cles was 10−4 - 105 cm). For this reason, it is clear that the mechanisms of transport of small nanoparticles should be close to those of conventional molecules, the mecha- nisms of transport of large nanoparticles should be simi- lar to those of Brownian particles. However, the indicated mechanisms of transport processes are significantly dif- ferent. Therefore, to clarify the momentum transfer char- acteristics of nanofluids that determine their viscosity, it is necessary to analyze both molecular systems and dis- perse systems with large macroscopic particles (Brownian, in particular). This will be done in the next two sections. However, before doing so, we note that even a cursory analysis of the size range of nanoparticles shows that the transport properties of nanofluids should depend on the size of the particles. This conclusion is unusual for the classical physics of transport processes. The classical relations for the Einstein viscosity [12] and Maxwell thermal conductivity [13] are independent of the size of the dispersed particles. Transport processes in gases at normal pressures are described by the kinetic Boltzmann equations, whose solution for the viscosity coefficient of binary gas mix- tures can be expressed as [14] 1 XY , (1) where 22 112 112 22 2 xx x X , 2 22 *112 121 2 112 11 0.6 0.52 2 x YA xx , 22 *2 2 1211 2 1 0.6 21 4 ZAxxx , * 12 2,2 2 π 5 16 π i i ii i mkT , * 12 12 12 2,2 2 12 12 π 5 16 π mkT . Here 12121 2 , x1 and x2 are the mole fractions of components 1 and 2, 12 mm , where m1 and m2 are the masses of the molecules of the first and second components, T is the temperature. * 2,2 1,1 * 12 1212 A * , where are reduced Ω-inte- grals, and ii * , 12 lm and ij are parameters of the pair inter- action potential (for example, the Lennard-Jones potential) which characterize the effective scattering cross sections of molecules of the same kind and the interaction between different kinds of molecules, respectively. If there is a mixture of gases with a small addition of one of them (say, the second) and this addition contains molecules with a large mass (analog of a gas suspension), small parameters appear in formulas (1) and these for- mulas are simplified to * * 2,2 2 12 12 1,1 12 11.22 1 s xO . (2) Thus, the addition of a small amount of a heavy gas to a lighter gas will lead to an increase in the viscosity of the mixture compared to the viscosity of the light component. Generally, however, this increase does not depend mono- tonically on the concentration of the heavy component and changes significantly with increasing temperature [15]. Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 268 Kinetic theory of gas nanosuspensions has been de- veloped (see papers [2,5,16-21]). In particular, it has been shown that the viscosity of rarefied gas nanosuspensions can be described by expression (1), where the subscript 2 refers to nanoparticles and 22R (R is the radius of the nanoparticle). Thus, as for molecular mixtures of gases, calculating the viscosity coefficient for gas nano- suspensions reduces to calculating the corresponding Ω- integrals for the RK molecule-nanoparticle interaction potential [19,22]. The viscosity coefficient of the gas nanosuspensions (1) is a multiparameter function and varies considerably with nanoparticle size and concentration and with the tem- perature of the gas suspension. For small mole fractions of the dispersed phase, , the coefficient (1) be- comes 21x 2 1* 12 2 ** 12 1 12 12 1 110.6 1 0.32 1.22 x A AA 1 2 . (3) Function (3) depends significantly on the mass ratio μ, nanoparticle radius, temperature, and interaction potential parameters. In particular, for certain values of these quan- tities, function (3) can change sign. This implies that the addition of small volume fractions of dispersed solid particles to a gas can both increase or decrease the effect- tive viscosity of the medium. Calculations have shown that this is indeed true. As an example, Figure 1 shows the dependence of the viscosity of a gas nanosuspension 2 U on the volume frac- tion of 1 nm diameter particles at different temperatures: T Figure 1. Effective viscosity (poise) of a gas suspensions of U nanoparticles in H2 (a) and Zn particles in Ne (b) versus volume concentration φ of nanoparticles. = 200 K (1), T = 300 K (2), T = 400 K (3), T = 500 K (4), T = 600 K (5), T = 800 K (6), and T = 1000 K (7) [5,23]. At concentrations of the order of 2 × 10−4 and room tem- peratures, the viscosity of the gas nanosuspension is 90% higher than the viscosity of the carrier gas. This effect depends significantly on the temperature, and at T = 1000 K, the ratio η/η1 ~2.3 at the same concentrations. On the other hand, the viscosity of a Zn-Ne gas sus- pension with nanoparticles of the same size decreases, as shown in Figure 2 (where the different curves correspond to the same temperatures as in Figure 1). At room tem- perature and a volume concentration of particles of 2 × 10−4, the effective viscosity of this gas suspension is about 15% lower than the viscosity of pure neon, and this effect increases with increasing temperature. The results derived from kinetic theory have been con- firmed experimentally by studies of the diffusion of na- noparticles [24-27]. The main conclusion that can be drawn is that the viscosity of gas nanosuspensions of small particles, first, differs significantly from the vis- cosity of ordinary molecular mixtures, and second, it is not described by the classical Einstein theory [12], ac- cording to which the effective viscosity of a disperse fluid depends only on the concentration of dispersed particles 012.5 , (4) and is always greater than the viscosity of the carrier fluid 0 , where φ is the volume fraction of dispersed particles. 3. Viscosity of Coarse Suspensions The effect of dispersed particles on the viscosity of sus- pensions was first studied in Einstein’s classical work cited above. Considering the motion of a small particle in a fluid, he determined the flow field perturbations caused by it, then calculated the effective stress tensor, and, as a result, obtained formula (4) for the effective viscosity coefficient. The volume concentration of particles was Figure 2. Normalized viscosity of a nanfluid versus volume concentration of particles for different ratios of the radius of the nanoparticle to that of the molecule. Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 269 assumed to be small enough to take into account the per- turbations caused by an isolated particle. Thus, the addi- tional momentum transfer in the liquid due to the presence of dispersed particles was determined only by hydrody- namic processes. Comparison of formula (4) with ex- periments has shown that it adequately describes the vis- cosity of suspensions at volume concentrations of parti- cles [28]. In this paper, we consider systems in which the particle concentrations are relatively low, up to about 10% - 15%. For this, it is necessary to find a cor- rection of order 2 10 2 to formula (4). To extend formula (4) to such particle concentrations within Einstein’s concept, it is necessary to take into account the hydrodynamic perturbations due to the mutual influence of closely spaced dispersed particles. This hydrodynamic interaction leads to an increase in the energy dissipation of viscous friction. As a result, the viscosity increases linearly with increasing particle concentration. Theory incorporating these effects was developed by Batchelor [29]. In addition, he took into account the contribution of Brownian motion to the average stress and obtained the following formula for the effective viscosity, accurate to the second order in concentration [30] 2 012.5 b , (5) where the coefficient b = 6.2. Similar ideas were deve- loped in [31] and some other papers. A fundamentally different approach to calculating the viscosity of suspensions was proposed by Mooney [32], who considered possible structuring of disperse systems. Later, this approach was developed in a number of papers. In particular, Krieger and Dougherty [33] obtained the formula 01 m , (6) where m is the volume fraction of particles at their maximum packing density and α is a parameter that de- pends on the properties of the medium. In particular, for a dilute suspension in which the particles do not interact with each other, α = 2.5. Later, formula (6) was modified in several papers (see [34,35]). A comprehensive list of the formulas used can be found in reviews [6,7], but it is important to emphasize that at not too high concentrations, almost all formulas lead to relation (5), in which the co- efficient b usually varies from 4.3 to 7.6. Thus, at a 10% concentration of dispersed particles, formulas of the type (5) gives an about 25% - 30% increase in the viscosity. It is worth noting that almost all classical theories of viscosity describe the dependence of the effective viscos- ity coefficient only on the volume concentration of parti- cles. However, the dependence of the viscosity of even a homogeneous liquid varies greatly with temperature. So far as is known, there is no consistent theory of the vis- cosity of liquids that would give universal formulas for fluid viscosity. In the absence of such a theory, almost all empirical or semi-empirical formulas for the viscosity coefficient actually describe its dependence on tempera- ture. A typical dependence was proposed by Andrade [36,37] T e , (7) where A and B are some constants determined experi- mentally for a particular fluid. The exponential depend- ence of viscosity on temperature is often violated near the liquid-solid phase transition. In practice, liquid viscosity is often calculated using the correlation proposed by Orrick and Erbar [15], 1 ln ln BT M , (8) here ρ is the density of the liquid, M is its molecular weight, and the constants A and B for a number of liquids can be found in [15]. Some other semi-empirical correla- tions (see, for example, [15]) are also used, but the tem- perature dependence of viscosity the remains qualita- tively the same as in (7). Formula (8) also takes into ac- count the physical properties of the liquid: its molecular weight and density. According to this formula, the liquid viscosity increases with increasing its density. Density, however, is not the only physical characteris- tic that affects liquid viscosity. In liquids, as opposed to gases, the viscosity is known to decrease with increasing temperature. In contrast, in gases it increases with in- creasing temperature. This is related to the different mechanisms of momentum transfer. In gases, smoothing of momentum is due to the kinetic mechanisms: the mo- mentum is transferred by molecules in motion and colli- sion. It is for this reason that in not too dense gases, the viscosity coefficient is proportional to the mean free path of the molecules l: η ~ l. As the density increases, the viscosity coefficient becomes a nonlinear function of den- sity and increases with increasing density. Increasing tem- perature increases the velocity of molecules, and, hence, the momentum transfer rate per unit time. This implies an increase in the viscosity with increasing gas tempera- ture. In liquids, the kinetic mechanism of momentum trans- fer also takes place. However, in liquids, the molecules are packed closely enough, so that it is difficult to speak about the mean free path of the molecules. Here, the main kinetic mechanism of momentum transfer is associated with collisions of molecules. On the other hand, although such collisions redistribute the momentum in the system, they do it locally, near a distinguished molecule. This is not sufficient to smooth out large-scale momentum fluc- tuations in a liquid. Liquids have short-range order and momentum transfer by molecules is accompanied by its Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 270 destruction. Thus, the viscosity of a liquid depends sig- nificantly on its structure. Attempts to take into account the liquid structure in calculations of liquid viscosity have been reported in the literature. This approach has been successfully applied to model the viscosity of non-New- tonian fluids (for example, see [38]). However, similar approaches are known for modeling the viscosity of sim- ple liquids. An example is the correlation proposed by Van Velzen, Cardozo, and Langenkamp [15] measurements (International Nanofluid Properties Bench- mark Exercise) also examined the dependence of viscosity only on the volume concentration of particles [40]. What has been established? At low concentrations, the viscosity of all measured nanofluids is several times higher than predicted by Einstein’s theory (4). However, the coeffi- cient of increase a was different in different studies. In paper [40] the data for three nanofluids with large (100 nm) Al2O3 nanoparticles in poly-alpha olefin (PAO) were presented. The coefficient a was found to be an order of magnitude larger than predicted by Einstein’s theory (4). Investigating an ethylene glycol based nanofluid with TiO2 particles Chen et al. [41,42] obtained a correlation coefficient a = 10.6. In these experiments, nanoparticles with an average size of 25 nm formed aggregates in the nanofluid with an average size of 140 nm. Colla et al. [43] proposed a correlation with a coefficient a = 18.64 based on the results of measurements for water-based nanofluids containing Fe2O3 particles with an average size of 67 nm. For an ethylene glycol based nanofluid containing 200 nm Cu particles, Garg et al., [44] obtained a correlation with a coefficient a ≈ 11. In a study [45] of the viscosity of a water-based nanofluid with Al2O3 nanoparticles, this factor equaled 7.3. The correlation used in this study was derived from experimental data [46-48]. It is worth to say that these experiments were performed with different nan- ofluids. *1 1 0 ln BT T , (9) where the parameters and 0 T are determined by the structure of the liquid molecules. * B Short-range order in liquids occurs at scales ranging from one to a few nanometers. Thus, whereas in gases, viscosity forms at scales of the order of the mean free path, in liquids it occurs at mesoscales ms much larger than the characteristic size of the molecules1 r0: rms > r0. r Thus, the dependence of the viscosity coefficient on the concentration of dispersed particles and temperature has been noted in all major studies (both experimental and theoretical). At low particle concentrations, the ef- fective viscosity coefficient of suspensions increased in proportion to φ compared to the viscosity coefficient of the carrier liquid. With further increase in the concentra- tion, the viscosity coefficient was described by formula (5). The dependence of viscosity on temperature gener- ally fits the classical relation (7). In experiments, correla- tions between viscosity and the size of dispersed particles were not found. Nevertheless, an attempt to take into account the effect of particle size on viscosity was made in studies [39] using a linear approximation for particle concentration. In accordance with the proposed formula, the effective viscosity coefficient increases with increas- ing particle size. Some more data can be given, but even those cited above are enough to see that there is no universality in the obtained correlations. In contrast, the Einstein formula for conventional suspensions is universal for all fluids and depends only on the volume concentration of particles. What are the reasons for the lack of universality for nan- ofluids? There may be two possible reasons. The coeffi- cient a may depend on: 1) the size of nanoparticles; 2) the density of nanoparticles (i.e., the nanoparticle material). 4. Dependence of Nanofluid Viscosity on Nanoparticle Concentration In all cases, as the volume (or mass) concentration of nanoparticles increases, a quadratic dependence of the viscosity on is obtained The viscosity of nanofluids has been persistently inves- tigated over about fifteen years in more than thirty groups throughout the world. However, a universal formula that would describe the viscosity coefficient of any nanofluid has not been derived. Moreover, measurements often lead to diametrically opposite results. Why does this occur? 2 01ab , (10) However, as in the case of the coefficient a, the coef- ficient b is not universal, but far exceeds that for conven- tional suspensions. Several correlations obtained at dif- ferent times are given below. One of the first correlations was obtained for a nanofluid with TiO2 particles [49] It was long thought, and is still being argued by many, that similarly to the viscosity of conventional suspensions, the viscosity of nanosuspensions is determined only by the mass concentration of particles. It is noteworthy that in special benchmark measurements made as part of an in- ternational project on viscosity and thermal conductivity 2 01 5.45108.2 . (11) A year later, the following experimental correlation was proposed for a water-based nanofluid containing Al2O3 nanoparticles [50] 1and larger than the mean free path of molecules, which can be calculated, e.g., for hard-sphere molecules and it is even smaller than the typical size of molecules. 2 017.3 123 . (12) Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 271 It is worth noting that in the same paper, a different correlation was proposed for a suspension of the same nanoparticles in ethylene glycol 2 010.19 306 . (13) This correlation, however, is certainly not universal because at low concentrations, it gives a reduction in the viscosity, which is physically unreasonable. Several more similar correlations have been proposed by different au- thors, but, for the mentioned reason, they will not be discussed in this paper. Chen et al. [41] proposed the following correlations for two different nanofluids: for an ethylene glycol based nanofluid with TiO2 particles, 2 01 10.610.6 , (14) and for a water-based nanofluid with Cu particles, 2 00.995 3.645468.72 . (15) The second correlation, however, is not entirely satis- factory in the limit 0 . From a study of nanofluids containing Al2O3 and CuO particles, Nguyen et al. [48] derived the correlation 23 01.475 0.3190.0510.009 . (16) However, it is also inadequate in the limit 0 and at low concentrations of nanoparticles. For water-based nanofluids with Fe2O3 particles, in paper [45] the following correlation based on experi- mental data [46-48] was proposed 2 01 18.64248.3 . (17) Summing up this brief overview, we note again that all formulas are dissimilar and not universal. The possible reasons are the same as before: the possible dependence of viscosity on nanoparticle size and material. 5. Dependence of the Viscosity of Nanofluids on the Size of Nanoparticles A fundamental disadvantage of all the correlations dis- cussed in the previous section is not the lack of univer- sality, but the fact that in the limit, none of them reduce to the corresponding formulas for the viscosity of conven- tional suspensions. In the first part of the paper, it was noted that nanoparticles are intermediate in size d between conventional molecules and macroscopic dispersed parti- cle. Moreover, the largest nanoparticles are close in size to usual Brownian particles. Therefore, the properties of nan- ofluids with such particles should be similar to the prop- erties of suspensions of submicron particles. In this regard, it is reasonable to expect that the formula for the viscosity of nanofluids with large particles reduces to the corre- sponding formula for conventional suspensions when , where D is the diameter of the conventional dispersed particle. It is therefore reasonable to assume that the viscosity of nanofluids should be a function of nanopar- ticle size. It was shown in Section 2 that the viscosity of gas nanosuspensions depends significantly on the size of the nanoparticles. dD Experimentalists came to the understanding that nano- particle size can affect the viscosity of nanofluids almost a decade ago. Nevertheless, the dependence of the viscosity on nanoparticle size has been the subject of very few studies. According to [7], they are only about one-quarter of the total number of papers devoted to the viscosity of nanofluids. This is not surprising since determining the dependence of the viscosity on nanoparticle size is much more difficult than determining viscosity for a particular size. First, measurements should be performed simulta- neously for, at least, three or four sizes of nanoparticles in the same base fluid. Second, one has to carefully monitor the particle size distribution in the nanofluid. Third, it is possible that many have been discouraged by conflicting information on the influence of nanoparticle size. Thus, He with colleagues [51] asserts that the viscosity increases with increasing size of nanoparticles. A similar assertion is made by Nguyen et al. [52]. They state that at low concentrations of nanoparticles, their size has virtually no effect on the viscosity of nanofluids. On the other hand, as the particle concentration increases, the viscosity coeffi- cient depends strongly on nanoparticle size and is higher for nanofluids with larger particles. In paper [53], it is noted that the viscosity of nanofluids is virtually inde- pendent of the size of nanoparticles. In contrast, studies [46,54,55] showed a reduction in the viscosity of nanofluids with increasing particle size. This is supported by molecular dynamics simulations [56,57]. Before analyzing these experimental data, we present the main result of these molecular dynamics simulations. In studies [56,57], nanofluids were simulated using the hard sphere interparticles interaction potential. In the calcula- tions, the dimensionless radius of nanoparticles Rr (where r is the radius of the carrier-fluid molecule) was 2, 3, and 4. The dependence of the viscosity coefficient of this nanofluid on the volume concentration of nanoparti- cles is shown in Figure 2. Here curves 1 - 3 correspond to R/r = 2, 3, 4. Here the dependence of nanofluid viscosity on nanopar- ticle size is quite obvious: the viscosity coefficient in- creases with decreasing particle size. These data, however, have a significant drawback. They were obtained for rather small nanoparticles. In addition, molecular dynamics simu- lation is an ideal experiment. In real experiments, nano- suspensions are never monodisperse. A nanofluid always contains nanoparticles of different sizes, and the viscosity of the nanofluid depends on the size distribution of the Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 272 nanoparticles. Thus, in experiments, one should carefully monitor the nanoparticle size distribution. At the same time, the molecular dynamics method is, in fact, the only method that can be used to model an “ideal nanofluid” and rigorously examine the effect exerted on the viscosity and other transport coefficients by not only the concentration of nanoparticles, but also by their material and size. It is necessary, however, to clearly distinguish between the effects of the volume concentration of nanoparticles and their size. Of course, for a fixed number of nanoparticles in a fluid, the volume fraction of the particles will increase with their size. However, nanofluids with particles of different sizes are different. Therefore, the results of mo- lecular dynamics simulations of water-based nanofluids [58] should be treated with caution. Let us now analyze the data of experimental studies of the effect of nanoparticle size on the effective viscosity of nanofluids. The suggestion that the viscosity of nanofluids can increase with increasing size of nanoparticles can be found in two papers we are aware of [51,52]. He with colleagues [51] studied the viscosity of a water-based nanofluid with relatively large particles of TiO2 (95, 132, and 230 nm). The volume concentrations of nanoparticles were rather small (less or equal than 1.2%). At such low concentrations, the viscosity coefficient should still in- crease almost linearly with increasing particle concentra- tion. In the graph given in [51] this is not so. On the other hand the measurement accuracy, apparently, does not exceed 2% - 3%, but an increase in the viscosity with increasing nanoparticle size is observed in exactly this range. In addition, in these experiments, the size distribu- tion of particles and their possible agglomeration were not monitored. Prasher, Song and Wang [53] studied a propylene glycol based nanofluid with Al2O3 nanoparticles. Nanoparticles of three sizes, 27, 40, and 50 nm were used, but it is not clear what as the distribution of nanoparticles in each of the nanofluids. The accuracy of viscosity measurements in these experiments is not high: about 3% at 20˚C and about 11% at 40˚C. The examined concentrations of nanoparti- cles were not great: 0.5%, 2%, and 3%. The independence of the viscosity on particle size stated in [53] can well be explained by the inaccuracy of the measurements. This is suggested, in particular, by the nonsystematic temperature dependence of the viscosity of the nanofluid. Namburu et al. [46] were among the first to show that nanofluid viscosity increases with decreasing particle size. They studied the viscosity of a suspension of Al2O3 na- noparticles of three sizes, 20, 50, and 100 nm, in an aqueous solution of ethylene glycol. The effect depended significantly on temperature and was greater at lower temperature of the nanofluid. The dependence of the viscosity of water-based na- nofluids with SiC particles was studied in sufficient detail by Timofeeva et al. [55]. They considered nanofluids with four particle sizes: 16, 29, 66, and 90 nm. Maximum viscosity was observed for nanofluids with the smallest particles, and the lowest viscosity for nanofluids with the largest particles. Furthermore, the viscosity of the nan- ofluid (4.1% concentration of nanoparticles) with 90 nm particles was 30% higher and that of the nanofluid with 16 nm particles was about 85% higher than the viscosity of the base fluid. Finally, recently a special series of experiments was performed to measure the dependence of the viscosity of an ethylene glycol based nanofluid with SiO2 particles on the size of nanoparticles [59]. The mass concentration of nanoparticles in ethylene glycol was varied from 0.5% to 14%, which was equivalent to a volume concentration of 0.25% to 7%. Viscosity measurements were performed on a Brook field LVDV-II+Pro rotational viscometer equipped with a small sample adapter (cup diameter 20 mm) using an SC4-18 spindle with an outer diameter of 17.5 mm. The measurement accuracy was not less than one percent. A VPZh 2 viscometer with a capillary diameter of 1.31 mm was used for reference measurements. The experi- ments were conducted using a thermostat to provide meas- urements at a given temperature. Test measurements of the viscosity of pure ethylene glycol were performed. The resulting viscosity 17.1 sP at a temperature Т = 25˚C agrees to within one percent with available experimental data [42]. The data obtained by the capillary and rotational viscometers were identical within the measurement error. Since the main objective of this work was to determine the dependence of the viscosity of the nanofluid on na- noparticle size, it was necessary to accurately determine the average size of the particles and their size distribution. A typical electronic photograph of nanoparticles with an average size of 28.3 nm is shown in Figure 3. The dif- ferential particle size distributions f obtained after proc- essing of an ensemble of such photograph are presented in Figure 3. Electronic photograph of silica nanoparticles with an average size of 28.3 nm. Copyright © 2013 SciRes. ANP 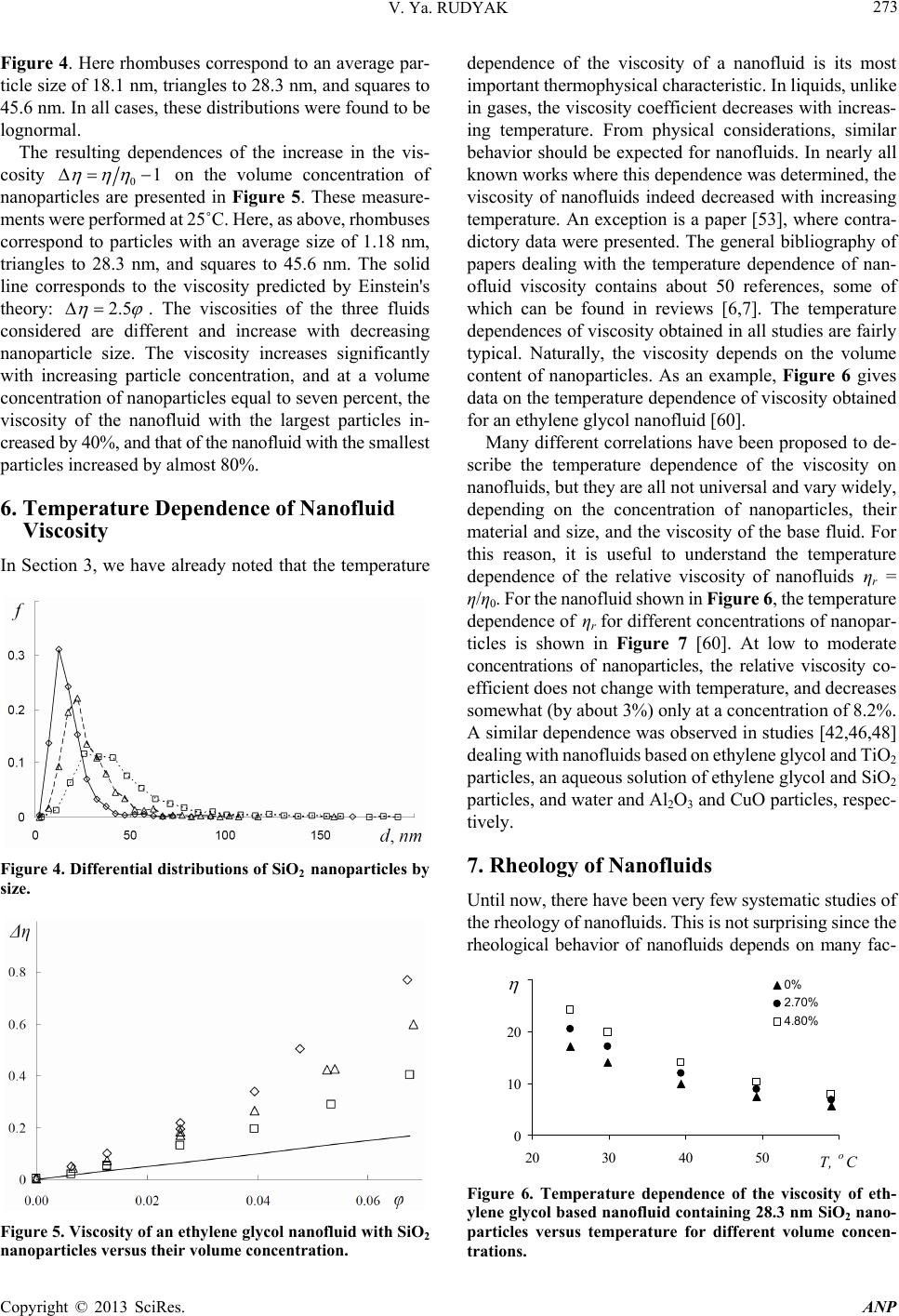 V. Ya. RUDYAK 273 Figure 4. Here rhombuses correspond to an average par- ticle size of 18.1 nm, triangles to 28.3 nm, and squares to 45.6 nm. In all cases, these distributions were found to be lognormal. dependence of the viscosity of a nanofluid is its most important thermophysical characteristic. In liquids, unlike in gases, the viscosity coefficient decreases with increas- ing temperature. From physical considerations, similar behavior should be expected for nanofluids. In nearly all known works where this dependence was determined, the viscosity of nanofluids indeed decreased with increasing temperature. An exception is a paper [53], where contra- dictory data were presented. The general bibliography of papers dealing with the temperature dependence of nan- ofluid viscosity contains about 50 references, some of which can be found in reviews [6,7]. The temperature dependences of viscosity obtained in all studies are fairly typical. Naturally, the viscosity depends on the volume content of nanoparticles. As an example, Figure 6 gives data on the temperature dependence of viscosity obtained for an ethylene glycol nanofluid [60]. The resulting dependences of the increase in the vis- cosity 01 on the volume concentration of nanoparticles are presented in Figure 5. These measure- ments were performed at 25˚C. Here, as above, rhombuses correspond to particles with an average size of 1.18 nm, triangles to 28.3 nm, and squares to 45.6 nm. The solid line corresponds to the viscosity predicted by Einstein's theory: 2.5 . The viscosities of the three fluids considered are different and increase with decreasing nanoparticle size. The viscosity increases significantly with increasing particle concentration, and at a volume concentration of nanoparticles equal to seven percent, the viscosity of the nanofluid with the largest particles in- creased by 40%, and that of the nanofluid with the smallest particles increased by almost 80%. Many different correlations have been proposed to de- scribe the temperature dependence of the viscosity on nanofluids, but they are all not universal and vary widely, depending on the concentration of nanoparticles, their material and size, and the viscosity of the base fluid. For this reason, it is useful to understand the temperature dependence of the relative viscosity of nanofluids ηr = η/η0. For the nanofluid shown in Figure 6, the temperature dependence of ηr for different concentrations of nanopar- ticles is shown in Figure 7 [60]. At low to moderate concentrations of nanoparticles, the relative viscosity co- efficient does not change with temperature, and decreases somewhat (by about 3%) only at a concentration of 8.2%. A similar dependence was observed in studies [42,46,48] dealing with nanofluids based on ethylene glycol and TiO2 particles, an aqueous solution of ethylene glycol and SiO2 particles, and water and Al2O3 and CuO particles, respec- tively. 6. Temperature Dependence of Nanofluid Viscosity In Section 3, we have already noted that the temperature 7. Rheology of Nanofluids Figure 4. Differential distributions of SiO2 nanoparticles by size. Until now, there have been very few systematic studies of the rheology of nanofluids. This is not surprising since the rheological behavior of nanofluids depends on many fac- 0 10 20 20 3040 50 60 T, o C 0% 2.70% 4.80% Figure 6. Temperature dependence of the viscosity of eth- ylene glycol base d nanofluid containing 28.3 nm SiO2 nano- particles versus temperature for different volume concen- trations. Figure 5. Viscosity of an ethylene glycol nanofluid with SiO2 nanoparticles versus their volume concentration. Copyright © 2013 SciRes. ANP 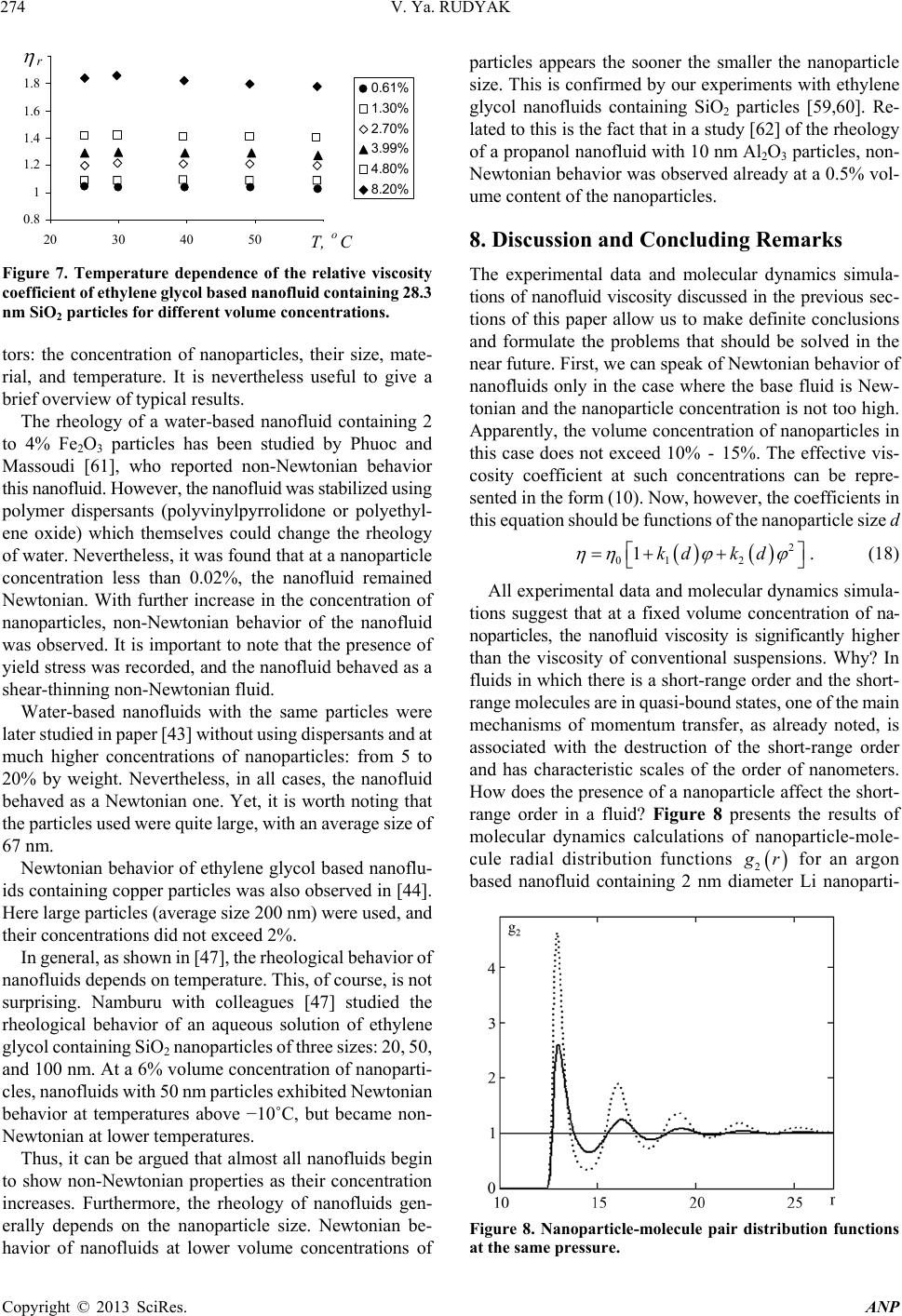 V. Ya. RUDYAK 274 0.8 1 1.2 1.4 1.6 1.8 2 20 30 40 50 60 T, o C r 0.61% 1.30% 2.70% 3.99% 4.80% 8.20% Figure 7. Temperature dependence of the relative viscosity coefficient o f eth ylene gl ycol based nanofluid containing 28.3 nm SiO2 particles for different volume conce ntr ations. tors: the concentration of nanoparticles, their size, mate- rial, and temperature. It is nevertheless useful to give a brief overview of typical results. The rheology of a water-based nanofluid containing 2 to 4% Fe2O3 particles has been studied by Phuoc and Massoudi [61], who reported non-Newtonian behavior this nanofluid. However, the nanofluid was stabilized using polymer dispersants (polyvinylpyrrolidone or polyethyl- ene oxide) which themselves could change the rheology of water. Nevertheless, it was found that at a nanoparticle concentration less than 0.02%, the nanofluid remained Newtonian. With further increase in the concentration of nanoparticles, non-Newtonian behavior of the nanofluid was observed. It is important to note that the presence of yield stress was recorded, and the nanofluid behaved as a shear-thinning non-Newtonian fluid. Water-based nanofluids with the same particles were later studied in paper [43] without using dispersants and at much higher concentrations of nanoparticles: from 5 to 20% by weight. Nevertheless, in all cases, the nanofluid behaved as a Newtonian one. Yet, it is worth noting that the particles used were quite large, with an average size of 67 nm. Newtonian behavior of ethylene glycol based nanoflu- ids containing copper particles was also observed in [44]. Here large particles (average size 200 nm) were used, and their concentrations did not exceed 2%. In general, as shown in [47], the rheological behavior of nanofluids depends on temperature. This, of course, is not surprising. Namburu with colleagues [47] studied the rheological behavior of an aqueous solution of ethylene glycol containing SiO2 nanoparticles of three sizes: 20, 50, and 100 nm. At a 6% volume concentration of nanoparti- cles, nanofluids with 50 nm particles exhibited Newtonian behavior at temperatures above −10˚C, but became non- Newtonian at lower temperatures. Thus, it can be argued that almost all nanofluids begin to show non-Newtonian properties as their concentration increases. Furthermore, the rheology of nanofluids gen- erally depends on the nanoparticle size. Newtonian be- havior of nanofluids at lower volume concentrations of particles appears the sooner the smaller the nanoparticle size. This is confirmed by our experiments with ethylene glycol nanofluids containing SiO2 particles [59,60]. Re- lated to this is the fact that in a study [62] of the rheology of a propanol nanofluid with 10 nm Al2O3 particles, non- Newtonian behavior was observed already at a 0.5% vol- ume content of the nanoparticles. 8. Discussion and Concluding Remarks The experimental data and molecular dynamics simula- tions of nanofluid viscosity discussed in the previous sec- tions of this paper allow us to make definite conclusions and formulate the problems that should be solved in the near future. First, we can speak of Newtonian behavior of nanofluids only in the case where the base fluid is New- tonian and the nanoparticle concentration is not too high. Apparently, the volume concentration of nanoparticles in this case does not exceed 10% - 15%. The effective vis- cosity coefficient at such concentrations can be repre- sented in the form (10). Now, however, the coefficients in this equation should be functions of the nanoparticle size d 2 01 2 1kd kd . (18) All experimental data and molecular dynamics simula- tions suggest that at a fixed volume concentration of na- noparticles, the nanofluid viscosity is significantly higher than the viscosity of conventional suspensions. Why? In fluids in which there is a short-range order and the short- range molecules are in quasi-bound states, one of the main mechanisms of momentum transfer, as already noted, is associated with the destruction of the short-range order and has characteristic scales of the order of nanometers. How does the presence of a nanoparticle affect the short- range order in a fluid? Figure 8 presents the results of molecular dynamics calculations of nanoparticle-mole- cule radial distribution functions 2 r for an argon based nanofluid containing 2 nm diameter Li nanoparti- Figure 8. Nanoparticle-molecule pair distribution functions at the same pressure. Copyright © 2013 SciRes. ANP 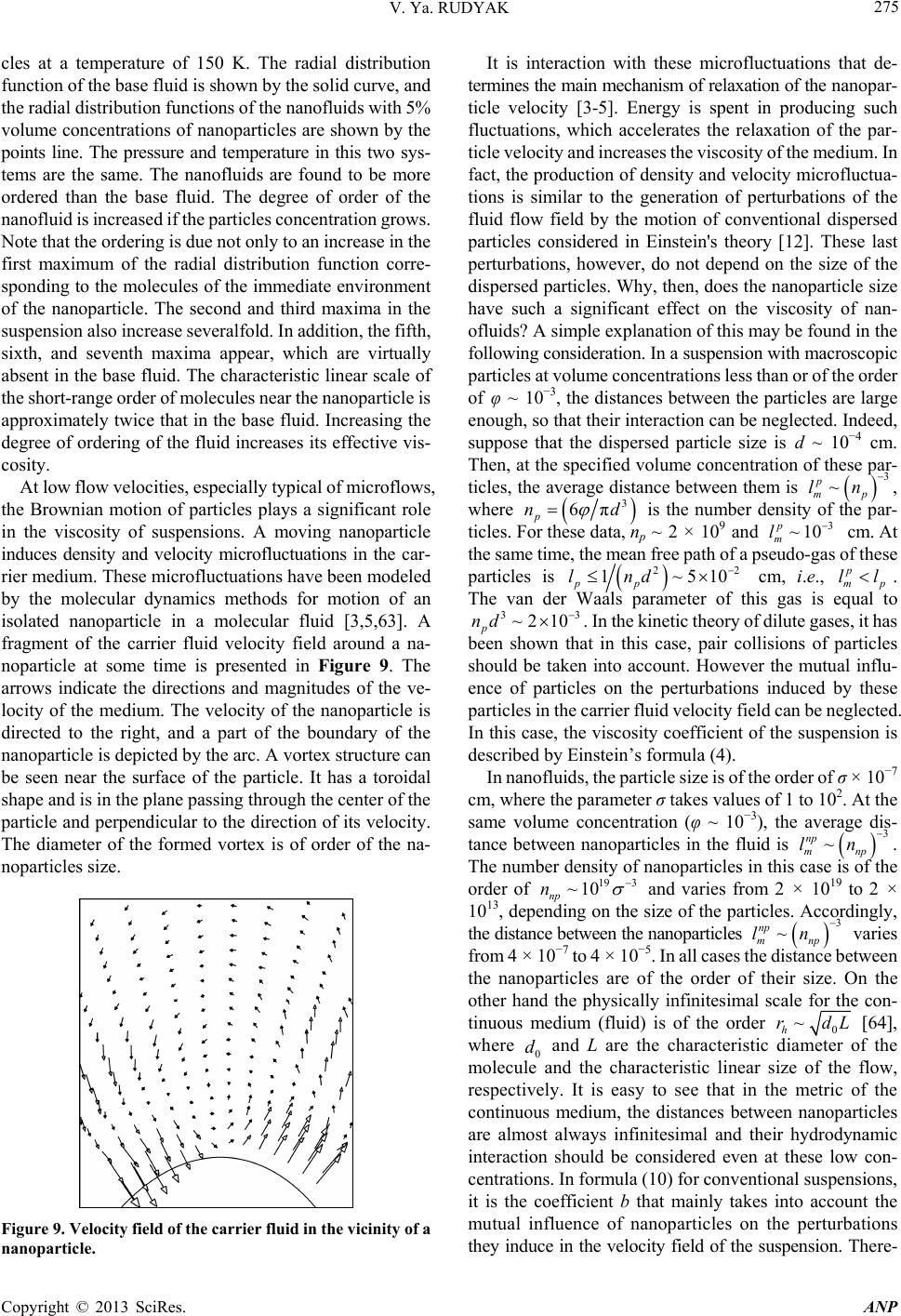 V. Ya. RUDYAK 275 cles at a temperature of 150 K. The radial distribution function of the base fluid is shown by the solid curve, and the radial distribution functions of the nanofluids with 5% volume concentrations of nanoparticles are shown by the points line. The pressure and temperature in this two sys- tems are the same. The nanofluids are found to be more ordered than the base fluid. The degree of order of the nanofluid is increased if the particles concentration grows. Note that the ordering is due not only to an increase in the first maximum of the radial distribution function corre- sponding to the molecules of the immediate environment of the nanoparticle. The second and third maxima in the suspension also increase severalfold. In addition, the fifth, sixth, and seventh maxima appear, which are virtually absent in the base fluid. The characteristic linear scale of the short-range order of molecules near the nanoparticle is approximately twice that in the base fluid. Increasing the degree of ordering of the fluid increases its effective vis- cosity. It is interaction with these microfluctuations that de- termines the main mechanism of relaxation of the nanopar- ticle velocity [3-5]. Energy is spent in producing such fluctuations, which accelerates the relaxation of the par- ticle velocity and increases the viscosity of the medium. In fact, the production of density and velocity microfluctua- tions is similar to the generation of perturbations of the fluid flow field by the motion of conventional dispersed particles considered in Einstein's theory [12]. These last perturbations, however, do not depend on the size of the dispersed particles. Why, then, does the nanoparticle size have such a significant effect on the viscosity of nan- ofluids? A simple explanation of this may be found in the following consideration. In a suspension with macroscopic particles at volume concentrations less than or of the order of φ ~ 10−3, the distances between the particles are large enough, so that their interaction can be neglected. Indeed, suppose that the dispersed particle size is d ~ 10−4 cm. Then, at the specified volume concentration of these par- ticles, the average distance between them is 3 ~ p mp ln , where 3 6π p n At low flow velocities, especially typical of microflows, the Brownian motion of particles plays a significant role in the viscosity of suspensions. A moving nanoparticle induces density and velocity microfluctuations in the car- rier medium. These microfluctuations have been modeled by the molecular dynamics methods for motion of an isolated nanoparticle in a molecular fluid [3,5,63]. A fragment of the carrier fluid velocity field around a na- noparticle at some time is presented in Figure 9. The arrows indicate the directions and magnitudes of the ve- locity of the medium. The velocity of the nanoparticle is directed to the right, and a part of the boundary of the nanoparticle is depicted by the arc. A vortex structure can be seen near the surface of the particle. It has a toroidal shape and is in the plane passing through the center of the particle and perpendicular to the direction of its velocity. The diameter of the formed vortex is of order of the na- noparticles size. d is the number density of the par- ticles. For these data, np ~ 2 × 109 and 3 ~10 p m l cm. At the same time, the mean free path of a pseudo-gas of these particles is 22 1~510d pp ln cm, i.e., p mp ll . The van der Waals parameter of this gas is equal to 3 ~2 10 p nd 3 . In the kinetic theory of dilute gases, it has been shown that in this case, pair collisions of particles should be taken into account. However the mutual influ- ence of particles on the perturbations induced by these particles in the carrier fluid velocity field can be neglected. In this case, the viscosity coefficient of the suspension is described by Einstein’s formula (4). In nanofluids, the particle size is of the order of σ × 10−7 cm, where the parameter σ takes values of 1 to 102. At the same volume concentration (φ ~ 10−3), the average dis- tance between nanoparticles in the fluid is 3 ~ np mnp ln . The number density of nanoparticles in this case is of the order of 19 3 ~10 np n and varies from 2 × 1019 to 2 × 1013, depending on the size of the particles. Accordingly, the distance between the nanoparticles 3 n p n~ np m l varies from 4 × 10−7 to 4 × 10−5. In all cases the distance between the nanoparticles are of the order of their size. On the other hand the physically infinitesimal scale for the con- tinuous medium (fluid) is of the order 0 ~ h [64], where 0 and L are the characteristic diameter of the molecule and the characteristic linear size of the flow, respectively. It is easy to see that in the metric of the continuous medium, the distances between nanoparticles are almost always infinitesimal and their hydrodynamic interaction should be considered even at these low con- centrations. In formula (10) for conventional suspensions, it is the coefficient b that mainly takes into account the mutual influence of nanoparticles on the perturbations they induce in the velocity field of the suspension. There- rd L d Figure 9. Ve loc ity f ield of the ca rri er f lui d i n the vic in it y of a nanoparticle. Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 276 fore, for nanofluids with low concentrations (in the lin- earized approximation for the concentration) of nanopar- ticles viscosity, the viscosity coefficient should be repre- sented as: 01ab . Batchelor [29,30], took into account the contribution of the hydrodynamic inter- action and Brownian motion of dispersed particles and obtained a coefficient b = 6.2. If this value is substituted into the above formula, the viscosity coefficient in the linear approximation for the concentration is equal to 018.7 . This value would provide a good fit to most of the available experimental data for nanofluids with small volume concentration of nanoparticles. Figure 10. Viscosity of an ethylene glycol nanofluid con- taining SiO2 particles versus nanopartic le size . There is also a second important point. The van der Waals parameter of a pseudo-gas of nanoparticles is of the order . It is known from kinetic theory that this corresponds to a fairly dense gas in which not only pair collisions of particles but also multiparticle (three-particle, etc.) collisions should be taken into ac- count. A nanoparticle interaction potential that takes into account the forces of both attraction and repulsion was constructed in [65]. The scale of the attractive forces is of the order of several sizes of nanoparticles. It follows that, even at such low concentrations, the contribution of the direct interaction of nanoparticles is also appreciable and should be considered when developing a coherent theory of nanofluid viscosity. 3 ~2 10 np nd 2 molecule. Thus, correlation (21) allows for the possible dependence of nanofluid viscosity on the physical char- acteristics of the base fluid. Moreover it may hope that correlation in form (21) will be applied for description of the viscosity coefficient at any temperature. Certainly, the volume fraction of the nanoparticles should be rather low. However, it does not take into account the possible dependence of nanofluid viscosity on nanoparticle mate- rial. Unfortunately, as yet, there have been no experiments giving a clear answer to the question of whether such dependence exists or not. Molecular dynamics simula- tions [56,59,66] indicate that for sufficiently small parti- cles, this dependence exists. However, the results of the kinetic theory of gas nanosuspensions [5,21] indicate that starting from certain sizes of nanoparticles (about 10 nm), this dependence should disappear. In constructing a correlation for nanofluid viscosity, it is necessary to proceed from formula (18). It is important, however, that in the limit of macroscopic fluids, it would reduce to the classical relations. Therefore, (18) needs to be represented as With further increase in the concentration of nanopar- ticles, it is necessary to take into account the possible structuring of the pseudo-gas of nanoparticles. In addition, due to the Van der Waals forces between nanoparticles, they can coagulate to form agglomerates. In this case the structure of nanofluids may resemble the structure of polymer solutions. From this point of view, it is not sur- prising that at high concentrations of nanoparticles, nan- ofluid become non-Newtonian. The study of the rheologi- cal properties of liquids requires systematic experiments with varying concentration, material, and shape of nanopar- ticles and varying properties of the base fluid. Interesting results can also be expected in the case where the base fluid is itself non-Newtonian. 2 01 1 12.5 6.2mD mD , (19) Here, the coefficient b is taken to be the value obtained by Batchelor [29,30], which provides a good fit to many experimental data. To specify the dependence of the co- efficients mi on the particle size, it is necessary to take into account two factors. First, it is desirable that in the limit of large particles, this correlation reduce to the classical one. Second, the number of the parameters in the correlation should not be too large. Figure 10 shows the dependence of nanofluid viscosity on nanoparticle size obtained in experiments [59,60]. This dependence is well enough described by an exponential. Therefore, correlation (19) can be written as 2 01 2 12.5 6.2 Dd Dd nen e . (20) REFERENCES Data [59,60] are well described by the formula 0 0 0.013 0 0.013 2 12.5 13.43 7.35 38.33 dd dd e e , (21) [1] S. Choi, “Enhancing Thermal Conductivity of Fluids with Nanoparticles,” In: D. A. Siginer and H. P. Wang, Eds., Developments Applications of Non-Newtonian Flows, Vol. 231, ASME, New York, 1995, pp. 99-105. [2] V. Ya. Rudyak and S. L. Krasnolutskii, “On Kinetic The- ory of Diffusion of Nanoparticles in a Rarefied Gas,” At- mospheric and Oceanic Optics, Vol. 16, No. 5-6, 2003, where d0 is the characteristic size of the carrier-fluid Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 277 pp. 468-471. [3] V. Ya. Rudyak and A. A. Belkin, “Mechanisms of Col- lective Nanoparticles Interaction with Condensed Sol- vent,” Thermophysics & Aeromechanics, Vol. 11, No. 2, 2004, pp. 54-63. [4] V. Ya. Rudyak, “Kinetic Theory and Modern Aerohy- dromechanics,” Journal of Applied and Industrial Mathe- matics, Vol. 8, No. 3, 2005, pp. 120-148. [5] V. Ya. Rudyak, A. A. Belkin and S. L. Krasnolutskii, “Statistical Theory of Nanoparticle Transport Processes in Gases and Liquids,” Thermophysics & Aeromechanics, Vol. 12, No. 4, 2005, pp. 506-516. [6] S. Sh. Hosseini, A. Shahrjerdi and Y. Vazifeshenas, “A Review of Relations for Physical Properties of Nanoflu- ids,” Australian Journal of Basic and Applied Sciences, Vol. 5, No. 10, 2011, pp. 417-435. [7] I. M. Mahbubul, R. Saidur and M. A. Amalina, “Latest Developments on the Viscosity of Nanofluids,” Interna- tional Journal of Heat and Mass Transfer, Vol. 55, No. 4, 2012, pp. 874-885. doi:10.1016/j.ijheatmasstransfer.2011.10.021 [8] D. C. Venerus, et al., “Viscosity Measurements on Col- loidal Dispersions (Nanofluids) for Heat Transfer Appli- cations,” Applied Rheology, Vol. 20, No. 4, 2010, Article ID: 44582. [9] G. Paul, J. Philip, B. Raj, P. K. Das and I. Manna, “Syn- thesis Characterization and Thermal Property Measure- ment of Nano-Al95Zn05 Dispersed Nanofluid Prepared by a Two-Step Process,” International Journal of Heat and Mass Transfer, Vol. 54, No. 15-16, 2011, pp. 3783- 3788. doi:10.1016/j.ijheatmasstransfer.2011.02.044 [10] W. Yu, H. Xie, Y. Li and L. Chen, “Experimental Inves- tigation on Thermal Conductivity and Viscosity of Alu- minum Nitride Nanofluid,” Particuology, Vol. 9, No. 2, 2011, pp. 187-191. doi:10.1016/j.partic.2010.05.014 [11] F. Perrin, “Etude Mathématique du Mouvement Brow- nien de Rotation,” Annales Scientifiques de L’Ecole Nor- male Superieure, Vol. 3, No. 45, 1928, pp. 1-51. [12] A. Einstein, “Eine Neue Bestimmung der Molekiildi- mensionen,” Annalen der Physik, Vol. 19, Ser. 4, 1906, pp. 289-306. doi:10.1002/andp.19063240204 [13] J. C. Maxwell, “A Treatise on Electricity and Magnet- ism,” Clarendon Press, Oxford, 1873. [14] J. O. Hirschfelder, Ch. F. Curtiss and R. B. Bird, “Mo- lecular Theory of Gases and Liquids,” Wiley, New York, 1954. [15] R. C. Reid, J. M. Prausnitz and T. K. Sherwood, “The Properties of Gases and Liquids,” McGraw-Hill Book Comp., New York, 1977. [16] V. Ya. Rudyak, “Kinetics of Finely Dispersed Gas Sus- pension,” Soviet Technical Physics Letters, Vol. 18, No. 10, 1992, pp. 681-682. [17] V. Ya. Rudyak, “The Kinetic Equations of Rarefied Gas Suspensions,” Proceedings of the 21st International Sym- posium on Rarefied Gas Dynamics, 1999, pp. 271-278. [18] V. Ya. Rudyak and S. L. Krasnolutskii, “Kinetic De- scription of Nanoparticle Diffusion in Rarefied Gas,” Doklady Physics, Vol. 46, No. 12, 2001, pp. 897-899. doi:10.1134/1.1433539 [19] V. Ya. Rudyak and S. L. Krasnolutskii, “Diffusion of Nanoparticles in a Rarefied Gas,” Technical Physics, Vol. 47, No. 7, 2002, pp. 807-812. doi:10.1134/1.1495039 [20] V. Ya. Rudyak and S. L. Krasnolutsky, “Effective Vis- cidity Coefficient for Rarefied Nano Gas Suspensions,” Atmosphere and Ocean Optics, Vol. 17, No. 5, 2004, pp. 468-475. [21] V. Ya. Rudyak, S. L. Krasnolutskii and E. N. Ivaschenko, “Influence of the Physical Properties of the Material of Nanoparticles on Their Diffusion in Rarefied Gases,” Journal of Engineering Physics and Thermophysics, Vol. 81, No. 3, 2008, pp. 520-524. doi:10.1007/s10891-008-0063-y [22] V. Ya. Rudyak and S. L. Krasnolutskii, “The Interaction Potential of Dispersed Particles with Carrier Gas Mole- cules,” Proceedings of the 21st International Symposium on Rarefied Gas Dynamics, Vol. 1, 1999, pp. 264-270. [23] V. Ya. Rudyak, S. L. Krasnolutskii, “About Viscosity of Rarefied Gas Suspensions with Nanoparticles,” Doklady Physics, Vol. 48, No. 10, 2003, pp. 583-586. doi:10.1134/1.1623543 [24] V. Ya. Rudyak, S. L. Krasnolutskii, A. G. Nasibulin and E. I. Kauppinen, “Methods of Measuring the Diffusion Coefficient and Sizes of Nanoparticles in Rarefied Gas,” Doklady Physics, Vol. 47, No. 10, 2002, pp. 758-761. doi:10.1134/1.1519325 [25] V. Ya. Rudyak and S. L. Krasnolutskii, “The Calculation and Measurement of Nanoparticles Diffusion Coefficient in Rarefied Gases,” Journal of Aerosol Science, Vol. 35, No. 1, 2003, pp. 579S-580S. [26] V. Ya. Rudyak, S. N. Dubtsov and A. M. Baklanov, “Temperature Dependence of the Diffusion Coefficient of Nanoparticles,” Technical Physics Letters, Vol. 34, No. 6, 2008, pp. 519-521. doi:10.1134/S1063785008060217 [27] V. Ya. Rudyak, S. N. Dubtsov and A. M. Baklanov, “Measurements of the Temperature Dependent Diffusion Coefficient of Nanoparticles in the Range of 295 - 600K at Atmospheric Pressure,” Journal of Aerosol Science, Vol. 40, No. 10, 2009, pp. 833-843. doi:10.1016/j.jaerosci.2009.06.006 [28] W. B. Russel, D. A. Saville and W. R. Schowalter, “Col- loidal Dispersions,” Cambridge University Press, Cam- bridge, 1989. [29] G. R. Batchelor, “Brownian Diffusion of Particles with Hydrodynamic Interaction,” Journal of Fluid Mechanics, Vol. 74, Pt. 1, 1976, pp. 1-29. doi:10.1017/S0022112076001663 [30] G. R. Batchelor, “The Effect of Brownian Motion on the Bulk Stress in a Suspension of Spherical Particles,” Jour- nal of Fluid Mechanics, Vol. 83, Pt. 1, 1977, pp. 97-127. doi:10.1017/S0022112077001062 [31] A. Acrivos and E. Y. Chang, “A Model for Estimating Transport Quantities in Two-Phase Materials,” Physics of Fluids, Vol. 29, No. 3-4, 1986, pp. 459-464. [32] M. Mooney, “The Viscosity of a Concentrated Suspen- sion of Spherical Particles,” Journal of Colloid Science, Vol. 6, No. 1, 1951, pp. 162-170. [33] I. M. Krieger and T. J. Dougherty, “A Mechanism for Non-Newtonian Flow in Suspensions of Rigid Spheres,” Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK 278 Journal of Rheology, Vol. 3, No. 1, 1959, pp. 137-145. doi:10.1122/1.548848 [34] N. A. Frankel and A. Acrivos, “On the Viscosity of a Concentrated Suspension of Solid Spheres,” Chemical Engineering Science, Vol. 22, No. 6, 1967, pp. 847-853. doi:10.1016/0009-2509(67)80149-0 [35] I. M. Krieger, “Rheology of Monodisperse Lattices,” Advances in Colloid and Interface Science, Vol. 3, No. 1, 1972, pp. 111-132. doi:10.1016/0001-8686(72)80001-0 [36] E. N. da C. Andrade, “Viscosity of Liquids,” Nature, Vol. 125, 1930, pp. 309-324. doi:10.1038/125309b0 [37] E. N. da C. Andrade, “A Theory of the Viscosity of Liq- uids,” Philosophical Magazine, Vol. 17, No. 112, 1934, pp. 497-514. [38] A. Ya. Malkin and A. I. Isaev, “Rheology, Concepts, Methods, & Applications,” Chemical Publishing, Toronto, 2006. [39] A. Graham, “On the Viscosity of Suspensions of Solid Spheres,” Applied Scientific Research, Vol. 37, No. 3-4, 1981, pp. 275-286. doi:10.1007/BF00951252 [40] D. C. Venerus, et al., “Viscosity Measurements on Col- loidal Dispersions (Nanofluids) for Heat Transfer Appli- cations,” Applied Rheology, Vol. 20, No. 4, 2010, Article ID: 44582. [41] H. Chen, Y. Ding, Y. He and C. Tan, “Rheological Be- havior of Ethylene Glycol Based Titania Nanofluids,” Chemical Physics Letters, Vol. 444, No. 4-6, 2007, pp. 333-337. doi:10.1016/j.cplett.2007.07.046 [42] H. Chen, Y. Ding and C. Tan, “Rheological Behavior of Nanofluids,” New Journal of Physics, Vol. 9, No. 10, 2007, p. 367. [43] L. Colla, L. Fedele, M. Scattolini and S. Bobbo, “Wa- ter-Based Fe2O3 Nanofluid Characterization: Thermal Conductivity and Viscosity Measurements and Correla- tion,” Advances in Mechanical Engineering, Vol. 2012, No. 1, 2012, Article ID: 674947. doi:10.1155/2012/674947 [44] J. Garg, et al., “Enchanced Thermal Conductivity and Viscosity of Copper Nanoparticles in Ethylene Glycol Nanofluid,” Applied Physics Letters, Vol. 103, No. 7, 2008, Article ID: 074301. doi:10.1063/1.2902483 [45] F. S. Oueslati and R. Bennace, “Heterogeneous Nanoflu- ids: Natural Convection Heat Transfer Enhancement,” Nanoscale Research Letters, Vol. 6, No. 3, 2011, p. 222. doi:10.1186/1556-276X-6-222 [46] P. K. Namburu, D. P. Kulkarni, A. Dandekar and D. K. Das, “Experimental Investigation of Viscosity and Spe- cific Heat and Silicon Dioxide Nanofluids,” Micro & Nano Letters, Vol. 2, No. 3, 2007, pp. 67-71. doi:10.1049/mnl:20070037 [47] P. K. Namburu, D. P. Kulkarni, D. Misra and D. K. Das, “Viscosity of Copper Oxide Nanoparticles Dispersed in Ethylene Glycol and Water Mixture,” Experimental Ther- mal and Fluid Science, Vol. 32, No. 2, 2007, pp. 397-402. doi:10.1016/j.expthermflusci.2007.05.001 [48] C. T. Nguyen, et al., “Viscosity Data for Al2O3-Water Nanofluid-Hysteresis: Is Heat Transfer Enhancement Us- ing Nanofluids Reliable?” International Journal of Thermal Sciences, Vol. 47, No. 2, 2008, pp. 103-111. doi:10.1016/j.ijthermalsci.2007.01.033 [49] B.C. Pak and Y. I. Cho, “Hydrodynamic and Heat Trans- fer Study of Dispersed Fluids with Submicron Metallic Oxide Particles,” Experimental Heat Transfer, Vol. 11, No. 2, 1998, pp. 151-170. doi:10.1080/08916159808946559 [50] X. Wang, X. Xu and S. U. S. Choi, “Thermal Conductiv- ity of Nanoparticle-Fluid Mixture,” Journal of Thermo- physics and Heat Transfer, Vol. 13, No. 4, 1999, pp. 474- 480. doi:10.2514/2.6486 [51] Y. He, Y. Jin, H. Chen, Y. Ding, D. Cang and H. Lu, “Heat Transfer and Flow Behaviour of Aqueous Suspen- sions of TiO2 Nanoparticles (Nanofluids) Flowing Up- ward through a Vertical Pipe,” International Journal of Heat and Mass Transfer, Vol. 50, No. 11-12, 2007, pp. 2272-2281. doi:10.1016/j.ijheatmasstransfer.2006.10.024 [52] C. T. Nguyen, F. Desgranges, G. Roy, N. Galanis, T. Mareґ, S. Boucher and H. Mintsa, “Temperature and Par- ticle-Size Dependent Viscosity Data for Water-Based Nanofluids—Hysteresis Phenomenon,” International Jour- nal of Heat and Fluid Flow, Vol. 28, No. 6, 2007, pp. 1492-1506. doi:10.1016/j.ijheatfluidflow.2007.02.004 [53] P. Prasher, D. Song and J. Wang, “Measurements of Na- nofluid Viscosity and Its Implications for Thermal Ap- plications,” Applied Physics Letters, Vol. 89, No. 13, 2006, Article ID: 133108. doi:10.1063/1.2356113 [54] J. Chevalier, O. Tillement and F. Ayela, “Rheological Properties of Nanofluids Flowing Through Microchan- nels,” Applied Physics Letters, Vol. 91, No. 23, Article ID: 233103. [55] E. V. Timofeeva, D. S. Smith, W. Yu, D. M. France, D. Singh and J. L. Routbo, “Particle Size and Interfacial Ef- fects on Thermo-Physical and Heat Transfer Characteris- tics of Water-Based α-SiC Nanofluids,” Nanotechnology, Vol. 21, No. 21, 2010, Article ID: 215703. doi:10.1088/0957-4484/21/21/215703 [56] V. Y. Rudyak, A. A. Belkin, E. A. Tomilina and V. V. Egorov, “Nanoparticle Friction Force and Effective Vis- cosity of Nanofluids,” Defect and Diffusion Forum, Vol. 273-276, No. 6, 2008, pp. 566-571. [57] V. Y. Rudyak, A. A. Belkin and V. V. Egorov, “On the Effective Viscosity of Nanosuspensions,” Technical Phy- sics, Vol. 54, No. 8, 2009, pp. 1102-1109. doi:10.1134/S1063784209080039 [58] G. Balasubramanian, S. Sen and I. K. Puri, “Shear Visco- sity Enhancement in Water—Nanoparticle Suspensions,” Physics Letters, Vol. A 376, No. 6-7, 2012, pp. 860-863. [59] V. Y. Rudyak, S. V. Dimov, V. V. Kuznetsov and S. P. Bardakhanov, “Measurement of the Viscosity Coefficient of an Ethylene Glycol-Based Nanofluid with Silicon Di- oxide Particles,” Doklady Physics, Vol. 58, No. 5, 2013, pp. 173-176. doi:10.1134/S1028335813050042 [60] V. Y. Rudyak, V. Dimov and V. V. Kuznetsov, “About Dependence of the Nanofluid Viscosity Coefficient on the Temperature and Size of the Particles,” Technical Physics Letters, Vol. 39, No. 17, 2013, pp. 53-59. [61] T. X. Phuoc and M. Massoudi, “Experimental Obser- vations of the Effects of Shear Rates and Particle Con- centration on the Viscosity of Fe2O3-Deionized Water Nanofluids,” International Journal of Thermal Sciences, Copyright © 2013 SciRes. ANP  V. Ya. RUDYAK Copyright © 2013 SciRes. ANP 279 Vol. 48, No. 7, 2009, pp. 1294-1301. doi:10.1016/j.ijthermalsci.2008.11.015 [62] A. D. Sommers, K. L. Yerkes and A. R. Runion, “A Stu- dy of the Thermal-Hydraulic Performance and System- Level Effects of Aluminum Oxide-Propanol Nanofluid,” Proceedings of the 14th International Heat Transfer Conference, Washington DC, 2010, Article ID: 22931. [63] V. Y. Rudyak and A. A. Belkin, “Simulation of the Trans- port Coefficients of Nanofluids,” Nanosystems: Physics, Chemistry, Mathematics, Vol. 1, No. 1, 2010, pp. 156- 177. [64] V. Y. Rudyak, “Nonlocal Solution of the Boltzmann Equation,” Zhurnal Tekhnicheskoі Fiziki, Vol. 65, No. 11, 1995, pp. 29-40. [65] V. Y. Rudyak, S. L. Krasnolutskii and D. A. Ivanov, “The Interaction Potential of Nanoparticles,” Doklady Physics, Vol. 57, No. 1, 2012, pp. 33-35. doi:10.1134/S1028335812010053 [66] V. Y. Rudyak, S. L. Krasnolutskii and D. A. Ivanov, “Molecular Dynamics Simulation of the Nanofluid Vis- cosity Coefficient,” Proceedings Russian Conference Mo- dern Problems of the Rarefied Gas Dynamics, Novosi- birsk, 26-30 July 2013, pp. 98-101
|