On the Sub-Critical Bifurcation of Anti-Phase and In-Phase Synchronized Vortex Shedding Forms

doi:10.4236/jmp.2013.45B015

Paper Menu >>

Journal Menu >>

Journal of Modern Physics, 2013, 4, 89-95

doi:10.4236/jmp.2013.45B015 Published Online May 2013 (http://www.scirp.org/journal/jmp)

On the Sub-Critical Bifurcation of Anti-Phase and

In-Phase Synchronized Vortex Shedding Forms

Yih Ferng Peng

Department of Civil Engineering, National Chi Nan University, Puli 545, Taiwan, China.

Email: yfpeng@ncnu.edu.tw

Received 2013

ABSTRACT

Transition of flows past a pair of side-by-side circular cylinders are investigated by numerical simulations and the bi-

furcation analysis of the numerical results. Various flow patterns behind the cylinder-pair have been identified by the

gap ratio (G) and Reynolds number (Re). This study focus on transition of in-phase and anti-phase vortex shedding

synchronized forms. A nested Cartesian-grid formulation, in combination with an effective immersed boundary method

and a two-step fractional-step procedure, has been adopted to simulate the flows. Numerical results reveal that the

in-phase and anti-phase vortex shedding flows at Re = 100 can co-exist at 2.08 2.58G



. Hysteresis loop with in-

creasing/decreasing G at constant Reynolds number Re = 100 is reported.

Keywords: In-phase Vortex Shedding; Anti-phase Vortex Shedding; Hysteresis

1. Introduction

Because of its fundamental importance and engineering

significance, unstable flow interferences across bluff

bodies have been investigated extensively. Flow inter-

ference with a pair of cylinders is complex in which both

relative-gap between the cylinders and arrangements of

relative position (in tandem, side-by-side, or in staggered)

play crucial roles in the physical transition. Among flows

around a pair of cylinders in various configurations, those

behind circular cylinders in a side-by-side arrangement

have been mostly extensively studied [1-11]. It is now

well established that the flow patterns behind a pair of

side-by-side cylinders can be classified [3,12] by the gap-

ratio G (surface-to-surface distance divided by cylinder-

diameter) and the Reynolds number (Reynolds number,

Re, is defined as/

ReU D



, where o

U is the free-

stream velocity, D is the cylinder diameter, and



is the

kinematic viscosity). At very small Gap ratios, the two

cylinders may behave in a similar fashion to a single bluff-

body [1]. At intermediate Gap ratios, the two side-by-

side cylinders is known [2] to exhibit a deflected or bi-

ased flow patterns, which are bi-stable in nature. The

deflected flow pattern is characterized by a gap flow bi-

ased towards one of the two cylinders. The gap flow in

this regime switches spontaneously from one side to the

other and thus corresponds to the flip-flopped regime [5].

For weak coupling (with relatively large G, 1



many of the past researchers report occurrences of both

anti-phase and in-phase synchronized vortex shedding

behind a pair of circular cylinders. Findings of William-

son [4] confirm that the shedding vortices (for 40



160) remain synchronized either in phase or in anti-

phase. Anti-phase streets often preserve the phase-locked

identity of the vortices even at a far downstream location.

However, for strong coupling (with relatively lower G)

only in-phase vortex shedding has been reported, and the

associated physical process eventually leads to formation

of a complex asymmetrically evolving Benard von Kar-

man streets.

Although there are varieties of flow patterns behind a

pair of side-by-side cylinders have been identified (which

include semi-single and twin vortex street formations,

symmetric and deflected flows, stationary, biased and

flip-flopped-type vortex shedding, periodic, quasi-peri-

odic, and weakly-chaotic flows, and in-phase and anti-

phase vortex synchronizations), very restriction results

have been reported on transition of those various flow

patterns. Examples can be found in the studies of Mizu-

shima & Ino [13] and Peng et al. [14]. In [13], parameter

space of the gap ratio and the critical Reynolds number

of symmetry/deflected vortex shedding flows and in-

phase/anti-phase vortex shedding flows behind a pair of

circular cylinders at low Reynolds number have been

reported by results of numerical simulations and linear

stability analyses. While in the study [14], transition from

semi-single symmetry vortex shedding flow to semi-

single deflected vortex shedding flow as well as transi-

tion from twin symmetry vortex shedding to twin de-

flected vortex shedding and then transition to the flipped-

Y. F. PENG

flopped vortex shedding regime behind a pair of elliptical

cylinders at low Reynolds number are shown by results

of direct numerical simulations. Although there are a lot

of experimental and numerical studies on the side-by-

side cylinders, the important transition phenomenon from

in-phase to anti-phase vortex shedding synchronization

and vs. are still unclear. Purpose of this study is then fo-

cus on transition of in-phase/anti-phase vortex shedding

synchronized forms behind a pair of side-by-side circular

cylinders. High resolution numerical methods based on a

nested Cartesian grid formulation, in combination with

an effective immersed boundary method and a two-step

fractional-step procedure, have been adopted to simulate

flows past a pair of side-by-side circular cylinders. Hys-

teresis loop with increasing/decreasing Re at constant gap

ratio describing the hysteresis phenomenon of in-phase/

anti-phase vortex shedding synchronized forms are re-

ported.

2. Numerical Methods and Validations

In this study, transitions of in-phase and anti-phase vortex

shedding flows behind a pair of circular cylinders in the

side-by-side arrangement are numerically investigated. A

nested Cartesian-grid formulation, in combination with

an effective immersed boundary method and a two-step

fractional-step procedure, has been adopted to simulate

the flows. Extensive related details of the discretization

schemes consisting of inside fine/coarse grid-areas and

the associated immersed boundary method may be found

in Peng et al. [14-15].

Here we briefly describe the implemented numerical

method. Governing equations used are unsteady incom-

pressible Navier–Stokes equations in primitive variables.

In integral forms, the dimensionless governing equations

(with lengths normalized by the diameter D of cylinders,

velocities normalized by the uniform inflow velocity U0,

and time by D /U0) appear as the following.

The mass conservation equation

CS un S

 , (1)

and the momentum conservation equation

d()d

CV CS

CS CS

uVuun S

pn Sun S





 







n inner fine-gri

(2)

CS and CV in Eqs. (1) and (2) denote the control-sur-

face and control-volume, respectively, and is a unit

vector normal to the control-surface. While advancing in

time, a second order accurate two-step fractional-step

method is used. A second-order Adams-Bashforth scheme

is employed for discretizing the convective terms, and

diffusion terms are discretized using an implicit Crank



colson scheme.

In the iterations of the discretized equations, a local

grid refinement technique is adopted through the intro-

duction of two nested blocks in the computational domain.

The implemented nested-block finite-volume based Carte-

sian-grid method is noted to facilitate effective/accurate

simulation of the presently investigated unsteady viscous

incompressible flows past multiple immersed boundaries.

The procedure adopted here allows systematic simulation

of flows past the cylinder-pair, and preserves global sec-

ond-order accuracy [15]. A sketch for the computational

domain with implemented boundary conditions and a

side-by-side arrangement of cylinder-pair is provided in

Figure 1. Various domain-lengths used for simulations

under the present study are defined as: L1 = 5D, L2 = 50D,

L3 = 12D, L4 = 4D, L5 = 8D, and L6 = 5.5D, facilitating

generation of a physical domain of size 55D × 24D, con-

sisting ad (Grid 2) area 12D × 11D. Upon

taking 0.1



the outer Grid1 (the coarse

grid), and 0.05

  for



  for the inner Grid 2, the

total grid size became 168,000, with Grid 1 = 120,000,

ted body force in the Na-

vier-Stokes equation, i.e.,

d Grid 2 = 48,000.

The simple concept of immersed boundary (IB) method

adopted here helps to simulate effectively the wake evo-

lutions past the cylinders. The virtual presence of the

cylinders within the flow domain is facilitated by intro-

ducing a locally active distribu

()

uuup uf,



tRe



 







in which the distributed body force

 is defined as

(( )1/)fuupReu











, and

represents the

volume-fraction of the solid body within a computational

cell. For a cell entirely occupied by the cylinders,

= 1

is used; and for a cell fully occupied by fluid,

= 0 is

taken. However, for an interface-cell, partially occupied

by a cylinder and partially by fluid, 0 <

< 1 is devoted.

Thereafter, the governing equations are solved everywhere

in the computational domain, including cells which are

ccupied by the elliptic cylinders.

Grid



u/ y=v=0



u=1,

v=0

u/x = 0

v/x = 0



Figure 1. Schematic plot of the flow domain.

Y. F. PENG 91

It is noted that an extensive validation of the underly-

ing method has been well-documented in [14-15]. In [14],

computations of important critical Reynolds numbers

(Recr,v) that correspond to onsets of vortex shedding for

uniform flows past a circular cylinder, an elliptical cyl-

inder, and two side-by-side attached elliptical cylinders

were performed. As listed on Table 1, for a circular cyl-

inder, our previous study observed this Recr,v to be 47.2,

which compares quite well with the experimentally pre-

dicted values 46.9 - 47.9 [16-18], and the theoretical val-

ues 46.1 - 47.3, as obtained by those linear stability

analysis [19-20] and the bifurcation analysis of Dusek et

al. [21].

3.1. Overview of Flows behind a Pair of

are

3. Results

Side-by-Side Circular Cylinders

This study begins with the investigation of critical transi-

tion characteristics in the narrow gap range, and extracts

the underlying bifurcation patterns. For this, first, flow

properties past two side-by-side circular cylinders in the

gap-ratio range 0.2 ≤ G ≤ 3.0 and 40 ≤ Re ≤ 100 are ex-

tensively simulated. The observed distinctive physical

properties of these flows sequentially characterized in

Table 2, in which ,1.5Cx

V denotes the teraged

transverse velocity at (x, y) = (1.5, 0.0), ,1 2L

ime-av



is the

temporal combined lift-coefficient (subscripe- t 1 + 2 d

mu-

ted data, the readers may note that at all Reynolds.

f vortex shed-

ding for flow pass a circular cylinder.

Source

notes upper plus lower cylinder effects, i.e., ,12,1,2LLL

CCC

),

and T is the period of vortex shedding. “Flow types” (last

column, Table 2) are classified based on the following

three special characteristics. The first letter in the abbre-

viated flow-type, “S,” corresponds to the semi-single flow,

and “T” corresponds to twin flow. For the second letter,

“S” represents symmetric flow, and “D” denotes the de-

flected flow. In the third and fourth places, “SS” indicates

steady-state flow, “VP” represents periodic vortex shed-

ding flow, “VQ” stands for quasi- periodic vortex shed-

ding flow, and “VC” denotes the chaotic vortex sh edd ing.

Various vortex shedding regimes, including flip-flopped,

in-phase, and anti-phase vortex shedding flows are also

denoted by superscripts in last column. From the si

Table 1. Critical Reynolds number of onset o

Recr,v Analytic Method

Present 47.2 bifis urcation analys

Provansal et al. [16]

47.45)

0] li

47.0 experiments

Williamson [147.9 experiments

Norberg [18] ( ± 0. experiments

Jackson [19] 46.2 linear stability analysis

Kumar & Mittal [247.3 near stability analysis

Dusek et al. [21] 46.1 bifurcation analysis

Table 2. Simulated results of flows past two side-by-side

circular cylinders at 40 ≤ Re ≤ 100 and 0.2 ≤ G ≤ 3.0.

No. G Re,1.5Cx

V F

,1 2L

C T low type

1 0.2400.0 0.593 10.80 S,S,VP

2 0.2600.0 0.921 9.75 S,S,VP

3 0.2800.0 0.786 9.20 S,S,VP

4 0.21000.0 0.258 9.08 S,S,VP

5 0.4400.0 0.005 13.61 S,S,VP

6 0.4600

NA S

NA T,

0 5.23

0 5.19

0 5.13

0 5.15

5.00 T

5.04 T

5.10 T

5.1 T

60 3.01000.0 0.0 5.17 T,S,VP A

.1110.00112.76 S,D,VP

7 0.4800.0 NA NA S,S,VQ F

8 0.41000.0 NA ,S,VC F

9 0.6400.0 0.0  T,S,SS

10 0.6600.0 0.0  T,S,SS

11 0.6800.0 NA  T, S, VC F

12 0.61000.0 NA  ,S,VC F

13 0.8400.0 0.0  T,S,SS

14 0.8600.0 NA NA T,S,VQ F

15 0.8800.0 NA NA T,S,VC F

16 0.81000.0 NA S,VC F

17 1.0400.0 0.0  T,S,SS

18 1.0600.0 NA NA T,S,VQ F

19 1.0800.0 NA NA T,S ,VQ F

20 1.01000.0 NA S,VC F

21 1.2400.0 0.0  T,S,SS

22 1.2600.0 NA NA T,S,VQ F

23 1.2800.0 NA NA T,S,VQ F

24 1.21000.0 NA S,VQ F

25 1.4400.0 0.0  T,S,SS

26 1.4600.0 NA NA T,S,VQ F

27 1.4800.0 0.439 5.53 T,S,VP I

28 1.41000.0 .622T,S,VP I

29 1.6400.0 0.0  T,S,SS

30 1.6600.0 NA NA T,S,VQ F

31 1.6800.0 0.415 5.50 T,S,VP I

32 1.61000.0 .588T,S,VP I

33 1.8400.0 0.0  T,S,SS

34 1.8600.0 NA NA T,S,VQ F

35 1.8800.0 0.402 5.45 T,S,VP I

36 1.81000.0 .570T,S,VP I

37 2.0400.0 0.0  T,S,SS

38 2.0600.0 0.197 6.05 T,S,VP I

39 2.0800.0 0.398 5.47 T,S,VP I

40 2.01000.0 .564T,S,VP I

41 2.2400.0 0.0  T,S,SS

42 2.2600.0 0.192 6.04 T,S,VP I

43 2.2800.0 .3995.50 T,S,VP I

44 2.21000.0 0.0 ,S,VP A

45 2.4400.0 0.0  T,S,SS

46 2.4600.0 0.196 6.06 T,S,V P I

47 2.4800.0 .4065.56 T,S,VP A

48 2.41000.0 0.0 ,S,VP A

49 2.6400.0 0.0  T,S,SS

50 2.6600.0 .2006.11 T,S ,V P I

51 2.6800.0 0.0 5.37 T,S,VP A

52 2.61000.0 0.0 ,S,VP A

53 2.8400.0 0.0  T,S,SS

54 2.8600.0 .2086.08 T,S,VP I

55 2.8800.0 0.0 5.41 T,S,VP A

56 2.81000.0 0.0 1 ,S,VP A

57 3.0400.0 0.0  T,S,SS

58 3.0600.0 0.0 5.94 T,S,VP A

59 3.0800.0 0.0 5.49 T,S,VP A

Y. F. PENG

numbers (Re ≥ 40) the single vortex shedding street is

reached in the range G ≤ 0.4. However, for larger G (G ≥

0.6), the approach to the vortex shedding flow remained

dependent on Re. The flip-flopped vortex-shed-ding oc-

curred in the gap-ratio range 0.4 ≤ G ≤ 1.8 with Re ≥ 60.

In-phase vortex shedding is detected at 0.4 ≤ G ≤ 1.8, and

anti-phase vortex shedding is founded at large G (G ≥

2.2). Notably, while Table 2 presents the explicit physi-

cal details of various flows, for the sake of facilitating

immediate comprehension of a trend, the parameter

space diagram is suitably summarized in Figure 2. As

shown in Figure 2, it is clear that flows are semi-single

at G < 0.5. At intermediate Gap ratios the two

side-by-side cylinders is known to exhibit a deflected or

biased flow patterns, which are bi-stable in nature. The

deflected jets through circular gap are further affected by

the shedding vortices at higher Re and flows become

flip-flopped consequently. The range of Gap ratios where

the flip-flopped flow pattern is observed extends from

approximately Gap ratios between 0.4 - 1.8 depending on

the Reynolds number. At higher Gap ratios, i.e., the cyl-

inders are spaced sufficiently far apart, the pair of cylin-

ders may behave as two independent bluff bodies. Prox-

imity interference effects, however, lead to various

modes of synchronization, anti-phase and in-phase, in the

vortex formation and shedding processes and the result-

ing parallel vortex streets. For example, in-phase and

anti-phase vortex shedding flows at Re = 100 are clearly

revealed at G = 2.0 and G = 3.0, respectively.

3.2. Hysteresis Scenario of In-phase and

Anti-phase Synchronized Forms

To investigated the transition of in-phase and anti-phase

synchronized forms in flows past a pair of side-by-side

circular cylinders, two sets of computations including

anti-phase and in-phase branches are carried out. The

anti-phase branch started from the anti-phase vortex

20 30 40 50 60 70 80 90100110120

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

2.4

2.6

2.8

3.0

3.2

3.4

3.6

SSSS

SSSSSSSSS

SSS

DDDDDD

FFF

FFFF FF

FFF

FFFF

 









AAA

Twin street

Semi-single street

S: symmetric flowsD: deflected flowsF: flip-flopped flows

I: in-phase flowsA: anti-phase flows

: steady flows

: periodic flows

: quasi-periodic flows

: chaotic flows

Figure 2. Simulated different wake patterns observed be-

hind two side-by-side circular cylinders.

shedding flow at G = 3.0 and Re = 100 and are calculated

by progressively decreasing G in very small steps. In the

meanwhile, the in-phase branch started from the in-phase

vortex shedding flow at G = 2.0 and Re = 100 and are

calculated by progressively increasing G in small steps.

The observed distinctive physical properties of these

flows are sequentially characterized in Table 3. It is

noted that in anti-phase branch, the solution at a higher G

is used as the initial condition for the next lower G.

Similarly, in in-phase branch, the solution at a lower G is

used as the initial condition for the next higher G.

The flow past cylinder-pair at constant Reynolds num-

ber (Re = 100) retains anti-phase vortex shedding syn-

chronized forms at high gap ratio (), as

indicated by our extracted data on Table 3(a). Once G is

decreased to G = 2.06, the anti-phase vortex shedding

flow transits to the in-phase synchronized vortex shed-

ding form. For clarity, the existence of the anti-phase

vortex shedding flow pattern at Re = 100, and G = 2.32 is

exhibited in Figure 3. It reveals clearly the anti-phase

vortex shedding behavior of the simulated flow in the

sub-domain x = [−5, 50], y = [−9, 9]. The continuation of

zero central-line velocity (Figure 3(d)), and perfectly

anti-phase synchronized growth of the lift (CL,1, CL,2)

coefficients (Figures 3(b) and (c)) ensure the inherent

anti-phase characteristic of vortex shedding (Figure 3(a))

in the wake. Note that, unlike for in-phase vortex shed-

ding flow (Figure 4), the equal but opposite natured

variations of CL,1 and CL,2 in the present case contribute

to the continued vanishing of CL,1+2 (Figure 3(d)) during

the entire time-evolution.

2.08 3.0G

Upon maintaining anti-phase synchronized vortex shed-

ding forms with the past findings related to side-by-side

cylinder-pair (Re = 100, ), once the gap-

ratio was subsequently increased (from

2.08 3.0G

2.0G



), the

in-phase synchronized vortex shedding were encountered

behind the cylinder-pair (Re = 100, ). The

distinguishable physical characteristics associated with

the in-phase vortex shedding flows past the cylinder-pair

at Re = 100 and again G = 2.32 is extracted in Figure 4.

It can be noted from the figure that the gap-flow quickly

lost stability; however, the shedding vortices appeared

clearly in-phase synchronized at least up to x ≤ 12.

Thereafter, instability is seen to quickly grow, leading to

the development of a combined binary vortex street

within 12 < x <26, and beyond that there occurred an

irregular flow pattern over a conversion point. Physical

details of this in-phase flow in terms of enhanced CL,1+2,

and significantly modulated transient evolution (in-phase)

of individual lift (CL,1 and CL,2) coefficients are extracted

in Figures 4(d), (b) and (c).

2.0 2.58G

3.3. Hysteresis Loop

From the simulated data on Table 3, the reader may note

that at constant Reynolds number (Re = 100), the anti-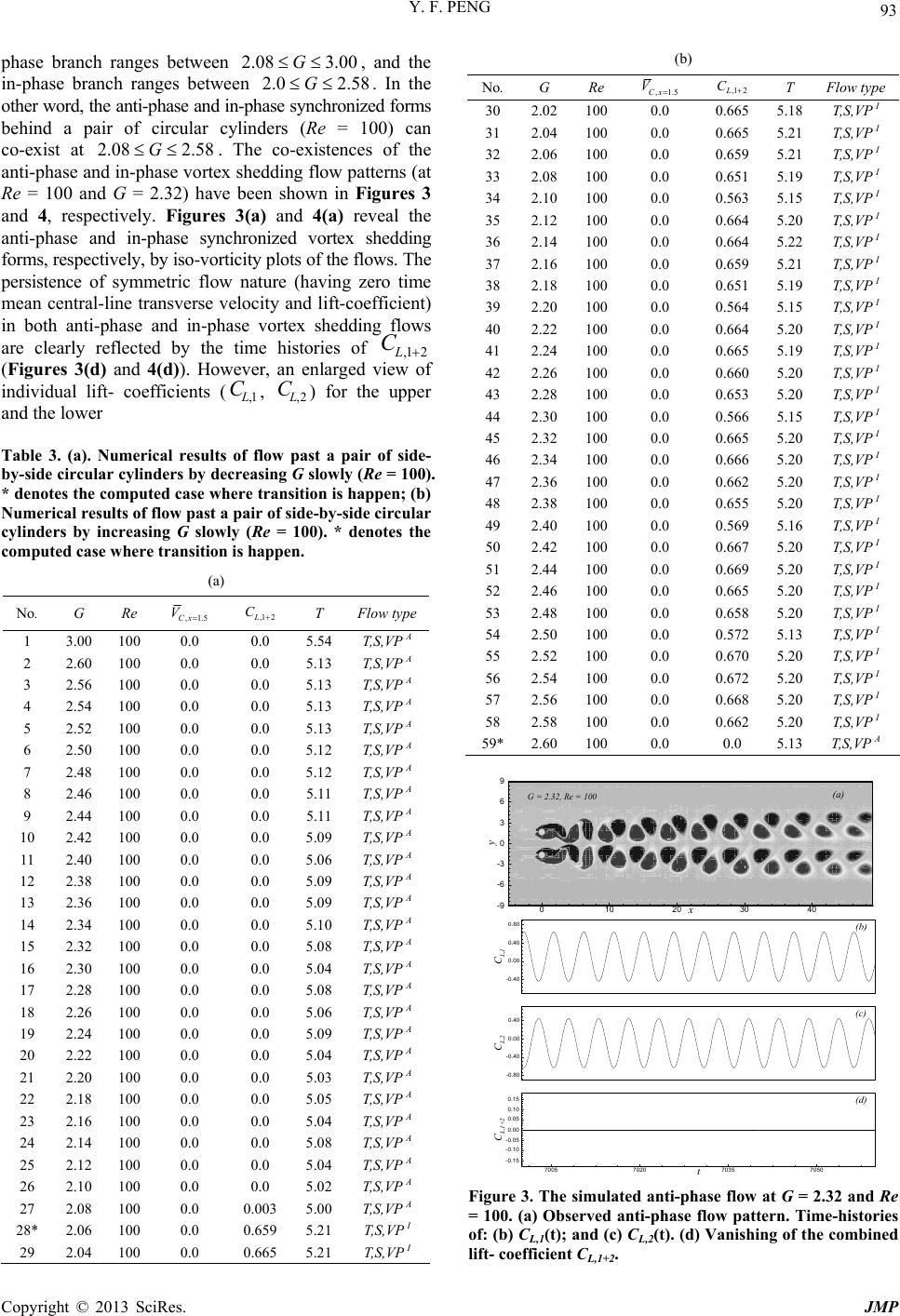

Y. F. PENG 93

phase branch ranges between , and the

in-phase branch ranges between . In the

other word, the anti-phase and in-phase synchronized forms

behind a pair of circular cylinders (Re = 100) can

co-exist at . The co-existences of the

anti-phase and in-phase vortex shedding flow patterns (at

Re = 100 and G = 2.32) have been shown in Figures 3

and 4, respectively. Figures 3(a) and 4(a) reveal the

anti-phase and in-phase synchronized vortex shedding

forms, respectively, by iso-vorticity plots of the flows. The

persistence of symmetric flow nature (having zero time

mean central-line transverse velocity and lift-coefficient)

in both anti-phase and in-phase vortex shedding flows

are clearly reflected by the time histories of ,1 2L

2.08 3.00G

2.0 2.58G

2.08 2.58G



(Figures 3(d) and 4(d)). However, an enlarged view of

individual lift- coefficients (, ) for the upper

and the lower

,1L

C,2L

Table 3. (a). Numerical results of flow past a pair of side-

by-side circular cylinders by decreasing G slowly (Re = 100).

* denotes the computed case where transition is happen; (b)

Numerical results of flow past a pair of side-by-side circular

cylinders by increasing G slowly (Re = 100). * denotes the

computed case where transition is happen.

(a)

No. G Re ,1.5Cx

V ,12L

C T Flow type

1 3.00 100 0.0 0.0 5.54 T,S,VP A

2 2.60 100 0.0 0.0 5.13 T,S,VP A

3 2.56 100 0.0 0.0 5.13 T,S,VP A

4 2.54 100 0.0 0.0 5.13 T,S,VP A

5 2.52 100 0.0 0.0 5.13 T,S,VP A

6 2.50 100 0.0 0.0 5.12 T,S,VP A

7 2.48 100 0.0 0.0 5.12 T,S,VP A

8 2.46 100 0.0 0.0 5.11 T,S,VP A

9 2.44 100 0.0 0.0 5.11 T,S,VP A

10 2.42 100 0.0 0.0 5.09 T,S,VP A

11 2.40 100 0.0 0.0 5.06 T,S,VP A

12 2.38 100 0.0 0.0 5.09 T,S,VP A

13 2.36 100 0.0 0.0 5.09 T,S,VP A

14 2.34 100 0.0 0.0 5.10 T,S,VP A

15 2.32 100 0.0 0.0 5.08 T,S,VP A

16 2.30 100 0.0 0.0 5.04 T,S,VP A

17 2.28 100 0.0 0.0 5.08 T,S,VP A

18 2.26 100 0.0 0.0 5.06 T,S,VP A

19 2.24 100 0.0 0.0 5.09 T,S,VP A

20 2.22 100 0.0 0.0 5.04 T,S,VP A

21 2.20 100 0.0 0.0 5.03 T,S,VP A

22 2.18 100 0.0 0.0 5.05 T,S,VP A

23 2.16 100 0.0 0.0 5.04 T,S,VP A

24 2.14 100 0.0 0.0 5.08 T,S,VP A

25 2.12 100 0.0 0.0 5.04 T,S,VP A

26 2.10 100 0.0 0.0 5.02 T,S,VP A

27 2.08 100 0.0 0.003 5.00 T,S,VP A

28* 2.06 100 0.0 0.659 5.21 T,S,VP I

29 2.04 100 0.0 0.665 5.21 T,S,VP I

(b)

No. G Re ,1.5Cx

V ,12L

C T Flow type

30 2.02100 0.0 0.665 5.18 T,S,VP I

31 2.04100 0.0 0.665 5.21 T,S,VP I

32 2.06100 0.0 0.659 5.21 T,S,VP I

33 2.08100 0.0 0.651 5.19 T,S,VP I

34 2.10100 0.0 0.563 5.15 T,S,VP I

35 2.12100 0.0 0.664 5.20 T,S,VP I

36 2.14100 0.0 0.664 5.22 T,S,VP I

37 2.16100 0.0 0.659 5.21 T,S,VP I

38 2.18100 0.0 0.651 5.19 T,S,VP I

39 2.20100 0.0 0.564 5.15 T,S,VP I

40 2.22100 0.0 0.664 5.20 T,S,VP I

41 2.24100 0.0 0.665 5.19 T,S,VP I

42 2.26100 0.0 0.660 5.20 T,S,VP I

43 2.28100 0.0 0.653 5.20 T,S,VP I

44 2.30100 0.0 0.566 5.15 T,S,VP I

45 2.32100 0.0 0.665 5.20 T,S,VP I

46 2.34100 0.0 0.666 5.20 T,S,VP I

47 2.36100 0.0 0.662 5.20 T,S,VP I

48 2.38100 0.0 0.655 5.20 T,S,VP I

49 2.40100 0.0 0.569 5.16 T,S,VP I

50 2.42100 0.0 0.667 5.20 T,S,VP I

51 2.44100 0.0 0.669 5.20 T,S,VP I

52 2.46100 0.0 0.665 5.20 T,S,VP I

53 2.48100 0.0 0.658 5.20 T,S,VP I

54 2.50100 0.0 0.572 5.13 T,S,VP I

55 2.52100 0.0 0.670 5.20 T,S,VP I

56 2.54100 0.0 0.672 5.20 T,S,VP I

57 2.56100 0.0 0.668 5.20 T,S,VP I

58 2.58100 0.0 0.662 5.20 T,S,VP I

59* 2.60100 0.0 0.0 5.13 T,S,VP A

0 10203040

-9

-6

-3

G = 2.32, Re = 100

(a)

-0.40

0.00

0.40

0.80

CL,1

(b)

-0.80

-0.40

0.00

0.40

CL,2

(c)

7005 7020 7035 7050

-0.15

-0.10

-0.05

0.00

0.05

0.10

0.15

CL,1+2

(d)

Figure 3. The simulated anti-phase flow at G = 2.32 and Re

= 100. (a) Observed anti-phase flow pattern. Time-histories

of: (b) CL,1(t); and (c) CL,2(t). (d) Vanishing of the combined

lift- coefficient CL,1+2.

Y. F. PENG

0 10203040

-9

-6

-3

G = 2.32, Re = 100

(a)

11440 11456 11472 11488

-0.80

-0.40

0.00

0.40

0.80

L,1+2

(d)

-0.40

-0.20

0.00

0.20

0.40

0.60

L,1

(b)

-0.60

-0.40

-0.20

0.00

0.20

0.40

L,2

(c)

Figure 4. The simulated periodic in-phase flow at G = 2.32

and Re = 100. (a) In-phase vortex shedding behavior.

Time-histories of: (b) CL,1(t); and (c) CL,2(t). (d) Enhance-

ment of the combined lift-coefficient CL,1+2.

1.8 2.0 2.2 2.4 2.6 2.8 3.0

-0.2

0.0

0.2

0.4

0.6

0.8

1.0

1.2

L,1+2

: byincreasingG gradually

: by decreasing G gradually

the in-phase branch

the anti-phase branch

Figure 5. The hysteresis region with G of in-phase and anti-

hase synchronized vortex shedding forms for flows past a

pair of circular cylinders at Re = 100.

cylinders (Figures 3(b) and (c)/Figures 4(b) and (c))

reveals occurrence of anti-phase/in-phase vortex shed-

ding vortices of the upper and lower vortex streets.

Readers may note that the corresponding lift-amplitudes

(,12 ) in anti-phase vortex shedding flows become

neutralized as shown in Figure 3(d), on the contrary, the

corresponding lift-amplitudes () in in-phase vortex

shedding flows become enhanced as shown in Figure

4(d), respectively. Since the value ofstands as a

characteristic value of anti-phase/in-phase synchronized

vortex shedding forms, it is worthy to show the

C

,1 2L

C

,1 2L

C

,1 2L



distributions. As shown in Figure 5, the ,1 2L



distri-

bution along the anti-phase branch (,1 2

C) combines

the in-phase branch (

L

,1 2L

C0



) becomes a hysteresis

loop. Particularly, the anti-phase branch starting from G

= 3.0 trace along a straight segment, ending at G = 2.08,

and then merges to the in-phase branch. While the in-

phase branch starting from G = 2.0 trace along a wavy

line, ending at G = 2.58, and then merges to the

anti-phase branch.

4. Conclusions

Numerical results have been presented for the in-phase

and anti-phase vortex shedding synchronized forms of

flows behind a pair of side-by-side circular cylinders.

Flows are restricted in low-Reynolds-number (Re



100)

laminar regime for various small/middle gap ratio

(0.23.0G



). The computations have been carried out

in two-dimensional, using a high resolution numerical

method based on a nested Cartesian grid formulation, in

combination with an effective immersed boundary method

and a two-step fractional-step procedure.

Hysteresis phenomenon of the in-phase/anti-phase

vortex shedding synchronized forms of flows has been

studied in detail. For flows behind a pair of side-by-side

circular cylinders at Re = 100, the hysteresis loop with

width ranges between is clearly found.

2.08 2.58G

5. Acknowledgements

This work was supported in part by the National Science

Council of the Republic of China (Taiwan) under Con-

tract No. NSC 101-2221-E-260-038-.

REFERENCES

[1] H. M. Spivac, “Vortex Frequency and Flow Pattern in the

Wake of Two Parallel Cylinders at Varied Spacing Nor-

mal to An Airstream,” Journal of the Aeronautical Sci-

ences, Vol. 13, 1946, pp. 289-301.

[2] P. W. Bearman and A. J. Wadcock, “The Interference

between A Pair of Circular Cylinders Normal to A

Stream,” Journal of Fluid Mechanics, Vol. 61. No. 3,

1973, pp. 499-511. doi:10.1017/S0022112073000832

[3] M. M. Zdravkovich, “Review of Flow Interference Be-

tween Two Circular Cylinders in Various Arrangements,”

ASME, Vol. 99, No. 4, 1977, pp. 618-633.

doi:10.1115/1.3448871

[4] C. H. K. Williamson, “Evolution of a Single Wake behind

A Pair of Bluff Bodies,” Journal of Fluid Mechanics, Vol.

159, 1985, pp. 1-18. doi:10.1017/S002211208500307X

[5] H. J. Kim and P. A. Durbin, “Investigation of the Flow

between a Pair of Circular Cylinders in the Flopping Re-

gime,” Journal of Fluid Mechanics, Vol. 196, 1988, pp.

431-448. doi:10.1017/S0022112088002769

[6] D. Sumner, S. S. T. Wong, S. J. Price and M. P. Päidous-

sis, “Fluid Behavior of Side-by-side Circular Cylinders in

Steady Cross-flow,” Journal of Fluids and Structures,

Vol. 13. No. 3, 1999, pp. 309-339.

doi:10.1006/jfls.1999.0205

Y. F. PENG

[7] Y. Zhou, H. J. Zhang and M. W. Yiu, “The Turbulent

Wake of Two Side-by-side Circular Cylinders,” Journal

of Fluid Mechanics，Vol. 458, 2002, pp. 303-332.

doi:10.1017/S0022112002007887

[8] S. J. Xu, Y. Zhou and R. M. C. So, “Reynolds Number

Effects on the Flow Structure behind Two Side-by-side

Cylinders,” Physics of Fluids, Vol. 15. No. 5, 2003, pp.

1214-1219. doi:10.1063/1.1561614

[9] S. Kang, “Characteristics of Flow over Two Circular

Cylinders in A Side-by-side Arrangement at Low Rey-

nolds Numbers,” Physics of Fluids, Vol. 15, 2003.

[10] S. Kumar, B. Gonzalez and O. Probst, “Flow Past Two

Rotating Cylinders,” Physics of Fluids, Vol. 23, No. 1,

2011, 01402. doi:10.1063/1.3528260

[11] Md Mahbub Alam, Y. Zhou, and X. W. Wang, “The

Wake of Two Side-by-side Square Cylinders,” Journal of

Fluid Mechanics, Vol. 669, 2011, pp. 432-471.

doi:10.1017/S0022112010005288

[12] D. Sumner, “Two Circular Cylinders in Cross-flow: A

Review,” Journal of Fluids and Structures, Vol. 26. No. 6,

2010, pp. 849-899.

doi:10.1016/j.jfluidstructs.2010.07.001

[13] J. Mizushima and Y. Ino, “Stability of Flows Past A Pair

of Circular Cylinders in A Side-by-side Arrangement,”

Journal of Fluid Mechanics, Vol. 595, 2008, pp. 491-507.

doi:10.1017/S0022112007009433

[14] Y. F. Peng, A. Sau, R. R. Hwang, W. C. Yang and C. M.

Hsieh, “Criticality of Flow Transition behind Two

Side-by-side Elliptic Cylinders,” Physics of Fluids, Vol.

24. No. 3, 2012, 034102.

doi:10.1063/1.3687450

[15] Y. F. Peng, R. Mittal, A. Sau and R. Hwang, “Ested Car-

tesian Grid Method in Incompressible Viscous Fluid

Flow,”Journal of Computational Physics, Vol. 229,

No.19, 2010, pp. 7072-7101.

doi:10.1016/j.jcp.2010.05.041

[16] M. Provansal, C. Mathis and L. Boyer, “Be’nard-von

Ka’rma’n Instability: Transient and Forced Regimes,”

Journal of Fluid Mechanics, Vol. 182, 1987, pp. 1-22.

doi:10.1017/S0022112087002222

[17] C. H. K. Williamson, “Oblique and Parallel Modes of

Vortex Shedding in the Wake of a Circular Cylinder at

Low Reynolds Numbers,” Journal of Fluid Mechanics,

Vol. 206, 1989, pp. 579-627.

doi:10.1017/S0022112089002429

[18] C. Norberg, “An Experimental Investigation of the Flow

around a Circular Cylinder: Influence of Aspect Ratio,”

Journal of Fluid Mechanics, Vol. 258, 1994, pp. 287-316.

doi:10.1017/S0022112094003332

[19] C. P. Jackson, “A Finite-element Study of the Onset of

Vortex Shedding in Flow past Variously Shaped Bodies,”

J ournal of Fluid Mechanics, Vol. 182, 1987, pp. 23-45.

doi:10.1017/S0022112087002234

[20] B, Kumar and S. Mittal, “Effect of Blockage on Critical

Parameters for Flow past A Circular Cylinder,” Interna-

tional Journal for Numerical Methods in Fluids, Vol. 50.

No. 8, 2006, pp. 987-1001. doi:10.1002/fld.1098

[21] J. Dusek, P. Le Gal and P. Fraunie, “A Numerical and

Theoretical Study of the First Hopf Bifurcation in A Cyl-

inder Wake,” Journal of Fluid Mechanics, Vol. 264, 1994,

pp. 59-80. doi:10.1017/S0022112094000583