Creative Education
2010. Vol.1, No.3, 154-161
Copyright © 2010 SciRes. DOI:10.4236/ce.2010.13024
Creativity: Cultural Capital in the Mathematics Classroom
Rae Ann Hirsh
Carlow University, Pittsburgh, USA.
Received August 28th, 2010; revised October 2nd, 2010; accepted October 10th, 2010.
Contemporary students face unique economic, environmental, and humanitarian challenges. The problem solv-
ing required to address these challenges requires solutions that have never been thought of before. In order to
tackle these problems, teachers must challenge the traditional problem solving methodologies used in math
classes and encourage new problem solving strategies through incorporation of the arts and facilitating of crea-
tive problem solving. This article will explore the research surrounding creativity, the arts, and creative problem
solving and suggest future applications of creativity in the mathematics classroom.
Keywords: Creativity, Math, Problem Solving, Arts, Curriculum, National Council for the Teaching of
Mathematics
Introduction
Memories of past math classes are filled with algorithms,
worksheets, tests, and memorization. Math activities consisted
of timed multiplication tests, working out algorithms on the
chalkboard, and following teacher-given directions. Math was
often thought of as memorization of facts and algorithms. Many
math textbooks, workbooks, and resources reinforced this tradi-
tional memorization methodology. While this type of math
instruction may have had its place in the past, contemporary
math instruction should reflect society‟s growing need for ad-
vanced problem solving skills to deal with current and future
economic, humanitarian, and environmental challenges. This
paper will challenge the traditional math methodology and in-
vestigate the use of creativity in problem solving to deal with
contemporary challenges. The research will define creativity
and the creative process; illustrate ways creativity can be in-
corporated into the math curriculum through the arts; explore
creative problem solving; and suggest future applications of
creativity in the mathematics class-room.
Creativity: A New Direction for Mathematics
Instruction
Contemporary views of creativity recognize it as the “cultur-
al capital of the twenty-first century” (Sheridan-Rabideau,
2010), for it is “among the most important and pervasive of all
human activities” (Simonton, 2000). Creativity invites experi-
mentation, formulation of new hypotheses, and opens possibili-
ties. Creativity involves personality, affect, motivation, culture,
potential, and beliefs (Ivcevic, 2009). With so many variables,
the definition of the word itself is quite elusive (Hope, 2010).
However, creativity is more easily defined when it is specific in
its application (Hope, 2010). For example, when creativity is
associated with art, poetry, or music, the definition becomes
clearer. In addition to the application, creativity requires the
work of others who support or use the creative work (Hope,
2010). From these perspectives, creativity is the ability to re-
spect and transcend rules in order to cause a change or create a
product that is valued, appreciated, and or used (Isenberg &
Jalongo, 2010; Gardner, 2006). Creativity is a necessary and
vital tool for dealing with the economic, environmental, and
humanitarian challenges of the 21st century (Sheridan-Rabideau,
2010) and helps prepare children for the real world (Sternberg,
2006). Creativity is a basic requirement that is highly respected
and valued in most disciplines and professions (Gardner, 2009;
Christensen, Johnson, & Horn, 2008).
With this in mind, one would expect creativity to be nurtured
and encouraged in the school environment. Unfortunately a
skills-based emphasis continues in contemporary schooling in
favor of more direct instruction of math and reading skills
(Gardner, 2006). Traditional math instruction has been devoid
of methodologies that encourage creativity. In contemporary
society, members have access to facts and algorithms through
calculators, computers, and other tools. While understanding
facts and algorithms is important to foundational math skills,
applying, using, and creating from these skills becomes more
accessible through the tools available. The potential for math
application and problem solving has increased and encourages a
different definition of mathematical ability. Gardner (Gardner,
1993) describes logical/mathematical intelligence as the “ability
to recognize significant problems and then to solve them.” This
definition challenges the „follow an algorithm‟ definition of
math that many school students have (Tsao, 2005) and encou-
rages creativity in the problem solving process through en-
couraging the identification and solution of significant prob-
lems. Creativity is a necessary tool for brainstorming, strate-
gizing, and solving problems (Wallace, Abbott, & Blary, 2007).
Creative problem solving can be developed through integration
of the arts and student-led problem solving strategies.
The Arts: Subjects Left Behind
With the contemporary emphasis on testing and standards,
less time in the classroom is dedicated to the arts and more time
is dedicated towards math and reading. No Child Left Behind
(2000) is an education law enacted to help all children become
proficient in reading and writing. Unfortunately, the No Child

R. A. HIRSH
155
Left Behind Act (2000) has turned into “subjects left behind”
(National Education Association, 2004). More time is spent on
reading and math and less time dedicated to the arts. In some
schools, arts have been eliminated to allow more time for read-
ing and math remediation (National Education Association,
2004). This unfortunate trend has further isolated many stu-
dents from developing their full mathematical potential. It may
be the artistic endeavors that encourage or help to develop math
ability. Artistic development is an integral part of math (Wilson,
2009), and math is an integral part of artistic development
(Schattschneider, 2006).
The arts, which include music, movement, art, and drama,
significantly contribute to mathematical understanding and
application (Wilson, 2009; Schattschneider, 2006; Gardner,
2006; Jensen, 2005). Children display different levels of crea-
tive talent in the arts which include technical skill, visual
thinking, and creativity (Wilson, 2009). Technical skill in the
arts is demonstrated by “the ability for students to manipulate
materials to convey an intended purpose” (Wilson, 2009).
Teachers can take advantage of this definition by allowing stu-
dents the opportunity to draw pictures to solve problems, use
graphic organizers, offer a choice of mathematic expression,
and by providing opportunities to present information visually
(Wilson, 2009). Visual thinking is “the ability of people to un-
derstand and interpret visual information” (Wilson, 2009).
Teachers can tap into this method of learning through inviting
children to create storyboards to illustrate steps to an algorithm,
organizational charts, visual story problems, and other visual
representation of math concepts (Wilson, 2009). Figure 1 de-
monstrates a kindergarten student‟s ability to visually demon-
strate a problem solving strategy.
The student was playing in the doll corner. She had four
dolls and twelve cookies. Her teacher asked her how she would
divide the cookies equally amongst the dolls. The student had a
difficult time explaining and thinking of a strategy. Her teacher
encouraged her to draw her strategy and she was able to solve
the problem through the visual representation (See Figure 1).
Creativity in the arts is “the ability of students to think flexi-
bly and generate novel ideas” (Wilson, 2009). Teachers can take
advantage of creativity in students through allowing brains-
torming sessions, attribute listing, and through encouraging
multiple problem solving perspectives (Wilson, 2009). Tech-
nical skills, visual thinking skills, and creativity in music, art,
and movement can be infused into the mathematics classroom to
Figure 1.
Kindergarten division.
help more children reach their full mathematical potential. Spe-
cific arts, such as music, art, and movement, can offer key entry
points into math lessons, and provide opportunities to develop,
explore, and assess math skills (Gardner, 2006).
Music and Art: Contemporary Tools for
Mathematic Success
Music and art, although overlooked, are necessary compo-
nents of the contemporary curriculum that contribute to the
development of mathematical knowledge and understanding
(Sloboda, 2001). Musical tasks offer the student the opportunity
to develop concepts of number through beat, rhythm, tempo,
time, and scale (Harris, 2008; Hardesty, 2008). An understand-
ing of music provides a foundation for the mathematical under-
standing of frequencies, geometric progressions, ratios, and
proportions (Harris, 2008). Music helps build a foundation in
young children for spatial-temporal reasoning (Harris, 2008;
Royal, 2007) and is related to higher math achievement test
scores (Rauscher, 1998). Movement encourages exploration of
time, measurement, number, rhythm, and placement. To some
students, mathematical knowledge doesn‟t make sense in its
traditional realm, but understanding unfolds when applied in
different activities and domains (Hirsh, 2004).
Art can provide teachers with specific strategies that may
help a child understand math concepts. Spatial strategies may
include charts, tessellations, geometrical grids, graphs, logic
puzzles, flip charts, origami, information tables, and games
(Wilson, 2009). These strategies take advantage of artistic
strengths and interests and present mathematic concepts in a
more accessible (Wilson, 2009).
Gabi, a third grade student, completed a unit on geometry.
For her comprehensive test, her teacher took advantage of her
interest in dogs and art. Her task was to design a theme park
for puppies. The theme park incorporated the mathematical
terminology, concepts, and reasoning of the unit and met the
math geometry, trigonometry, and problem solving standards
through the various design tasks such as Geometric German
Shepherd cups, Rover Roller Coaster, Congruent Café, and the
Puppy Treat Box.
In designing the various attractions at the theme park, Gabi
needed to be able to identify, visually represent, problem solve,
and apply the knowledge of the geometry unit through her ar-
tistic design of the theme park (See Figures 2 & 3).
Figure 2.
Dog treat container.

R. A. HIRSH
156
Figure 3.
Geometric german sheppard cups.
In contrast, the unit test was a multiple choice test that re-
quired knowledge of terminology. In using the unit test, her
teacher would have missed an opportunity for Gabi to demon-
strate an advanced ability to apply the mathematic concepts and
problem solve.
While art can be a tool for the development of math skills,
math can be a tool in the creation, analysis, and teaching of art
(Schattschneider, 2006). Math is used in the creation of art
through the use of fractals and algorithms. Patterns, sequences,
and ratios can be discovered in works of art. Math vocabulary
can be used to analyze art and help to define cultural and artis-
tic preferences and patterns (Schattschneider, 2006). Math can
be used to teach art as students study perspective, create de-
signs, solve puzzles, and study formulas (Schattschneider,
2006).
A fourth grade student, Tori, was having a difficult time me-
morizing her multiplication tables. It was difficult for her to see
the patterns in the numbers. She did, however, have advanced
art ability. Her teacher decided to take advantage of that ability
and had her construct a multiplication board out of nails and
wood. The board is represented in Figure 4. After constructing
the board, the student used string to represent each of the mul-
tiplication facts. Visual patterns emerged from this experience.
The student recorded the patterns in a notebook and began to
understand the mathematic patterns presented in this visual
form (Figure 5). She then was able to understand and recall
her multiplication tables. This method was inspired by the
Waldorf philosophy.
Waldorf education infuses music and art with all core sub-
jects (Steiner, 1996). Students produce their own textbooks and
create elaborate pictorial representations of math concepts such
as multiplication, geometry, banking, and detailed physics ap-
plications. Eurhythmy is another music/movement-based strat-
egy Waldorf teachers use. Eurhythmy encourages rhythmic
movement, chants, and music to facilitate the development of
language and mathematic skills (Steiner, 1996). Students often
discover patterns in number ranging from skip counting to the
Fibonacci number sequence in eurhythmic activities. Waldorf
students are typically advanced in mathematical understanding
and application in comparison to their non-Waldorf peers by
the end of 8th grade (Oberman, 2008).
Figure 4.
Multiplication board.
Figure 5.
Drawing of multiplication board.
The Movement Arts: More Subjects Left Behind
Time for movement in the classroom has been diminishing.
Recess and physical education have been replaced with teacher-
structured academic tasks.
Movement in other classes during the school day is very li-
mited. However, movement offers unique problem solving
opportunities for the math student. Movement in the arts in-
volves gross and fine motor manipulation and (Gardner, 2006).
These bodily/kinesthetic arts “contribute to the development
and enhancement of critical neurobiological systems, including
cognition, emotions, immune, circulatory, and perceptual-motor
skills” (Jensen, 2005). These arts improve timing, coordination,
motivation, and attention (Hirsh, 2004). Children labeled with
various disabilities often move, fidget, touch things, and get out
of their seats. While some see this as misbehavior, other teach-
ers can use this as an opportunity to take advantage of the need

R. A. HIRSH
157
to move in the mathematics classroom (Armstrong, 2010).
Movement can be accessed in the classroom through three dis-
tinctive realms: industrial, recreational, and dramatic (Jensen,
2005).
Industrial arts refer to skills often thought of as trade work
such as woodworking, sculpting, design, basket weaving, and
graphic arts (Hirsh, 2004). This type of art requires a specific
skill set, yet the different types of industrial arts rely heavily on
the same set of math skills to be successful. Proportion, mea-
surement, geometry, ratios, formulas, material analyses, and
number concepts are all necessary skills in industrial design and
work. The industrial arts can be useful motivators for applying
and understanding math concepts.
Jason was a sixth grade student who had difficultly with
many math concepts, but displayed exceptional skill in the in-
dustrial arts. During a measurement unit, Jason’s teacher as-
signed him a different task as an alternative to a math exam. He
was to design and build a small bench for the classroom. His
teacher provided him with measurement specifications, the
wood, and measuring devices. Jason drew his design, had it
approved by this teacher, and then began to measure, cut, and
sand the wood. He assembled the bench and his teacher used a
rubric for assessment. When Jason reviewed the rubric, he
exclaimed that he had no idea that he was that smart. When
Jason saw how his industrial art skills were related to math
concepts, his confidence in problem solving in the classroom
improved and so did his math skills.
Recreational arts include participation in gross motor activi-
ties for enjoyment (Jensen, 2001). These activities may include
exercise, games, obstacle courses, and sports. The distinctive
attribute of recreational arts is the essence of recreation or free
choosing of the activity. Recreational arts can be incorporated
into the mathematics classroom through scavenger hunts,
sport-related activities, games, and obstacle courses. Scoring,
calculation, timing, measurement, trajectory, speed, specific
skill games, and activities can be used to capture the interest
and motivation of otherwise disinterested students.
One disinterested student was John. He was a seventh grade
student struggling with traditional math. At lunch, a debate
broke out among students about the effectiveness of Gatorade
on sports performance. John was particularly interested. Dur-
ing math class, John’s teacher asked him if he would like to
design an experiment that would test his hypothesis of the effec-
tiveness of Gatorade. John expressed great enthusiasm for the
project and designed several recreational sport activities that
would be used in the experiment. He had volunteers try each
activity with and without Gatorade. He recorded all the data
which included scoring, timing, measurement, speed, and vari-
ous calculations. In math class, John would usually give up
quickly if the calculations and data were challenging. However,
he was determined to test his hypothesis and his perseverance
was greatly enhanced in this situation. After analyzing the data,
he came to the conclusion that Gatorade did not help sports
performance and presented his findings to the class. His inter-
est in recreational arts contributed to a successful application
of math skills.
Dramatic arts involve dance, drama, role play, and (Jensen,
2001). Dance allows the opportunity to develop beat, rhythm,
tempo, time, measurement, and problem solving which are
foundational problem solving math skills. Through drama, ma-
thematical concepts can be explored, developed, and commu-
nicated. Students can create body sculptures of geometric
shapes and act out scenarios that demonstrate area, perimeter,
and volume. Role play provides an opportunity to dramatize
problem solving strategies.
A group of older students had the task of designing a math
game for kindergarten students. They had to incorporate con-
cepts of number and counting in the game. They decided to
create a life-size game board (See Figure 6). The kindergarten
students were to be the game pieces. The spaces on the game
board had different addition story problems written on them
and would have to be acted out if landed upon. A box of props
was next to the game board. A giant die was created out of a
cardboard box. Kindergarten students took turns throwing the
die and then walking that number of spaces on the game board.
When they landed on a space, they would need to act out the
addition story problem using the props in the box. The kinder-
garten students were very excited to participate in the game
and came up with additional story problems for the game in
class after the experience was over. The new story problems
were creative and involved different thinking processes than the
original problems.
Figure 6.
Life-Size game board.

R. A. HIRSH
158
Creativity: Problem Solving in the
Twenty-First Century
Albert Einstein stated that “we can‟t solve problems by using
the same kind of thinking we used when we created them.”
These profound words express the critical importance of nur-
turing creative problem solving skills in children. Creative
problem solving is useful in most vocations. For example, in
business, creativity can disrupt the normal trajectory of product
development to inspire a new product or technology (Christen-
sen, Johnson, & Horn, 2008); in literature, creativity is recog-
nized and valued through awards, book sales, and impact; and
in sales, successful salespeople need innovative techniques and
strategies to compete for customers. Thinking outside-the-box
produces new and improved products, materials, and services
and is valued in most professions.
Traditionally, students in math classes are presented with an
algorithm, encouraged to follow the algorithm step by step, and
produce a correct answer. This process negates the student‟s
responsibility of brainstorming, creating, producing, and strate-
gizing solutions to problems (Gardner, 2006). In school, the
situations for applying algorithms are controlled. Out of school,
those situations are not controlled and algorithms may not be
applicable or useful for dealing with real-world problems.
The traditional approach to math is evidenced in conversa-
tions with elementary school students. A group of elementary
school students were interviewed about their thoughts and
feelings of math class (See Table 1). A common theme appeared.
Students expressed concerns about testing. The student with the
highest grades in math stated she knew a lot more than the test
showed. Students with the lowest grades believed the tests con-
tained new material and they were not able to remember the
correct algorithm when the problems were mixed together. All
students believed that success in math was equated with the
ability to follow an algorithm and arrive at a correct answer.
When students had something that was difficult in math, par-
ents or teachers would reiterate the algorithm. Often, this was
confusing for the students with the lower grades, if they didn’t
understand it the first time, saying it again did not help them
either. Most of the students did not enjoy math class unless
games, art, or other activities were involved.
Table 1.
Student mathematics questionnaire.
Student
What grades do you
have in math?
Do you like math in school?
How do you solve math
problems in school?
What happens if you
don’t understand it?
Do you think tests you have
in school show what you
have learned?
Student 1
A
I sometimes like math games.
When we used art and games to
learn it, I really liked it. I found
math really easy.
I do the problem step by
step until I know the
whole lesson. My teacher
tells me the steps to follow.
I ask my teacher and she
tries to help me by telling
me what I did wrong.
I really think that the teacher
would know better than the
test or other work. Sometimes
test shows them, but not all
the time. I knew more than
what was on the test.
Student 2
A’s & B’s
Yes, I liked math class when
I played games like around the
world.
I do it mental in my head.
I ask my teacher, and
sometimes she will help
me by explaining the
steps or tell me to ask
someone else.
Yes, because it proves that
I can do it.
Student 3
B’s & C’s
No, I don’t like the math work
that we did. If we finished our
morning work, we could play
around the world and eat
pretzels – that’s the only part
that I liked.
I don’t. I can’t. Well,
I need help figuring out
the steps.
I ask my teacher for help,
but she says to try a
different way. But I can’t
remember the steps to
each of the different ways
No, there’s stuff that we
didn’t even learn on the test.
I don’t recognize a lot of the
problems that are on the test.
Student 4
B’s & C’s
Most of the time I didn’t like
math because our teacher
wouldn’t explain things
clearly – she would just
say – just because. If art was
involved or writing, I would
understand it better.
When I solve math problems
I try to work it out as slowly
as I can on graph paper so
I can figure out the process.
My teacher tells us how to
do it – not step by step, but
how to solve the problem.
I get extremely upset.
I usually ask my teacher,
but she explains the
problem the same way
she does in class and
I still don’t understand it.
Absolutely not! They are hard
for me because there are too
many different steps to
remember or too many
different kinds of problems
on the same test. I can’t
remember them all.
Student 5
A’s & B’s
Yes, my teacher is awesome.
She makes math class fun by
making up games (she tells us
she stays up to 4:00 am to
make math games for us.)
Pretty simply, I understand,
plan, solve, and check.
She makes small groups
and helps us with what
we don’t understand.
Yes, they make me smarter.
I do well on them and I know
what to do.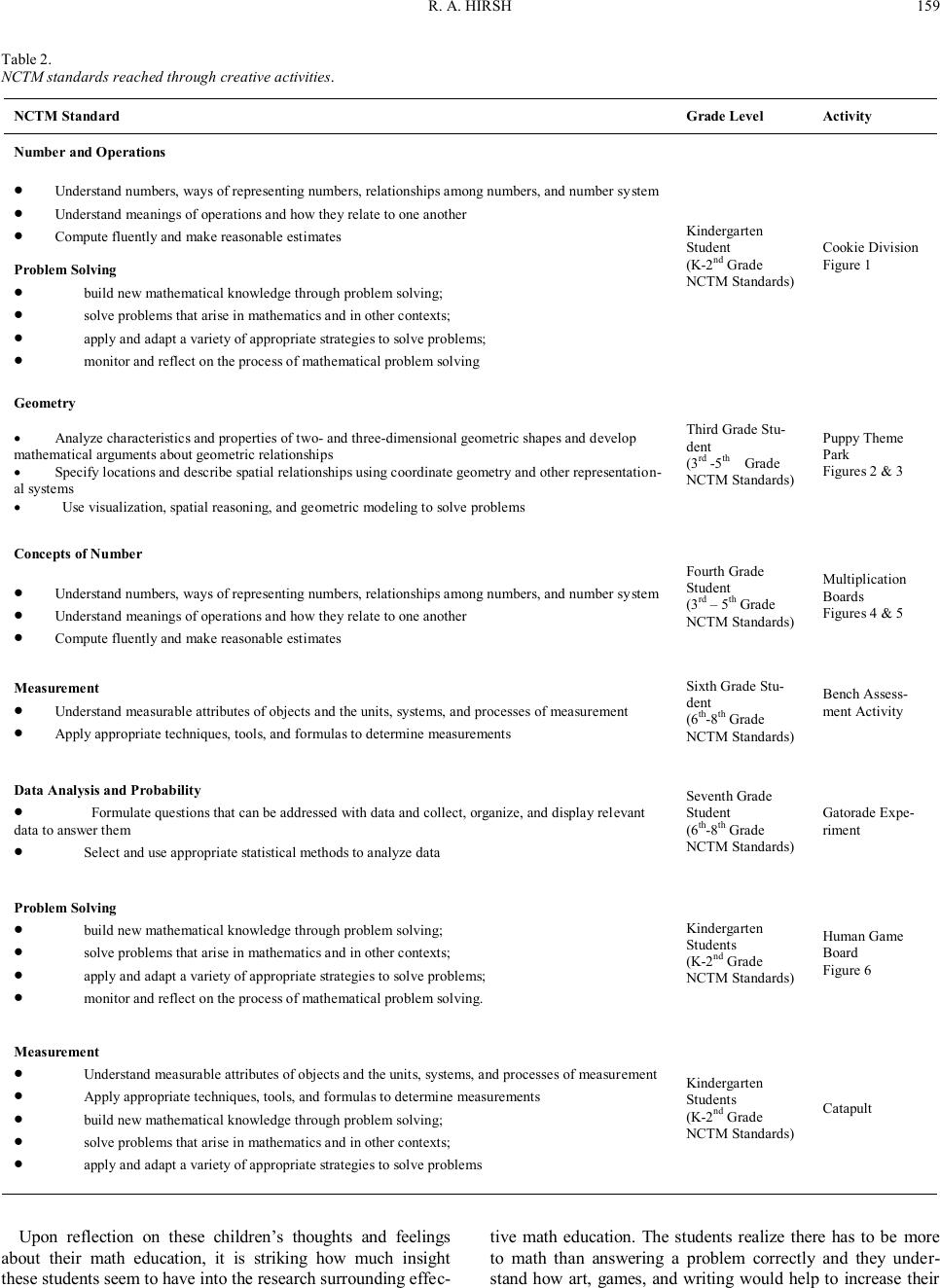

R. A. HIRSH
159
Table 2.
NCTM standards reached through creative activities.
NCTM Standard
Grade Level
Activity
Number and Operations
 Understand numbers, ways of representing numbers, relationships among numbers, and number system
 Understand meanings of operations and how they relate to one another
 Compute fluently and make reasonable estimates
Problem Solving
 build new mathematical knowledge through problem solving;
 solve problems that arise in mathematics and in other contexts;
 apply and adapt a variety of appropriate strategies to solve problems;
 monitor and reflect on the process of mathematical problem solving
Kindergarten
Student
(K-2nd Grade
NCTM Standards)
Cookie Division
Figure 1
Geometry
 Analyze characteristics and properties of two- and three-dimensional geometric shapes and develop
mathematical arguments about geometric relationships
 Specify locations and describe spatial relationships using coordinate geometry and other representation-
al systems
 Use visualization, spatial reasoning, and geometric modeling to solve problems
Third Grade Stu-
dent
(3rd -5th Grade
NCTM Standards)
Puppy Theme
Park
Figures 2 & 3
Concepts of Number
 Understand numbers, ways of representing numbers, relationships among numbers, and number system
 Understand meanings of operations and how they relate to one another
 Compute fluently and make reasonable estimates
Fourth Grade
Student
(3rd – 5th Grade
NCTM Standards)
Multiplication
Boards
Figures 4 & 5
Measurement
 Understand measurable attributes of objects and the units, systems, and processes of measurement
 Apply appropriate techniques, tools, and formulas to determine measurements
Sixth Grade Stu-
dent
(6th-8th Grade
NCTM Standards)
Bench Assess-
ment Activity
Data Analysis and Probability
 Formulate questions that can be addressed with data and collect, organize, and display relevant
data to answer them
 Select and use appropriate statistical methods to analyze data
Seventh Grade
Student
(6th-8th Grade
NCTM Standards)
Gatorade Expe-
riment
Problem Solving
 build new mathematical knowledge through problem solving;
 solve problems that arise in mathematics and in other contexts;
 apply and adapt a variety of appropriate strategies to solve problems;
 monitor and reflect on the process of mathematical problem solving.
Kindergarten
Students
(K-2nd Grade
NCTM Standards)
Human Game
Board
Figure 6
Measurement
 Understand measurable attributes of objects and the units, systems, and processes of measurement
 Apply appropriate techniques, tools, and formulas to determine measurements
 build new mathematical knowledge through problem solving;
 solve problems that arise in mathematics and in other contexts;
 apply and adapt a variety of appropriate strategies to solve problems
Kindergarten
Students
(K-2nd Grade
NCTM Standards)
Catapult
Upon reflection on these children‟s thoughts and feelings
about their math education, it is striking how much insight
these students seem to have into the research surrounding effec-
tive math education. The students realize there has to be more
to math than answering a problem correctly and they under-
stand how art, games, and writing would help to increase their

R. A. HIRSH
160
mathematical understanding. This same concept is supported in
the literature surrounding effective mathematics instruction
(Tsao, 2005; Wallace, Abbott, & Blary, 2007; Kamii, 1999;
2000). Math involves more than following directions and re-
quires multiple strategies for all students to reach their mathe-
matics potential. Students communicated that following direc-
tions did not necessarily mean mastery of a math concept. They
felt the need to experiment, brainstorm, and develop problem
solving strategies of their own. These few students share the
view of many American school students (Tsao, 2005) and real-
ize the traditional mathematics model used in most of their
schools of lecture, memorization, workbook practice, and test-
ing needs revised to incorporate creative problem solving strat-
egies.
Children benefit from a creative, autonomous problem solv-
ing approach to contextual problems (Kamii, 1999; 2000). The
students interviewed with lower grades could not apply a
learned algorithm in a new situation or in context when pre-
sented with new problems on a test. In order to develop trans-
ference of their skills, they need opportunities to present ideas,
develop their own algorithms, and explore possibilities and
solutions. Teachers can facilitate this through games, conversa-
tions, debate, and play/exploration (Kamii, 1999; 2000).
Conversation and debate offer unique insights into the child‟s
thought process and construction of concepts and content. This
can be facilitated by posing a problem and asking children for
solutions (not answers, but strategies for a solution). When a
solution is presented, other children can be encouraged to ac-
cept the solution, offer one of their own, and/or respectfully
debate the other child‟s thought process. These strategies en-
courage reflection and create an autonomous environment for
creating and experimenting with algorithms and problem solv-
ing strategies.
Play and exploration invite participation in physical-knowl-
edge activities (Kamii, Miyakawa, & Kato, 2007). These activi-
ties encourage the child to explore blocks, levers, patterns,
pendulums, water, sand, indoor and outdoor materials and to
develop their own problems and solutions with those materials.
Time for exploration is a critical component of an autonomous
mathematics classroom. Traditional scheduling and formats
may need restructured in order to accommodate the needs of the
creative problem solver. Often, debate and conversation can be
incorporated into play and exploration experiences.
In a kindergarten classroom, a teacher is hit in the back of
the head with a tiny plastic doll. She turns to find children in
the block area constructing catapults and launching tiny fig-
ures over the book shelf. She observes and listens to their con-
versations about the catapult construction. While the room was
too small to safely launch figures over the bookshelf, the teach-
er asks students to gather their materials and leads the students
towards a gymnasium where they can experiment freely. She
provides students with measurement devices and asks students
to record their estimation and measurement data. She also asks
students to draw designs of effective and ineffective catapults.
Students explored materials, discussed and debated designs,
and tested their designs through estimation and measurement.
In this scenario, the kindergarten teacher recognized a wonder-
ful opportunity to develop problem solving skills by recogniz-
ing the benefits of play and exploration and encouraging debate
and discussion.
Curricular Considerations
Each activity presented in this paper addresses con-
tent-specific standards outlined by the National Council for the
Teaching of Mathematics (See Table 2). While these content
specific standards can be addressed in many ways in the class-
room, each of the projects mentioned help facilitate the Repre-
sentation, Communication, Reasoning and Proof, and Connec-
tion Standards listed as well. These standards are often over-
looked in the classroom, but integrating the arts and facilitating
creative problem solving skills invite these applications and
synthesizing standards. It is through application and synthesis
of math concepts that ideas can be challenged, created, and
improved. Traditional tests may demonstrate standard content
knowledge, but integrated projects inspire new applications and
new possibilities.
In reflecting on the strategies presented in this paper, one
wonders if the children interviewed would have different an-
swers and attitudes if the arts were integrated into their mathe-
matics classroom. Not every child loves math, music, art, dra-
ma or industrial arts, however most children like one of these.
When that interest or talent is accessed, it can provide a tool for
developing challenging and disinteresting concepts (Gardner,
2006).
If teachers of mathematics continue to teach what they know
and ask students to memorize and regurgitate it, how can one
ever expect any advancements to be made in math, engineering,
science, technology or business? Integrating the arts into the
mathematics classrooms provides students access to content,
multiple perspectives on a topic, and invites them to think, ap-
ply, understand, create, and participate in their learning. It is in
this participation that new ideas emerge and become possible.
Math education requires restructuring to promote an autonom-
ous classroom that facilitates creativity through the arts and
creative problem solving to effectively prepare children for the
economic, environmental, and humanitarian challenges of the
new century (Sheridan-Rabideau, 2010). The restructuring ef-
forts should be at the forefront of education policy and reform
and should include teacher education, scheduling, curricular,
and environmental strategies that support creativity in the ma-
thematics classroom. As Short (Short, Kauffman, & Kahn,
2000) suggests, “In their lives outside of school, children natu-
rally move between art, music, movement, mathematics, drama,
and language as ways to think about the world. It is only in
schools that students are restricted to using one sign system at a
time.”
References
Armstrong, T. (2010). Neurodiversity: Discovering the extraordinary
gifts of autism, ADHD, dyslexis, and other brain differences. Cam-
bridge, MA: Da Capo Press.
Christensen, C., Johnson, J., & Horn, M. (2008). Disrupting class: How
disruptive innovation will change the way the world learns. New
York, NY: McGrawHill.
Gardner, H. (1993). Frames of mind. New York: Perseus Books.
Gardner, H. (2006). Multiple intelligences: New horizons in theory and
practice. New York: Perseus Books.
Gardner, H. (2009). Five minds for the future. Boston, MA: Harvard
Business School Publishing.
Hardesty, L. (2008). The geometry of sound. Technology Review, 111,
m7. Retrieved from ttp://www.technologyreview.com/

R. A. HIRSH
161
Harris, M. (2008). The effects of music instruction on learning the
Montessori classroom. Montessori Life: A Publication of the Ameri-
can Montessori Society, 20, 24-31. Retrieved from http://www.
amshq.org/publications.htm
Hirsh, R. (2004). Early childhood curriculum: Incorporating multiple
intelligences developmentally appropriate practice, and play. Boston:
Allyn & Bacon.
Hope, S. (2010). Creativity, content, and policy. Arts Education Policy
Review, 111, 39-47. doi:10.1080/10632910903455736
Isenberg, J., & Jalongo, M. (2010). Creative thinking and arts-based
learning: Preschool through fourth grade. Upper Saddle River, NJ:
Pearson.
Ivcevic, Z. (2009). Creativity maps: Toward the next generation of
theories of creativity. Psychology of Aesthetics, Creativity, and the
Arts, 3, 17-21. Retrieved from http://www.apa.org/pubs/journals/
aca/index.aspx
Jensen, E. (2005). Teaching with the brain in mind, 2e. Alexandria, VA:
Association for the Supervision of Curriculum Development.
Jensen, E. (2001). Arts with the brain in mind. Alexandria, VA: Asso-
ciation for the Supervision of Curriculum Development.
Kamii, C. (1999). Young children reinvent mathematics: Implications
of Piaget’s theory, 2e. New York, NY: Teachers College Press.
Principles and standards for school mathematics. (2000). Reston, VA:
National Council for the Teaching of Mathematics.
Kamii, C., Miyakawa, Y., & Kato, T. (2007). Trying to make a lever
work at ages 1 to 4: The development of “functions” (logico- ma-
thematical thinking). Early Education and Development, 18,
145-161.
National Education Association. (2004). No subjects left behind? Think
again. National Education Association Today, 23, 26-27. Retrieved
from: http://www.nea.org/neatoday/
Oberman, I. (2008). Waldorf education and its spread into the public
sector. Encounter, 21, 10-14. Retrieved from http://www.great-ideas.
org
Rauscher, F., & Shaw, G. (1998). Key components of the Mozart effect.
Perceptual and Motor Skills, 86, 835-841. Retrieved from http://
www.ammonsscientific.com/AmSci/
Royal, K. (2007). Mind, music, & math. Direct Administration, 43, 18.
Retrieved from http://www.districtadministration.com/
Schattschneider, D. (2006). Math and art in the mountains. The Ma-
thematical Intelligencer, 28, 31-37. doi:10.1007/BF02986882
Sheridan-Rabideau, M. (2010). Creativity repositioned. Arts Education
Policy Review, 111, 54-58. doi:10.1080/10632910903455876
Short, K. G., Kauffman, G., & Kahn, L. H. (2000). I just need to draw:
Responding to literature across multiple sign systems. The Reading
Teacher, 54, 160-71
Simonton, D. (2000). Creativity: Cognitive, personal, developmental,
and social aspects. American Psychologist, 55, 151-158.
doi:10.1037/0003-066X.55.1.151
Sloboda, J. (2001). Emotion, functionality, and the everyday experience
of music: Where does music education fit? International Research in
Music Education Conference, England: Exeter University.
Steiner, R. (1996). The education of the child: and early lectures on
education. New York, NY: Anthroposophic Press.
Sternberg, R. (2006). Arts at the core: How six school districts integrate
arts education into the curriculum. American School Board Journal,
193, 44-47. Retrieved by http://www.nsba.org
Tsao, Y. (2005). A comparison of american and taiwanese students:
Their math perception. Journal of Instructional Psychology, 31,
206-213.
Wallace, A., Abbott, D., & Blary, R. (2007). The classroom that math
built: Encouraging young mathematicians to pose problems. Young
Children, 62, 42-49.
Wilson, H. (2009). The Picasso in your classroom: How to meet the
needs of talented artists in elementary school. Gifted Child Today, 32,
36-45. Retrieved form http://www.prufrock.com/