Paper Menu >>
Journal Menu >>
 Journal of Modern Physics, 2013, 4, 486-494 http://dx.doi.org/10.4236/jmp.2013.44069 Published Online April 2013 (http://www.scirp.org/journal/jmp) Scaling Symmetry and Integrable Spherical Hydrostatics Sidney Bludman1, Dallas C. Kennedy2 1Departamento de Astronomía, Universidad de Chile, Santiago, Chile 2Natick, USA Email: sbludman@das.uchile.cl, dalet@stanfordalumni.org Received October 17, 2012; revised December 10, 2012; accepted December 25, 2012 Copyright © 2013 Sidney Bludman, Dallas C. Kennedy. This is an open access article distributed under the Creative Commons At- tribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is prop- erly cited. ABSTRACT Any symmetry reduces a second-order differential equation to a first integral: variational symmetries of the action (ex- emplified by central field dynamics) lead to conservation laws, but symmetries of only the equations of motion (exem- plified by scale-invariant hydrostatics) yield first-order non-conservation laws between invariants. We obtain these non- conservation laws by extending Noether’s Theorem to non-variational symmetries and present an innovative variational formulation of spherical adiabatic hydrostatics. For the scale-invariant case, this novel synthesis of group theory, hydro- statics, and astrophysics allows us to recover all the known properties of polytropes and define a core radius, inside which polytropes of index n share a common core mass density structure, and outside of which their envelopes differ. The Emden solutions (regular solutions of the Lane-Emden equation) are obtained, along with useful approximations. An appendix discusses the n = 3 polytrope in order to emphasize how the same mechanical structure allows different thermal structures in relativistic degenerate white dwarfs and zero age main sequence stars. Keywords: Lagrangian Mechanics; Symmetry; Hydrodynamics; Astrophysics; Stellar Structure 1. Symmetries of Differential Equations and Reduction of Order Noether’s Theorem relates every variational symmetry, a symmetry of an action or similar integral, to a conserva- tion law, a first integral of the equations of motion [1]. By an extension of Noether’s Theorem, non-variational symmetries—symmetries of the equations of motion which are not in general variational symmetries—also lead to first integrals, which are not conservation laws of the usual divergence form, as discussed in a previous article [2]. There it was shown that a Lagrangian ,,tq q ,, dStqq ii and action ii , with degrees of freedom i, can be transformed under an infinitesimal point tran- sformation : t q ,, , iji tqq tq d d d ii i iii tq q q t Gqqt d dd , dd i i qt q tt tt , i qqt (1) in terms of the total derivative of the Noether charge, :Gt ii p and the variational deriva- tive :dd ii i qqt . For transformations that leave initial and final states unchanged, the variation in action is d d, d f ifi i i SGfGitqt tt (2) if the term in ddtt ,qt is integrated by parts. If the system evolution obeys an action principle, that this va- riation vanish for independent variations i 0 that vanish at initial and final times, the system obeys the Euler-Lagrange equations i and ddtt 0 i , the rate of change of the Hamiltonian in non-conserva- tive systems. On-shell, where , d f if i StGfGi (3) d:dd d Gtt t . (4) This is Noether’s equation, giving the evolution of a symmetry generator or Noether charge, in terms of the Lagrangian transformation that it generates. It expresses the Euler-Lagrange equations of motion as the diver- gence of the Noether charge. This divergence vanishes C opyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY 487 for a variational symmetry, but not for any other symme- try transformation. Noether’s Equation (4) could have been derived direct- ly from the definition of the Noether charge. But using the action principle makes manifest the connection be- tween Noether’s equation and the Euler-Lagrange equa- tions. We use the action principle and this connection to reformulate the theory of hydrostatic barotropic spheres, which is integrable if they are scale symmetric, even where this scale symmetry is not a symmetry of the ac- tion (Section 2). The first integrals implied by any sym- metry of the equations of motion, while generally not va- nishing-divergence conservation laws, are still useful dy- namical or structural first-order relationships. Because it neglects all other structural features, scaling symmetry is the most general simplification that one can make for any dynamical system. For the radial scaling transformations we consider, rr 2; , the Lagrangian scales as some scalar density S and the ac- tion scales as . The Noether charge gen- erating the scale transformation evolves according to a non-conservation law 12S 12 ddGt , a first-order equation encapsulating all of the consequences of scaling symmetry [2]. From this first-order equation follow di- rectly all the properties of index-n polytropes, as estab- lished in classical works [3,4], modern textbooks [5,6], and the recent, excellent treatments of Horedt and Liu [7,8]. Our secondary purpose is to present an original varia- tional formulation of spherical hydrostatics and to extend Noether’s Theorem to non-variational scaling symmetry, which yields a scaling non-conservation law (Section 2). For spherical hydrostasis, we define a core radius, inside which all stars exhibit a common mass density structure. Outside this core, polytropes of different index n show different density structures as the outer boundary is felt (Section 3). Section 4 completes the integration of the Lane-Emden equation by quadratures and obtains useful approximations to the Emden function n . An appendix reviews the thermodynamic properties of the physically important polytropes of index n = 3 [2,5,6]. What is original here is the explanation of the the differ- ences between relativistic degenerate white dwarf stars and ideal gas stars on the zero-age main sequence (ZAMS), following from their different entropy structures. Our original approximations to 3 should prove useful in such stars. 2. Scaling Symmetry and Integrability of Hydrostatic Spheres 2.1. Variational Principle for Hydrostatic Spheres A non-rotating gaseous sphere in hydrostatic equilibrium obeys the equations of hydrostatic equilibrium and mass continuity 2 2 dd , dd 4π, PrGmr mr r (5) where the pressure, mass density, and included mass Pr, r , mr depend on radius r. For dependent variables, we use the gravitational potential 2d r VrGmr r and the thermodynamic potential (specific enthalpy, ejection energy) 0d Pr H rP , so that (5) and its integrated form become dd dd, , Hr Vr GM Vr HrR (6) expressing the conservation of the specific energy as the sum of gravitational and internal energies, in a star of mass M and radius R. The two first-order Equations (5) are equivalent to a second-order equation of hydrostatic equilibrium, Poisson’s Law in terms of the enthalpy H r: 2 2 1d d4π0, dd H rGH rr r (7) We assume a chemically homogeneous spherical structure, and thermal equilibrium in each mass shell, so that r , Pr, H r are even functions of the ra- dius r. At the origin, spherical symmetry requires dd 0Pr and mass continuity requires, to order , 2 r 2 33 35 225 1, 4π34π 1. 35 3 c c rAr rr mr Arr (8) The average mass density inside radius r is 35 325 :4π3c rmr rr 0W . In a previous paper [2], we showed that hydrostatic equilibrium (7) follows from the variational principle minimizing the Gibbs free energy, the integral of the Lagrangian : 0 :d,, , R WrrHH (9) 22 ,, 4π8πd, :dd, rHHrHG Pr 'r dr (10) W is the sum of the gravitational and internal specific energies per radial shell . The canonical momentum and Hamiltonian, 2 22 2 :, ,,2 4π, mHrHG rHmGmrrP H (11) are the included mass and energy per mass shell. The Copyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY 488 canonical equations are 2 2 , 4π. GmrmH H mr (12) Spherical geometry makes the system nonautonomous, so that 2rrr vanishes only as- ymptotically, as the mass shells approach planarity. The equations of hydrostatic equilibrium (5) can be rewritten dlogdlog =3, dlogdlog1dlog 1 ururnrvr vruvr dlog ,nr r (13) in terms of the logarithmic derivatives :dlogd log, :d logd : d urm r vr P wr nrvr log , logd log, r r nr (14) and an index :dlog 1 1: dlo nr nr d log, gdlog , P P (15) which depends on the local thermal structure. The mass density invariant w makes explicit the universal mass density structure of all stellar cores, which is not appar- ent in the conventional pressure invariant v. 2.2. Scaling Symmetry and Reduction to First-Order Equation between Scale Invariants Following the our results [2], a hydrostatic structure is completely integrable, if the structural Equations (5) are invariant under the infinitesimal scaling transformation ,, 1, where :21 n n rr n HH n , , nn H H (16) generated by the Noether charge, for constant n, 2 2 : 4π 2 nn GrmH H rP . n H H Hr GG 2 (17) The Lagrangian (10) then transforms as a scalar den- sity of weight n 12 12 , n SS n 12 2, n (18) so that only for the polytrope 5 12 n is the action invariant and scaling a symmetry of the action. Both structural Equations (13) are autonomous, if and only if n is constant, so that, 11n K r Pr , with the same constant K (related to the entropy) at each ra- dius. When this is so1, ddlog 3, ddlog 1 n nnn uruuw wrwuwn (19) dlog d logd log dlog 13 n nn wum r uwnuwu . (20) In this section, we consider only the first equality in (20) 1 d d3 nn n n wu wn w uuuw c (21) between scale invariants, which encapsulates all the ef- fects of scale invariance. We consider only simple poly- tropes with finite central density , so that the regular- ity condition (8) requires that all be tangent to n wu 53 3u at the origin. Such Emden polytropes are the regular solutions n wu of the first-order Equation (19), for which 53 3 n wu u 3 for u. In terms of the dimensional constant, dimensional ra- dius, and the central enthalpy and pressure 211 1 1 :,:, 4π :11 ,, n c n ccc c nKr G H nPnKP (22) the second-order equation of hydrostatic equilibrium (7), takes the dimensionless form of the Lane-Emden equa- tion 22 d d0. dd n n n (23) In terms of the dimensionless enthalpy nc H H , the dimensional included mass, mass density, average included mass density, and specific gravitational force are 32 3 2 4π, , :3, 4π3 :4π cn n ncn ncn cn mr r mr rr gr (24) where prime designates the derivative ':dd . The 1These characteristic equations are equivalent to a predator/prey equa- tion in population dynamics [12,13]. With time t replacing-log r, they are Lotka-Volterra equations, modified by additional spontaneous growth terms −u2, 2 n wn on the right side. The uw cross-terms lead to growth of the predator w at the expense of the prey u, so that a popula- tion that is exclusively prey initially (u = 3, w = 0) is ultimately de- voured u 0. For the weakest predator/prey interaction (n = 5), the p redator takes an infinite time to reach the finite value w5 5. For stronger predator/prey interaction (n < 5), the predator grows infinitely in finite time. n w Copyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY Copyright © 2013 Sci JMP 489 Res. scale invariants are 11 :, n nn n n nn uv uv 1 :, :. n n nn n (25) The Noether charge 22 2 21 n cn n H GGn 1 , n nnn (26) evolves radially according to 221 d1 21 n ncnn n GH n Gn n 2 d5 12 . (27) This non-conservation law expresses the radial evolu- tion of energy density per mass shell, from entirely inter- nal 11 n nn at the center, to entirely gravitational 2 2 n wu at the stellar surface. Figure 1 shows the first integrals n for n = 0, 1, 2, 3, 4, 5. For n = 5, scaling is a variational symmetry so that (26) reduces to a conservation law for the Noether charge 5 5 1 constant. v u 226 255 5 212 3 55 1 262 3 c c H GG Huvv u G (28) For the Emden solution, 5 is finite at the stellar boundary , the constant vanishes, and 0 55 5 53 3 v u 5nv wu everywhere. For , n diverges at the stellar radius 1 , but 0nn 0u , a finite constant characterizing each Emden function. At the boundary , our density invariant diverges as u n w1 1 0 n n n n u , and 3n 2 1 1 01 n nn 0n . (29) Table 1 lists these constants , along with the global mass density ratios cn and the ensuing dimensional radius-mass relation R 113 14π n nnn M 0n nKG R . Together with the well-known [3,5,6] third, fourth and fifth columns, all of this table follows directly from the regular solutions of the first-order Equation (21). In addition, the sixth and seventh columns express mass concentration in an origin- nal way. 3. Increasing Polytropic Index and Mass Concentration Emden functions are the normalized regular solutions of the Lane-Emden Equation (23) for which the mass den- sity is finite at the origin, so that 01, 00 nn . Each Emden function of index n is characterized by its first zero 0 1nn , at dimensionless boundary radius 1n . As an alternative measure of core concentration, we define the core radius core :2 core u implicitly by , where gravitational and pressure gradient forces are maximal. This core radius, where and the mass density has fallen to 2 n w corennc 0.4 1n for all polytropes , is marked by red dots in Figures 1-3. The sixth and seventh columns in Table 1 list dimensionless values for the fractional core radius corn rR ecore 1n and fractional included mass coren m. Within the core , the internal energy dominates over the gravita- tional energy, so that for , M 2u 1n 5 2 core 53, 3 16,for2, , n nn wu wuu u (30) consistent with the universal density structure (8) all stars enjoy near their center. For n = 0, the mass is uniformly distributed, and the entire star is core. As 0 < n < 5 increases, the radial distribution concen- trates, and the envelope outside the core grows. With Table 1. Scaling exponents, core parameters, surface parameters, and mass-radius relations for polytropes of increasing mass concentration. Columns 3 - 5 are well-known [3,5,6]. Columns 6 - 7 present a new measure of core concentration. Radius-Mass Relation n n 1n cn n R R 0n corecore 1nn rR coren mM 31 0 nn n RM 0 −2 2.449 1 0.333 1 1 R M; mass uniformly distributed 13 3.142 3.290 ... 0.66 0.60 1 R independent of M 1.5 4 3.654 5.991 132.4 0.55 0.51 13 RM R 2 2 4.353 11.403 10.50 0.41 0.41 3 1 6.897 54.183 2.018 0.24 0.31 M independent of R 4 2/3 14.972 622.408 0.729 0.13 0.24 4.5 4/7 31.836 6189.47 0.394 0.08 0.22 5 1/2 0 0 0.19 for any M; mass infinitely concentrated 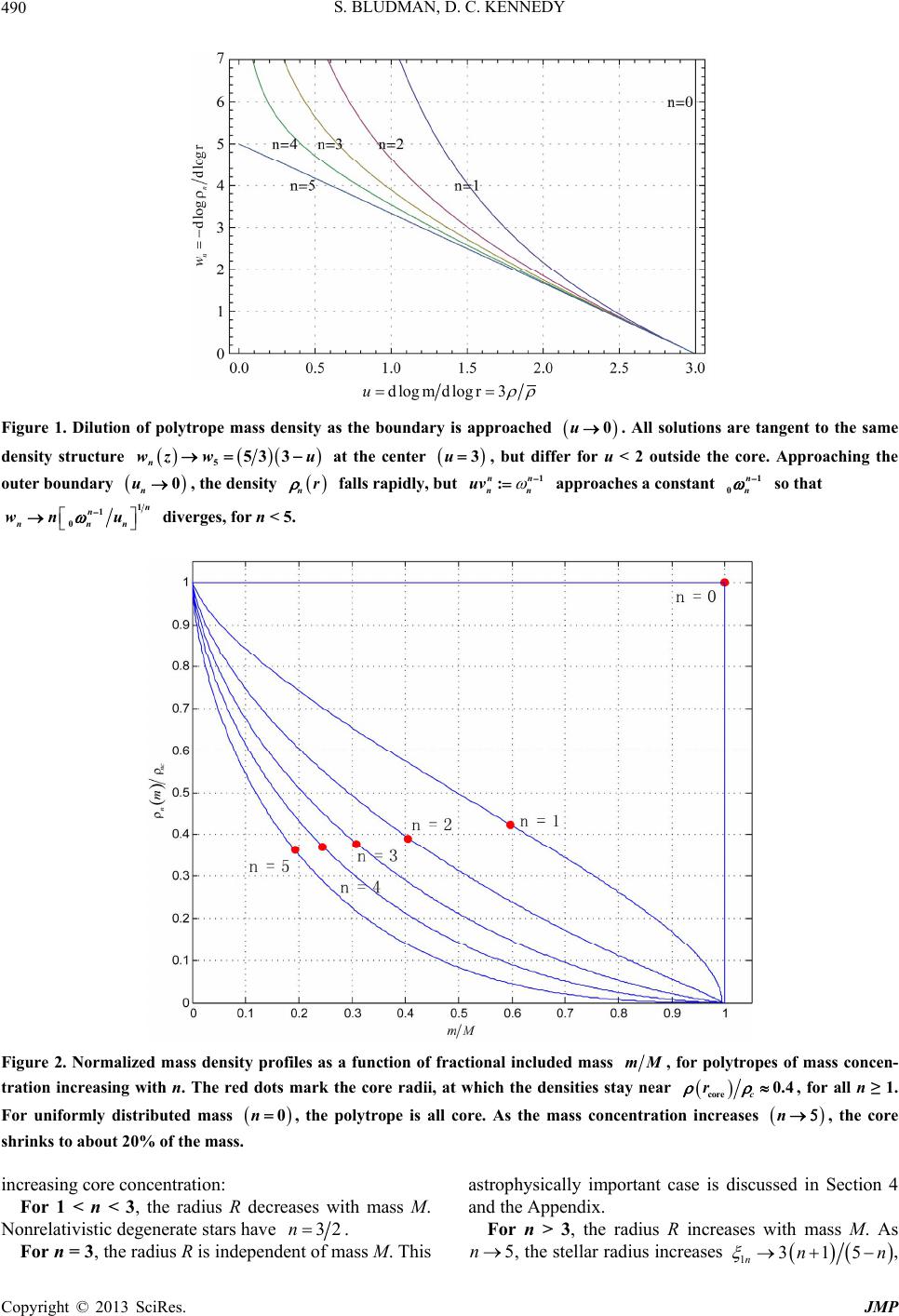 S. BLUDMAN, D. C. KENNEDY 490 dlogmudlogr 3 Figure 1. Dilution of polytrope mass density as the boundary is approached 0u. All solutions are tangent to the same density structure 5n wz w533u at the center 3u , but differ for u < 2 outside the core. Approaching the outer boundary 0 n u, the density nr falls rapidly, but 1n n : n n uv approaches a constant 1 0 n n so that 1 1 0 n n nnn wn u diverges, for n < 5. Figure 2. Normalized mass density profiles as a function of fractional included mass mM , for polytropes of mass concen- tration increasing with n. The red dots mark the core radii, at which the densities stay near c rcore 0.4 0n n , for all n ≥ 1. For uniformly distributed mass , the polytrope is all core. As the mass concentration increases , the core shrinks to about 20% of the mass. increasing core concentration: For 1 < n < 3, the radius R decreases with mass M. Nonrelativistic degenerate stars have 32n 5n . For n = 3, the radius R is independent of mass M. This astrophysically important case is discussed in Section 4 and the Appendix. For n > 3, the radius R increases with mass M. As , the stellar radius increases 1315 nnn , Copyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY 491 Figure 3. Normalized mass density profiles as function of fractional radius r/R. The density is uniform for n = 0, but is maxi- mally concentrated at finite radius for the n = 5 polytrope, which is unbounded R . The density at the core radius stays about core c r0.4 1n, for any . the core radius shrinks core 103n, the fractional core radius 0.045 5rR n corecore 1n, core 0.19 n mM, and 01 30 nn R . For n = 5, the mass is infinitely concentrated toward the center, and the stellar radius for any mass M . Scaling becomes a variational symmetry, so that the Noether charge 5 in (40) is constant with radius. For the regular solution this constant vanishes: G core 5 12 3 55 10 3 31 nG uvv u 26 55 5 5 1 26 2 0, (31) so that 3 55 13, 3vu 5. Integrating then yields 12 2 13, 1 5 50 (32) after normalizing to . For n > 5, the central density diverges, so that the total mass M is infinite. 4. Regular Emden Solutions and Their Approximations In place of u, we now introduce an equivalent homology invariant : 3dlogdlogzu r n , where 3 :3 4π nmrr is the average mass density inside radius r. In term of z, wn, the characteristic differential Equations (20) are dlog ddlog g . 3 w zm rz dl o 32 n nn zw z zwn (33) Incorporating the boundary condition, the first of Equations (40) takes the form of a Volterra integral equa- tion [9] 0 Pic 2 d3 5113: , :9 107. n zn nn n J nn n zwn wzzw zw z J zwz Jnn (34) The Picard approximation is defined by inserting the core values 53 n wz z 0, 5n inside the preceding inte- gral. For , this Picard approximation is every- where exact. For intermediate polytropic indices 0 < n < 5, the Picard approximation breaks down approaching the boundary, where wn diverges as 1 1 0 n n nn wn u 3n , . and is poorest for After obtaining :dlog dlogr nn wz , either nu- merically or by Picard approximation, another integration gives [9] 0 52 d exp 3 13 zn ncn n zw z zwz zz z (35) 1 0 52 Pic d exp 3 13: n nn cn zn n n n z zw z nw zzz z (36) 32 3 32 13 exp d 32 3 z n z mz Mzz wz z z (37) Copyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY 492 1 12 3 12 exp d3 3. 3 n z n rz R zzzw z z 11 32z z z RM 3n (38) All the scale dependance now appears in the integra- tion constants M and , which except for depends on M. Inserting the core values 53wz z n inside the integral, the Picard approximations 2 Pic 16, n N nn NN :535 n n 0, 5n (39) to the Emden functions are obtained and tabulated in the last column of Table 2. For polytropic indices , this Picard form is exact. For intermediate polytropic indices , the Picard approximation remains a good approximation through order 05n 6 , but breaks down approaching the outer boundary. Unfortunately, the Picard approximation is poorest near , the astro- physically most important polytrope. Figure 4 compares three approximations to this most important Emden func- tion, shown in yellow, whose Taylor series expansion is 3n 24 6 3 8 10 164019 5040 619 1088640 2743 39916800. 24 6 810 1 0.16666670.0250.0037698 0.00056860.00006872, (40) to this Taylor series expansion 3core 2.51.7 (41) shown in red, diverges badly for . 54 2 3Pic 24 6 12 15 1640 133600 24 6 1 0.16666670.0250.003611, 3.9 (42) (43) shown in dashed green, converges and remains a good approximation over the bulk of the star, with ≤10% error out to , more than twice the core radius and more than half-way out to the stellar boundary at 13 6.897 . nPic to emden functions Table 2. Taylor series and picard approximations . n n Emden Function n and Taylor Series :53 5 n Nn Picard Approximation 2 Pic :1 6 n N nn N 0 2 16 –1 2 16 1 24 6 sin1 6 1205040 –5/2 52 2246 11516 12010800 n 24 6 1612085 15120nnn 53 5n 224 6 16161206 510800 n N n Nnnn 5 12 2 13 1/2 12 2 13 Figure 5. The exact Emden function 3 (solid yellow) and its polynomial (red), Picard (green dashed) and Padé (heavy black dashed) approximations. Even in this worst case, the Picard approximation holds out to twice the core radius at 2ξ3core = 3.3, before breaking down near the boundary. The Padé approximation is indistinguishable from the exact solution, vanishing t ξ1 = 6.921, very close to the true boundary at ξ13 = 6.897. a Copyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY 493 This approximation suffices in white dwarf and ZAMS stars, except for their outer envelopes, which are never polytropic and contain little mass. Because it satisfies the central boundary condition, but not the outer boundary condition, the Picard approximation underestimates and overestimates outside 3.9. Padé rational approximation [10,11]: 24 3Pad 24 24 1108 1145360 1 171081008 1 0.1666670.025 0.0005686 0.0000857 6 810 0.00376984 618 , 6.921 (44) shown in dashed heavy black, is a simpler and much bet- ter approximation. By construction, it agrees with the series expansion (40) through fourth order. In fact, this Padé approximation is almost exact out to its first zero at 1 13 , very close to the true outer boundary 6.897. These simple analytic approximations to 3 sim- plify structural modeling of massive white dwarfs and ZAMS stars. 5. Conclusions We have explored how a symmetry of the equations of motion, but not of the action, reduces a second-order dif- ferential equation to first-order, which can be integrated by quadrature. In scale-invariant hydrostatics, the sym- metry of the equations yields a first integral, which is a first-order equation between scale invariants, and yields directly all the familiar properties of polytropes. We observe that, like all stars, polytropes of index n share a common core density profile and defined a core radius outside of which their envelopes differ. The Em- den functions n , solutions of the Lane-Emden equation that are regular at the origin, are finally obtain- ed, along with useful approximations. The Appendix reviews the astrophysically most impor- tant n = 3 polytrope, describing relativistic white dwarf stars and zero age main sequence stars. While reviewing these well-known applications [5,6], we stress how these same mechanical structures differ thermodynamically and the usefulness of our original (Section IV) approxi- mations to these Emden functions. 6. Acknowledgements Thanks to Andrés E. Guzmán (Universidad de Chile) for calculating the figures with Mathematica and proofread- ing the manuscript. SAB was supported by the Millen- nium Center for Supernova Science through grant P06- 045-F funded by Programa Bicentenario de Ciencia y Tecnología de CONICYT and Programa Iniciativa Cien- tífica Milenio de MIDEPLAN. REFERENCES [1] G. W. Bluman and S. C. Anco, “Symmetry and Integra- tion Methods for Differential Equations,” Springer-Verlag, Berlin, 2010. [2] S. Bludman and D. C. Kennedy, “Invariant Relationships Deriving from Classical Scaling Transformations,” Jour- nal of Mathematical Physics, Vol. 52, 2011, Article ID: 042092. [3] S. Chandrasekhar, “An Introduction to the Study of Stel- lar Structure, Chapters III, IV,” University of Chicago, 1939. [4] M. Schwarzschild, “Structure and Evolution of the Stars,” Princeton University Press, Princeton, 1958. [5] R. Kippenhahn and A. Weigert, “Stellar Structure And Evolution,” Springer-Verlag, Berlin, 1990. [6] C. J. Hansen and S. D. Kawaler, “Stellar Interiors: Physi- cal Principles, Structure, and Evolution,” Springer-Verlag, Berlin, 1994. [7] G. P. Horedt, “Polytropes: Applications in Astrophysics and Related Fields,” Kluwer, Dordrecht, 2004. [8] F. K. Liu, “Polytropic Gas Spheres: An Approximate Analytic Solution of the Lane-Emden Equation,” Monthly Notices of the Royal Astronomical Society, Vol. 281, No. 4, 1996, pp. 1197-1205. [9] S. A. Bludman and D. C. Kennedy, “Analytic Models for the Mechanical Structure of the Solar Core,” The Astro- physical Journal, Vol. 525, No. 2, 1999, pp. 1024-1031. [10] P. Pascual, “Lane-Emden Equation and Padé’s Approxi- mants,” Astronomy & Astrophysics, Vol. 60, 1977, pp. 161-163. [11] Z. F. Seidov, “Lane-Emden Equation: Picard vs Pade,” arXiv:astro-ph/0107395. [12] W. E. Boyce and R. C. DiPrima, “Elementary Differential Equations and Boundary Value Problems,” 7th Edition, John Wiley and Sons, Hoboken, 2001. [13] D. W. Jordon and P. Smith, “Nonlinear Ordinary Differ- ential Equations,” 3rd Edition, Oxford University Press, Oxford, 1999. Copyright © 2013 SciRes. JMP  S. BLUDMAN, D. C. KENNEDY 494 Appendix: Astrophysical Applications of the n = 3 Polytrope The polytrope, which is realized in white dwarfs of maximum mass and in the Eddington standard model for ZAMS stars just starting hydrogen burning, is distin- guished by a unique 3n - M R relation: the mass 32 πKG 03 πM 4 is independent of radius R, but depends on the constant 43 :KP 0WU . In these stars, the gravitational and internal energies cancel, making the total energy . Because these stars are in neutral mechanical equilibrium at any radius, they can expand or contract homologously. 1.1. Relativistic Degenerate Stars: K Fixed by Fundamental Constants The most massive white dwarfs are supported by the degeneracy pressure of relativistic electrons, with num- ber density eeH nm , where H m is the atomic mass unit and the number of electrons per atom 2 eZA , because these white dwarfs are composed of pure He or 12 16 CO mixtures. Thus, 13 43 83π WDH e Khcm WD depends only on funda- mental constants. This universal value of K leads to the limiting Chandrasekhar mass 22 Ch 2 π815 1.456 2 MM M 2 5.824 ee M [5,6]. 1.2. Zero-Age Main Sequence Stars: Mass and KM Dependent on Specific Radiation Entropy In an ideal gas supported by both gas pressure gas :PTP and radiation pressure 3: 1T P 4 rad Pa , the radiation/gas pressure ratio is 3 :. 3 Ta rad gas 1 P P (45) The specific radiation and ideal monatomic gas entro- pies are 52 l og, Tr r 3 rad gas 4, 3 aT SSr (46) so that the gas entropy gradient gas d51 dlog 2ad ad S P (47) depends on the difference between the adiabatic gradient 25 ad and the star’s actual thermal gradient :dlog dlogTP , which depends on the radiation transport. Bound in a polytrope of order n, the ideal gas thermal gradient and gas entropy gradient are gas d5 :1 1,1 dlog21 S nPn . (48) For 32n 0.4 150 , the thermal gradient is subadiabatic, the star’s entropy increases outwards, so that the star is sta- ble against convection. M ZAMS stars, with mass MM SM 1 , have nearly constant radiation entropy rad, because radiation transport leaves the luminosity generated by interior nuclear burning everywhere proportional to the local transparency (inverse opacity) . Assuming constant SM 3n rad , we have Eddington’s standard model, an polytrope with rad 41SM and 13 4 43 31 ,KM Pa (49) M depends only on , which is itself determined by Eddington’s quartic equation [3,5,6] 2 2 4 32 03 343 1, 310 :18.3 . πH M M hc M M Gm (50) The luminosity Edd 3 4 4 Edd 1 0.003 , LL M LMMM (51) depends on the Eddington luminosity Edd :4π p LcGM through the photospheric opacity p 1 . This mass-lumi- nosity relation is confirmed in ZAMS stars: on the lower- mass ZAMS, , ; on the upper-mass ZAMS, 3 LM 2 21MM LM, [6]. Copyright © 2013 SciRes. JMP |

