Journal of Software Engineering and Applications
Vol.10 No.13(2017), Article ID:81501,34 pages
10.4236/jsea.2017.1013053
Fault Tolerance for Lifeline-Based Global Load Balancing
Claudia Fohry, Marco Bungart, Paul Plock
Research Group Programming Languages/Methodologies, University of Kassel, Kassel, Germany

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 16, 2017; Accepted: December 26, 2017; Published: December 29, 2017
ABSTRACT
Fault tolerance has become an important issue in parallel computing. It is often addressed at system level, but application-level approaches receive increasing attention. We consider a parallel programming pattern, the task pool, and provide a fault-tolerant implementation in a library. Specifically, our work refers to lifeline-based global load balancing, which is an advanced task pool variant that is implemented in the GLB framework of the parallel programming language X10. The variant considers side effect-free tasks whose results are combined into a final result by reduction. Our algorithm is able to recover from multiple fail-stop failures. If recovery is not possible, it halts with an error message. In the algorithm, each worker regularly saves its local task pool contents in the main memory of a backup partner. Backups are updated for steals. After failures, the backup partner takes over saved copies and collects others. In case of multiple failures, invocations of the restore protocol are nested. We have implemented the algorithm by extending the source code of the GLB library. In performance measurements on up to 256 places, we observed an overhead between 0.5% and 30%. The particular value depends on the application’s steal rate and task pool size. Sources of performance overhead have been further analyzed with a logging component.1
Keywords:
Fault Tolerance, Task Pool, Load Balancing, GLB, Resilient X10

1. Introduction
Hardware failures such as breakdown of a computational node are increasingly recognized as impediments to the efficient execution of large-scale parallel programs. The traditional fault tolerance technique, checkpoint/restart, has high costs that increase with the system size. So alternatives are being looked at.
A promising direction is application-specific resilience. Here, the user program is notified of the failure and can handle it in an appropriate way. Application-specific resilience increases the programming expense. Therefore, implementation in reusable libraries is desirable.
This paper studies fault tolerance for a parallel programming pattern, the task pool. This pattern has many variants and is widely used in runtime systems of task-based parallel programming systems, as well as for load-balancing of irregular applications. We consider a particular variant, which is called lifeline-based global load balancing, or shortly the lifeline scheme. It is an advanced task pool variant with low communication costs and efficient termination detection.
The lifeline scheme is used in the Global Load Balancing framework GLB [1] that is part of the standard library of the parallel programming language X10. It targets distributed-memory architectures in the Partitioned Global Address Space (PGAS) setting. Here, place denotes a set of computational resources together with a memory partition, i.e., typically a cluster node.
We extend the lifeline scheme by the ability to handle permanent place failures, i.e., fail-stop failures of a whole place. Other failures types such as silent errors are not considered. The algorithm has been implemented by extending the GLB code, which is open-source.
When designing our algorithm, we assumed that failures are rare and unrelated, but may coincide. Two failures are denoted as quasi-simultaneous if the second failure occurs before the first one has been recovered from. Quasi-simultaneous failures coincide if the workers on the failed places were cooperating with each other at the time of failure, according to one of the protocols described in Section 3.
Network communication is supposed to be reliable. If both sender and receiver of a message are alive, the message is eventually delivered. There is no presumption on message ordering, though. Even messages from the same sender to the same receiver may overtake.
The lifeline scheme deploys one worker per place, who processes tasks in a single thread of execution. When it has no tasks, it tries to steal tasks from a co-worker. Stealing is cooperative, i.e., the worker does not access the co-worker’s memory, but sends a message in which it asks for tasks. The lifeline scheme supposes the following task model, which is common for application-level task pools:
・ All tasks carry out the same code and are parameterized by a task descriptor.
・ Task execution is free of side effects.
・ Each task computes a partial result, and the overall result is calculated by reduction from the partial results. Reduction uses a commutative and associative operator.
This task model differs from nested fork-join parallelism insofar as children do not return their results to the parent. In fact, children can outlive their parents. Task execution adopts the help-first policy [2] , i.e., after spawning a task, a worker continues with the parent such that the child can be stolen away.
Our fault-tolerant algorithm has been developed incrementally, and earlier versions have been published in [3] [4] [5] . The current paper sums up that work and presents the overall algorithm in a unified way. Unlike earlier work, it includes a detailed discussion of correctness and a performance analysis. Experimental data refer to the ULFM backend of X10 [6] . Base ideas of the overall algorithm include
・ a ring structure for backups,
・ an actor-like communication structure that allows to reorder and prioritize messages,
・ a low-overhead consistence-maintaining steal protocol,
・ transaction and linkage schemes to reduce the steal-related backup expense,
・ a restore protocol whose execution can be nested to recover from multiple coincident failures, and
・ timeout control and an emergency mode to facilitate recovery.
The algorithm is correct in the sense that it either outputs the correct result or halts with an error message. Beyond that, it is robust, i.e., program aborts are rare. There are three reasons for such aborts:
・ Our programming system lacks support for failure of place 0.
・ We restrict redundancy to one copy per task descriptor. If both original and copy go lost due to coincident failures, the program aborts.
・ Ultimate timeout may enforce termination, e.g. after unusually long network delays (see Section 4.2).
A third design goal has been efficiency, i.e., a low overhead during failure-free operation, and quick recovery from failure. Fast recovery reduces the likelihood that another failure occurs before the program execution has returned to a consistent state.
The program has been tested extensively, by triggering failures with kill calls in the program. Performance measurements used the Unbalanced Tree Search (UTS) and Betweenness Centrality (BC) benchmarks. During failure-free operation on up to 256 places, we observed an overhead of 0.5% to 30% over the original GLB version. The overhead for recovery was negligible. In addition to time measurements, we analyzed sources of overhead by logging entrance and exit from interesting states during program execution. The analysis revealed that most overhead is due to steal-related backups, which are frequent at the beginning and end of a program’s execution. So the overhead can be reduced by switching to another resilient scheme during steal-intensive periods.
The paper is organized as follows. Section 2 provides background on X10, GLB, and the lifeline scheme. We refer to an own actor-like implementation, which we took as our basis to incorporate fault tolerance. The fault-tolerant algorithm is explained in Section 3. Correctness and robustness are discussed in Section 4. Section 5 describes experiments and discusses results. The paper finishes with related work and conclusions in Sections 6 and 7, respectively.
2. Background
2.1. X10
In line with the Partitioned Global Address Space (PGAS) model, X10 assumes a global address space that is subdivided into partitions. A partition, together with computational resources, is denoted as place. An X10 programmer controls the mapping of data and computations to places with the at keyword. Data may be accessed locally only. For a remote access, the computation must be moved to the remote place with at, which is more expensive than a local operation. These place changes can be considered as active messages. In place changes, data from the origin place is transparently copied and sent along, if accessed remotely.
More specifically, X10 follows the Asynchronous PGAS (APGAS) model [7] . Accordingly, it expresses computations by light-weight activities that are transparently mapped to threads by the runtime system. An activity may release its thread by calling Runtime.probe(). In this case, all pending activities are executed before the calling activity resumes. Program execution starts with a single activity on place 0. New activities are spawned with the async keyword and run asynchronously to their parent. Activities can be moved to a different place with at. The spawning of activities can be encapsulated in a finish block. At the end of this block, the program execution suspends until all activities, including nested ones, have terminated.
X10 supports a mode called Resilient X10, in which the user program is notified in the event of a permanent place failure. Three notification mechanisms are available:
1) Dead Place Exceptions can be caught at the end of an at or finish block. They cannot be caught at the end of an async block.
2) Function isDead (place) can be invoked at any time to inquire a particular place’s liveness.
3) Function register Place Removed Handler registers a piece of code at the current place. It is automatically invoked when another place dies.
X10 programs can be compiled into either Java or C++. The latter option, called Native X10, is more efficient. Native X10 can run with a sockets-based backend or an MPI-based backend. For Resilient X10, the MPI backend is based on the User-Level Failure Mitigation (ULFM) extension of MPI [6] [8] .
2.2. Lifeline Scheme
Independent from the place-internal mapping of activities to threads, X10’s standard library offers the Global Load Balancing framework GLB for inter-place load balancing [1] . GLB tasks are different from X10 activities, and must be explicitly defined. Internally, GLB achieves load balancing with the lifeline scheme, which is a particular realization of the task pool pattern.
In general, a task pool processes a typically large number of tasks with a fixed number of workers. The concept of tasks differs between task pool variants. As stated before, we assume that all tasks carry out the same code, are side effect-free and produce a result. The final result is calculated by reduction from task results, using a commutative and associative operator. Tasks may generate new tasks, but are otherwise independent.
In most task pool variants, including the lifeline scheme, each worker maintains a local data structure, called local pool. The worker repeatedly takes a task out of the pool, processes it, inserts new tasks if generated, then takes the next task etc. Additionally, it accumulates the results of its tasks into a partial result. Initially, at least one local pool contains a task. The overall computation ends when all tasks are finished. Then, the final result is computed by reduction from the partial results of all workers.
If a worker has no tasks left, it tries to steal tasks from a co-worker. Correspondingly, the workers are called thief and victim, respectively. In cooperative work stealing, the thief sends a message, and the victim responds by sending another message back. The return message contains either the loot (tasks) or a reject notice. The lifeline scheme deploys a quite sophisticated pattern of victim selection: A thief contacts up to w random victims, followed by up to z lifeline buddies, until it finds work. The lifeline buddies are preselected and form a low-diameter graph [9] . When a lifeline buddy rejects a steal request, it additionally stores the identity of the thief. If it obtains work later, it shares the work with the stored thieves.
After unsuccessful steal attempts, a worker becomes inactive. This state differs from termination in that the worker may be re-activated if a lifeline buddy later sends work. When all workers have become inactive, the overall computation ends.
2.3. GLB Framework
A GLB user must specify the local pool data structure by providing the following functions:
・ boolean process(n): takes up to n tasks from the local pool, processes them, inserts new tasks, and returns a flag to indicate whether n tasks were available
・ TaskBag split(): splits the local pool such that one part can be sent to a thieve as loot in a TaskBag.
・ void merge(TaskBag): integrates the received TaskBag into the own pool.
GLB implements the lifeline scheme with a single worker per place. By setting environment variables, it moreover enforces sequentialization of all user activities on a place. Thus, there is no need for place-internal synchronization. Communication between workers is accomplished by at async calls, which correspond to active messages, and are shortly denoted as messages. If a message arrives at a place, it is queued until the receiver suspends by calling Runtime.probe().
This scheme resembles the well-known actor model [10] , in which parallel entities progress in a message-driven way: Except for message processing, a worker is passive and only reacts to message receipt. While the original GLB implementation occasionally violates the actor pattern by using blocking communication, we slightly modified the code for a clear structure. The modified variant is called GLB-Actor. It was the starting point for the development of our fault-tolerant algorithm. For clarity of presentation, we only describe GLB-Actor in the following. Further information on the differences between GLB and GLB-Actor can be found in [4] .
In GLB-Actor, all communication is asynchronous, and a sender never blocks to wait for an answer. Asynchronous communication has two merits: First, it enables parallelism between task processing and communication, which speeds up the program. Second, it keeps workers responsive despite the restriction to a single activity per place.
Recall that messages contain code. Thus, their receipt initiates a sequence of actions, which may change the worker’s state and/or cause sending other messages. GLB-Actor deploys three types of messages:
・ noTasks: This is the reject notice from an attempted victim. Upon receipt of this message, the worker contacts the next victim or, after unsuccessful attempts, sets variable stealFailed to true.
・ give: A victim sends tasks. The victim may have been contacted right before, or be a lifeline buddy that registered the request much earlier. On the thief site, function give() internally calls the user-defined function merge() to integrate the tasks into the local pool. If the message give() arrives at an inactive worker, the message additionally re-activates it.
・ trySteal: The receiver of this message is the victim of a steal attempt. If its queue is empty, it answers with noTasks. Otherwise, it calls split(), and sends the extracted tasks back in a give message.
Recall that messages are always received at the next Runtime.probe() call following their arrival. Then, most of the respective actions are carried out immediately. An exception is a steal request that arrives at a victim with a non-empty pool. In this case, the request is recorded. Recorded actions are carried out only when all pending messages have been received. This way, random steals can be handled in preference (i.e., before) lifeline steals, and are thus answered by tasks in more cases. In the GLB-Actor code, each worker runs the following main loop, where queue denotes the worker’s local pool:

Method processUpToN() is the same as process(), except that it updates state information. At Runtime.probe(), all pending messages are received, i.e., the respective remote activities perform their actions immediately or record them. Recorded actions are carried out later when the worker resumes and calls processRecorded().
Beside by messages, a worker’s progress may be driven by local events. GLB-Actor defines only one type of local event, that of the local pool having become empty. This event is recorded by processUpToN() and handled by processRecorded(), when the worker starts stealing. This subdivision has the advantage that the event is handled after a possible give, which is handled during Runtime.probe() and makes the empty pool event obsolete (if applicable).
Behind the main loop, the worker activity ends. To re-activate the worker, a lifeline buddy starts a new activity on its place. This activity continues to use the worker’s state. Inactivity is reflected by a state variable. In GLB-Actor, inactive workers do not call processRecorded(). This call is not necessary since inactive workers may not receive messages of a type that requires recording.
3. Fault-Tolerant Algorithm
Our fault-tolerant algorithm extends GLB-Actor. It defines many new types of messages and local events that are related to backup, failure recognition, and recovery. Table 1 gives an overview and contains more technical information. The third column lists major actions only, whereas others are discussed in the text. Immediate actions are displayed in italics. For recorded actions, their order in the table reflects the execution order in processRecorded(). An arriving restore, for instance, is handled before a give, since the former appears higher up in the table. The last two columns are explained later.
Despite the higher number of messages and local events, the actor scheme works the same way as before. With this scheme, the worker simultaneously pursues different computational issues: task processing, stealing, backup, monitoring, and recovery. The fault-tolerant algorithm makes extensive use of the actor scheme’s ability to record actions such that they can be performed in a well-defined order and with different priorities. Unlike in GLB-Actor, even inactive workers must regularly call processRecorded(), and we will ensure that.
In every message receipt, the message’s sender is inspected. If the message does not match any ongoing protocol, a message-specific action is taken. In most cases, the message is discarded for being orphan, i.e., it must have come from a place that died after sending. Orphan messages are no longer needed. In some cases, an unexpected message indicates a new failure or it is due to protocol nesting. These cases are explicitly described in the text, whereas discarding of orphans is the default and not further mentioned.
A message receipt may initiate multiple immediate actions. An interesting observation regarding the actor scheme is the fact that these can be carried out in any order. If a worker fails while modifying its state, all updates are lost, no
Table 1. Types of messages and actions to be carried out upon arrival. Immediate actions are displayed in italics. For recorded actions, their order in the table indicates the execution order. The leftmost column uses different fonts for messages and local events. Abbreviations: Em = emergency mode, Ti = timeout control, n/a = not applicable, (−) = in emergency mode only.
matter whether performed before or after the failure. Message-sending actions may be reordered w.r.t. local actions as well, if the message contents are independent. From this observation, we always perform the most urgent actions first. Typically, we start sending messages, and thereafter update the worker’s state.
The rest of this section is structured along the different computational issues and core ideas of the algorithm. An overview of the algorithm is given in Figure 1.
Figure 1. Flow chart.
3.1. Algorithm in Failure-Free Operation
1) Regular backups: Each worker regularly saves a copy of its local pool contents in the main memory of another. For that, workers are arranged in a ring. For simplicity, we assume the ring order to coincide with place numbering (plus wraparound). This setting has no negative impact on failure coincidence, if successively-numbered places are mapped to distinct physical network nodes.
If worker i writes its backup to worker j, we say that i has backup partner j, or briefly Back(i) = j. Vice versa, i = Forth(j). After failures, the ring structure is repaired by bridging gaps and updating the respective Back and Forth variables.
Backup writing is uncoordinated. Each worker independently counts iterations of its main loop and sends a backup every k iterations. The backup includes the tasks to be saved, the current value of the accumulated partial result, the current value of the sender’s Forth variable, and the identity of the sender itself. Regular backups are sent with message type REGreq, and acknowledged with message type REGack (see Table 1). If a REGreq’s sender differs from the current value of the receiver’s Forth variable, it must be an orphan message and is discarded as described before.
2) Failure recognition: As noted in Section 2, Resilient X10 supports three mechanisms for failure notification:
・ Dead Place Exceptions cannot be used in our program since they cannot be caught at the end of an async block and the whole program is spanned by a single finish.
・ The register Place Removed Handler functionality is not available for Native X10.
・ Therefore, we rely on isDead(). More specifically, each worker i regularly calls isDead(Back(i)) within processRecorded(). In case of failure, it invokes the restore protocol described in Sect. 3.2. Sometimes, failure of Back(i) is detected by a different worker, who reports that to i with message deathNotice.
3) Ghost activities: An inactive worker must call processRecorded() to
a) fulfill regular duties such as invoking isDead(Back(i)), and
b) timely perform the actions that are recorded by incoming messages.
For issue 1, all active workers send the following monitor message to their backup place during each processRecorded(). By recursion, all inactive workers are captured this way.

For issue 2, every message that records an action at an inactive worker spawns a ghost activity. A ghost calls processRecorded() and, like any other activity, is scheduled after some time. A flag ensures that at most one ghost activity is spawned, including the call in monitor.
4) Timeout Control: Although, in the actor scheme, a worker never explicitly waits for an answer to a message sent, the worker may need a reply before it can return to normal state. In the backup protocol described above, for instance, the worker must wait for the completion of a previous backup before it can send the next. Otherwise, the second backup may overtake the first one and is overwritten. Message delays may be due to network delays or place failures. After failures, a failed place’s Back is not always able to notify the waiting place. Shortly after trySteal, for instance, Back does not yet know of the steal attempt. Therefore, we deploy a timeout control scheme that supplements the regular isDead() calls.
Timeout control stores awaited messages in a list, called awaitedMsgs. For each message, it records type, source, and a deadline (wallclock time). The last column of Table 1 marks the message types covered by timeout control. Backup acknowledgements are usually not included, since failure of Back is recognized by the regular isDead() calls.
Each invocation of processRecorded() goes through awaitedMsgs and, if a deadline has passed, checks liveness of the respective source via isDead(). If the source is alive, the message is re-inserted into awaitedMsgs with a new deadline, until an ultimate deadline is reached (see below). If the source is dead, a timeout has occurred. In this case, a deathNotice is sent to the place’s Forth, which is determined by going backwards through the ring until the next place alive. Afterwards, the timeout is dealt with specifically for the particular type of lost message, as explained in Sect. Note that inactivity of a worker does not stall timeout control, since monitoring ensures regular processRecorded() calls.
5) Transactions: At Runtime.probe(), multiple trySteal messages may be received. For efficiency, we combine their handling into a transaction. Transactions include successful requests only, whereas the others are rejected by sending noTasks. Similarly, transactions do not contain duplicates, i.e., the same thief may not be contained twice.
Transactions are numbered by tans, which are assigned consecutively by each victim and include its id. Tans are included wherever appropriate, e.g. they are sent with all messages of the steal protocol. Beside the tan, a transaction descriptor stored by the victim holds the list of thieves.
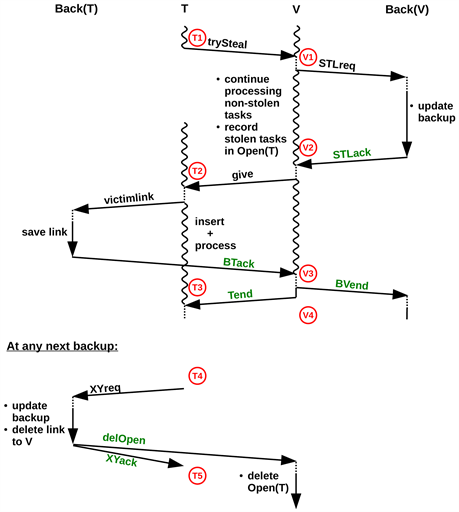
6) Steal Protocol: The steal protocol is depicted in Figure 2. For clarity, only a single thief T and victim V are shown, but there may be several thieves. Dotted lines denote waiting times for Runtime.probe(), and wavy lines mark task processing (depicted at T and V only). Messages STLreq, STLack and BVend are sent once per transaction, whereas the other messages are sent once per thief.
Message STLreq initiates a steal backup, which updates the data saved at Back(V) and includes the list of thieves. The backup is acknowledged by STLack.
As noted in the figure, V saves the task bags to be stolen in an array of lists, called Open, before sending them out via give. Thus, entry Open(T) holds all task bags that were sent to T but have not yet been acknowledged. When T receives loot, it first enters the corresponding tan into an array called tanGOT. This array has one entry per place i and holds the last tan of loot received from i.
Figure 2. Steal Protocol, adapted from [3] .
Then, T informs Back(T) by sending a victimLink message containing a link to V. In case T dies, Back(T) will use this link to request the tasks from V. As a recorded action, T later inserts the tasks into its own pool and resumes task processing.
After Tend, any next backup brings Back(T) up to date, making the saved links superfluous. Notations XYreq and XYack in Figure 2 denote backups that are part of the steal protocol. XY can stand for REG, STL or TO (explained later). XY-backups are marked by a flag and instruct Back(T) to delete all links saved (other backups do not cause deletion). In particular, Back(T) sends a delOpen message to V, which in turn deletes all tasks up to the tan provided.
Backup writing is permitted after Tend only. Outstanding Tends are maintained in a list, called openTends. There may be several, since T may receive multiple give messages at a time. If a backup is scheduled when openTends is non-empty, it is postponed until the next processRecorded() call.
A victim V processes one transaction at a time. Upon receipt of BTack, it deletes the thief from the transaction descriptor. When all thieves have acknowledged, BVend is sent. At Back(V), the period between receiving STLreq and BVend is denoted as queasy. During this period, Back(V) does not know whether T and Back(T) have already adopted the tasks.
3.2. Restore after Single Failure
1) Restore Protocol: Figure 3 depicts our restore protocol. It is initiated by Forth(P) after having detected P’s failure via isDead() or a deathNotice. Forth(P) locates Back(P) as being the next place alive in the ring. When receiving restore, Back(P) makes sure that the failed place P is its own Forth, and that the message’s sender is Forth(P). Only then recovery is possible. Otherwise, the program needs to abort since a gap in the ring indicates that two neighbored places went lost. If recovery is possible, Back(P) inserts P’s saved tasks into its own pool, updates the accumulated partial result, and temporarily invalidates Forth, as noted in the figure. If necessary, Back(P) is re-activated.
Figure 3. Restore protocol, adapted from [3] .
Back(P) also takes care of the case that P was the victim and/or thief of ongoing steals at the time of failure. For the victim case, it contacts all thieves of the current transaction, to make sure they received the tasks. This is accomplished with GOTcheck and GOTok messages. A thief receiving GOTcheck obeys the following three cases, in which waiting is accomplished by postponing the action to the next processRecorded call:
a) tan Î tanGOT Ù tan Ï openTends ® Send GOTok
b) tan Ï tanGOT ® Wait a few seconds to compensate network delays. Then abort the program for loss of two copies.
c) tan Î tanGOT Ù tan Î openTends ® Wait until openTends is empty, except possibly for the affected tan (for which Tend is unlikely to arrive after V’s death). Then send an XYreq (of type TOreq) to Back(T). Upon receipt of TOack, openTends is reset and GOTok is sent.
For the thief case, Back(P) goes through saved links, and contacts the respective victims via linkResolve. They respond by sending a linkTasks message that contains either tasks or null. The latter indicates that V has already taken back the tasks itself, which may happen after a timeout of BTack (see Section 3.4).
When Back(P) has successfully checked/collected all of P’s former tasks and updated its local pool correspondingly, it writes a taken-over backup, represented by messages TOreq and TOack. Note that this backup type is used for different purposes.
Then, Back(P) signals completion via RSTack. Upon receipt, Forth(P) installs Back(P) as its new backup partner by sending an inauguration backup with message IAreq. If Forth(P) was between V1 and V4 when the failure occurred, the IA-backup also includes the (possibly updated) transaction descriptor, such that the new backup place can resume queasy state. Furthermore, Forth(P) and Back(P) update their respective Back and Forth variables. An IAreq must always be the first backup on a new backup place.
Note that, as any backups, TOreq and IAreq may only be sent after any previous backup has been acknowledged. TOreq may correspond to an XYreq in Figure 2. IAreq may not, since any previously sent links went to the failed place. Nevertheless, IAreq brings its backup partner up to date, making XYreq superfluous. If Back(T) fails while T is between T2 and T3 , T sends replacement messages for BTack and delOpen when reaching C3 .
2) Emergency mode: Any execution of the restore protocol is time-critical. Therefore, only urgent and short messages are processed at Forth(P) and Back(P) between c1 and R5 . In particular, processing of tasks pauses, and non-urgent recorded messages are postponed. Immediate actions are always performed.
In emergency mode, timeout control is only applied to messages that may be relevant for restore. For these, timeout control is time-critical. While active workers are constantly calling processRecorded() in this mode (since task processing pauses), the normal monitoring of inactive workers is too infrequent. Therefore, we run a long-term ghost between c1 and C2 . It is launched on Forth(P), and carries out code

If Forth(P) is active, it starts a ghost on Back(P) the same way within processRecorded. This guarantees frequent timeout control on both Forth(P) and Back(P). Unlike monitoring, the long-term ghost is not recursive.
3.3. Nested Restore
During the restore protocol, one of the involved workers may fail. Failure of a former victim or thief has already been discussed in the previous section. Coincident failures of both victim and thief lead to timeout onlinkTasks and are discussed in Section 3.4. In the following, we consider all cases in which Forth(P), Back(P), or Back(Back(P)) fail.
An overview is given in Table 2, where row and column headings denote the role that the same worker takes in the 1st and 2nd protocol, respectively. The interior of the table indicates the failed place’s identity. For instance, the first entry of the table refers to a place that has Forth(P) role in the first protocol. When the 1st protocol’s Back(P) fails, the place takes over the Forth role in the 2nd protocol, as well. For any given row/column, the identity of the failed place is unique. Sign “+” marks cases in which recovery is possible, and “−” marks cases in which it is not. For “(+)”, recovery may or may not be possible, depending on the particular timing.
In the following, notation X ® Y means that a worker is performing role X in the first restore protocol, and then receives a message that puts it into role Y in the second. Forth is abbreviated by F, Back by B, and Back(Back) by BB.
Case B ® B Since a place may only restore another if it holds the failed place’s backup, the program needs to abort if message restore2 is processed before the
Table 2. Recovery after two failures: Rows/columns denote the same worker’s roles in the two protocols. The interior indicates the second failed place’s identity. Abbreviations: + recovery possible, − abort, (+) recoverability depends on timing.
arrival of IAreq1. Recovery is facilitated by the order in Table 1, If restore is received first, the algorithm waits for a few seconds before aborting the program.
Case F ® F This case is illustrated in Figure 4. Recovery is possible if and only if restore(Back(P)) arrives after TOreq. Otherwise, Back(P)’s data are unsecured. After the second failure, outstanding messages of the first protocol are orphan.
Case F ® B This case is not interesting if F receives restore after C2, and thus after having sent IAreq. Here, the second protocol’s TOreq2 is just delayed until the first protocol’s IAack1 arrives, as usual.
If F receives restore before RSTack, it instantly commences its B role, to utilize the waiting time before C2 . However, our worker must not send TOreq2 before IAack1. In fact, TOreq2 and IAreq1 are redundant. Therefore, the worker waits until the second protocol has come to R3 , and the first protocol has come to C2 , and then sends a single (combined) IAreq. Upon receipt of IAack, it sends RSTack2.
Case B ® F If B is at or behind R4 when detecting the failure, the recovery procedures are independent. If B is before R4 , it first attends to the second protocol, because it needs an inaugurated backup place before it can send TOreq. There is no difference between states R3 and R4 , since TOreq went lost. Similar to the previous case, TOreq1 and IAreq2 are combined. After IAack, the second protocol is complete, whereas the first protocol is continued with sending RSTack.
Case F ® BB Here, F can receive the TO-backup independent from its participation in the first protocol.
Case BB ® F Similarly, the roles are independent.
Case B ® BB This case coincides with case F ® B on B’s predecessor. This case can only occur after B’s inauguration.
Case BB ® B Similarly, this case coincides with F ® F. Recovery is possible if and only if the TO-backup is written before receipt of restore. Again, the probability for encountering the two messages in this order is increased by the order in Table 1, as well as by waiting for a few seconds if message restore arrives first.
Case BB ® BB This case coincides with B ® B and requires program abort.
More than two failures: From the above case-by-case analysis, BB involvement is either independent or coincides with another case. Therefore, we concentrate
Figure 4. Recovery in F ® F case.
on roles F and B. From case B ® B, a worker cannot be in more than one B role. From case F ® F, it can be in more than one F role, but then the first role is essentially finished when the second one is started with. Consequently, a place can be in at most one B role and one active F role, such that the above consideration of cases F ® B and B ® F is sufficient.
3.4. Specific Timeouts
Recall from Section 3.1 that each worker maintains an awaitedMsgs list. Timeout control regularly runs through this list to check liveness of the respective sources. When recognizing a failure, we speak of a timeout. Then, the place’s Forth is informed by a deathNotice and the particular type of lost message is dealt with. This section handles the type-specific treatment of lost messages. Recall that timeout control covers the message types marked in the last column of Table 1.
Timeout of RSTack corresponds to case F ® F. Here, Forth determines the next place alive in the ring and sends restore. Similarly, timeout of IAack initiates the next restore protocol.
If timeout of GOTok or linkTasks reveals a failure, the program must be aborted for loss of two copies. The same holds for timeout of IAreq.
In some cases, the causer of a timeout may be different from the source of an outstanding message. In Figure 2, for instance, timeout of BVend may be due to a failure of Back(T), despite liveness of V. The typical approach in these cases is non-transitive, i.e., each worker only checks the source of its own outstanding messages. In the example, message BTack will be controlled by V.
An interesting exception is timeout of BTack. The message is expected from Back(T), but V contacts T. The exception is made for the reason that Back(T) does not wait for the victimLink message. If T is alive, BTack is kept in awaitedMsgs, since the timeout may be due to a network delay. If Back(T) is dead, that will be detected by T later on. In this case, T sends a replacement for BTack, as noted in Section 3.2.
If timeout of BTack reveals failure of T, V takes back the tasks from Open(T), and re-inserts them into its own pool. Moreover, V removes T from the transaction descriptor. Thereafter, V informs Back(V) by sending a new backup, for which it overloads message types TOreq and TOack again.
It may happen that T failed, but Open(T) does not contain the tasks. In this case, linkResolve must have overtaken BTack, and no further action is needed.
Timeout control for noTasks and give coincides. Timeout requires no further action beyond sending a deathNotice and contacting the next victim. At this point, defects of the lifeline graph can be tackled as well, as described in [10] .
At timeout of Tend, T writes the next backup as soon as possible, i.e., when openTends has become empty except for the lost message. Again, a TO-backup is used for this purpose. After receipt of TOack, the missing Tend is removed from openTends.
At timeout of BVend, Back(V) sends a deathNotice, but takes no further action until receipt of restore.
3.5. Variants of Algorithm
In addition to the algorithm described, we considered two variants:
1) Forward-and-collect: This variant is inspired by a modification of cooperative work stealing, which was introduced by Prell [11] . Recall rejects of unsuccessful steal attempts are normally returned to the thief, who in turn contacts the next random victim. The forwarding variant from [11] replaces these two messages by a single one to reduce communication costs. For that, the first victim selects a second random victim, and sends the steal request along on behalf of the original thief. If the second victim has no work either, it forwards the request again, and so on. When work is discovered, it is sent back to the original thief only.
We modified the scheme and call our variant forward-and-collect. Here, a forwarded request includes the identities of the original thief, and of all victims encountered along the way. Note that these victims are normally out of tasks.
To state it in more detail, the original thief selects w random victims, and then sends its own id, a steal id and the list of selected victims to the first victim. We call this message type forward. It is covered by timeout control. Receipt of forward is similar to receipt of trySteal, but the request is always recorded. The victim can respond in three ways:
・ Case 1: The victim has no work to share and there are victims left in the list. In this case, the message is forwarded to the next victim and a corresponding forwardedTo message is sent to the original thief. Moreover, the victim adds itself as thief. Added thieves are denoted as fellows.
・ Case 2: The victim has no work to share and there are no victims left in the list. This case corresponds to w failed random steals in the original GLB. The victim sends a noTasks message to the original thief. Fellows are not informed, since they have another open steal request of their own.
・ Case 3: The victim has work to share. The victim opens a transaction for all thieves on the list (subject to the availability of enough work).
The forwardedTo messages inform the thief about the identity of the current victim. They are used for timeout control. When a thief receives a noTasks message, it starts stealing from lifeline buddies as usual.
Forward-and-collect fits well with the lifeline scheme, since the scheme can naturally handle simultaneous give’s. Forward-and-collect offers the advantage of an increased transaction size, which may increase our fault tolerance scheme’s efficiency.
2) Ahead-of-time stealing: In this variant, a worker initiates a steal attempt before it runs out of tasks, i.e., when its pool size has fallen under some threshold [11] . The scheme can improve the efficiency of work stealing, since it reduces idle times.
4. Correctness and Robustness
4.1. Correctness
Recall that correctness requires the program to either output the correct result or halt with an error message. Correctness follows from observations 1 to 3:
Observation 1: If the program yields a result, exactly one result per task has been included in the reduction. Outside of stealing, a backup partner takes over both the failed worker’s tasks and the corresponding accumulated partial result at the time of backup writing. Thus, even though a task may be executed twice, its result is included only once.
The steal protocol ensures that, after a failure, open tasks (including their copies) are consistently adopted by either the thief or the victim sides:
・ If Back(T) fails, the restore protocol involves an IA-backup from T to a new Back(T). The backup includes all tasks for which links have been sent before. The victim side is not involved in the restore, and so the tasks are consistently adopted by the thief side.
・ Similarly, if Back(V) fails, V inaugurates a successor. The IA-backup includes information about the ongoing transaction, and puts the new Back(V) into queasy state. Since T is not involved, the tasks are consistently adopted by the victim side.
・ If both T and Back(T), or both V and Back(V) fail, the program aborts for loss of a place and its backup partner. This is taken care of by the restore protocol.
・ If V fails before V1 , T is informed by a timeout, but the tasks have never moved away from V.
・ If V fails between V1 and V4 , Back(V) is in queasy state and sends GOTcheck messages. From the three cases in Section 3.2, they are answered by GOTok only when it is clear that both T and Back(T) have adopted the copies. Note that this includes cases in which Back(T) is replaced due to failure.
・ If T fails before T2 , V is notified by a timeout of BTack and takes over the tasks. The subsequent TOreq brings Back(V) up to date. Since T failed before T2 , Back(T) did not yet receive any links. Therefore, the tasks are consistently seen at V.
・ If T fails between T2 and T3 , V is again notified by a timeout of BTack. Independently, Back(T) discovers the failure and sends linkResolve. This gives rise to a race condition, in which either Back(T) or V adopts the tasks. In either case, the tasks are removed from Open(T) during adoption, and therefore cannot be adopted twice. If the tasks are adopted by V, the argumentation is the same as in the previous case (Back(T) receives null). If the tasks are adopted by Back(T), Back(V) need not be informed as it already sees the tasks at the thief side.
・ After V4 , the tasks are consistently seen at the thief side.
Observation 2: Provided that number and duration of tasks are finite, the program terminates. Termination detection is primarily provided by Resilient X10, as our program starts all activities within the scope of a single finish. The number of steal attempts is finite, since a worker becomes inactive after attempts. It is re-activated only when it receives tasks, and then it processes at least one task itself. Moreover, the duration of each steal attempt is finite, since it is eventually limited by the ultimate timeout scheme. Consequently, completion of tasks implies a worker activity’s termination, and Resilient X10 detects when all activities have either terminated or failed.
In our scheme, a task is executed at most times, where denotes the number of failures. Thus, the overall time for task processing is finite. Workers are constantly processing tasks (if available), except in emergency mode and inactive state. Emergency mode is left from Observation 3, and inactive state is handled by the lifeline scheme. Even if unfavorably coincided failures cut off a subgraph of the lifeline graph, the two subgraphs do not share work anymore, but still each task is computed by one of the subgraphs. So this case can lead to slowdown, but does not compromise the correctness.
Deadlock is impossible, since the code of all messages is wait-free, i.e., it finishes after a bounded time. Livelocks are precluded by the ultimate-timeout scheme discussed in Section 4.2.
Observation 3: After failures, the program is guaranteed to return to normal operation. In particular, the following observations hold.
3a) All failures are detected. This is guaranteed by regular isDead() calls and monitoring.
3b) The ring structure is repaired. Since Back(P) checks both its own and the failed place’s Forth variables (see Sect. 3.2), acceptance of restore guarantees that there are no gaps left in the ring. This issue has been discussed in more depth in [3] , where it was called log.
3c) Ongoing protocols are aborted such that participants either return to a consistent state or the program halts. This statement has been verified with an informal, but systematic analysis. We considered all possible states and message types, and made sure they are handled appropriately.
The following discussion includes interesting cases only. Many other cases are obvious, since the respective message belongs to an ongoing protocol, or can be easily seen to be orphan. An example for an orphan message is state C1 with message IAack. This indicates case F ® F. From Figure 4, the message must have come from Back(P), which meanwhile failed. Discarding the message is therefore appropriate.
Other message receipts are impossible. For instance, an IAack cannot be received in state T2 , since IAreq may not be sent when openTends is non-empty.
An interesting case for a message receipt in a certain state is a give message that arrives after its timeout. Here, Back(V) must be in queasy state. The message can be accepted as usual, and a successive GOTcheck may later be answered by GOTok.
Another interesting case is state C1 with message IAreq. Candidate situations in which that may happen are cases F ® B and B ® F. From the explanation in Section 3.3, case F ® B is not possible, since F cannot have sent RSTack while in state C1 , and thus its predecessor cannot have sent IAreq. In case B ® F, the second failure cannot have been detected before R4 , since the F-role protocol would have been carried out until C2 before sending the (combined) IAreq. This contradicts our place being in state C1 . Consequently, the situation can only occur in case B ® F when the second failure is detected after R4 . Consequently, the protocols are independent, and IAreq can be handled as usual.
Abort of the steal protocol has already been discussed in Observation 1. The restore protocol obviously returns to a consistent state in the single-failure case: Former Back(P) becomes Forth(P)’s Back and vice versa, such that the gap is bridged. Tasks are adopted by Back(P), and all involved workers get a consistent view of the new state by the backups.
The tanGOT array contains only the largest tan from each victim. This is sufficient since V processes one transaction at a time. Any larger tan in tanGOT indicates that the previous transactions have been successfully completed as well. Therefore, it is no problem if Back(V) sends GOTcheck when T is already in state T3 .
The occurrence of a second failure during a restore protocol’s execution has already been handled in Sect. 3.2. For instance, the first line of Table 2 covers all possibilities for the second failure, when complemented with the observation that a failure of Forth causes program abort.
3d) The program is free from leakage. Orphan messages are discarded, as discussed before. Both the tanGOT array and the awaitedMsgs list have finite size. The Open list may not overflow, since any delOpen message deletes all tan’s up to the one provided as a parameter. This scheme cannot cause premature deletion since V processes one transaction at a time, and the links must be received in the same order. A transaction may not contain the same thief twice, as is taken care of by V.
4.2. Robustness and Efficiency
Recall that robustness denotes the program’s ability to usually output the correct result despite one or several, possibly coincident, failures. Thus, cases in which the program halts with an error message are rare.
Robustness has principle limitations. First, in the current X10 version, only resilience mode 1 can be selected, which halts the program after a failure of place 0.
Second, our fault-tolerant algorithm has a limited redundancy of one copy per task descriptor. While the particular value of one is rather arbitrary, any resilience scheme must restrict the redundancy level in some way, to trade off backup overhead against recovery chances. A higher value than one would increase robustness, but any value will leave cases in which the program aborts.
In our case, if both original and copy go lost quasi-simultaneously, recovery is fundamentally impossible. For uniform protection, the algorithm keeps exactly one copy per task descriptor. Between T2 and T5 , these copies are spread over different victim places. Therefore, the probability of data loss is somewhat higher than that of a quasi-simultaneous failure of a place and its backup partner. The difference is, however, small, since the spread copies are collected regularly.
If either original or copy of each relevant task descriptor is intact, our algorithm is normally able to recover. A few rare exceptions are due to unusually long network delays. These cases are practically excluded since the program waits for a few seconds before abort.
Moreover, the algorithm leaves one loophole for livelocks: Occasionally, recorded actions are postponed from one processRecorded() call to the next, to first wait for a certain message. This may give rise to a group of workers who cyclically wait for each other’s message. Such cycles may involve additional workers who do not postpone actions, but carry out a protocol whose progress depends on the arrival of the next message. A particularly vulnerable protocol state is R2 , since further progress depends on multiple outstanding messages. Table 3 lists all cases in which actions are postponed. It also includes some vulnerable states, to facilitate further discussion.
An example of a livelock cycle is the following: In the restore protocol, worker Back(P) sends GOTcheck and thus waits in state R2 . The inquired thief finds the tan in tanGOT and also in openTends. According to case 3 from Section 3.2, it waits until openTends is almost empty, and then needs to send an XYreq. If
Table 3. Situations in which actions are postponed to next process recorded.
accidentally Back(T) has failed as well, a new Back(T) must first be inaugurated. The corresponding restore protocol may, symmetrically to the first one, hang in R2 , such that none of the involved workers makes progress.
Possibly, cycles like that could be eliminated at the price of further increasing the algorithm’s complexity. We took a different approach and built into the algorithm an ultimate timeout scheme. The scheme is an extension of timeout control and has already been mentioned in Section 3.1. If a message is being waited for since a long time, ultimate timeout aborts the program. Like normal timeout, ultimate timeout refers to wallclock time. The value should be chosen large enough to account for unusually long network delays, which may, e.g., be due to temporary network congestion from other jobs. Feedback about the current load, if available, could be used to adjust the value. We never observed ultimate timeout in our experiments.
We rely on ultimate timeout for several practical reasons. First, eliminating livelocks, if possible, would be difficult and error-prone. Second, even if the algorithm was livelock-free, any programming error (or network fault) may still stall the program, and then ultimate timeout can help. Finally, we expect that the likelihood of a program abort due to livelock is much lower than that of loosing an original and its copy.
To consolidate this conjecture, consider Table 3, which includes all cases in which actions are postponed.
The following discussion assumes that the awaited message is not subject to timeout. Similarly, for outstanding backup acknowledgements, the case that Back fails is ignored. In these cases, the restore protocol takes appropriate action such that the respective situation is left. In case 4, if a Tend is affected by timeout, the backup is sent despite openTends holding the problematic message. Only if the restore protocol’s execution leads to a new vulnerable state, a livelock may occur. From the discussion of specific timeouts in Section 3.4, this is rarely the case.
Case 1 of the table can only occur if V has sent BVend before the backup request, and the messages have just overtaken. Thus, from our assumption of a reliable network, BVend will eventually arrive. Cases 2 and 3 cannot cause the program to hang, since backup writing is never postponed (except for case 1, where the delay is finite) and thus the awaited message will be delivered for sure. Similarly in case 4, both victimLink and BTack are always processed immediately, and thus Tend is guaranteed to be sent. For the same reason, situation 5 is left. Case 6 embraces several situations in which a problem would actually require program abort, but it may be caused by a network delay. For instance, GOTcheck may be received before the corresponding tasks, or restore(P) may be received before P’s backup. Since waiting for a few seconds does no harm to the program’s progress, case 6 may not lead to livelock.
In case 7, none of the postponed messages may stall recovery, as can be verified with Table 1 and Table 3. Leaving situation 8 is implied by the previous discussion of cases 2, 3 and 4 and the observation that linkResolve is processed immediately. In consequence, the restore protocol cannot stick in state R2 . Therefore, RSTack is guaranteed to be sent, which beats case 9. Note that the same arguments apply to combined IAreq/TOreq messages in the B ® F and F ® B cases. In consequence, emergency mode is guaranteed to be left, and thus the delays from case 5 are finite. This observation applies in particular to give, resolving case 10. In case 11, the TO-backup will succeed since Back(V) is either alive, or will be replaced by a new Back(V). Execution of the corresponding restore protocol is not hindered by the delay of BVend. Finally, case 12 may occur if the tasks just received by give have been consumed before the corresponding Tend arrives. The case cannot stall the program, since the steal protocol is guaranteed to progress outside of failures.
From the above discussion, compromises to robustness are chiefly due to coincident failures. We have designed the algorithm so as to minimize them. In particular, we keep the recovery period short, by switching to emergency mode and by using an efficient restore protocol. If coincident failures occur, nested executions of the restore protocol may still permit recovery.
Regular isDead() calls guarantee that all failures are recognized. Closer meshed monitoring could further reduce the probability of quasi-simultaneous failures at the price of a higher performance overhead. Regarding efficiency, place failures slow down a program for three reasons:
1) decreased number of computational resources
2) recovery overhead, and
3) defects of the lifeline graph.
Issue 1 cannot be avoided. Unlike other computations, task pools have the advantage of being naturally malleable. After a failure, Back takes over the tasks, but the burden for re-execution is automatically balanced among workers by stealing. We addressed issue 2 with an efficient design of our restore protocol. For instance, all linkResolve and GOTcheck messages are issued at the same time. Local actions such as checking Forth are performed afterwards, while waiting for the outstanding answers. Issue 3 arises since failures reduce the number of lifeline buddies that may re-activate a worker. Thus, the worker tends to remain inactive for a longer period of time, in which it does not contribute to task processing. This effect can be eliminated by restructuring the lifeline graph, as discussed in [12] . Lifeline graph degeneration is problematic only when multiple, or even all, lifeline buddies of a worker are affected. From our assumption of only few failures, we expect the performance impact of issue 3 to be low, and therefore have not taken any further provision. Similar to issue 3, our algorithm may send steal requests to dead victims. Again, we did not try to eliminate that, from our assumption of only few failures.
Experimental data in Section 5 show our algorithm’s efficiency during failure-free operation. Efficiency has been obtained with different algorithmic ideas. Foremost, we strive to send as few messages as possible, and to keep their volume low. We focused on communication since it is expensive in PGAS systems. The steal protocol’s concept of maintaining links instead of sending more backups to Back(T) reduces the communication volume, and requires less handshaking. Similarly, our transaction scheme reduces steal overhead, since it requires less steal backups and reduces handshaking. The consistent use of asynchronous communication often allows to continue task processing while waiting for the next message of an ongoing protocol. Finally, we took care for implementation details. For instance, we avoid copying unnecessary data in place changes, and perform local actions in an appropriate order.
5. Experiments
Experiments were conducted on an Infiniband-connected cluster with 16 nodes. Each node has two Intel Xeon E5-2680 v3 Processors as well as 64 GB of main memory. Hyperthreading was disabled. We started up to 16 places per physical node. More specifically, experiments with up to 16 places used one node, experiments with 17 to 32 places used two nodes etc. Places were mapped cyclically to nodes, to avoid quasi-simultaneous failures of a place and its Back. X10 does not optimize data access between places on the same node, such that communication costs are almost identical inside and across the nodes.
As benchmarks, we used Unbalanced Tree Search (UTS) [13] and Betweenness Centrality (BC) [14] . Both are part of the X10 distribution, and utilize the GLB framework. UTS counts the number of nodes in a highly irregular tree, and BC calculates a centrality score for each node in a graph. The benchmark versions used in this paper differ from less-efficient ones used in [5] insofar as they store open tasks in a compact format. BC includes long-running tasks. To allow their interruption by Runtime.probe(), we slightly modified the original benchmark, as described in [3] . The modification is necessary to store the result of partially finished tasks separately from the overall result. Thus it is not included in backups, as long as the task is not finished. Both benchmarks insert given tasks at the bottom of the local pool. Regarding GLB usage, the main differences between UTS and BC are:
・ BC distributes the initial work load statically, such that each worker starts with about the same number of tasks. UTS, in contrast, maps a single initial task to one worker, and relies on work stealing to distribute the load.
・ The result of UTS is a single long value, whereas the result of BC is a long-array of size N, where N is the number of nodes in the graph.
All programs were compiled and executed with X10 2.6, gcc 4.9.4 and MPI-ULFM version 1.7.
Table 4 gives an overview of the parameters used to configure the benchmarks and the GLB frameworks. GLB denotes the original GLB framework from the X10 library, and FTGLB denotes our fault-tolerant extension from Section 3. As further explained in [13] , UTS uses geometric tree shape with tree depth d, branching factor b, and a random seed r. For BC, N denotes the number of
Table 4. Parameter settings.
graph nodes, parameters a, b, c, d determine the graph shape, and s is a random seed [14] . GLB-parameter n was set to its default-value of 511. The value of k (which determines the interval for regular backups) was set to 2048 in UTS and to 32768 in BC. The choice of k will be discussed below.
Prior to the actual experiments, we determined appropriate values for the GLB-parameters w (number of random steals) and z (number of lifeline buddies per worker) by exploring the parameter space for w and z for different number of places. We found that and yield the best performance. Such experiments should be conducted prior to any GLB usage, and do not privilege our fault-tolerant extension.
Next, we measured performance with these values on 1 to 256 places. Figure 5 depicts the overhead of FTGLB’s execution time over that of GLB, calculated by . The overhead for UTS is depicted in Figure 5(a). It ranges from 0.5% to 10% on up to 64 places, and is about 30% on 128 and 256 places. The increased overhead on 128 and 256 places can be attributed to a high steal rate. On 64 places, about 33% of all backups written were found to be steal backups, on 256 places it was about 70%. This mirrors our result from [14] , where steal backups were always dominating regular backups. We will discuss a possible solution for this problem further below.
Figure 5(b) shows the overhead of BC. It ranges from 8% to 18%. The BC curve is more even than the UTS curve. We expect this to be due to static initialization, which eliminates the initial stealing phase.
Similar to w and z, the value of k should to be determined experimentally. The value corresponds to writing approximately one backup per second. An inappropriate value of k may cause significant overhead, as illustrated with the case in Figure 5(c). Experiments with and a larger number of places were not conducted due to the bad performance on up to 8 places.
In a next group of experiments, we analyzed the performance with a logging component. The generated phase diagrams for a run on 64 places (4 nodes) are depicted in Figure 6. In these diagrams, the horizontal axis represents processing time. For any time value, the height of the red bar indicates the percentage of places whose worker is processing tasks at this time. Analogously, the yellow bar represents the percentage of places whose worker is active but does
Figure 5. Performance overhead of (a) UTS, (b) BC with and (c) BC with in FTGLB compared to GLB.
not process tasks. In particular, the place may be inside the Runtime.probe() call, run incoming activities such as trySteal or give, or perform the split(), merge() and processRecorded() functions. Note that even if a Worker has no incoming messages, some portion of time is attributed to the yellow bar. In FTGLB, the yellow bar additionally comprises sending and receiving backups, calling isDead(), and checking timeouts. We decided to call this phase “Communicating”, since most of these activities are related to communication. Times spent waiting for a victim’s answer to a steal requests are depicted in blue. Note that part of the time spent waiting is used for communication and therefore attributed to the yellow bar. Idling times in inactive state are depicted in green.
For the BC runs in Figure 6(a) and Figure 6(b), it is noticeable that FTGLB has a longer finish phase than GLB, i.e., termination detection is less efficient. This can be explained by the fact that FTGLB (Figure 6(b)) has to write one backup per steal, and by the large backup volume in BC. Towards the end of the calculation, more workers run out of work and begin to steal, resulting in a large number of steal backups. GLB took 9.99 s to execute, whereas FTGLB took 11.24 s. This makes for an overhead of about 12.5%.
Figure 6. Phase diagrams for the BC benchmark with GLB and FTGLB ((a) and (b) respectively), as well as for the UTS benchmark with GLB and FTGLB ((c) and (d) respectively).
For UTS, the plots in Figure 6(c) and Figure 6(d) are similar. Execution time was 17.29 s for GLB and 19.04 s for FTGLB, which corresponds to an overhead of about 10.12%. In UTS, the result is a single long value, such that the backup volume is smaller. It can be observed that FTGLB spends more time on communication. Steal backups account for most of the communication overhead. Thus, reducing this communication by switching to another fault tolerance scheme during steal-intensive time periods can reduce the overall overhead.
A closer look at the starting phases of FTGLB for both UTS and BC executions (Figure 6(b) and Figure 6(d)) reveals that all places are either idling or communicating. The latter denotes the time spent to write the initial backup. Like result reduction, this time does not count to the program’s execution time.
It is noticeable that both BC-executions show a phase towards the end of the execution where all places are idle. This phase is actually present in all four executions (BC and UTS), but much more prominent in BC. This represents result reduction. For BC, a long-array of length N must be collected, as compared to a single long-value for UTS. The time needed for result reduction is not part of the overall computation time. For both BC executions, result reduction took about 0.3 s, whereas result reduction took about 0.04 s for the two UTS executions.
In a last group of experiments, we measured performance for the variants presented in Section 3.5. For forward-and-collect, the execution time was almost the same as that of FTGLB. Ahead-of-time-stealing had bad performance when the threshold was set to a large value. This was especially problematic for the UTS benchmark since the local pool sizes are typically small. Therefore, the parameter had to be set to a small value. With the optimum threshold value, the performance was about the same as that of FTGLB.
Summarizing experimental results, the overhead of FTGLB vs. GLB varies between 0.5% and 30%. The value increases with an application’s steal rate and backup volume.
6. Related Work
In recent years, fault tolerance received much attention [15] [16] [17] . Research addresses both permanent failures and silent errors [18] [19] .
A common fault tolerance technique is system-level checkpoint/restart. It regularly saves checkpoints, typically on disc, and upon failure resets to the last valid checkpoint. Checkpoint/restart can be combined with message logging [20] . Current research investigates improvements such as multi-level schemes [21] . Compared to our approach, checkpoint/restart has a different cost structure: Writing a single checkpoint is expensive, and the checkpointing frequency must rise with the system size to account for an increased failure rate. In our approach, backup writing is comparatively cheap, and the checkpointing frequency depends on the steal rate.
Other research considers application-level approaches. Application-level checkpointing reduces the size of the state that needs to be saved [22] [23] . Application-specific techniques include the exploitation of redundancy in matrix computations, which is often denoted as algorithm-based fault tolerance (ABFT) [24] . Application-specific approaches require a failure notification mechanism in the underlying programming system, as it is available in an increasing number of systems [6] [25] [26] . In some applications such as Monte Carlo algorithms, failures can be ignored [25] . Ali et al. [27] use redundant communication to continuously update shadow data structures. Other user-level approaches target arrays [28] as well as the MapReduce [29] and hierarchical master/worker patterns [30] . Task scheduling in grids and clouds differs from our work in coarser-grained tasks and centralization (e.g. [31] [32] ).
Previous work on resilient task pools considered recovery from silent errors [33] , and coping with side effects [34] . Closest to our work is fault-tolerance for divide-and-conquer algorithms and nested fork-join programs [35] [36] [37] . This research direction considers a different task model, in which each child task returns a result to its parent. The parent outlives the child and can therefore function as a kind of supervisor. In particular, the parent re-spawns tasks after a child’s failure. Kestor et al. [37] introduce a particularly efficient realization of this approach, which avoids re-computing grandchildren on live nodes when the child failed. Like ours, their approach can cope with multiple permanent place failures in a PGAS setting. Unlike ours, their scheme accumulates large amounts of computed information in a single location (roots of computation subtrees), whereas our scheme steadily maintains a copy of each valuable piece of information. Thus, the scheme from [37] needs to be combined with checkpointing, whereas our scheme can be used independently. Moreover, the scheme from [37] requires global failure notification, whereas our scheme gets along with local notification.
In [4] , we considered a modification of our algorithm’s previous version from [3] . The modification may further reduce the backup volume for the case that local pools are organized as stacks. In [12] , we considered an extension that supports both fault tolerance and the dynamic addition of places. The resilient A* algorithm in [38] shares some similarity with our algorithm, but in a simpler setting.
Application-level fault tolerance schemes can make use of system-level facilities for resilient storage such as X10’s Resilient Store [39] or Hazelcast’s IMap [40] . Such facilities simplify the implementation of fault-tolerance [41] , but do not support integration with the application. In particular, our approach of saving links at Back(T) requires a custom fault tolerance scheme.
7. Conclusions
This paper has introduced a fault-tolerant extension of lifeline-based global load balancing, which is able to recover from one or several permanent place failures. We combined several algorithmic ideas to achieve both robustness and efficiency. Among them are a transaction scheme for stealing, emergency mode, timeout control, and nested execution of restore protocols.
Correctness was discussed theoretically, and confirmed by experimental tests. In performance measurements, we observed an overhead between 0.5% and 30%. The particular value is application-dependent and increases with the steal rate and the backup volume. Consequently, the overhead can be reduced by switching to another resilience scheme in steal-intensive times. If recovery from a failure is not possible, the algorithm halts with an error message. Such cases are rare, as has been discussed in the paper.
The presented algorithm is tied to the lifeline scheme. Nevertheless, we expect its main ideas to be applicable to more task pool variants. In particular, the algorithm does not seem to exploit the lifeline scheme’s pattern of victim selection. Possibly, some of our ideas are also useful for other task models and non-cooperative work stealing. Similarly, silent errors are an important topic, and possibly our algorithm can be combined with replication techniques to handle both types of failures.
Our performance analysis can be further strengthened by including more benchmarks and attributing cost savings to different algorithmic ideas. Moreover, a formal verification would be desirable. Formal methods might especially help to find all cases of livelock.
Acknowledgements
This work is supported by the Deutsche Forschungsgemeinschaft, under grant FO 1035/5-1. Experiments were conducted on the Lichtenberg high performance computer of the TU Darmstadt.
Cite this paper
Fohry, C., Bungart, M. and Plock, P. (2017) Fault Tolerance for Lifeline-Based Global Load Balancing. Journal of Software Engineering and Applications, 10, 925-958. https://doi.org/10.4236/jsea.2017.1013053
References
- 1. Zhang, W., Tardieu, O., Herta, B., et al. (2014) GLB: Lifeline-Based Global Load Balancing library in X10. Proceedings of the 1st Workshop on Parallel Programming for Analytics Applications, Orlando, FL, 16 February 2014, 31-40. https://doi.org/10.1145/2567634.2567639
- 2. Guo, Y., Barik, R., Raman, R. and Sarkar, V. (2009) Work-First and Help-First Scheduling Policies for Async-Finish Task Parallelism. International Parallel and Distributed Processing Symposium (IPDPS), Rome, 25-29 May 2009, 1-12.
- 3. Fohry, C., Bungart, M. and Posner, J. (2015) Fault Tolerance Schemes for Global Load Balancing in X10. Scalable Computing: Practice and Experience, 16, 169-185.
- 4. Fohry, C., Bungart, M. and Posner, J. (2015) Towards an Efficient Fault-Tolerance Scheme for GLB. Proceedings of the ACM SIGPLAN Workshop on X10, Portland, OR, 14 June 2015, 27-32. https://doi.org/10.1145/2771774.2771779
- 5. Fohry, C. and Bungart, M. (2016) A Robust Fault Tolerance Scheme for Lifeline Based Taskpools. Proceedings of the International Conference on Parallel Processing Workshops (P2S2), Philadelphia, 16-19 August 2016, 200-209.
- 6. Bland, W. (2012) User Level Failure Mitigation in MPI. Proceedings of Euro-Par, Springer LNCS 7640, Rhodes Island, 27-31 August 2012, 499-504.
- 7. Saraswat, V., Almasi, G., Bikshandi, G., et al. (2010) The Asynchronous Partitioned Global Address Space Model. Proceedings of ACM SIGPLAN Workshop on Advances in Message Passing, Toronto, 5-10 June 2010, 1-8.
- 8. Hamouda, S.S., Herta, B., Milthorpe, J., Grove, D. and Tardieu, O. (2016) Resilient X10 over MPI User Level Failure Mitigation. Proceedings of the 6th ACM SIGPLAN Workshop on X10, Santa Barbara, CA, 14 June 2016, 19-23. https://doi.org/10.1145/2931028.2931030
- 9. Saraswat, V., Kambadur, P., Kodali, S., et al. (2011) Lifeline-Based Global Load Balancing. Proceedings of the 16th ACM Symposium on Principles and Practice of Parallel Programming, San Antonio, TX, 12-16 February 2011, 201-212. https://doi.org/10.1145/1941553.1941582
- 10. Agha, G.A. and Kim, W. (1999) Actors: A Unifying Model for Parallel and Distributed Computing. Journal of Systems Architecture, 45, 1263-1277. https://doi.org/10.1016/S1383-7621(98)00067-8
- 11. Prell, A. (2016) Embracing Explicit Communication in Work-Stealing Runtime Systems. Ph.D. Thesis, Universität Bayreuth, Bayreuth.
- 12. Bungart, M. and Fohry, C. (2017) A Malleable and Fault-Tolerant Task Pool Framework for X10. 2017 IEEE International Conference on Cluster Computing, Honolulu, HI, 5-8 September 2017. https://doi.org/10.1109/CLUSTER.2017.27
- 13. Olivier, S., Huan, J., Liu, J., et al. (2006) UTS: An Unbalanced Tree Search Benchmark. Proceedings of Workshop on Languages and Compilers for High Performance Computing, Springer LNCS 4382, New Orleans, 14-21 July 2006, 235-250.
- 14. HPCS Scalable Synthetic Compact Applications #2: Graph Analysis. http://www.graphanalysis.org/benchmark/HPCS-SSCA2_Graph-Theory_v2.0.pdf
- 15. Snir, M., Wisniewski, R.W., Abraham, J.A., et al. (2014) Addressing Failures in Exascale Computing. International Journal of High Performance Computing Applications, 28, 129-173.
- 16. Herault, T. and Robert Y. (2015) Fault-Tolerance Techniques for High-Performance Computing. Springer, Berlin. https://doi.org/10.1007/978-3-319-20943-2
- 17. Hukerikar, S. and Engelmann, C. (2017) Resilience Design Patterns: A Structured Approach to Resilience at Extreme Scale. Supercomputing Frontiers and Innovations, 4, 1-38.
- 18. Ni, X., Meneses, E., Jain, N. and Kale, L.V. (2013) ACR: Automatic Checkpoint/Restart for Soft and Hard Error Protection. Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis, Denver, CO, 17-21 November 2013, Article No. 7. https://doi.org/10.1145/2503210.2503266
- 19. Benoit, A., Cavelan, A., Cappello, F., Raghavan, P., Robert, Y. and Sun, H. (2017) Identifying the Right Replication Level to Detect and Correct Silent Errors at Scale. Proceedings of the 2017 Workshop on Fault-Tolerance for HPC at Extreme Scale (FTXS@HPDC 2017), Washington DC, 26 June 2017, 31-38. https://doi.org/10.1145/3086157.3086162
- 20. Meneses, E. (2013) Scalable Message-Logging Techniques for Effective Fault Tolerance in HPC Applications. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL.
- 21. Benoit, A., Cavelan, A., Fèvre, V.L., Robert, Y. and Sun, H. (2017) Towards Optimal Multi-Level Checkpointing. IEEE Transactions Computers, 66, 1212-1226. https://doi.org/10.1109/TC.2016.2643660
- 22. Bautista-Gomez, L., Komatitsch, D., Maruyama, N., et al. (2011) FTI: High Performance Fault Tolerance Interface for Hybrid Systems. Proceedings of 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Seattle, 12-18 November 2011, Article No. 32. https://doi.org/10.1145/2063384.2063427
- 23. Moody, A., Bronevetsky, G., Mohror, K. and de Supinski, B.R. (2010) Design, Modeling, and Evaluation of a Scalable Multi-Level Checkpointing System. SciTech Connect, 1-11. https://doi.org/10.2172/984082
- 24. Ali, N., Krishnamoorthy, S., Halappanavar, M., et al. (2013) Multi-Fault Tolerance for Cartesian Data Distributions. International Journal of Parallel Programming, 41, 469-493. https://doi.org/10.1007/s10766-012-0218-5
- 25. Cunningham, D., Grove, D., Herta, B., et al. (2014) Resilient X10: Efficient Failure-Aware Programming. Proceedings of the 19th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, 49, 67-80. https://doi.org/10.1145/2555243.2555248
- 26. Panagiotopoulou, K. and Loidl, H.-W. (2015) Towards Resilient Chapel: Design and Implementation of a Transparent Resilience Mechanism for Chapel. Proceedings of the 3rd International Conference on Exascale Applications and Software (EASC), Edinburgh, 21-23 April 2015, 86-91.
- 27. Ali, N., Krishnamoorthy, S., Govind, N. and Palmer, B. (2011) A Redundant Communication Approach to Scalable Fault Tolerance in PGAS Programming Models. 2011 19th International Euromicro Conference on Parallel, Distributed and Network-Based Processing, Ayia Napa, Cyprus, 9-11 February 2011, 24-31. https://doi.org/10.1109/PDP.2011.72
- 28. Chien, A., Balaji, P., Beckman, P., et al. (2015) Versioned Distributed Arrays for Resilience in Scientific Applications: Global View Resilience. Procedia Computer Science, 51, 29-38. https://doi.org/10.1016/j.procs.2015.05.187
- 29. Hadoop Homepage. https://hadoop.apache.org/
- 30. Bendjoudi, A., Melab, N. and Talbi, E.-G. (2014) FTH-B&B: A Fault-Tolerant Hierarchical Branch and Bound for Large Scale Unreliable Environments. IEEE Transactions on Computers, 63, 469-493.
- 31. Favarim, F., da Silva Fraga, J., Lung, L.C. and Correia, M. (2007) GRIDTS: A New Approach for Fault-Tolerant Scheduling in Grid Computing. 6th IEEE International Symposium on Network Computing and Applications, Cambridge, MA, 12-14 July 2007, 187-194. https://doi.org/10.1109/NCA.2007.27
- 32. Murray, D.G., Schwarzkopf, M., Smowton, C., et al. (2011) CIEL: A Universal Execution Engine for Distributed Data-Flow Computing. Proceedings of USENIX Conference on Networked Systems Design and Implementation, Berkeley, 30 March-1 April 2011, 113-126.
- 33. Wang, Y., Ji, W., Shi, F. and Zuo, Q. (2013) A Work-Stealing Scheduling Framework Supporting Fault Tolerance. Proceedings of Design, Automation and Test in Europe, EDA Consortium/ACM DL, Grenoble, 19-22 March 2013, 695-700.
- 34. Ma, W. and Krishnamoorthy, S. (2012) Data-Driven Fault Tolerance for Work Stealing Computations. Proceedings of the 26th ACM International Conference on Supercomputing, Venice, 25-29 June 2012, 79-90.
- 35. Blumofe, R.D. and Lisiecki, P.A. (1997) Adaptive and Reliable Parallel Computing on Networks of Workstations. Proceedings of the USENIX Annual Technical Symposium, Anaheim, 6-10 January 1997, 133-147.
- 36. Wrzesinska, G., Nieuwpoort, R.V.V., Maassen, J. and Bal, H.E. (2005) Fault-Tolerance, Malleability and Migration for Divide-and-Conquer Applications on the Grid. Proceedings of the 19th IEEE International Parallel and Distributed Processing Symposium (IPDPS), Denver, CO, April 2005.
- 37. Kestor, G., Krishnamoorthy, S. and Ma, W. (2017) Localized Fault Recovery for Nested Fork-Join Programs. 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), Orlando, FL, 29 May-2 June 2017, 397-408. https://doi.org/10.1109/IPDPS.2017.75
- 38. Kabir, U. and Goswami, D. (2015) Identifying Patterns towards Algorithm Based Fault Tolerance. In: International Conference on High Performance Computing & Simulation, Amsterdam, 20-24 July 2015, 508-516.
- 39. X10 Homepage. http://x10-lang.org/
- 40. Hazelcast Reference Manual. http://docs.hazelcast.org/docs/3.7/manual/html-single/index.html
- 41. Posner, J. and Fohry, C. A Java Task Pool Framework providing Fault Tolerant Global Load Balancing. International Journal of Networking and Computing, 8, in press.
Appendix: Nomenclature
1. General
BC Betweenness Centrality (benchmark)
FTGLB Fault-Tolerant GLB variant developed in this paper
GLB Global Load Balancing framework of X10 class library
GLB-Actor minor modification of GLB according to actor scheme
PGAS Partitioned Global Address Space (programming model)
ULFM User-Level Failure Mitigation (MPI branch)
UTS Unbalanced Tree Search (benchmark)
X10 parallel programming language
2. Places
P a place
V victim of a transaction
T thief of a transaction
Back(P) successor of P, holds P’s backup
Forth(P) predecessor of P, saves its backup on P
3. Framework Parameters
n max. number of tasks processed per main loop iteration
k number of main loop iterations between regular backups
w number of random victims
z number of lifeline buddies per worker
4. Backup-Related Messages
REG regular backup
STL steal backup
TO taken-over backup
IA inauguration backup
req backup send request
ack acknowledgement of receipt
5. Steal-Related Messages (See Figure 2 and Table 1)
trySteal, noTasks, give, victimLink, BTack, Tend, BVend, delOpen
6. Restore-Related Messages (See Figure 3 and Table 1)
deathNotice, restore, linkResolve, linkTasks, GOTcheck, GOTok, RSTack
7. Liveness-Check-Related Messages (See Table 1)
monitor, isDead(Back)
8. User-Implemented
Classes: TaskBag, Result, Queue
Methods: process, merge, split, getResult
NOTES
1This paper is an extended version of C. Fohry, M. Bungart: A Robust Fault Tolerance Scheme for Lifeline-Based Taskpools; Proc. Int. Conf. on Parallel Processing Workshops (P2S2), 2016, pp. 200-209.