ABSTRACT

A dynamically reconfigurable system can change its configuration during operation, and studies of such systems are being carried out in many fields. In particular, medical technology and aerospace engineering must ensure system safety because any defect will have serious consequences. Model checking is a method for verifying system safety. In this paper, we propose the Dynamic Linear Hybrid Automaton (DLHA) specification language and show a method to analyze reachability for a system consisting of several DLHAs.

Keywords:

Formal Method, Model Checking, Hybrid Automata, Embedded Systems, Dynamically Reconfigurable Systems

1. Introduction

Dynamically reconfigurable systems can change their configuration during operation. Such systems are being used in a number of areas [1] - [4] of an apparatus that involves human lives or expensive manufactured goods (e.g., in medical or aerospace engineering). Here, it is very important to guarantee safety. The major methods of checking system safety include simulation and testing; however, it is difficult for them to ensure safety precisely, since large systems can have infinite state spaces. In such a case, model checking that performs exhaustive searches is a more effective method.

In this paper, we propose the Dynamic Linear Hybrid Automaton (DLHA) specification language for describing dynamically reconfigurable systems and provide a reachability analysis algorithm for verifying system safety.

1.1. Our Proposal

The target of our research is an embedded system in which a CPU and dynamically reconfigurable hardware, e.g., DRP (Dynamically Reconfigurable Processor) or dynamically reconfigurable FPGA (Field-Programmable Gate Array) [5] [6] operate cooperatively. The DRP is a coarse-grained programmable processor developed by NEC Corporation [4] , and it manages both the power conservation and miniaturization. The DRP is used to accelerate the computations of a general purpose CPU through cooperative operations, and it has the following features:

・ Dynamic creation/destruction of functions: when a process occurs, the DRP constitutes a private circuit for processing it. The circuit configuration is released after the process finishes.

・ Hybrid property: the operation frequency changes whenever a context switch occurs.

・ Parallel execution: the DRP executes several processes on the same board at the same time.

・ Queue for communication: the DRP asynchronously receives processing requests from the CPU.

1.1.1. Specification

We devised the following new specification techniques for dynamically reconfigurable systems consisting of CPUs and DRPs:

・ We use linear hybrid automata [7] describing changes in the operating frequency.

・ We use linear hybrid automata that have creation/destruction events describing dynamic creations and destructions of configuration components.

・ We use FIFO queues describing asynchronous communication.

We developed a new specification language (DLHA) based on a linear hybrid automaton with both creation/destruction events and unbounded FIFO queues. DLHA is different from existing research in the following points:

・ V. Varshavsky and J. Esparza proposed the GALA (Globally Asynchronous - Locally Arbitrary) modeling approach including timed guards [8] . This approach cannot describe hybrid systems since it is the specification language based on discrete systems. Thus, GALA cannot represent changes in operating frequency.

・ S. Minami and others have specified a dynamically reconfigurable system using linear hybrid automata and have verified it by using a model checker, H YT ECH [9] . Since linear hybrid automata cannot describe changes to the configuration and asynchronous communications, the system has been specified as a static system. Therefore, the specification presented in their work is unsuitable for representing dynamically reconfigurable systems. Moreover, they verified only the schedulability property of the system, whereas we have verified several other properties in our work.

1.1.2. Verification Method

The originality of our work on the verification method is twofold:

・ Our method targets systems that dynamically change their configurations, which is something the existing work, such as H YT ECH, has studied. We extend the syntax and semantics of linear hybrid automata with special actions called creation actions and destruction actions. We define a state in which an automaton does not exist and transitions for creation and destruction.

・ Our method is a comprehensive symbolic verification for hybrid properties, FIFO queues and creation/destruction of tasks.

1.1.3. Experiments on Verifying Dynamically Reconfigurable Systems

For the experiments, we specified a dynamically reconfigurable embedded system consisting of a CPU and DRP, and verified some of its important features. This is the first time that specification and verification of dynamic changes have been tried in a practical case.

1.2. Related Work

Here, we describe related work and how it differs from our work.

・ P. C. Attie and N. A. Lynch specified systems whose components are dynamically created/destroyed by using I/O automata [10] . I/O automata cannot describe changes in variables, for example, changes in the clock and operating frequency.

・ H. Yamada and others proposed hierarchical linear hybrid automata for specifying dynamically reconfigurable systems [11] . They introduced concepts such as class, object, etc., to the specification language. However, as the scale of the system to be specified increases, the representation and method of analysis in the verification stage tend to be complex.

・ B. Boigelot and P. Godefroid specified a communication protocol in terms of finite-state machines and unbounded FIFO buffers (queues), and they verified it [12] . Since the finite-state machine also cannot describe changes in variables, it is unsuitable in our case.

・ A. Bouajjani and others proposed a reachability analysis for pushdown automata and a symbolic reachability analysis for FIFO-channel systems [13] [14] . However, since their analysis don’t provide for continuous changes in variables, in languages cannot be used for designing hybrid systems.

2. Dynamic Linear Hybrid Automaton

2.1. Preliminaries

Definition 1 (Constraint). Let V be a finite set of variables. A constraint 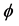on V is defined as

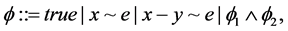
where, , 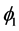and 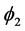are constraints on V, and. denotes the set of all constraints on V.

Definition 2 (Flow condition). Let 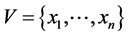be a finite set of (real-valued) variables. A flow condition f on V is defined as

where. is the set of all flow conditions.

For each variable x, we use the dotted variable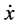, to denote the first derivative of x.

Definition 3 (Update Expression). Let V be a finite set of variables. An update expression upd on V is defined as

where and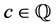. 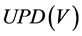is the set of all update expressions can be written.

2.2. Syntax

A dynamic linear hybrid automaton (DLHA) is a tuple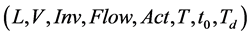, where

・ is a finite set of locations.

・ is a finite set of (real-valued) variables.

・ is a function that assigns a constraint to each location.

・ is a function that assigns a flow condition to each location.

・ is a finite set of actions.

- is a finite set of input actions, and each input action has the form. An input action denotes receiving the message m.

- is a finite set of output actions, and each output action has the form. An output action denotes sending the message m to each DLHA.

- is a finite set of internal actions that denote changing a state of a DLHA.

Moreover, we formalize the following special actions:

- A creation action that has the form or denotes a message for creation of DLHA. is an input action, and it represents that has been created. is an output action, and represents a request for creating.

- A destruction action that has the form or denotes a message for a destruction of DLHA. is an input action that indicates has been destroyed.

- An enqueue action that has the form denotes enqueueing of message m into a queue q. This action is an internal one, that is,.

- A dequeue action that has the form denotes dequeueing of message m from the top of q.

・ is a finite set of transitions. A constraint is called a guard condition.

・ is an initial transition.

・ is a finite set of destruction-transitions.

2.3. Operational Semantics

A state of a DLHA is defined as

where is a location, is an assignment called evaluation of variables, and denotes an undefined value.

We define the semantics of the DLHA by, where

・ is a set of states.

・ is a set of time transitions and discrete transitions.

・ is the initial state.

The following rules define time and discrete transitions:

Definition 4 (Time transition of a DLHA). For any,

・

・ if

where denotes an evaluation such that , and denotes that satisfies the constraint for any.

Definition 5 (Discrete transition of a DLHA). For an evaluation and update expressions, denotes an evaluation updated by, that is, for any,

・ For any transition, if and .

・ (Creation of a DLHA) For the initial transition, , where is an evaluation such that.

・ (Destruction of a DLHA) For any destruction-transition, if

For the initial transition, the initial state is defined as

3. Dynamically Reconfigurable Systems

To describe an asynchronous communication among DLHAs in a dynamically reconfigurable system (DRS), we use a queue (unbounded FIFO buffer) as a model of the communication channel. We assume that the system performs lossless transmission, so we can let the queue be unbounded.

3.1. Syntax of DRS

A dynamically reconfigurable system (DRS) is defined by a tuple consisting of a finite set of DLHAs and a finite set of queues.

3.2. Semantics of DRS

A state of a DRS is a tuple, where

・ is a vector of the states of DLHAs.

・ is a vector of the content of the queues, where each is the set of all messages that can be stored in queue.

Definition 6 (Time Transition of a DRS). For an arbitrary, the time transition is defined as

Definition 7 (Discrete Transition of a DRS). Let and be , , , and.

・ For any output action,

An output action is broadcasted to all DLHAs, and a DLHA receiving the action moves by synchronization if the guard condition holds in the state.

・ For an internal action,

- in the case of, ,

- while in the case of, ,

- otherwise, if.

A run (or path) of the system is the following finite (or infinite) sequence of states.

where between and is defined as

The initial state of a dynamically reconfigurable system is where each is the initial state of DLHA and each is empty; that is,.

Example 1 (DLHA and DRS). A DLHA is represented by a directed graph, where each node represents a location and each edge represents a transition. Figure 1 shows a dynamically reconfigurable system consisting of three DLHAs and one queue.

where

This system runs as follows:

1) requires to be created from by enqueueing a message, and it waits for the message to return from.

2) When receives the message, it creates.

3) After finishes processing the job, it sends the message to and is destroyed.

4) This system infinitely repeats steps 1) to 3).

For example, (1) shows a run of this system is shown.

(1)

4. Reachability Analysis

4.1. Reachability Problem

We define reachability and the reachability problem for a DRS as follows:

Definition 8 (Reachability). For a DRS and a location, reaches if there exists a path such that

where

Definition 9 (Reachability Problem). Given a DRS and a location, we output “yes” if can reach, and “no” otherwise.

4.2. Reachability Analysis

4.2.1. Convex Polyhedra

Our method introduces convex polyhedra for the reachability analysis in accordance with [15] .

A polyhedron is convex if it can be defined by a formula which is a conjunction of linear formulae. For a set of variables, a convex polyhedron on V is a n-dimensional real space. In particular, we define true and false as and.

Example 2 (Convex Polyhedron). The formula is a convex polyhedron. From linear formula, the existential quantifier can be eliminated effectively. Therefore, we obtain

4.2.2. Algorithm of Reachability Analysis

We define a state s in the reachability analysis as, where

・ is a finite set of locations.

・ is a convex polyhedron.

・ is a vector of the content of the queues.

Figure 2, Figure 3 and Figure 4 show the algorithm of the reachability analysis.

Figure 2 is an overview of the reachability analysis, and this algorithm is performed using the expanded method of [16] with a set of queues. The analysis is performed as follows:

1. Compute an initial state of the system (ll.1-3).

2. Initialize a traversed set and a untraversed set of states by and (line 4).

3. While is not empty, repeat the following process (ll.5-16).

(a) Take a state from and remove the state from (ll.6-7).

(b) If the set of locations contains the target location, return “yes” and terminate (ll.8-10).

(c) If the state has not been traversed yet () (line 11),

i. add the state into (line 12),

ii. compute the set of successors by using the subroutine (line 13), and

iii. add all components of to (line 14).

Subroutine Succ Figure 3 shows the subroutine to compute the successors of a state. In this algorithm, we make the following assumptions.

where

Let the initial state of be; is, where

Here, is a function that assigns a convex polyhedron to each state.

is a function that returns a convex polyhedron after performing a time transition on a given set L of locations and a convex polyhedron (line 4). We define this function in accordance with [15] as follows:

Let the set of all variables in the system and their derivatives be and.

where

For a convex polyhedron and a set of update expressions, denotes the convex polyhedron updated by for. Let the set of reset variables and set of shifted variables be and . can be computed as

where

Given a state and a system, the successors are computed using the procedure described below.

1. For each transition (or destruction-transition) outgoing from a location, the set of post states is computed as follows (ll.5-31):

(a) Compute the convex polyhedron for the time transition (line 4).

(b) If a is an internal action, is computed as follows:

i. Compute the set of locations (line 8)

ii. Compute the convex polyhedron for the discrete transition (line 9)

iii. If a is an enqueue action (ll.11-15),

where

iv. If a is a dequeue action (ll.16-20),

v. If a is another internal action (line 22),

(c) If a is an output action, is computed with the subroutine Syncs (line 26 and 29).

(d) If a is an input action,.

Subroutine Syncs Figure 4 shows the subroutine Syncs of Succ to compute successors by using the transition that has an output action. Given a state, a transition (or destruction-transition), and a system, a set of successors is computed as follows:

1. Initialize as (line 1).

2. Compute a convex polyhedron for the time transition (line 2).

3. For each in the system, compute the set of transitions that are outgoing from the state by using an input action (ll.3-5),

4. Compute the set of combinations of (line 6).

5. For each combination, the successor is computed as follows (ll.7-29):

(a) Compute the set of transitions (line 9).

(b) Compute the set of locations (ll.9-14, line 21).

where

(c) Compute the update expression (ll.9-14).

where

(d) Compute the conjunction of guard conditions (ll.9-14).

(e) Compute the convex polyhedron (ll.22-24).

where

(f) If, the successor is added to (ll.26-27).

The correctness of this algorithm is implied by Lemma 1 and Lemma 2.

Lemma 1. If the algorithm terminates and returns “is not reachable”, the system has the safety property.

Lemma 2. If this algorithm terminates and returns “is reachable”, the system does not hold the safety property.

By definition, all linear hybrid automata are DLHAs. Our system dynamically changes its structure by sending and receiving messages. However, the messages statically determine the structure, and the system is a linear hybrid automaton with a set of queues. It is basically equivalent to the reachability analysis of a linear hybrid automaton. Therefore, the reachability problem of DRSs is undecidable, and this algorithm might not terminate [16] .

Moreover, in some cases, a system will run into an abnormal state in which the length of a queue becomes infinitely long, and the verification procedure does not terminate.

5. Practical Experiment

5.1. Model Checker

We implemented a model checker of DRSs consisting of DLHAs in Java (about 1600 lines of code) by using the LAS, PPL, and QDD external libraries [12] [17] - [19] . For the verification, we input the DLHAs of the system, a monitor automaton, and the error location to the model checker, and it output “yes (reachable)” or “no (unreachable)” (Figure 5). The monitor automaton had a special location (we call it the error location), and checked the system without changing the system’s behavior [15] . The monitor automata had to be specified to reach the error location if the system didn’t satisfy the properties.

For the specification of the input model, we extended the syntax and semantics of DLHA as follows:

・ A transition between locations can have a label asap (that means “as soon as possible”). For a transition labeled asap, a time transition does not occur just before the discrete transition.

・ Each DLHA can have constraints and update expressions for the variables of another DLHA in the same system. That is, for each DLHA, invariants, guard conditions, update expressions and flow conditions can be used by all DLHAs.

For example, Figure 6 shows the input file for checking whether the system in Figure 1 reaches the location Execute.

5.2. Specification of Dynamically Reconfigurable Embedded System

5.2.1. A Cooperative System Including CPU and DRP

We have specified a dynamically reconfigurable embedded system consisting of a CPU and DRP for the model described in our previous research [9] . A DRP is a processor that can execute exclusive processes at the same time by dynamically changing the circuit configuration, and it is used to accelerate CPU computations, for example, in image processing and cipher processing. A DRP has computation resources called tiles (or processing elements), and it dynamically sets the context of a process if there are enough free tiles. In addition, a DRP can change the operating frequency in accordance with running processes. In this paper, we assume that the number of tiles and the operating frequency for each process have been set in advance and that the operating frequency of the DRP is always the minimum frequency of the running co-tasks.

Figure 7 shows an overview of the system. This system processes jobs submitted from the external environment through the cooperative operation of the CPU and DRP. The CPU Dispatcher creates a task when it receives a call message of the task from the external environment. When a task on the CPU uses the DRP, The CPU Dispatcher sends a message to the DRP Dispatcher. The DRP Dispatcher receives the message asynchronously and creates a co-task (it means “cooperative task”) in a first-come, first-served manner if there are enough free tiles. Here, we will assume that this system has two tasks and two co-tasks that have the parameters shown in Table 1 & Table 2.

The system, whose components are illustrated in Figure 8, consists of 11 DLHAs and 1 queue. We show part of the state-transition diagram in Figure 9. The external environment consists of EnvA (Figure 10) and EnvB (Figure 11) that periodically create

TaskA (Figure 12) and TaskB (Figure 13). That is, EnvA uses Crt_taskA! to create TaskA every 70 milliseconds, and EnvB uses Crt_taskB! to create TaskB with every 200 milliseconds. The Scheduler (Figure 14) performs scheduling in accordance with the priority and actions for creation and destruction of DLHAs. For example, when TaskA is created by EnvA with Crt_taskA! and TaskB is already running, The Scheduler receives Crt_taskA? from EnvA and sends Act_Preempt! to TaskA and TaskB. Then, Act_Preempt! causes TaskA to move to RunA and TaskB to move to WaitB.

TaskA and TaskB send a message to The Sender if they need a co-task. The Sender (Figure 15) enqueues the message to create a co-task to q when it receives a message from tasks. When TaskA sends Act_Create_a0! and moves to RunA from WaitA, The Sender receives Act_Create_a0? and enqueues cotask_a0 in q with q! cotask_a0.

The DRP_Dispatcher (Figure 16) dequeues a message and creates cotask_a0 (Figure 17), cotask_a1 (Figure 18), and cotask_b0 (Figure 19) if there are enough free tiles. The Frequency_Manager (Figure 20) is a module that manages the operating frequency of the DRP. When a DLHA of a co-task is created, The Frequency_Manager moves to the location that sets the frequency to the minimum value.

5.2.2. Other Cases

We have the parameters of the model in subsection 5.2.1 and conducted experiments with it.

・ Modified Tasks: We modified the parameters of the tasks on the CPU as shown in Table 3. Here, the parameters of the co-tasks are the same as those in Table 2.

・ Modified co-tasks: We modified the parameters of the co-tasks on the DRP, as shown in Table 4. The parameters of the tasks are the same as those in Table 1.

5.3. Verification Experiment

We verified that the embedded systems described in subsection 5.2 provide the following properties by using monitor automata (Figures 21-25). The verification experiment was performed on a machine with an Intel (R) Core (TM) i7-3770 (3.40 GHz) CPU and 16 GB RAM running Gentoo Linux (3.10.25-gentoo).

The experimental results shown in Table 5 indicate that the modified tasks cases and the modified co-tasks cases were verified with less computation resources (memory and time) than were used by the original model. This reduction is likely due to the following reasons:

・ Regarding the schedulability of the modified tasks model, the processing time is shorter than that of the original model since the verification terminates if a counterexample is found.

・ In the cases of the modified co-tasks, the most obvious explanation is that the state- space is smaller than that of the original model since the number of branches in the search tree (i.e. nondeterministic transitions in this system) is reduced by changing the start timings of the tasks and co-tasks with the parameters.

・ In cases other than those of the modified tasks, it is considered that the state-space is smaller than that of the original model because this system is designed to stop processing when a task exceeds its deadline.

5.3.1. Schedulability

Here, schedulability is a property in which each task of the system finishes before its deadline. Let be the total processing time and be the deadline in task A (Figure 13); the remaining processing time is represented as, and the remaining time till the deadline is represented as. Therefore, the monitor automaton moves the error location if the task A is created and it satisfies the condition (Figure 21). In the case of Table 1, since and. Similarly, the condition for task B is.

5.3.2. Creation of Co-Tasks

In the embedded system, each co-task must be created before the remaining time in the task calling it reaches its deadline. When the message is received from task A, the monitor automaton starts counting time for co-task a0. If the waiting time exceeds the deadline of task A before it receives the message, the monitor moves to error location. Figure 22 shows The monitor automaton for the case of Table 1 for co-task a0. Monitor automata for co-tasks a1 and b0 can be similarly described.

5.3.3. Destruction of Co-Tasks

Each co-task must be destroyed before the waiting time reaches its deadline. For the co-task a0, when the message is received from the dispatcher DRP_ Dispatcher, the monitor automaton checks the message. Figure 23 shows the monitor automaton for the case of Table 2.

5.3.4. Frequency Management

Creating or destroying a co-task, the DRP changes the operating frequency corresponding to the co-tasks being processed. Since this system requires that the frequency is always at the minimum value, the monitor checks whether the frequency manager (Frequency_Manager) moves to the correct location when it receives a message for creating a co-task. For example, when co-task a0 and co-task b0 are running on the DRP, Frequency_Manager must be at location. Figure 24 show the monitor automaton for the case of Table 2.

5.3.5. Tile Management

When the DRP receives a message for creating of a co-task and the number of free tiles is enough to process it, the dispatcher creates the co-task. The dispatcher then updates the number of used tiles. The monitor automaton checks whether the number tiles in DRP_Dispatcher is always between 0 and the maximum number, 8 in this case (Figure 25).

6. Conclusion and Future Work

We proposed a dynamic linear hybrid automaton (DLHA) as a specification language for dynamically reconfigurable systems. We also devised an algorithm for reachability analysis and developed a model checker for verifying the system. Our future research will focus on a more effective method of verification, for example, model checking with CEGAR (Counterexample-guided abstraction refinement) and bounded model checking based on SMT (Satisfiability modulo theories) [20] [21] .

Cite this paper

Yanase, R., Sakai, T., Sakai, M. and Yamane, S. (2016) Specification and Verification of Dynamically Reconfigurable Systems Using Dynamic Linear Hybrid Automata. Journal of Software Engineering and Applications, 9, 452- 478. http://dx.doi.org/10.4236/jsea.2016.99030

References