Journal of Modern Physics
Vol.08 No.03(2017), Article ID:74438,7 pages
10.4236/jmp.2017.83021
Accounting for Some Aspects of Dark Matter and Dark Energy via Noncommutative Geometry
Peter K. F. Kuhfittig
Department of Mathematics, Milwaukee School of Engineering, Milwaukee, WI, USA

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 25, 2016; Accepted: February 25, 2017; Published: February 28, 2017
ABSTRACT
The purpose of this paper is to seek a connection between noncommutative geometry, an offshoot of string theory, and certain aspects of dark matter and dark energy. The former case is based on a simple mathematical argument showing that the main manifestation of dark matter in connection with flat galactic rotation curves is also a consequence of noncommutative geometry. The latter case requires an examination of the local effect of noncommutative geometry and the subsequent extension to the global phenomenon of an accelerating Universe.
Keywords:
Noncommutative Geometry, Dark Matter, Dark Energy

1. Introduction
While it is generally assumed that dark matter is needed to account for galactic rotation curves in the outer region of galaxies, it has already been observed that a noncommutative-geometry background can accomplish this goal equally well [1] [2] . In the first part of this paper, we seek a mathematical explanation for this outcome: both dark matter and noncommutative geometry predict that the mass inside a sphere of radius 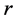 increases linearly with
increases linearly with 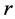 in the outward radial direction. It follows that dark matter is not needed to account for flat galactic rotation curves.
in the outward radial direction. It follows that dark matter is not needed to account for flat galactic rotation curves.
The second part of this paper makes an analogous connection between noncommutative geometry and dark energy. An analysis of the local effect of noncommutative geometry suggests an extension thereof to the global phe- nomenon of an accelerating Universe.
The main conclusion is that string theory in the form of a noncommutative- geometry background can account for certain aspects of both dark matter and dark energy.
2. Noncommutative Geometry
Suppose we start with the general metric of a static spherically symmetric line element, using units in which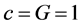 :
:
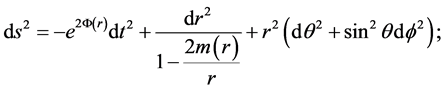 (1)
(1)
here 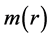 is the effective mass inside a sphere of radius
is the effective mass inside a sphere of radius 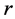 with
with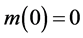 . We also require that
. We also require that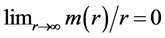 .
.
Because of the spherical symmetry, the only nonzero components of the stress-energy tensor are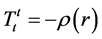 , the energy density,
, the energy density, 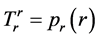 , the radial pressure, and
, the radial pressure, and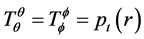 , the lateral pressure. The Einstein field equations can be written in the following form:
, the lateral pressure. The Einstein field equations can be written in the following form:
 (2)
(2)
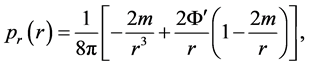 (3)
(3)
and
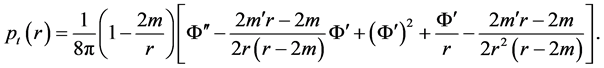 (4)
(4)
The conservation law 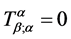 implies that
implies that
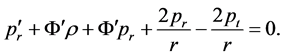 (5)
(5)
As a result, only Equations (2) and (3) are actually needed, an observation that will be taken advantage of later.
Next, we take a brief look at noncommutative geometry, an area that is based on the following outcome of string theory: coordinates may become noncommuting operators on a  -brane [3] [4] . Here the commutator is
-brane [3] [4] . Here the commutator is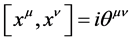 , where
, where 


The point is that the mass 

To make use of Equation (6), one can keep the standard form of the Einstein field equations in the sense that the Einstein tensor retains its original form but the stress-energy tensor is modified [7] . It follows that the length scale need not be restricted to the Planck scale. It is further noted in Ref. [7] that noncom- mutative geometry is an intrinsic property of spacetime and does not depend on any particular feature such as curvature.
The gravitational source in Equation (6) results in a smeared mass. As in Refs. [5] [6] , the Schwarzschild solution of the Einstein field equations associated with the smeared source leads to the line element

Here the smeared mass is found to be

Since

Due to the smearing, the mass of the particle depends on


So the modified Schwarzschild solution becomes an ordinary Schwarzschild solution in the limit.
3. The Dark-Matter Hypothesis
The existence of dark matter was already hypothesized in the 1930’s by Zwicky and others. The implications thereof were not recognized until the 1970’s when it was observed that galaxies exhibit flat rotation curves (constant velocities) sufficiently far from the galactic center [11] . This observation indicates that the matter in the galaxy increases linearly in the outward radial direction.
To recall the reason for this, suppose 




where 


as asserted. Equation (10) essentially characterizes the dark-matter hypothesis.
Consider next a thin spherical shell of radius

which is simply a translation in the 

Observe that, analogously,
So the mass of the shell is zero at 

Since we are moving in the outward radial direction, we can replace “mass of the shell” by “mass per unit length in the 



Either way, 


(So 
It follows that 

in agreement with Equation (10). Not only does this provide an alternative to the dark-matter hypothesis, the geometric interpretation of the gravitational pull due to dark matter is very much in the spirit of Einstein’s theory, which replaces the concept of gravitational force by the geometric concept of curvature.
Remark: It is important to note that we are examining only one aspect of dark matter, accounting for galactic rotation curves. Evidence for dark matter also comes from other sources, such as the need to explain the CMB temperature anisotropy, which is beyond the scope of this study. On the other hand, it is shown in Ref. [12] that dark matter also emerges from noncommutative geometry in a more general cosmological setting.
4. Dark Energy
A major discovery in the late 1990’s was that our Universe is undergoing an accelerated expansion [13] [14] , i.e., 

Here 



To make use of
in the cosmological model (15), we need to recall that our Universe is a 3-sphere, having neither a center nor an edge. So any point can be chosen for the origin of the above


refers to Equation (15). Equation (16) now suggests that 


where 
Recalling that

but only near the origin.
Before trying to generalize this result to a cosmological setting, let us examine 



The result can best be seen qualitatively by plotting 


Figure 1. 

before approaching zero asymptotically. The asymptotic behavior is to be expected since from a distance, the smearing is no longer apparent.
We can now assert that

in the neighborhood of every particle. Moreover, we are now in a vacuum, which is teeming with virtual particles. These particles are extremely short lived, but given that all particles have a finite lifetime, it is generally assumed that there is no absolute distinction between virtual and ordinary particles. Inequality (20) would therefore hold in the vicinity of every point. The cumulative effect would therefore be an accelerated expansion on a cosmological scale.
Inequality (20) is consistent with the discussion in Ref. [7] , which asserts that the collapse of a smeared particle to a point mass is prevented by a kind of “quantum pressure”, an outward push induced by noncommuting coordinate quantum fluctuations.
5. Conclusions
This paper discusses certain manifestations of string theory in the form of noncommutative geometry. The first part of this paper examines a particular aspect of dark matter, accounting for flat galactic rotation curves. It is shown that a noncommutative-geometry background agrees with the dark-matter assumption, whose basic manifestation is the linearly increasing mass in the outward radial direction. Connections to other aspects of dark matter, such as structure formation, are thereby left open. However, according to Ref. [12] , dark matter does emerge from noncommutative geometry in a cosmological setting; the same is true for dark energy.
The second part of this paper discusses a particular aspect of dark energy by examining the local effect of the smearing that characterizes noncommutative geometry. Since the Universe is a 3-sphere, any point can serve as the origin for

Concluding comment: accounting for both dark matter and dark energy may be considered a promissing step toward obtaining empirical evidence for string theory, given that noncommutative geometry is an offshoot thereof.
Cite this paper
Kuhfittig, P.K.F. (2017) Accounting for Some Aspects of Dark Matter and Dark Energy via Noncommutative Geometry. Journal of Modern Physics, 8, 323-329. https://doi.org/10.4236/jmp.2017.83021
References
- 1. Rahaman, F., Kuhfittig, P.K.F., Chakraborty, K., Usmani, A.A. and Ray, S. (2012) General Relativity and Gravitation, 44, 905-916.
https://doi.org/10.1007/s10714-011-1320-5 - 2. Kuhfittig, P.K.F. and Gladney, V. (2014) Journal of Modern Physics, 5, 1931-1937.
https://doi.org/10.4236/jmp.2014.517187 - 3. Witten, E. (1996) Nuclear Physics B, 460, 335-350.
https://doi.org/10.1016/0550-3213(95)00610-9 - 4. Seiberg, N. and Witten, E. (1999) Journal of High Energy Physics, 9909, Article ID: 032.
- 5. Smailagic, A. and Spallucci, E. (2003) Journal of Physics A, 36, L-467-L-471.
https://doi.org/10.1088/0305-4470/36/33/101 - 6. Smailagic, A. and Spallucci, E. (2003) Journal of Physics A, 36, L-517-L-521.
https://doi.org/10.1088/0305-4470/36/39/103 - 7. Nicolini, P., Smailagic, A. and Spallucci, E. (2006) Physics Letters B, 632, 547-551.
https://doi.org/10.1016/j.physletb.2005.11.004 - 8. Kuhfittig, P.K.F. (2013) International Journal of Pure and Applied Mathematics, 89, 401-408.
https://doi.org/10.12732/ijpam.v89i3.11 - 9. Nozari, K. and Mehdipour, S.H. (2008) Classical and Quantum Gravity, 25, Article ID: 175015.
https://doi.org/10.1088/0264-9381/25/17/175015 - 10. Kuhfittig, P.K.F. (2015) International Journal of Modern Physics D, 24, Article ID: 1550023.
https://doi.org/10.1142/S0218271815500236 - 11. Rubin, V., Thonnard, N. and Ford, W.K. (1980) Astrophysical Journal, 238, 471-487.
https://doi.org/10.1086/158003 - 12. Chamsedding, A.H., Connes, A. and Mukhanov, V. (2015) Physical Review Letters, 114, Article ID: 091302.
- 13. Riess, A.G., et al. (1998) Astronomical Journal, 116, 1009-1038.
https://doi.org/10.1086/300499 - 14. Perlmutter, S.J., et al. (1999) Astrophysical Journal, 517, 565-586.
https://doi.org/10.1086/307221 - 15. Carmeli, M. (2001) Accelerating Universe, Cosmological Constant and Dark Energy. arXiv: asro-ph/0111259.







