Journal of Modern Physics
Vol.08 No.01(2017), Article ID:73278,11 pages
10.4236/jmp.2017.81003
Hubble’s Constant and Flat Rotation Curves of Stars: Are Dark Matter and Energy Needed?
Alexandre Chaloum Elbeze
University Pierre et Marie Curie, Paris, France

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 9, 2016; Accepted: January 1, 2017; Published: January 4, 2017
ABSTRACT
Although dark energy and dark matter have not yet been detected, they are believed to comprise the majority of the universe. Observations of the flat rotation curve of galaxies may be explained by dark matter and dark energy. This article, using Newton’s laws and Einstein’s theory of gravitation, shows that it is possible to define a new term, called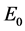 , variable in time and space, of which one of its limits is the Hubble constant
, variable in time and space, of which one of its limits is the Hubble constant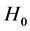 . I show that
. I show that 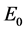 is strongly linked to an explanation of the flat rotation curve of galaxies. This strong correlation between Hubble’s constant
is strongly linked to an explanation of the flat rotation curve of galaxies. This strong correlation between Hubble’s constant  and
and  enables us to solve the mystery of the surplus of gravity that is stabilizing the universe.
enables us to solve the mystery of the surplus of gravity that is stabilizing the universe.
Keywords:
Hubble’s Law, General Relativity, Cosmological Constant, Expanding Universe, Dark Energy

1. Introduction
Galaxies appear to rotate more quickly than allowed by the gravity of its observable matter. Logically, they should have been destroyed a long time ago, as should galaxy clusters. Because of this disagreement between theory and observations, some undetectable element is believed to be providing galaxies with the additional mass that they need to avoid breaking up. This mysterious element has been called “dark matter”. Over the years, coherent theories on dark matter and dark energy have been formulated to explain the stability of galactic systems. Attempts have been made to modify Newton’s laws of gravity, for example, Milgrom’s MOND theory [1] , which explains rather well the flat rotation curves of stars for many galaxies. However, these theories have not yet offered a sufficiently well explained source; they are rather empirical theories. In this article, using Newton’s laws and Einstein’s theory of general relativity [2] , I show that a coherent theory is possible that can explain, at the same time, flat rotation curves, the expansion of the universe, and the acceleration of the expansion. I will define a new term, 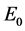 , one limit of which is the Hubble constant, and I clearly show its relationship with the flat rotation curves of galaxies. This new term
, one limit of which is the Hubble constant, and I clearly show its relationship with the flat rotation curves of galaxies. This new term  is universal because it applies without restriction to all celestial bodies.
is universal because it applies without restriction to all celestial bodies.
2. Hubble’s Constant and Defining the New Term 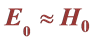
The Hubble constant 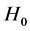 is the constant of proportionality between the distance and speed of apparent recession of galaxies relative to any point in the observable universe. It is connected to the famous Hubble’s law, which describes the expansion of the universe. Although referred to as a constant,
is the constant of proportionality between the distance and speed of apparent recession of galaxies relative to any point in the observable universe. It is connected to the famous Hubble’s law, which describes the expansion of the universe. Although referred to as a constant, 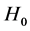 actually varies depending on time and distance. It thus describes the growth rate of the universe at one moment and at a given distance from the point of observation. The most precise value of
actually varies depending on time and distance. It thus describes the growth rate of the universe at one moment and at a given distance from the point of observation. The most precise value of  (from optical observations, May 2001) is 72 ± 8 km∙s−1∙Mpc−1.
(from optical observations, May 2001) is 72 ± 8 km∙s−1∙Mpc−1.
However, the current definition of 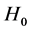 does not relate expansion of the universe to the flat rotation curves of galaxies and galaxy clusters. I must thus extend the concept of expansion of the universe to a comparison of the gravitational acceleration for small and large distances. Thus Newtonian acceleration can be written as
does not relate expansion of the universe to the flat rotation curves of galaxies and galaxy clusters. I must thus extend the concept of expansion of the universe to a comparison of the gravitational acceleration for small and large distances. Thus Newtonian acceleration can be written as  for small distances (less than kpc), and
for small distances (less than kpc), and 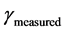 and
and 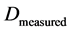 (for distances greater than kpc) are the measured acceleration and distance, respectively, between gravitationally interacting masses. We can therefore write the following relationship for a galactic system in gravitational balance:
(for distances greater than kpc) are the measured acceleration and distance, respectively, between gravitationally interacting masses. We can therefore write the following relationship for a galactic system in gravitational balance:
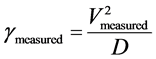 (1)
(1)
where 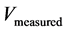 is the measured speed of rotation. Einstein’s relativity theory may also be applied to Newtonian gravitational acceleration
is the measured speed of rotation. Einstein’s relativity theory may also be applied to Newtonian gravitational acceleration 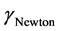 so that the masses vary as
so that the masses vary as
![]() and the distances in the moving reference frame (for the observer) shorten according to
and the distances in the moving reference frame (for the observer) shorten according to![]() . In fact, Newton’s second law in relativistic mechanics (special
. In fact, Newton’s second law in relativistic mechanics (special
relativity) may be applicable in my calculations. Here, ![]() represents the radial velocity between two gravitationally interacting objects (not to be confused with the rotation speed
represents the radial velocity between two gravitationally interacting objects (not to be confused with the rotation speed ![]() of planets, stars, galaxies, and galaxy clusters around the center of their respective system). This radial velocity
of planets, stars, galaxies, and galaxy clusters around the center of their respective system). This radial velocity ![]() can also be regarded as the recessional velocity of the object of interest (galaxies, stars, planets) similar to the relationship
can also be regarded as the recessional velocity of the object of interest (galaxies, stars, planets) similar to the relationship![]() , where
, where ![]() is the Hubble constant and D is the distance.
is the Hubble constant and D is the distance.
On the other hand, I take into account the relativistic function of acceleration ![]() developed by Elbeze [3] [4] , in which I include the recessional rate of the universe defined by function
developed by Elbeze [3] [4] , in which I include the recessional rate of the universe defined by function ![]() (added at the possible radial speed
(added at the possible radial speed![]() ), which will be defined below (and is equivalent to the Hubble expression
), which will be defined below (and is equivalent to the Hubble expression![]() ), and obtain:
), and obtain:
![]() (2)
(2)
From these relationships, I can define a rate of variation of acceleration ![]() between the Newtonian acceleration (for all distances) and the measured acceleration
between the Newtonian acceleration (for all distances) and the measured acceleration ![]() as follows:
as follows:
![]() (3)
(3)
I can compare Equation (3) with the Hubble constant ![]() as follows:
as follows:
![]() (4)
(4)
where ![]() is the equivalent of
is the equivalent of ![]() in this article, and
in this article, and ![]() is the reference radial velocity, which I will define below. By replacing accelerations
is the reference radial velocity, which I will define below. By replacing accelerations ![]() and
and ![]() with their equivalent in speed and distance in Equations (1), (2), (3), and (4), so that radial velocity is negligible in calculating the rate
with their equivalent in speed and distance in Equations (1), (2), (3), and (4), so that radial velocity is negligible in calculating the rate![]() , while applying the relativistic principle for distance and masses in radial motion (defined above and according to Newton’s second law in special relativity to a radial dimension along
, while applying the relativistic principle for distance and masses in radial motion (defined above and according to Newton’s second law in special relativity to a radial dimension along![]() ), and with
), and with
![]() , I obtain:
, I obtain:
![]() (5)
(5)
where ![]() is the recessional speed of mass M2 from mass M1 (Figure 1).
is the recessional speed of mass M2 from mass M1 (Figure 1).
Here, D is the distance between masses M1 and M2, their relative speed ![]() (radial velocity) is negligible, and
(radial velocity) is negligible, and ![]() is the measured speed of rotation of M2 around mass M1. Solving Equation (4) and Equation (5) for
is the measured speed of rotation of M2 around mass M1. Solving Equation (4) and Equation (5) for ![]() gives two universal solutions:
gives two universal solutions:
![]() (6)
(6)
We can already assume that M1 and the gravitational constant G (from equation 2) disappear from Equation (6), because they are factors in the elements ![]() com-
com-
posing it. Only speeds ![]() and
and![]() , distance D, and the reference speed V0, which will be defined low, are present in Equation (6). Thus Equation (6) is universal, independent of M1 and M2, and applies to all points in the universe with no distinctions. Let us write the recessional velocities
, distance D, and the reference speed V0, which will be defined low, are present in Equation (6). Thus Equation (6) is universal, independent of M1 and M2, and applies to all points in the universe with no distinctions. Let us write the recessional velocities ![]() and
and ![]() as follows:
as follows:
![]()
Figure 1. Measurement of the proposed recessional rate ![]() for coupled masses M1 and M2.
for coupled masses M1 and M2.
![]() (7)
(7)
3. Relationship between ![]() and
and ![]() and the Flat Rotation Curves of Galaxies
and the Flat Rotation Curves of Galaxies
One possible solution for the speed of rotation![]() , which solves Equation (6), is:
, which solves Equation (6), is:
![]() (8)
(8)
where ![]() is the acceleration of the expansion of the universe (which is here regarded as small compared with gravitational acceleration
is the acceleration of the expansion of the universe (which is here regarded as small compared with gravitational acceleration ![]() for distances < 1 Mpc); G is New- ton’s gravitational constant; Mg is the mass of the planet, star, galaxy, or galaxy cluster; D and
for distances < 1 Mpc); G is New- ton’s gravitational constant; Mg is the mass of the planet, star, galaxy, or galaxy cluster; D and ![]() are the distance and relative radial speed, respectively, between masses M1 and M2 (Figure 1);
are the distance and relative radial speed, respectively, between masses M1 and M2 (Figure 1); ![]() is the recessional velocity of the object of interest;
is the recessional velocity of the object of interest; ![]() is the atomic radius of hydrogen; and the two functions
is the atomic radius of hydrogen; and the two functions ![]() (value between 1 and 2) and
(value between 1 and 2) and![]() , which is on the order of
, which is on the order of ![]() depending on the nature of the celestial body (e.g., galaxy, star), are defined in Appendix 1 and Appendix 2, respectively. By replacing
depending on the nature of the celestial body (e.g., galaxy, star), are defined in Appendix 1 and Appendix 2, respectively. By replacing
![]() (Equation (8)) in Equation (6), the term
(Equation (8)) in Equation (6), the term ![]() from Equation (8) (which defines the Newtonian part of
from Equation (8) (which defines the Newtonian part of![]() ) disappears before the factors
) disappears before the factors![]() , so that with
, so that with
![]()
then Equation (5) becomes
![]() (9)
(9)
I can apply Equation (8) (e.g., to our galaxy) in the case of gravitational balance of the Milky Way, and assume the acceleration of the expansion of the universe to be equal to ![]() (defined low), here
(defined low), here ![]() is the acceleration in
is the acceleration in![]() , we obtain the Figures 2-4.
, we obtain the Figures 2-4.
In Figure 2, the position of our Sun is at approximately 8.2 kpc and its speed is![]() . The speed returns to its Newtonian form to 2.5 Mpc. In my calculations, only the mass of the bulb is considered; I do not take account of the mass of the galactic gas clouds, which in any case do not influence the effective existence of the flat rotation curves of the galaxy, but modify only the form of the curve speeds. I apply Equation (9) to define
. The speed returns to its Newtonian form to 2.5 Mpc. In my calculations, only the mass of the bulb is considered; I do not take account of the mass of the galactic gas clouds, which in any case do not influence the effective existence of the flat rotation curves of the galaxy, but modify only the form of the curve speeds. I apply Equation (9) to define ![]() (the proposed new expansion rate) in relation to the Hubble constant
(the proposed new expansion rate) in relation to the Hubble constant ![]() (Hubble expansion rate) (Figure 3).
(Hubble expansion rate) (Figure 3).
Figure 3 shows four terms:![]() , the proposed expansion rate
, the proposed expansion rate![]() , and the Hubble constant
, and the Hubble constant![]() . Values of
. Values of ![]() are given in units of km・s−1/Mpc; in this article,
are given in units of km・s−1/Mpc; in this article, ![]() is equal to
is equal to ![]() km・s−1/Mpc for a distance of
km・s−1/Mpc for a distance of ![]() [5]
[5]
![]()
Figure 2. Flat velocity curve of the Milky way galaxy.
![]()
Figure 3. Relationship between the Hubble constant and![]() .
.
![]()
Figure 4. Acceleration of a celestial body of mass Mg and acceleration of expansion of the universe![]() .
.
[6] , and ![]() for a large distance (
for a large distance (![]() ) is equal to
) is equal to ![]() km・s−1/Mpc. I stated the position of the Sun in the Milky Way, which is approximately equal to 8.6 pc (0.0000068 Gpc) from the galactic center, with a rotation speed of 230 km∙s−1 and an expansion rate of
km・s−1/Mpc. I stated the position of the Sun in the Milky Way, which is approximately equal to 8.6 pc (0.0000068 Gpc) from the galactic center, with a rotation speed of 230 km∙s−1 and an expansion rate of![]() .
.
In Figure 3, we can see the difference between ![]() and
and![]() . For
. For![]() , the speed
, the speed ![]() represents a straight line with a fixed slope, whereas for
represents a straight line with a fixed slope, whereas for![]() , the slope is variable all along distance D. At large distances, the expansion rate
, the slope is variable all along distance D. At large distances, the expansion rate ![]() is positive (repulsion, i.e., galaxies move apart) and tends toward the speed of light c (thus conforming to Einstein’s relativity theory); at a smaller distance it becomes negative (attraction) and almost constant, for part of the curve after the reversal since the distance
is positive (repulsion, i.e., galaxies move apart) and tends toward the speed of light c (thus conforming to Einstein’s relativity theory); at a smaller distance it becomes negative (attraction) and almost constant, for part of the curve after the reversal since the distance![]() . This part of the curve is at small distances less than
. This part of the curve is at small distances less than![]() , particularly regarding the solar system and its planets for which the expansion function
, particularly regarding the solar system and its planets for which the expansion function ![]() also applies. I can also plot the curve of the acceleration of the expansion of the universe
also applies. I can also plot the curve of the acceleration of the expansion of the universe![]() , taking the derivative of
, taking the derivative of ![]() with respect to time as
with respect to time as
![]()
where ![]() (Figure 4).
(Figure 4).
In Figure 4, we can see three areas of acceleration: a zone from 0 to 0.5 pc where there is a constant rate of negative expansion (of![]() , attraction); a zone between 0.5 pc and 2 Gpc where there is an accelerated rate of positive expansion (repulsion); and a zone between 2 Gpc and above 3 Tpc where there is a decelerated rate of expansion (always repulsive). Finally, the acceleration
, attraction); a zone between 0.5 pc and 2 Gpc where there is an accelerated rate of positive expansion (repulsion); and a zone between 2 Gpc and above 3 Tpc where there is a decelerated rate of expansion (always repulsive). Finally, the acceleration ![]() produced by the expansion of the universe is much less than the acceleration
produced by the expansion of the universe is much less than the acceleration ![]() produced by mass
produced by mass ![]() up to the value of 2.9 Mpc for the Milky Way, and is negligible for our solar system. It seems that beyond 2.9 Mpc, other celestial bodies cannot be orbiting the Milky Way!
up to the value of 2.9 Mpc for the Milky Way, and is negligible for our solar system. It seems that beyond 2.9 Mpc, other celestial bodies cannot be orbiting the Milky Way!
4. Definition of the Value of the Speed of Reference ![]() in Our Solar System
in Our Solar System
I can rewrite an approximation of Equation (8) by neglecting the acceleration of the universe for the Earth (Figure 4) and by setting ![]() as follows (here for our solar system):
as follows (here for our solar system):
![]() (10)
(10)
This reference speed V0 will be calculated at the level of our solar system. This has two principal advantages: we know the precise Earth-Sun distance, and the flat expansion velocities are relatively stable (here attractive to the Sun; see Figure 3). Using universal Equations (8), (9), and (10), which also apply to our solar system, I deduce the value of![]() , depending on the position and speed of rotation of the Earth around the Sun (
, depending on the position and speed of rotation of the Earth around the Sun (![]() and
and![]() , respectively). By comparing the value of
, respectively). By comparing the value of![]() , which is given by Equation (10), with the value in Equation (9), I get:
, which is given by Equation (10), with the value in Equation (9), I get:
![]() (11)
(11)
In this relationship the value of ![]() is obtained by replacing the value of V0 in Equation (9) by
is obtained by replacing the value of V0 in Equation (9) by![]() . Indeed, the V0 value is similar at the speed of expansion of the universe, and this fact answers the classical formula of Hubble. The function
. Indeed, the V0 value is similar at the speed of expansion of the universe, and this fact answers the classical formula of Hubble. The function ![]() is a constant dependent on the zone of space considered. For a distance D (about the distances of the solar system)
is a constant dependent on the zone of space considered. For a distance D (about the distances of the solar system)![]() . Finally, the calculation of V0 in the solar system gives
. Finally, the calculation of V0 in the solar system gives![]() . To obtain this value, I have to check the equation
. To obtain this value, I have to check the equation
![]()
where ![]() (Figure 5).
(Figure 5).
The term ![]() depends on the nature of the star, galaxy, or planet in question; here for our solar system
depends on the nature of the star, galaxy, or planet in question; here for our solar system![]() , and for the Milky Way
, and for the Milky Way ![]() . The values of n and no define the function
. The values of n and no define the function![]() . Thus, the reference speed V0 will have a value dependent on the nature of the considered system, or:
. Thus, the reference speed V0 will have a value dependent on the nature of the considered system, or:
![]() (12)
(12)
For the solar system:![]() .
.
In the Milky Way galaxy:![]() .
.
Thus, ![]() is a universal speed of reference for all gravitational systems. This value
is a universal speed of reference for all gravitational systems. This value ![]() is thus directly related to the value of the expansion rate of the universe
is thus directly related to the value of the expansion rate of the universe![]() , as well as to the flat rotation curves of galaxies. Figure 6 shows the point where the distance of the Sun from the center of the Milky Way and the ratio
, as well as to the flat rotation curves of galaxies. Figure 6 shows the point where the distance of the Sun from the center of the Milky Way and the ratio ![]()
![]()
Figure 6. Distance from Sun to center of Milky Way for![]() .
.
coincide. This equality requires the conditions ![]() and
and ![]() to the center of the Milky Way equal to
to the center of the Milky Way equal to![]() .
.
5. Conclusion
I have shown in this article that it is possible to link the concept of expansion of the universe through a new term ![]() (which is comparable to the Hubble constant
(which is comparable to the Hubble constant![]() ), and the flat rotation curves of galaxies, with one limit according to galactic mass. For the Milky Way, the limit (end of the non-Newtonian rotation curves) is around 2.9 Mpc. This is possible using both the widely accepted gravitational theories of Newton and Einstein. I suggest a solution (Equations (8) and (10)) for the expression of the flat rotation speed of galaxies (or other galactic objects) which is derived from the universal relation of expansion of the universe
), and the flat rotation curves of galaxies, with one limit according to galactic mass. For the Milky Way, the limit (end of the non-Newtonian rotation curves) is around 2.9 Mpc. This is possible using both the widely accepted gravitational theories of Newton and Einstein. I suggest a solution (Equations (8) and (10)) for the expression of the flat rotation speed of galaxies (or other galactic objects) which is derived from the universal relation of expansion of the universe ![]() (Equation (9)). This solution gives excellent results. The first and second derivatives of the value of
(Equation (9)). This solution gives excellent results. The first and second derivatives of the value of ![]() (Equation (6)) are a function of time, and show that the universe is in acceleration until about
(Equation (6)) are a function of time, and show that the universe is in acceleration until about![]() , then in deceleration until approximately
, then in deceleration until approximately![]() . This is new information about the universe. Thus, we can legitimately ask whether dark matter is necessary to explain the flat rotation curves of galaxies? And because of this accelerating expansion, could it be that dark energy does not exist? In this article, I have shown that the basic concept of the expansion of the universe also applies to the solar system like with planets and their satellites. Based on this, the Hubble constant
. This is new information about the universe. Thus, we can legitimately ask whether dark matter is necessary to explain the flat rotation curves of galaxies? And because of this accelerating expansion, could it be that dark energy does not exist? In this article, I have shown that the basic concept of the expansion of the universe also applies to the solar system like with planets and their satellites. Based on this, the Hubble constant ![]() could be measured with more accuracy. The results presented in this article may solve some current issues such as the energy density of galaxies, their masses, and may help to solve the mystery of the formation of the universe and the presence of filaments of material connecting the clusters and super clusters of galaxies of the current standard model, all without the need to involve hypothetical dark matter and dark energy.
could be measured with more accuracy. The results presented in this article may solve some current issues such as the energy density of galaxies, their masses, and may help to solve the mystery of the formation of the universe and the presence of filaments of material connecting the clusters and super clusters of galaxies of the current standard model, all without the need to involve hypothetical dark matter and dark energy.
Cite this paper
Elbeze, A.C. (2017) Hubble’s Constant and Flat Rota- tion Curves of Stars: Are Dark Matter and Energy Needed? Journal of Modern Physics, 8, 24-34. http://dx.doi.org/10.4236/jmp.2017.81003
References
- 1. Milgrom, M. (1983) Astrophysical Journal, 270, 365-370.
https://doi.org/10.1086/161130
- 2. Einstein, E. (1950) The Meaning of Relativity. Princeton University Press, Princeton.
- 3. Elbeze, A.C. (2012) Earth, Moon, and Planets, 108, 151-163.
https://doi.org/10.1007/s11038-012-9388-9
- 4. Elbeze, A.C. (2013) SpringerPlus, 2, 513.
https://doi.org/10.1186/2193-1801-2-513
- 5. Wendy, L., et al. (1994) Nature, 371, 757-762.
https://doi.org/10.1038/371757a0
- 6. Riess, A.G., et al. (2016) A 2.4% Determination of the Local Value of the Hubble Constant. arXiv:1604.01424.
- 7. Elbeze (2005) New Atomic Physics (NAP).
Appendix 1: Calculation of ![]()
Let![]() , a relative coefficient taken as a reference for our galaxy, the Milky Way. Any other object in the universe will also have a number
, a relative coefficient taken as a reference for our galaxy, the Milky Way. Any other object in the universe will also have a number ![]() that varies according to the object’s characteristics such as its mass distribution, its linear density
that varies according to the object’s characteristics such as its mass distribution, its linear density![]() , and the shape of its flat rotation curves. For the Sun
, and the shape of its flat rotation curves. For the Sun![]() . In this article, the distribution of the masses is comparable to that of a thin disk (the spherical distribution does not change the final results) of apparent mass equal to
. In this article, the distribution of the masses is comparable to that of a thin disk (the spherical distribution does not change the final results) of apparent mass equal to![]() :
:
![]() (A1.1)
(A1.1)
where D is the distance from the center of the object of interest (e.g., galaxy, star) and ![]() is the radius of the central core, where for a galactic disk such as that of the Milky Way,
is the radius of the central core, where for a galactic disk such as that of the Milky Way, ![]() is generally taken as equal to
is generally taken as equal to![]() , for the sun and the earth their radius. The density
, for the sun and the earth their radius. The density ![]() is equal to
is equal to![]() .
.
The value of ![]() is defined as
is defined as![]() , where
, where ![]() is the hidden value of the galactic mass near to its actual value for the distance
is the hidden value of the galactic mass near to its actual value for the distance ![]() being considered. Let this mass be equal to
being considered. Let this mass be equal to
![]() (A1.2)
(A1.2)
I define the coefficients ![]() as being equal to
as being equal to
![]() (A1.3)
(A1.3)
and finally obtain ![]() as a function of distance
as a function of distance![]() .
.
Appendix 2: Calculation of ![]()
In this article, the value of ![]() for our purposes is
for our purposes is
![]() (A2.1)
(A2.1)
Here, ![]() is a function of at least three parameters:
is a function of at least three parameters: ![]() is the atomic radius of hydrogen;
is the atomic radius of hydrogen; ![]() is the average atomic radius in the galaxy (or other object of interest) in terms of the orbital radius of hydrogen, where
is the average atomic radius in the galaxy (or other object of interest) in terms of the orbital radius of hydrogen, where ![]() is defined in Appendix 1; and
is defined in Appendix 1; and ![]() is the electron rest energy.
is the electron rest energy.
The relationship giving ![]() is written as follows:
is written as follows:
![]()
![]()
The value ![]() is always very small compared with
is always very small compared with ![]() and
and ![]() (proton and electron rest energy), and we can write:
(proton and electron rest energy), and we can write:
![]() (A2.2)
(A2.2)
where ![]() and
and ![]() are the electron and proton rest energies, respectively;
are the electron and proton rest energies, respectively; ![]() and
and ![]() are modified wavelengths of the electron and the proton;
are modified wavelengths of the electron and the proton; ![]()
![]() and
and![]() ,
, ![]() are the radial and volumetric interaction energy between the electron and the proton in the hydrogen atom. These values define the volume and the binding energy of the electromagnetic reaction between the electron and the proton, and
are the radial and volumetric interaction energy between the electron and the proton in the hydrogen atom. These values define the volume and the binding energy of the electromagnetic reaction between the electron and the proton, and ![]() and
and ![]() are the energy charge (similar to electric charge) of the proton and electron in the hydrogen atom as follow table:
are the energy charge (similar to electric charge) of the proton and electron in the hydrogen atom as follow table:
By using the values in table, we obtain a value for our galaxy the Milky Way of![]() . For a more detailed explanation of these values, the reader may wish to refer to the book by Elbeze [7] .
. For a more detailed explanation of these values, the reader may wish to refer to the book by Elbeze [7] .
In fact, for a first reading of this appendix, we can neglect the values of the above table and consider only the value of ![]() as being a constant of integration.
as being a constant of integration.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org




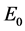 , variable in time and space, of which one of its limits is the Hubble constant
, variable in time and space, of which one of its limits is the Hubble constant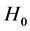 . I show that
. I show that 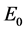 is strongly linked to an explanation of the flat rotation curve of galaxies. This strong correlation between Hubble’s constant
is strongly linked to an explanation of the flat rotation curve of galaxies. This strong correlation between Hubble’s constant  and
and  enables us to solve the mystery of the surplus of gravity that is stabilizing the universe.
enables us to solve the mystery of the surplus of gravity that is stabilizing the universe.
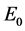 , one limit of which is the Hubble constant, and I clearly show its relationship with the flat rotation curves of galaxies. This new term
, one limit of which is the Hubble constant, and I clearly show its relationship with the flat rotation curves of galaxies. This new term  is universal because it applies without restriction to all celestial bodies.
is universal because it applies without restriction to all celestial bodies.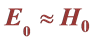
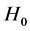 is the constant of proportionality between the distance and speed of apparent recession of galaxies relative to any point in the observable universe. It is connected to the famous Hubble’s law, which describes the expansion of the universe. Although referred to as a constant,
is the constant of proportionality between the distance and speed of apparent recession of galaxies relative to any point in the observable universe. It is connected to the famous Hubble’s law, which describes the expansion of the universe. Although referred to as a constant, 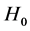 actually varies depending on time and distance. It thus describes the growth rate of the universe at one moment and at a given distance from the point of observation. The most precise value of
actually varies depending on time and distance. It thus describes the growth rate of the universe at one moment and at a given distance from the point of observation. The most precise value of  (from optical observations, May 2001) is 72 ± 8 km∙s−1∙Mpc−1.
(from optical observations, May 2001) is 72 ± 8 km∙s−1∙Mpc−1.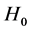 does not relate expansion of the universe to the flat rotation curves of galaxies and galaxy clusters. I must thus extend the concept of expansion of the universe to a comparison of the gravitational acceleration for small and large distances. Thus Newtonian acceleration can be written as
does not relate expansion of the universe to the flat rotation curves of galaxies and galaxy clusters. I must thus extend the concept of expansion of the universe to a comparison of the gravitational acceleration for small and large distances. Thus Newtonian acceleration can be written as  for small distances (less than kpc), and
for small distances (less than kpc), and 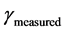 and
and 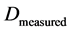 (for distances greater than kpc) are the measured acceleration and distance, respectively, between gravitationally interacting masses. We can therefore write the following relationship for a galactic system in gravitational balance:
(for distances greater than kpc) are the measured acceleration and distance, respectively, between gravitationally interacting masses. We can therefore write the following relationship for a galactic system in gravitational balance: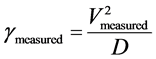 (1)
(1)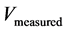 is the measured speed of rotation. Einstein’s relativity theory may also be applied to Newtonian gravitational acceleration
is the measured speed of rotation. Einstein’s relativity theory may also be applied to Newtonian gravitational acceleration 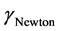 so that the masses vary as
so that the masses vary as


























































































































































































