Received 2 August 2014; revised 27 August 2014; accepted 16 September 2014

ABSTRACT

We examine the possibility of generating net forces on concave isolated objects from backgrounds consisting of randomly created waves carrying momentum. This issue is examined first for waves at the surface of a liquid, and second for quantum vacuum electromagnetic waves, both in relation with a one-side-open rectangular structure whose interior embodies a large number of parallel reflecting plates. Using known results about the Casimir-like effect and the original Casimir effect for parallel plates, we explain why and how such rectangular hollow structures should feel net oriented forces. We briefly describe real systems that would allow testing these theoretical results.

Keywords:

Casimir Effect and Analogs, Vacuum Energy, Propulsion Drive

1. Introduction

It is commonly believed that isolated objects in any background consisting of a spectrum of randomly created waves carrying momentum will not be subject to net forces due to this background. This belief rests upon the idea that such forces would then derive from a potential associated with the background energy. The energy of any isolated object in such a potential being independent of its position, no net forces should result from any configuration of the objects. The Casimir effect (see e.g. [1] ) contradicts the above naive presumption. The role played by the whole background potential of energy in this situation is similar to that of the collection of all sets in Set Theory. If this collection is considered as a set, then an intrinsic contradiction known as Cantor’s paradox follows [2] . The Casimir effect put forward that deriving forces from an energy potential can be inappropriate. General Relativity shows that the energy-momentum tensor has a more direct physical meaning than the one of a potential where just differences of energy matter. In this theory the curvature of space-time describes the energy content, and the absolute amount of energy has a meaning. Energy density curves space-time and an increase in the energy density causes an increase of its curvature (see e.g. [3] ).

In the original Casimir effect two ideal rigid conducting and uncharged parallel plates attract each other due to the quantum vacuum energy spectrum of the electromagnetic radiation at zero temperature. The effect results from an imbalance of the radiation forces on the inside and the outside surfaces of the plates, which both equal infinity. The plates discretize the spectrum of electromagnetic waves between and transverse to the plates. In the region between the plates the energy density is smaller than outside the plates, which causes the imbalance of the radiation forces. The net force is then proportional to the difference in the local energy density. Using a regularization procedure needed to evaluate the above indeterminate form, one can show that the force of attraction between the plates is inversely proportional to the fourth power of their separation distance [4] .

The Casimir effect is not restricted to the electromagnetic radiation of quantum vacuum. Casimir-like effects also exist. Here likeness means that the force between bodies results from a wave background different from that of the electromagnetic radiation of quantum vacuum. Such Casimir-like effects have been treated theoretically and observed experimentally for liquid surface waves [5] , and many other oscillating systems [6] -[8] . As for the original Casimir effect, the behavior in these naturally or artificially driven-wave systems can be seen as ensuing from an imbalance of radiation forces. It is observed that the analogy of the driven systems to the one of the original Casimir effect is not exact. First, the waves being driven in the Casimir-like systems, the energy densities of the wave spectra are not infinite, and therefore no regularization is required. Next, the behavior of the forces between the bodies is usually specific to the Casimir-like effect considered. For instance, in the case of liquid surface waves, the attractive force between the plates is independent of their separation distance and is proportional to the mean-square amplitude of the waves [5] .

In this paper, we shall consider the action of two different wave backgrounds on concave structures made up of many parallel and equally spaced plates. In each region between two adjacent plates the energy density is lower than the one outside the whole structure of plates. We are interested in the possibility of transforming this difference of energy density into a kinetic energy applying to the whole structure. The first wave background examined is that of liquid surface waves. The concave structure considered will then consist of many partly submerged parallel plates floating perpendicularly to the liquid surface and whose form seen from top would look like a comb. The second wave background will be that of the original Casimir effect. In this case, the concave structure will have the form of a rectangular parallelepiped made up of many parallel conducting plates, with one of its faces open showing one edge of each of its interior parallel plates. For other approaches to the project of extracting energy through the Casimir effect, see e.g. [9] -[12] .

2. Waves between Parallel Plates

Consider two flat and square plates of macroscopic area a² facing each other at a distance apart. We assume that the plates lie in a wave background where waves are randomly created with different frequencies. For liquid surface waves the frequencies are in a finite spectrum band. In this case the plates are assumed to reflect the totality of waves, of which amplitude is assumed to be sufficiently small for the geometric wave theory to apply. For the original Casimir effect, the wave-frequencies are in an infinite band. The plates are then assumed to be perfectly reflecting up to some frequency, and perfectly transparent for higher frequencies. In practice, 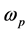can be identified with the plasma frequency of the plate material [13] .

Let us examine the collective behavior of a set of waves first between two infinite-size square plates a relatively short distance apart. We start with a single wave between the plates. Because of the boundary conditions imposed by the plates, this wave can effectively be created only if its half-wavelength fits a whole number of times into the distance b between the plates. Due to interference, a plurality of waves of the same wavelength but with different phases will gradually cancel out each other while moving between the plates. Therefore, only in-phase waves having as wavelength an integer divisor of 2b can exist between the two parallel plates. We now consider the set of in-phase waves characterized by a same wavelength which is an integer divisor of 2b. Using the Huygens-Fresnel principle, it is straightforward to show that between the plates these waves will form a wavefront moving perpendicularly to the plates [13] . The different sets of in-phase waves will thus manifest themselves as different sets of wavefronts, each one characterized by a specific wavelength.

We now determine what happens in the case of finite-size square plates. For the original Casimir effect, it can be shown that taking into account the edges of the two identical plates results into a slight increase of the effective area of the plates [14] . In the simplified theoretical model below for the original Casimir effect, we shall use the exact area of the plates with the consequence of slightly underestimate the considered force. For the Casimir- like effect caused by the waves at the surface of a liquid, we shall assume that the plate edges play the role of scatterers through which the waves created outside the space between the plates but in a position to reach their edges mostly undergo elastic isotropic diffuse reflections, a small part being transmitted through the plates. This last part is assumed to be dissipated by internal losses of various kinds. Principal among the mechanisms responsible for these losses are viscosity, thermal conduction, and energy interchange between plate molecules and atoms with differing external excitations. Because of the isotropic scattering by the plate edges, about half of the waves they re-emit will be in the spaces between the parallel plates. But due to the boundary conditions imposed by the plates, only the waves with wavelength equal to an integer divisor of 2b can effectively form there. Since there exists a smallest wavelength in the wave background in the case of Casimir-like effects, the preceding observations lead to the conclusion that the wave motion between the two finite-size plates must be negligible compared with the wave motion in its complementary region. This substantial reduction in wave motion between the plates has indeed been observed experimentally, as well as the ensuing attraction between the plates [5] . In the theoretical model below for the liquid surface waves, we shall assume that there is strictly no wave motion between the parallel plates of finite size.

3. Liquid Surface Waves Interacting with a Structure of Reflecting Fins

Consider two rigid square plates of area a² kept at a small distance b apart by an a × b rigid plate of the same material as for the square plates. Seen from top this structure would have the shape of a long square subset sign. The structure is partially but deeply submerged in a liquid whose surface is disturbed by waves of small amplitude, which are everywhere created with frequencies randomly selected within a limited band. The origin of the waves could be natural or artificial. Since both gravity and surface tension of the liquid contribute to the restoring force, these driven oscillations of the liquid surface are sometimes called deep gravity-capillary waves. The aim of the deep placement is twofold. First, it is to prevent the wave motion from passing under the structure and into the region between the plates. We thus assume that the plates are sufficiently deep so that they are subject to essentially all of the wave motion. Second, it is to increase the viscous damping in order to reduce the motion of the structure due to fluctuations of random waves. In practice, the distance of separation b is chosen so that the waves motion between the parallel plates is negligible compared with the one outside the square subset sign structure.

The asymmetry of the four lateral sides of the square subset sign structure causes an imbalance in the momentum it receives in the direction going through its open face and its opposite closed one. We have seen that almost all momentum of the waves created outside the structure with the possibility of propagating into the region between the square plates undergoes elastic isotropic diffuse reflections by the free edge of each plate cutting the liquid surface, a small part being absorbed by the structure. However, the waves created outside the square subset sign structure which meet its opposite closed face are reflected by it. It thus follows a net force acting on the structure in the sense going from its closed face toward its opposite open one. This force results from the asymmetry due to the concavity of the square subset sign structure.

The value of the above force can be estimated directly from [5] . To see this, we first observe that the value F_r of the force due to the difference in the local energy density related to the liquid surface waves on the two sides of one of two parallel square and perfectly reflective plates of area a² at a distance b apart, when they are free to move, is

,

where g is the acceleration due to gravity, 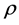is the liquid density, A_rms is the root-mean-square of the wave amplitude and a must be interpreted as the plate width [5] . If the face was perfectly absorbing instead of being perfectly reflecting, then the value of the force would be equal to half of.

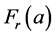We now consider a device D made up of N side-by-side square subset sign structures, N being such that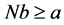. The width of the open face of D on which the force acts is then equal to Nb. It follows that D undergoes a net force whose direction goes from its closed face toward its opposite open one, and its value is given by

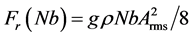. (1)

By keeping the distance b at the value which minimizes the wave motion between the parallel plates of D, and by increasing the number N of adjacent square subset sign structures, (1) shows that it would be possible, in principle, to generate an oriented net force having a value as large as one wishes.

In the above model, if the structure of parallel plates is first held fixed with respect to an observer and then released, it would in principle undergo a sustained acceleration. But this acceleration will fade out in practice. Indeed, as the structure of parallel plates moves with its open side ahead, the level of liquid between the plates and in front of its open side rises, becoming higher than elsewhere on the liquid surface. Combined with its friction with the liquid, this local accumulation of liquid will exert an extra force opposed to the structure movement, which in turn will gradually reduce the acceleration, until it completely disappears. The speed of the structure will then reach a constant value. This value is non-zero because otherwise the structure will undergo a new acceleration due to the appearance of a new difference in the local energy density between its inside and its outside regions. The movement of the structure generates waves on the liquid surface whose total energy compensates in part to the hollow of energy existing between the parallel plates. In principle, such a device should allow to extract a part of the surface wave energy.

To illustrate the above situation, let us use the physical characteristics of the experiment described in [5] . We thus assume that the liquid on which the waves are created is ethyl alcohol (ρ = 0.791 g/cm³), and that its root- mean-square surface vertical displacement is A_rms = 0.1 cm. According to (1), the net force starting value for a structure with b = 1.7 cm and N = 6 is approximately 9.9 dynes.

4. Background of Electromagnetic Waves on a Parallelepiped of Conducting Plates

We are now interested in the interaction of the quantum vacuum electromagnetic waves with a rectangular one-side-open parallelepiped P made up of N + 1 identical conducting uncharged parallel square plates of area a² kept at a same small distance b apart by three a × Nb rectangular plates of the same material as the square plates. One face of P is open toward its interior showing one edge of each square plate and the whole structure is electrically continuous. The local energy density of the quantum vacuum background of electromagnetic waves throughout the region between these square plates is lower than the one outside P. The electromagnetic waves stemming from the quantum vacuum which are created outside P and reach its open side, or the exterior closed face opposite to the open side, are respectively absorbed and reflected. A net force results from this difference of momentum on the two sides of this face of P.

Let us determine the value of the above net force. First, we know that the value of the force due to the difference in the local energy density related to the background of quantum vacuum electromagnetic waves on the two sides of one of two free to move parallel square and perfectly reflective plates of sides a, when they are at a distance b apart, is given by (see e.g. [1] )

, (2)

where h is Planck’s constant, c is the speed of light in vacuum and 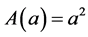is the area of each plate. Between each pair of facing parallel square plates of P the local density of energy is equal to that existing between two identical parallel square plates kept at distance b apart. Assuming that N is such that, then we can apply (2) to the face of P opposite to its open one. The total area of the region making up the far end interior side of P being Nab, the value of the force on P due to the reflection of quantum vacuum electromagnetic waves created outside P and arriving on the same area of the corresponding exterior side is given by

.

The value of the force on P due to the absorption by P of the electromagnetic waves created outside P and incident on its open face equals half of. Therefore, the net force acting on P will be in the direction going from the closed face opposite to its open one toward the latter, and its value will be

. (3)

Equation (3) shows that by increasing N it is possible, in principle, to generate an oriented net force having a value as large as wanted.

If the parallelepiped P is first held fixed with respect to an observer and then released, it would in principle undergo a sustained acceleration. But, similar to the model with liquid surface waves this acceleration will fade out in practice. Indeed, the movement of P deforms inward the regions of lower energy density between its parallel plates, because some electromagnetic waves created outside P then enter between the plates. The faster P goes, the more marked becomes the deformation. Consequently, the quantity of negative energy between the plates gradually decreases until the acceleration of P reduces to zero. The speed of P then stabilizes at a constant value. This value is non-zero because otherwise the structure would undergo a new acceleration due to a new difference in the local energy density between its inside and its outside regions. The value of this constant speed will be proportional to the depth a of the inter-plate spaces between the open and opposite closed faces of P.

The above device seems to allow the extraction of a part of the quantum vacuum electromagnetic wave energy. Let us illustrate this by assuming that the number of spaces between facing square plates is such that Nb = a, where b is sufficiently small to generate a noticeable attracting force between two adjacent parallel plates. The corresponding value of (3) is

. (4)

Hence, for a cube consisting of 5000 parallel square plates of sides a = 1 cm, of thickness τ = 10⁻⁴ cm, and at distance b = 10⁻⁴ cm apart, (4) yields a net force of 6.5 × 10⁻³ dyne as starting value.

5. Conclusion and Discussion

We have shown that in a background of randomly created waves a structure with a rectangular concave interior embodying parallel reflecting plates can be subject to net forces. This possibility has been put forward in two cases. The first one is related to a background of waves at the surface of a liquid which partially submerged the structure of reflecting plates. The second one involves a one-side-open parallelepiped of ideal parallel conducting plates in the background of quantum vacuum electromagnetic waves. The fact that a net force results from the latter concave configuration may be related to a similar theoretical outcome, which follows from calculations of the energy-momentum tensor expectation value due to the curvature of a perfectly conducting boundary [15] [16] . For each of our settings, we have proposed a real system that could be tested experimentally. These results show that it is, in principle, possible to propel a ship on the sea, or a spaceship into outer space, using devices made up of a large number of reflecting parallel plates. This kind of propulsion is much more effective than the dynamic Casimir effect described in [17] , where the spaceship is accelerated through the reaction of the electromagnetic radiation emitted when an uncharged mirror is properly accelerated in the quantum vacuum.

Let us now discuss the meaning of the very existence of such a net force acting on an isolated object in a background of randomly created waves. This violates the ordinary principle of conservation of energy-momen- tum. As shown by the Casimir effect, the level of energy of the background must not necessarily be referred to a potential of energy. Physically realistic phenomena related to the energy background of quantum field theory actually fail to satisfy various local energy conditions [18] . The present paper shows that it seems possible to extract energy from some wave backgrounds. For the naturally or artificially generated waves at the surface of a liquid, the energy extracted would come from what generates these waves. For the electromagnetic waves associated with the quantum vacuum, the energy extracted can be seen as originating from the curvature of space- time, which then would become less curved locally. In this perspective, an extended principle of conservation of energy-momentum could be applied to a delimited region of space-time. Similar situations are already known in General Relativity where, for instance, particular metrics describe a contraction of space-time in front of a spaceship in order to carry it at a speed that could be, non-locally, faster than light (see e.g. [19] ).

Within General Relativity, the original Casimir effect means that no electromagnetic vacuum state associated with two separated neutral and conducting plates corresponds to a stable space-time. The net forces put forward in this paper in relation first with a Casimir-like effect, and second with the original Casimir effect show that the backgrounds of the energy density of these settings are also unstable in the sense that they allow energy of these backgrounds to be transferred to a body in the form of kinetic energy.

Acknowledgements

The author is grateful to Normand Beaudoin, Roby Gauthier, Pierre Gravel and Doris LaChance for interesting discussions and useful comments.

References