Journal of Modern Physics
Vol.5 No.3(2014), Article ID:43125,5 pages DOI:10.4236/jmp.2014.53018
Cluster Model of Formation of Subnuclear and Subatomic Objects
Russian Federal Nuclear Center, All-Russia Research Institute of Experimental Physics, Sarov, Russia
Email: postmaster@ifv.vniief.ru, e.e.lin@ifv.vniief.ru
Copyright © 2014 E. E. Lin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property E. E. Lin. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 17, 2013; revised November 23, 2013; accepted December 21, 2013
Keywords: Cluster Model; Kinetics of Formation; Objects; Subnuclear/Nuclear Matter
ABSTRACT
The paper describes the development results on one-dimensional (1D) asymptotic model of the formation kinetics for the objects (clusters) of subnuclear (quark) and subatomic (nuclear) matters. A concept of the objects distribution density wave φ(a, t) in space of sizes a lies in the basis for analytical description of the processes under consideration. The proposed formalism makes it possible to describe in an adequate way the final outcomes of the well-known catastrophic phenomena in the world of elementary particles. Mass characteristics of different processes of approach to equilibrium in nuclear reactions are calculated.
1. Introduction
Different analytical and numerical methods are used to study the mechanism of reaching the equilibrium in nuclear processes (e.g., see [1-4]). Such investigations are based on the model concepts of the nature of nuclear matter and the dynamics of the processes under consideration. Work [5] describes an attempt to look at intranuclear phenomena from the unified point of view, treating them as processes of formation and growth of compact objects (clusters) with distinct collective quantum properties (strong interaction) in a closed stochastic system of nucleons oscillating around local positions of equilibrium. The closed system in question can be either a parent nucleus or two nuclei in contact after their colliding (a double system). At the initial moment of time, this system contains seeds of nuclear matter: alpha-particles and (or) their fragments — tritons and deuterons. The random interaction of these seeds results in their coalescence, and compact nuclear matter clusters are formed in the system. It is assumed that, as in the case of the growth processes of nanocrystals with strong interatomic bonds [6], oscillations of nucleons on the surface of contacting nuclear clusters with temporarily (virtually) broken external bonds can lead to the mutual compensation of these unused bonds. As a result, consolidation of adjacent clusters takes place and larger objects of nuclear medium with different masses are formed. Due to Coulomb repulsion, these objects can escape from the area of interaction. Values of most propable mass numbers of clusters-nuclides calculated in [5] correspond to the wellknown data for such processes of approach to equilibrium as cluster radioactivity, deep inelastic interaction of heavy ions, spontaneous nuclear fission and synthesis of superheavy elements in stars.
The aims of this work are as follows: 1) verification of the proposed cluster model using the example of hard collision processes of elementary particles and formation of stable hadron jets [7]; 2) consideration of the nuclide “stability islands” problem [8] on the basis of cluster model [5]; 3) determining average mass numbers of nuclei formed in the processes of spontaneous fission and nucleosynthesis in stars.
2. Analytical Approach
A concept of the objects distribution density wave φ(a, t) in space of sizes a lies in the basis of analytical method for describing the processes under consideration [5,6]. This 1D approach makes it possible to neglect deviations of the object geometric shape from the spherical one. An evolution of the wave φ(a, t) during the stochastic process of the objects aggregation can be described in the diffusion approximation with the help of Fokker-Planck kinetic equation written for the space of clusters sizes a (where t is time):
 (1)
(1)
Here, 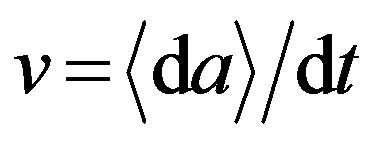 and
and  are the average rate of kinematic transfer of φ and the diffusion coefficient in the space a, respectively; m is the cluster mass; and
are the average rate of kinematic transfer of φ and the diffusion coefficient in the space a, respectively; m is the cluster mass; and 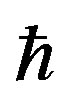 is the reduced Planck constant. The carried out study of the asymptotic properties of function φ(a, t) showed that in the end of the irreversible aggregation of objects as a result of interaction of large clusters with small seeds in a stochastic conservative system the distribution density of large clusters with a ? a0 (a0 is a size of a seed) is inversely proportional to their masses: j µ m–1 (an “inverse-mass” law) [6].
is the reduced Planck constant. The carried out study of the asymptotic properties of function φ(a, t) showed that in the end of the irreversible aggregation of objects as a result of interaction of large clusters with small seeds in a stochastic conservative system the distribution density of large clusters with a ? a0 (a0 is a size of a seed) is inversely proportional to their masses: j µ m–1 (an “inverse-mass” law) [6].
We define two mechanisms of growth of nuclear matter clusters: 1) the small flux of seeds, when each of them has time to occupy its place on the surface of the cluster before starting interaction with the next seed; 2) the high flux of seeds, when they affect the cluster almost simultaneously (equivalent to collision of clusters). Linearization of Equation (1) makes it possible to produce analytical expressions for increase in the mean size 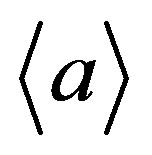 of large clusters (a ? a0) with time [6]. In case of the first growth mechanism the approximate law of increasing the average size of clusters can takes the following form
of large clusters (a ? a0) with time [6]. In case of the first growth mechanism the approximate law of increasing the average size of clusters can takes the following form
 . (2)
. (2)
Here, t1 is the unit of time in the processes with small flux of seeds, t0 is a typical time scale of objects interaction, m0 is the seed mass. The second mechanism has a typical time scale equal to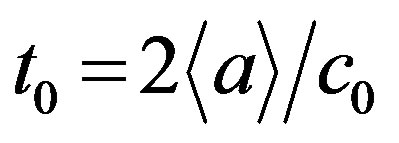 , where c0 = 5 × 107 m·s–1 is the “sound” velocity or average nucleon thermal velocity determined by the average thermal energy of the degenerate Fermi gas (22 MeV per nucleon [8,9]). Then, the law of increasing the average size can be written as
, where c0 = 5 × 107 m·s–1 is the “sound” velocity or average nucleon thermal velocity determined by the average thermal energy of the degenerate Fermi gas (22 MeV per nucleon [8,9]). Then, the law of increasing the average size can be written as
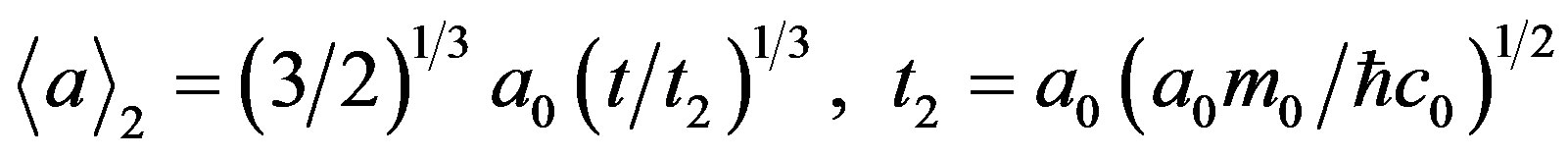 . (3)
. (3)
Here, t2 is a unit of time in the processes with a large flow of seeds.
The size of a spherical nucleus is related with mass number A in the following way [8,9]:
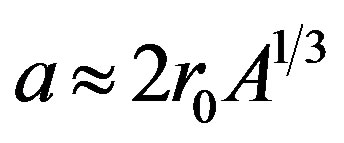 . (4)
. (4)
Here, r0 = 1.3 fm is a typical space scale of strong interaction. The total time of the process is determined by the Heisenberg rule basing on the level of shell energy: [10]. It is correct for isolated excitation of level in the quantum system.
The following formula can be written for the most probable mass numbers of cluster-nuclides [5]:
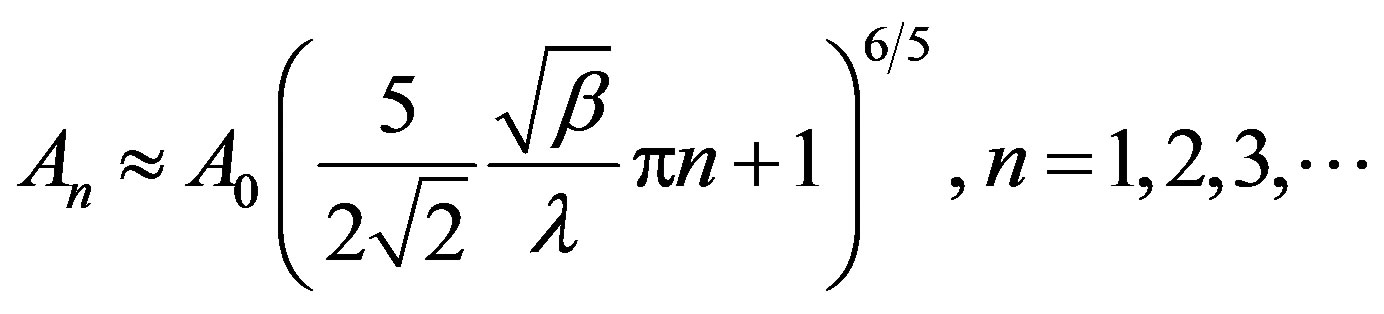 . (5)
. (5)
Here, A0 is the mass number of the seed; λ > 1 is an arbitrary real number; and small parameter  is defined by seed mass m0 and size a0, and by the characteristic time scale t0 of the objects interaction. A reasonable choice for this scale is the period of high-frequency nucleon oscillations in the nucleus. This parameter can be defined as t0 = 2r0/c0 » 5 × 10–23 s. The approximate quantity λ is found by matching the solutions for the first maximum of j, which corresponds to the seeds, and the maximum of j for small clusters [6]. The calculations yield
is defined by seed mass m0 and size a0, and by the characteristic time scale t0 of the objects interaction. A reasonable choice for this scale is the period of high-frequency nucleon oscillations in the nucleus. This parameter can be defined as t0 = 2r0/c0 » 5 × 10–23 s. The approximate quantity λ is found by matching the solutions for the first maximum of j, which corresponds to the seeds, and the maximum of j for small clusters [6]. The calculations yield .
.
3. Subnuclear Processes
Verification of the suggested formalism can be performed using the example of catastrophic (deeply inelastic) processes with hadrons [7,11]. One can consider these processes as the following chain of events: head-on collisions of “lepton-nucleon” or “nucleon-nucleon” ® the quark is split from the gluon cloud ® random interactions in the continuous intrahadron medium ® formation of new particles (hadron jets). New particles are considered as clusters containing the elements of a continuous intrahadron medium (partons): quarks, gluons, quark-antiquark pairs, and so on. Then the law of evolution of the mean cluster size (3) gives the following relation between the units of length aunit, time tunit and mass munit at deep inelastic interaction of fundamental particles:
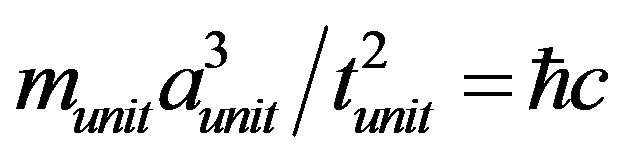 (6)
(6)
Here, c is maximum velocity of interaction propagation in hadron medium, namely, the velocity of light in vacuum. On the basis of this formula and other known data [7,11,12] for “conventional” quark masses (uand dquarks) deep inside hadrons and for typical space scales, it is possible to get the following evaluation of a time unit  for current quarks (cq) in the state of asymptotic freedom (af):
for current quarks (cq) in the state of asymptotic freedom (af):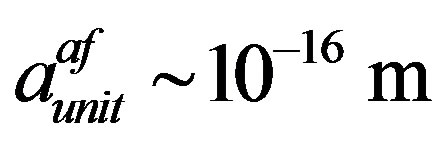 ,
, 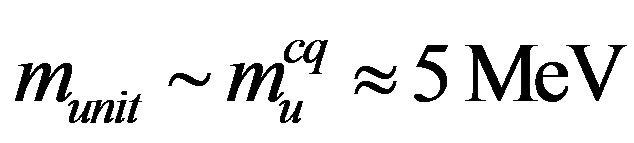 ,
, 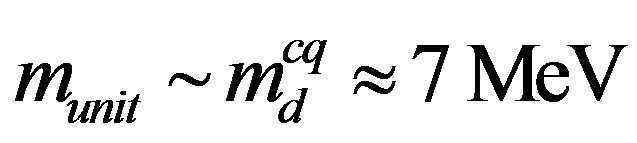 Þ
Þ . Transition time ttrans for quarks from asymptotic freedom to constrained state (confinement) inside the hadron is estimated by formula (3) as
. Transition time ttrans for quarks from asymptotic freedom to constrained state (confinement) inside the hadron is estimated by formula (3) as 
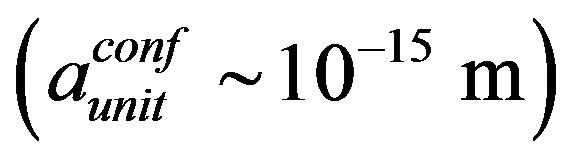 . The produced value corresponds to the time scale of strong interaction.
. The produced value corresponds to the time scale of strong interaction.
In the processes considered in [7], the minimum value of the length unit is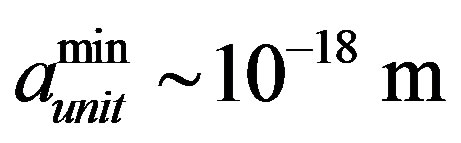 . It can be taken as a top estimation of the current quark size. Then, from the relation (6) we get that
. It can be taken as a top estimation of the current quark size. Then, from the relation (6) we get that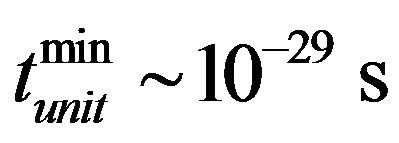 , and the time
, and the time  of hadron formation with mean size
of hadron formation with mean size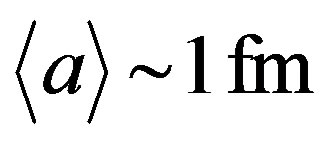 , in compliance with formula (3), makes
, in compliance with formula (3), makes
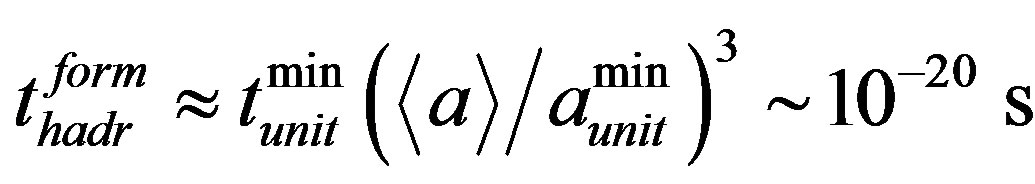 .
.
The produced value is much higher than the life time of unstable hadrons (resonances)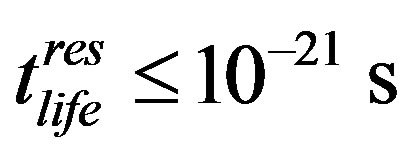 :
: . This reflects the formation of stable hadron jets in the processes of catastrophic collisions being described. If we take, in compliance with the results of [13], that the velocity of excitation propagation in quark-gluon medium is equal to the sound velocities cs = 0.3c and 0.57c, then multipliers 1.8 and 1.3 will appear in the evaluations given above for time units, the time of quark transition into the bound state, and the time of hadron formation. These corrections will not change the estimation of time scale for strong interaction and will make stronger inequality
. This reflects the formation of stable hadron jets in the processes of catastrophic collisions being described. If we take, in compliance with the results of [13], that the velocity of excitation propagation in quark-gluon medium is equal to the sound velocities cs = 0.3c and 0.57c, then multipliers 1.8 and 1.3 will appear in the evaluations given above for time units, the time of quark transition into the bound state, and the time of hadron formation. These corrections will not change the estimation of time scale for strong interaction and will make stronger inequality  that reflects the formation of stable hadron jets.
that reflects the formation of stable hadron jets.
Asymptotic distribution j µ m–1 means that: 1) the probability of nucleon fragmentation under deep inelastic scattering is higher than the chance of its preservation; 2) the number of pions in hadron jet is 1.5 times higher that the number of nucleons. These conclusions correspond to the notions on the nature of hard processes given in [7]. In particular, the following reaction takes place at frontal collision of protons: pp ® p0p+p+nn. One can see that there are 3 pions and 2 neutrons in the formed hadron jet.
Thus, the proposed formalism provides adequate determination of asymptotic states reached at well-known catastrophic phenomena in the world of subnuclear objects, namely, fundamental and elementary particles. This gives us a reason for making an attempt to apply this formalism for considering the intranuclear processes mentioned in the Section 1.
4. Processes in Nuclear Scales
The values A calculated in [5] correspond to the mass numbers of the nuclides and their isotopes over the currently known range, including the transfermium elements. In this paper we regard the problem of “stability islands” of nuclides [8,14]. As an example the element roentgenium with Z = 111 has the mass number of A = 273 [8]. In the proposed model, this value of A obtained from formula (5) corresponds to tritons as the seeds. At Z = 114, in compliance with 2β-stability, the number of neutrons is equal to 184 and the mass number is equal to A = 298 [14]. In our model, the mass numbers closed to it are 299 and 302. These values obtained from the formula (5) correspond to tritons and deuterons as the seeds, respectively. Work [15], which is dedicated to the production and the decay of element 114, mentions its isotopes with A = 288 and 289. In the model, the values A = 290 and 293 are the closest mass numbers corresponded to the tritons and deuterons as the seeds, respectively. Using various calculation options of the β-stability band the islands of stability are predicted also at Z = 164 and with neutron numbers of 272 or 318 [14]. Respective mass numbers A = 436 and 482 are closed to the approximate value of the mass number of the final nuclide Aend » 470 calculated in [5]. In the model, mass number A = 436 corresponds to deuterons as the seeds. The closest to the mass number of 482 are the following values calculated with the help of formula (5): A = 483 for the tritons as the seeds, and A = 485 for deuterons as the seeds. Thus, one can presume that the developed asymptotic model of clusters formation in the nuclear matter complements the method for predicting nuclear mass with the help of radial basis function [4], which makes it possible to find mass numbers in the range from 20 to 260.
One can rewrite expressions (2) and (3) in the following way more convenient for calculations:
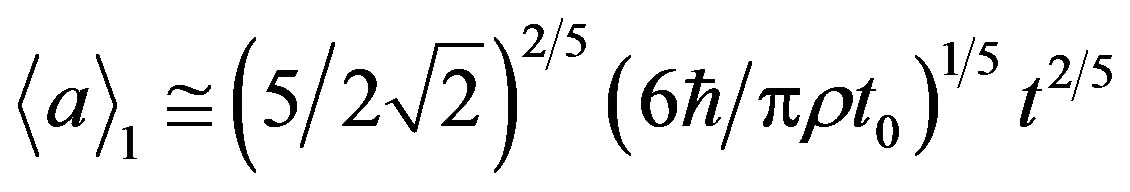 . (7)
. (7)
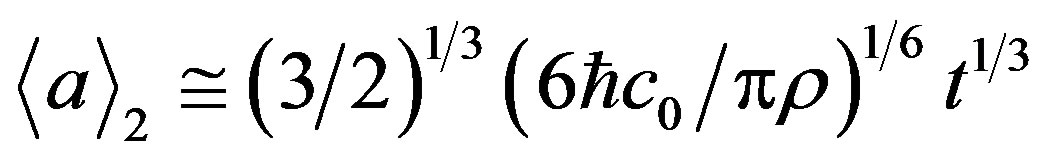 . (8)
. (8)
Here, r is the density of nuclear matter taken as equal to r = 2.5 × 1017 kg·m–3 [5]. In order to eliminate parameter a0 from the formulas it was taken that the mass of the seed is equal to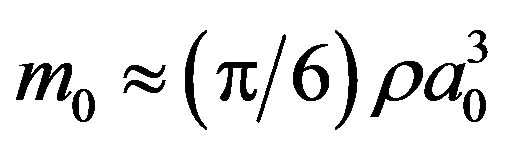 .
.
One can try to describe spontaneous nuclear fission as a result of excitation of the first rotational level with energy Grot = 100 keV using formulas (4) and (8). The total time of the intranuclear process that corresponds to the specified value of Grot is equal to trot = 6.287 × 10–21 s, and the average mass number of light fragments is evaluated to be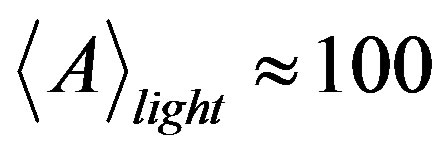 . Average mass number of heavy fragments
. Average mass number of heavy fragments 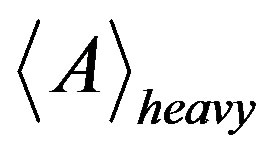 is determined by the mass conservation law
is determined by the mass conservation law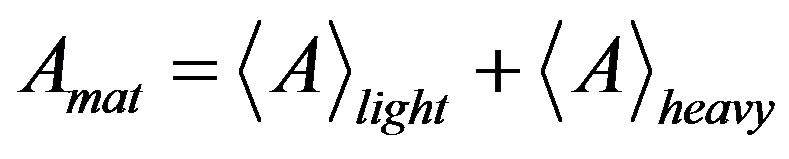 , Amat is the mass number of parent nucleus. In case of light actinides (Th, U) we get
, Amat is the mass number of parent nucleus. In case of light actinides (Th, U) we get . The diagrams of mass distribution for the fragments of spontaneous fission of heavy nuclei (A = 235, 238) given in [16] show that the average mass number of lighter fragments is 90 - 100, and the average mass number of heavier fragments is about 140.
. The diagrams of mass distribution for the fragments of spontaneous fission of heavy nuclei (A = 235, 238) given in [16] show that the average mass number of lighter fragments is 90 - 100, and the average mass number of heavier fragments is about 140.
If we presume that high-speed nucleosynthesis in stars takes placed as a result of transition of the system of nucleons from the high-frequency vibration level with the period of t0 = 2r0/c0 » 5 × 10−23 s to the first rotational level with the energy of 100 keV during the life time trot = 6.287 × 10−21 s of this level, then formulas (4) and (7) give the evaluation of the average mass number of superheavy elements as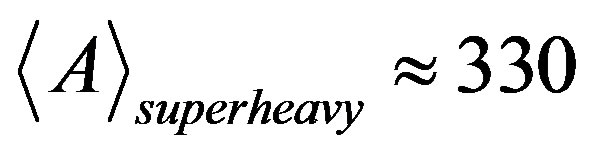 . As for the forced fission competed with the nucleosynthesis, in this case it is possible to take the travel time t = a/c0 of the sound wave in the nucleus formed as a result of nucleosynthesis as a time scale t0. With regard to formula (4) when
. As for the forced fission competed with the nucleosynthesis, in this case it is possible to take the travel time t = a/c0 of the sound wave in the nucleus formed as a result of nucleosynthesis as a time scale t0. With regard to formula (4) when  we get t0 = 3.6 × 10−22 s. Then from the formulae (4) and (7) we get that, when the lifetime of the first rotational level is 6.287 × 10−21 s, the average mass number of light fragments of superheavy elements is about
we get t0 = 3.6 × 10−22 s. Then from the formulae (4) and (7) we get that, when the lifetime of the first rotational level is 6.287 × 10−21 s, the average mass number of light fragments of superheavy elements is about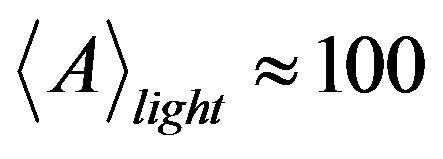 . In compliance with the mass conservation law the average mass number of heavy fragments is equal to
. In compliance with the mass conservation law the average mass number of heavy fragments is equal to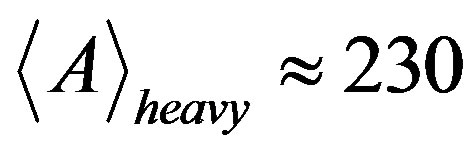 . The produced values approximately agree with the first and the last peaks of the final element abundance in the Galaxy [2]. This agreement gives the credibility to the above-given evaluation of the average mass number of superheavy elements, which can be formed as a result of nucleosynthesis in supernovae and neutron stars.
. The produced values approximately agree with the first and the last peaks of the final element abundance in the Galaxy [2]. This agreement gives the credibility to the above-given evaluation of the average mass number of superheavy elements, which can be formed as a result of nucleosynthesis in supernovae and neutron stars.
5. Discussion of Results
The proposed model corresponds to the problem of motion of 1D wave packet j(a, t) in the space a [6]. The group velocity 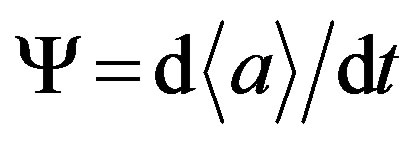 goes down with time:
goes down with time:
 .
.
This circumstance reflects the expansion of wave packet and the slower-down of its propagation. At the final stage of irreversible aggregation of clusters in the closed system this wave packet with non-Gaussian shape has an attenuating discontinuity in the wave “front” related to the maximum possible size of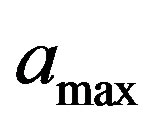 :
:
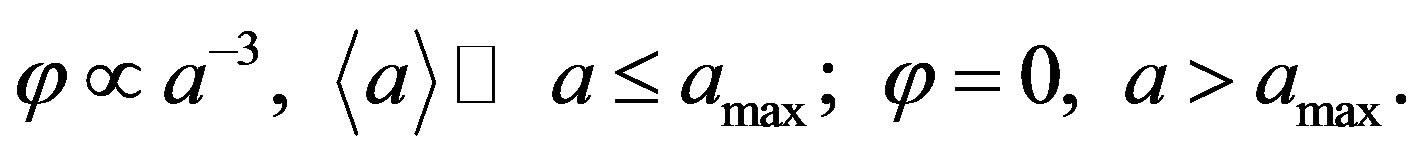
The presented results and notions allow us to make a conclusion that the developed in [6] asymptotic method for describing the formation of clusters under consideration has sufficiently general character to be implemented in respective problems of high-energy physics.
In Section 3 it was found that the least value of time unit in quark-gluon medium is 10−29 s, and the unit of time for current quarks in the state of asymptotic freedom is 10−26 s. Using relation (6) one can get the following evaluation of the unit of time in the interaction processes with constituent quarks in confinement state described in [11,12]: ,
, 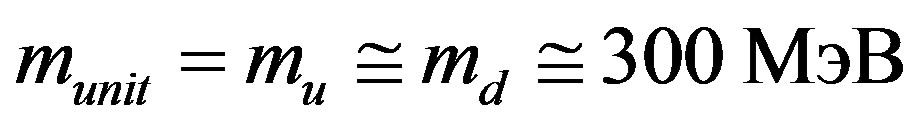 Þ
Þ
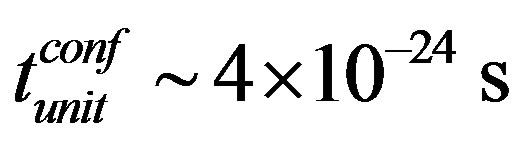 . The transfer time from asymptotic freedom to confinement is evaluated in Section 3 as
. The transfer time from asymptotic freedom to confinement is evaluated in Section 3 as 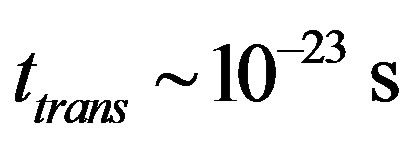 that agrees with the time scale of strong interaction, and the formation time of stable hadrons is estimated as
that agrees with the time scale of strong interaction, and the formation time of stable hadrons is estimated as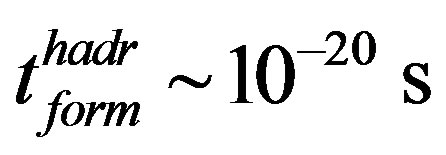 . Relation (6) shows that the processes in the world of fundamental and elementary particles are characterized with the spectrum of time units. Close to the upper boundary this spectrum overlaps with the “lower” area of times t = 10−23 - 10−22 s which are typical for direct nuclear reactions. Thus, formula (6), which shows that “regular” space-and-time relations are valid up to the distances of about 10−18 - 10−15 m and time of 10−29 - 10−26 s, complies with the generally accepted notions about space-and-time scales in microphysics [17].
. Relation (6) shows that the processes in the world of fundamental and elementary particles are characterized with the spectrum of time units. Close to the upper boundary this spectrum overlaps with the “lower” area of times t = 10−23 - 10−22 s which are typical for direct nuclear reactions. Thus, formula (6), which shows that “regular” space-and-time relations are valid up to the distances of about 10−18 - 10−15 m and time of 10−29 - 10−26 s, complies with the generally accepted notions about space-and-time scales in microphysics [17].
We can try to determine the value of phenomenological “fundamental mass” of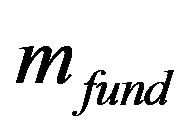 , if we take that the least space unit (a fundamental length) is the value of afund ~ 10−18 m and that this value is connected with the fundamental time scale tfund by the reasonable relation
, if we take that the least space unit (a fundamental length) is the value of afund ~ 10−18 m and that this value is connected with the fundamental time scale tfund by the reasonable relation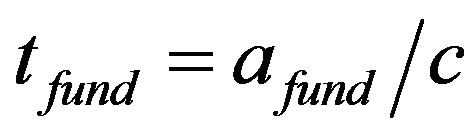 . Then, from relation (6) we get the following expression for the fundamental mass:
. Then, from relation (6) we get the following expression for the fundamental mass: . Then we get that
. Then we get that  [6]. The produced value lies within the supposed experimental range specified in [8], where mass
[6]. The produced value lies within the supposed experimental range specified in [8], where mass 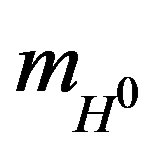 of the neutral Higgs boson H0 should be:
of the neutral Higgs boson H0 should be: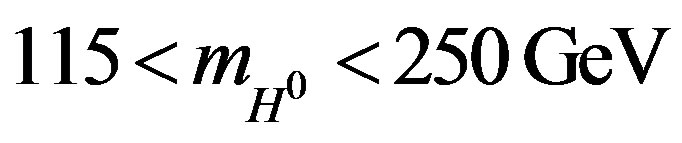 . Besides, this value is closed to the “critical” mass of 180 - 200 GeV, above which H0-boson can decay into the pairs of Wand Z-bosons [18]. The reason of the obtained agreement is in the fact that the proposed model of formation of “quantum” clusters is scalar and does not contain such parameters of spins and of electric charges, and, therefore, it can be applied to the scalar neutral boson H0 with the zero spin. It is also important to mark approximate correspondence of obtained evaluation for
. Besides, this value is closed to the “critical” mass of 180 - 200 GeV, above which H0-boson can decay into the pairs of Wand Z-bosons [18]. The reason of the obtained agreement is in the fact that the proposed model of formation of “quantum” clusters is scalar and does not contain such parameters of spins and of electric charges, and, therefore, it can be applied to the scalar neutral boson H0 with the zero spin. It is also important to mark approximate correspondence of obtained evaluation for 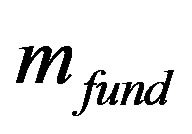 to the value of the upper limit of the Higgs mass identified in [19] as 170 GeV.
to the value of the upper limit of the Higgs mass identified in [19] as 170 GeV.
It could be interesting to carry out a qualitative analysis of various processes with fundamental and elementary particles with the help of relation (6). For example, we could try to estimate the state of the heaviest of all quarks — t-quark (tq), which has a conventional mass of 176 GeV [12]. One can get from relation (6) that the minimum time unit for t-quark, when having the size , is
, is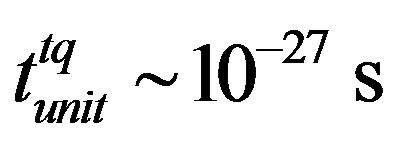 . Then, as it comes from formula (3), the time
. Then, as it comes from formula (3), the time 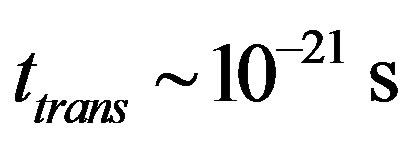 would be required to form bounded states with a characteristic size of about 10−15 m. The produced evaluation complies with the life time of unstable resonances, therefore, t-quark does not form the stable hadron. This result complies with the common notion, according to which a t-quark is the “only quark that is ‘born and dies free’” [12].
would be required to form bounded states with a characteristic size of about 10−15 m. The produced evaluation complies with the life time of unstable resonances, therefore, t-quark does not form the stable hadron. This result complies with the common notion, according to which a t-quark is the “only quark that is ‘born and dies free’” [12].
In the area of nuclear scales the suggested method allows to evaluate the time of approach to equilibrium basing on the typical mass numbers and respective nuclide sizes. This problem was solved in [20] with regard to the research on the kinetics of deep-inelastic interaction between the beam of copper ions and the gold target at the collision energy of 365 MeV [9]. It was shown that the formation time for the interaction products with the average mass numbers  and 100, typical for the process under consideration, is about of 10−20 s. The produced value is much less than the lifetimes of 10−16 - 10−14 s which are typical for the intermediate compound nucleus. This makes it possible to speak about comparatively quick (explosion) character of the process of deep inelastic heavy-ions interaction.
and 100, typical for the process under consideration, is about of 10−20 s. The produced value is much less than the lifetimes of 10−16 - 10−14 s which are typical for the intermediate compound nucleus. This makes it possible to speak about comparatively quick (explosion) character of the process of deep inelastic heavy-ions interaction.
6. Conclusion
The developed cluster model makes it possible to produce adequate evaluations of space-and-time and mass characteristics for the processes in the subnuclear (quark) matter and for the intranuclear processes of approach to equilibrium.
REFERENCES
- S. G. Kadmenskii, S. D. Kurgalin and Yu. M. Tchuvil’sky, Physics of Particles and Nuclei, Vol. 38, 2012, pp. 699-742. http://dx.doi.org/10.1134/S1063779607060019
- V. I. Panov, I. Yu. Korneev and F.-K. Thielemann, Physics of Atomic Nuclei, Vol. 72, 2009, pp. 1026-1033. http://dx.doi.org/10.1134/S1063778809060155
- P. Wagner and Y. M. Zhong, Nuclear Physics A, Vol. A592, 1995, pp. 385-412.
- N. Wang and M. Liu, Physical Review C, Vol. 84, 2011, Article ID: 051303.
- E. E. Lin, Bulletin of the Russian Academy of Sciences Physics, Vol. 76, 2012, pp. 881-883. http://dx.doi.org/10.3103/S1062873812080199
- E. E. Lin, “Qualitative Kinetic Models of Formation of Compact Objects with Strong Internal Bonds,” RFNCVNIIEF, Sarov, 2011 (in Russian).
- M. Jacob and P. Landshoff, Scientific American, Vol. 242, 1982, pp. 66-75. http://dx.doi.org/10.1038/scientificamerican0380-66
- B. S. Ishanov, I. M. Kapitonov and N. P. Yudin, “Particles and Atomic Nuclei,” LKI, Moscow, 2007 (in Russian).
- L. Valentin, “Physique Subatomique: Noyaux et Particles,” Nouvelle Édition Entièrement Refondue, Hermann, Paris, 1982.
- V. S. Olkhovscii, Soviet Journal of Particles and Nuclei, Vol. 15, 1984, pp. 130-148.
- G. Kane, “Modern Elementary Particle Physics,” Addison-Wesley, Boston, 1987
- L. B. Okun, Physics Uspekhi, Vol. 41, 1998, pp. 553-557. http://dx.doi.org/10.1070/PU1998v041n06ABEH000403
- R. B. Neufeld and B. Mueller, Physical Review Letters, Vol. 103, 2009, pp. 04301-04304. http://dx.doi.org/10.1103/PhysRevLett.103.042301
- I. P. Selinov, “Atomic Nuclei: Structure and Systematic,” Nauka, Moscow, 1990 (in Russian).
- Ch. E. Düllmann, M. Schädell and A. Yakushev, Physical Review Letters, Vol. 104, 2010, pp. 252701-252705. http://dx.doi.org/10.1103/PhysRevLett.104.252701
- A. I. Obukhov and I. S. Grigor’ev, “Fission of Nuclei,” In: I. S. Grigor’ev and E. Z. Meilikhov, Eds., Physical Quantities Handbook, Energoatomizdat, Moscow, 1991, pp. 1087- 1098 (in Russian).
- V. L. Ginzburg, Physics Uspekhi, Vol. 42, 1999, pp. 353- 373. http://dx.doi.org/10.1070/PU1999v042n04ABEH000562
- L. B. Okun, “Particle Physics: The Guest for the Substance of Substance,” Hardwood Academic Publishers, Newark, 1985.
- S. Khalil and S. Moretti, Journal of Modern Physics, Vol. 4, 2013, pp. 7-10. http://dx.doi.org/10.4236/jmp.2013.41002
- E. E. Lin, Technical Physics Letters, Vol. 19, 1993, pp. 669-670.

