Applied Mathematics
Vol. 4 No. 4 (2013) , Article ID: 30359 , 9 pages DOI:10.4236/am.2013.44084
Ant Colony Optimization Approach Based Genetic Algorithms for Multiobjective Optimal Power Flow Problem under Fuzziness
1Department of Mathematics and Statistics, Faculty of Sciences, Taif University, Taif, KSA
2Physics and Engineering Mathematics Department, Faculty of Engineering, Tanta University, Tanta, Egypt
3Department of Basic Engineering Science, Faculty of Engineering, Menoufia University, Shibin Al Kawm, Egypt
Email: a_mousa15@yahoo.com, galal5968@yahoo.com
Copyright © 2013 Abd Allah A. Galal et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 2, 2013; revised February 2, 2013; accepted February 9, 2013
Keywords: Ant Colony; Genetic Algorithm; Fuzzy Numbers; Optimal Power Flow
ABSTRACT
In this paper, a new optimization system based genetic algorithm is presented. Our approach integrates the merits of both ant colony optimization and genetic algorithm and it has two characteristic features. Firstly, since there is instabilities in the global market, implications of global financial crisis and the rapid fluctuations of prices, a fuzzy representation of the optimal power flow problem has been defined, where the input data involve many parameters whose possible values may be assigned by the expert. Secondly, by enhancing ant colony optimization through genetic algorithm, a strong robustness and more effectively algorithm was created. Also, stable Pareto set of solutions has been detected, where in a practical sense only Pareto optimal solutions that are stable are of interest since there are always uncertainties associated with efficiency data. The results on the standard IEEE systems demonstrate the capabilities of the proposed approach to generate true and well-distributed Pareto optimal nondominated solutions of the multiobjective OPF.
1. Introduction
The OPF optimizes a power system operating objective function (such as the operating cost of thermal resources) while satisfying a set of system operating constraints, including constraints dictated by the electric network. OPF has been widely used in power system operation and planning. In its most general formulation, the OPF is a non-linear, non-convex, large-scale, static optimization problem with both continuous and discrete control variables. Even in the absence of non-convex unit operating cost functions, unit prohibited operating zones, and discrete control variables, the OPF problem is nonconvex due to the existence of the nonlinear (AC) power flow equality constraints. The presence of discrete control variables, such as switchable shunt devices, transformer tap positions, and phase shifters, further complicates the problem solution [1-3]. Since there is instabilities in the global market, implications of global financial crisis and the rapid fluctuations of prices, for this reasons a fuzzy representation of the multiobjective optimal power flow has been defined, where the input data involve many parameters whose possible values may be assigned by the experts. In practice, it is natural to consider that the possible values of these parameters as fuzzy numerical data which can be represented by means of fuzzy subsets of the real line known as fuzzy numbers. Mathematical programming approaches, such as nonlinear programming, quadratic programming and linear programming, have been used for the solution of the OPF problem [4,5]. Unfortunately, the OPF problem is a highly nonlinear and a multimodal optimization problem. Therefore, conventional optimization methods that makes use of derivatives and gradients, in general, not able to locate or identify the global optimum. On the other hand, many mathematical assumptions such as analytic and differential objective functions have to be given to simplify the problem. Furthermore, this approach does not give any information regarding the trade-offs involved.
The development of meta-heuristic optimization theory has been flourishing. Many meta-heuristic paradigms such as genetic algorithm, simulated annealing, and tabu search have shown their efficacy in solving computationally intensive problems [6-9]. The studies on heuristic algorithms over the past few years have shown that these methods can be efficiently used to eliminate most of difficulties of classical methods. Since they are populationbased techniques, multiple Pareto-optimal solutions can, in principle, be found in one single run.
Recently, to meet the ever increasing demands in the design problems, a new evolutionary algorithm called ant colony optimization algorithm have all been used successfully to mimic the corresponding natural, or physical, or social phenomena [10-12]. Ant colony optimization (ACO) is a metaheuristic inspired by the shortest path searching behavior of various ant species. Since the initial work of Dorigo, Maniezzo, and Colorni on the first ACO algorithm, the ant system [13], several researchers have designed ACO algorithms to deal with multiobjective problems. The set of solutions achieved by a multiobjective evolutionary algorithm is required to satisfy both convergence and diversity criteria [14].
This paper intends to present a new hybrid algorithm for solving optimal power flow under fuzziness. The proposed approach integrates the merits of both ACO and GA and it has two characteristic features. Firstly, a fuzzy representation of the optimal power flow problem has been defined. Secondly, by enhancing ACO through GA, a strong robustness and more effectively algorithm was created. Several optimization runs of the proposed approach will be carry out on the standard IEEE systems to verify the validity of the proposed approach.
This paper is organized as follows. In Section 2, MOO is described. Section 3, provides a multiobjective formulation of EELD Problem. In Section 5, the proposed algorithm is presented. Implementation of the proposed approach is presented in Section 6. Results are given in Section 6. Finally, Sections 7 and 8 gives a brief discussion and conclusion about this study.
2. Defination of Multiobjective Optimization
A multiobjective Optimization Problem (MOP) can be defined as determining a vector of design variables within a feasible region to minimize a vector of objective functions that usually conflict with each other. Such a problem takes the form:
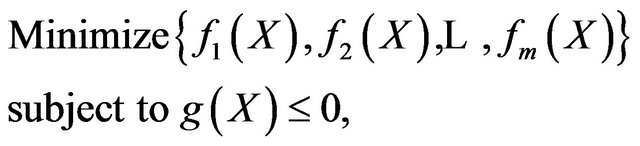
where X is vector of decision variables; 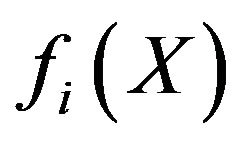 is the ith objective function; and
is the ith objective function; and 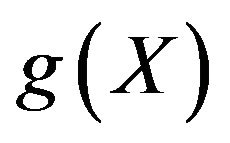 is constraint vector. A decision vector X is said to dominate a decision vector Y (also written as
is constraint vector. A decision vector X is said to dominate a decision vector Y (also written as ) iff:
) iff:
 for all
for all 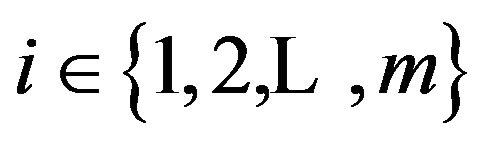 and
and  for at least one
for at least one 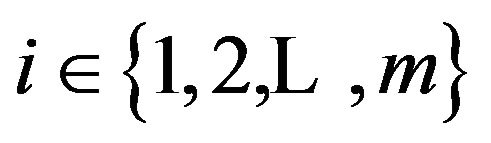
All decision vectors that are not dominated by any other decision vector are called nondominated or Paretooptimal. These are solutions for which no objective can be improved without detracting from at least one other objective.
3. Multiobjective Formulation of EELD Problem
The economic emission load dispatch involves the simultaneous optimization of fuel cost and emission objectives which are conflicting ones. The deterministic problem is formulated as described below.
Fuel Cost Objective. The classical economic dispatch problem of finding the optimal combination of power generation, which minimizes the total fuel cost while satisfying the total required demand can be mathematically stated as follows:

where C: total fuel cost ;
;
Ci: is fuel cost of generator i;
 : fuel cost coefficients of generator i;
: fuel cost coefficients of generator i;
 : power generated (p.u) by generator i;
: power generated (p.u) by generator i;
n: number of generator.
Emission Objective. The emission function can be presented as the sum of all types of emission considered, such as NOx, SO2, thermal emission, etc., with suitable pricing or weighting on each pollutant emitted. In the present study, only one type of emission NOx is taken into account without loss of generality. The amount of NOx emission is given as a function of generator output, that is, the sum of a quadratic and exponential function:
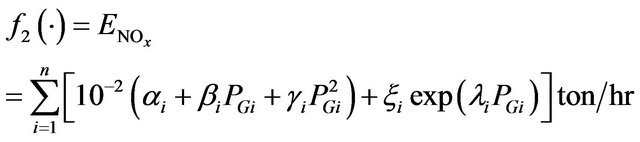
where,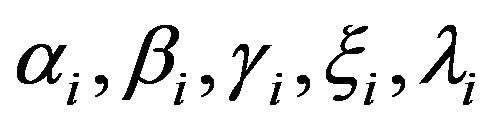 : coefficients of the ith generator’s NOx emission characteristic.
: coefficients of the ith generator’s NOx emission characteristic.
Constraints: The optimization problem is bounded by the following constraints:
Power balance constraint. The total power generated must supply the total load demand and the transmission losses.
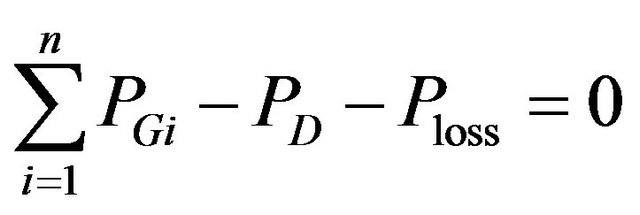
where : total load demand (p.u.), and
: total load demand (p.u.), and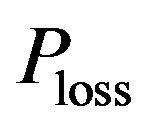 : transmission losses (p.u.).
: transmission losses (p.u.).
The transmission losses are given by [15]:
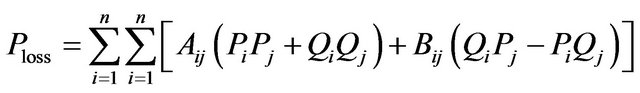
where
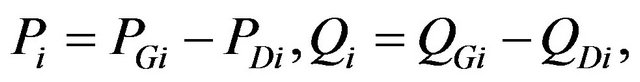
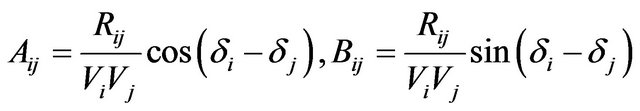
![]() : number of buses;
: number of buses;
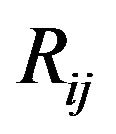 : series resistance connecting buses i and j;
: series resistance connecting buses i and j;
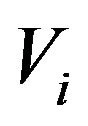 : voltage magnitude at bus i;
: voltage magnitude at bus i;
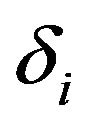 : voltage angle at bus i;
: voltage angle at bus i;
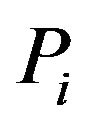 : real power injection at bus i;
: real power injection at bus i;
 : reactive power injection at bus i.
: reactive power injection at bus i.
• Maximum and Minimum Limits of Power Generation. The power generated 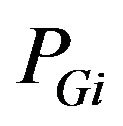 by each generator is constrained between its minimum and maximum limits, i.e.,
by each generator is constrained between its minimum and maximum limits, i.e.,

where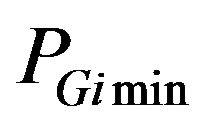 : minimum power generated, and
: minimum power generated, and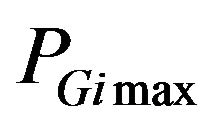 : maximum power generated.
: maximum power generated.
• Security Constraints. A mathematical formulation of the security constrained EELD problem would require a very large number of constraints to be considered. However, for typical systems the large proportion of lines has a rather small possibility of becoming overloaded. The EELD problem should consider only the small proportion of lines in violation, or near violation of their respective security limits which are identified as the critical lines. We consider only the critical lines that are binding in the optimal solution. The detection of the critical lines is assumed done by the experiences of the decision maker DM. An improvement in the security can be obtained by minimizing the following objective function.
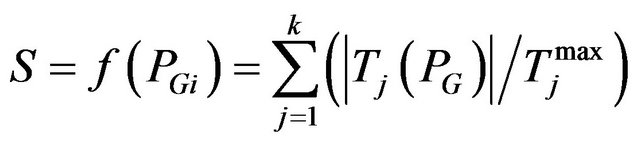
where, 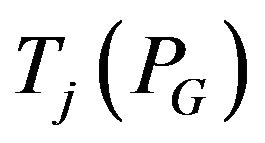 is the real power flow
is the real power flow 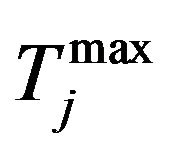 is the maximum limit of the real power flow of the jth line and k is the number of monitored lines. The line flow of the jth line is expressed in terms of the control variables
is the maximum limit of the real power flow of the jth line and k is the number of monitored lines. The line flow of the jth line is expressed in terms of the control variables , by utilizing the generalized generation distribution factors (GGDF) [1] and is given below.
, by utilizing the generalized generation distribution factors (GGDF) [1] and is given below.
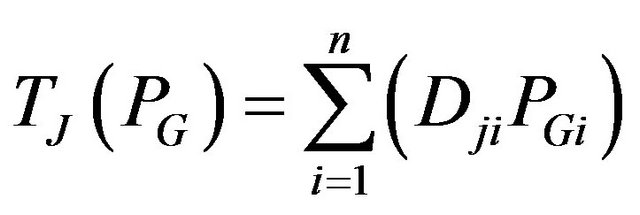
where,  is the generalized GGDF for line j, due to generator i.
is the generalized GGDF for line j, due to generator i.
For secure operation, the transmission line loading 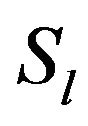 is restricted by its upper limit as
is restricted by its upper limit as

where 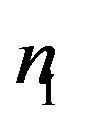 is the number of transmission line.
is the number of transmission line.
• Multiobjective Formulation of EELD Problem. The multiobjective EELD optimization problem is therefore formulated as:
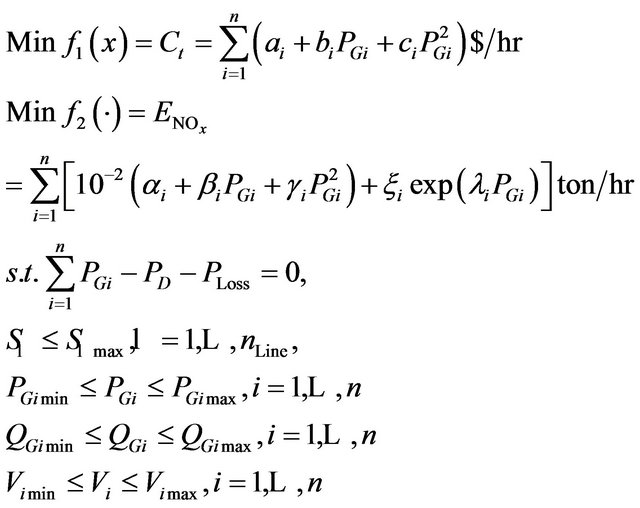
4. The Proposed Approach
This section presents a new hybrid algorithm for solving optimal power flow under fuzziness. The proposed approach integrates the merits of both ACO and GA and by enhancing ACO through GA, a strong robustness and more effectively algorithm was created. The main steps of the MACO are summarized as follows.
Step 1: Construct Q Colonies. In a multiobjective optimization problem, multiobjective functions  need to be optimized simultaneously, there does not necessarily existence a solution that is best with respect to all objectives because of incommensurability and confliction among objectives. For this step, the number of colonies is set to Q with its own pheromone structure, where
need to be optimized simultaneously, there does not necessarily existence a solution that is best with respect to all objectives because of incommensurability and confliction among objectives. For this step, the number of colonies is set to Q with its own pheromone structure, where 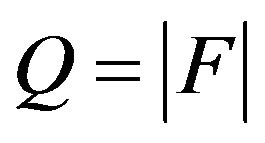 is the number of objectives to optimize.
is the number of objectives to optimize.
Step 2: Initialization. First, pheromones trails are initialized to a given value 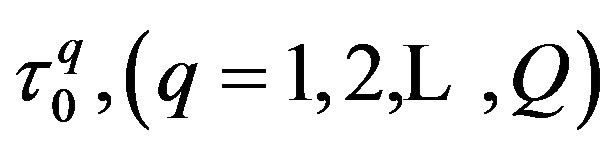 where
where  is the pheromone information in the current iteration and Pareto set are initialized to an empty set.
is the pheromone information in the current iteration and Pareto set are initialized to an empty set.
Implementing the multipheromone ant colony optimization for a certain problem requires a representation of n variables for each ant, with each variable i has a set of  options (nodes) with their values
options (nodes) with their values ![]() which we generate (a fully connected graph
which we generate (a fully connected graph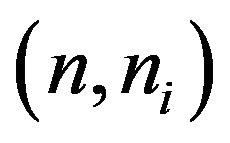 , and their associated pheromone oncentrations
, and their associated pheromone oncentrations 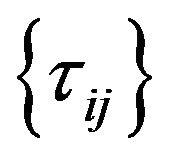 (see Figure 1); where
(see Figure 1); where , and
, and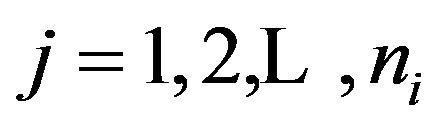 . The process starts by generating m ants’ position (solutions) from the population which is generated randomly, thus each ant k,
. The process starts by generating m ants’ position (solutions) from the population which is generated randomly, thus each ant k, 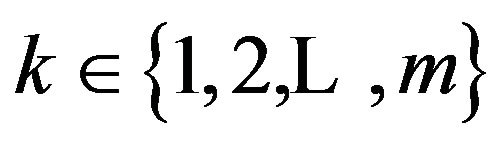 has a position with a selected value for each variable
has a position with a selected value for each variable 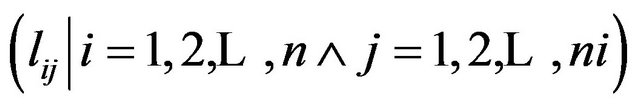 according
according

Figure 1. Ant representation.
to the associated pheromone with this value. This process continues for each objective. Consequently, path of each ant was consisted of ![]() nodes with a value
nodes with a value ![]() for each node.
for each node.
Step 3: Evaluation. The MACO parameterized by the number of ant colonies  and the number of associated pheromone structures. All the colonies have the same number of ants. Each colony
and the number of associated pheromone structures. All the colonies have the same number of ants. Each colony 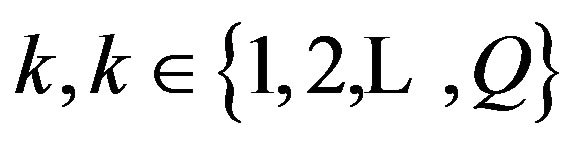 tries to optimize an objective considering the pheromone information associated for each colony, where each colony is determined knowing only the relevant part of a solution. This methodology enforces both colonies to search in different regions of the nondominated front.
tries to optimize an objective considering the pheromone information associated for each colony, where each colony is determined knowing only the relevant part of a solution. This methodology enforces both colonies to search in different regions of the nondominated front.
Step 4: Trail Update and Reward Solutions. When updating pheromone trails, one has to decide on which of the constructed solutions laying pheromone. The quantity of pheromone laying on a component represents the past experience of the colony with respect to choosing this component. Then, at each cycle every ant constructs a solution, and pheromone trails are updated. Once all ants have constructed their solutions, pheromone trails are updated as usually in Equation (2): first, pheromone trails are reduced by a constant factor to simulate evaporation to prevent premature convergence; then, some pheromone is laid on components of the best solution. Accordingly, pheromone concentration 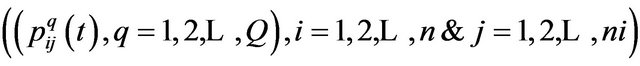 associated with each possible route (variable value) is changed in a way to reinforce good solutions, as in Equation (2) and the change in pheromone concentration
associated with each possible route (variable value) is changed in a way to reinforce good solutions, as in Equation (2) and the change in pheromone concentration  is expressed in equation
is expressed in equation
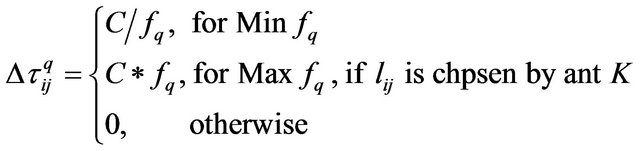
A possibility is to reward every nondominated solution of the current cycle as follows

where 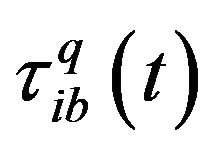 the revised concentration of pheromone is associated with option
the revised concentration of pheromone is associated with option  at iteration
at iteration ,
, 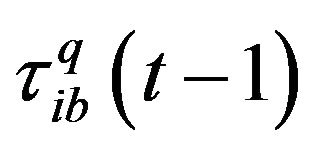 is the concentration of pheromone at the previous iteration
is the concentration of pheromone at the previous iteration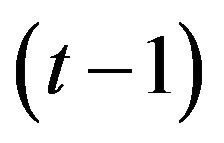 ;
; 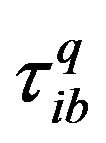 is change in pheromone concentration that can be determined according to Equation (6); and B is the size of reward solutions Step 5: Solution Construction. Once the pheromone is updated after an iteration, the next iteration starts by changing the ants’ paths (i.e. associated variable values) in a manner that respects pheromone concentration and also some heuristic preference. For each ant and for each dimension construct a new candidate group to replace the old one. As such, an ant
is change in pheromone concentration that can be determined according to Equation (6); and B is the size of reward solutions Step 5: Solution Construction. Once the pheromone is updated after an iteration, the next iteration starts by changing the ants’ paths (i.e. associated variable values) in a manner that respects pheromone concentration and also some heuristic preference. For each ant and for each dimension construct a new candidate group to replace the old one. As such, an ant 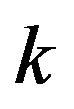 will change the value for each variable according to the transition probability. The transition probability is done for each colony
will change the value for each variable according to the transition probability. The transition probability is done for each colony  as expressed in the following equation.
as expressed in the following equation.

where 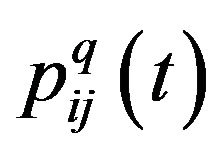 is Probability that option
is Probability that option ![]() is chosen by ant k for variable i at iteration t.
is chosen by ant k for variable i at iteration t.
Step 6: Nondominated Solutions. The set of nondominated solutions is stored in an archive. During the optimization search, this set, which represents the Pareto front, is updated. At each iteration, the current solutions obtained are compared to those stored in the Pareto archive; the dominated ones are removed and the nondominated ones are added to the set.
Step 7: Steady State Genetic Algorithm. Steady state genetic algorithm was implemented in such way that, two offspring are produced in each generation. Parents are selected to produce offspring and then a decision is made as to which individuals in the population to select for deletion to make room for the new offspring (Figure 2). A replacement/deletion strategy defines which member of the population will be replaced by the new offspring. Steady state genetic algorithms overlapping systems, since parents and offspring compete for survival.
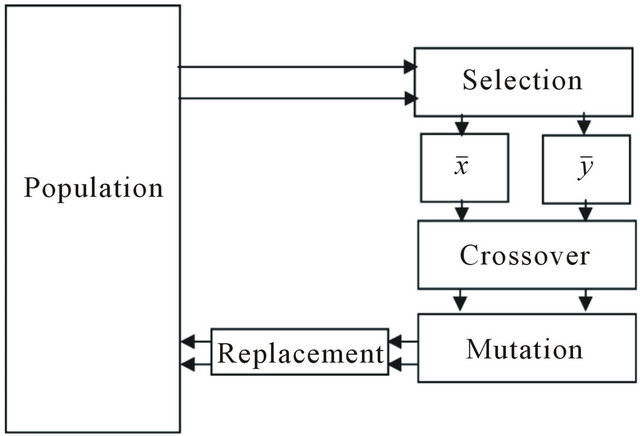
Figure 2. The model for steady state for genetic algorithms.
1) Selections: Selection determines which individuals of the population will have all or some of their genetic material passed on to the next generation of individuals. The mechanism for selecting the parents is based on a tournament selection. Tournament selection operates by choosing some individuals randomly from a population and selecting the best from this group to survive into the next generation. For example, pairs of parents 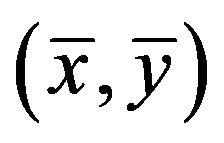 are randomly chosen from the initial population. Their fitness values are compared and a copy of the better performing individual becomes part of the mating pool. The tournament will be performed repeatedly until the mating pool is filled. That way, the worst performing patent in the population will never be selected for inclusion in the mating pool. Tournaments are held between pairs of individuals are the most common. In this way all parents necessary for a reproduction operator are selected.
are randomly chosen from the initial population. Their fitness values are compared and a copy of the better performing individual becomes part of the mating pool. The tournament will be performed repeatedly until the mating pool is filled. That way, the worst performing patent in the population will never be selected for inclusion in the mating pool. Tournaments are held between pairs of individuals are the most common. In this way all parents necessary for a reproduction operator are selected.
2) Recombination through Crossover and Mutation: After selection has been carried out, then the mechanisms of crossover and mutation are applied to produce an offspring, the following subsection outlines these genetic operators.
Crossover: Once the parents are created, the crossover step is carried out by replacing the current value with a new one which produced stochastically with a probability proportional to the crossover probability. Suppose the crossover probability set by the system is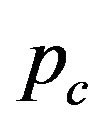 . Generating a random number
. Generating a random number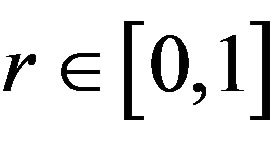 , the crossover operation could be carried out only if
, the crossover operation could be carried out only if . Suppose
. Suppose ![]() and
and ![]() are two parents and
are two parents and ![]() is a random number (i.e.
is a random number (i.e.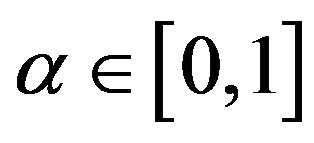 ). The result of crossover operation
). The result of crossover operation 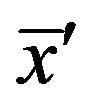 and
and  can be obtained by the following linear combination of
can be obtained by the following linear combination of ![]() and
and![]() :
:

Mutation: Once the, the crossover is performed, the mutation step is carried out by replacing the current value with a new one which produced stochastically with a probability proportional to the mutation probability . Generating a random number
. Generating a random number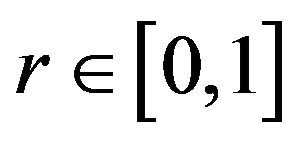 , the mutation operation is implemented only if
, the mutation operation is implemented only if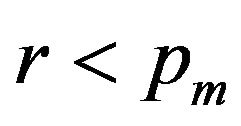 . Suppose
. Suppose  will be transformed into
will be transformed into 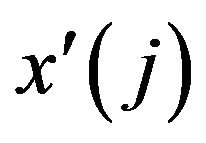 after mutation as follows:
after mutation as follows:
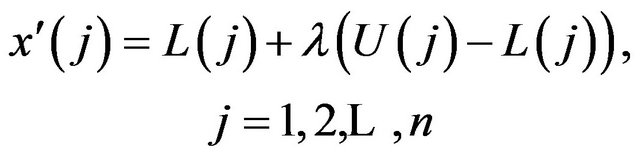
where ![]() is a random number (i.e.
is a random number (i.e.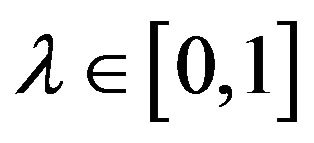 ). Here L and U are the lower and upper bounds respectively.
). Here L and U are the lower and upper bounds respectively.
3) Replacement/deletion strategy: A widely used combination is to replace the worst individual only if the new individual is better. In the paper, this strategy will be suggested that the individual will be deleted if it was dominated by the new offspring as in Algorithm 1.
Algorithm 1. The strategy of deletion.

5. Implementation of the Proposed Approach
The described methodology has been described for Mobjective function, but it is applied to the standard IEEE 30-bus 6-generator test system with two objectives. The single-line diagram of this system is shown in Figure 3 and the detailed data are given in [1,2]. The values of fuel cost and emission coefficients are given in Table 1. For comparison purposes with the reported results, the system is considered as losses and the security constraint is released. The techniques used in this study were developed and implemented on 1.7-MHz PC using MATLAB environment. Table 2 lists the parameter setting used in the algorithm for all runs.
Naturally, these data (cost and emission) involve many controlled parameters whose possible values are vague and uncertain. Consequently each numerical value in the domain can be assigned a specific “grade of membership” where 0 represents the smallest possible grade of membership, and 1 is the largest possible grade of membership. Thus fuzzy parameters can be represented by its membership grade ranging between 0 and 1.
The fuzzy numbers shown in Figure 4 have been obtained from interviewing DMs or from observing the instabilities in the global market and rate of prices fluctuations. The idea is to transform a problem with these fuzzy parameters to a crisp version using ![]() -cut level. This membership function can be rewritten as follows:
-cut level. This membership function can be rewritten as follows:
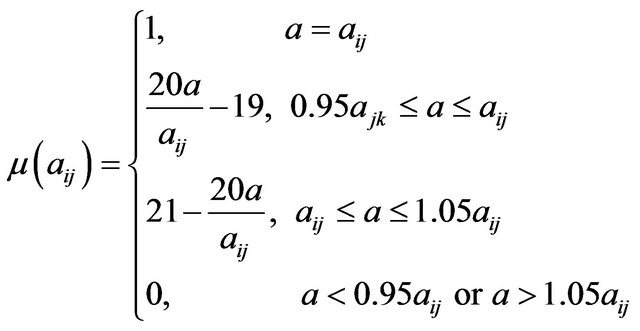
So, every fuzzy parameter 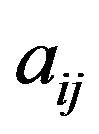 can be represented using the membership function. By using
can be represented using the membership function. By using ![]() -cut level, these fuzzy parameters can be transformed to a crisp one having upper and lower bounds
-cut level, these fuzzy parameters can be transformed to a crisp one having upper and lower bounds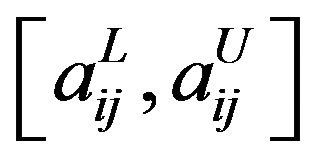 , which declared in
, which declared in
Table 1. Generator cost and emission coefficients.
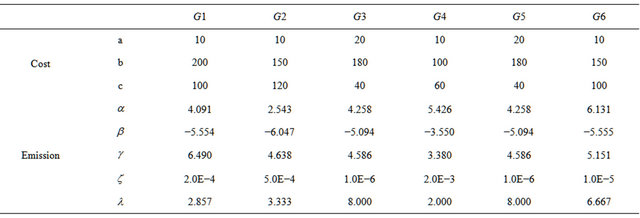
Table 2. Parameters for the proposed approach.
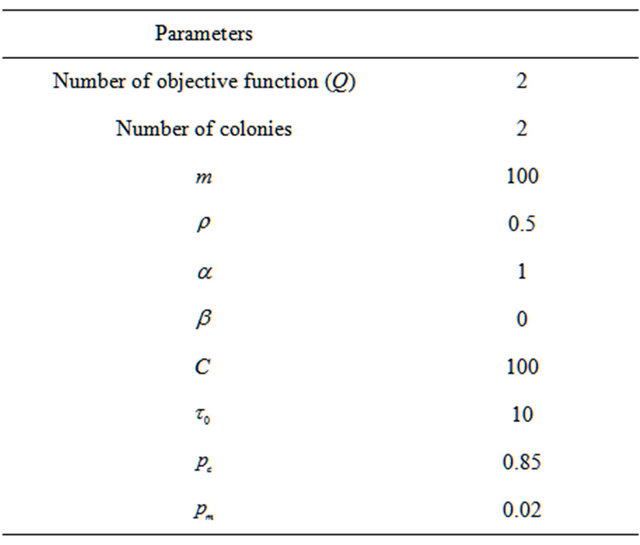
Figure 4. Consequently, each ![]() -cut level can be represented by the two end points of the alpha level.
-cut level can be represented by the two end points of the alpha level.
6. Results and Discussion
Here, the problem is how to determine the optimal power flow for considering the minimum cost and the minimum emission objectives simultaneously. In order to efficiently and effectively obtain the solution, the search for the optimal solution is carried out in two steps. Firstly, a set of nondominated solutions is obtained by exploring the optimal Pareto frontier using different ![]() cut level. To study the influence of fuzzy parameters on the obtained Pareto optimal solutions, all the range of the parameter fluctuation were scanned, two bounds of Alpha value have been considered
cut level. To study the influence of fuzzy parameters on the obtained Pareto optimal solutions, all the range of the parameter fluctuation were scanned, two bounds of Alpha value have been considered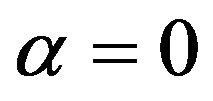 ,
,  , and also we take some values between these bounds
, and also we take some values between these bounds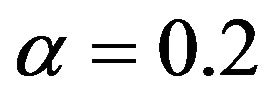 ,
, ![]() 0.4,
0.4, 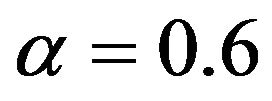 ,
,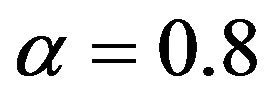 . Based on the definition of Pareto stability, the Pareto frontier may be reduced to a manageable size (i.e., Stable Pareto optimal solutions). MMACO is employed to deal with this problem. Graphical
. Based on the definition of Pareto stability, the Pareto frontier may be reduced to a manageable size (i.e., Stable Pareto optimal solutions). MMACO is employed to deal with this problem. Graphical

Figure 3. Single line diagram of IEEE 30-bus 6-generator test system.

Figure 4. Fuzzy numbers of the effectiveness of resource.
presentations of the experimental results on the six instances problem and are presented in Figures 5-10. It is obvious from Figures 5-10 that the results maintain the diversity and convergence for all ![]() cut level.
cut level.
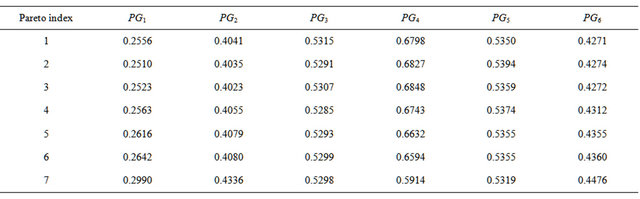
Further we need to determine stable Pareto set solution, which is a Pareto optimal for all runs (different ![]() cut level), there was 7 Pareto solution was detected as a stable Pareto solution. Table 3 lists the set of the stable set of optimal solution. On the basis of the application, we can conclude that the proposed method can provide a sound optimal power flow by simultaneously considering multiobjective problem.
cut level), there was 7 Pareto solution was detected as a stable Pareto solution. Table 3 lists the set of the stable set of optimal solution. On the basis of the application, we can conclude that the proposed method can provide a sound optimal power flow by simultaneously considering multiobjective problem.
In this section, a comparative study has been carried out to assess the proposed approach concerning Pareto solutions, DM preference, and computational time. On the one hand, evolutionary techniques suffer from the large-size of the Pareto set. Therefore the proposed approach has been used to reduce the Pareto front by detecting the stable Pareto solutions under uncertainty which enable the proposed approach to help the DM to take correct decision by visualizing the Pareto front, also it maintains the di-
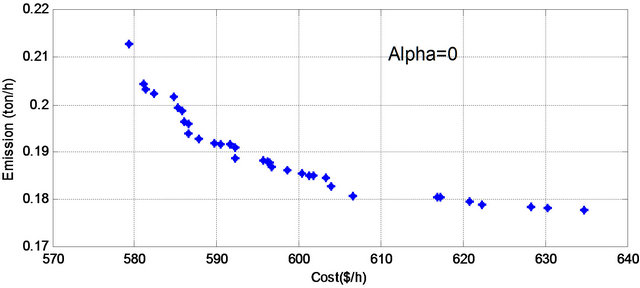
Figure 5. Pareto optimal set for α cut level = 0.
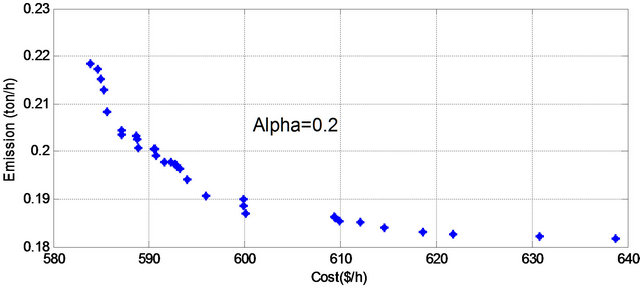
Figure 6. Pareto optimal set for α cut level = 0.2.
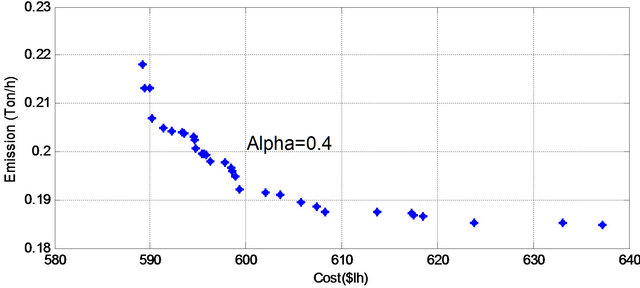
Figure 7. Pareto optimal set for α cut level = 0.4.
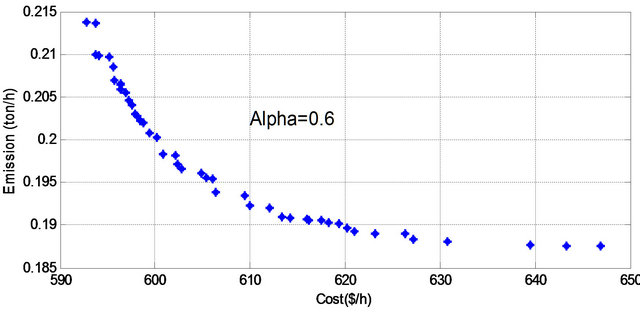
Figure 8. Pareto optimal set for α cut level = 0.6.
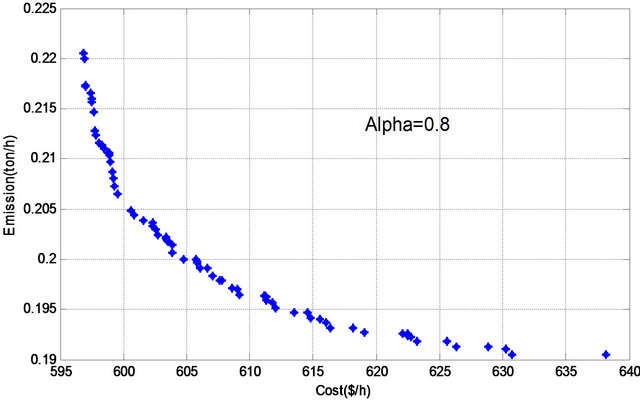
Figure 9. Pareto optimal set for α cut level = 0.8.
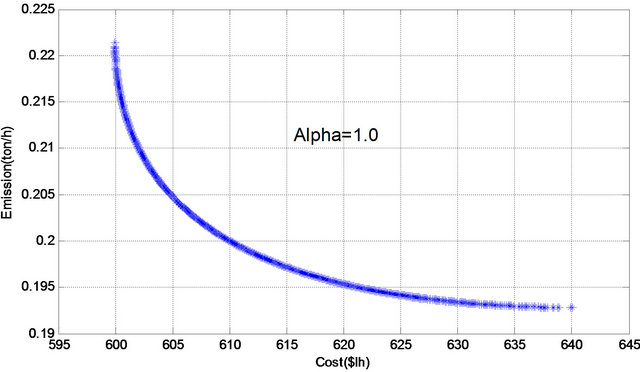
Figure 10. Pareto optimal set for α cut level = 1.0.
versity of the solutions and good distribution over the nondominated front and take the DM preference into consideration by choosing appreciate ![]() cut level. On the other hand, classical techniques aim to give a single point at each iterations of problem solving. On the contrary, the proposed approach generates a set of solutions at each iteration according to DM preference. Finally, the feasibility of using the proposed approach to handle multiobjective optimization problems has been empirically approved.
cut level. On the other hand, classical techniques aim to give a single point at each iterations of problem solving. On the contrary, the proposed approach generates a set of solutions at each iteration according to DM preference. Finally, the feasibility of using the proposed approach to handle multiobjective optimization problems has been empirically approved.
7. Conclusions
Ant colony optimization has been and continues to be a fruitful paradigm for designing effective combinatorial
Table 3. The stable optimal pareto solutions by MM-ACO.
optimization solution algorithms, in this paper; we proposed a new optimization system MM-ACO for solving multiobjective optimization with an application in optimal power flow considering two objectives (cost and emission). Our approach has two characteristic features. Firstly, a set of nondominated solutions is obtained by exploring the optimal Pareto frontier using different ![]() -cut level and subsequently, based on the definition of Pareto stability, the Pareto frontier may be reduced to a manageable size (i.e., Stable Pareto optimal solutions). The main features of the proposed algorithm could be summarized as follows:
-cut level and subsequently, based on the definition of Pareto stability, the Pareto frontier may be reduced to a manageable size (i.e., Stable Pareto optimal solutions). The main features of the proposed algorithm could be summarized as follows:
1) The proposed approach is capable of determining the stable Pareto optimal solution with two objectives, with no limitation in handing higher dimensional problems.
2) The size of the Pareto optimal set has been effectively reduced to a manageable size with no further information from DM.
3) Empirically, we demonstrate that our algorithm yields consistently better results.
The performance improvement of ACO algorithm still remain in the experimental stage for lack of solid theoretical support; thus, for future work, we intend to test the algorithm on more complex real-world applications. Also, conduct research on the parallel mechanism of the ant colony optimization algorithms so that it improves the efficiency of the algorithm used in the intelligent systems.
REFERENCES
- R. Yokoyama, S. H. Bae, T. Morita and H. Sasaki, “Multiobjective Generation Dispatch Based on Probability Security Criteria,” IEEE Transactions on Power Systems, Vol. 3, No. 1, 1988, pp. 317-324. doi:10.1109/59.43217
- A. Farag, S. Al-Baiyat and T. C. Cheng, “Economic Load Dispatch Multiobjective Optimization Procedures Using Linear Programming Techniques,” IEEE Transactions on Power Systems, Vol. 10, No. 2, 1995, pp. 731-738. doi:10.1109/59.387910
- M. S. Osman, M. A. Abo-Sinna and A. A. Mousa, “Epsilon-Dominance Based Multiobjective Genetic Algorithm for Economic Emission Load Dispatch Optimization Problem,” Electric Power Systems Research, Vol. 79, No. 11, 2009, pp. 1561-1567. doi:10.1016/j.epsr.2009.06.003
- Y. J. Feng, L. Yu and G. L. Zhang, “Ant Colony Pattern Search Algorithms for Unconstrained and Bound Constrained Optimization,” Applied Mathematics and Computation, Vol. 191, No. 1, 2007, pp. 42-56. doi:10.1016/j.amc.2006.09.142
- B. Baran and M. Schaerer, “A Multiobjective Ant Colony System for Vehicle Routing Problem with Time Windows,” Proceedings of 21st IASTED International Conference on Applied Informatics, Innsbruck, 10-13 February 2003, pp. 97-102.
- M. Azzam and A. A. Mousa, “Using Genetic Algorithm and Topsis Technique for Multiobjective Reactive Power Compensation,” Electric Power Systems Research, Vol. 80, No. 6, 2010, pp. 675-681. doi:10.1016/j.epsr.2009.10.033
- A. A. Mousa, R. M. Rizk-Allah and W. F. Abd El-Wahed, “A Hybrid Ant Colony Optimization Approach Based Local Search Scheme for Multiobjective Design Optimizations,” Electric Power Systems Research, Vol. 81, No. 4, 2011, pp. 1014-1023. doi:10.1016/j.epsr.2010.12.005
- A. A. Mousa and K. A. Kotb, “Hybrid Multiobjective Evolutionary Algorithm Based Technique for Economic Emission Load Dispatch Optimization Problem,” Scientific Research and Essays, Vol. 7, No. 25, 2012, pp. 2242- 2250. doi:10.5897/SRE11.197
- E. Zitzler and L. Thiele, “Multiobjective Evolutionary Algorithms: A Comparative Case Study and the Strength Pareto Approach,” IEEE Transactions on Evolutionary Computation, Vol. 3, No. 4, 1999, pp. 257-271.
- S. Goss, S. Aron, J. L. Deneubourg and J. M. Pasteels, “The Self-Organizing Exploratory Pattern of the Argentine Ant,” Journal of Insect Behavior, Vol. 3, No. 2, 1990, pp. 159-168. doi:10.1007/BF01417909
- B. Baran and M. Schaerer, “A Multiobjective Ant Colony System for Vehicle Routing Problem with Time Windows,” Proceedings of 21st IASTED International Conference on Applied Informatics, Innsbruck, 10-13 February 2003, pp. 97-102.
- G. Fuellerer, K. F. Doerner, R. F. Hartl and M. Iorib, “Ant Colony Optimization for the Two-Dimensional Loading Vehicle Routing Problem,” Computers & Operations Research, Vol. 36, No. 3, 2009, pp. 655-673. doi:10.1016/j.cor.2007.10.021
- M. Dorigo and T. Stützle, “Ant Colony Optimization,” MIT Press, Cambridge, 2004. doi:10.1007/b99492
- M. S. Osman, M. A. Abo-Sinna and A. A. Mousa, “ITCEMOP: An Iterative Co-Evolutionary Algorithm for Multiobjective Optimization Problem with Nonlinear Constraints,” Journal of Applied Mathematics & Computation, Vol. 183, No. 1, 2006, pp. 373-389. doi:10.1016/j.amc.2006.05.095
- B. S. Kermanshahi, Y. Wu, K. Yasuda and R. Yokoyama, “Environmental Marginal Cost Evaluation by Non-Inferiority Surface,” IEEE Transaction on Power Systems, Vol. 5, No. 4, 1990, pp. 1151-1159. doi:10.1109/59.99365

