ABSTRACT

In this second part, we thoroughly examine the types of higher-order asymptotic variation of a function obtained by all possible basic algebraic operations on higher-order varying functions. The pertinent proofs are somewhat demanding except when all the involved functions are regularly varying. Next, we give an exposition of three types of exponential variation with an exhaustive list of various asymptotic functional equations satisfied by these functions and detailed results concerning operations on them. Simple applications to integrals of a product and asymptotic behavior of sums are given. The paper concludes with applications of higher-order regular, rapid or exponential variation to asymptotic expansions for an expression of type.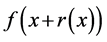

Keywords:

Higher-Order Regularly-Varying Functions, Higher-Order Rapidly-Varying Functions, Smoothly-Varying Functions, Exponentially-Varying Functions, Asymptotic Functional Equations, Asymptotic Expansions

6. Introduction to Part II

We continue the exposition and the section numbering in Part I [1] .

-In §7 we thoroughly examine the types of higher-order asymptotic variation of functions obtained by all basic algebraic operations on higher-order varying functions. For smooth variation the proofs are quite easy using the Balkema-Geluk-de Haan characterization, but proofs for regular or rapid variation require lenghty calculations and careful use of Leibniz’s, Faà Di Bruno’s or Ostrowski’s formulas for higher derivatives of, respectively, a product, a composition or an inversion; these results are not to be found in the literature. Unlike the first-order case the results for higher orders are not granted a priori and in fact restrictions are necessary for definite results in each single case: exhaustive counterexamples are exhibited.

-In §8 we highlight three concepts related to exponential variation which we label as “hypo-exponential” or “exponential” or “hyper-exponential” variation. These classes of functions, though classical, are cursorily treated in the literature and we have collected together all the basic properties, especially many useful “asymptotic functional equa- tions”. Types of higher-order exponentiality are then easily defined.

-§9 contains a detailed account of operations with the three types of exponential variation; results about composition require careful statements and lengthy calculations as in §7. The class of hypoexponentiality is too large and that of hyperexponentiality is too vague to obtain definite results but the additional assumption of rapid variation (in our restricted sense) turns out to be the right one to obtain useful results.

-§10 exhibits two simple applications: an elementary result about the value of the limit of the two ratios

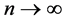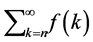and an improvement of a fundamental classical result about the principal part, as, of a sum or. Results more general than the classical ones are obtained by simpler proofs.

-§11 concludes the paper with a number of asymptotic expansions for an expression of type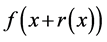, as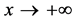, under assumptions of higher-order variations on f, results which reveal useful in iterative processes to determine the behavior of solutions of some functional equations, such as implicit functions.

For later references we quote some known “Combinatorial formulas for composition and inversion”.

-Faà Di Bruno’s formula for derivatives of a composition, Bourbaki( [2] ; p. I.47) or Comtet ( [3] ; p. 137):

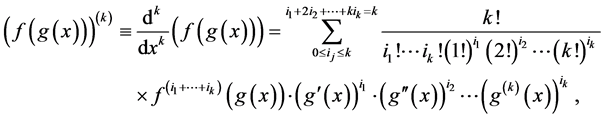(6.1)

where the summation is taken over all possible ordered k-tuples of non-negative integers 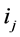such that

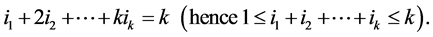(6.2)

Notice that in the preceding sum there is only one term containing 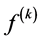and only one term containing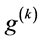, both with coefficient 1, namely:

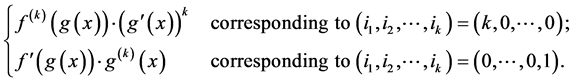(6.3)

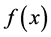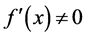-A formula for higher derivatives of an inverse function, Ostrowski ( [4] ; pp. 20-21, 290-293). For, the inverse function of a k-time differentiable with, the formula holds true:

(6.4)

where the summation is taken over all ordered k-tuples of non-negative integers 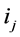such that

(6.5)

Another version of this formula has been proved by Johnson [5] using combinatorial reasonings.

In this paper, the symbol always denotes the inverse function of f on a suitable neighborhood of.

7. Operations with Higher-Order Regular and Rapid Variation

We examine in this section what can be asserted about the order of variation of the product, composition and inverse of regularly-, smoothly- or rapidly-varying functions of higher order. The reader may notice that in the theory of Hardy fields the main results in this section are assumed to hold true whereas we, assuming that the involved functions belong to some of the studied classes, show that their product, composition and inverse belong to a specified class; and this requires a certain computational effort the proofs being based on the above-reported formulas for composition and inversion. Let us start from smooth variation.

7.1. Operations with Higher-Order Smoothly-Varying Functions

Balkema, Geluk and de Haan, ( [6] ; p. 412), and Bingham, Goldie and Teugels, ( [7] ; p. 46) notice that the properties

(7.1)

imply

(7.2)

with the appropriate indexes specified in Proposition 2.1 and with a restriction on the index of g. These inferences require no painful direct proofs because the corresponding properties for the associated functions, defined in (3.24), are easily checked. Here is a statement completed with a result about linear combination and a few remarks. Whenever a power appears, the positivity of is tacitly assumed if this is required by the exponent.

Proposition 7.1. (Operations with smoothly-varying functions). If and then:

(7.3)

For a linear combination, we have the results:

(7.4)

Proof. Without loss of generality suppose. Here is a list of the associated functions except for the linear combination:

(7.5)

The relations in (3.24) being assumed for and the analogous ones for, our claims follow from inspecting the structures of the formulas for higher-order derivatives of composition and inverse regardless of the effective coefficients appearing in (6.1) and (6.4). To prove (7.4) we need a preliminary

Lemma 7.2.

(7.6)

(7.7)

(7.8)

Proof of the Lemma. The argument is quite easy if based on relations (3.21). To prove (7.7) we use the assumptions “”, whence

(7.9)

as if all the quantities are positive and in the other case. In the case of (7.6) and (7.8), we have

(7.10)

as we have “” and “”.

We can now prove properties in (7.4) writing

(7.11)

For we have by (7.3) that hence (7.7) implies that also under any of the stated restrictions. Again by (7.3) the product on the right in (7.11) belongs to the class . If then hence (7.6) implies that and the product on the right in (7.11) belongs to the class. The proof of Proposition 7.1 is over. ,

7.2. Operations with Higher-Order Regularly- or Rapidly-Varying Functions

We rewrite here the inclusions in (3.39):

(7.12)

which imply that the results involving only regular variation follow at once from the corresponding ones in Proposition 7.1 adding the restriction that the final index is not an integer whereas results involving rapid variation cannot be inferred from properties of the associated functions, as remarked in §4 after (4.25), but must be proved by directly working on formulas (6.1) and (6.4). For rapid variation of higher order we are using the strong concept in Definition 4.1.

Proposition 7.3. (Product of higher-order varying functions). (I) If

(7.13)

then

(7.14)

(II)

(7.15)

(7.16)

(III)

(7.17)

(Notice the assumption on g, milder than.)

Proof. For part (I) we have, by Proposition 7.1, that

(7.18)

a class of functions coinciding with if. For part (II), we shall prove relations in (4.10) for the product assuming their validity when is replaced by or.

First case:. In this case, all functions have ultimately one and the same strict sign so we may suppose and this will prove vital in the following calculations:

(7.19)

Here, by the positivity of all the terms in the sum, the expression may be factored out of the sum and a suitable grouping of the factors and yields:

(7.20)

Second case: of order n. In this case the functions have ultimately alternate signs so we may suppose. This implies that all the terms in the second sum in (7.19) have ultimately the same sign and the subsequent calculations are still valid.

The proof of part (III) requires a different device made clear by the case. Write

(7.21)

having used relations in (4.9) for and those in (3.21) for. Moreover, “”, implies that the first term inside braces has the greatest growth-order and we get

(7.22)

Now from both assumptions “” we get:

(7.23)

And replacing this last relation into the right-hand side in (7.22), we finally get the sought-for relation

(7.24)

For, we start from the first equality in (7.19) using relations in (4.10) for f and in (3.21) for with suitable constants:

(7.25)

where for. Using the remark preceding (7.22), we get

(7.26)

,

Remarks on the case of regular variation. 1. A direct proof for could be done but this particular case would imply the claim for only with the restrictions

(7.27)

instead of the sole condition for, how is apparent for writing “”, where the restriction “” is needed to grant and to apply again the case.

2. About the restrictions on the indexes notice that, if

(7.28)

then it is not always true that

(7.29)

with a well-defined depending only on the numbers; may well depend on the particular functions. In fact, using functions like those in (3.40) it is quite easy to exhibit pair of functions such that

(7.30)

Example 1:

(7.31)

Example 2:

(7.32)

Example 3:

(7.33)

3. The function in (7.33) offers an example of a function of order 1 but not of order 2 such that. Hence a possible factorization

which is basic and trivially true for, see (2.18), is in general false for without the restrictions “”, a case wherein it follows from Proposition 7.3-(I).

Proposition 7.4. (Quotient). (I) If

(7.34)

then

(7.35)

(II)

(7.36)

Proof. In both cases (7.3) implies; in part (I), again by (7.3), we have “” hence, by (7.12), the restrictions on grant the thesis. The claim in part (II) follows from Propositon 7.3-(III). This argument avoids the supplementary restrictions “” to grant “”. ,

As concerns composition we give some general results with different restrictions on the indexes and exhibit counterexamples concerning the restrictions.

Proposition 7.5. (Composition involving only regular variation). Assumptions for all the cases to be treated:

(7.37)

for the values of k specified in each statement. We already know that with no restrictions on whereas for higher-order variation we give three distinct statements.

(I) (The case). If are of order 2 then

(7.38)

with no restriction on. Whenever and, (which, by Proposition 2.6, is certainly true if and, due to), then “”.

(II) (The regular case). If are of order and if

(7.39)

then Proposition 7.1 and (7.12) imply:

(7.40)

(III) (The exceptional case). If are of order and if

(7.41)

then

(7.42)

The above results apply to the special case of a power, with and satisfying (7.39); in particular “” implies “” so that conditions in (7.41) are satisfied and “” with “”.

Proof. Part (I) is easily proved applying the definition of “”, i.e. relation in (2.1) with f replaced by either or:

(7.43)

For part (III) let us notice that, by part (I), we already know that

(7.44)

hence we have to prove that h is of order. Faà Di Bruno’s formula yields for each:

(7.45)

with suitable coefficients whose explicit expressions are not presently needed. Using relations in (3.7), we express the quantities in terms of and the quantities in terms of, and this last is the right device to obtain the claim in part (III); in so doing we get the following asymptotic form for the general term in the preceding sum:

(7.46)

with suitable constants, and

(7.47)

with a new constant. To apply Proposition 3.1-(II), we must know that the’s, save the last, are nonzero, and this follows from Proposition 2.6 and the restrictions in (7.41). In fact, for, (7.47) yields:

(7.48)

which implies. For we have:

(7.49)

which, together with (7.44) and (7.48), implies. And so on.

Notice that retracing the foregoing steps by expressing the quantities in terms of one obtains a direct proof of part (II) with the restrictions in (7.39).,

Counterexamples showing the non-existence of a definite result in case.

Two counterexamples with::

(7.50)

(7.51)

A similar counterexample with::

(7.52)

Proposition 7.6. (Composition involving rapid variation in the sense of Definition 4.1).

(I)

(7.53)

(II)

(7.54)

In particular, if then.

(III)

(7.55)

Proof. With the position in (7.44) are ultimately and we shall prove the relations:

(7.56)

already knowing, by Proposition 2.2, that belongs to the class specified in each statement. For various simple proofs are available and we write down only those devices for which also apply to the general cases. For the claim in (I):

(7.57)

We have used the assumption “” which grants that the foregoing quantity within square brackets is “~1”.

For we start from equation (7.45) showing that the one term containing, i.e., is the “asymptotically-leading” term. First we factor out this term:

(7.58)

where the indexes in the sum are subject to the restrictions specified in (7.45) plus condition. Now, a bit differently than in (7.46), we use (3.6) expressing only the quantities in terms of so obtaining:

(7.59)

with suitable constants. The general term in the sum in (7.58) assumes the form:

(7.60)

and

(7.61)

and relations in (7.56) are proved for part (I). For the claim in (II) the situation is different as all the terms have the same growth-order. Expressing and in terms of and we get:

(7.62)

For let us examine each term in the sum in (7.45) expressing and in terms of and:

(7.63)

And so we get

(7.64)

From (7.45) we get:

(7.65)

and it remains the task of proving that, a fact directly checked for. We know that and, fortunately enough, the simple remark at the end of §4, preceding Proposition 4.2, grants this conclusion avoiding cumbersome calculations. For the claim in (III):

(7.66)

For the general term in the sum in (7.45), apart from the “leading” term, now assumes the form:

(7.67)

Replacing into the sum we get

(7.68)

,

The restriction in (7.53)-(7.54) is obviously necessary; the composition of a slowly-varying and a rapidly-varying function may give any result as shown by “” according as “”.

It remains to look for some result about inversion. The simple example of, shows that: (i) the inverse of a function regularly varying of some order n (of any order n, in this case) is not necessarily regularly varying of the same order; (ii) the inverse of a function regularly varying of some order but not of order may well be regularly varying of any order n. Here again natural restrictions on the indexes are to be imposed.

Proposition 7.7. (Inversion of a divergent function). (I) If

(7.69)

then the inverse function (which is well defined on some neighborhood of) satisfies

(7.70)

(II)

(7.71)

(III)

(7.72)

Proof. Part (I) follows from Proposition 7.1 and (7.12). In this proof notations stand for the derivatives of. For part (II), we already know that, by Proposition 2.2-(iv); and from (4.10) we get

(7.73)

For we have:

(7.74)

i.e.. For it is enough to show that

(7.75)

its exact value being determined by Proposition 2.6 and the restrictions in (7.69). From formula (6.4):

(7.76)

with suitable coefficients and where the summation is taken over all ordered k-tuples of non-negative integers satisfying (6.5). Replacing each quantity by its principal part we get:

(7.77)

wherein, by (6.5):

(7.78)

Hence we have:

(7.79)

for some constant and (7.75) follows. For part (III) the relations to be used are those in (4.36):

(7.80)

where x must be replaced by. If we already know that; but if is of order 2 and then, instead of (7.74), we have:

(7.81)

which, by Proposition 4.1, states that in the restricted sense of Definition 4.1. For higher derivatives we now get from (7.76) and (7.78):

(7.82)

with a suitable constant. That can be indirectly proved in the same way as after (7.65) and the proof is over. ,

Applying the preceding results to one gets the following

Proposition 7.8. (Inversion of an infinitesimal function). If f is a continuous strictly decreasing function on such that “” then, trivially, the function has an inverse g such that:

(7.83)

Moreover the following inferences hold true:

(7.84)

(7.85)

(7.86)

8. Concepts Related to Exponential Variation

Whereas the study of the asymptotic behavior as of integrals leads in a natural way to introducing the concepts of regular and rapid variation, the study of the asymptotic behavior as of sums leads to introducing a different classification at based on the limit of the logarithmic derivative: see Hardy ( [8] ; Th. 33, p. 48) or Dieudonnè ( [9] ; pp. 100-103).

8.1. The Three Concepts of Exponential Variation and Basic Properties

Definition 8.1. If large enough, then f is termed “hypo(ºsub)-exponentially varying” or “exponentially varying” or “hyper(ºsuper)-expo- nentially varying” at (in the strong sense) if the following relation, as , holds true respectively:

(8.1)

For brevity we use the symbol to denote the class of the functions such that

(8.2)

studying separately the properties in the four cases:. The elementary case justifying the terminology is that of the exponential of a power (refer to the notations in Definition 2.1):

(8.3)

-Typical hypoexponentially-varying functions are:

(8.4)

and any regularly-varying function obviously belongs to the class.

-All the exponentially-varying functions have the following structure:

(8.5)

as trivially follows from.

-Typical hyperexponentially-varying functions are:

(8.6)

Any exponentially-varying or hyperexponentially-varying function obviously is rapidly varying but there are rapidly-varying functions which are hypoexponentially varying, as in (8.3).

Proposition 8.1. (Basic properties of hypoexponentially-varying functions). For, the following properties hold true:

(i) An integral representation of type:

(8.7)

(ii) The asymptotic estimates:

(8.8)

(8.9)

(iii) The asymptotic functional equation:

(8.10)

and in particular:

(8.11)

(More precise asymptotic functional equations cannot be proved for a generic as the class contains rapidly-varying functions.)

(iv) The asymptotic relations involving anti-derivatives:

(8.12)

which state that, in the respective cases, either or belongs to the same class of;

(8.13)

(v) The asymptotic functional equations involving integrals of:

(8.14)

(8.15)

Compare with (5.10) for similar relations where.

Proof. Representation in (8.7) follows from (2.12) and; the estimates in (8.8)-(8.9) follow at once from (8.7). To prove (8.10) let be such that for x large enough; we get from (8.7)

(8.16)

because for each there exists such that:

(8.17)

whence

(8.18)

The two relations in (8.12) are proved by direct application of L’Hospital’s rule with a preliminary remark for the second relation. The assumptions are “” which imply the convergence of the integral; this in turn implies which, together with the convergence of, imply and L’Hospital’s rule may be applied to evaluate the . Relations in (8.13) follow from (8.10) applied to either or or directly by L’Hospital’s rule. For (8.14) apply the mean-value theorem of the integral calculus:

(8.19)

A proof of the special case of (8.15), “”, is essentially contained in ( [9] ; p. 102) or ( [2] ; p. V.31) and is based on the mean-value theorem applied to . Our exposition is much more elementary. ,

Proposition 8.2. (Basic properties of exponentially-varying functions). For the following properties hold true:

(i) An integral representation of type:

(8.20)

(ii) The asymptotic estimates:

(8.21)

(8.22)

(iii) The asymptotic functional equations:

(8.23)

(8.24)

(8.25)

and in particular:

(8.26)

(iv) The asymptotic relations involving antiderivatives:

(8.27)

which state that, in the respective cases, either or belongs to the same class of, and that, for this special class of functions, the asymptotic relations in (2.84)-(2.85) hold true without the additional condition.

(v) The asymptotic functional equations involving integrals of:

(8.28)

(8.29)

It follows from the above relations that the four functions

(8.30)

have the same order of growth as for each fixed, in the case. Analogous conclusion in the case for the four functions

(8.31)

Proof. Representation in (8.20) follows from (2.12), putting; and (8.22) are simple consequences of (8.20). As in (8.16) we now have:

(8.32)

whence relations in (8.23)-(8.25) follow. Relations in (8.27) are simply proved by L’Hospital’s rule and those in (8.28) either by L’Hospital’s rule and (8.25) or, directly, by (8.25) applied to a suitable antiderivative of f. To prove (8.29) just notice that either for, or for, in which last case the second relation in (8.27) implies:

(8.33)

In both cases L’Hospital’s rule may be applied:

(8.34)

,

Proposition 8.3. (Basic properties of hyperexponentially-varying functions). We are using the notation defined in (1.12). (I) If the following properties hold true:

(8.35)

(8.36)

(8.37)

(8.38)

(8.39)

(8.40)

(8.41)

(8.42)

(II) If the following properties hold true:

(8.43)

(8.44)

(8.45)

(8.46)

(8.47)

(8.48)

(8.49)

(8.50)

Proof. (I) Estimate in (8.37) follows from (8.35) by writing

(8.51)

relations in (8.38) follow from the identity “”; relation in (8.39) follows from L’Hospital’s rule and those in (8.40) follow either from L’Hospital’s rule or from (8.38) applied to. The first relation in (8.41) trivially follows from; the second one follows, e.g., from (8.39) and (8.38) applied to:

(8.52)

or also from L’Hospital’s rule:

(8.53)

by the second relation in (8.38). Strangely enough any elementary attempt to prove the third relation in (8.41) failed and we report a proof under the restriction “f convex”; in this case we have at disposal the elementary inequality ( [10] , p. 15):

(8.54)

Analogous procedures for the relations in (8.42) and for the claims in part (II) up to (8.48). For those in (8.49), putting, we now have:

(8.55)

(8.56)

Analogously for (8.50). ,

The values of the following limit are contained in the foregoing three propositions:

(8.57)

interchanging the values “0” and “” for. Special results in §11 give asymptotic expansions for the quantity under various assumptions on f.

As a simple but meaningful application of the preceding functional equations consider a function of the type “” where denotes the “integer part” of the real number x. From the trivial relation “” the following facts follow:

(8.58)

(8.59)

(8.60)

8.2. Higher-Order Exponential Variation

The right concepts of higher-order types of exponential variation are a consequence of some simple relationships between the types of exponential variation of and.

Proposition 8.4. (Types of exponential variation for a derivative). Let and

(8.61)

Then: “if”, and “if”. In the case “” we have that:

(8.62)

It follows that, whenever “”, then: “”.

Proof. If then “” implies by (8.22) that: either “” or “”. In any case the following application of L’Hospital’s rule is legitimate:

(8.63)

If “” then “” and (8.60) is still valid. Last,

(8.64)

and we shall show that “” excluding the other cases: (i) “” would imply “” and (8.63) would give a contradiction; (ii) ““ would imply “” whence “” against (8.63); (iii) “” means “” which, together with the integral representation in (8.64), would imply by (8.13) that “”. Let us examine the circumstance “”; if it were “” then, as we have just remarked, “” and (8.63) would give again a contradiction. If then Proposition 8.2 applied to implies “” and the relations in (8.62) follow.,

Examples for:

(8.65)

(8.66)

as, in this last case,

Definition 8.2. If then f belongs to one of the classes

(8.67)

iff all the functions belong to the corresponding classes This implies that “for all large enough and”. Equivalently:

(8.68)

(8.69)

(8.70)

wherein the correct index “” or “” is determined by the single limit “”.

According to our agreements, an is supposed strictly positive whereas an is supposed to be of one strict sign. For also the highest-order derivative in (8.69)-(8.70) is ultimately of one strict sign. More precisely, if and then:

(8.71)

The above definition excludes the circumstance that:

(8.72)

Using (8.62) it is immediately proved that (8.72) occurs iff there exists a polynomial of exact algebraic degree k such that:

(8.73)

We shall not give this class a special name.

Proposition 8.5. (Relationships between higher-order exponentiality and higher-order rapid variation in the strong restricted sense). If then:

(I) If then its derivatives satisfy the relations

(8.74)

implying that if, and where “” is in accord with the sign of c.

(II) If, then iff the additional conditions are satisfied:

(8.75)

Proof. (I) Relations in (8.74) are stronger that those in (4.6), Definition 4.1, and imply those in (4.8) with; the assertion follows from Proposition 4.1. (II) In this case relations in (8.70) may be read as

(8.76)

which are stronger that those in (4.6) and the assertion again follows from Proposition 4.1. ,

9. Operations with Higher-Order Exponentially-Varying Functions

Rules governing multiplication and composition of functions of the above classes can be proved; the results are not obvious a priori and restrictions on the indexes may be necessary. Some cases would remain completely undecided due to the intrinsic nature of two classes: contains both regularly- and rapidly-varying functions whereas the functions in are “very” rapidly varying; however the additional assumption of rapid variation (in our restricted sense) turns out to be the right one to obtain useful results.

Proposition 9.1. (Product). (I) Results for variation of order 1. If then their powers, product and quotient belong to the following classes:

(9.1)

provided that the quantities represent well-defined extended real numbers, i.e. they do not give rise to some indeterminate form. A trivial counterexample concerning the product with “” is “”, with and

(II) Results for variation of order. If, then

with, provided that this sum unambiguously defines an extended real number other than zero, hence there is no definite result in the case “”. The trouble whenever is that a product may be a polynomial of algebraic degree so that some derivative of its, of order, may be. (For the result on the power see Proposition 9.4-(I).)

Proof. It is enough to prove the claims about the product only for. (I) Quite trivially: “” and

(9.2)

For part (II) we separate three cases: “”; “”; “”. In the first case:

(9.3)

and the thesis follows from (8.69). In case “” we would have relations

(9.4)

which do not grant that “”. In the second and third cases similar calculations would give relations “” which are not enough; we must prove the chain in (8.70) with f replaced by. In the second case the claim follows from the remarkable relation:

(9.5)

and “”. Relation in (9.5) is proved using (8.69)-(8.70) in the Leibniz’s formula:

(9.6)

In the third case, for, we have:

(9.7)

wherein the last but one equality is legitimate by the fact that the two products and have ultimately the same strict sign: it is essential that either “” or “”. For we write:

(9.8)

If “” all the involved quantities (coefficients and functions) are positive and we get:

(9.9)

If “” we use (8.71) for the signs of the derivatives and get:

(9.10)

whence:

(9.11)

having used once again (8.68) and Leibniz’s formula to obtain the last equality. ,

For inversion there is no special result: we can only assert that an, with has an inverse defined on a suitable neighborhood of which, by Proposition 2.2-(iv), is slowly varying in the strong sense. For composition we face the following situation: evaluating the limit of the ratio is easy for but for it is necessary to find the exact principal part at of each derivative. Our restricted notion of rapid variation turns out to be the right one to obtain general results. Separate accounts are presented: for order 1 under the least possible hypotheses and with counterexamples; for order 2 with some restrictions and via elementary calculations; and more complete results for order which are also valid for but obtained via elaborated calculations requiring a further restriction in a few cases.

Proposition 9.2. (Composition: order 1). Let the functions be either regularly or exponentially varying as specified in each statement, hence they are ultimately strictly positive; and let so that we may classify the type of variation at, if any, of the composite function.

(I) If

(9.12)

then provided that the product is not the indeterminate form “” in which case any conclusion may hold true as shown by the simple counterexamples:

(9.13)

The positive part of the statement is examplified by: .

(II) If

(9.14)

then

(9.15)

If and if the quantity

(9.16)

defines an extended real number, then.

There is no definite result for the excluded cases. A counterexample for “and” is “” and a counterexample for “and” is “”: in both cases the indexes of exponential variation depend on the value of “”. A counterexample for “and” is

(9.17)

the index of exponential variation depending on the value of “”. For this is a counterexample for “and”.

(III) If both functions are exponentially varying with various indexes, namely

(9.18)

then according as or. Simple counterexamples for the cases “or” are provided by the pair

(9.19)

each of them in the role either of H or f. In both cases: does not exist though. Some results for the cases “” are reported in Proposition 9.4-(III).

Proof. For part (I) write

(9.20)

and use “”. For the non-ambiguous cases in part (II) just write

(9.21)

recalling that “or” according as or. For part (III) we have

(9.22)

because the first limit is and the second limit is as either “” or “” and. ,

Proposition 9.3. (Composition: order 2). Let the functions be either regularly or exponentially varying of order 2 as specified in each statement and ultimately strictly positive, and.

(I) Let

(9.23)

and both the products “” be not the indeterminate form “”. Then provided that in the case “” the restriction be added (see Proposition 8.5):

(9.24)

For the special case

(9.25)

and f as in (9.23) we have that:

(9.26)

In particular: if. Notice that in case “” we are not assuming “” in the strong restricted sense of our Definition 4.1.

(II) If

(9.27)

then:

(9.28)

If and if the expression

(9.29)

defines an extended real number, then.

(III) If both functions are exponentially varying, namely

(9.30)

then according as or, provided that in the case “and” the restriction (9.24) is added.

Proof. By Proposition 9.2 we need to estimate the behavior of the sole ratio

(9.31)

For part (I) we use the last expression in (9.31) trivially checking that:

(9.32)

whereas for the remaining cases wherein “” the assumption in (9.24) implies by Proposition 8.5-(II) that so that:

(9.33)

taking account that:. For part (II) we use the first equality in (9.31); for and the index of is due to condition, and we get:

(9.34)

as well as the corresponding results for and for. The same equality is used for part (III) wherein the assumptions imply “”; for and, and according to the various circumstances, we have:

(9.35)

Now let; if the very same calculations give “” whereas, for and to avoid the indeterminate form “”, we need (9.24) namely relation, so getting:

(9.36)

,

Proposition 9.4. (Composition: order). Let the functions be either regularly or exponentially varying of order as specified in each statement; ultimately strictly positive, and.

(I) (H regularly or rapidly varying). If

(9.37)

then:

(9.38)

and these relations imply: if, and

(9.39)

If

(9.40)

and

(9.41)

then in each of the four cases we have:

(9.42)

and these relations imply: either if, or if.

For the special choice we get the inference:

(9.43)

and if belongs to one of the classes in (9.41) then belongs to the same class.

If

(9.44)

then:

(9.45)

whence:.

If

(9.46)

then:

(9.47)

whence:.

(II) (H exponentially varying, f smoothly varying of positive index). Assume

(9.48)

If

(9.49)

then:

(9.50)

which implies

(9.51)

wherein agrees with the sign of c.

If

(9.52)

then:

(9.53)

which implies:, with the sign of agreeing with the sign of c.

If then quite different circumstances occur according as H is regularly or rapidly varying and the pertinent results are contained in Propositions 7.1, 7.5, 7.6.

(III) (H exponentially varying, f slowly varying). Notwithstanding the counterexample in (9.19) some positive results can be given for and they depend on the behavior of. To be precise assume:

(9.54)

Condition implies that the index of variation of is −1 so that and we have three different inferences. First:

(9.55)

wherein the last relation follows from “”. This implies: and Second:

(9.56)

with some constants and this implies by Proposition 3.4 that: . Third:

(9.57)

wherein “”. This implies: . A trivial example to visualize these results is the following:

(9.58)

This example also shows that, if and is a natural number, then it is not granted that

.

(IV) (Both exponentially varying). Let

(9.59)

Case:. The following relations hold true:

(9.60)

(9.61)

Case:. If satisfies the additional condition in (9.52) then:

(9.62)

(9.63)

Relations in (9.63) coincide with the first group of relations in (9.47) obtained under the assumption for H in (9.46) which is independent of the present assumption “”.

In each case it is checked that “” that is “” according as or. Moreover, (9.60) and (9.62) grant the additional property

(9.64)

that is “”, whereas this last property follows from either (9.61) or (9.63) under the additional condition for H in (9.46) which implies that both relations in (9.61) and (9.63) can be rewritten as:

(9.65)

For “or” there is no general result as shown in Proposition 9.2-(III).

Proof. Remember that all the claims are already known for order 1 and that, in each single case, one has to replace the appropriate asymptotic relations into the Faà Di Bruno’s formula for which, with the present notations, we write in the more succinct form:

(9.66)

always taking into account restrictions in (6.2) and that all the coefficients are positive numbers.

Part (I). Under conditions in (9.37), , we have relations

(9.67)

(9.68)

whence

(9.69)

Let us now consider the family of polynomials:

(9.70)

where, by (6.2), has algebraic degree k, and let us try to find a closed form of. For fixed k let be two -functions on some interval satisfying conditions in (9.37) with, e.g., and then and. By Proposition 9.2-(I) we get:

(9.71)

This, together with the value, implies which our reasoning has shown true for each; being a polynomial this must be an identity on; hence we have given an indirect proof of the useful equality:

(9.72)

wherein the coefficients and the indexes are specified in (6.1)-(6.2). The relation in (9.37) for follows. For the pertinent assumption on H in (9.37) implies relations

(9.73)

and quite similar calculations as above yield:

(9.74)

having used the obvious equality: whenever Under the assumptions in (9.40)-(9.41) we use relations in (9.67) or in (9.73) for, and relations

(9.75)

and we get:

(9.76)

and the analogous relation in case. Hence for we have:

(9.77)

(9.78)

Analogous procedure in case and the claims are proved. If conditions in (9.44) are assumed we use both relations in (9.68) for and the scale

(9.79)

Instead of (9.69) we now get:

(9.80)

taking into account the fact that into the summation the term with the highest growth-order is the one term corresponding to “”, that is: “”, with coefficient 1. By the assumption on H, see (4.8), these last relations imply:

(9.81)

Under conditions in (9.46) we use (9.75) and the scale in (9.79) so getting:

(9.82)

which yield the same relations as in (9.81).

Part (II). The common relations for H are:

(9.83)

If (9.49) holds true then:

(9.84)

(9.85)

wherein. Condition “” implies that the leading term in the sum is the one corresponding to “”. As relation in (9.50) follows. From this we infer:

(9.86)

Under condition in (9.52), we use relations in (9.75) for so getting:

(9.87)

Part (III). Under assumptions in (9.54), we have the following relations for:

(9.88)

(9.89)

with suitable nonzero coefficients which may have any signs. The extra assumption implies that the leading term into the last sum is the one corresponding to “”, i.e. “” so that and the relations in (9.55) follow; in particular Condition “”, i.e. “”, implies that

(9.90)

(9.91)

where the sum is some number which may have any sign including zero. This is (9.56). In the third case condition “” implies that the leading term is the one corresponding to “”; now and (9.57) follows. This in turn implies:

(9.92)

Part (IV). If then:

(9.93)

wherein the leading term is the one corresponding to and (9.60) follows. If and then:

(9.94)

wherein the leading term is, once again, the one corresponding to due to the scale in (9.79), and (9.61) follows. If and then, using relations in (9.75), we get:

(9.95)

If then

(9.96)

and (9.62) follows. If and if also the scale in (9.79) is taken into account then the last expression in (9.95) implies:

(9.97)

that is (9.63). ,

10. Two Simple Applications of Exponential Variation

10.1. Relations between the Integral of a Product and the Product of Integrals

From elementary calculus we know that, generally speaking, an integral of type has no precise quantitative relationships with and inequalities linking the two quantities are known: see, e.g., ( [11] ; §2.13, pp. 70-74), ( [12] ; Chap. X). Similar remarks apply to the pair and. The concepts related to exponential variation yield asymptotic information about the ratios of these quantities as.

Proposition 10.1. Let; ultimately.

(I) In the case “” we have the following contingencies:

(10.1)

(II) Under the assumptions “” we have the following contingencies:

(10.2)

(III) For regularly varying (hence hypoexponentially varying) we have the exact principal parts at of the above ratios, namely

(10.3)

(10.4)

Proof. By L’Hospital’s rule we have:

(10.5)

and then we apply the various results in Propositions 8.1-8.3. The last claims in (10.1) and (10.2) simply follow noticing that the two limits on the right-hand sides in (10.5) are not smaller than the limits of the sole ratios involving f. Part (III) follows from Proposition 2.4-(I). ,

For rapidly varying in the strong restricted sense of Definition 4.1, Proposition 2.4-(II) would give relation

(10.6)

and a similar one for. More precise results depend on the types of exponential variation of which provide information on the and the foregoing results are reobtained under the unnecessary restrictions on the second derivatives.

Proposition 10.2. Let each of the two functions belong to one of the three classes in Definition 8.1

(I) In the case “” we have the following contingencies:

(10.7)

(II) Under the assumptions: “and”, we have the following contingencies:

(10.8)

Proof. Again by L’Hospital’s rule:

(10.9)

,

10.2. Sums of Exponentially-Varying Terms

If has a definite type of exponential variation at according to Definition 8.1, then classical results going back to Hardy ( [8] ; Th. 33, p. 48) under stronger regularity assumptions, express the asymptotic behavior of a sum or via either or, the behavior of the integral being then detected by some of the results in Proposition 2.4. Our exposition allows simplified proofs and we also point out to what extent the classical results apply to more general series of type. It turns out that the functional Equations (8.14) and (8.15) impose drastic restrictions on the sequence.

Proposition 10.3. For, with, the following equivalence holds true:

(10.10)

together with the following asymptotic comparisons between sums and integrals.

(I) If and is a sequence of real numbers such that:

(10.11)

then:

(10.12)

(10.13)

If and is a sequence of real numbers such that:

(10.14)

then:

(10.15)

(10.16)

In the particular case “” the asymptotic relations in (10.15)- (10.16) respectively become, by Proposition 2.4-(I):

(10.17)

(10.18)

(II) If and satisfies conditions in (10.14) then:

(10.19)

(10.20)

(III) If and is a sequence of real numbers such that:

(10.21)

then:

(10.22)

(10.23)

Proof. (I) Under conditions in (10.11) it follows from (8.14) that:

(10.24)

(10.25)

and the analogous relation in case of convergence. Under conditions in (10.14) we get from (8.15):

(10.26)

(10.27)

and the analogous relation in case of convergence. And also the equivalence in (10.10) is proved.

(II) From (8.29) we get:

(10.28)

(10.29)

and the analogous relation in case of convergence. (III) For “”is ultimately strictly monotonic and, for the argument’s sake, we may suppose that is strictly monotonic on the whole interval. For, is strictly increasing so that:

(10.30)

whence:

(10.31)

Analogously for, is strictly decreasing and

(10.32)

whence:

(10.33)

The equivalence in (10.10) in cases (II) and (III) is implicit in the previous relations. ,

Remarks. 1. Condition “” is adequate in part (III) whereas the stronger condition “” is needed in part (I) to apply (8.15) and get a precise asymptotic result. A sequence such that “” may not work in each of the above three circumstances dramatically changing the type of exponential variation; take for instance “” checking the three cases pertinent to: “”, “”, “”. If the inequalities concerning “” in (10.11) and in (10.21) are satisfied only for each n large enough this does not affect the principal parts of the sums though the given relations might be quite inaccurate from a numerical standpoint.

2. The equivalence in (10.10) for the case is remarkable in so far it does not require the monotonicity of in which case it trivially follows from the inequalities:

(10.34)

or from the inverted ones. Another classical criterion grants the equivalence in (10.10) under conditions “” regardless of the sign of.

3. The mentioned original proofs by Hardy for implicitly assume that. The proofs by Dieudonné in ( [9] ; pp. 101-103), assuming, are reported in ( [2] ; pp.V.30-V:31) with some simplifications.

Comments and examples on applying the foregoing results. Suppose that the asymptotic behavior of the given sequence is described by an expansion with several terms, say “” with “”. If f has a definite type of asymptotic variation then, generally speaking, there is only one case wherein the mere principal part suffices to find the principal part of the pertinent sum, namely:

(10.35)

separating the cases of convergence and divergence. If the expansion has the simpler form “” with “” then the inferences in (10.35) hold true for the larger class of whereas, for a generic “” all the divergent and convergent terms in the expansion must be taken into consideration save further simplifications. The results in part (III), with the mild restriction on the sequence, may yield interesting relations difficult to achieve by other methods.

Example 1. For “” we have two quite equivalent ways of applying (10.19) to evaluate the sum:

(10.36)

In the first procedure we put and which last satisfies conditions in (10.14) with; in the second we notice that “”and choose “” getting the same result.

Example 2. For “”, where “”, we have:

(10.37)

The sole relation “” is enough in this case.

Example 3. For, where “”, (10.19) cannot be applied with the choice as “”; but noticing that “” we get from (10.22):

(10.38)

And the same argument can be used to establish the relation:

(10.39)

Example 4. Let

(10.40)

To evaluate we cannot apply neither (10.19) with the choice as “” nor, generally speaking, a direct method save, e.g., the case wherein “” with “”, as in the preceding example. But there is an indirect method which works well for any though not very “natural”. Starting from the expansion:

(10.41)

it can be checked that:

(10.42)

Hence for we have and:

(10.43)

for: For the sequence we have that and we may apply (10.22) with so getting:

(10.44)

which is a remarkable relation due to the presence of the possibly oscillatory term.

11. Asymptotic Expansions for

In iterative processes aiming at determining the asymptotic behavior of solutions of a functional equation it is sometimes useful to know asymptotic expansions of a quantity like. We preliminarly state a few elementary facts about the asymptotic relation

(11.1)

from a different viewpoint than that in §5. If, (11.1) is trivially true for any r such that; otherwise it makes sense for and, in such a case, it is satisfied by any: see (5.6). Weakening the hypothesis on f useful results hold true under strong conditions on the growth-order of r. This point is highlighted in the following preliminary result containing a classification of various asymptotic functional equations, partly overlapping the results in Proposition 5.1.

Lemma 11.1. (I) If, f ultimately, then:

(11.2)

(11.3)

(11.4)

(11.5)

without any restrictions on sign and monotonicity of, and on the sign of r apart from the first inference. The four inferred asymptotic relations are listed in order of decreasing logical strength.

(II) Relation in (11.1) holds true under the following conditions:

(11.6)

which means that, no matter what the growth-order of, (11.1) is practically granted for any nonnegative and sufficiently small r. This result implies those in (11.3)-(11.5) but with additional unnecessary assumptions, hence it is better used in the case “unbounded”. For results with a nonpositive r see ( [2] ; p. V.44) and ( [9] ; exercise 6, p. 113).

Proof. Using the first equality in (5.20) all claims in part (I) reduce to proving that either or is “” under the different assumptions on r: this is elementary and left to the reader. For part (II) it is simpler to apply the mean-value formula after a few preliminary remarks. First we may suppose and the assumptions imply that exists in; so we have to study the two nontrivial cases “either 0 or”. Moreover it is easily seen that the case is brought back to the other case referred to. Hence we are supposing and so that the monotonicity of implies that is ultimately decreasing (to zero) as. Now we have:

(11.7)

and all the assumptions on and r imply:

(11.8)

,

Simple counterexamples show the necessity of the restrictions on r in (11.6); in fact, even if is monotonic, condition may not work:

Various types of expansions for can be obtained using “higher-order types of variation” for f.

Proposition 11.2. (Higher-order regular or rapid variation). (I) If , and then the ordered n-tuple is an asymptotic scale at, i.e.

(11.9)

and the following asymptotic expansion of Poincaré’s type holds true:

(11.10)

If, with, we have the remainder estimate:

(11.11)

(II) If, monotonic, and then we have the asymptotic scale in (11.9) and the asymptotic expansion of Poincaré’s type in (11.11). The conditions on f are granted when assuming.

In part (I) the sign of r may be arbitrary. The result in part (II) shows another context wherein our concept of higher-order rapid variation reveals appropriate: the hypothesis “” is the right one to grant the asymptotic scale in (11.9); the other assumptions serve to get a simple estimate of the remainder. According to Proposition 8.5 this result also is the right one to be applied to hyperexponentiality of higher order.

Proposition 11.3. (Higher-order hypoexponentiality). (I) If and is bounded then the following expansion holds true:

(11.12)

where is an asymptotic scale at by (8.68). This is an asymptotic expansion with variable coefficients; it is of a more general type than Poincaré’s, see, e.g., ( [2] ; p. V.17), ( [9] ; pp. 84-85), and has been introduced by Erdélyi: ( [13] ; p. 2), ( [14] ; p. 222). If then, under a monotonicity assumption for, we have the remainder estimates:

(11.13)

(II) If and then the following expansion holds true for each fixed:

(11.14)

which may be thought of as an asymptotic expansion either of Poincaré’s type with respect to the asymptotic scale or of Erdélyi’s type with respect to the scale. In particular:

(11.15)

and, under the additional assumption of monotonicity for, we have the remainder estimates:

(11.16)

inverting the estimates for. Notice that, though does not appear in some of the previous expansions, the given remainder-estimates have been obtained using some property of granted by the assumptions.

Proofs. The common formula for the various claims is Taylor’s formula with initial point x and Lagrange remainder:

(11.17)

For the claim in Proposition 11.2-(I), we start from formula (3.5): “” with suitable constants; whence

(11.18)

and this, because of condition, implies (11.9) if. If for then the foregoing argument yields “” whereas the regular variation of gives

(11.19)

In any case (11.9) holds true. For the remainder we know that there exists a number (using the notation in Definition 3.1) such that:

(11.20)

whence (11.10) and (11.11) follow. For part (II) in Proposition 11.2, the assumption is that be rapidly varying of order in the strong restricted sense of Definition 4.1 hence, by Proposition 4.1,

(11.21)

and

(11.22)

for, and (11.9) follows. From the nonnegativity of r and (11.21) we also get:

(11.23)

Applying Lemma 11.1-(II) to the three quantities on the right and using the monotonicity of:

(11.24)

whence (11.11). For part (I) in Proposition 11.3 we have so that the assumption “hypoexponentially varying” and (8.10) yield the following two relations as:

(11.25)

whence (11.12) follows. Under the monotonicity assumption we have

(11.26)

and (11.13) follows. The proof for (11.14) is quite the same: relations in (11.25) still hold true and the quantity in (11.12) is now replaced by. ,

We now briefly examine to what extent the powers in (11.14) can be replaced by their full binomial expressions with suppression of the parentheses. It is clear that a correct arrangement depends on the relative growth-orders between and and there are too many possible cases to be collected together in a readable result except for one special case in which is not too small and a “natural” arrangement of the terms occur.

Proposition 11.4. (Different arrangements in the expansion of). Let so that we have the expansion in (11.14) with, and n replaced by; but we shall consider just the expansion in (11.14) with the stronger remainder-estimate. Under any one of the following further restrictions, either

(11.27)

or

(11.28)

then the asymptotic expansion in (11.14) can be rewritten as the new expansion:

(11.29)

where all the terms, in the given order and with no grouping inside each sum, form an asymptotic scale at, that is

(11.30)

Example. For all the function r:

(11.31)

satisfies the conditions in (11.27), and also the conditions in (11.28) with respect to, ,.

Proof. The chain obviously follows from and. For the right hand-side in (11.29) is an asymptotic expansion if “”; for this happens if both conditions are satisfied: “,”; and in general the right-hand side in (11.29) is an asymptotic expansion if the following conditions are satisfied:

(11.32)

Now, if two circumstances can occur; if then conditions in (11.32) are satisfied iff “” i.e. “”. If this is not the case then, by Proposition 2.6-(I), there exists such that:

(11.33)

As above we see that conditions in (11.32) are satisfied for iff , whereas the condition for is certainly satisfied if ; and our claim is proved.

If then we have the set of relations in (4.8) whence it follows that

(11.34)

,

For an exponentially-varying f a possible expansion with more than one term must be of a different type as the n-tuple is no asymptotic scale at, and here is the corresponding result.

Proposition 11.5. (Higher-order exponentiality). Let , , be represented, by (8.5), in the form where, so that we have:

(11.35)

If then we may replace by its n-term expansion in powers of and by its expansion of type (11.14) to get an expansion for the left-hand side in (11.35). For we get:

(11.36)

For the expansion reduces to the identity. For we have “” and the expansion is a disguised form of

(11.37)

which is directly obtained from (8.26) and the decomposition

(11.38)

12. Conclusions and Open Problems

As cursorily stated in the general introduction to this two-part paper in §1, our job consisted in: first, collecting all almost elementary and standard material about basic properties of regularly-, rapidly- and exponentially-varying functions; second, giving appropriate definitions for higher-order types of asymptotic variation; third, exhibiting several characterizations of higher-order smooth and rapid variation and highlighting the role of a lemma by Balkema, Geluk and de Haan about smooth variation, a role somewhat hidden in the original concise proof. Afterwards, a great deal of work has been required to prove complete results concerning the possible types of asymptotic variation for functions obtained by means of algebraic operations; in so doing much of the material in the previous sections have been used including (seemingly) futile remarks and (seemingly) minor results. On the contrary §5 on asymptotic functional equations is expository in nature its only merit being that of collecting in a systematized way as many such equations as possible. And the same can be said for such types of equations satisfied by exponentially-varying functions and grouped in §8.

All the material in both parts of the paper must be considered as the systematized general theory of higher-order asymptotic variation including the few simple applications in §§10,11. A (here again) semi-expository paper on the applications of such a theory should collect known and new results about asymptotic expansions of parameter-dependent integrals and sums, solutions of differential-functional equations, implicit functions and so on. But this requires a separate long effort.

We end by pointing out a few open problems in the just developed theory.

Open Problem 1. About the limit for an exponentially-varying function f:

-If “” all possible circumstances can occur for “” due to the great variety of functions in this class.

-If “” then “” and relations in (8.22) imply that:

either “” or “” accordind to the sign of c.

-If “” then “” and relation in (8.37) implies that “”.

-But if “” then “” and “”, and this does not automatically implies “”. Prove that “” for each f in this class or find a counterexample. It is easily checked that if “” exists in then necessarily “”; hence the only possible counterexample consists in a function “” such that “” does not exist in. See Remark 3 after the proof of Proposition 2.3 and Proposition 2.5-(III).

Open Problem 2. Provide a proof for the third relation both in (8.41) and in (8.42) without the restriction “f convex”, or exhibit a counterexample.

Open Problem 3. A counterexample to monotonicity condition in Lemma 11.1:

Find a pair of functions (f, r) satisfying all conditions in (11.6) except monotonicity such that (11.1) does not hold true.

Open Problem 4. The first sentence after (9.11), concerning the inversion of a function with a definite type of exponential variation is in fact inaccurate; for instance, if the index of exponential variation is a real nonzero number c, then the principal part of the inverse is 1/c times a logarithm and something can be said about higher-order variation of the inverse. Find results for each extended real number c.

Cite this paper

Granata, A. (2016) The Theory of Higher-Order Types of Asymp- totic Variation for Differentiable Functions. Part II: Algebraic Operations and Types of Exponential Variation. Advances in Pure Mathematics, 6, 817-867. http://dx.doi.org/10.4236/apm.2016.612064

References