World Journal of Mechanics
Vol. 1 No. 4 (2011) , Article ID: 7127 , 12 pages DOI:10.4236/wjm.2011.14024
Numerical Modelling of Non-Similar Mixed Convection Heat and Species Transfer along an Inclined Solar Energy Collector Surface with Cross Diffusion Effects
1Biomechanics and Energy Research, Aerospace Engineering, Sheffield Hallam University, Sheffield, England
2Department of Mathematics, Assiut University, Assiut, Egypt
3Department of Mathematics, Madanapalle Institute of Technology and Science, Madanapalle, India
4Department of Mathematics, Narajole Raj College, West Bengal, India
E-mail: O.Beg@shu.ac.uk, g_swapan2002@yahoo.com
Received May 10, 2011; revised June 14, 2011; accepted July 10, 2011
Keywords: Heat and mass transfer, inclined plate, Soret/Dufour effects, buoyancy, Numerical, Solar energy
ABSTRACT
An analysis is performed to study thermo-diffusion and diffusion-thermo effects on mixed convection heat and mass transfer boundary layer flow along an inclined (solar collector) plate. The resulting governing equations are transformed and then solved numerically using the local nonsimilarity method and Runge-Kutta shooting quadrature. A parametric study illustrating the influence of thermal buoyancy parameter (x), Prandtl number (Pr), Schmidt number (Sc), Soret number (Sr), Dufour number (Du) and concentration-tothermal-buoyancy ratio parameter, N, on the fluid velocity, temperature and concentration profiles as well as on local skin-friction, Nusselt and Sherwood numbers is conducted. For positive inclination angle of the plate (g = 70 degrees), flow velocity (f') is strongly increased i.e. accelerated, with thermal buoyancy force parameter (x), in particular closer to the plate surface; further into the boundary layer, x has a much reduced effect. Conversely temperature (q) and concentration (f) is decreased with increasing thermal buoyancy parameter, x. For negative plate inclination, the flow is accelerated whereas for positive inclination it is decelerated i.e. velocity is reduced. Conversely with negative plate inclination both the temperature and concentration in the boundary layer is reduced with the opposite apparent for positive inclination. Increasing Prandtl number strongly reduces temperature in the regime whereas an increase in Schmidt number boosts temperatures with temperature overshoots near the plate surface for Sc = 3 and 5 (i.e. for Sc > 1). Concentration is reduced continuously throughout the boundary layer, however, with increasing Schmidt number. A positive increase in concentration-to-thermal-buoyancy ratio parameter, N, significantly accelerates the flow in the domain, whereas negative N causes a deceleration. A velocity overshoot is also identified for N = 20, at intermediate distance from the plate surface. Negative N (thermal and concentration buoyancy forces oppose each other) induces a slight increase in both fluid temperature and concentration, with the reverse observed for positive N (thermal and concentration buoyancy forces assisting each other). Increasing Dufour number respectively causes a rise in temperature and a decrease in concentration, whereas an increase in Soret number cools the fluid i.e. reduces temperature and enhances concentration values. In the absence of Soret and Dufour effects, positive N causes a monotonic increase in local Nusselt number, Nux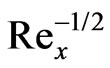 with x Cosg; for N = -1 the local Nusselt number remains constant for all values of parameter, x Cosg. Local Sherwood number,
with x Cosg; for N = -1 the local Nusselt number remains constant for all values of parameter, x Cosg. Local Sherwood number, 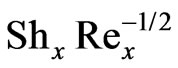 is boosted considerably with higher Schmidt numbers and also with positive N values. The computations in the absence of Soret and Dufour effects correlate accurately with the earlier study by Chen et al. (1980).
is boosted considerably with higher Schmidt numbers and also with positive N values. The computations in the absence of Soret and Dufour effects correlate accurately with the earlier study by Chen et al. (1980).
1. Introduction
Combined heat and mass transfer from inclined surfaces finds numerous applications in solar energy systems, geophysics, materials processing etc. Many studies have appeared concerning natural and also mixed convection flows. Kierkus [1] studied isothermal inclined plate natural convection boundary layer flow using a perturbation method for a Prandtl number of 0.7. Fujii and Imura [2] studied experimentally free convection from an inclined plate. Chen et al. [3] analyzed combined heat and mass transfer in mixed convection along vertical inclined plates. Uniform surface flux effects on inclined plate thermal convection were reported by Armaly et al. [4]. The combined buoyancy and wall transpiration effects on mixed convection along an inclined plate were studied by Lee and Hsu [5]. Wickern [6] examined the laminar boundary layer flow over an arbitrarily sloping plate showing that for opposing buoyancy forces singular as well as regular behaviour may prevail. Further studies have been communicated by Yan and Soong [7] in the context of evaporating inclined boundary layer convection and by Sheu and Lin [8] in combusting inclined flat plate flows. All the studies neglected Soret and/or Dufour effects. Such effects are significant when density differences exist in the flow regime. The Soret or thermo-diffusion effect refers to mass flux produced by a temperature gradient and was first reported by Ludwig [9] and Soret [10], these studies showing an increase (decrease) of salt concentration at the cold (hot) end of a tube filled with salty water. The Dufour effect refers to heat flux produced by a concentration gradient. The Soret and Dufour effects are usually minor and can be neglected in simple models of coupled heat and mass transfer. According to Platten and Legros [11], the mass fraction gradient established under the effect of thermal diffusion is very small. However, it has a disproportionately large influence on hydrodynamic stability relative to its contribution to the buoyancy of the fluid. They also argued that in most liquid mixtures the Dufour effect is negligible, but this may not be the case in gases. Mojtabi and Charrier-Mojtabi [12] have confirmed this by noting that in liquids the Dufour coefficient is an order of magnitude smaller than the Soret effect. Many investigations of Soret/Dufour effects on convection flows have been presented. Twefik and Yang [13] experimentally investigated Helium mass transfer via a porous horizontal cylinder and also confirmed the major influence of Soret and Dufour phenomena on transpiration-cooled boundary layer flows. Sparrow et al. [14] studied convection along a horizontal cylinder for a Helium-air system. Sparrow et al. [15] further conducted experiments using Hydrogen, Helium, Carbon Dioxide and Freon-12, injected via a horizontal porous cylinder, showing the strong influence of Soret effects on the flow regime for injected gases with a lower density than air (i.e. Helium and Hydrogen). Abreu et al. [16] used the Adomian’s polynomial method to study both forced and free convection laminar boundary layer heat and mass transfer with Soret and Dufour effects. Hort et al. [17] analyzed in detail the thermal convection and mass transfer in binary gas mixtures with Dufour effects. Coelho and Silva Telles [18] studied the Graetz problem with thermo-diffusion effects with conduction in the axial and transverse directions plus longitudinal advection. Weaver and Viskanta [19] reported numerical results for the Soret/Dufour effects on free convection heat and mass transfer in a cavity, indicating that species interdiffusion reduces the overall heat transfer, but increases the mass transfer through the cavity. They also showed that heat transfer due to Dufour effects is comparable to that by heat conduction and that the total mass flux through the cavity due to Soret diffusion can reach 10% to 15%. Further excellent studies of Soret and/or Dufour effects on mixed-free-forced convection, have been communicated by Kafoussias and Williams [20] for temperature-dependent viscosity and for the case of a Darcian porous regime by Anghel et al. [21]. Postelnicu [22] studied the influence of chemical reaction on heat and mass transfer from vertical surfaces in porous media considering Soret and Dufour effects. Bég et al. [23] presented the first computational study of micropolar convection boundary layers in nonlinear porous media with Soret and Dufour cross-diffusion effects, employing a finite element method with a focus on suspension polymer chemical process engineering applications. More recently Bég et al. [24] investigated (using the SparrowQuack-Boerner local non-similarity numerical method) the collective first order chemical reaction and Soret and Dufour diffusional influence on heat transfer from an inclined plate, with applications in solar energy systems. Bég et al. [25] have further studied numerically the effects of transverse magnetic field on magnetohydrodynamic convection from a stretching polymeric sheet embedded in a porous medium in the presence of Soret and Dufour effects. Bhargava et al. [26] extended the model in [25] to consider the oscillatory magneto-convection and species diffusion in a porous medium with Soret and Dufour effects with applications in magnetic materials processing. Rawat and Bhargava [27] studied viscous dissipation (Eckert number) effects in buoyancydriven micropolar convection heat transfer in a Darcian porous medium. Very recently Bég et al. [28] employed the implicit Keller box method to study Soret/Dufour effects on micropolar convection flow from a spherical body. Osalusi et al. [29] have used numerical shooting methods to study the rotating hydromagnetic disk flow with Soret/Dufour and Ohmic heating effects. In the context of combustion systems, Miller et al. [30] have described the effects of Soret and Dufour diffusion on laminar flame diffusion dynamics. Partha et al. [31] have analyzed the interaction of dispersion, buoyancy (Rayleigh number), mass transfer (Lewis number) an Soret/ Dufour gradients on magnetohydrodynamic convection in a porous regime. OKong’o and Bellan [32] have also studied Soret and Dufour effects in compressible gas flow with binary species mixing for mixtures of supercritical heptane and nitrogen and oxygen and hydrogen using fluctuation dissipation theory. They derived similarity solutions for velocity, temperature and mass fraction profiles, highlighting the strong influence of Soret and Dufour effects. The objective of the present work is to investigate the combined Soret and Dufour effects and also the influence of the inclination of the plate on the mixed convection heat and mass transfer over an inclined plate (solar energy collector) system using boundary layer theory. The effects of governing thermophysical parameters on heat and mass transfer characteristics are analyzed in detail. Numerical solutions are obtained using the Sparrow-Quack-Boerner local non-similarity numerical method and very efficient Runge-Kutta shooting quadrature., incorporating the applicable criteria that follow.
2. Mathematical Model
Consider the combined thermal convection and diffusion mass transfer in laminar boundary layer flow parallel to a flat plate which is inclined to the vertical with angle, 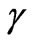 , with free stream velocity,
, with free stream velocity, 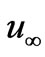 , as depicted in figure 1. The temperature of the ambient medium is
, as depicted in figure 1. The temperature of the ambient medium is 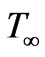 and wall temperature is
and wall temperature is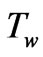 . The flow along the plate contains a species, A, slightly soluble in the fluid, B with the concentration at the plate surface being
. The flow along the plate contains a species, A, slightly soluble in the fluid, B with the concentration at the plate surface being  and the solubility of A in B far away from the plate is
and the solubility of A in B far away from the plate is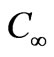 . The streamwise coordinate, x, is measured from the leading edge of the plate, parallel to the plate and the transverse coordinate, y, normal to the plate in the outward direction, for flow regimes both above and beneath the plate. Following Sparrow et al. [15], we assume the Dufour effect may be described by a second order concentration derivative with respect to the transverse coordinate in the energy conservation equation, and the Soret effect by a second order temperature derivative in the concentration equation.
. The streamwise coordinate, x, is measured from the leading edge of the plate, parallel to the plate and the transverse coordinate, y, normal to the plate in the outward direction, for flow regimes both above and beneath the plate. Following Sparrow et al. [15], we assume the Dufour effect may be described by a second order concentration derivative with respect to the transverse coordinate in the energy conservation equation, and the Soret effect by a second order temperature derivative in the concentration equation.
The forced flow, following Chen et al. [3] exists above the plate for g > 0 in the clockwise direction and beneath the plate for g < 0 (in the anti-clockwise direction). The fluid properties are assumed to be constant except the density variation in the buoyancy force term. Along with the Boussinesq approximation, the laminar boundary layer equations can be written with Soret and Dufour effects as follows:
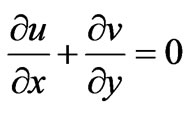 (1)
(1)
 (2)
(2)
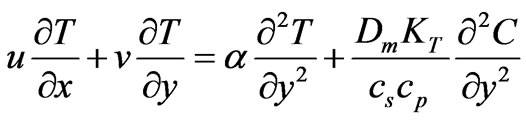 (3)
(3)
The first two terms on the RHS of equation (2) correspond to the streamwise pressure gradients induced by the combined buoyancy forces, with the plus and the minus signs representing, respectively, flows above and below the plate. The third and fourth terms correspond to the buoyancy forces generated by thermal and mass diffusion, with the plus and minus signs referring, respectively, to upward and downward forced flows. The final term in (2) on the right hand side is the viscous diffusion term. The initial and boundary conditions at the plate and in the free stream are:
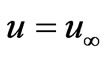 ,
, 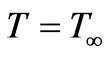 ,
,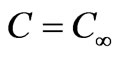 at x = 0
at x = 0
 ,
, 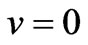 ,
, 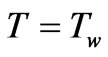 ,
, 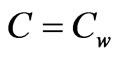 at y = 0
at y = 0
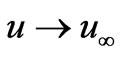 ,
, 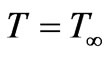 ,
,  as
as 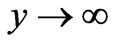 (5)
(5)
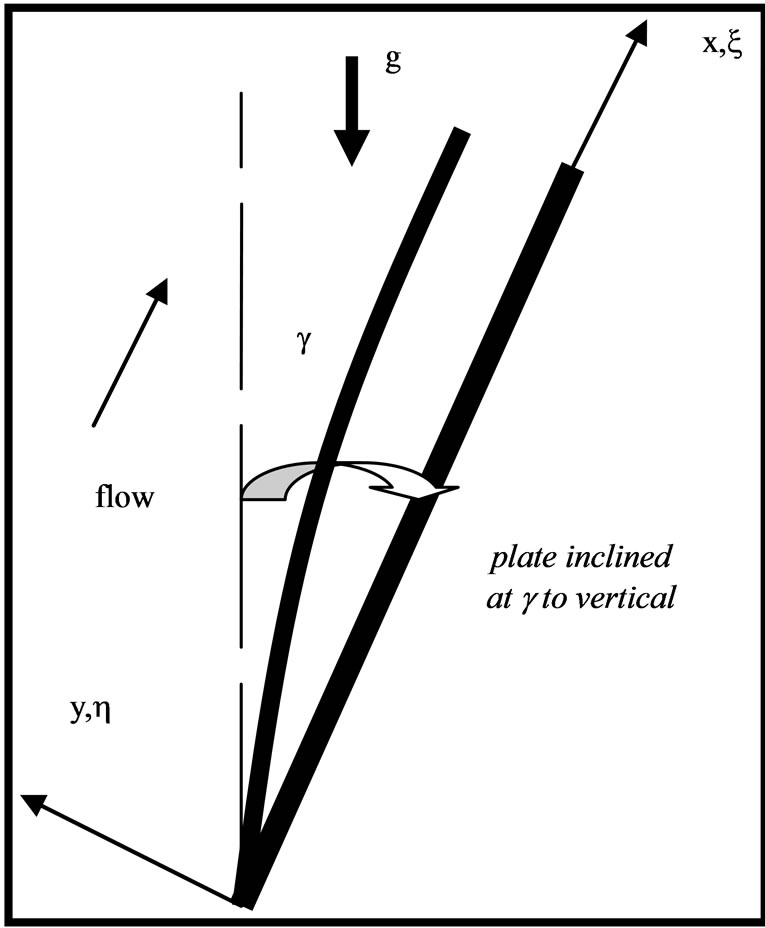
Figure 1. Physical model and coordinate system.
where u and v denote the velocity components in the xand y-directions respectively, v is the kinematic viscosity,  and
and 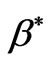 are the coefficients of thermal expansion and concentration expansion, respectively, T and C are the temperature and concentration, respectively,
are the coefficients of thermal expansion and concentration expansion, respectively, T and C are the temperature and concentration, respectively, 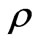 is the density, Dm is the mass diffusivity, cp is the specific heat capacity, cs is the concentration susceptibility,
is the density, Dm is the mass diffusivity, cp is the specific heat capacity, cs is the concentration susceptibility, 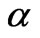 is the thermal diffusivity, Tm is the mean fluid temperature, KT is the thermal diffusion ratio. Also, as indicated by Chen et al. [3], equation (2) indicates the existence of both buoyancy induced streamwise pressure gradient terms and the buoyancy force terms for an inclined surface. The relative magnitude of these terms, however is controlled by the angle of inclination of the plate to the vertical,
is the thermal diffusivity, Tm is the mean fluid temperature, KT is the thermal diffusion ratio. Also, as indicated by Chen et al. [3], equation (2) indicates the existence of both buoyancy induced streamwise pressure gradient terms and the buoyancy force terms for an inclined surface. The relative magnitude of these terms, however is controlled by the angle of inclination of the plate to the vertical,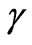 . Chen et al. [3] have shown using an orderof-magnitude analysis that the buoyancy-induced streamwise pressure gradient terms can be neglected in comparison with the buoyancy force terms provided:
. Chen et al. [3] have shown using an orderof-magnitude analysis that the buoyancy-induced streamwise pressure gradient terms can be neglected in comparison with the buoyancy force terms provided:
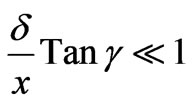 (6)
(6)
Chen et al. [3] have further shown that in terms of dimensionless boundary layer thickness  (the
(the  value for which
value for which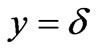 ), the condition (6) is also equivalent to the following condition:
), the condition (6) is also equivalent to the following condition:
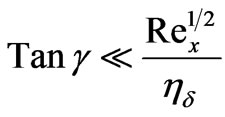 (7)
(7)
where 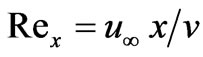 denotes the local Reynolds number. Effectively the condition (6) or (7) is valid for Tan
denotes the local Reynolds number. Effectively the condition (6) or (7) is valid for Tan 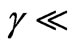 3 ~ 30 i.e. angles of inclination,
3 ~ 30 i.e. angles of inclination, 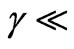 72 ~ 88 degrees. In this situation, the buoyancy-induced streamwise pressure gradient terms are omitted in equation (2) which reduces to the much simpler form:
72 ~ 88 degrees. In this situation, the buoyancy-induced streamwise pressure gradient terms are omitted in equation (2) which reduces to the much simpler form:
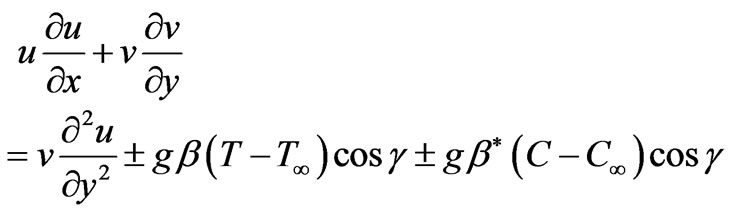 (8)
(8)
The governing boundary layer equations then comprise equations (1), (3), (4) and (8), with boundary conditions (6) subject to the condition given by (6) and (7). The special case of a vertical plate is retrieved from (8) for 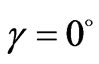 i.e.
i.e.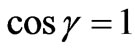 . Proceeding with the analysis we introduce the following dimensionless variables:
. Proceeding with the analysis we introduce the following dimensionless variables:
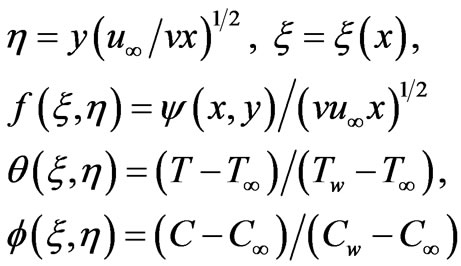 (9)
(9)
where h is the pseudo-similarity variable, x is transformed x-coordinate which represents the thermal buoyancy effect, f is a reduced stream function, q is dimensionless temperature and f is the dimensionless concentration function. The stream function 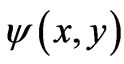 satisfies the mass conservation equation (2) with
satisfies the mass conservation equation (2) with
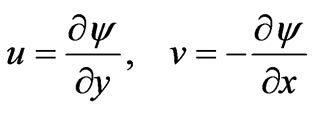 (10)
(10)
Implementing equations (9) and (10) into equations (8) and (3), (4), (5), we obtain:
 (11)
(11)
 (12)
(12)
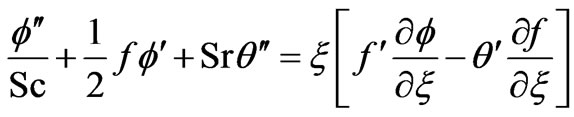 (13)
(13)
The transformed dimensionless boundary conditions are:
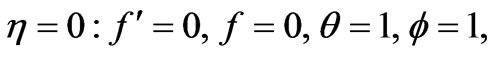 (14a)
(14a)
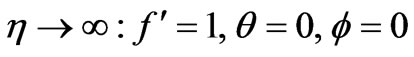 (14b)
(14b)
where denotes differentiation with respect to
denotes differentiation with respect to , Pr is the Prandtl number, Sc is the Schmidt number, the thermal buoyancy force parameter,
, Pr is the Prandtl number, Sc is the Schmidt number, the thermal buoyancy force parameter,  (which is a measure of thermal buoyancy force effect on forced convection),
(which is a measure of thermal buoyancy force effect on forced convection), 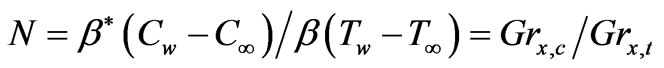 is a parameter quantifying the relative effects between buoyancy forces that arise from mass diffusion and thermal diffusion,
is a parameter quantifying the relative effects between buoyancy forces that arise from mass diffusion and thermal diffusion, 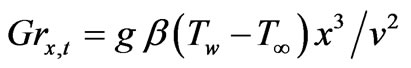 denotes local Grashof number for thermal diffusion,
denotes local Grashof number for thermal diffusion,

denotes the local Grashof number for mass diffusion respectively,
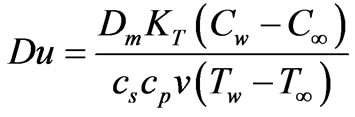
is the Dufour number,
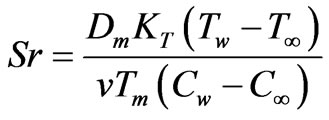
is the Soret number. The engineering design quantities of physical interest include the skin-friction coefficient (a function of local Reynolds number), Nusselt number function and Sherwood number function, which in dimensionless form are given by:
 (15)
(15)
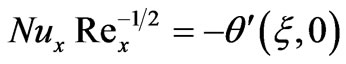 (16)
(16)
 (17)
(17)
3. Numerical Solutions
We now obtain approximate solutions to Equations (11) - (13) based on the local similarity and local nonsimilarity methods developed by Sparrow et al. [33]. More recently this approach has been employed by Bég et al. [34] to simulate electromagnetic induction flows. Chang et al. [35] employed local nonsimilarity modeling to investigate unsteady rheological flow. Bég et al. [36] studied gravity-driven magneto-micropolar flow on a slope using both local nonsimilarity and network simulation methods. Details and convergence aspects are described in [34] to [36]. For the first level of truncation the 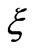 derivatives in equations (10) - (13) can be neglected. Thus, the governing equations for the first level of the truncation are:
derivatives in equations (10) - (13) can be neglected. Thus, the governing equations for the first level of the truncation are:
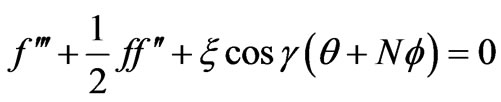 (18a)
(18a)
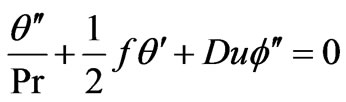 (18b)
(18b)
 (18c)
(18c)
subject to the boundary conditions:
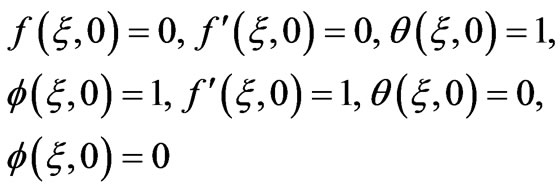 (19)
(19)
For the second level of truncation, we introduce,
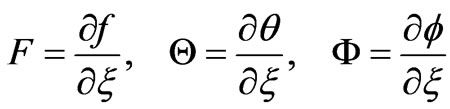 (20)
(20)
and restore all of neglected terms in the first level of truncation. Thus, the governing equations are:
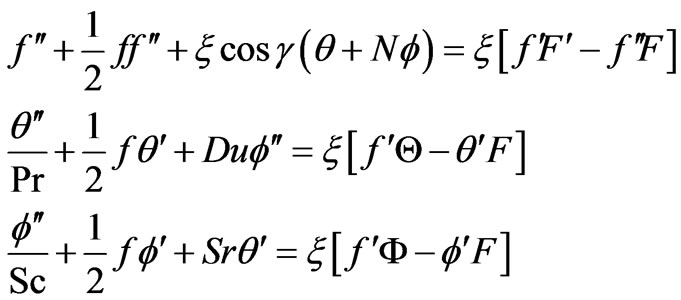 (21)
(21)
subject to the boundary conditions:
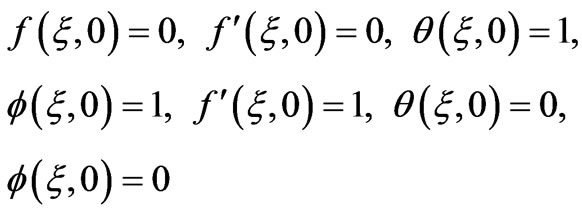 (22)
(22)
The introduction of the three new dependent variables 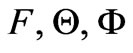 in the problem requires three additional equations with appropriate boundary conditions. This can be obtained by differentiating equations (21) with respect to
in the problem requires three additional equations with appropriate boundary conditions. This can be obtained by differentiating equations (21) with respect to  and neglecting the terms
and neglecting the terms 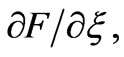
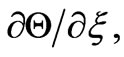 and
and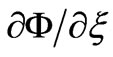 , which leads to:
, which leads to:
 (23)
(23)
 (24)
(24)
The coupled non-linear eqautions (18), (21) and (23) with the boundary conditions (19), (22) and (24) are solved using fourth order Rung-Kutta method with a shooting technique. This method has also been applied very recently to simulate viscoelastic flow in porous media by Bég and Makinde [37] and nanofluid thermal convection by Rashidi et al. [38], showing excellent efficiency compared with semi-analytical methods such as the differential transform technique with Padé approximants. The step size 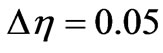 is used to obtain the numerical solution with five-decimal place accuracy as the criterion of convergence.
is used to obtain the numerical solution with five-decimal place accuracy as the criterion of convergence.
4. Results and Discussion
The values of Sr and Du have been selected to ensure that the product Sr Du is constant, assuming that the mean temperature is constant. The default values for the control parameters are selected as: Pr = 0.7 (air), Sr = 1, Du = 0.05 [i.e. Sr Du = 0.05], N = 1, Sc = 0.2 (hydrogen gas as the species diffusing in air). In all computations we present the variation of f', q and f versus h for the velocity, temperature and species diffusion boundary layers, and also
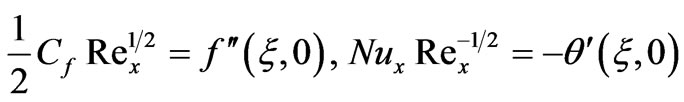
and 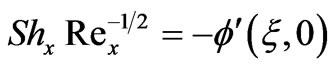 versus x as a simulation of skin friction function, Nusselt number function and Sherwood number, respectively. In figures 2 to 4 we have plotted the variation of dimensionless velocity, temperature and concentration function with the thermal buoyancy parameter,
versus x as a simulation of skin friction function, Nusselt number function and Sherwood number, respectively. In figures 2 to 4 we have plotted the variation of dimensionless velocity, temperature and concentration function with the thermal buoyancy parameter, .
.
For positive inclination angle of the plate (g = 70 degrees), we observe flow velocity (f') is strongly increased i.e. accelerated, with a rise in thermal buoyancy force parameter (x), in particular closer to the plate surface; further into the boundary layer, the profiles begin to converge for all values of x i.e. they tend towards unity as specified in the boundary conditions. A distinct velocity overshoot is identified for x values greater than or equal to unity; for x = 0 and 0.1, this overshoot vanishes. Strong thermal buoyancy therefore has a significant acceleration effect on the boundary layer flow. Temperature function (q) however, as illustrated in figure 2 is adversely affected with increasing thermal buoyancy parameter, x. Profiles all descend smoothly from the maximum value at the wall to zero in the free stream. The value N = 1 implies that the thermal and concentration (species diffusion) buoyancy forces are of the same order of magnitude. Dimensionless concentration function (f) is decreased also with increasing thermal buoyancy parameter, x, as shown in figure 4. The differences in values are however smaller over the same range of x values, compared with the temperature distribution (figure 3). In all cases the velocity, temperature and concentration are minimized with x = 0.
In figures 5 to 7 the effects of plate inclination on the dimensionless velocity, temperature and concentration function with coordinate transverse to the plate (h) are illustrated, again with both Soret and Dufour effects present, for N = 1. When g < 0 i.e. negative plate inclination, in figure 5, the velocity (f') is reduced at first i.e. flow is initially decelerated nearer the plate surface; however further away it is accelerated and infact overshoots. For the case of the vertical plate (g = 0 degrees) and for positive inclination, velocities are always monotonic distributions and no overshoot is present.
With g > 0 i.e. 30 degrees and 80 degrees, velocity is reduced i.e. flow is decelerated, largely owing to gravitational effects. Conversely in figure 6, with negative plate inclination (g < 0) the temperature (q) decreases slightly;

Figure 2. f' versus η for various ξ values.
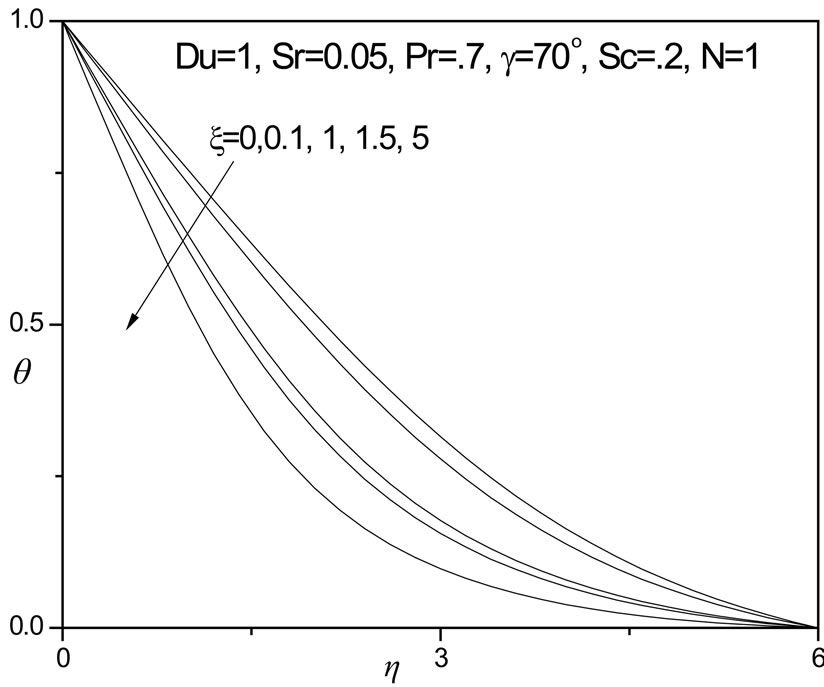
Figure 3. θ versus η for various ξ values.
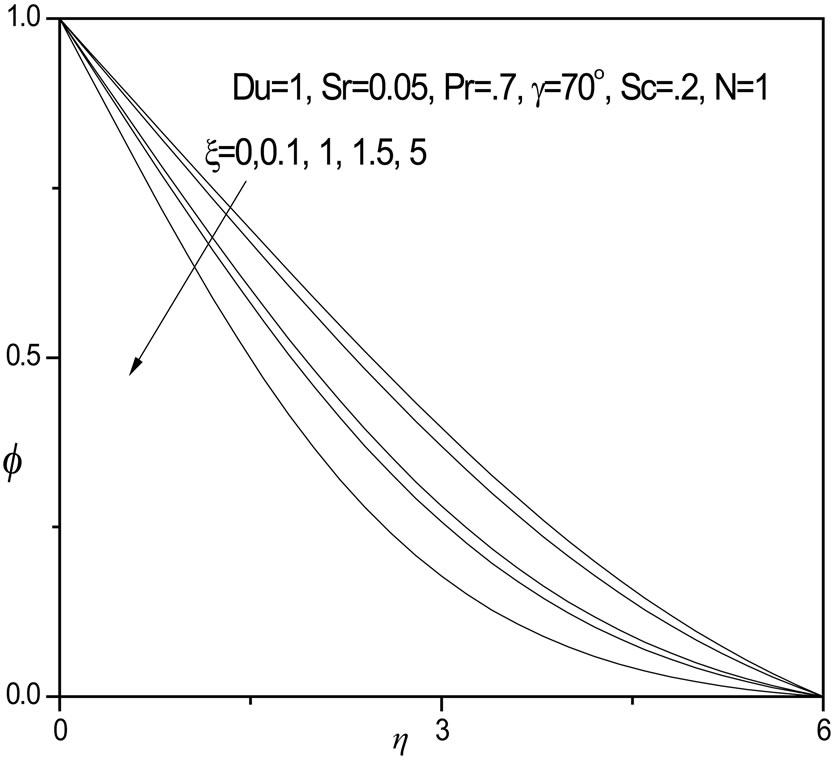
Figure 4. 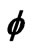 versus η for various ξ values.
versus η for various ξ values.
Figure 5. f' versus η for various γ values.

Figure 6. θ versus η for various γ values.
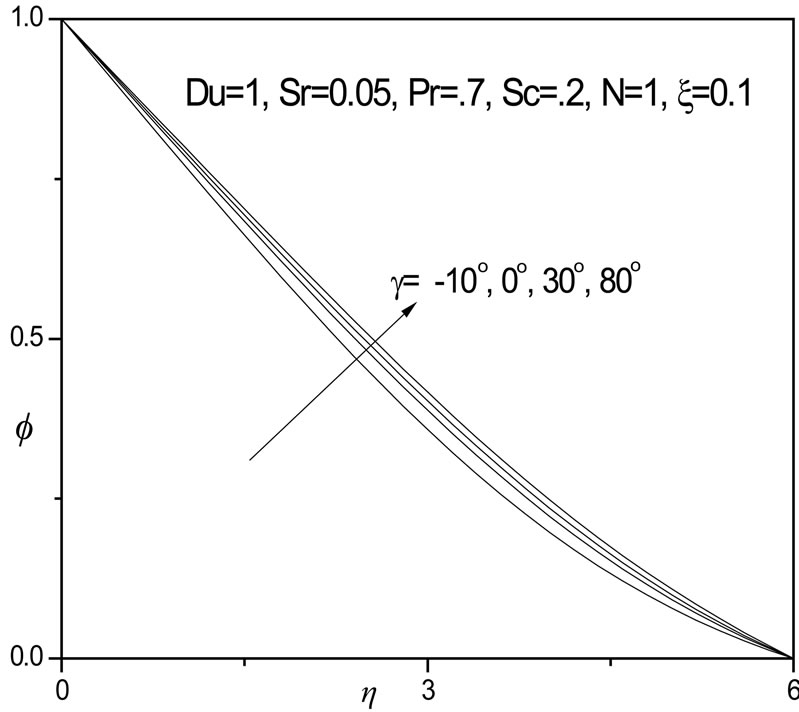
Figure 7.  versus η for various γ values.
versus η for various γ values.
for a vertical plate temperatures are greater than for the negatively inclined plate; temperatures are further increased marginally with positive inclination of the plate. In figure 7, a similar response is observed for the concentration distributions (f) which as with temperature are reduced with negative plate inclination, but enhanced with positive inclination and also for a vertical plate scenario (g = 0 degrees).
Figure 8 shows the response of temperature function through the boundary layer regime to Prandtl number, Pr. Larger Pr values imply a thinner thermal boundary layer thickness and more uniform temperature distributions across the boundary layer. Smaller Pr fluids have higher thermal conductivities so that heat can diffuse away from the vertical surface faster than for higher Pr fluids (thicker boundary layers). Physically Pr = 0.7 is representative for air or hydrogen and Pr = 1 for water. Pr = 10, 20 may correspond to oils and lubricants. Pr encapsulates the ratio of momentum diffusivity to thermal diffusivity. With a decrease in Pr temperatures as seen in figure 8 are substantially increased. The lowest temperatures correspond to the highest value of Prandtl number (Pr = 20). No temperature overshoot is observed. In figure 9 the effect of Schmidt number, Sc on temperature profiles (q) is plotted, for low value of thermal buoyancy parameter (x = 0.1). Larger values of Sc correspond to Methanol diffusing in air (Sc = 1.0) and Ethylbenzene in air (Sc = 2.0), as indicated by Gebhart et al. [39]. When Pr and Sc differ, then the thermal and species diffusion regions are of different extents. Temperature is continuously decreased from the wall for Sc = 0.1 and Sc = 0.5. For Sc = 0.5 the profile is almost linear in decay. For Sc = 1, the concentration and velocity boundary layers will have approximately the same thickness; temperatures also

Figure 8. θ versus η for various Pr values.

Figure 9. θ versus η for various Sc values.
decrease smoothly from the plate surface to the free stream. For Sc > 1 we observe a significant temperature overshoot a short distance from the plate surface. The highest temperature corresponds to Sc = 5 (maximum Schmidt number). For both Sc = 3 and 5, temperature profiles descend sharply after attaining the velocity overshoot. Figure 10 indicates that concentration (f) is reduced continuously throughout the boundary layer, however, with increasing Schmidt number. Sc measures the relative effectiveness of momentum and mass transport by diffusion. Larger values of Sc are equivalent to reducing the chemical molecular diffusivity i.e. less diffusion therefore takes place by mass transport. As a result concentration is decreased in the boundary layer.
The influence of the concentration-to-thermal-buoyancy ratio parameter, N, on dimensionless velocity (f'), temperature (q) and concentration function (f) with coordinate transverse to the plate (h) are shown again with both Soret and Dufour effects present, in figures 11 to
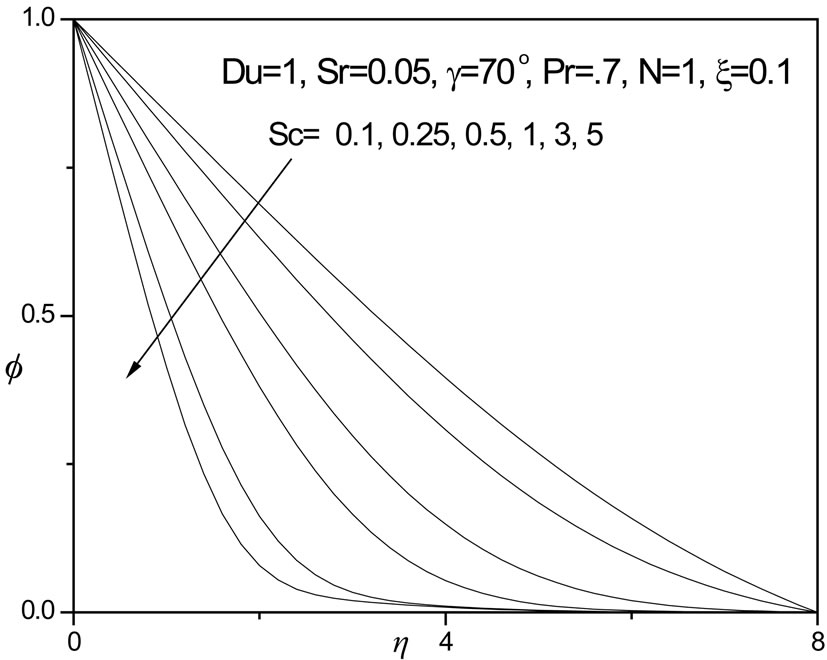
Figure 10. 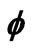 versus η for various Sc values.
versus η for various Sc values.
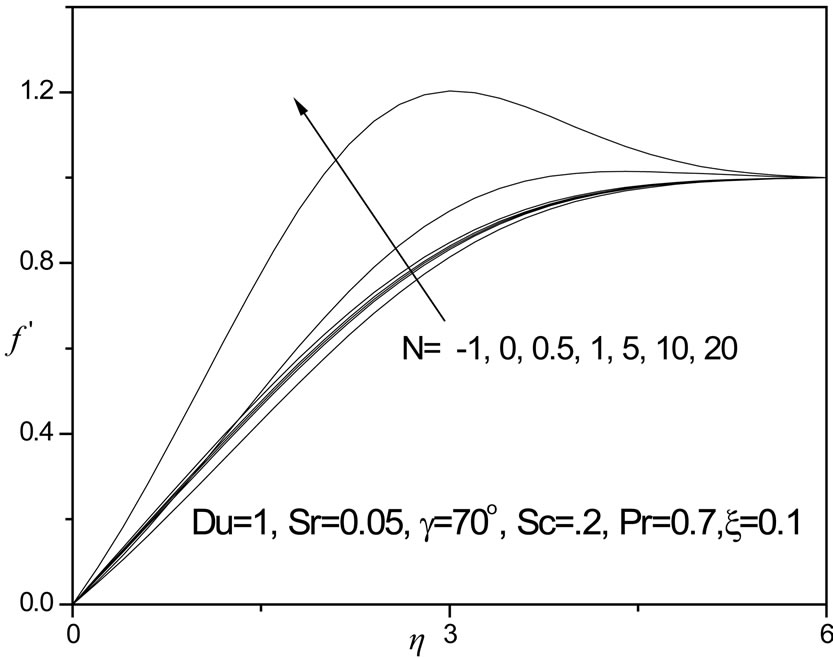
Figure 11. f' versus η for various N values.
13. A positive rise in N clearly induces an increase in velocity as seen in figure 11; the flow is significantly accelerated for N = 20, where once again a velocity overshoot is computed at intermediate distance from the plate surface (h ~ 3). For N = 0.5, 1, 5, 10, no velocity overshoot is apparent although velocities are increased in the regime continuously. For N < 0 i.e. -1, the thermal and species buoyancy forces oppose each other and this causes a decrease in flow velocity compared with the scenario where both forces are absent (N = 0) or are aiding each other (N > 0). In figure 12 negative N causes a very slight rise in fluid temperature i.e. heats the fluid regime slightly; for N = 0, and for positive N (thermal and concentration buoyancy forces assisting each other), this trend is reversed with a decrease in temperature i.e. cooling of the boundary layer regime. In figure 13, a similar response for the concentration distribution is observed as in the case of the temperature distribution, with f values increasing fractionally with a negative N value and decreasing with positive N values. Opposing buoyancy forces (N < 0) therefore enhance species diffusion in the regime whereas aiding buoyancy forces (N > 0) inhibit species diffusion in the boundary layer. A similar response was reported by Rawat and Bhargava [27] and also Partha et al. [31].
In figures 14 and 15 the combined effect of Dufour number (Du) and Soret number (Sr) on the temperature and concentration distributions, respectively, in the regime are shown. We study the simultaneous increase (and decrease) of these parameters so that their product remains constant at 0.05, following Anghel et al. [21] and Postelnicu [22]. Increasing Dufour number causes a rise in temperature whereas an increase in Soret number cools the fluid i.e. reduces temperature, as observed in figure 14. Conversely in figure 15, we observe that a rise in Du decreases the concentration values in the boundary layer, whereas a rise in Soret number increases values.
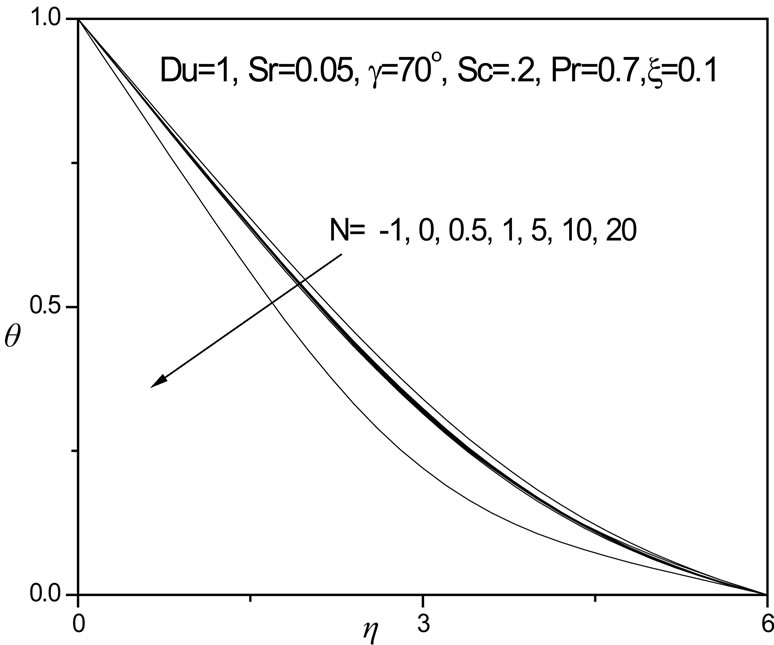
Figure 12. θ versus η for various N values.
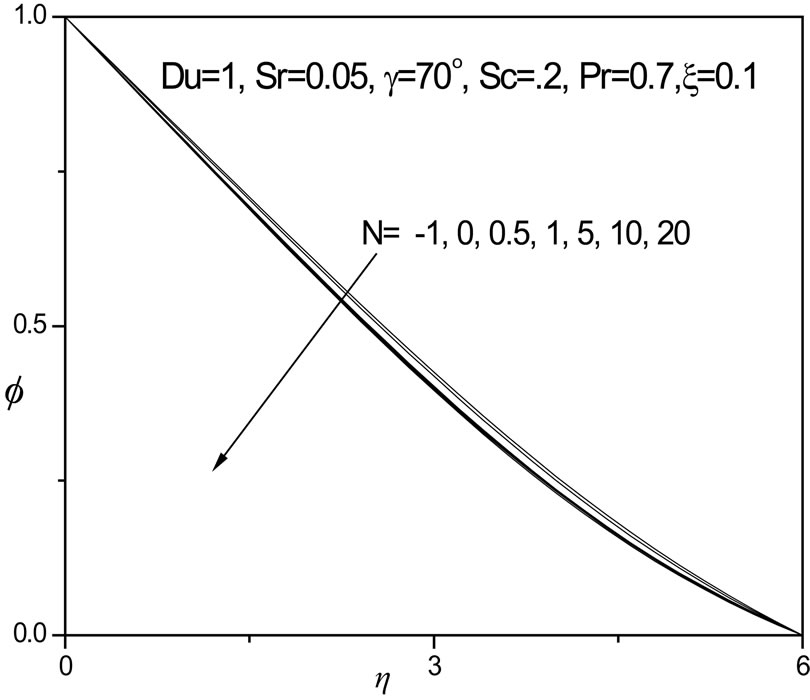
Figure 13.  versus η for various N values.
versus η for various N values.
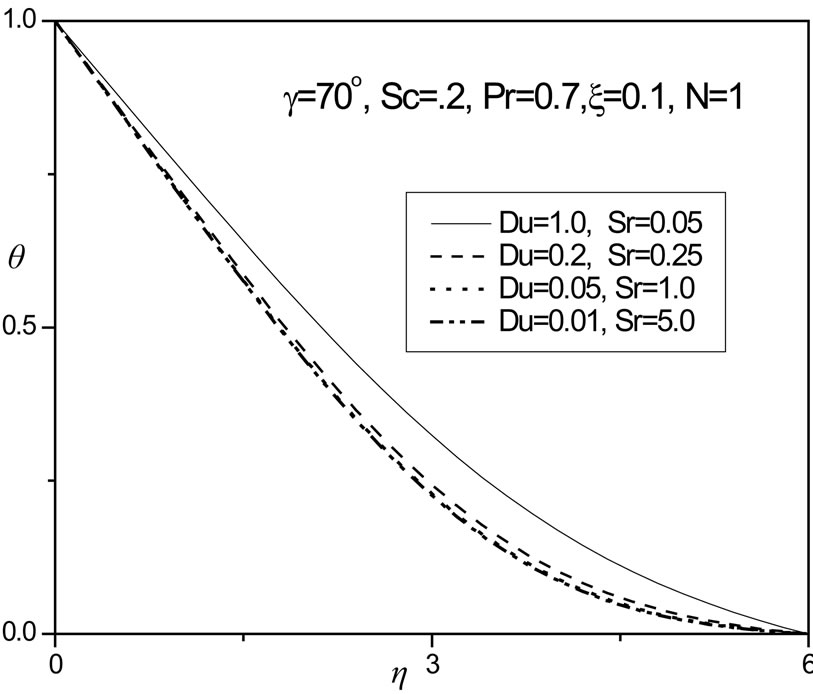
Figure 14. θ versus η for various Du & Sr values.
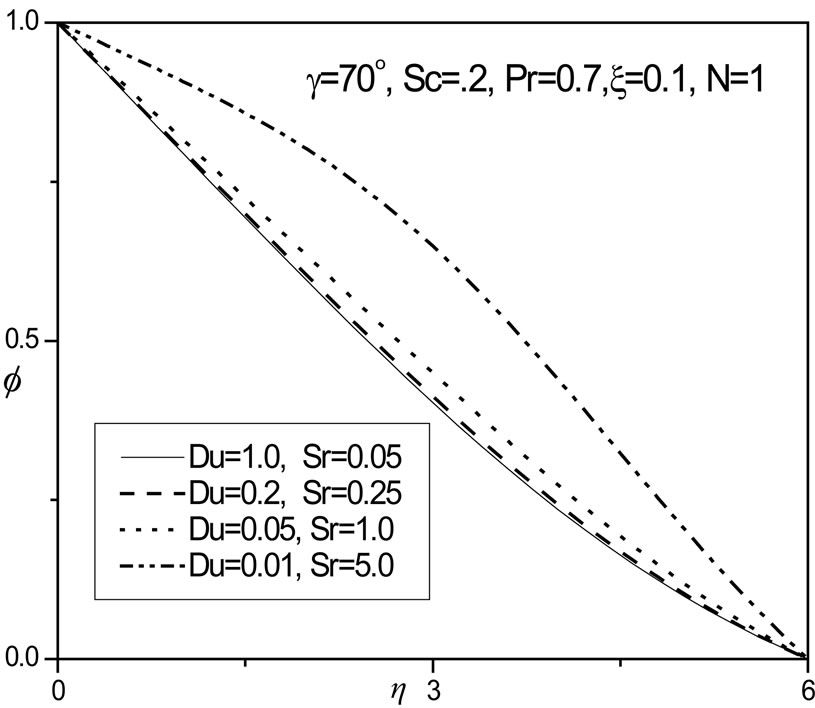
Figure 15. 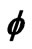 versus η for various Du & Sr values.
versus η for various Du & Sr values.
In figures 16 and 17, we have presented the variation of the local Nusselt number, 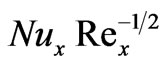 and local Sherwood number,
and local Sherwood number,  , respectively with the product of the thermal buoyancy force parameter, x, and Cosg i.e.
, respectively with the product of the thermal buoyancy force parameter, x, and Cosg i.e. 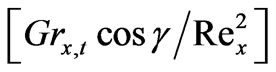 as originally computed by Chen et al. [3], with Soret and Dufour effects neglected. Our results agree almost exactly with the computations in [3]. We infer from figures 16 and 17 that in the absence of Soret and Dufour effects, the situations where N = 0 (buoyancy forces absent) and N > 0 (aiding buoyancy forces), generate a continuous increase in local Nusselt number,
as originally computed by Chen et al. [3], with Soret and Dufour effects neglected. Our results agree almost exactly with the computations in [3]. We infer from figures 16 and 17 that in the absence of Soret and Dufour effects, the situations where N = 0 (buoyancy forces absent) and N > 0 (aiding buoyancy forces), generate a continuous increase in local Nusselt number, 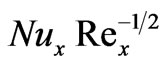 with thermal buoyancy force parameter, x; for N = -1 (opposing buoyancy forces) the local Nusselt number remains unchanged for all values of thermal buoyancy parameter, x. Local Sherwood number,
with thermal buoyancy force parameter, x; for N = -1 (opposing buoyancy forces) the local Nusselt number remains unchanged for all values of thermal buoyancy parameter, x. Local Sherwood number,  as seen in figure 17, is boosted considerably with an increase in Schmidt number from 0.7 through 1.0 to 7.0, for N > 0; however it is reduced with N < 0 compared with N = 0 and N > 0.
as seen in figure 17, is boosted considerably with an increase in Schmidt number from 0.7 through 1.0 to 7.0, for N > 0; however it is reduced with N < 0 compared with N = 0 and N > 0.

Figure 16. Local Nusselt number results.
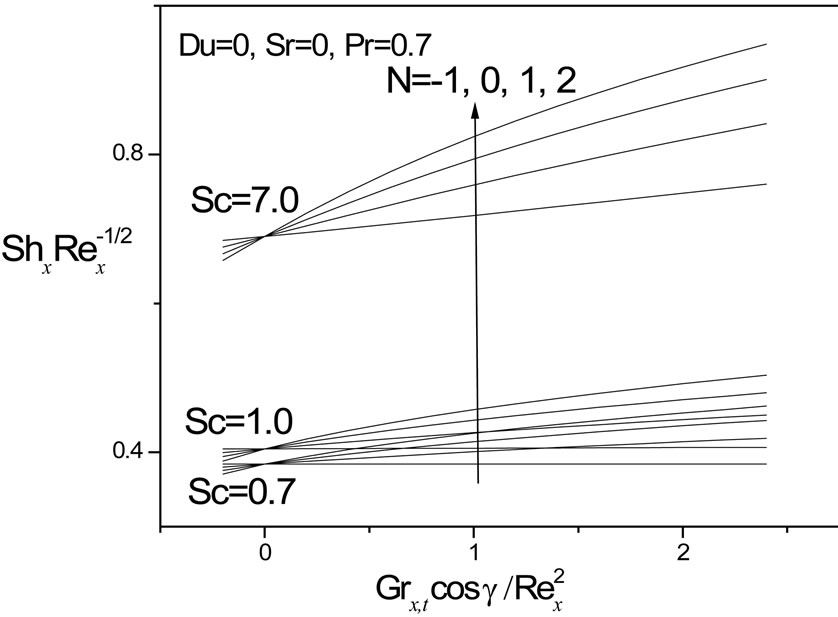
Figure 17. Local Sherwood number results.
We finally note that the local nonsimilarity method (LNM) has been extensively validated by the authors recently, as has the numerical shooting quadrature used in the present article, with other techniques including network simulation, finite elements and differential quadrature methods. Details of validation are provided in Bég et al. [24,25] and also in Bég et al. [34], Chang et al. [35] and Bég et al. [36]. There is great confidence therefore in the present numerical solutions and comparisons have been omitted herein for conservation of space.
5. Conclusions
Numerical solutions have been obtained for the mixed convection heat and mass transfer boundary layer flow along an inclined plate in the presence of Soret and Dufour thermo-diffusion effects, using the local nonsimilarity method and a Runge-Kutta shooting technique. For positive inclination of the plate (g > 0), a rise in Dufour number (Du) increases temperatures in the boundary layer but decreases the concentration; conversely an increase in Soret number (Sr) reduces temperature and elevates concentration values. For positive inclination angle of the plate (g = 70 degrees), flow is accelerated, with thermal buoyancy force parameter (x) whereas temperature (q) and concentration (f) are reduced with increasing thermal buoyancy parameter, x. For negative and positive plate inclinations (g < 0 and g > 0), the flow is accelerated and decelerated respectively; for these plate orientations however the temperature and concentration functions are decreased and increased respectively. Temperatures are enhanced and concentrations reduced in the regime with increasing Schmidt number. A positive increase in concentration-to-thermal-buoyancy ratio parameter, N, significantly increases flow velocity with the converse effect for negative N. A velocity overshoot is also identified for N = 20, at intermediate distance from the plate surface. With Soret and Dufour effects neglected, N > 0 induces a continuous rise in local Nusselt number, 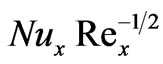 and local Sherwood number,
and local Sherwood number,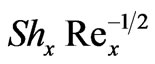 .
.
The present study is being extended to consider Soret/ Dufour effects in rotating disk flows [40] of interest in membrane oxygenators and also consider dusty (fluidparticle suspension) effects in photovoltaic collector systems [41]. It is also envisaged that homotopy methods will be employed in such studies [42]. The results of these investigations will be reported in the near future.
REFERENCES
- W. T. Kierkus, “An Analysis of Laminar Free Convection Flow and Heat Transfer about an Inclined Isothermal Plate,” International Journal of Heat and Mass Transfer, Vol. 11, No. 2, 1968, pp. 241-252. doi:org/10.1016/0017-9310(68)90153-1
- T. Fujii and H. Imura, “Natural-Convection Heat Transfer from a Plate with Arbitrary Inclination,” International Journal of Heat and Mass Transfer, Vol. 15, No. 4, 1972, pp. 755-764. doi:org/10.1016/0017-9310(72)90118-4
- T. S. Chen, C. F. Yuh and A. Moustsoglou, “Combined Heat and Mass Transfer in Mixed Convection along Vertical and Inclined Plates,” International Journal of Heat and Mass Transfer, Vol. 23, No. 4, 1980, pp. 527- 537. doi:org/10.1016/0017-9310(80)90094-0
- B. F. Armaly, T. S. Chen and N. Ramachandran, “Correlations for Laminar Mixed Convection on Vertical, Inclined and Horizontal Flat Plates with Uniform Surface Heat Flux,” International Journal of Heat and Mass Transfer, Vol. 30, No. 2, 1987, pp. 405-408. doi:org/10.1016/0017-9310(87)90129-3
- S. L. Lee and K. Hsu, “Interaction of Surface Suction/Blowing with Buoyancy Force on Mixed Convection Flow Adjacent to an Inclined Flat Plate,” International Journal of Heat and Mass Transfer, Vol. 32, No. 10, 1989, pp. 1989-1991. doi:org/10.1016/0017-9310(89)90167-1
- G. Wickern, “Mixed Convection from an arbitrarily Inclined Semi-Infinite Flat Plate—I. The Influence of the Inclination Angle,” International Journal of Heat and Mass Transfer, Vol. 34, No. 8, 1991, pp. 1935-1945. doi:org/10.1016/0017-9310(91)90205-S
- W. M. Yan, and C. Y. Soong, “Convective Heat and Mass Transfer along an Inclined Heated Plate with Film Evaporation,” International Journal of Heat and Mass Transfer, Vol. 38, No. 7, 1995, pp. 1261-1269. doi:org/10.1016/0017-9310(94)00241-M
- W. J. Sheu and M. C. Lin, “Thermal Ignition in Buoyancy-Driven Boundary Layer Flows along Inclined Hot Plates,” International Journal of Heat and Mass Transfer, Vol. 39, No. 10, 1996, pp. 2187-2190. doi:org/10.1016/0017-9310(95)00283-9
- C. Ludwig, “Diffusion Zwichen Unfleigh Erwarmten Orten Gleich Zusammengesetz Losungen,” Sitzungbsber. Kaiser. Akad. Wiss. (Mathem.-Naturwiss. Cl.), Wien, Vol. 65, 1856, pp. 539.
- C. Soret, “Sur l’état d’équilibre que prend, du point de vue de sa Concentration, une Dissolution Saline Primitivement Homogène, Dont Duex parties Sort Portèes à des Temperatures Différentes,” C. R. Arch. Science Physical Nature, Genève, Vol. 2, 1879, pp. 48-61.
- J. Platten and J. C. Legros, “Convection in Liquids,” Springer, Berlin, 1984.
- A. Mojtabi and M. C. Charrier-Mojtabi, “Double Diffusive Convection in Porous Media,” Handbook of Porous Media, Marcel Dekker, New York, 2000, pp. 559-603.
- O. E. Tewfik and J. W. Yang, “The Thermodynamic Coupling between Heat and Mass Transfer in Free Convection with Helium Injection,” International Journal of Heat and Mass Transfer, Vol. 6, No. 10, 1963, pp. 915-923. doi:org/10.1016/0017-9310(63)90082-6
- E. M. Sparrow, W. J. Minkowycz and E. R. G. Eckert, “Effects of Diffusion Thermo and Thermal Diffusion on Heat Transfer, Flow and Mass Transfer for the Helium-Air Boundary Layer in Stagnation Flow,” ASME Journal of Heat Transfer, Vol. 86C, 1964, p. 508.
- E. M. Sparrow, C. J. Scott, R. J. Frostron and W. A. Ebert, “Experiments on the Diffusion Thermo Effect in a Binary Boundary Layer with Injection of Various Gases,” ASME Journal of Heat Transfer, Vol. 87, 1965, pp. 321-327.
- C. R. A. Abreu, M. F. Alfradique and A. S. Telles, “Boundary Layer Flows with Dufour and Soret Effects. I: Forced and Natural Convection,” Chemical Engineering Science, Vol. 61, No. 13, 2006, pp. 4282-4289. doi:org/10.1016/j.ces.2005.10.030
- W. Hort, S. J. Linz and M. Lucke, “Onset of Convection In Binary Gas Mixtures: Role of the Dufour Effect,” Physical Review A, Vol. 45, No. 6, 1992, pp. 3737-3748. doi:org/10.1103/PhysRevA.45.3737
- R. M. L. Coelho and A. Silva-Telles, “Extended Graetz Problem Accompanied by Dufour and Soret Effects,” International Journal of Heat and Mass Transfer, Vol. 45, No. 15, 2002, pp. 3101-3110. doi:org/10.1016/S0017-9310(02)00043-1
- A. Weaver and R. Viskanta, “Natural Convection Due to Horizontal Temperature and concentration Gradients: 2- Species Interdiffusion, Soret and Dufour Effects,” International Journal of Heat and Mass Transfer, Vol. 34, No. 12, 1991, pp. 3121-3133. doi:org/10.1016/0017-9310(91)90081-O
- N. G. Kafoussias and E. M. Williams, “Thermal-Diffusion and Diffusion-Thermo Effects on Mixed FreeForced Convective and Mass Transfer Boundary Layer Flow with Temperature Dependent Viscosity,” International Journal of Engineering Science, 1995, pp. 1369- 1384.
- M. Anghel, H. S. Takhar and I. Pop, “Dufour and Soret Effects on Free Convection Boundary Layer over a Vertical Surface Embedded in a Porous Medium,” Studia University Babes-Bolyai Mathematica, Vol. XLV, No. 4, 2000, pp. 11-21.
- A. Postelnicu, “Influence of Chemical Reaction on Heat and Mass Transfer by Natural Convection form Vertical Surfaces in Porous Media Considering Soret and Dufour Effects,” Heat and Mass Transfer, Vol. 43, No. 6, 2007, pp. 595-602. doi:org/10.1007/s00231-006-0132-8
- B. O. Anwar, R. Bhargava, S. Rawat and E. Kahya, “Numerical Study of Micropolar Convective Heat and Mass Transfer in a Non-darcian Porous Regime with Soret/Dufour Diffusion Effects,” Emirates Journal of Engineering Research, Vol. 13, No. 2, 2008, pp. 51-66.
- B. O. Anwar, A. B. Tasveer, A. Y. Bakier and V. Prasad, “Chemically-Reacting Mixed Convective Heat and Mass Transfer along Inclined and Vertical Plates with Soret and Dufour Effects: Numerical Solutions,” International Journal of Applied Mathematics and Mechanics, Vol. 5, No. 2, 2009, pp. 39-57.
- O. Anwar Bég, A. Y. Bakier and V. R. Prasad, “Numerical Study of Free Convection Magnetohydrodynamic Heat and Mass Transfer from a Stretching Surface to a Saturated Porous Medium with Soret and Dufour Effects,” Computational Materials Science, Vol. 46, No. 1, 2009, pp. 57-65. doi:org/10.1016/j.commatsci.2009.02.004
- R. Bhargava, R. Sharma and O. Anwar Bég, “Oscillatory Chemically-Reacting MHD Free Convection Heat and Mass Transfer in a Porous Medium with Soret and Dufour Effects: Finite Element Modeling,” International Journal of Applied Mathematics and Mechanics, Vol. 5, No. 6, 2009, pp. 15-37.
- S. Rawat and R. Bhargava, “Finite Element Study of Natural Convective Heat and Mass Transfer in a Micropolar Fluid-Saturated Porous Regime with Soret/Dufour Effects,” International Journal of Applied Mathematics and Mechanics, Vol. 5, No. 2, 2009, pp. 58-71.
- O. Anwar Bég, V. R. Prasad, B. Vasu, N. Bhaskar Reddy, Q. Li and R. Bhargava, “Free Convection Heat and Mass Transfer from an Isothermal Sphere to a Micropolar Regime with Soret/Dufour Effects, International Journal of Heat and Mass Transfer, Vol. 54, 2011, pp. 9-18. doi:org/10.1016/j.ijheatmasstransfer.2010.10.005
- E. Osalusi, J. Side and R. Harris, “Thermal-Diffusion and Diffuse-Thermal Effects on Combined Heat and Mass Transfer of a Steady MHD Convective and Slip Flow Due to a Rotating Disk with Viscous Dissipation and Ohmic Heating,” International Communications in Heat Mass and Transfer, Vol. 35, No. 8, 2008, pp. 908-918. doi:org/10.1016/j.icheatmasstransfer.2008.04.011
- R. S. Miller, S. Palle and C. Nolan, “Effects of Soret and Dufour Diffusion on Laminar Diffusion Flames at Large Pressures,” 56th Annual Meeting of Fluid Dynamics Division, American Physical Society, Meadowlands, New Jersey, November 23-25, 2003.
- M. K. Partha, P. V. S. N. Murthy and G. P. Raja-Sekhar, “Soret and Dufour Effects in a Non-Darcy Porous Medium,” ASME Journal of Heat Transfer, Vol. 128, No. 6, 2006, pp. 605-610. doi:org/10.1115/1.2188512
- N. OKong’o and J. Bellan, “Real-Gas Effects on Mean Flow and Temporal Stability of Binary Species Mixing Layers,” AIAA Journal, Vol. 41, No. 12, 2003, pp. 2429-2443. doi:org/10.2514/2.6842
- E. M. Sparrow, H. Quack and J. Boerner, “Local Nonsimilarity Boundary Layer Solutions,” AIAA Journal, Vol. 8, No. 11, 1970, pp. 1936-1942. doi:org/10.2514/3.6029
- O. A. Bég, A. Y. Bakier, V. R. Prasad and S. K. Ghosh, “Nonsimilar, Laminar, Steady, Electrically-Conducting Forced Convection Liquid Metal Boundary Layer Flow with Induced Magnetic Field Effects,” International Journal of Thermal Sciences, Vol. 48, No. 8, 2009, pp. 1596-1606. doi:org/10.1016/j.ijthermalsci.2008.12.007
- T-B. Chang, A. Mehmood, O. Anwar Bég, M. Narahari, M. N. Islam and F. Ameen, “Numerical Study of Transient Free Convective Mass Transfer in a Walters-B Viscoelastic Flow with Wall Suction,” Communications in Nonlinear Science and Numerical Simulation, Vol. 16, No. 1, 2010, pp. 216-225. doi:org/10.1016/j.cnsns.2010.02.018
- O. A. Bég, J. Zueco and T. B. Chang, “Numerical Analysis of Hydromagnetic Gravity-Driven Thin Film Micropolar Flow along an Inclined Plane,” Chemical Engineering Communications, Vol. 198, No. 3, 2011, pp. 312- 331.
- O. Anwar Bég and O. D. Makinde, “Viscoelastic Flow and Species Transfer in a Darcian High-Permeability Channel,” Journal of Petroleum Science and Engineering, Vol. 76, No. 3-4, 2011, pp. 93-99. doi:org/10.1016/j.petrol.2011.01.008
- M. M. Rashidi and O. Anwar Bég, “DTM-Padé Modeling of Natural Convective Boundary Layer Flow of a Nanofluid Past a Vertical Surface,” International Journal of Thermal and Environmental Engineering, Vol. 4, 2012, pp. 13-24.
- B. Gebhart, et al., “Buoyancy-Induced Flows and Transport,” Hemisphere, New York, 1988.
- O. Anwar Bég, J. Zueco and L. M. López-Ochoa, “Network Numerical Analysis of Optically-Thick Hydromagnetic Slip Flow from a Porous Spinning Disk with Radiation Flux, Variable Thermophysical Properties and Surface Injection Effects,” Chemical Engineering Communications, Vol. 198, No. 3, 2011, pp. 360-384.
- J. Zueco, P. Eguía, E. Granada, J. Míguez and O. Anwar Bég, “An Electrical Network for the Numerical Solution of Transient MHD Couette Flow of a Dusty Fluid: Effects of Variable Properties and Hall Current,” International Communications in Heat and Mass Transfer, Vol. 37, No. 10, 2010, pp. 1432-1439. doi:org/10.1016/j.icheatmasstransfer.2010.07.025
- M. M. Rashidi, M. Rastegari and O. Anwar Bég, “A Study of Non-Newtonian Flow and Heat Transfer over a Non-Isother-Mal Wedge Using the Homotopy Analysis Method,” Chemical Engineering Communications, 2011.

