International Journal of Astronomy and Astrophysics
Vol.2 No.4(2012), Article ID:26045,6 pages DOI:10.4236/ijaa.2012.24026
Precise Underground Observations of the Partial Solar Eclipse of 1 June 2011 Using a Foucault Pendulum and a Very Light Torsion Balance
1Astronomical Observatory, Stefan cel Mare University, Suceava, Romania
2Main Astronomical Observatory of National Academy of Sciences, Kiev, Ukraine
Email: dimitrieolenici@hotmail.com, pugach@mao.kiev.ua, pugach@yandex.ru
Received July 3, 2012; revised August 12, 2012; accepted August 21, 2012
Keywords: Solar Eclipse; Allais Effect; Torsion Balance
ABSTRACT
Simultaneous observations of the solar eclipse on 06/01/2011 were carried out using a Foucault pendulum and a torsion balance. The instruments were installed in a salt mine, where the interference was minimal. Both instruments clearly reacted to the eclipse. We conclude that these reactions should not be considered as being gravitational effects.
1. Introduction
Interest in the study of nonconventional phenomena during solar eclipses was largely triggered by the researches in the 1950s by Maurice Allais, who later became a Nobel laureate. While observing the behavior of a paraconical pendulum during an eclipse, he discovered an anomaly, in particular an abrupt variation of the speed of precession of the oscillation plane [1,2]. Similar phenomena during solar eclipses were recorded many times, but data collected have not been able to convince scientists. Many scientists remain at their opinion that the observed changes can be properly explained by a very trivial way—fluctuations in temperature, atmospheric pressure or other environmental parameters. However, C. Duif presented in 2004 a review article [3] which argued that none of the external factors may not be the cause of such sudden changes.
This effect, now known as the Allais Effect (AE), has been quite widely studied over the years by a number of researchers (for a list of references, see [4]).
In particular, parallel observations using torsion balances (TB) and pendulums of different designs have recently been conducted. These simultaneous observations have showed that devices which differ in their operating principles can react to the solar eclipse in similar ways [5,6].
The results of these and similar experiments make the Allais effect yet more puzzling. As yet, no general approach has been formulated for the interpretation of the measurement results. Moreover, the new attitude is growing that the AE is not primarily related to gravity, or at least is not best explained as a phenomenon framed purely in terms of Newtonian/Einsteinian gravitational physics [4].
This paper continues the description of a series of simultaneous observations made with the use of a pendulum and a torsion balance (TB).
2. Observations
2.1. Context of the Observations
The partial solar eclipse of 01.06.2011 took place over the northern hemisphere, and was visible in East Asia, Canada, Greenland and Iceland. It was not visible in Romania, and there it occurred late at night. The eclipse began at 19 h 25 m UT and terminated at 23 h 07 m. Conjunction in right ascension (21 h 22 m) and the time of maximum phase (21 h 16 m) almost coincided. The Sun at this time was in the constellation of Taurus.
In order to minimize possible interference, our measurements were performed in a disused salt mine in Cacica (northern Romania). The mine is an extensive network of passages and chambers, dug through a huge monoblock of sodium chloride (NaCl), of size roughly some cubic kilometers. A torsion balance was installed in a small isolated chamber at a depth of 40 m, and a Foucault pendulum was set up in a huge chamber of area more than 1000 m2 at a depth of about 75 m.
The observations thus were performed in an underground environment in almost ideal conditions:
• absence of any mechanisms within 50 m, such as motors and generators or moving objects;
• absence of electrical and wireless devices;
• cool still air;
• no mechanical vibrations;
• complete silence and absence of strong light and heat radiation;
• very good temperature stability maintained over decades;
• In addition, the salt monoblock provided reliable protection from external electromagnetic radiation.
2.2. Observations with the Torsion Balance
The observations were made with the instrument WEB_3, of which a basic description is given in [7]. However, in this instrument a very light aluminum disk with a diameter of 120 mm and weighing about 80 mg was used instead of a straw beam. This disc was suspended in a horizontal position inside a cubical enclosure, using a thin monofilament (25 - 30 microns) from a silkworm cocoon.
The faces of the cube were made of glass plates measuring 24 × 24 cm2 and having thickness of 2 mm. The edges of the cube were treated on the outside with silicone sealant and sealed with tape (Figure 1).
A webcam connected to a computer was mounted above the upper face of the cube. The image from the camera was processed by custom software that determines the position of a marker and calculates its polar coordinates relative to the vertical axis of symmetry of the cube. One measurement was taken each minute. The torsion balance was installed, adjusted and put into operation on the afternoon of 30 May, i.e. more than 50 hours before the eclipse, which was a period sufficient for the instrument to reach a state of thermodynamic equilibrium with the environment. Over this period, no outsiders entered the torsion balance chamber.
2.3. Observations with the Foucault Pendulum
In this experiment we utilized a Foucault pendulum of 8 m length with a bob (B) of lead 8 kg mass and having an aerodynamic form, being shaped as a horizontal lens with diameter of 20 cm and 4 cm central thickness (Figure 2).
The suspension was provided by an aluminum ring (R) of 6 cm diameter having, at the top of its inner circumference, a pivot (p) whose point was supported upon a ball (b). The ball oscillated in a spherical cup (c) of 10 cm radius. The spherical cup was attached to a bracket firmly fixed to the ceiling of the experimental chamber.
To the lower side of the ring, opposite to the pivot, there was fixed a small rod (r), from which was suspended a steel wire (w) of 1 mm diameter that supported the bob.
The distance between the ball and the center of the

Figure 1. A demonstration model of a disk torsion balance.
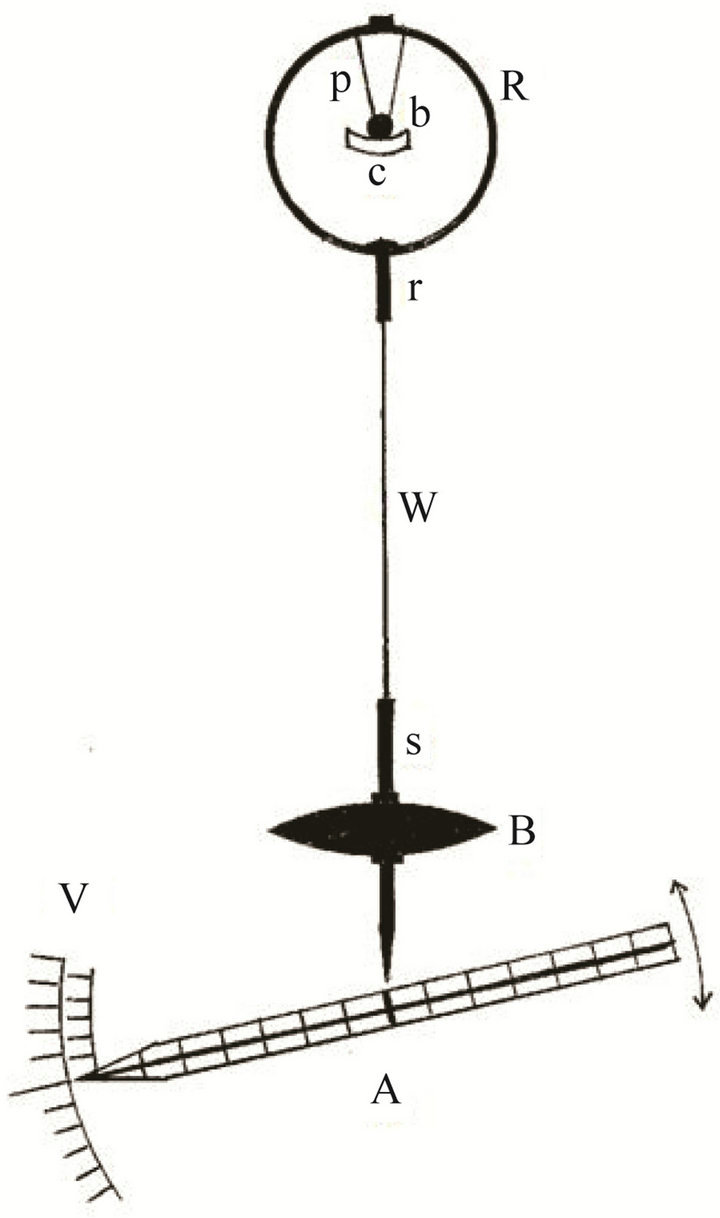
Figure 2. Schematic representation the experiment with the Foucault pendulum.
pendulum bob was 8 m.
Through the bob passed a support screw (s) of 8 mm diameter and 70 cm length. The bob was mounted on this screw, held between two nuts. The part of screw under the bob was 20 cm long, and had a sharp lower end which served as a pointer and oscillated over an alidade (A).
The upper part of the screw was 46 cm long, and had on its upper end a nut like a cap, to which was attached the steel wire hanging from the suspension ring.
An angular vernier (V) having precision of 0.1˚ was provided to the point of the alidade. At the center of the alidade there was provided a millimetric cross, with which it was possible to perform measurements of the semi-axis of the ellipse of oscillation of the pendulum.
3. The Results
3.1. Measurements with the Torsion Balance
The measurement results for 1 and 2 June are shown in Figure 3. The red and blue lines show different phases of the reaction of the apparatus. The dashed vertical lines show the beginning and end of the contact of the Moon’s penumbra with the Earth. The azimuth is measured clockwise from south.
3.2. Measurements with a Foucault Pendulum
For comparison, the determinations with the Foucault pendulum were performed on three nights at approximately the same time interval straddling the eclipse maximum, as follows:
31 May: 20 h 0 m - 22 h 50 min (three series of determinations) (Table 1).
1 June: 19 h 40 m - 22 h 40 m (five series of determinations) (Table 2).
2 June: 19 h 05 m - 21 h 0 m (four series of determinations) (Table 3).
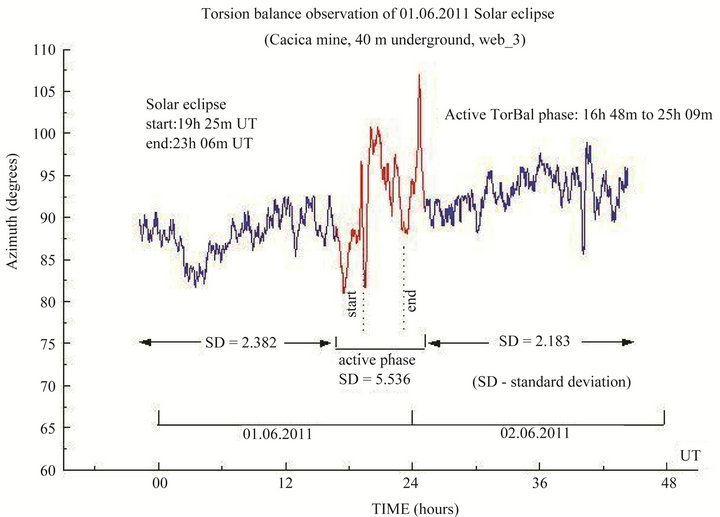
Figure 3. Results of torsion balance observations of 1st June, 2009 solar eclipse.

Table 1. The azimuths on 31 May.

Table 2. The azimuths on 1 June.

Table 3. The azimuths on 2 June.
Each time, the pendulum was started at the same initial amplitude (a) of 68 cm.
After every start the azimuth readings were taken in a series of five determinations at intervals of 7 minutes 6 seconds, which corresponded to 75 oscillations.
In the tables below we present the start times of the pendulum and the incremental azimuth values after each interval of 7 min 06 sec.
The average values (Av.val.) of corresponding determinations at the same times after start (T.af.st.) are shown in bold.
If we compare the graphs of final values of azimuth we see that on the night of the eclipse the azimuth was dramatically reduced (Figure 4). The average values were: 9.06˚ ± 1.43˚ in night before eclipse; 5.34˚ ± 0.14˚ in the night of eclipse and 7.2˚ ± 0.18˚ in the night after eclipse.
We therefore affirm that in this experiment the Allais effect was again confirmed. Speed of precession of the oscillation plane of a pendulum during a solar eclipse does change.
On the other hand we know that the Foucault effect at the latitude of Cacica (47˚38′) is 0.17008˚/min.
In Table 4, we give the values of the Foucault effect and the average values we obtained.
In the graphs below, Figure 5, we see that the curves of azimuth in the nights before and after eclipse were above the Foucault effect (F.ef.) curve, while the curve during eclipse was below the Foucault effect curve.
An interesting fact is that the curves before and after the eclipse had a tendency to be concave, whereas the curve during eclipse had a tendency to be convex. This show very clearly that during the eclipse a horizontal effect like a torsion appeared, with a tendency to brake the precession of the plane of oscillation of the pendulum. In the case of torsion balance this force was able to rotate the balance, because it had extremely low mass.
The fact was very interesting that the torsion balance graph during the eclipse had a tendency to decrease. Also the final azimuth values of the Foucault pendulum (5.7˚; 5.2˚; 5.4˚; 5.5˚; 4.9˚) exhibited the same tendency. So this experiment demonstrated excellent correlation.
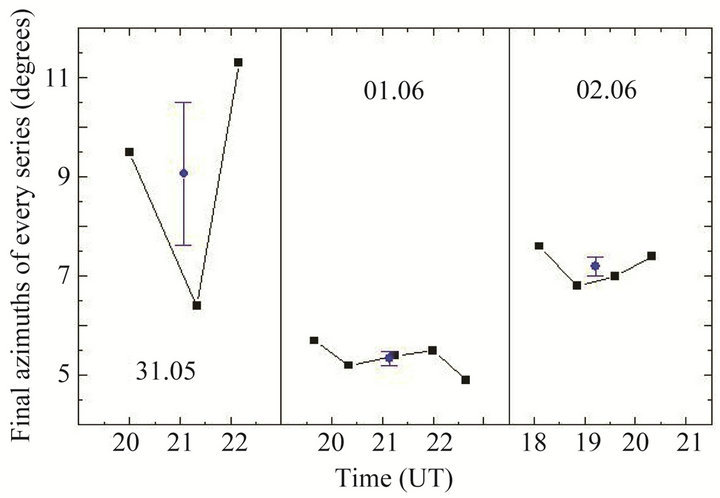
Figure 4. The diagram shows that on June 1 azimuths measured were minimal.
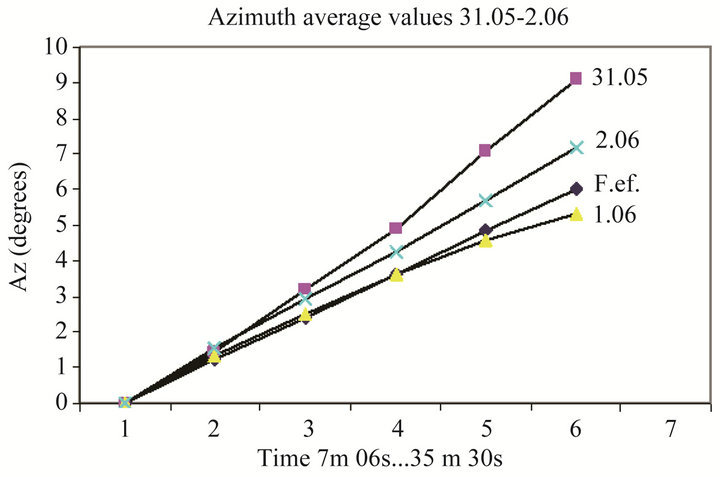
Figure 5. The curve during eclipse (1.06) had a tendency to be convex and located below the F.ef. line.
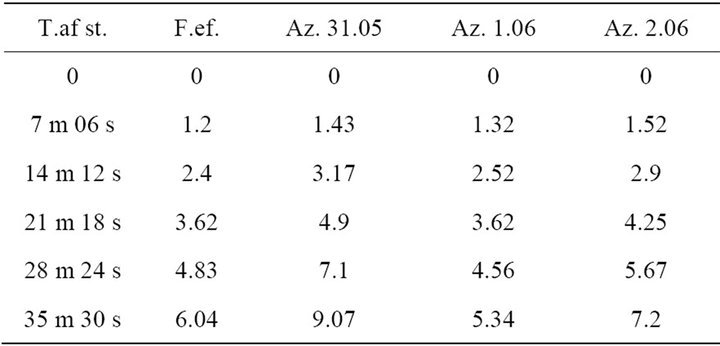
Table 4. Resulting azimuths.
4. Analysis of the Results
A simple analysis of the TB results shows that, during the entire observational period, the most severe reaction of WEB_3 device was during the period of the eclipse. At this time, the amplitudes of the samples significantly increased. Thus the entire series of measurements may be conceptually divided into 3 parts:
1) an interval before the eclipse (pre-eclipse portion), from 20 h 51 m on 31 May to 16 h 48 m on 1 June.
2) a central portion including all phases of the eclipse, from 16 h 48 m on 1 June to 25 h 09 m (corresponding to 01 h 09 m on 2 June);
3) an interval after the eclipse (post-eclipse portion), from 25h 09m to the end of measurement.
The central portion we will conditionally call the active phase of the eclipse. Simple statistical calculations show that the above division has an objective justification. We calculated the standard deviations (SD) of the random variable for each of the three conditional fragments and obtained the following values:
1. SD1 = ±2.382 2. SD2 = ±5.536 3. SD3 = ±2.183 Thus the active phase is objectively present, because the parameter SD2 over interval 2 is almost 2.5 times higher than the average values over intervals of 1 and 3. Moreover, the fact that the active phase coincided with the eclipse indicates that the eclipse bore a causal relationship with this phenomenon.
From this we may conclude that the increased reaction of the torsion balance during a solar eclipse was caused by this phenomenon. It is noteworthy that the duration of the active phase (around 8 h 21 m) was much longer than the duration of the eclipse itself (3 h 41 m). In fact, the torsion balance ‘experienced’ the eclipse for 2.5 h before it started.
There are also two other arguments which reinforce our opinion that on 1 June our torsion balance reacted to a solar eclipse, and that the increased TB reaction during the interval 2 was not caused by other random factors.
First of all, we have found some common structural elements in the reactions of torsion balances during the solar eclipses of 2009, 2010 and 2011.
Different colored lines in Figure 6 show the reactions of torsion balances during solar eclipses of the last three years. The arrow labeled with “max” shows the maximum phases of the eclipses. Listed below are several items easily identified which are common to all the curves.
1) All the curves have a preceding minimum (preminimum) of different width and length, denoted by A.
2) There always is a sharp peak P between this preminimum and the maximum value (these are not marked on the graphs because they are obvious). It is significant
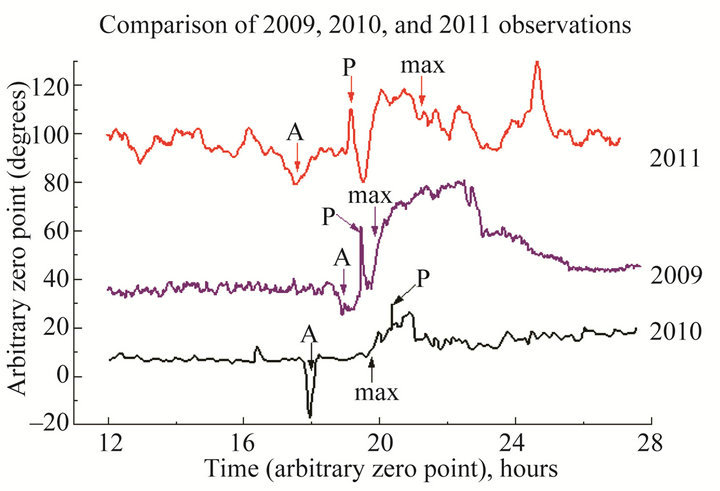
Figure 6. Symbols “A”, “P” and “max” indicate common structural elements for three solar eclipses of 2009, 2010 and 2011.
that a similar peak was also recorded during paraconical pendulum observations of the solar eclipse on 26.01.2009 (see reference [5]).
3) The reaction of a torsion balance to an eclipse is commonly manifested by increase of its readings, i.e. the TB generally rotates in a clockwise direction. Therefore, the average of the readings after the eclipse is generally higher than before the eclipse. This tendency is also evident in Figure 4.
The same features, with varying degrees of clarity, can be found in our other observations of solar eclipses performed during other years [8].
Second, we have found that there is statistically significant rather than just visual correlation between the curves for 2009 and 2011. From the curve obtained in 2011, we isolated the segment AB between the time points A = 14 h 18 m and B = 20 h 45 m. This time segment corresponds to the initial stage of the eclipse.
This segment is shown in Figure 5 by the red line. From the 26.01.2009 observations we extracted the analogous segment beginning from the time 08 h 14 m (for 26.01.2009 years); this is shown in Figure 5 by the purple line. Visual assessment shows that the red and purple lines in this graph exhibit an obvious similarity.
Rigorous statistical analysis confirms that the similarity of these two curves is objectively justified. These two numerical value series are compared in Figure 7. The calculated correlation coefficient CC is:
СС = 0.651.
This relatively high correlation coefficient (Figure 8) indicates that the basis of both processes is some common cause, which in our case can be considered as determinative. We think that this common determining factor is the solar eclipse affecting the behavior of the torsion balance. Since this fact is global in nature, it is quite plausible that it might affect the behavior of a Foucault pendulum and/or a paraconical pendulum.

Figure 7. The similarity of the two curves (2009 and 2011) eliminates the possibility of accidental coincidence.

Figure 8. The high value of the correlation coefficient (CC = 0.651) confirms the similarity of the two curves.
This is supported by the analysis of our 1-2 June 2011 measurements with the Foucault pendulum, as presented above.
The above combined analysis of data obtained in different year convincingly demonstrates that the torsion balance really does react to solar eclipses. Moreover, it does not seem to matter in what part of the planet and at what time this astronomical phenomenon occurs. In addition, a number of scientific publications (see for example [4]), as well as our earlier works [5,6]) have claimed that a solar eclipse has some impact on the behavior of physical pendulums of different designs.
5. Conclusions
Some further evidence has been obtained that non-conventional phenomena occur during solar eclipses. These phenomena are called “non-conventional” because they do not fit into the framework of established scientific beliefs about the world (paradigm), and as yet no adequate explanation has been found.
Half a century ago scientists assumed that the Allais effect was due to gravity, but now this view appears rather questionable, and many workers in the field regard it with skepticism. The results presented in this paper reinforce the position of the skeptics: the torsion balance of our design is not sensitive to changes in the gravitational potential, but nevertheless it appears to “feel” the solar eclipse. Thus, the Allais effect seems more complex and mysterious than it appeared a couple of decades ago. This mystery should stimulate the enthusiasm of scientists and promote more research in this direction.
6. Acknowledgements
Both authors thank Thomas Goodey for help with the experiment organization and preparation of this article. We also are grateful to Mr. Corneliu Zup—director of the Salina Cacica, and Mr. Doru Slevoaca—chief of the Cacica salt mine for permission and help in organization of our experiments.
REFERENCES
- M. F. C. Allais “Mouvement du Pendule Paraconique et Eclipse Totale de Soleli du 30 Juin 1954,” French Academy of Science, Vol. 245, No. 1, 1957, pp. 2001- 2003.
- M. Allais, “L’anisotropie de L’espace,” Clement Juglar, Paris, 1998.
- C. Duif, “A Review of Conventional Explanations of Anomalous Observations during Solar Eclipses,” Proceedings of the Conference on the Pioneer Anomaly, Bremen, May 2004.
- H. A. Munera, “Should the Laws of Gravitation Be Reconsidered?” Apeiron, Montreal, 2011, p. 448.
- T. J. Goodey, A. F. Pugach and D. Olenici, “Correlated Anomalous Effects Observed during the August 1st 2008 Solar Eclipse,” Journal of Advanced Research in Physics, Vol. 1, No. 2, 2010, Article ID: 021007.
- A. F. Pugach and D. Olenici, “Observations of Correlated Behavior of Two Light Torsion Balances and a Paraconical Pendulum in Separate Locations during the Solar Eclipse of 26.01.2009,” Advances in Astronomy, Vol. 2012, 2012, Article ID 263818. HUdoi:10.1155/2012/263818U
- A. F. Pugach and D. P. Vorobiov, “The Device for Registration of Beam Position of an Extralight Torsion Balance,” Kinematics and Physics of Celestial Bodies, Vol. 26, No 6, 2010, pp. 76-81. HUdoi:10.3103/S088459131006005XU
- A. F. Pugach “Observations of the Astronomical Phenomena by Torsion Balance,” Physics of Consciousness and Life, Cosmology and Astrophysics, Vol. 9, No. 2, 2009, pp. 30-51.

