ABSTRACT

DNA separation techniques have drawn attention because of their uses in applications such as gene analysis and manipulation. There have been many studies utilizing micro-fabricated devices for faster and more efficient separations than traditional methods using gel electrophoresis. Although many experimental studies have presented various new devices and methods, computational studies have played a pivotal role in this development by identifying separation mechanisms and by finding optimal designs for efficient separation conditions. The simulation of DNA separation methods in micro-fabricated devices requires the correct capture of the dynamics and the structure of a single polymer molecule that is being affected by an applied flow field or an electric field in complex geometries. In this work, we summarize the polymer models (the bead-spring model, the bead-rod model, the slender-body model, and the touching-bead model) and the methods, focusing on Brownian dynamics simulation, used to calculate inhomogeneous fields taking into consideration complex boundaries (the finite element method, the boundary element method, the lattice-Boltzmann method, and the dissipative particle dynamics simulation). The worm-like chain model (adapted from the bead-spring model) combined with the finite element method has been most commonly used but other models have shown more efficient and accurate results. We also review the applications of these simulation approaches in various separation methods and devices: gel electrophoresis, post arrays, capillary electrophoresis, microchannel flows, entropic traps, nanopores, and rotational flows. As more complicated geometries are involved in new devices, more rigorous models (such as incorporating the hydrodynamic interactions of DNA with solid boundaries) that can correctly capture the dynamic behaviors of DNA in such devices are needed.

Keywords:

DNA Separation, Single Polymer Dynamics, Brownian Dynamics Simulation, Microfluidics, Electrophoresis, Entropic Trap, Microchannel

1. Introduction

Gene analysis is one of the essential tasks for advances in biotechnology. Gene analysis would not be possible without DNA manipulation techniques. With the advent of lab-on-a chip technology in the early 2000s, the manipulation of DNA molecules in micro-fabricated microfluidic devices began to flourish [1] [2] [3] . This led to further research regarding the properties and the dynamics of DNA in micro or nano-scale geometries [4] [5] [6] . Among the DNA manipulation techniques, DNA separation is a crucial step in gene analysis such as genome mapping and sequencing [7] . It has also been used in other applications such as DNA sorting, diagnosis and fingerprinting [8] .

The mobility of DNA molecules is an important transport property in DNA separation techniques. DNA molecules tend to have size-independent similar mobility in free solution because the overall charge to mass ratio does not change much with molecular weight. This leads to difficulties in separating longer molecules [9] [10] . However, it has been found that size-dependent flow behaviors are possible in a flow system where DNA molecules interact with complex geometries. Examples of this include the porous structure in gel electrophoresis and microscale flows with inhomogeneous force (or flow) fields [11] [12] . Indeed, microfluidic devices have become increasingly attractive in the field of DNA separation due to their ability to operate rapidly with only a small volume of sample [11] . Nevertheless, it is expensive and time consuming to optimize the geometry of the device through new fabrications and numerous runs [13] , or slab gel modifications in the case of gel electrophoresis [14] . Hence, several theoretical models have been developed to estimate overall mobility and diffusion coefficients [15] [16] [17] . However, computer simulations can give specific details of DNA trajectory and structure, rather than simplified ensemble average properties. Therefore, computational simulations of DNA dynamics in microscale flows have contributed to the development of experimental separation techniques and in identifying separation mechanisms [13] [18] . In this study, we review the computational simulation approaches for DNA dynamics, specifically the size-based separation of double stranded DNA, in microscale flows.

As mentioned earlier, for DNA separation to be feasible, size-dependent dynamics or mobility must be caused by interactions with solid boundaries in the flow system. Therefore, single polymer dynamics and inhomogeneous force field calculations must be calculated simultaneously and self-consistently [19] . Through these combined simulations, separation mechanisms can be identified. This approach can be applied to other recent studies of DNA in confinement [2] , such as DNA within nanochannels [5] . It can also be applied to flowing colloidal systems, such as drug delivery particles in the bloodstream [20] .

2. Single Polymer Dynamics

The time and length scales for DNA separations are typically in similar or larger ranges of a single DNA molecule in a free space (length scales of 10 - 100 μm and relaxation times of 0.01 - 1 s). These scales are also larger than the base-pair molecular level so molecular dynamic simulation is not suitable. Indeed, the sequence of base-pairs does not affect the physical properties of DNA. Additionally, DNA separations are usually performed in a dilute concentration of DNA solution, which leads to an assumption that interaction with other DNA molecules can be neglected in modeling. In those situations, Brownian dynamics (BD) simulation of a coarse-grained single polymer model is used for DNA separation simulation [21] [22] [23] . One of the advantages of utilizing coarse grained models is reduced complexity. This allows for model properties to be calculated quickly while maintaining sufficient accuracy for molecular properties. However, the polymer model must be carefully chosen to minimize the loss of polymer physics details required to describe the separation behaviors in interest [21] [22] [23] [24] . In this section, we summarize the polymer models and corresponding BD simulation methods used in DNA separation simulations by focusing on the commonly used bead-spring model and briefly mentioning other models. Note here that we excluded Monte-Carlo (MC) approaches, which were used in earlier times [25] [26] or in recent studies on DNA structure in nano-scale confinements [5] [27] .

2.1. Bead-Spring Model

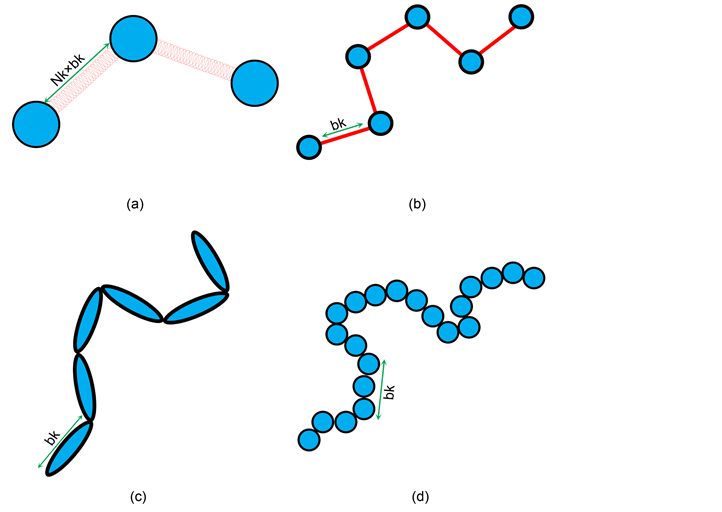
The most common polymer model for DNA separation is the “bead-spring” model. Each “bead” represents a sub-chain larger than a Kuhn length, b_k (a shortest polymer segment length which is not bent or stretched by thermal fluctuation. DNA has b_k~0.1 nm which is much larger than that of typical polymer), and the “springs” lie between these beads. These springs are used to maintain the conformational entropy inside a sub-chain (represented by the beads). This is shown in Figure 1(a) [28] [29] . This model is a basic model used for many other polymer systems, such as entangled polymeric liquids [30] , or networks [31] because the bead-spring model can describe the elasticity of these polymer systems in a simple way. The number of beads, N, (or the number of springs, N-1) must be carefully chosen so that computational time and the details of dynamics are balanced.

The force balance on the i-th bead in a bead-spring chain model is given by Equation (1):

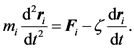(1)

Here, m is the mass of the bead, r_i is the position vector of the bead, t is the time, F is the total net hydrodynamic force acting on the bead, and ζ is the drag coefficient. Stokes flow condition is usually applicable to microscale flows, hence, to DNA separations, too. When using Stokes flow condition, inertial effect is considered negligible (overdamping system). Thus, the left hand side of Equation (1) can be assumed to be 0. Electric fields are used in gel electrophoresis, a common method of DNA separation. Thus, along with considering flow field, electric field (non-hydrodynamic force) is also evaluated to give an equation of motion:

(2)

Here, U(r_i) is the unperturbed fluid velocity at the bead position, μ is the electrophoretic mobility, E(r_i) is the electric force at the bead position, 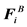is the Brownian force, 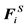is the net spring force, 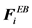is the net excluded volume force between the other beads, 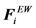is the excluded volume force with a wall (solid boundary). In many DNA separation studies only one field is applied, either the electric or flow field. Therefore, either U(r_i) or E(r_i) becomes 0. The evaluation of U(r_i) or E(r_i) with consideration to the micro-fabricated structure of the device is one of the most important parts in DNA separation simulations. This is discussed further in Section 3. The drag coefficient, ζ, is related to the bead diffusivity, D_i. For typical electrophoresis conditions, DNA, which is a negatively charged molecule, is always surrounded by counter ions. This cancels the hydrodynamic interactions (HI) in strong ionic concentration [32] [33] [34] . Therefore, the diffusivity can be regarded as a free-draining (not affected by other particles) property, based on the Stokes-Einstein law:

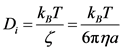(3)

Here, k_B is the Boltzmann constant, T is the absolute temperature, η is the solvent viscosity, and a is the bead radius. The bead radius, a, is typically chosen to match the experimental diffusivity data [21] [23] . Including HIs requires the use of a different tensor form instead of the scalar coefficient. This will be discussed later in this section.

The Brownian force for a free-draining bead is evaluated at each time step from the fluctuation dissipation theorem, which must satisfy the following conditions:

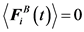(4)

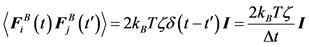(5)

Here, 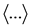is the ensemble average. 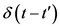is a delta function, which is non-zero at. I is the identity tensor. The actual expression to evaluate Brownian force used in simulation is:

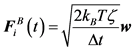(6)

Here, w is a random vector, of which average is 0 and variance is 1, evaluated by any random vector generator algorithm [21] [23] . The discretized time step size is Δt.

The net spring force is the sum of the spring forces between adjacent beads:

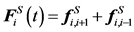(7)

Here, the sub-index i,i + 1 represents the force between the i-th and the i + 1 th beads. For the beads at both ends (i = 1 and i = N), only one of these spring forces exists. There are various models used to describe the spring force, which is closely related to polymer conformation. The simplest spring force model is the Gaussian chain model also known as the Hookean spring model [24] . Streek et al. used this basic model for their simulations of DNA separation [21] [35] [36] . A disadvantage of this model is that the spring can violate its maximum stretch length, l. To overcome this problem, the finite extensibility nonlinear elastic chain (FENE) spring model is also used in some simulations [37] [38] or an additional constraint force is added [39] . However, for an accurate simulation of polymer finite extensibility and stiffness, the use of Worm-Like Chain (WLC) model was proposed [40] [41] :

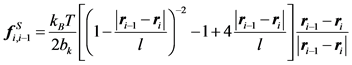(8)

Note here that the persistence length for WLC model is the half length of b_k. Underhill and Doyle examined the nonlinearity of the extension-force relation further to propose a correction method by incorporating the “effective” persistence length [28] . The WLC model has become one the most popular polymer models for DNA dynamics.

The excluded volume force is the sum of each excluded volume force between each bead:

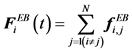(9)

Streek et al. used a force derived from a truncated Leonard-Jones potential equation [21] [35] [36] . However, Jendrejack et al. proposed a model based on experimental observation [42] :

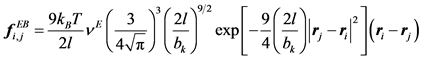(10)

Here, is the excluded volume parameter. Equation (10) is derived from a Gaussian excluded volume potential. This is softer than the truncated Leonard-Jones potential and is used to prevent small time step sizes [43] [44] . The excluded force from a wall can be evaluated from the same equation by replacing r_j with the nearest boundary position [45] , whereas Jendrejack et al. used its simplified form [43] [44] .

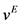
Numerical integration of Equation (2) is required to get the new bead position at a new time step t + Δt. An explicit Euler scheme requires a very small Δt to prevent numerical instability attributed to new spring lengths exceeding l or new bead positions overlapping the solid boundaries of the model. Although an implicit Euler scheme can be used to avoid spring overstretch, the new position must be solved using Newton-Raphson iterations. This also results in long computational times. Therefore, Jendrejack et al. devised a semi-implicit scheme where an implicit Euler scheme is applied only to the integration of the term related to the spring force and the rest of the terms are integrated by an explicit Euler scheme [41] . Kim and Dolye also adapted the semi-implicit scheme [45] . They included an additional “re-position” step to consider the bead-wall overlap for irregular boundaries based on Heyes and Melrose’s algorithm [46] .

As mentioned earlier, Equation (3) can be only used when HIs are neglected. This assumes that DNA undergoing gel electrophoresis is uniformly negatively charged and the Debye length is smaller than the persistence length of DNA. With these conditions, HIs are assumed to be screened due to counterion movement [32] [33] [34] . However, an experimental study [47] and later simulation studies including HIs claimed that the HI effects cannot be negligible, where the channel size is on a Debye length scale [48] [49] [50] . Due to these concerns, whether inclusion of HIs within DNA separation simulations is important or not has been a controversial topic.

Inclusion of HIs for the bead-spring model is described by Jendrejack et al. [41] [42] [43] [44] . Diffusivity in Equation (3) must be evaluated in a tensor form, D, in order for HIs to be considered:

(11)

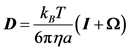
Here, Ω is the HI tensor. For HIs with beads to be evaluated, the Oseen-burger tensor or Rotne-Prager tensor is used [24] [51] . The latter is used to avoid situations when D becomes a non-positive definite tensor. Bead-wall HIs are numerically evaluated from each grid point. The diffusivity tensor from Equation (11) is then used with Equation (2), which can be rewritten as:

(12)

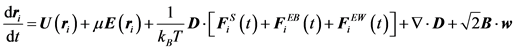
Here, B is the decomposed tensor of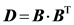. Note that the last term is the Brownian displacement term considering HIs. The position gradient of D is a correction term for numerical integration that considers the change of D over a time step. Despite the importance of HIs, including HIs in the bead-spring model has limitations: 1) HIs are concentrated on each bead. 2) multi-body interaction is not included as much level as in Stokesian dynamics [19] 3) it is computationally expensive to evaluate these Equations (11) and (12) at each time step. To overcome these problems other approaches have been applied. These include slender-body model and other simulation methods, which will be presented in later sections. In summary, it is noted that the Equations (1)-(12) are introduced here as an example of bead-spring WLC model, which have been widely used in DNA dynamics simulations.

2.2. Other Polymer Models

While the bead-spring model is the most widely used model in DNA separation simulations, other polymer models can be applied to simulation of DNA. Below we discuss bead-rod model, slender-body model, and touching-bead model.

1) Bead-rod model: As shown in Figure 1(b), this model defines a polymer molecule as a chain of beads connected by rigid rods, instead of flexible springs as in the bead-spring model. The vectors which represent the orientation of connecting rods are not dependent on each other. Thus, this can be considered as a freely-jointed chain. The connecting rod length is set as b_k, which leads to a less coarse-grained model than when using the bead-spring model. Compared to when using the bead-spring model, penetration between chains is not allowed. Constraint forces are assigned to maintain a constant rod length between beads and prevents an overstretch of the chain [5] [24] . With the bead-spring model, various spring force models and numerical scheme for the equation of motions were proposed to prevent the overstretch, as discussed in Section 2.1. In the absence of a stretching force and the presence of strong longitudinal stiffness in the polymers the freely-jointed chain model can describe the dynamic behavior of the chain well. These conditions correspond to an entropy-dominated situation [52] . On the other hand, this model is not suitable under strong deformation or confinement situations less than 4b_k because bending within the rods is neglected [52] . Therefore, this model was used to study DNA structures confined within nanochannels, of which channel size is larger than 4b_k [53] . Patel and Shaqfeh used this model for simulation of DNA flowing in post arrays, where a DNA molecule hooked on a post is highly stretched [18] .

2) Slender-body model: As shown in Figure 1(c), a DNA chain is represented by a series of connected rods (slender-bodies). In contrast to the bead-rod model, which carries resistance on each bead, the slender body model includes continuous resistance over contour length. This is a better representation of a real DNA molecule. Additionally, based on the HIs included on the slender-body connectors, multibody HIs can be included, which is the similar level as in Stokesian dynamics simulations. Bead based models have difficulties with including these interactions [19] [54] . However, for this model to be the freely-jointed chain, as in the bead-rod model, additional correction forces must be added [54] . In later studies, this model was applied to the simulation of DNA flows in pressure driven flow. HI with walls was also included using a Green’s function for a point source between two boundaries [55] [56] . This allowed for shear-induced migration to be simulated. Even DNA fragments shorter than b_k can be simulated as single slender-bodies [57] [58] . Michelleti further modified this model by incorporating the bending energy between connecting rods to study linear and circular DNA chains in slit confinement structures [59] .

3) Touching-bead model: As shown in Figure 1(d), all the beads in this model are connected to each other without any springs or connecting rods in between. The length between beads is set to a < b_k and can allow for bending within the model. This aspect makes this model more accurate than the bead-rod model. This flexibility within b_k enables us to calculate rotational diffusivity more accurately [5] . However, a larger number of beads is required for this model compared to the bead-rod or bead-spring models. This causes an increase in the computational time needed to evaluate the model. If a is set too large (a ≈ b_k), the actual effective persistence length becomes smaller than 0.5b_k, which results in inaccurate prediction of DNA stretch [5] . Tree et al. computed the relaxation times of bacteriophage λ-DNA in a high ionic strength buffer confined in a nanochannel using this model. They also proved that as channel size decreases, there is a significant drop in relaxation time. This is due to a major decline in chain extension fluctuation [27] . Muralidhar et al. tested the underlying assumption under this method. They showed that their predictions for the chain extension and confinement free energy in the system agree with the simulation data for adequately long chains [60] . Dai et al. predicted DNA diffusivity in slit confinement using MC simulations using this model. Simulated DNA diffusivities are validated by experimental data [61] .

2.3. Comparison of Polymer Models

In summary, the bead-spring models, more specifically the WLC model, have been widely used in simulations of DNA separations due to their efficiency. However, too much coarse-graining, in other words not enough beads, may result in an inaccurate description of dynamics and crossing of polymer chains. The bead-rod model can prevent the overstretch issue and the slender-body model can include HI more accurately. However, connector rigidity can cause limitations in the length scale of confinement. The touching-bead model can simulate DNA properties on a more realistic scale, but at the cost of a high computational load. Therefore, this model is mainly used in the study of DNA structure in nano-confinement.

3. Field Calculation in Complex Geometry

As explained earlier, DNA separation simulations require local flow or force values , as in U(r_i) and E(r_i) in Equations (2) and (12), for polymer motion in the flow or force field of the separation device. If the geometry of the separation device is simple, such as a straight microchannel, its force or flow values at each position can be solved analytically. However, advances in DNA separation methods utilize DNA flows in complex geometries which induce nonlinear force or flow fields. These must be solved numerically. Therefore, DNA separation simulations require a proper combination of DNA dynamics predictions and field calculations.

3.1. Finite Element Method

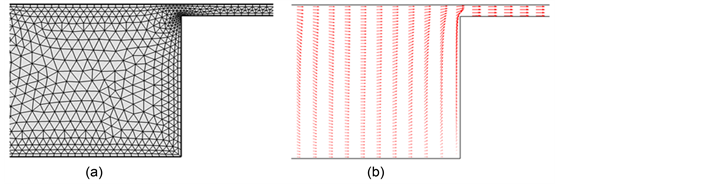
The finite element method (FEM) is a numerical method for solving differential equation within a boundary. This method discretizes the domain of the problem into smaller sub-domains, called finite elements or meshes, as shown in Figure 2(a). The discretized form of the governing equation results in a system of equations. Approximate solutions of these equations are obtained at each node of each element. Once the unknowns are solved, the values at the positions of interest are evaluated by interpolation. FEM is especially useful for complex geometries. For example, if the domain can be divided into a series of

rectangles, as with structured microchannels, the finite difference method can be used [21] [35] [36] . However, for a domain near a circular object, which can be easily discretized with fine triangular shaped elements, it is suitable to use FEM [62] .

As mentioned earlier, FEM can be used for electric field calculations with DNA electrophoresis simulations. The electric field of potential is denoted by Φ. The governing Laplace equation, in the fluid domain, Ω, is shown below:

(13)

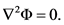
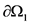
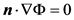
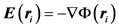
The boundary where the electric potential is explicitly applied, given as Φ = Φ_given, is. The boundary condition on the insulating walls, where potential is not applied, is. Here n is a normal vector pointing out of the fluid domain. The solutions of Equation (13) along with the boundary conditions obtained by FEM are then used to evaluate. Figure 2 shows an example of a meshed fluid domain and the calculated electric field in a microfluidic device with entropic traps, arrays of microchannels with different sizes [12] [63] . This is then combined with BD simulations of DNA polymer models by being used in Equations (2) or (12). Kim and Doyle tested this combination of FEM and BD simulations [45] . They used FEM to obtain the inhomogeneous electrical field around a spherical obstacle. DNA movement and deformation under the electric field around the obstacle was also simulated [62] .

3.2. Boundary Element Method

Boundary element method (BEM) is a numerical method used to solve “linear” partial differential equation in a boundary. In this method, the fundamental solution of the linear differential equation (Green’s function) must be available first. Compared to FEM, discretization is only required on boundaries, which results in fewer mesh points and more efficient calculations. Instead of the interpolation used in FEM, the boundary integral equation is used in BEM to evaluate flow or electric potential values at the positions of interest. The surface integrals of the Green’s function and its derivative are utilized for this [13] [64] . The Laplace equation, Equation (13), and the Stokes equation are linear differential equations and thus this method can be applied to solve inhomogeneous electric fields [13] [64] and to consider HIs of DNA in microchannel flows [43] [44] . HIs induced by DNA are difficult to calculate using FEM because DNA strands must be considered as moving boundaries. However, when using BEM, Green’s functions for bead-bead interactions (Rotne-Prager solution [51] ) or bead-wall interactions (Blake solution [65] ) are adapted to consider the HI effects on DNA flow behaviors in microchannels. Jendrejack et al. studied the center-of-mass distribution of DNA in microchannel by evaluating Oseen-burger tensor or Rotne-Prager solution on each grid point on microchannel wall [43] [44] . Without incorporating these effects, the cross-sectional center-of-mass distribution of DNA is different from experimental observations. As explained after Equation (12), inclusion of HI is computationally expensive. However, Zhang et al. proposed more efficient and accurate method to simulate DNA flowing on nanopit arrays [66] . They combined the general-geometry Ewald-like method [67] with a variant of the immersed boundary method [68] . Additionally, instead of using Cholesky decomposition [69] , Chebyshev polynomial approximation [70] was used to decompose D = B・B^T much more efficiently. This method can be applied to complex geometries and hydrodynamic interaction is considered as much level as Stokeian dynamics simulation [19] [66] .

3.3. Lattice-Boltzmann Method

The lattice-Boltzmann Method (LBM) is a numerical method for the simulation of fluid using the discrete Boltzmann equation instead of conservative momentum balance equations like the Navier-Stokes equation [71] [72] . For small Knudsen and Mach numbers, the discrete Boltzmann equation becomes the Navier-Stokes equation. This method is known to be suitable for fluid flow calculations in complex geometries and colloidal suspensions due to its basis in the Bhatnagar-Gross-Krook model [73] . This is a particle or fluid molecule collision model. For the LBM, a particle velocity distribution function describes the mass density and the velocity of a particle in a discretized lattice. The time evolution of this function is described by the discrete Boltzmann function and it can be converted to evaluate fluid hydrodynamic properties. LBM has been applied to the simulation of DNA dynamics in microfluidic devices by combining the flow field calculated from LBM with BD simulations of polymer chains. LBM can easily include the inertial and the HI effects in the simulation. However, electric field must be calculated explicitly. Therefore, if inertia and HIs are not important or there is no flow (only an electric field), FEM is more efficient. Additionally, LBM is more efficient if polymer concentration is higher [74] [75] . LBM was applied to the simulation of DNA in microchannel flows to show the cross sectional lateral migration of DNA induced by polymer-wall HI [71] [72] . LBM was also used in a study on the translocation of DNA through nanopores [76] and in the calculation of rotational flow fields for DNA separation simulations using streaming flow [77] .

3.4. Dissipative Particle Dynamics

As in LBM, mesoscale models can accurately represent the hydrodynamic properties of a flow system and they are not as expensive as atomic models in terms of computation load. Dissipative Particle Dynamics (DPD) is a simulation technique for fluid which utilizes the dynamic simulation of coarse-grained particles on a mesoscale. Mesoscale methods are intermediate methods between atomic scale and microscale [78] [79] [80] . Compared to molecular dynamic simulations, the atomic structure of the fluid and solvent molecules is not considered. Clusters of molecules are defined as individual particles instead. Instead of using the particle velocity distribution function in a lattice used with LBM, fluid and polymer particle positions and velocities are calculated using stochastic differential equations with this method. Solid boundaries are simulated as a layer of “frozen” particles [78] [79] [80] . However, the soft potential causes large density fluctuation. Pan et al. adapted a double layer of frozen particles to remove this problem [50] .

As in LBM, DPD is suitable for the calculation of flow fields in complex geometries including HIs. Another similarity is that electric force fields must be calculated explicitly. Additionally, the original DPD technique has a low Schmidt number, which is the ratio between kinematic viscosity to diffusivity. This causes slower momentum transfer when compared to mass transfer. This can be a major problem when simulating fluids within complex geometries [37] . Fan et al. proposed a possible solution to this problem. They modified the weight function in the dissipative force and decreased the cut off radius [81] . Litvinov proposed a modified DPD method called Smoothed DPD to study the static and dynamic behavior of DNA molecules in the flow. This method is based on second order discretization of Navier-Stokes equations and is good in better prediction of thermodynamic properties [82] .

DPD was applied to DNA separation simulations in microfluidic devices that utilized electrophoresis and structured microchannels to examine the HI effects [50] [83] . Pan et al. found that a specific separation mechanism, corner trapping, that was identified by Streek et al. [35] was not identified while using DPD [50] . They claimed that the difference was due to the HI inclusion [49] . Ranjith investigated the effect of rotational flow in microchannels on the transport and dynamics of DNA molecules. He utilized a modified DPD model called finite-size DPD which considers the size effects on the dynamic modeling of different particles. Rotational flow in the microchannel is also considered by adding a rotational dissipative force to the dynamics of the system [84] .

3.5. Comparison of Models

In summary, inhomogeneous electric field considering complex geometry can be calculated either by FEM or BEM. BEM is more efficient but there are many available popular commercial tools for FEM. If flow field considering complex geometry can be calculated by FEM, LBM [85] , and DPD [80] . However, BEM can be used only for Stokes flow condition (negligible inertia). BEM, LBM, and DPD are used for the HI inclusion. Accurate and efficient method for including HI in BEM was developed by Zhang et al. [66] . LBM is also widely used but adaptation for irregular boundary is required [85] . DPD is also popular for its flexibility but modifications are required to prevent problems like low Schmidt number or large density fluctuation near a boundary [81] . There were studies comparing the methods for BD with HI as in Equations (11)-(12) and LBM [74] [75] . The agreements of both methods were confirmed. For the situation of highly stretched polymer conformation, small enough spatial and times step sizes are required [75] . Table 1 summarizes the comparison with these models.

4. Simulations of DNA Separations

In this section, we summarize the simulations of popular DNA separation methods.

4.1. Gel Electrophoresis

Gel electrophoresis is one of the most popular DNA separation tools. It is still widely used in many DNA related experiments [86] . A gel solution, usually made of agarose or polyacrylamide, is prepared. Once a gel is made from the gel solution, it is considered a porous media. Porous media is defined as a random array of obstacles with colloidal size. DNA samples are applied to the gel and an electric field is applied either in a constant or pulsed field. As mentioned earlier, long DNA molecules have similar electrophoretic mobility in free solution. However, interaction with the gel structure induces differences in mobility according to DNA length. After a certain period, the electric field is stopped and the band positions of the DNA sample are compared to those of a reference sample. A reference sample is a set of molecules with known lengths [14] . Various simulation studies elucidated the DNA-gel structure interaction mechanisms which cause the differences in DNA mobility within the gel.

Duke and Viovy adapted a MC simulation for studying DNA motion in gel electrophoresis [26] . They called the mechanism of the DNA motion as the “hopping rule”. The gel structure was considered as a randomly connected 3D network of pores with uniform diameter. DNA motion was simulated as strands moving through the tube-like pores, like a snake, which is called as “reptation”

[87] . Using this gel structure, they studied crossed-field electrophoresis, where the direction of the electric field is switched periodically. They studied how DNA responds to different electric fields in the gel structure. Their simulation found that the separation of relatively long DNA is positively affected when the angle between fields is elevated above 90 degrees.

Azuma and Takayama performed a BD simulation of DNA in a constant electric field gel electrophoresis. They modeled DNA as a bead-spring model and the gel structure as immobilized bars, simulated as lines of beads, in a 3D periodic box. They tracked the evolution of the radius of the longer principal axis and the velocity of the center-of-mass and found that those values show periodic behaviors in relatively strong fields. This was inferred as the “elongation-contraction” mechanism in DNA. The period of the elongation-contraction mechanism was also found to be proportional to DNA length. They used this finding to explain why long DNA strands cannot be separated under a constant electric field gel electrophoresis [39] . Streek performed BD simulation of bead-spring model to study the effect of pulsed electric field in gel electrophoresis [21] .

4.2. Arrays of Posts

Although gel electrophoresis is a very common method, its limitations were described previously in this paper: time consuming procedures, inconsistency of random gel structure, and difficulty in the separation of relatively long DNA chains [14] . To overcome these limitations, microlithography techniques have been utilized and introduced to the development of micro-fabricated devices used in DNA separations [29] [88] [89] [90] . Instead of a random distribution of the colloidal size obstacles in the gel structure, the arrays and the sizes of the obstacles, or posts, can be fabricated as designed. Devices with post arrays have been used for the separation of relatively large molecules.

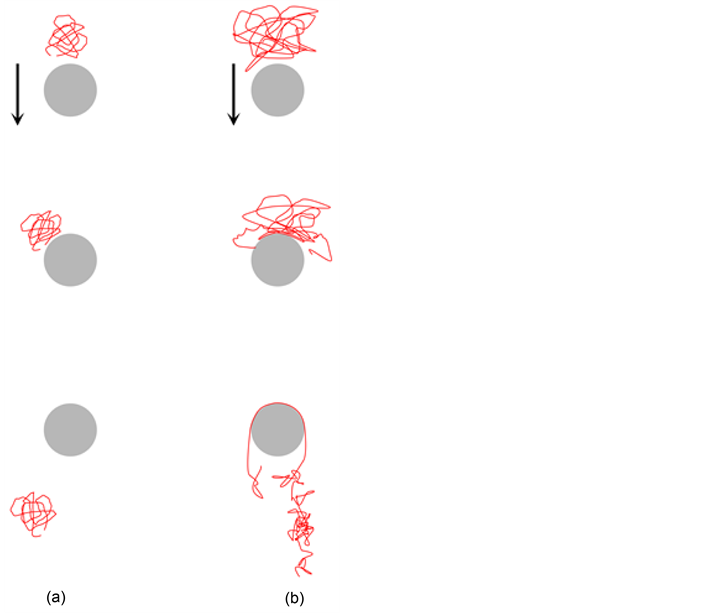
With advances in post array devices, simulation studies have been used to both identify separation mechanisms and to explore optimal array designs. Saville and Sevick performed a BD simulation of a bead-spring model flowing around an obstacle [91] . This study identified two mechanisms: 1) “hooking” and 2) “roll-off”, as shown in Figure 3. If a DNA molecule, moving under the influence of an electric field, hits a post, it may get hooked on the obstacle. In that case, the DNA conforms to a U-shape known as a hairpin. The DNA is likely to remain hooked on until it gets unhooked after some time. It has been found that hooking probability is proportional to chain length, therefore DNA molecule mobility is affected by its chain length [18] . However, if the size of a post is relatively larger than the DNA molecule, the molecule hits the obstacle and rolls around the obstacle with little change in conformation. This mechanism is independent of DNA size, and is not a desirable condition for separation [92] .

Randall and Doyle incorporated an analytical expression for the inhomogeneous electric field around a circular object for more accurate DNA motion.

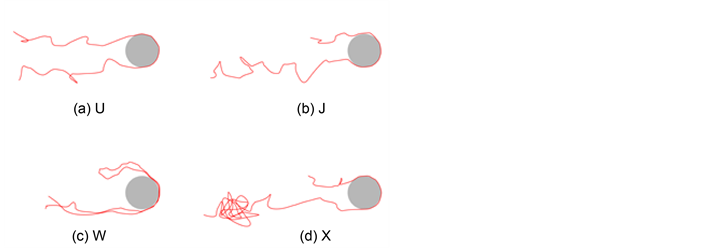
They identified the trends of these mechanisms in terms of the radius of gyration of DNA, Rg, the size of the obstacle, and the electric field strength. For example, when the field is strong enough and the obstacle’s diameter is small, the dominant mechanism is hooking [93] . They also further investigated the hooking mechanism in more detail. They identified four hooking modes: symmetric U-shaped hook, asymmetric J-shaped hook with constant extension, rare entangled W-hook, and asymmetric X-hook with increasing extension, as shown in Figure 4 [62] [93] . Previously, J-shaped hook, which is similar to a rope-on-pulley motion, was conjectured to be dominant. However, the simulation results validated experimental data that X-hook was the most dominant mode in hooking mechanisms. Kim and Doyle also extended the inhomogeneous electric field calculations for arbitrary objects using FEM [45] . Later, it was shown that BEM is a more efficient method for electric field calculations [13] [64] .

Studies on the effects of different array types have been performed systematically with the help of simulations. Patel and Shaqfeh investigated BD of a freely-jointed bead-rod chain in a sparse array of posts when they are ordered versus

randomly dispersed. They concluded that disordered arrays in strong electric fields are optimal conditions for separation [18] . Later, calculations of inhomogeneous electric field values used with post arrays were performed by a commercial FEM solver for more accurate calculations [94] . BEM was also applied to electric field calculations in post arrays [13] [64] . Ou et al. also confirmed the importance of inhomogeneous electric field calculations. The results show a better prediction of mobility but underestimate diffusion coefficient values [95] .

4.3. Capillary Electrophoresis

Capillary electrophoresis (CE) separates macromolecules in a capillary when an electric field is applied to the system. CE needs less time to separate DNA and gives higher resolutions and sensitivities compared to typical gel electrophoresis. CE has mainly contributed to human genome analysis [1] and has taken over as the dominant separation method, especially for smaller DNA strands. CE also has the potential to become automated. The ends of the capillary tube are under a voltage and this creates an electrical field. The capillary is filled with a concentrated entangled polymer solution which substitutes the porous structure used in traditional gel electrophoresis. The DNA samples race through the capillary and their mobility is affected by their chain length, due to polymeric conformation. As a result, the samples are separated by molecular size into different peaks each with a specific width that characterizes the CE performance [96] .

Kekre et al. performed a BD simulation of DNA in CE [49] . While many studies assumed that HI is screened in the electrophoretic condition (high ionic strength limit) [48] [49] [50] , there exists electrically induced hydrodynamic interaction between charged polymers [97] . The simulation used the bead-spring model with the electrically induced HI. It was experimentally observed that DNA migrates across the electric field line and concentrates near the capillary wall if pressure gradient is applied in the opposite direction to the electric field [98] . Their simulation results agreed with the experimental phenomenon and found that DNA conformation is stretched by shear flow and that contributes to the migration towards the wall. Their finding suggests that the weak dependence of DNA mobility on length is mainly due to its average spherical conformation rather than the screened HI [46] [47] . Pandey and Underhill recently developed a coarse-grained model for DNA in CE by considering internal DNA strand interactions [99] .

4.4. Straight Microchannel

Studies on DNA dynamics in “straight” (this is different from the structured microchannel discussed in Section 4.5) microchannel flows have been performed for basic understanding of DNA and solid boundary interactions. It is well known that if a pressure drop is applied to a Newtonian fluid between two parallel plates, a parabolic shape velocity distribution is created at steady state. Therefore, the velocities of DNA flowing in a microchannel are dependent on its cross-sectional position (faster elution for DNA flowing near a center) and any factors affecting the cross-sectional DNA position can be a separation mechanism. Jendrejack et al. performed BD simulation considering DNA-wall HI [43] [44] . They showed that the DNA-wall HI resulted in shear-induced lateral migration of DNA: longer DNA tends to migrate away from the wall, which results in faster elution. This migration has been shown by using slender-body models in different simulation methods [56] [58] , and LBM [71] [72] . However, DPD requires adjustment of parameters for showing proper migration behaviors [37] , [81] . There is a size-based particle separation technique, called field-flow fractionation. This technique applies an extra flow or force field in the cross-sectional direction while samples are flowing in the parabolic channel flow [100] . The applied field induces the cross-sectional position differences according to particle size. There were theoretical studies for applying this technique to DNA separation [101] [102] .

4.5. Structured Microchannel Arrays for Entropic Trap

Periodically constricted channels were introduced as an effective way of creating entropic traps to separate DNA chains based on their length. The mechanism used in the entropic constriction of polymer molecules was first studied by Arvanitidou et al. [103] . It has been shown that long polymer chains are severely affected by entropic constriction when the size of the confinement is smaller than 2Rg of the polymer [12] [63] .

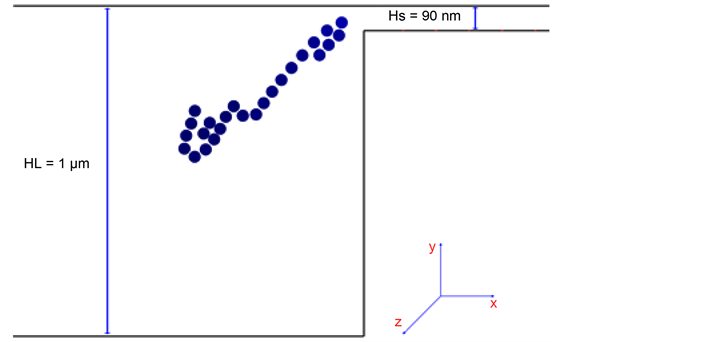
As shown in Figure 2 and Figure 5, the device consists of both large and small periodic channels, which are fabricated using a lithographic method. The electric force is applied in the x-direction to move DNA through the channels. The height of the small channel, HS, is designed to be smaller than 2Rg of DNA molecule. Therefore, DNA molecule will be trapped in the larger channel until they manage to overcome the entropic barrier. However, the amount of free energy lost in this process is dependent on the length of the molecule. Consequently, the mobility of the DNA molecule is also length dependent. Surprisingly,

it was shown that longer strands of DNA molecules elute faster. Initially, this was explained by Han et al. [12] [63] . For a DNA molecule to pass through the small channels of the device, it only takes a portion of the molecule to be close to the entrance and the rest of the molecule will be dragged into the channel accordingly. Longer molecules have more surface area and thus they have a higher probability of being dragged into the smaller channels. This causes these long molecules to exit the device faster than shorter DNAs [12] [63] .

The first attempt to simulate the device designed by Han et al. and to prove their theory was done by Tessier et al. [104] . They used a bound fluctuation MC method to simulate the behavior of long strands of DNA through the entropic trap device. The results of the simulation agreed with the experimental results by Han et al. The simulation could show the DNA conformation in the small channel region in detail. It was also found that the strength of the field directly affects deformation of the chain. When the field was weak, the initial energy needed to break the entropic barrier could not be obtained. In a strong field, the escape was rapid but the DNA did not have enough time to conform to the small channel.

Streek et al. performed BD simulation using the bead-spring model with a Hookean spring force. HI was ignored and the electric field was calculated using FDM [35] . The experimental results by Han et al. were accurately reproduced, although the authors claim that they found a new mechanism which dominated the mechanism, previously proposed by Han et al. The new mechanism was based on the diffusion coefficient of DNA. Small molecules have higher diffusion coefficients than larger molecules. Therefore, they are more likely to diffuse to the dead corners of the larger channel and spend more time there. Streek et al. also extended the study to the device with Hs > 2Rg. The new mechanism was also detected in that device and the elution order was found to be similar (faster elution for longer DNA) at low electric field. However, the reverse elution order and non-equilibrium bistable behavior were found at high electric field [36] .

Panwar and Kumar performed BD simulation with the bead-rod model [105] . They investigated the effects of DNA length and field strength on time scales in three distinctive regions: 1) placing the chain near the small channel, 2) breaking the entropic barrier, and 3) transporting the molecules through the small channel. Later, Lee and Joo performed a similar BD simulation to compare the motions of linear and star-branched polyelectrolyte molecules through an entropic array [106] . Their findings showed that the mobility of star branched molecules was significantly lower than linear polymers with the same molecular weight.

In earlier works, HIs were neglected in simulations of DNA separation by electrophoresis. The decision to neglect these interactions was based on the assumption that HIs are screened if the Debye length of the DNA is smaller than the scale of the device confinements. Therefore, this is a questionable assumption in the small channels. Application of DPD to the entropic trap simulation enables to investigate the HI effects. Moeendarbary et al. found that larger molecules have higher probability of hernia (kink) formation entering the smaller channel. These chain dynamics contribute to the higher mobility of longer DNA chains [49] . Pan et al. found that applying small voltages to the device resulted in a longer time required for separation. Higher voltages gave a quick but less efficient separation. They also found that the corner trapping that was reported by Streek et al. did not contribute to the overall separation process [50] . Additionally, electroosmotic effect was also investigated by DPD [107] .

Along with investigating the HI effects on separation simulations, the effects of using short DNA fragments and the effects of different entropic trap geometries have also been studied. Laachi et al. investigated the transport of shorter, or rigid, DNA molecules through periodic arrays of narrow channels [57] . Their theoretical analysis showed that it is unnecessary to operate near equilibrium to separate short DNA strands. According to their findings, long rigid DNA branches elute faster in strong electric fields. Fayad and Hadjiconstantinou did similar work, but they studied the effects of different geometrics on entropic trap arrays [108] . Fayad and Hadjiconstantinou used BD simulation with WLC model considering HI to study the effect of device geometry on the separation process for shorter DNAs. Optimization of the device was also studied [109] . Choi et al. used BD simulations to show the separation of shorter DNA chains in an alternating deep-shallow area nanofilter [110] . They suggested a new mechanism responsible for separating molecules in strong electric fields. The effect of the deep region’s wall angle was studied on the separation process. They found that the shape of the entropic trap and the size of the rigid molecules were key factors that caused molecules to move along different electrophoretic streamlines. Results showed that the shorter branches were more likely to migrate to the bottom streamlines and stay there. Zhang et al. performed BD simulation with HI to study the separation of DNA using a device with nanoslits and nanopits with a similar design as in the entropic traps, but DNA is moved by flow. They found that HI plays important role in the separation mechanism [66] .

4.6. Rotational Flow

Microscale rotational flows, or streaming flows, with counter-rotating vortices have been known as another method for trapping particles, or DNA strands [77] [111] [112] [113] . The vortices can be generated by acoustically driven bubbles [111] or by local heating [112] . An inhomogeneous shear gradient in the vortices causes a difference in the deformation of DNA molecules according to DNA lengths. As a result, the position and conformation of DNA molecules in those vortices will also be length dependent.

Watari et al. performed a BD simulation using WLC model and an analytic stream of Taylor-vortex flow. The inclusion of HIs were conducted in the same manner as in the Equations (11)-(12), excluding DNA-wall HI. They investigated the effect of vortex flow conditions on DNA conformations and positions to show the potential for trapping DNA in vortices [113] . Alfahani et al. [77] used the LBM to evaluate the rotating flow field and to include HIs. The LBM followed the same methodology as in the work done by Usta et al. [71] [72] . BD simulation of WLC in the rotating flow was performed. It is noteworthy that one wall of the microfluidic device was modeled as a “stick wall” on which DNA was trapped by a temperature gradient [112] . The simulation showed that there was a condition that needed to be fulfilled to separate DNA strands by length. If flow was strong enough, DNA strands were pushed out of the vortex and compressed against the wall. However, if the wall did not have enough strength to hold the compressed DNA, it was pulled by the hydrodynamic drag force back into the vortex. If the flow strength and the wall trapping force are tuned, short DNA strands are trapped in the trap region, the region between two vortices on the stick wall, and long DNA strands rotate freely in the vortices [77] .

4.7. Nanopore Translocation

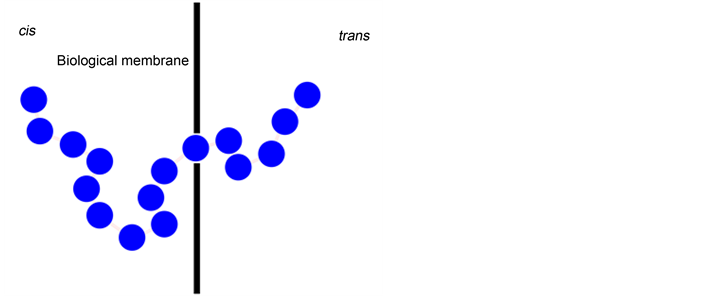
It was discovered that the sequencing and detection of DNA and RNA strands can be possible by forcing them through a narrow biological nanopore using an electric field, as shown in Figure 6 [114] [115] . If the size difference between the molecules and the pores is large, molecules are squeezed through the pore. This is called nanopore translocation. This method enables DNA sequencing to be faster than conventional gel electrophoresis methods because base pair identification can be done as soon as strands pass through the pore. In order for the translocation process to be better understood for further applications, the conformational behavior of the DNA chain during the process needs to be investigated using simulation methods.

A BD simulation of this process was done by Tian and Smith and considered the repulsive force from the nanopore’s walls [116] . In the simulation, it was assumed that the process was dominated by the force field rather than the entropic

barrier effect. Investigation of the conformation difference before and after translocation, found that the polymer chains were not in equilibrium during the process. Izmitli et al. took HI into account in their simulation study [117] . They used a bead-spring model to represent the DNA chain and LBM to simulate the streamlines. They found that HI effects are a minor factor in determining residence time of the polymer. Luo et al. performed a 3D simulation of the process under an external force field to find the correct relation of residence time and external force. For slow and fast translocation processes the dependencies were found to be different [118] . Smiatek and Schmid performed a DPD to consider the effects of solvent choice on translocation. They considered the effect of different salt concentrations and surface slip conditions. The results of simulation showed that the role of surface slippage in polymer migration was very strong and may be considered as an important parameter in future microfluidic designs [119] . A different aspect of DNA translocation through a nanopores was investigated by de Haan et al. They used coarse-grained simulations that took the Peclet number, the ratio between convection and diffusion, as a regime deterministic parameter in the simulation. They found that the probability of translocation to occur was found to be highly dependent on the Peclet number [120] .

Similar to the studies on DNA structure in nanoconfinement [5] , many MC simulation approaches have been used to investigate the mechanism [121] and the relation between the average residence time in a pore and the DNA length [122] . Molecular Dynamic simulation can be used in simulating the nanopore translocation of polyelectrolyte molecules [123] [124] as well because structures on a nanopore scale are similar to those on an atomic scale.

5. Concluding Remarks and Perspectives

In this study, we have reviewed the computational studies of DNA separations in micro-fabricated devices. We focused on the dynamic simulation of double stranded DNA in geometries related to separation methods and devices. The reviewed simulation approaches can also be extended to the dynamic simulation of other biopolymers in microscale flows [2] . The simulation approaches covered combining single polymer dynamic calculations and inhomogeneous field calculations consistently. The general simulation approach is to use a BD simulation of a WLC model, a special from of the bead-spring model adapted for semi-flexible polymers like DNA, with the calculation of an inhomogeneous flow, or force, field using FEM. However, other methods may be adapted depending on specific conditions to maximize efficiency and accuracy. With advances in the field of micro-fabricated devices, more complex and confined geometries have been involved in new design of DNA separation/manipulation devices. Therefore, polymer models and field calculation methods must be developed to accurately capture and predict DNA behaviors in those new devices. Furthermore, the importance of the inclusion of HIs has been emphasized in conditions of nano-scale confinement [50] or high shear rate [49] . In recent advancements, there have been attempts to utilize commercial computational tools to perform DNA separation simulations. We have been directly involved with this by utilizing COMSOL Multiphysics®, a physics modeling tool, to simulate DNA separation [125] .

Acknowledgements

The authors gratefully acknowledge financial supports from Missouri University of Science and Technology (UMRB and OURE).

Cite this paper

Monjezi, S., Behdani, B., Palaniappan, M.B., Jones, J.D. and Park, J. (2017) Computational Studies of DNA Separations in Micro-Fabricated Devices: Review of General Approaches and Recent Applications. Advances in Chemical Engineering and Science, 7, 362-392. https://doi.org/10.4236/aces.2017.74027

References

Glossary

BD: Brownian dynamics simulation

BEM: Boundary element method

CE: Capillary electrophoresis

DPD: Dissipative particle dynamics

FDM: Finite difference method

FEM: Finite element method

FENE: Finite extensibility nonlinear elastic chain

HI: Hydrodynamic interaction

LBM: Lattice-Boltzmann method

MC: Monte-Carlo

WLC: Worm-like chain model