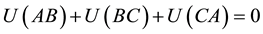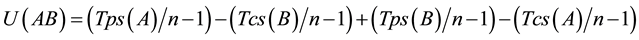Social Networking
Vol.03 No.03(2014), Article ID:45217,13 pages
10.4236/sn.2014.33021
Novel Epistemic and Predictive Heuristic for Semantic and Dynamic Social Networks Analysis
Christophe Thovex, Francky Trichet
Laboratory of Computer Sciences (LINA, UMR-CNRS 6241), University of Nantes, Nantes, France
Email: christophe.thovex@univ-nantes.fr, francky.trichet@univ-nantes.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 February 2014; revised 21 March 2014; accepted 11 April 2014
ABSTRACT
Using Kripke semantics, we have identified and reduced an epistemic incompleteness in the metaphor commonly employed in Social Networks Analysis (SNA), which basically compares information flows with current flows in advanced centrality measures. Our theoretical approach defines a new paradigm for the semantic and dynamic analysis of social networks including shared content. Based on our theoretical findings, we define a semantic and predictive model of dynamic SNA for Enterprises Social Networks (ESN), and experiment it on a real dataset.
Keywords:
Graph, Analysis, Interdisciplinary, Modal, Logic, Semantics, Social, Networks

1. Introduction
Social Networks Analysis (SNA) is an approach of graph-mining based on sociology and applied to social graphs, i.e. some graphs representing people and their social relationships, such as Moreno’s sociograms [1] . It integrates dynamic models based on the comparison of information flows to electric flows [2] [3] , in order to improve SNA standard centralities introduced in [4] [5] , for instance. As an example, the betweenness centrality of a node 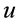 is a topological measure comparing the number of shortest paths connecting each pair of nodes (i, j) including u in a graph, to the total number of shortest paths in the graph. It is calculated for each node of a social network and the higher betweenness values indicate the leaders in terms of information sharing, within the studied social network [4] . Newer definitions of betweenness in [2] [3] are based on the idea that information doesn’t necessarily follow the shortest path between people, within a social network. These well-known definitions in SNA are flow-based measures which compare the value of an edge to a resistance and compare a node to an interconnection of resistances respecting the Kirchhoff’s point law and Kirchhoff’s mesh law. They use the point law to calculate the current output, based on the current input for each connected node, and so on following a random walk within social networks. [2] [3] centralities are implemented in most of the SNA applications and libraries (e.g., Pajek, NetMiner, Gephi―http://gephi.org) and recognized for the results they provide. However, 1) these models force all the resistances to be equivalent within the studied network, and 2) they omit the Ohm’s law in the simulation of current flow distribution they entail, although Kirchoff’s laws are based on the Ohm’s law.
is a topological measure comparing the number of shortest paths connecting each pair of nodes (i, j) including u in a graph, to the total number of shortest paths in the graph. It is calculated for each node of a social network and the higher betweenness values indicate the leaders in terms of information sharing, within the studied social network [4] . Newer definitions of betweenness in [2] [3] are based on the idea that information doesn’t necessarily follow the shortest path between people, within a social network. These well-known definitions in SNA are flow-based measures which compare the value of an edge to a resistance and compare a node to an interconnection of resistances respecting the Kirchhoff’s point law and Kirchhoff’s mesh law. They use the point law to calculate the current output, based on the current input for each connected node, and so on following a random walk within social networks. [2] [3] centralities are implemented in most of the SNA applications and libraries (e.g., Pajek, NetMiner, Gephi―http://gephi.org) and recognized for the results they provide. However, 1) these models force all the resistances to be equivalent within the studied network, and 2) they omit the Ohm’s law in the simulation of current flow distribution they entail, although Kirchoff’s laws are based on the Ohm’s law.
Since information flows and information sharing are recognized as key indicators in SNA, the semantics intrinsic to the shared content related to social networks (i.e., the endogenous content) has been studied, resulting in semantic SNA models. Semantic SNA attempts are sustained since a few years, with important contributions such as [6] and [7] .
While we were defining new semantic SNA models in line with the Socioprise project, funded by the French State Secretariat at the prospective and development of the digital economy [8] , we had to accept various resistances values within our model of social networks analysis. It has led us to identify a semantic incoherence in the interdisciplinary bridge-building between graph analysis and electrophysics commonly accepted in SNA. Our findings might also concern other application domains-e.g., traffic networks.
This paper presents: (a) the demonstration of a semantic incoherence and its resolution in current SNA; (b) a socio-semantic graph structure based on (a) and entailing a metric of semantic tension for a social network; (c) a semantic and predictive model of dynamic SNA (patented model), dedicated to Enterprises Social Networks (ESNs).
Our theoretical work is based on Kripke semantics. Our applicative work is dedicated to economic performance and social climate optimization, and experimented in line with the Socioprise project. Socioprise was realized in partnership with the OpenPortal Software company, which provides French leading software solutions for human capital management.
In this paper, the Section 2 presents the principles and methods related to our contributions, encountered in SNA. Section 3 introduces our theoretical and epistemic contribution. Section 4 sums up the purpose of the Socioprise project and defines a skills network structure as a base for the experimentation of our theoretical contribution. Section 5 presents the predictive model of recommendations we define, based on knowledge engineering and on the natural balance of electronic flows. Section 6 presents the results obtained with a real dataset in the context of the Socioprise project. Lastly, Section 7 presents the conclusions and perspectives of our work.
2. Interdisciplinary Semantics
The section sums up the main semantic principles and methods encountered in SNA models, from the sociograms presented in [1] , to the latest outcomes in SNA for the Semantic Web presented in [9] .
2.1. Graphs Analysis and Interdisciplinarity
In [1] , some social graphs named sociograms were introduced in sociology for the analysis of dynamic behavior in people groups. The graph theory and sociology were intuitively associated yet. Then in another domain, as electrophysics and graph theory evoked an epistemic equivalence, their interdisciplinary study enabled outcomes such as the demonstration of current flows unity and continuity in large graphs, established in [10] .
Introducing electro-physical phenomenons in Social Networks Analysis, [2] [3] betweenness centralities improves the standard betweenness centrality defined in [4] . Interdisciplinary bridge-building between SNA and electromagnetic force1 is useful to SNA models, but also to physics. For instance, in [11] physicians have recourse to centrality measures so as to prevent defaults in electric power grids. Our theoretical work defines and experiments a semantic completion of the electro-physic metaphor commonly employed in SNA.
2.2. Semantics of Endogenous Content
An ontology is an explicit specification of a shared formalization. It represents the concepts, objects and other entities supposed to exist in an interest area, with their relationships [12] . Semantic SNA studies the conceptual aspects of social networks. It is based on knowledge and ontology engineering coupled with SNA principles, and concerns the Social and Semantic Web [6] . Since [7] , more and more works are published in the domain and various domains are waiting for innovative applications resorting to semantic SNA―e.g., collaborative enterprises, marketing, mobile and social apps.
Basically, text analysis and mining produce a set of statistical models which provide a gateway between syntactic and semantic levels in text analysis. The Jaccard index refinement defined in [13] , improves the Jaccard’s measure of semantic similarity between terms and corpora. The standard Term Frequency (TF) measure introduced in [14] , and the Inverse Document Frequency (IDF) defined in [15] are frequently improved as refinements of TF.IDF measures or so called, such as in [16] . Semantic SNA and ontology building benefit each other, as defined in [17] with a three-dimensional model crossing social graphs, annotations (tags) and consensual ontologies. The latest works in semantic SNA aim at making operational the outlines of SNA using ontologies and Semantic Web languages, and pave the way for statistical and semantic analysis of the Social Web [9] [18] . Our applicative work defines and experiments a structure of social graph based on the semantics of the endogenous content and dedicated to semantic SNA. It enables 1) to retrieve the communities and individuals sharing knowledge denoted by keywords, 2) to rank people activities within communities sharing common knowledge, and 3) to detect and to balance stress at work, based on the collective/individual knowledge use and on the knowledge commonly developed within an enterprise social network.
3. Epistemic Equivalence
Based on Kripke semantics [19] , we have detected and resolved a semantic incoherence due to an incompleteness of the electro-physic metaphor introduced in SNA to represent the information behavior in social networks [2] [3] 2.
Definition 1. In a Kripke model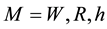 ,
, 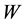 is a set of worlds
is a set of worlds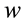 ,
, 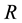 is a binary relationship of accessibility in
is a binary relationship of accessibility in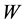 , and
, and 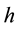 is a function representing all the propositions
is a function representing all the propositions 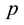 such as
such as 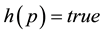 in all worlds
in all worlds . The formalism
. The formalism 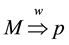 means
means 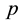 is true in the world of the model
is true in the world of the model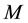 .
.
Definition 2. Some propositions are Kripke-satisfiable if it exists at least one world of a model in which they are true. A proposition is Kripke-valid if it is true in every world of every Kripke model, or in every world of a unique Kripke model.
Definition 3. A proposition p is Kripke-equivalent to 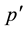 if
if 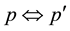 in every world of every defined Kripke model, or in every world of a unique Kripke model.
in every world of every defined Kripke model, or in every world of a unique Kripke model.
Let a proposition 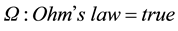
and a proposition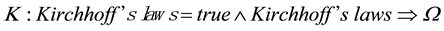


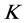
Let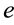




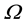
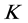
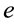
In the world
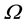
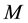


We obtain the Equation (1), meaning 

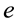


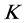
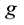


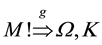
Rightfully observing Kripke semantics, 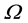

Furthermore, releasing constraints by replacing 
is not sufficient to make it Kripke-valid, as long as Ω remains false in
Therefore, according to Kripke semantics, the demonstration of a semantic incoherence within the electrophysical metaphor commonly employed in SNA is established.
Finally, we introduce an epistemic completion resolving the semantic incoherence we have demonstrated.
Making 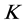

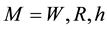
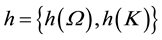


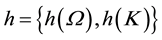

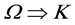
3.1. Shared Knowledge and Stress at Work
The linguistic Term Frequency metric TF is defined in [14] as the number of occurrences of a term 

Regarding people within a social network platform/database, 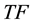
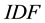
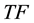
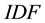
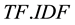
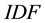
We use 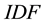
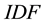

In the context of the Socioprise project, we are interested in Enterprises Social Networks Analysis (ESNA). For a person in an ESN, we state stress at work increases in proportion to the knowledge use intensity and to the knowledge rarity. In other words, the semantic intensity metric combined to the rarity metric 

3.2. Semantic Coherence
Respecting our epistemic equivalence, we introduce the Ohm’s law6 in



Theorem 1.
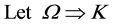

3The Kripke model entails 
4We compare a digital resource within the social network to a document.
5We do not consider noise words and stop words as terms denoting knowledge.
6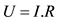
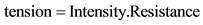
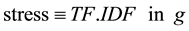
then
and

Based on Kripke semantics, theorem 1 defines knowledge use intensity (i.e., the semantic intensity) coupled to knowledge rarity as a factor of stress in 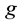


Equation (3) represents the semantic equivalence between stress and electrophysical tension for interdisciplinary graph analysis.
Proof.
Introducing equation (3) in 
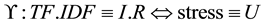
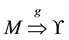




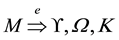
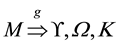





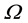

Introducing the Ohm’s law in the world 

Introducing the Ohm’s law prior to the Kirchhoff’s point law in SNA, our epistemic paradigm improves the interdisciplinary bridge-building between information flows behavior and electronic flows behavior previously introduced in [2] and [3] . This theoretical contribution paves the way for graph-based applications taking advantage of electronic flow-based rules in graph theory, so as to discover further heuristics merging knowledge engineering and electrophysics in SNA.
4. Socio-Semantic Networks
We experiment our improvement of the interdisciplinary bridge-building between electro-physics and SNA. Our theoretical approach is applicable to various social graph structures. We apply it to a socio-semantic structure of social network. This structure that we name skills network, facilitates our applicative approach in order to make our theoretical contributions easier to perceive. It is defined below, after the presentation of our applicative purpose.
Our applicative objective is to define an innovative and decisional model based on dynamic and semantic SNA, which purpose is to foster the performance and to improve the social climate within workgroups. This model produces some visual indications and predictive recommendations for the performance optimization and the reduction of psychosocial risk, fostering the agile and skills-based work organization defined in [21] . Our experimentations aim at the discovery of multidimensional synergies between knowledge engineering and physical aspects of the analysis of Collaborative Enterprises Social Networks (CESN). We define a CESN as a heterogeneous graphic structure, based on the numerical marks and contents available in enterprises information systems and representing collaborative relationships within enterprises.
We define a hybrid graph structure, named skills network, which represents the studied CESN and the semantic network induced by its endogenous dataset. The nodes of the semantic network represent the meaningful terms found in the endogenous content and indexed. The arcs of the semantic network represent some semantic relationships, such as synonymy and/or hyponymy, defined in a thesaurus or an ontology. In the context of the Socioprise project, we solely represent synonyms found in a predefined thesaurus, for each term denoting knowledge found in the endogenous content. Our theoretical findings provides a new heuristic for defining coherent semantic weighs within skills networks, which is going to be presented in Section 5.
7We do not study the possible uses of Equation (4), which semantics is coherent in
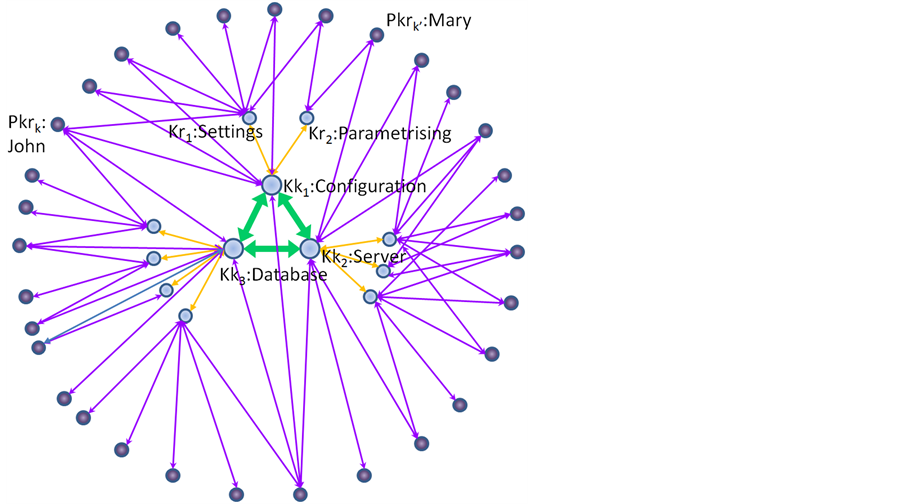
We have developed a skills network research system enabling the automatic building of skills networks based on keywords researches. These restricted networks are named skills networks on demand. They make knowledge communities and noticeable individuals accurately identifiable regarding seized keywords, with the help of SNA metrics. The Figure 1 shows an example of skills network on demand.
Figure 1. Basic structure of skills network on demand.
The Figure 1 illustrates the result of a query on “Configuration, Server, Database”. It returns a skill networks entailing 31 individuals producing and/or consuming the 3 keywords and/or their respective related knowledge.
For instance, John produces and/or consumes content in the domain “database configuration and settings”, while Mary produces and/or consumes content in the domain of “parameterizing server”. The figure only shows the skills network structure, and how it represents a part of the competencies of John and Mary related to the knowledge domain denoted by the keywords.
In our current experimentations as in Figure 1, a skills network on demand comprises three types of nodes and four types of relationships8. The nodes are either of a type (1) keyword-Key knowledge (Kk), (2) term associated to keyword-Relative knowledge (Rk) or (3) People (Pkr).
The relationships are either of a type (1) Key knowledge/Key-knowledge, (2) Key knowledge / Relative knowledge, (3) People/Key knowledge or (4) People/Relative knowledge.
The set of arcs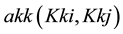
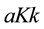


An individual is associated to the key and/or relative knowledge present in the endogenous content with which he interacts. His interactions within the CESN are typed by two generic roles, production (P) and consumption (C). The role P represents information flows produced by individuals and the role C represents information flows consumed by individuals. An individual 


5. A Graph Weighing Paradigm
Within skills networks on demand, individuals act as flow producers and/or consumers, whilst keywords act as flow collectors. Our keywords-based and automatic process of skills networks building stands on a lexico-se- mantic indexation of the endogenous resources associated to individuals―i.e., the resources produced and consumed by the enterprise members, through the collaborative software environment.
First, we apply our theoretical approach thanks to a process propagating initial values calculated by the BM25 formula, in respect to the Ohm’s law and Kirchhoff’s laws. Our process enables to calculate values of semantic tension/stress, semantic intensity and resistance for each element of a skills network, respecting the epistemic paradigm we introduce. Then, we define a predictive recommendation model based on a retro-propagation process and on the natural balance of electronic flows.
5.1. Lexico-Semantic Research
Skills networks on demand are automatically built depending on keywords. They use a lexico-semantic research service requiring indexation of the endogenous content. The enterprises corpora being usually consequent, for their semantic indexing, we momentarily reject the hypothesis of rich (and time-consuming) ontologies built by the experts. The software architecture deployed in the context of Socioprise comprises 1) lexical analysers for French and English language, 2) noise words lists, 3) French and/or English thesaurus, and 4) some multilingual full-text indexing-search services. It supports about 50 languages and remains quickly adaptable to various datasets.
In our main experimentation with a French corpus, the noise words list and the thesaurus are simply built using French lexicons and synonyms dictionaries. This part of our indexation and research process could be improved with specialized dictionaries, ontologies and/or domain-specific thesauri such as SKOS thesauri9, in order to provide more relevant skills networks on demand.
Thanks to the BM25 formula integrated in our experimental architecture, we are in measure to calculate values of production 


5.2. Interdisciplinary Rules of Flow Distribution
The Kripke model defined in Section 3 provides an epistemic equivalence between graph theory and electrophysics, based on the coherence of Ohm’s law and the Kirchhoff,’s point law and represented in Equation (3). It introduces a rational improvement of the interdisciplinary paradigm defined in [2] [3] and commonly accepted in SNA.
Within skills networks, a person 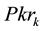


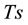
For a same term denoting knowledge, the 

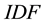


Based on the values

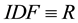
For instance, the total resistance 
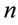

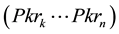



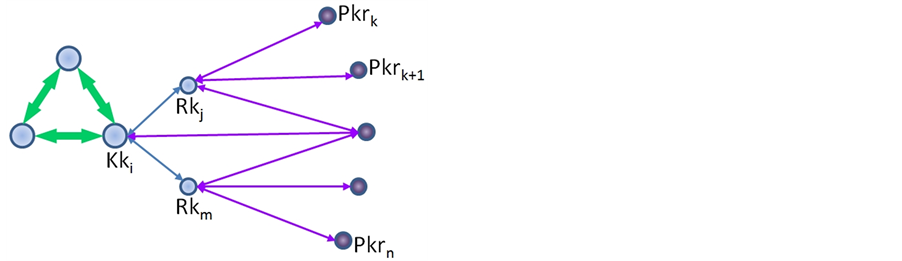
Figure 2. Graphic component as parallel resistances.
Let
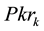
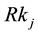
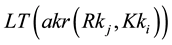
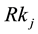
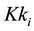

Formula (8) defines how the intensity produced and/or consumed in a group of parallel resistances is collected and converted to tension in a serial-parallel component such as illustrated in Figure 3.
Figure 3. Serial-parallel component.
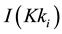
Figure 4. Parallel hierarchy of components.
For 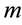

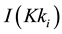


In the Formula (9), all the arcs connected to a node 
5.3. Balanced Tension Core Values
Theorem 2.
Kirchhoff’s mesh law:
Let a mesh defined by the points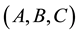
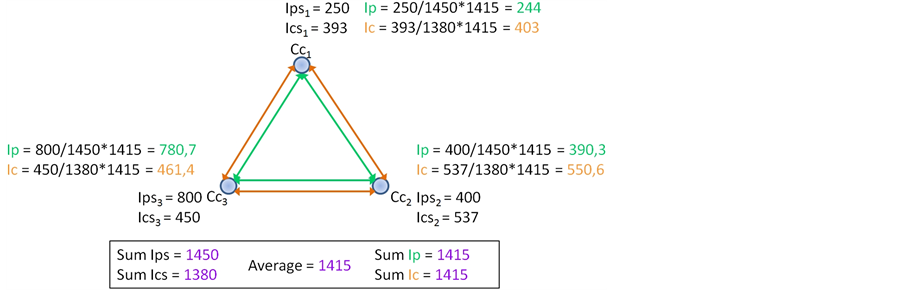
Within skills networks on demand resulting from multiple keywords queries, we note 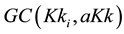

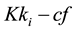
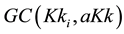


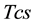
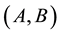
We state the arcs in 
All the meshes we have experimented with skills networks comprising up to 5 nodes rightfully observe the Kirchhoff’s mesh law and confirm the accuracy of our propagation process.
5.4. Balanced Intensity Core Values
Theorem 3.
Kirchhoff’s point law
The sum of incoming current intensities in a node is equal to the sum of outgoing current intensities.
Each node 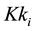

Thus, we define a principle for smoothing tension, based on the average intensity value within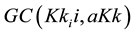
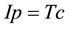


Figure 5. Balancing a three-keywords mesh.
Figure 5 shows how balanced values 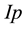

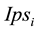
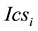
5.5. A Natural Load-Balancing Recommendation
We use a propagation process to collect semantic values produced and/or consumed within skills networks on demand. The process respects the epistemic paradigm we define in dynamic Social Networks Analysis, and implements the Ohm’s law and Kirchhoff’s laws. Semantic values are collected by the keywords representing the core of skills networks on demand, and production/consumption flows are balanced depending on an average value, respecting our epistemic paradigm.
The retro-propagation of new balanced values, from the core to the extremities of the studied skills network, produces balanced semantic values to be compared to the initial values, for each element within the network. Theoretically, the balanced values represent the optimal stress and activity distribution, in respect to individual knowledge and knowledge communities-i.e., a dynamic and predictive recommendation.
Figure 6 presents a simulation of our process, showing initial and balanced values calculated thanks to our model. The electric circuit at bottom-left in the figure shows the corresponding circuit implemented in an electronic solver, so as to verify the accuracy of our model.
Figure 6. Initial and balanced semantic weights.
Our retro-propagation process isolates dependant sources of intensity, to avoid a useless recursive complexity. Excepting this, it rightfully respects the electronic distribution rules in serial/parallel circuits. This represents a
significant improvement of the analogy between networks flows and current flows, since the works of [2] and [3] .
6. Predictive Recommendation
The corpus we use in line with the Socioprise project stems from a real business process, supported by a workflow application running over a relational database. The studied dataset comprises about 250 000 commented steps, regarding 33,000 entries-i.e., some initial actions of entry in the workflow. These entries comes from about 540 persons and are carried through issues by 80 collaborators. Entries and steps comprise various textual metadata and comments.
We generate skills networks automatically built from a research with the French keywords “validation, message, erreur”. In Figure 7, we present our predictive model of recommendations with 4 illustrations in which the networks are disposed in space thanks to the same algorithm (i.e., a Force Atlas 2 spatialization algorithm). The color gradient at the center of the picture represents the values amplitude, from blue to red for minimum to maximum values.
In Figure 7, the graphs at the left are coloured and dimensioned depending on the difference of produced minus consumed semantic intensity, at the top, and of produced minus consumed tension, at the bottom. The graphs at the right of the picture are colourised and dimensioned depending on the difference of balanced intensities produced minus consumed, at the top of the picture, and of balanced tension produced minus consumed, at the bottom10.
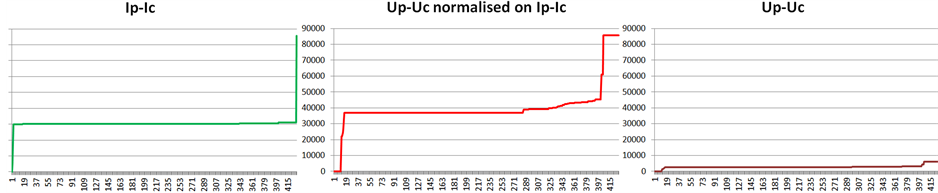
Figure 9 presents the distribution of the balanced values of the arcs of our experimental skills networks, for the graphs at the left of the picture 7.
Figure 8 presents the distribution of the balanced values for the arcs of the studied network. Visualizing the weighed networks illustrated in Figures 7-9, we note that:
1) intensities are stronger than tensions, for both the initial and the balanced values―i.e., warmest colours in Figure 7 and level of the mean values in Figure 9;
2) initial values are more sparse than balanced values―i.e., less population in initial mean values, cf. Figure 9 and colour temperature in Figure 7;
Figure 7. Predictive recommendation―real dataset.
Figure 8. Initial values distribution.
Figure 9. Initial values distribution.
3) the balanced tension values don’t present hot spot (cf. node“Utilitaire Compile”) and are strongly redistributed around the average level-cf. nodes colour and dimension in the graph Predictive , Figure 7 and curve at the center of Figure 8.
4) maximums are lower for balanced values than for initial values, about 5 times lower for the intensity values and 60 times lower for the tension values-cf. vertical scales and curves in Figure 8 and Figure 9; average values are lower for the balanced values than for the initial values, about 2,5 times lower for the intensity values and 14 times lower for the tension values-cf. vertical scales and curves in Figure 8 and Figure 9.
5) average values are lower for the balanced values than for the initial values, about 2,5 times lower for the intensity values and 14 times lower for the tension values-cf. vertical scales and curves in Figure 8 and Figure 9.
Studying the skills networks presented in Figure 7, we have begun to identify visual and interesting particularities. For instance, within the initial networks, the keywords “erreur” and “message” appear as main activity and tension sources whilst “erreur” concerns much more collaborators than “message”-cf., Figure 7. The overall recommendation exhibited by the balanced networks seems to make sense, whilst it foresees intensity increasement about “message”, and it foresees the tension decreasement of the electronic account “Utilitaire Compile”, counterbalanced by the increased number of collaborators working about “message”.
Concerning the biggest “hot” spot appearing in the initial weighed networks, which corresponds with a generic account shared by various collaborators (i.e., node Utilitaire Compile), we observe an unexpected particularity. The spot disappears in the predictive recommendation and a new red coloured group appears, related to the keyword “message”.
We have been positively surprised when retrieving most of the individuals who used the shared account within the new recommended group, although there was absolutely no explicit information associating these individuals to the shared account in the studied database. We also have noticed two related knowledge exhibited by the initial tensions weighs and denoted by the terms “lettre, faute”-trad., “letter, fault or default”. The relevance of synonyms in our example could be improved using better semantic referentials (cf. Section 5.1), however these terms possibly represent a recommendation for social capital management within the studied workgroup.
Our experimentation shows that at constant total intensity, predictive recommendation decreases the tension values within the studied skills network. According to our epistemic paradigm, the recommendation resulting from our predictive model is susceptible to foster the performance of workgroups and the amelioration of social climate.
According to the experts, the dynamic model of predictive SNA we have defined produces 1) a principle of reduction of the tension/stress at work, 2) some precise indications for training management (training plan), and 3) some recommendations for human and social capital management―e.g., employs and careers management and development. The validity of these outcomes is confirmed by the experts in Human Resources Management (HRM) and in Human Capital Management (HCM) involved in the Socioprise project12. The first results presented reveal numerous indications and recommendations looking propitious to the amelioration of perfor- mance and social climate, but they still need to be studied in order to release more easy-to-understand in- dications.
Future applications of the Socioprise project have been presented in a large professional event (Human Resources 2012, Paris-France), and a new project has been studied. It is based on the development of spanning- tree and graph factorization models aiming at the production of innovative end-user software.
7. Conclusion and Perspectives
Based on Kripke semantics [19] , we have detected and reduced a semantic incoherence due to an incompleteness of the electro-physic metaphor commonly employed in Social Network Analysis. Our theoretical approach defines an epistemic paradigm applicable to various social graph structures. We apply it to a socio-semantic structure of social network named skills network on demand, which contributes to semantic and dynamic SNA and makes our theoretical findings easier to perceive.
From an applicative standpoint, our epistemic paradigm produces first a metric of stress at work based on individual/collective knowledge and on spontaneous numerical activity, which bias might be lower than questions-based surveys. Based on our epistemic paradigm, we define a semantic and predictive model of dynamic SNA for Enterprises Social Networks, experimented with a professional dataset (patent). Its application to social capital management helps in fostering psychosocial risk reduction, professional well-being and overall, peaceful social climate.
From a theoretical standpoint, the metaphysic approach we develop paves the way for electrodynamics and thermo-dynamics metaphors in graph models, possibly resulting in future dynamic SNA measures. The applicative perspective of our findings can extend to various interdisciplinary applications based on graph theory.
Categories and Subject Descriptors
H.1.0 [Information Systems Applications]: Models and Principles, General; M.4 [Knowledge Management]: Knowledge Modeling; K.4.2 [Computing Milieux]: Computers and Society, Social Issues.
General Terms
Social Networks Analysis, Semantics, Modal Logic, Knowledge Engineering.
References
- Moreno, J. (1934) Who shall survive?―(Trad. fr) Fondements de la sociométrie. PUF.
- Brandes, U. and Fleischer, D. (2005) Centrality Measures Based on Current Flow. 22nd Symp. Theoretical Aspects of Computer Science (STACS 05), number 3404 in LNCS, 533-544, Springer Verlag.
- Newman, M. (2005) A Measure of Betweenness Centrality Based on Random Walks. Social Networks, 27, 39-54. http://dx.doi.org/10.1016/j.socnet.2004.11.009
- Freeman, L. (1977) A Set of Measures of Centrality Based on Betweenness. Sociometry, 40, 35-41. http://dx.doi.org/10.2307/3033543
- Shimbel, A. (1953) Structural Parameters of Communication Networks. Bulletin of Mathematical Biophysics, 15, 501- 507. http://dx.doi.org/10.1007/BF02476438
- Gruber, R.T. (2008) Collective Knowledge Systems: Where the Social Web Meets the Semantic Web. Web Semantics: Science, Services and Agents on the World Wide Web, 6, 4-13. http://dx.doi.org/10.1016/j.websem.2007.11.011
- Mika, P. (2005) Ontologies Are Us: A Unified Model of Social Networks and Semantics. International Semantic Web Conference, Volume 3729 of Lecture Notes in Computer Science, 522-536. International Semantic Web Conference 2005, Springer.
- The Socioprise Project, 2009-2012.
- Erétéo, G. (2011) Semantic Social Network Analysis. Ph.D. Thesis, Université de Nice Sophia-Antipolis, Laboratoire d’Informatique, Signaux et Systèmes de Sophia-Antipolis (L3S, UMR6070 CNRS).
- Thomassen, C. (1990) Resistances and Currents in Infinite Electrical Networks. Journal of Combinatorial Theory, Series B, 49, 87-102. http://dx.doi.org/10.1016/0095-8956(90)90065-8
- Wang, Z., Scaglione, A. and Thomas. R. (2010) Electrical Centrality Measures for Electric Power Grid Vulnerability Analysis. Proceedings of the 49th IEEE Conference on Decision and Control, CDC 2010, December 15-17, 2010, Atlanta, Georgia, 5792-5797.
- Gruber, T. (1995) Toward Principles for the Design of Ontologies Used for Knowledge Sharing. International Journal of Human Computer Studies, 43, 907-928, http://dx.doi.org/10.1006/ijhc.1995.1081
- Rogers, D. and Tanimoto, T. (1960) A Computer Program for Classifying Plants. Science, 132, 1115-1118. http://dx.doi.org/10.1126/science.132.3434.1115
- Salton, G. and MacGill, M. (1986) Introduction to Modern Information Retrieval, Chapter 6―Retrieval Refinements, 201-215. McGraw-Hill Book Company.
- Sparck Jones, K. (1972) A Statistical Interpretation of Term Specificity and Its Application in Retrieval. Journal of Do- cumentation, 28, 11-21. http://dx.doi.org/10.1108/eb026526
- Robertson, S.E. and Sparck Jones, K. (1976) Relevance Weighting of Search Terms. Journal of the American Society for Information Science, 27, 129-146. http://dx.doi.org/10.1002/asi.4630270302
- Jung, J. and Euzenat, J. (2007) Towards Semantic Social Networks. ESWC 07: Proceedings of the 4th European Semantic Web Conference, 267-280, Springer-Verlag, Berlin, Heidelberg.
- Thovex, C. and Trichet, F. (2012) Semantic Social Networks Analysis: Towards a Sociophysical Knowledge Analysis. Social Network Analysis and Mining Journal (SNAM), 2.
- Kripke, S.A. (2011) Philosophical Troubles: Collected Papers, Volume 1. Oxford University Press, Oxford.
- Zaragoza, H., Craswell, N., Taylor, M., Saria, S. and Robertson, S.E. (2004) Microsoft Cambridge at Trec-13: Web and Hard Tracks. Proceedings of Text REtrieval Conference, TREC 2004.
- Demailly, L. (2008) Politiques de la relation: approche sociologique des métiers et activités. Presses Universitaires Septentrion.
NOTES
1In modern physics, the electromagnetic force is one of the 4 forces enabling the creation of Universe. The 3 others forces are: gravitation, weak nuclear force and strong nuclear force.
2Our findings concern all graph analysis models entailing the Kirchhoff’s laws (not only SNA models).
8Types and number of relationships can change depending on the semantic referential used for skills graph automatic building.
9Simple Knowledge Organization System (SKOS) is a re-quest for comments (W3C) specific to multilingual thesaurus management.
10The calculated values are normalized in so as to be loaded in a graph visualization software―i.e., Gephi, http://gephi.org
11We have not yet proofed this particularity as a result of the regular behavior of the model.
12The involved experts in HRM and HCM are specialized consultants of the company OpenPortal Software, managing large client relationships.