Advances in Linear Algebra & Matrix Theory
Vol.2 No.4(2012), Article ID:25472,4 pages DOI:10.4236/alamt.2012.24008
On the Minimal Polynomial of a Vector
Faculty of Mathematics and Computer Science, Hubei University, Wuhan, China
Email: dzheng@hubu.edu.cn, ghliu@hubu.edu.cn
Received October 26, 2012; revised November 30, 2012; accepted December 9, 2012
Keywords: Finite dimensional linear space; Linear transformation; Minimal polynomial
ABSTRACT
It is well known that the Cayley-Hamilton theorem is an interesting and important theorem in linear algebras, which was first explicitly stated by A. Cayley and W. R. Hamilton about in 1858, but the first general proof was published in 1878 by G. Frobenius, and numerous others have appeared since then, for example see [1,2]. From the structure theorem for finitely generated modules over a principal ideal domain it straightforwardly follows the Cayley-Hamilton theorem and the proposition that there exists a vector v in a finite dimensional linear space V such that v and a linear transformation of V have the same minimal polynomial. In this note, we provide alternative proofs of these results by only utilizing the knowledge of linear algebras.
1. Introduction
Let 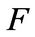 be a field,
be a field, 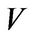 be a vector space over
be a vector space over 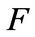 with dimension
with dimension![]() , and
, and ![]() be a linear transformation of
be a linear transformation of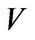 . It is known that
. It is known that 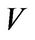 becomes a
becomes a 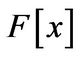 -module according to the following definition:
-module according to the following definition:
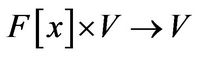
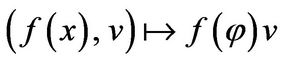 .
.
For a fixed linear transformation ![]() and a vector
and a vector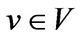 , the annihilator of
, the annihilator of ![]() with respective to
with respective to ![]() is defined to be
is defined to be
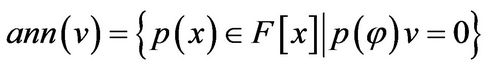 .
.
Similarly, the annihilator of 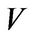 with respective to
with respective to ![]() is defined to be
is defined to be
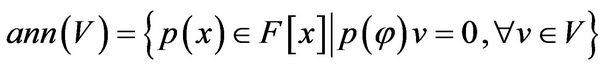 .
.
Since 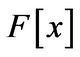 is a principal ideal domain the ideals
is a principal ideal domain the ideals 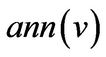 and
and 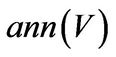 can be generated by the unique monic polynomials, denote them by
can be generated by the unique monic polynomials, denote them by 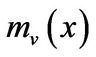 and
and 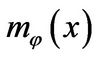 , respectively. Which are called the order ideals of
, respectively. Which are called the order ideals of ![]() and
and 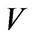 in abstract algebras, respectively. They are also called the minimal polynomials of
in abstract algebras, respectively. They are also called the minimal polynomials of ![]() and
and 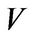 with respective to
with respective to ![]() in linear algebras, respectively. It is clear that the minimal polynomial of zero vector (or zero transformation) is 1. By the structure theorem for finitely generated modules over a principal ideal domain [3,4], the module
in linear algebras, respectively. It is clear that the minimal polynomial of zero vector (or zero transformation) is 1. By the structure theorem for finitely generated modules over a principal ideal domain [3,4], the module 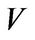 can be decomposed into a direct sum of finite cyclic submodules:
can be decomposed into a direct sum of finite cyclic submodules:
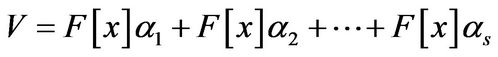 , (1)
, (1)
and 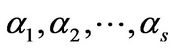 are vectors in
are vectors in 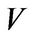 such that
such that
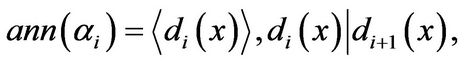 (2)
(2)
where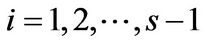 . Let
. Let 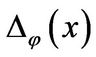 be the characteristic polynomial of
be the characteristic polynomial of![]() . By (1) and (2) one has
. By (1) and (2) one has
• 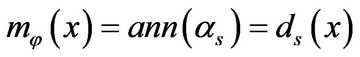 ;
;
• 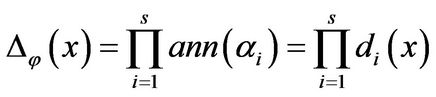 .
.
Furthermore, these results straightforwardly imply the following theorem:
Theorem 1. [3,4] With the notations as above, we have 1) [Cayley-Hamilton Theorem]
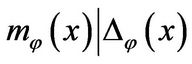 , and so
, and so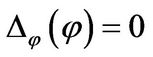 .
.
2) There exists a vector 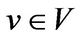 such that
such that
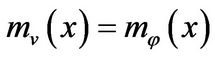 .
.
2. Proofs Based on Linear Algebras
In this section we give an alternative proof of Theorem 1 by only utilization of knowledge of linear algebras. To demonstrate an interesting proof of some proposition in linear algebras and its applications, we present two proofs of (2) in Theorem 1 for infinite fields and arbitrary fields, respectively, and then use the related results to prove the Cayley-Hamilton theorem.
The following lemma provide an interesting proof of an proposition in linear algebras that a vector space over an infinite field can not be an union of a finite number of its proper subspaces by Vandermonde determinants.
Lemma 1. Let 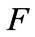 be an infinite field, and
be an infinite field, and 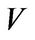 be a vector space over
be a vector space over 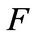 with dimension
with dimension![]() , and
, and 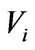 be nontrivial subspaces of
be nontrivial subspaces of 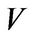 for
for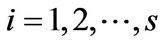 . Then there exists infinite many bases of
. Then there exists infinite many bases of 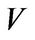 such that any element of them is not in each
such that any element of them is not in each 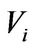 for
for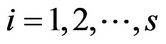 . Therefore, if
. Therefore, if ![]() then
then 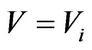 for some i .
for some i .
Proof: Let 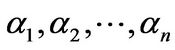 be a F-base of
be a F-base of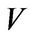 . For any
. For any 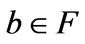 we set
we set
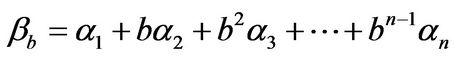 .
.
Let 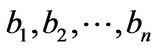 distinct elements in
distinct elements in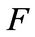 . We have
. We have
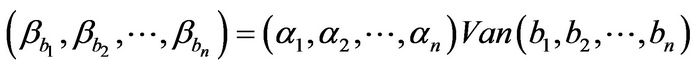
where 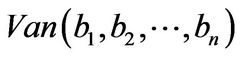 is a Vandemonde matrix. So
is a Vandemonde matrix. So 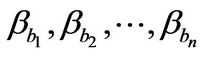 is a base of
is a base of  because the determinant of
because the determinant of 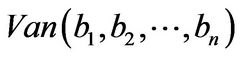 is nonzero. Let
is nonzero. Let ![]() be the following set with an infinite number of vectors:
be the following set with an infinite number of vectors:
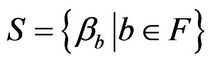 .
.
Since 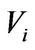 with
with 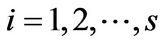 is a nontrivial subspace of
is a nontrivial subspace of 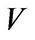 one can verify that
one can verify that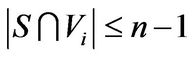 . And so
. And so
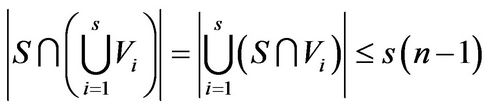 .
.
Therefore, 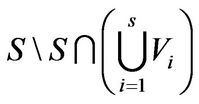 is infinite, and any distinct
is infinite, and any distinct
![]() vectors in the set constitute a base of
vectors in the set constitute a base of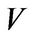 .
.
Proposition 1. Let 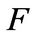 be an infinite field. Let
be an infinite field. Let 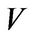 be a
be a 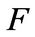 -vector space with dimension
-vector space with dimension![]() , and
, and ![]() be a linear transformation of
be a linear transformation of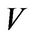 . Then there exists a vector
. Then there exists a vector 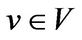 such that
such that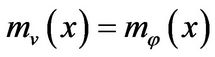 .
.
Proof: It is clear that 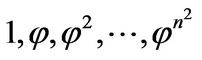 are linearly dependent over
are linearly dependent over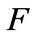 . So the degree
. So the degree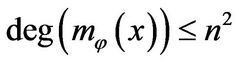 . For any
. For any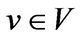 , the minimal polynomial
, the minimal polynomial 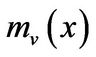 of
of ![]() is a monic factor of
is a monic factor of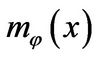 . So there exist finite number of vectors
. So there exist finite number of vectors 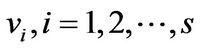 such that
such that
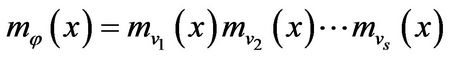 where
where 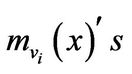 are mutually coprime irreducible polynomials. Set
are mutually coprime irreducible polynomials. Set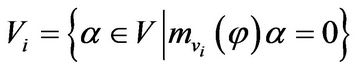 . One can verify that
. One can verify that
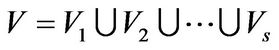 .
.
By Lemma 1, there exists 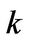 with
with 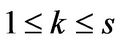 such that
such that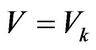 . Which shows that
. Which shows that
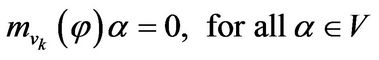 and so
and so 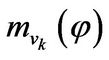 is a zero linear transformation. Hence we have
is a zero linear transformation. Hence we have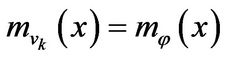 .
.
In fact, Proposition 1 holds for arbitrary fields from the introduction. To obtain a general proof we first give the following lemma.
Lemma 2. Let 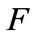 be a field,
be a field, 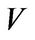 be a
be a ![]() -dimensional linear space over
-dimensional linear space over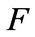 , and
, and ![]() be a linear transformation of
be a linear transformation of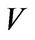 . For any
. For any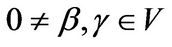 , there exists
, there exists 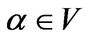 such that
such that
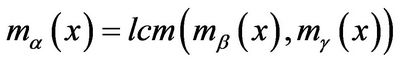 here
here 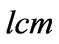 and the following
and the following 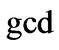 stand for the least common multiple and greatest common divisor of two polynomials, respectively.
stand for the least common multiple and greatest common divisor of two polynomials, respectively.
Proof: By properly arrangement, the minimal polynomials of ![]() with respective to
with respective to ![]() have the following irreducible factorization respectively,
have the following irreducible factorization respectively,
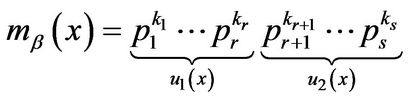 ,
,
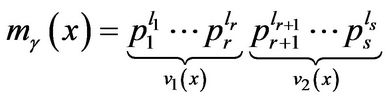 .
.
Moreover, 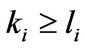 for
for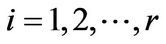 , and
, and 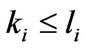 for
for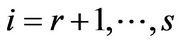 . So, we have
. So, we have
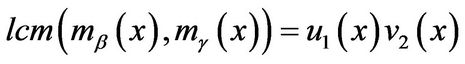 ,
,
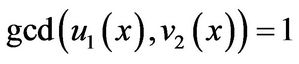 .
.
One can verify that the minimal polynomials of 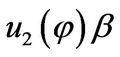 and
and 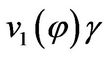 are
are
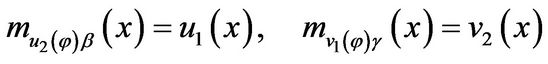 respectively. Set
respectively. Set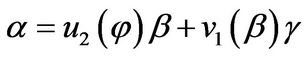 , then
, then
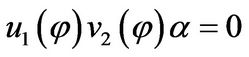 .
.
Which implies that
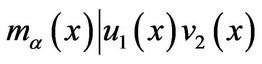 . (3)
. (3)
Conversely, from 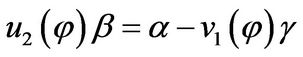 it follows that
it follows that
![]() .
.
Which shows that
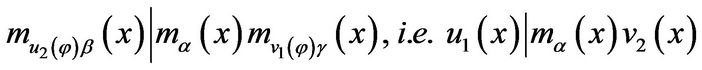
So, 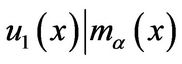 since
since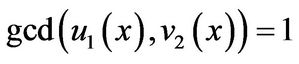 Similarly,
Similarly,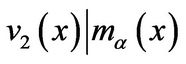 . By
. By 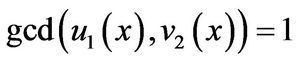 again, we have
again, we have
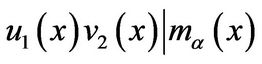 . (4)
. (4)
Equations (3) and (4) imply that
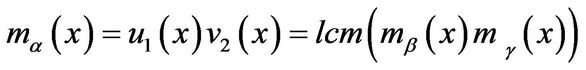 .
.
Proposition 2. Let 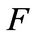 be a field. Let
be a field. Let 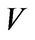 be a
be a 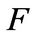 -vector space with dimension
-vector space with dimension ![]() and
and ![]() be a linear transform of
be a linear transform of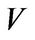 . Then there exists a vector
. Then there exists a vector 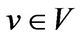 such that
such that
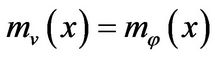 .
.
Proof: Let 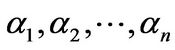 be a
be a  -base of
-base of . One can verify that
. One can verify that
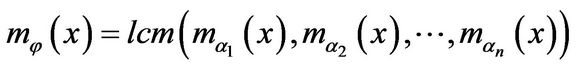 .
.
By repeatedly utilization of Lemma 2, we can find a vector 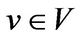 such that
such that
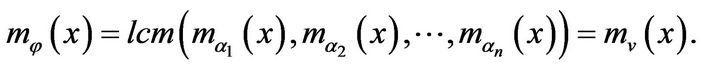
According to Proposition 2, we can easily deduce the Cayley-Hamilton theorem.
Proof of Cayley-Hamilton Theorem: Let 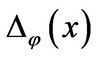 be the characteristic polynomial of
be the characteristic polynomial of![]() . We show
. We show 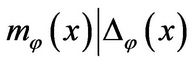 . By Proposition 2 there exists
. By Proposition 2 there exists 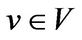 such that
such that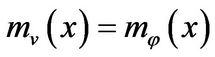 . Let
. Let
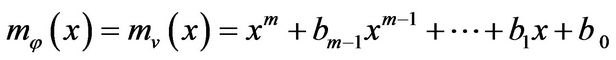 .
.
So, one can verify that vectors 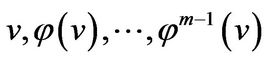 are linearly independent over
are linearly independent over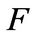 . We extend them to a basis of
. We extend them to a basis of 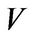 as follows:
as follows:
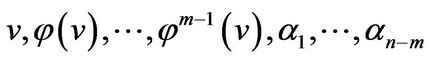 .
.
We have
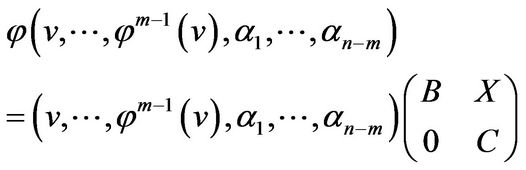
where the ![]() square matrix
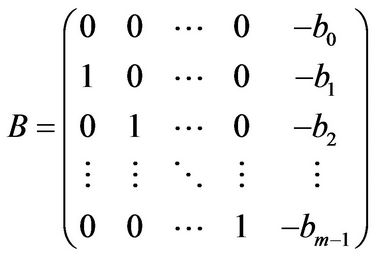
square matrix 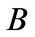 has the form
has the form
and 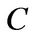 is an
is an ![]() square matrix, and
square matrix, and 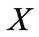 is an
is an 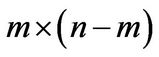 matrix. So the characteristic polynomial of
matrix. So the characteristic polynomial of ![]() is
is
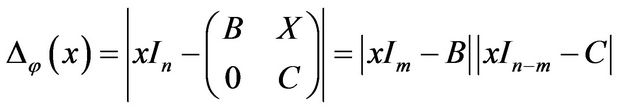 and
and
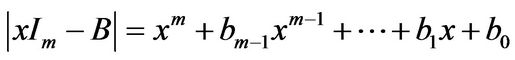 .
.
Hence, 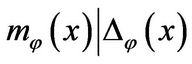 , and
, and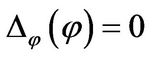 .
.
Actually, the Cayley-Hamilton theorem can be obtained by only using the minimal polynomial of a vector.
Another Proof of Cayley-Hamilton Theorem: Let 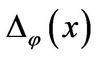 be the characteristic polynomial of
be the characteristic polynomial of![]() . For any
. For any 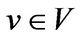 let
let 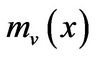 be the minimal polynomial of the vector
be the minimal polynomial of the vector ![]() with respective to
with respective to![]() . To prove the CayleyHamilton theorem, it is enough to show that
. To prove the CayleyHamilton theorem, it is enough to show that
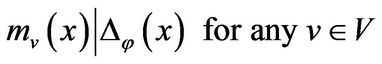 .
.
This statement can be verified by the same arguments as that in above proof.
3. Acknowledgements
The authors would like to thank the anonymous referees for helpful comments. The work of both authors was supported by the Fund of Linear Algebras Quality Course of Hubei Province of China. The work of D. Zheng was supported by the National Natural since Foundation of China (NSFC) under Grant 11101131.
REFERENCES
- K. Hoffman and R. Kunze, “Linear Algebra,” 2nd Edition, Prentice Hall Inc., Upper Saddle River, 1971.
- R. A. Horn and C. R. Johnson, “Matrix Analysis,” Cambridge University Press, Cambridge, 1986.
- N. Jacobson, “Basic Algebra I,” 2nd Edition, W. H. Freeman and Company, New York, 1985.
- Th. W. Hungerford, “Algebra, GTM 73,” Springer-Verlag, New York, 1980. doi:10.1007/978-1-4612-6101-8

