ABSTRACT

Let 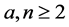be two natural numbers. C. K. Chui and X. L. Shi proved that for any affine frame of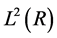, and the family 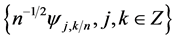is also a frame with the same bounds if is relatively prime to. In this paper we prove that is relatively prime to which is also necessary.

Keywords:Affine Frame; Oversampling

1. Introduction

Let denote, as usual, the space of all complex-valued square integrable functions on the real line with inner product 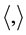and norm. For any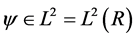, we will use the notation

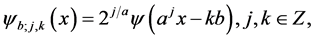(1)

where 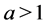and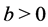. A function 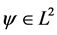is said to generate an affine frame

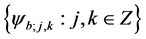(2)

of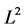, with frame bounds and, where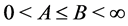, if it satisfies

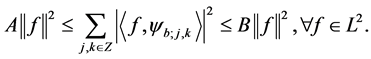(3)

The frame (2) of is called a tight frame, if (3) holds with, see [1] and [2]. In 1993, C. K.Chui and X. L. Shi [3] proved the following oversampling theorem:

Theorem A. Let 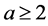be any positive integer and. Also, let 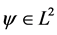generate a frame 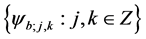with frame bounds and as given by (3). Then for any positive integer which is relatively prime to, the family

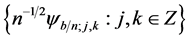(4)

remains a frame of 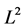with the same bounds. If, this result does not hold. But they only gave a countexample for the case where 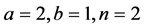as in [4]. For other positive integer and which satisfy, they did not prove. The aim of this paper is to establish the inverse proposition of Theorem A, and then we following:

Theorem 1.1. Let 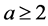be any positive integer and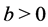. Also, let 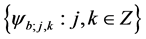be any affine frame of with frame bounds and. The family (4) remains a frame of 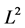with the same bounds: that is,

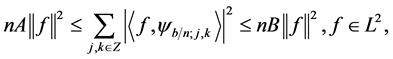(5)

if and only if and are relatively prime.

2. Proofs

The sufficiency has been included in the theorem 4 of [3]. In the following we will prove the necessary part of the theorem.

Suppose for any affine frame (2) of 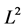with frame bounds and, the family (4) is also a frame of 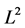with the same bounds. Then when (1) forms an orthonormal basis, the family (4) forms a tight frame with frame bound. So we just need to prove that there exists a function such that the family (1) forms the orthonormal basis, but for any two positive integers and which satisfy, there exist two functions and 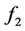such that

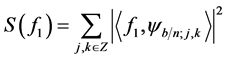
Doesn’t equal

.

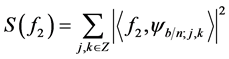Let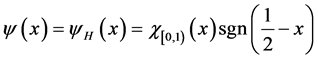, then 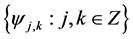forms an orthonormal basis, which is called Haar basis. Set

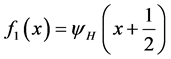and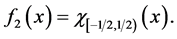

We prove that if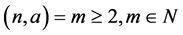, then

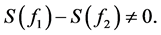(6)

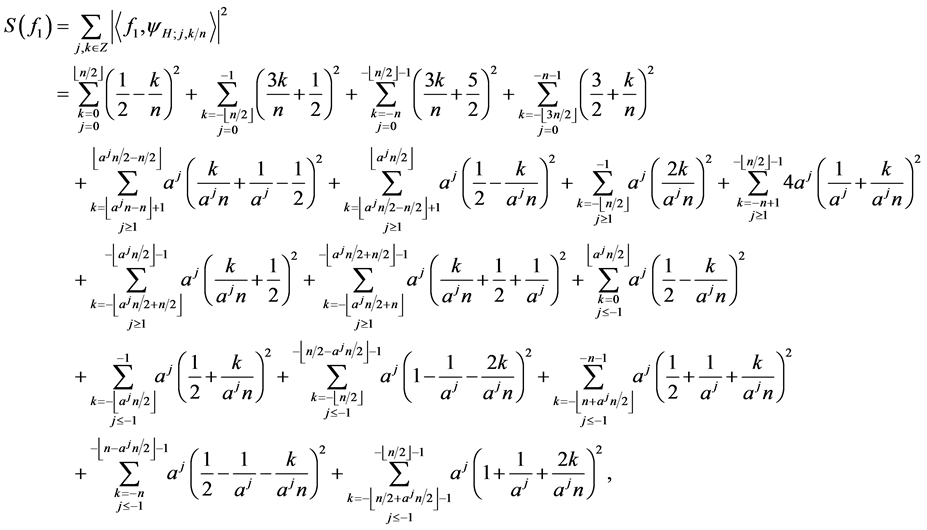
and

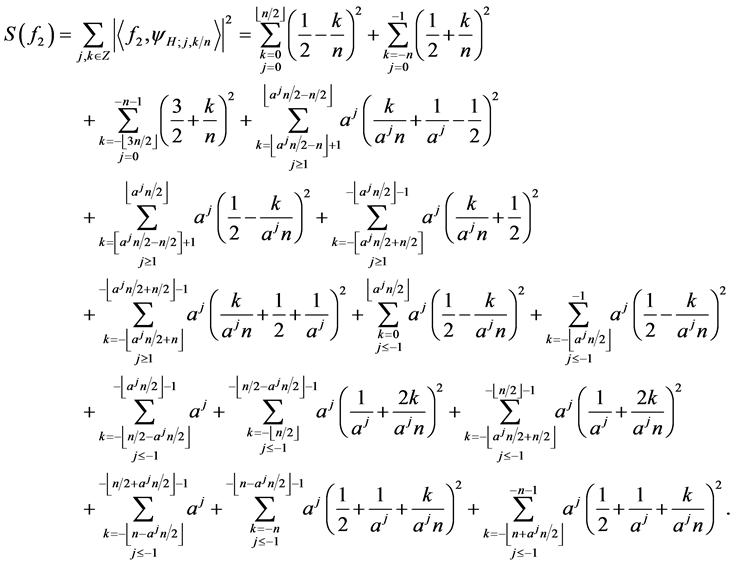
Denote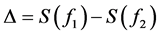. We have

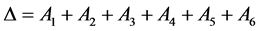where

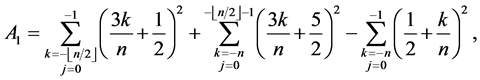
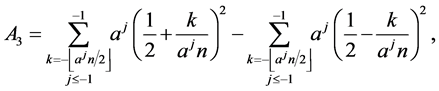
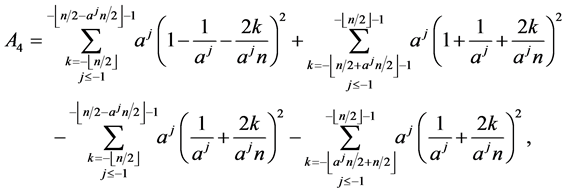
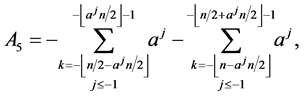
and

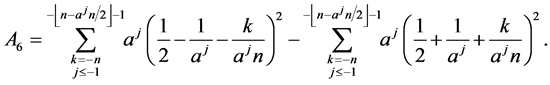
In order to prove the theorem, we have three cases.

Case 1. When.

We have 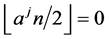if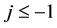. Thus, if is an even integer, we can get

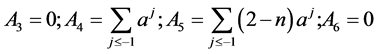
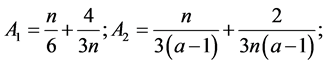
So, we have

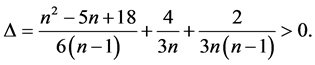
If is an odd integer, we have

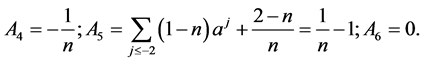
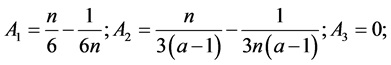
So, we have

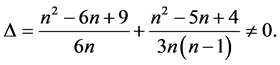
Case 2. When.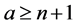

If is an even integer, we have

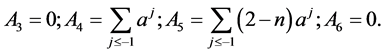
Thus

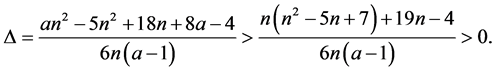
If is an odd integer, we can get 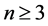because of 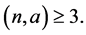As in the case, we also have

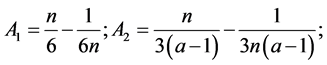
So, we get

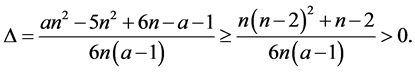
Case 3. When.

If is an even integer. Let

and

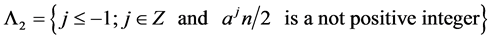
When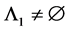, there exists an integer satisfying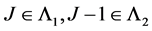. Therefore we have

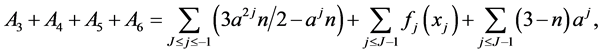
where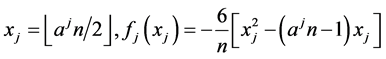. When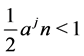, we have 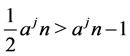and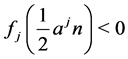. Thus we have

Therefore

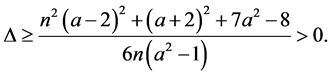
When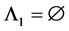, similar to the case, we also have

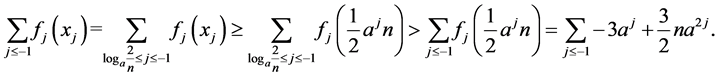
So we have

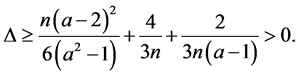
If is an odd integer. We have

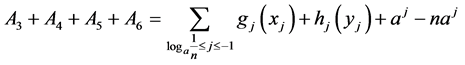
where

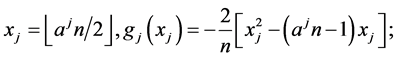
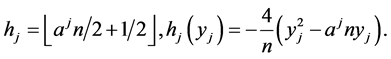
A familiar calculation shows

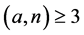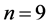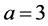Since and, we have. Also when and, we have

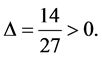
When and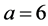, obviously we have

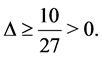
When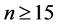,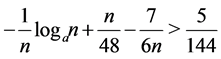. So we have in this case. This completes the proof of the theorem.

Acknowledgements

The authors would like to thank anonymous reviewers for their comments and suggestions. The authors are partially supported by project 11226108, 11071065, 11171306 funded by NSF of China, and project Y201225301. Project 20094306110004 funded by RFDP of high education of China.

REFERENCES