Open Journal of Modern Hydrology
Vol.07 No.02(2017), Article ID:75363,20 pages
10.4236/ojmh.2017.72006
Estimation Accuracy for Reciprocal Analysis of Sensible and Latent Heat Flux Focusing on Radiometric Temperature and Lag-Time
Toshisuke Maruyama*, Manabu Segawa
Faculty of Environmental Science, Ishikawa Prefectural University, Ishikawa, Japan
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 17, 2017; Accepted: April 9, 2017; Published: April 12, 2017
ABSTRACT
There is no word to describe the importance of evapotranspiration research for water resource utilization. We have already proposed a new method for the reciprocal estimation of the sensible (H) and latent heat fluxes (lE) by using a single height temperature (Tz) and humidity (rehz) based on the observed net radiation (Rn) and ground heat flux (G). This research is more advanced than the previous research because it uses a Ts observed by a radiometer and identifies the observed data satisfactorily heat balance relationship in every hour at nine sites. First, we confirmed that the estimated H and lE are very close reproductions of the identified H and lE. Second, by analyzing the relative ground surface temperature (Ts - T0) [Ts: ground surface temperature, T0: observed temperature near the soil surface], the hourly and seasonal changes of (Ts - T0) were clarified, resulting in a marked difference in the (Ts - T0) from previous research in arid and semi-arid regions. Next, the estimation accuracy of H, lE and rehs (the humidity of the soil surface) was determined by observing the slope of the estimated and observed relationship, resulting in the reasonable accuracy (0.85 - 1.15 times) of rehs at seven of the nine sites. Furthermore, the annual evapotranspiration was estimated by com- paring the identified and estimated H and lE, resulting in a reasonable accuracy (0.85 - 1.15) at five of the nine sites in the case of the application of constraint b. Moreover, the effect of the lag-time between the net radiation Rn and both Tz and Ts for the estimation accuracy on H and lE was tested, and no remarkable difference was found because the effect was included already in the original data. The above results will contribute greatly to the advance of water resource planning and hydrometeorology. This research was conducted using FLUXNET data.
Keywords:
Bowen Ratio Method, Radiometric Temperature, Lag-Time between Net Radiation and Temperature, Single Height Temperature and Humidity, Evapotranspiration

1. Introduction
The precise estimation of evapotranspiration (ETa) is very important not only for reasonable water resource utilization and irrigation planning but also for analyzing the hydrologic cycle of water on the earth. The ETa is currently estimated by using the Penman, Penman-Monteith, Bowen ratio and complementally relationship methods. However, those methods have some shortfalls that must be solved [1] [2] [3] .
Based on the above reason, we proposed a new method for the reciprocal analysis of the sensible (H) and latent heat fluxes (lE) by using a single height air temperature (Tz), air humidity (rehz), net radiation (Rn) and ground heat flux (G). The method will remarkably increase utilization for estimating ETa because the method uses only the single height Tz and rehz along with common climate elements. The result will achieve an outstanding development in hydrometeorology, especially in the estimation of ETa.
However, the observed data used for the validation of the method are not sufficiently accuracy because the data do not satisfy the heat balance relationship. To compensate for this shortcoming, this research conducted the validation by using a completely satisfied heat balance relationship with corrected data. The details of the method are described in Section 2.3.
The data used here are from nine sites of FLUXNET, which observes the Ts by using a radiometer and includes required items for our method. In addition, the analysis method is almost the same as that used in previous research, which used the GRG (General Reduced Gradient). The algorithm is provided in the previous research [2] [3] as an Appendix.
2. Methods
2.1. Fundamental Concept of This Research
Figure 1 describes the fundamental concept of this research to compare the data correction (identified), and general solution (estimated results). First, we esti- mated H, lE and rehs by using the radiometric temperature (Ts) from the previously proposed method [1] [2] [3] . Second, because the observed data obtained by FLUXNET do not satisfy the heat balance relationship, as described in a previous report [1] [2] [3] , the observed data were corrected, i.e., identified, Third,
Figure 1. Schematic presentation for the approach of the research.
the validity was confirmed by comparing the estimated H, lE and rehs with the identified data. In addition, the heat balance relationship was determined on an hourly basis.
2.2. Outline of the General Solution
The general solution briefly describes what was reported in the previous research
[1] [2] [3] . Near the soil surface, the following heat balance relationship can be satisfied. Here, Rn is the net radiation, H is the sensible heat flux, lE is the latent heat flux and G is the heat flux in the ground.
 (1)
(1)
If there is only one unknown variable, the variable can be uniquely determined mathematically by using the following formula:
 (2)
(2)
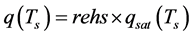
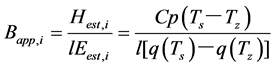 (3)
(3)
 and
and 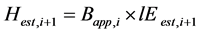 (4)
(4)
Here, i is iteration times.
The estimation procedure of the unknown variable is as follows. First, if the Ts is observed by the radiometer, rehs is assumed, and the values are put into Equation (3). The resulting Bapp,i is obtained. Next, the Bapp,i is put into Equation (4), resulting in a more accurate estimation of lE and H. By repeating the same procedure, the ε is reduced finally to its minimum; i.e., it is converged. In this paper, the suffix est means estimation, app means approximated at the process, sat means saturated, and q is the specific moisture.
The following constraints are applied:
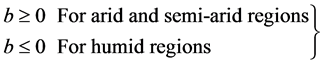 (5)
(5)
Here,
 (6)
(6)
To stabilize the process, the following constraints also applied:
 (7)
(7)
Furthermore, the Ts, T0 and G use is estimated by extrapolating as follows:
 (8)
(8)
Here, DT0 is the measurement of the depth of T0, Kt is the heat conductivity of the soil, and RTs is the adjustment factor.
In the optimization process, RTs/Kt is automatically modified according to the applied T0 and G.
2.3. Correction of Observed Data
As noted in previous research, the data of the FLUX NET unfortunately occasionally do not satisfy the heat balance relationship because these data cannot provide an accurate observation of related items. A great effort has been made to achieve an accurate observation, but such an improvement cannot be expected in the near future. Thus, the following procedure can be applied to compensate for the observation error. This concept is based on the assumption that the observation error is divided into two parts, which is proportional to the observed H and lE as shown in Equation (9) on an hourly basis.
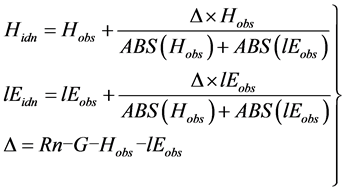 (9)
(9)
Here, Hobs is the observed value of the sensible heat flux, lEobs is the observed value of the latent heat flux, Hidn is the corrected sensible heat flux, and lEidn is the corrected latent heat flux. The other items have already been described.
If the Hidn and lEidn are applied, the heat balance relationship is completely satisfied.
2.4. Identification of rehsidn with H’idn,lE’idn
Because rehs is not observed, rehsidn should be estimated by using an optimization process. If Ts is observed, the rehsidn can be determined by the following Equation (10) and by using Equation (2), Equation (3), Equation (4) and Equation (7).
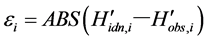 (10)
(10)
Here, H’idn,i is identified as the sensible heat flux at i times.
In addition, the H’idn,i, lE’idn,i and rehsidn are the same as a result of following criteria: ABS(lE’idn,i − lE’obs,i) = εi; here, lE’idn is identified as the latent heat flux at time i.
The H’idn and lE’idn obtained by this procedure differ from the Hidn and lEidn obtained by Equation (9). Therefore, the values are estimated by using Equation (10) and are expressed as H’idn, lE’idn.
To guarantee the reliability of the rehsidn, the reproducibility of H’idn, lE’idn with Hidn, and lEidn should be checked and may be coincident to each other.
2.5. Hourly Change of Ts - T0 and Ts - Tz
Due to the difficulties of Ts observation, the relationship between Ts andT0 or Ts and Tz has rarely been clear, and they are supposed to be closely related. Fortunately, because the tested sites have the observed data for both Ts and T0, the difference (Ts - T0) and (Ts - Tz) can be calculated by observed data. And also those items can be compared by estimated data using previous research [2] [3] .
2.6. Evaluation of the Lag-Time between Rn and TzorTs
On the ground surface, it is requires the time between receiving Rn and both Tz and Ts must be increased because the temperature changes the air space between the ground surface and height z. The time difference is defined here as lag-time. We have concerns regarding the effect that the lag-time will have on the evaluation of lEest and Hest.
To investigate the lag-time, the hourly changes in Rn, Ts and Tz are first arranged by using the observed data for all of the tested sites. Then, the typical sites are selected as an example. For the sites, the analysis was conducted by assuming the various lag-times of rehz, Ts and Tz. Then, we identified the most reasonable lag-time from the analyzed data between the estimated and identified values.
2.7. Outline of the Experimental Sites
The outline of the experimental sites is described in Table 1. The sites are selected from the FLUXNET having the necessary data, such as RnG, Tz, rehz, H and lE, with Ts observed by a radiometer worldwide. As shown Table 1, three sites were located in the USA (Billesbach, et al. [4] : Woodward (US-AR2) Data; Meyers, Tilden P.: Goodwin Creek of US-Goo Data [5] ; Prueger, John H.: Brooks Field Site 11 of the US-Br3 Data [6] ), three sites in Australia (Beringer J. and L. Hutley [7] : Dry River (AU-Dry) Ozflux L2 Data; Beringer et al. [8] : Sturt Plains (AU-Stp) Ozflux L2 Data; Eamus and Cleverly [9] : Ti Tree East (AU- TTE) Ozflux L2 Data), two sites in Europe (Ceschia and Tallec [10] : Lamasquere (FR-Lam) Data; Arnaud C. and Cristina G.: Valld’Alinya of ES-VDA Data [11] ) and one site in Chaina (Yanhong et al. [12] : Qinghai Flux Research Site (CN- QHB) AsiaFlux Data), for a total of nine sites. Of these, six dry and semidry sites were recorded as having under 1000 mm of annual precipitation, whereas the three humid sites recorded over 1000 mm of annual precipitation. In Table 1, the names of the country and region, the latitude and longitude, the elevation of
Table 1. Outline of the Experimental sites [2] [3] .
Note: *QHB is AsiaFlux ID.
the sites, the year of testing and the measurement depth of the temperature near the soil surface T0 are provided.
The heat balance relationship of the observed data and the data gap is described in Table 2. The measurement instruments of the climate element is described in the previous report [2] [3] .
3. Results of the Analysis
3.1. Comparison of the Identified and Observed H and lE
In previous research, we found that the heat balance relationship of the observed data is occasionally not guaranteed [13] [14] [15] [16] . Therefore, the observed data should be corrected to guarantee the relationship. If heat balance relationship is satisfied, the (Rn-G) should be equal to the (Hobs + lEobs) from the heat balance Equation (1). To confirm this fact, the observed (Rn-G) is compared with the (Hobs + lEobs) directory, resulting in an unsatisfied relationship. To revise the relationship, Equation (9) is applied for every hour of the observed H and lE. The results are described in Figure 2. The blue circle describes the corrected vales (Hidn + lEidn), and the red circle describes the observed (Hobs + lEobs). The (Rn-G) versus (Hidn + lEidn) completely coincide with the observed values. The following analysis is conducted by using the Hidn and lEidn as reasonable variables. In addition, the order of those figures is arranged from low to high annual precipitation.
Figure 2. Comparison of the (Rn − G) versus (H + lE), identified and observed.
Table 2. Heat balance relationship and data gap [2] [3] .
Note: Data gap does not used, one of which G, Tz, T0, P (atomospheric pressure), rehz, Rn, Hobs and lEobs is not observed, Imbalance is estimated by Imb = Rn − G − lE − H using yearly observed data and the imbalance ratio defined as Raimb = Imb/(Rn − G).
3.2 Comparison of lE, H, rehs and Ts, Identified and Estimated, in the Applied Case of b
By using the radiometer-observed Ts, Hest, lEest and rehsest were estimated. To confirm the validity of those results compared with Hidn, lEidn and rehsidn.
Figure 3 describes the result of the comparison at all of the sites. The vertical axis describes Hest. lEestrehsest, nd the horizontal axis describes Hidn, lEidn and rehsidn. All of the sites described coincide with each other, which indicates the effectiveness of the proposed method. Of course, in arid and semi-arid regions, H is greater than lE, whereas in humid regions, lE is greater than H.
Furthermore, the humidity displays a relatively smooth relationship in the arid and semi-arid regions (AU-TTE, CN-QHB, AU-Dry and AU-Stp) but is mostly random in the humid regions (ES-VDA, US-Goo and US-Br3). The other sites show an intermediate relationship. AU-TTE, AU-Stp and CN-QHB have an especially smooth relationship, whereas US-AR2, AU-Dry and FR-Lam have a relatively random one. Consequently, the variation (R2) of rehsidn versus rehsest is larger in the humid regions than in the arid and semi-arid regions.
Moreover, both the estimated and identified hourly changes of H and lE coincide very well, as do the yearly changes. The reproducibility seemed to be a little better than Figure 3 in previous research [2] and Figure 4 in previous report [3] ; because of the space limitation, those figures are abbreviated.
Furthermore, if the H’idn and lE’idn do not coincide with the Hidn and lEidn, then the reliability of rehsidn is not guaranteed. Based on this idea, the comparison of the H’idn with Hidn and lE’idn with lEidn were conducted, resulting in three sites (US-Br3, ES-VDA and CN-QHB) being in complete agreement and six sites (AU-Dry, AU-Stp, AU-TTE, US-Goo, US-AR2 and FR-Lam) being almost in agreement. Thus, the validity of rehsidn is confirmed. In addition, the related figure


Figure 3. (a) Comparison of H, lE and rehs, identified and estimated (arid and semi-arid region); (b) Comparison of H, lE and rehs, identified and estimated (humid region).
is abbreviated because of the space limitation.
Additionally, the reciprocal analysis was conducted by using Equations (2)- (4), and the constraints were applied in Equation (5), Equation (6) and Equation (7). The constraint of b was applied to the arid and semiarid regions as b > 0, whereas that applied for the humid regions was b < 0. The initial condition was set as rehs = rehz for all cases by reason of Figure 2 in previous report [3] . To prevent the small fluctuation of H and lE in the optimization process, five hours of a moving average was applied in the result [17] . The calculation was conducted in hourly units and summarizes the daily results. The solver precision was set at 0.000001, and the limit of convergence was set at 0.001.
3.3. Hourly Change of the Relative Temperature (Ts - T0) and (Ts - T0)
Figure 4 describes the hourly change of the relative temperature (Ts - T0) and (Ts - T0) in the summer (late June). The magnitude of the variation of those items varies by region.
Generally, the difference of (Ts - T0) in the arid and semi-arid regions is distributed in 10˚C - 25˚C, whereas in the humid regions the difference is distributed 2˚C - 12˚C. The difference is very large in the arid and semi-arid regions and is relatively small in the humid regions. Most notably, CN-QHB was relati-
Figure 4. Hourly change in observed (Ts − Tz) and (Ts − T0) at the various sites.
vely dry and at a high elevation (3250 m) and had a remarkably large difference of 25˚C. The sites where there are larger differences in the air temperature [(Ts - T0) > (Ts - T0)] are the arid and semi-arid regions [US-AR2, CN-QHB, AU-Dry, AU-Stp, and US-Br3], and the smaller differences [(Ts - T0) < (Tz - T0)] are the wet regions (US-Goo). AU-TTE, FR-Lam. ES-VDA has almost the same difference. Especially AU-TTE has deeper measurement of T0 as 10 cm. In contrast, the Ts is usually higher than the Tz at AU-TTE, US-AR2, CN-QHB, AU-Dry FR-Lam and ES-VDA while the Ts is lower than the Tz atUS-Br3 and US-Goo. AU-Stpis changed alternatively plus and minus.
3.4. Seasonal Change of Ts and T0
The seasonal changes (February, May, June, September and November) of the Ts and T0 are described in Figure 5, where AU-Dry is representative of a semi-arid region, US-Goois a humid region, and CN-QHB is an extreme climate region. The relative temperature (Ts - T0) of AU-Dry in the yearly average is approximately 9.0˚C + 7.2˚C = 16.2˚C, whereas US-Goo is approximately (−1.0) ? (−3.4) = 2.4˚C. The extreme climate region CN-QHB is approximately 15.2 + 12.8 = 28.0˚C. Generally, the winter seasons in February and November (June and September at the AU-sites) show relatively large changes compared with the summer season. In fact, at CN-QHB, there is a 25˚C difference in summer and a 32˚C difference in February.
3.5. Lag-Time among Rn, Tz and Ts
To investigate the lag-time, the hourly changes in Rn, Tz and Ts during the end of June are shown in Figure 6. The figure shows that the lag-time appeared very
Figure 5. Seasonal changes in observed (Ts - Tz) and (Tz - T0).
Figure 6. Hourly change in observed Rn, Tz and Ts (lag-time).
clearly. When Rn is supplied, the Ts increased approximately one to three hours later. Then, one to three hours later, the Tz increased. This tendency has is not clear across the sites, although there are small, site-specific differences. In addition, to clarify the peak difference, a five-hour moving average is applied to all data.
Because H and lE were estimated by using the observed RnTs, Tz and rehz, the estimated results already include the effect of the lag-time on Hest and lEest, Reasonability of this estimation was verified by the fact that the peak times ofHest and Hcor or lEest and lEcor was well coincided as Figure 3 in previous report [2] and Figure 4 in previous report [3] .
4. Consideration
4.1. Estimation of the Accuracy of H and Le Depend on b
Although Figure 3 describes the apparent relationship between the estimated and the identified H and lE, it does not show a qualitative evaluation. In this section, the estimation accuracy is qualitatively evaluated by the slope of Figure 3 (Hest versus Hidn,lEidn versus lEest, and rehsidn versus rehsest) and the determination coefficients R2. The effectiveness of b is also considered.
The b is an experimental constraint for increasing the estimation accuracy. Therefore, if the same accuracy is obtained, it is better to not apply the b. Table 3 describes the estimation accuracy for all of the sites in the case of b being applied. For the estimation of H and lE, the AU-TTE site certainly required the b because if the b had not been applied, then the estimation accuracy would have decreased markedly. However, the other sites do not necessarily require it because the estimation accuracy is mostly reasonable, regardless of whether b is applied.
To evaluate the qualitative estimation accuracy, the slope of the related items ranging from 0.85 - 1.15 is shown in red. In Table 3, the reasonable estimation of rehs is shown for seven of the nine sites. The number of the red character is almost the same, regardless of whether b was applied.
Table 3. Slope of Hest versus Hidn, lEidn versus lEest, rehsidn versus rehs and R2.
Note: Red character indicate the accuracy of 0.85 - 1.15.
4.2. Estimation Accuracy of the Sensible (HTa) and Latent Heat Flux (ETa)
The annual evapotranspiration (ETa) is required for water resources planning because the available water resources are evaluated by the annual precipitation minus the evapotranspiration. Based on this concept, the ETa and HTa were estimated and described in Table 4. In addition, the ETa and HTa were estimated to be 100 W∙m−2 of the heat flux equivalent for 3.53 mm・day-1 [18] . The second row of Table 4 describes the ratio of the identified HTaidn and ETaidn against the estimated HTaest and ETaest for each site.
To qualitatively estimate the accuracy, the slope of the related items ranging from 0.85 - 1.15 is shown in red. The ratios show that the case of the applied b was slightly more reasonable than when b was not applied. In fact, the estimation was conducted at five sites for the HTaest and ETaest at nine sites. The difference in the ratio between when b is applied or not is not significant. Although the hourly changes of the estimated H and lE is very well matched with the identified ones, that fact is not reflected clearly on the ETa and HTa. In addition, monthly change of the HTa and ETa is almost the same of Figure 7 in previous report [2] and Figure 8 in previous report [3] . Because of space limitation, the Figures are abbreviated.
Table 4. Comparison of the annual HTaest and ETaest with HTaidn and ETaidn (mm∙year−1).
Note: Red character indicate the accuracy of 0.85 - 1.15.
Figure 7. Effect of Lag-time on Hestand lEestat US-Goo: “cor” indicate the corrected data by regression analysis with maintaining yearly heat balance relationship [2] [3] .
4.3. Result of the Lag-Time Evaluation
In Figure 6, the lag-time of the Rn, Ts and Tz is shown clearly among the nine test sites. Because the reciprocal analysis was conducted by using the observed data, the lag-time effect is already included.
However, the heat storage between the soil surface and the air temperature at the observation height is not considered during the heat transfer process; i.e., the continuity relationship of the Hest and lEest between those spaces is not yet considered.
To investigate the effects on the Hest and lEest by the lag-time, an experimental calculation is conducted by changing the lag-time from zero to two hours at US-Goo and at US-Br3, with a one-hour interval used as an example. The lag- time effect was evaluated that the observed data of the Tz and Ts after of the given lag-time were put into the calculation. The results are described in Figure 7 for US-Goo. An irregular phenomenon appeared in the one- and two-hour lag-time at US-Goo.
This result indicates that the heat storage changes in the air spaces will be very small; i.e., the effect of the discontinuity on the Hest and lEest between those spaces will be negligible. However, the one hour interval of analysis may be too large for this purpose.
In addition, Figure 7 (the zero-hour lag-time) show the validity of the analysis because the estimated H and lE are very well agreed with the identified data; this result is seen at all of the tested sites as noted before, but the result is not shown due to the space limitation. In addition, to make the lag-time difference clear, a five-hour moving average was applied.
5. Discussion
5.1. Advantage of the Ts and rehs Determination in Previous Research
In the previous section, we discussed the reciprocal analysis by using the Ts observed by a radiometer. However, we have already proposed another reciprocal analysis method-that uses two parameters (Ts and rehs) determined by two simultaneous equations [2] [3] (the two parameter method). Generally, there are many cases which have no observed Ts by a radiometer, thus the two parameter method has advantages which are more applicable for other many regions.
The accuracy of the two-parameter method has been described in previous research [2] [3] . However the one-parameter method (the long wave analysis) discussed here may be more accurate than the two-parameter method (the simultaneous analysis) because only one rehs is estimated by one equation. Nonetheless, the estimation accuracy is not significantly different between those methods [3] .
The reason is not clear, but the one-parameter method seemed to be restricted in the optimization process because it had less freedom in parameter determination than did the two-parameter method. If not only the observed Ts but also the Rn, G, Tz and rehz contained some observation error, then the estimation accuracy of the rehs was reflected directly, whereas the two-parameter method would be adjusted by the Ts or rehs together. Thus, the determination freedom would increase. Consequently, if there is some observed error in the data, H and lE are estimated with almost the same accuracy.
5.2. Comparison of Relative Temperature Difference (Ts - T0) with the Previous Research
Because Ts was observed by a radiometer, the relative temperature difference (Ts - T0) can be analyzed precisely in the research. (Ts - T0) has also been discussed in previous research in Figure 6 [2] and in Figure 7 [3] . The difference in (Ts - T0) causes great concern. Table 5 summarizes the (Ts - T0) of this method (late June to beginning of July) and the two-parameter method (simultaneous analysis) with the conventional method [2] [3] and its relationship of rehs and rehz at the nine test sites. Here the conventional method estimated H and lE by one equation, which does not guarantee the uniqueness of the estimated Ts and rehs mathematically [2] [3] , but the reproducibility is quite reasonable.
As shown in the Table, the difference (Ts - T0) is quite large in the one-para- meter method but is relatively small in the two-parameter method; the conventional method is especially small. The estimated rehs tracks the observed rehz for almost all methods and all cases. However, the method specific features are recognized; the two-parameter method has a relatively small difference between the rehs and rehz, whereas the one-parameter method has a larger difference be-
Table 5. Comparison of the hourly change (Ts - T0) and the difference of rehs and rehz: rehs trucked almost the same pass with the rehz, So amount of the diffrence showed relatively small in long wave, small in simultaneous analysis and quiet small in conventional analysis.
Note: Period of investigation is 6/23 - 7/1. Simultaneous analysis: Ts and rehs estimated simultaneously by two equations that unified the variables [2] [3] . Convetional analysis: Ts and rehs estimated by one equation that not unified mathematically the variables [2] [3] .
tween them. The conventional method has the smallest difference between them, regardless there are some exceptions.
This feature is considered as follows: the one-parameter method has less freedom for the determination of rehs, whereas the two-parameter method has a larger determination freedom. Therefore, the former method achieved the heat balance by adjusting only rehs, and the latter achieved the balance by adjusting both Ts and rehs. Thus, the determined difference of the rehs and rehz will be enlarged in the former but not in the latter. The conventional method has a larger freedom for the determination of Ts and rehs because there is only one governing equation. Thus, the heat balance relationship is achieved easily by the small (Ts - T0) and (rehs-rehz) mentioned above, and the estimated accuracy of the H and lE does not produce a remarkable difference among the three methods, although the reason for the coincidence is different.
In contrast, the temperature difference (Ts - T0) will occur as a result of a heat transfer mechanism, such as a heat conduction or radiation. In this research, the Ts is evaluated by the radiation dominance, whereas the two-parameter method evaluates the Tsby the heat conduction dominance by using the T0 and G as estimated by Equation (9). Therefore, the former’s estimate of the difference is large, and the latter’s is small.
5.3. Initial Values and Constraints
Because this method is based on the Bowen’ ratio concept, the sensitivity of the Ts and rehs to the convergence of the objective function is very small. Therefore, determining the initial values is very important. We proposed a new idea for solving the problem and explained it precisely in Figure 2 of the previous report [3] . In addition, this research examined the constraint b. This is an experimental variable; thus, it is desirable to avoid using the b as much as possible. However, the extreme climate conditions, such as US-TTE, required the constraint b. In addition, the constraint of Equation (7), as noted in previous research, plays a role in preventing the abnormal fluctuation of the Bowen ratio in the convergence process.
5.4. Issues to Be Solved in Future
The primary issues to be solved in future are as follows: (1) The estimation of the H and lE by a single height temperature and humidity, and the sensitivity of the Ts and rehs in the convergence process, is relatively small. Therefore, a way to increase the sensitivity is a very important issue. (2) The accuracy of the original data that were used for the verification was not sufficient. At present, much research on increasing the accuracy of the observations are making new efforts in this area throughout the world. We are expecting a successful result. (3) By improving the governing equations, a more efficient optimization procedure can be identified.
6. Summary and Conclusions
The previous research concept is that H and lE are estimated by using a single height Tz and rehz based on the Rn and G observation. This research conducted the same analysis by using the Ts observed by a radiometer at nine sites distributed worldwide. By selecting such a method, there is only one unknown parameter rehs that is expected to increase the estimation accuracy of the H and lE. To examine the accuracy of the analysis, the observation data of the H and lE were corrected to guarantee the heat balance relationship on an hourly basis, in contrast to the previous research.
First, after the observed data are corrected to guarantee the heat balance relationship on an hourly basis, the reproducibility of the H and lE is confirmed. This resulted in a very strong agreement not only for the Hest,lEest with Hidn, and lEidn but also for the relationship of rehsest with rehsidn. The relationship of rehsest with rehsidn was very smooth (high R2) in the arid and semiarid regions but was relatively random (low R2) in the humid regions.
Second, the hourly change of the relative temperature (Ts - To) was discussed and is the base of the research. In summer, the result of this is a large difference in the Ts and T0 of approximately 10˚C - 25˚C, with an average of 18˚C in the arid and semi-arid regions, whereas there is a small difference in the humid regions of approximately 2˚C - 12˚C, with an average of 8.7˚C. In particular, at CN-QHB, which has a high altitude, the difference is 25˚C and is quite large. This difference, more than the air temperature [(Ts - Tz) < (Ts - T0)], is found in the arid and semi-arid regions, whereas a small difference [(Ts - Tz) > (Ts - T0)] is found in the humid regions.
Next, the qualitative accuracy of the H and lE estimation was determined. As a result, a reasonable accuracy (0.85 - 1.15 times of the identified rehs) of rehs is observed at seven of the nine sites. Although we expected a more correct estimation of this method than the method with two unknown parameters [2] [3] , the results do not show a remarkable difference. The reason for this is considered to be the determination freedom of the unknown parameter.
Moreover, the lag-time effect on the estimation accuracy for the lEest and Hest was evaluated. We recognized that there is no marked difference in the accuracy because the observed Ts, Tz and rehz are already included in the lag-time effect. Furthermore, by comparing the yearly H and lE, i.e., the accuracy of the yearly HTa and ETa, an estimation was conducted. Five of the nine sites had a relatively reasonable result of 0.85 - 1.15 times of the identification.
To confirm the validity of estimated Hest,lEest and rehsest using radiometric temperature, the comparison of identified Hidn,lEidn and rehsidn with estimated of those. Resulted in mostly coincided with each other as noted Figure 3(a) and Figure 3(b).
In addition, the accuracy of this method and the reciprocal estimation of the H and lE by using the Ts observed by a radiometer are almost the same as the two-parameter method that was used to determine the Ts and rehs in previous research [2] [3] . Therefore, if there is no Ts observed by a radiometer, the reciprocal determination of the Ts and rehs can be determined by using the two- parameter method.
Above result is very useful to estimate the ETa which acts an important role of actual water resources and irrigation planning.
Acknowledgements
We express sincere thanks to the AmeriFlux, EuroFlux and AsiaFlux principal investigation for data accessed July 5, 2015. We thank Dr. Fujihara Yooich and Dr. Takimoto Hiroshi for providing valuable comments for the optimization procedure. We acknowledge the following AmeriFlux sites for their data records: site IDs. In addition, funding for AmeriFlux data resources was provided by the US Department of Energy’s Office of Science.
Cite this paper
Maruyama, T. and Segawa, M. (2017) Estimation Accuracy for Reciprocal Analysis of Sensible and Latent Heat Flux Focusing on Radiometric Temperature and Lag-Time. Open Journal of Mo- dern Hydrology, 7, 105-124. https://doi.org/10.4236/ojmh.2017.72006
References
- 1. Maruyama, T. and Segawa, M. (2016) Reciprocal Analysis of Sensible and Latent Heat Fluxes in a Forest Region Using Single Height Temperature and Humidity Based on the Bowen Ratio Concept. Journal of Water Resource and Protection, 8, 724-742.
https://doi.org/10.4236/jwarp.2016.87059 - 2. Maruyama, T. and Segawa, M. (2016) Application of the Reciprocal Analysis for Sensible and Latent Heat Fluxes with Evapotranspiration at a Humid Region. Open Journal of Modern Hydrology, 6, 230-252.
https://doi.org/10.4236/ojmh.2016.64019 - 3. Maruyama, T. and Segawa, M. (2016) Estimation of the Sensible and Latent Heat Fluxes by Reciprocal Analysis at an Arid and Semi-Arid Region. Open Journal of Modern Hydrology, 7, 38-64.
- 4. Billesbach, D.B., Torn, J.A. and Margaret, S. (2010) ARM USDA UNL OSU Woodward Switchgrass 2 (US-Br3) AmeriFlux L2 Data.
http://cdiac.esd.ornl.gov/programs/ameriflux/data_system/aaARM_USDA_UNL_OSU_Woodward_Switchgrass_2_pf.html - 5. Meyers, T.P. (2006) Goodwin Creek (US-Goo) AmeriFlux L2 data.
http://cdiac.esd.ornl.gov/programs/ameriflux/data_system/aaGoodwin_Creek_pf.html - 6. Prueger, J.H. (2010) Brooks Field Site 11 (US-Br3) AmeriFlux L2 data.
http://cdiac.esd.ornl.gov/programs/ameriflux/data_system/aaBrooks_Field_Site_11_pf.html - 7. Beringer, J., Cunningham, S. and Hutley, L. (2014) Sturt Plains Ozflux L2 Data.
- 8. Beringer, J. and Hutley, L. (2010) Dry River Ozflux L2 Data.
- 9. Eamus, D. and Cleverly, J. (2013) Ti Tree East Ozflux L2 Data.
- 10. Ceschia, E. and Tallec, T. (2008) Lamasquere (FR-Lam) European Fluxes Database Cluster L2 Data.
- 11. Carrara, A. and Gimeno, C. (2008) ValldAlinya (ES-VDA) European Fluxes Data-Base Cluster L2 Data.
http://gaia.agraria.unitus.it/home/data/request-data - 12. Tang, Y., Du, M. and Kato, T. (2004) Qinghai Flux Research Site (CN-QHB) AsiaFlux L2 Data
- 13. Twine, T.E., Kustas, W.P., Norman, J.M., Cook, D.R., Houser, P.R., Meyers, T.P., Prueger, J.H., Starks, P.J. and Wesely, M.L. (2000) Correcting Eddy-Covariance Flux Underestimates over a Grassland. Agricultural and Forest Meteorology, 103, 279-300.
- 14. Allen, R. (2008) Quality Assessment of Weather Data and Micrometeorological Flux—Impact on Evapotranspiration Calculation, Journal of Agricultural Meteorology, 64, 191-204.
https://doi.org/10.2480/agrmet.64.4.5 - 15. Wison, K., Goldstein, A., Falge, E., Abbinet, M., Baldocchi, D., Berbingier, C., Ceulemans, R., Dolman, H., Field, C., Grelle, A., Ibrom, A., Law, B., Kowalski, A., Meyers, T., Moncrieff, J., Monson, R., Oechel, W., Tenhunen, J., Valentini, R. and Verma, S. (2002) Energy Balance Closure at FLUXNET Sites. Agricultural and Forest Meteorology, 113, 223-243.
- 16. AsiaFlux Steering Committee (2003) Observation of CO2 Flux on the Ecosystem of the Earth. Center of Global Environmental Research, National Institute for Environmental Studies, Japan
- 17. Kondo, J. (1996) Water and Heat Balance on Soil Surface. Meteorology on Water Environment, Asakura Publishing Ltd., 128-159.
- 18. Kondo, J. (2015) Heat balance and climate on soil surface.
http://www.asahi-net.or.jp/~rk7j-kndu/kenkyu/ke03.htm








