Open Journal of Acoustics
Vol.3 No.2(2013), Article ID:33465,5 pages DOI:10.4236/oja.2013.32007
Weakly Nonlinear Quantum Dust Ion-Acoustic Waves
Plasma Physics Group, Faculty of Sciences-Physics, Theoretical Physics Laboratory, University of Bab-Ezzouar, USTHB, Algiers, Algeria
Email: mouloudtribeche@yahoo.fr
Copyright © 2013 Siham Ghebache, Mouloud Tribeche. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 11, 2013; revised March 12, 2013; accepted March 20, 2013
Keywords: Dusty Plasmas; Dust Ion-Acoustic Waves; Quantum Plasmas; QHD Model; Solitary Waves; Deformed K-dV Equation
ABSTRACT
The one-dimensional quantum hydrodynamic (QHD) model for a three-specie quantum plasma is used to study the quantum counterpart of the well known dust ion-acoustic wave (DIAW). It is found that owing to the quantum effects, the dynamics of small but finite amplitude quantum dust ion-acoustic waves (QDIA) is governed by a deformed Korteweg-de Vries equation (dK-dV). The latter admits compressive as well as rarefactive stationary QDIA solitary wave solution. In the fully quantum case, the QDIA soliton experiences a spreading which becomes more significant as electron depletion is enhanced.
1. Introduction
Linear as well as nonlinear collective processes in dusty or complex plasmas have received special attention in the past decade mainly due to the realization of their occurrence in both the laboratory and space environments [1-3]. A dusty plasma is a normal electron-ion plasma with an additional highly charged component of small micron or sub-micron sized extremely massive charged particulates (dust grains). Wave propagation in such complex systems is therefore expected to be substantially different from the ordinary two component plasmas and the presence of charged dust can have a strong influence on the characteristics of the usual plasma wave modes, even at frequencies where the dust grains do not participate in the wave motion. It has been found that the presence of static charged dust grains modifies the existing plasma wave spectra. On the other hand, it has been shown that the dust dynamics introduces new eigenmodes, such as, dust-acoustic (DA) mode [4] (weak coupling regime), dust-lattice (DL) mode [5] (strong coupling regime), dust Bernstein-Greene-Kruskal (DBGK) modes [6-8], etc. Among the host of modified dusty modes discussed in the literature, the dust ion-acoustic wave (DIAW) has received wide attention as well as experimental confirmation in several low-temperature dusty plasma devices [9-14]. Shukla and Silin [15] have first theoretically shown that due to the conservation of equilibrium charge density and the strong electron depletion, a dusty plasma (with negatively charged static dust grains) supports low-frequency DIA waves. The latter is the usual ion-acoustic mode modified by the presence of dust particles. In contrast to the DAWs, the frequency of the DIAWs is much larger (smaller) than the dust (ion) plasma frequency, whereas their phase velocity is much larger (smaller) than the ion and dust (the electron) thermal velocities (velocity). Hence, in the DIAWs, the restoring force comes from the pressure of the inertialess electrons, while the ion mass provides the inertia to maintain the DIAWs. On a time scale much longer (shorter) than the ion (dust) plasma period, the dust grains remain almost immobile. Recent technological advances on miniaturized semiconductor devices and nanoscal objects have made it possible to envisage practical applications of plasma physics where the quantum nature of the particles plays a crucial role. One reason is that the great degree of miniaturization of today’s electronic components is such that the De Broglie wavelength of the charge carriers becomes comparable to the system length and the tunneling effects are therefore no longer negligible. The topic of quantum plasmas has then attracted considerable attention [16-35]. For instance, quantum plasma echoes [19], the expansion of a quantum electron gas into vacuum [20], the quantum two and three stream instabilities [21-23], the self-consistent dynamics of Fermi gases [24], the quantum ion-acoustic waves [25], the quantum corrected electron holes [27], the modified quantum Zakharov equations [28], and the quantum dust modes have been the subject of intense investigations [29-33]. Recently [34], we have reported, for the first time, the nonlinear features of the quantum counterpart of the well known DIAW. The aim of the present paper is therefore to show the existence, formation and possible realization of weakly nonlinear quantum dust-ion acoustic (QDIA) solitary waves. The derivation goes parallel to that done in standard quantum hydrodynamic analysis [25]. The manuscript is organized as follows. The one-dimensional quantum hydrodynamic (QHD) model for three species quantum dusty plasma describing the dynamics of low phase velocity dust ionacoustic oscillations is given in Section 2. A weakly nonlinear analysis is carried out in Section 3. A summary of our results and findings is given in Section 4.
2. Theoretical Model
We consider a system consisting of electrons, singly charged positive ions, equiradius spherical dust grains carrying identical charge and mass. The nonlinear dynamics of low phase velocity QDIA oscillations is governed by the one-dimensional quantum hydrodynamic (QHD) model
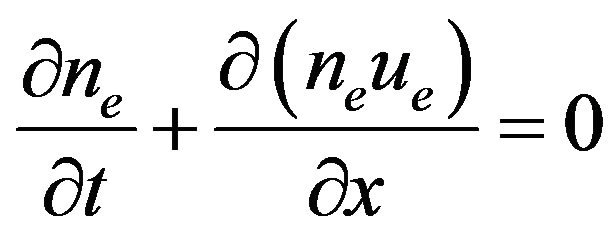 (1)
(1)
 (2)
(2)
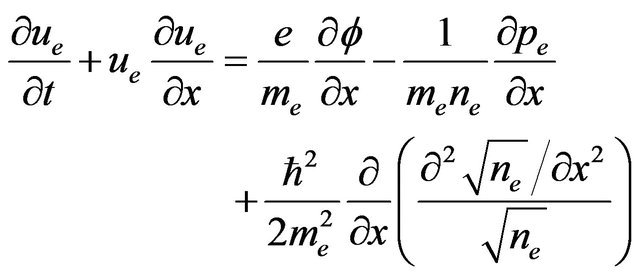 (3)
(3)
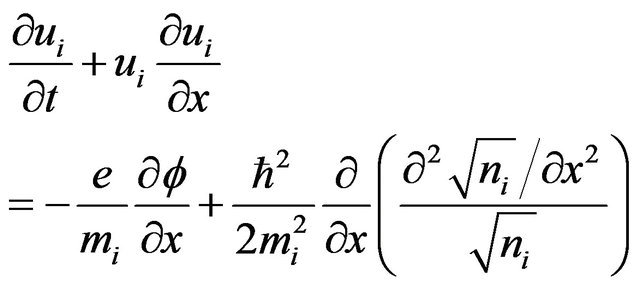 (4)
(4)
 (5)
(5)
The dust grains are usually much heavier than the ions and electrons and their dynamics is on a much longer time. They are taken to be immobile and negatively charged, 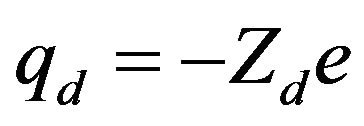 , where
, where 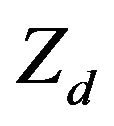 is the number of charges residing on the dust grain, ue,i is the electron (ion) fluid velocity,
is the number of charges residing on the dust grain, ue,i is the electron (ion) fluid velocity, 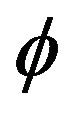 is the electrostatic potential,
is the electrostatic potential, 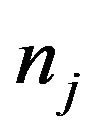 refers to the charged particles number density,
refers to the charged particles number density, 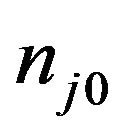 indicates the corresponding equilibrium values with obvious labels e, i and d, mj are the mass, while
indicates the corresponding equilibrium values with obvious labels e, i and d, mj are the mass, while  represents the scaled Planck’s constant. We assume that the electrons obey the following pressure law in a one-dimensional zero-temperature Fermi gas [24,25,35].
represents the scaled Planck’s constant. We assume that the electrons obey the following pressure law in a one-dimensional zero-temperature Fermi gas [24,25,35].
 (6)
(6)
where  is the electron Fermi speed, kB the Boltzmann constant, and TFe the electron Fermi temperature. For the sake of simplicity, pressure effects are disregarded for ions. Notice that the quantum corrections (quantum diffraction and quantum statistics) appear through the terms proportional to
is the electron Fermi speed, kB the Boltzmann constant, and TFe the electron Fermi temperature. For the sake of simplicity, pressure effects are disregarded for ions. Notice that the quantum corrections (quantum diffraction and quantum statistics) appear through the terms proportional to  in (3) and (4) and via the equation of state (6). Adopting the following normalization
in (3) and (4) and via the equation of state (6). Adopting the following normalization
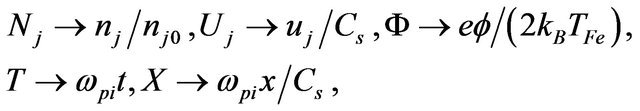
where  is the corresponding ion plasma frequency, and
is the corresponding ion plasma frequency, and 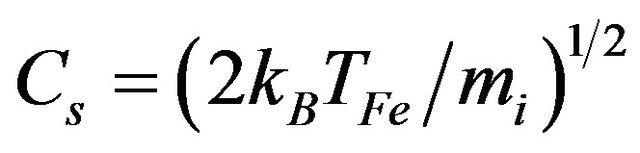 is a quantum ion-acoustic velocity, Equations (1)-(5) can be rewritten as
is a quantum ion-acoustic velocity, Equations (1)-(5) can be rewritten as
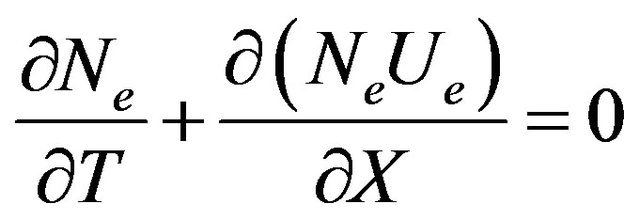 (7)
(7)
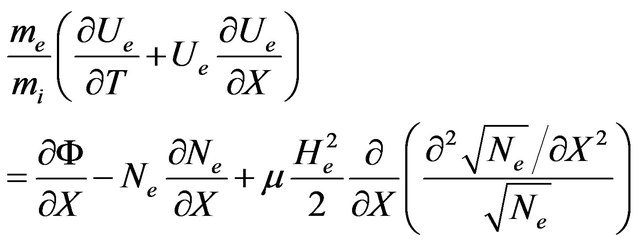 (8)
(8)
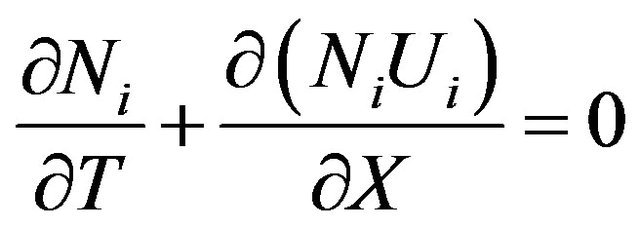 (9)
(9)
 (10)
(10)
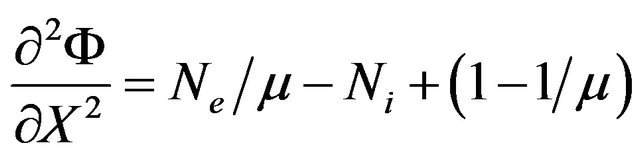 (11)
(11)
Here, 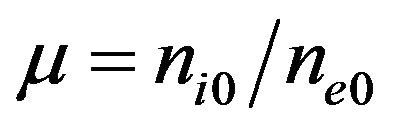 measures the unperturbed ion and electron number density imbalance, and
measures the unperturbed ion and electron number density imbalance, and
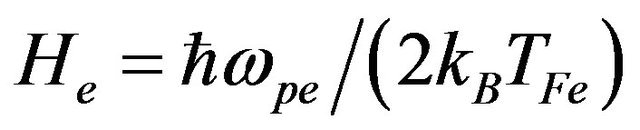 is a nondimensional quantum parameter determining the ratio between the electron plasmon energy and the electron Fermi energy, where
is a nondimensional quantum parameter determining the ratio between the electron plasmon energy and the electron Fermi energy, where
 is the corresponding electron plasma frequency. Neglecting the left-hand side of Equation (8) due to
is the corresponding electron plasma frequency. Neglecting the left-hand side of Equation (8) due to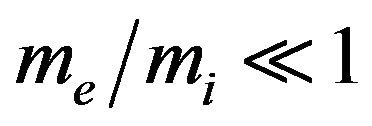 , integrating once and discarding terms proportional to
, integrating once and discarding terms proportional to 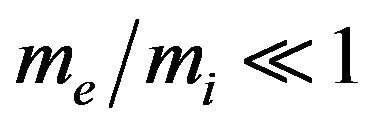 in Equation (10), we obtain the following reduced model
in Equation (10), we obtain the following reduced model
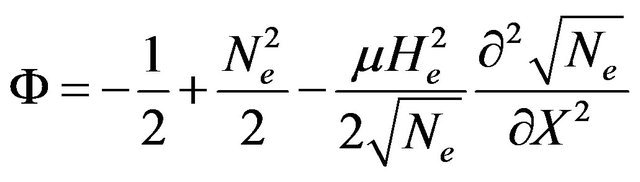 (12)
(12)
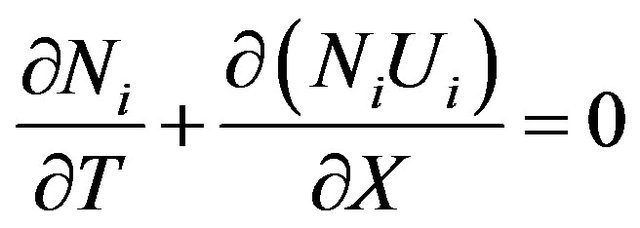 (13)
(13)
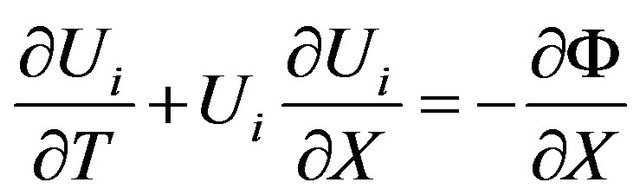 (14)
(14)
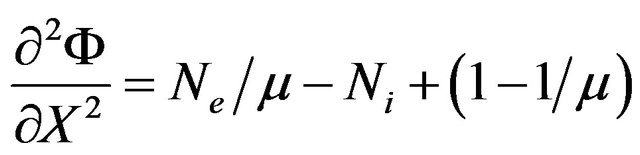 (15)
(15)
It may be useful to note that in the linear limit, the system (12)-(13) gives
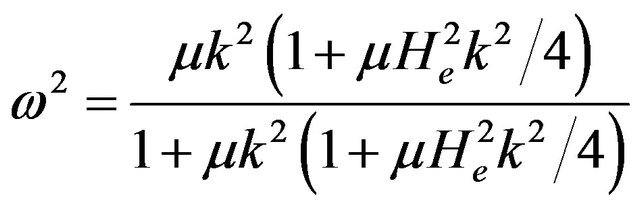 (16)
(16)
where ω and k represent, respectively, the normalized wave frequency and the normalized wave number.
3. Weakly Nonlinear QDIA Waves
To study small but finite amplitude QDIA solitary waves, we follow the well known reductive perturbation technique [36]. We first introduce the stretched variables 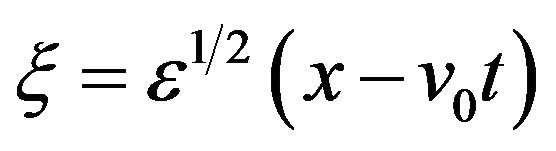 and
and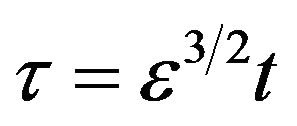 , where ε is a smallness expansion parameter, measuring the amplitude of the wave or the strength of nonlinearity, and
, where ε is a smallness expansion parameter, measuring the amplitude of the wave or the strength of nonlinearity, and 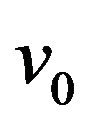 is the unknown soliton velocity normalized to Cd, to be determined later. Substituting power series expansions of
is the unknown soliton velocity normalized to Cd, to be determined later. Substituting power series expansions of  and
and 
 (17)
(17)
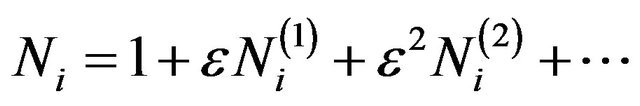 (18)
(18)
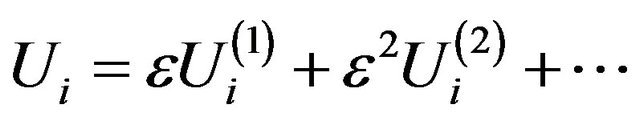 (19)
(19)
into Equations (12)-(15) gives to lowest order in ε, 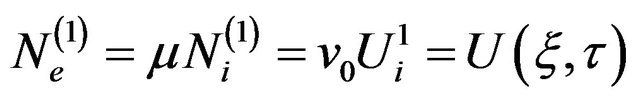 and
and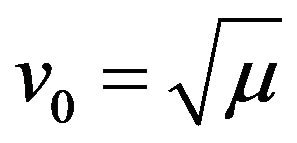 . Considering the next higher order in ε, we obtain the following set of equations
. Considering the next higher order in ε, we obtain the following set of equations
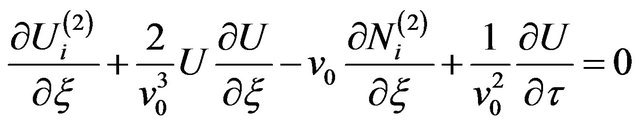 (20)
(20)
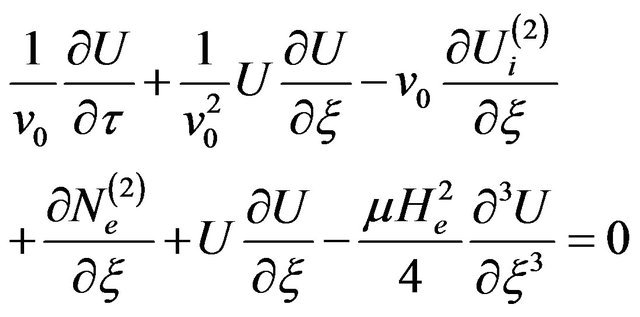 (21)
(21)
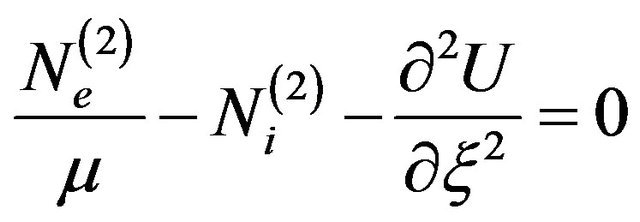 (22)
(22)
from which we derive the following equation
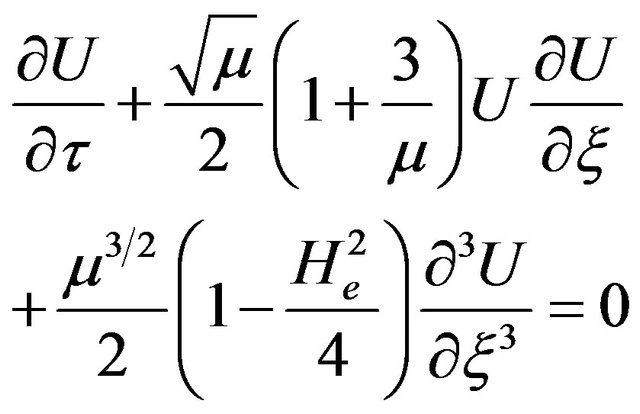 (23)
(23)
Equation (23) is a deformed Korteweg-de Vries equation (dK-dV) in which quantum diffraction is responsible for the term proportional to . For
. For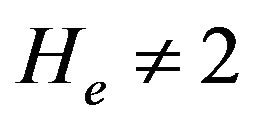 , we can transform the independent variables
, we can transform the independent variables ![]() and τ to
and τ to  and
and![]() , where
, where 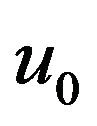 is a normalized constant speed and impose appropriate boundary conditions for localized perturbations, namely
is a normalized constant speed and impose appropriate boundary conditions for localized perturbations, namely
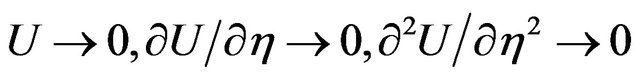 as
as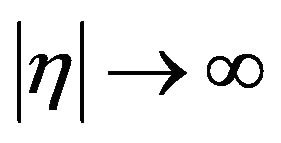 . Performing the last step in deriving soliton solutions, one gets
. Performing the last step in deriving soliton solutions, one gets
 (24)
(24)
where 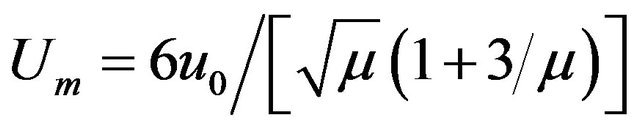 and
and
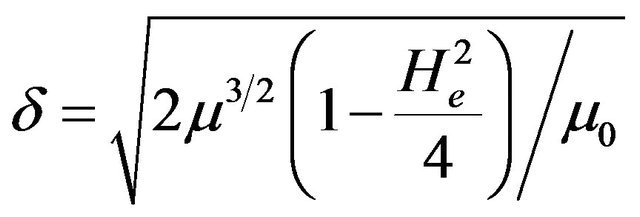 represent the amplitude and the width of the solitary wave, respectively. Note that Um does no longer depend on He. Despite the fact that quantum effects leave the absolute amplitude of the QDIA soliton unaffected, for He smaller or greater than 2 the soliton may exhibit compression (with a phase spped
represent the amplitude and the width of the solitary wave, respectively. Note that Um does no longer depend on He. Despite the fact that quantum effects leave the absolute amplitude of the QDIA soliton unaffected, for He smaller or greater than 2 the soliton may exhibit compression (with a phase spped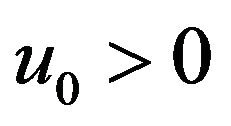 ) or rarefaction (with a phase speed
) or rarefaction (with a phase speed ). As a result of quantum effects, the QDIA soliton experiences either a compression for He < 2 (Figure 1) or a spreading in the fully quantum case (Figure 2). This spreading is more significant as the unperturbed ion and electron number density imbalance (or electron depletion) is enhanced (Figure 3) (it is worth to note that certain values
). As a result of quantum effects, the QDIA soliton experiences either a compression for He < 2 (Figure 1) or a spreading in the fully quantum case (Figure 2). This spreading is more significant as the unperturbed ion and electron number density imbalance (or electron depletion) is enhanced (Figure 3) (it is worth to note that certain values
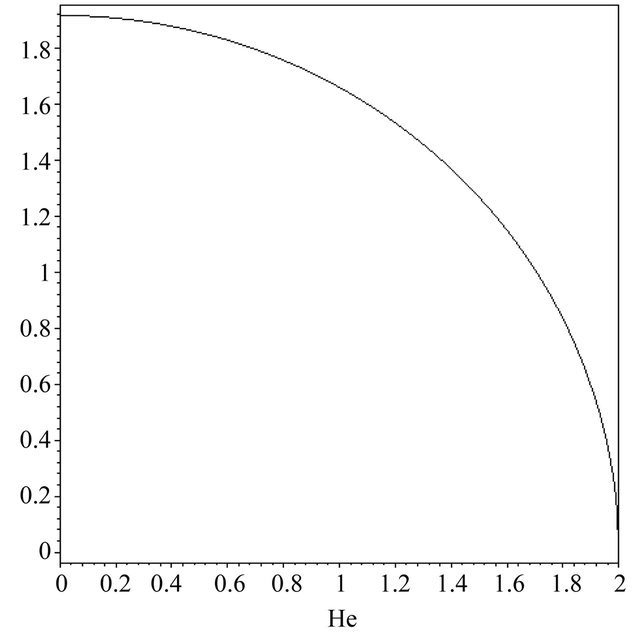
Figure 1. Plot of the QDIA soliton width δ versus He < 2 with u0 = 1 and μ = 1.2.

Figure 2. Plot of the QDIA soliton width δ versus He > 2 with u0 = −1 and μ = 1.2.
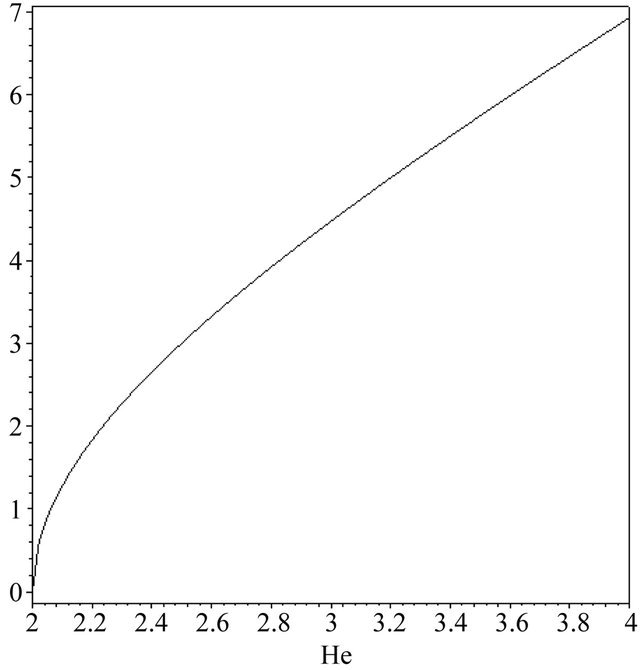
Figure 3. Plot of the QDIA soliton width δ versus He > 2 with u0 = −1 and μ = 4.
of δ and He which make Um large enough to break the validity of the weakly nonlinear analysis have to be discarded).
4. Conclusion
To conclude, we have addressed the problem of quantum dust ion-acoustic solitary waves. The dynamics of small but finite amplitude QDIA waves is governed by a deformed Korteweg-de Vries equation. The latter admits compressive as well as rarefactive stationary solitary wave solution. For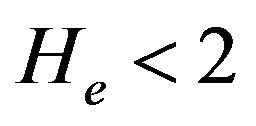 , the quantum effects tend to lower the soliton width. In the fully quantum case, the QDIA soliton experiences a spreading which becomes more significant as the unperturbed ion and electron number density imbalance is enhanced. Our results should help for diagnostics of charged impurities in micloelectronics and to understand the salient features of coherent nonlinear structures that may occur in space quantum dusty plasmas.
, the quantum effects tend to lower the soliton width. In the fully quantum case, the QDIA soliton experiences a spreading which becomes more significant as the unperturbed ion and electron number density imbalance is enhanced. Our results should help for diagnostics of charged impurities in micloelectronics and to understand the salient features of coherent nonlinear structures that may occur in space quantum dusty plasmas.
REFERENCES
- D. A. Mendis and M. Rosenberg, “Cosmic Dusty Plasma,” Annual Review of Astronomy and Astrophysics, Vol. 32, 1994, pp. 419-463. doi:10.1146/annurev.aa.32.090194.002223
- M. Horanyi, “Charged Dust Dynamics in the Solar System,” Annual Review of Astronomy and Astrophysics, Vol. 32, 1996, pp. 383-418. doi:10.1146/annurev.astro.34.1.383
- P. K. Shukla and A. A. Mamun, “Introduction to Dusty Plasma Physics,” Institute of Physics, Bristol, 2002. doi:10.1887/075030653X
- N. N. Rao, P. K. Shukla and M. Y. Yu, “Dust-Acoustic Waves in Dusty Plasmas,” Planetary and Space Science, Vol. 38, No. 4, 1990, pp. 543-546. doi:10.1016/0032-0633(90)90147-I
- F. Melandso, “Lattice Waves in Dust Plasma Crystals,” Physics of Plasmas, Vol. 3, No. 11, 1996, p. 3890. doi:10.1063/1.871577
- M. Tribeche, R. Hamdi and T. H. Zerguini, “Effects of Electron Depletion on Nonlinear Dusty Plasma Oscillations,” Physics of Plasmas, Vol. 7, No. 10, 2000, p. 4013. doi:10.1063/1.1290618
- M. Tribeche, H. Houili and T. H. Zerguini, “Nonlinear Oscillations in Dusty Plasmas with Variable Charges on Dust Particles,” Physics of Plasmas, Vol. 9, No. 2, 2002, p. 419. doi:10.1063/1.1436127
- M. Tribeche, L. Ait Gougam and T. H. Zerguini, “Large Amplitude Electrostatic Solitary Structures in a ChargeVarying Dusty Plasma with Two-Temperature Trapped Ions,” Physica Scripta, Vol. 75, No. 3, 2007, p. 354. doi:10.1088/0031-8949/75/3/022
- R. L. Merlino, A. Barkan, C. Thompson and N. D’Angelo, “Laboratory Studies of Waves and Instabilities in Dusty Plasmas,” Physics of Plasmas, Vol. 5, No. 5, 1998, p. 1607. doi:10.1063/1.872828
- R. L. Merlino, A. Barkan, C. Thompson and N. D’Angelo, “Experiments on Waves and Instabilities in Dusty Plasmas,” Plasma Physics and Controlled Fusion, Vol. 39, No. 5A, 1997, p. 421. doi:10.1088/0741-3335/39/5A/039
- Y. Nakamura, H. Bailung and P. K. Shukla, “Observation of Ion-Acoustic Shocks in a Dusty Plasma,” Physical Review Letters, Vol. 83, No. 8, 1999, pp. 1602-1605. doi:PhysRevLett.83.1602
- Y. Nakamura and H. Bailung, “A Dusty Double Plasma Device,” Review of Scientific Instruments, Vol. 70, No. 5, 1999, p. 2345. doi:10.1063/1.1149761
- Y. Nakamura and A. Sarmaa, “Observation of IonAcoustic Solitary Waves in a Dusty Plasma,” Physics of Plasmas, Vol. 8, No. 9, 2001, p. 3921. doi:10.1063/1.1387472
- X. Liang, J. Zheng, J. X. Ma, W. D. Liu, J. Xie, G. Zhuang and C. X. Yu, “Experimental Observation of IonAcoustic Waves in an Inhomogeneous Dusty Plasma,” Physics of Plasmas, Vol. 8, No. 5, 2001, p. 1459. doi:10.1063/1.1362530
- P. K. Shukla and V. P. Silin, “Dust Ion-Acoustic Wave,” Physics of Plasmas, Vol. 45, No. 5, 1992, p. 508. doi:10.1088/0031-8949/45/5/015
- N. C. Kluksdahl, A. M. Kriman, D. K. Ferry and C. Ringhofer, “Self-Consistent Study of the Resonant-Tunneling Diode,” Physical Review B, Vol. 39, No. 11, 1989, pp. 7720-7735. doi:PhysRevB.39.7720
- F. Cornu, “Quantum Plasmas with or without a Uniform Magnetic Field. II. Exact Low-Density Free Energy,” Physical Review E, Vol. 58, No. 5, 1998, pp. 5293-5321. doi:PhysRevE.58.5293
- B. Shokri and A. A. Rukhadze, “Quantum Surface Wave on a Thin Plasma Layer,” Physics of Plasmas, Vol. 6, No. 9, 1999, p. 3450. doi:10.1063/1.873604
- G. Manfredi and M. R. Feix, “Theory and Simulation of Classical and Quantum Echoes,” Physical Review E, Vol. 53, No. 6, 1996, pp. 6460-6470. doi:PhysRevE.53.6460
- S. Mola, G. Manfredi and M. R. Feix, “Expansion of a Quantum Electron Gas,” Journal of Plasma Physics, Vol. 50, No. 1, 1993, pp. 145-162. doi:10.1017/S0022377800026969
- F. Haas, G. Manfredi and M. R. Feix, “Multistream Model for Quantum Plasmas,” Physical Review E, Vol. 62, No. 2, 2000, pp. 2763-2772. doi:PhysRevE.62.2763
- F. Haas, G. Manfredi and J. Goedert, “Nyquist Method for Wigner-Poisson Quantum Plasmas,” Physical Review E, Vol. 64, No. 2, 2001, Article ID: 026413. doi:PhysRevE.64.026413
- D. Anderson, B. Hall, M. Lisak and M. Marklund, “Statistical Effects in the Multistream Model for Quantum Plasmas,” Physical Review E, Vol. 65, No. 4, 2002, Article ID: 046417. doi:PhysRevE.65.046417
- G. Manfredi and F. Haas, “Self-Consistent Fluid Model for a Quantum Electron Gas,” Physical Review B, Vol. 64, No. 7, 2001, Article ID: 075316. doi:PhysRevB.64.075316
- F. Haas, L. G. Garcia, J. Goedert and G. Manfredi, “Quantum Ion-Acoustic Waves,” Physics of Plasmas, Vol. 10, No. 10, 2003, p. 3858. doi:10.1063/1.1609446
- R. Redmer, “Physical Properties of Dense, Low-Temperature Plasmas,” Physics Reports, Vol. 282, No. 2-3, 1997, p. 35-157. doi:10.1016/S0370-1573(96)00033-6
- A. Luque, H. Schamel and R. Fedele, “Quantum Corrected Electron Holes,” Physics Letters A, Vol. 324, No. 2-3, 2004, pp. 185-192. doi:10.1016/j.physleta.2004.02.049
- L. G. Garcia, F. Haas, L. P. L. de Oliveira and J. Goedert, “Modified Zakharov Equations for Plasmas with a Quantum Correction,” Physics of Plasmas, Vol. 12, No. 1, 2005, Article ID: 012302. doi:10.1063/1.1819935
- P. K. Shukla, “A New Dust Mode in Quantum Plasmas,” Physics Letters A, Vol. 352, No. 3, 2006, pp. 242-243. doi:10.1016/j.physleta.2005.11.065
- S. Ali and P. K. Shukla, “Dust Acoustic Solitary Waves in a Quantum Plasma,” Physics of Plasmas, Vol. 13, No. 3, 2006, Article ID: 022313. doi:10.1063/1.2173518
- S. Ali and P. K. Shukla, “Erratum: Dust Acoustic Solitary Waves in a Quantum Plasma,” Physics of Plasmas, Vol. 13, No. 3, 2006, Article ID: 129902. doi:10.1063/1.2402917
- P. K. Shukla, L. Stenflo, “Jeans Instabilities in Quantum Dusty Plasmas,” Physics Letters A, Vol. 355, No. 4-5, 2006, pp. 378-380. doi:10.1016/j.physleta.2006.02.054
- A. P. Misra and A. R. Chowdhury, “Modulation of Dust Acoustic Waves with a Quantum Correction,” Physics of Plasmas, Vol. 13, No. 7, 2006, Article ID: 072305. doi:10.1063/1.2217933
- M. Tribeche, S. Ghebache, K. Aoutou and T. H. Zerguini, “Arbitrary Amplitude Quantum Dust Ion-Acoustic Solitary Waves,” Physics of Plasmas, Vol. 15, No. 3, 2008, Article ID: 033702. doi:10.1063/1.2899325
- I. Nagy, “Short-Range Correlation in A Two-Dimensional Electron Gas,” Physical Review B, Vol. 52, No. 3, 1995, pp. 1497-1499. doi:PhysRevB.52.1497
- Washimi, H., Washimi, T. Taniuti, “Propagation of Ion Acoustic Solitary Waves of Small Amplitude,” Physical Review Letters, Vol. 17, No. 19, 1966, pp. 996-998. doi:PhysRevLett.17.996

