Theoretical Economics Letters
Vol. 2 No. 2 (2012) , Article ID: 19271 , 5 pages DOI:10.4236/tel.2012.22023
Profit-Sharing and the Endogenous Order of Moves in Oligopoly
1Faculty of Economics, Oita University, Oita, Japan
2Graduate School of Economics, Kobe University, Kobe, Japan
Email: htakami@oita-u.ac.jp, nakamura@econ.kobe-u.ac.jp
Received March 7, 2012; revised April 1, 2012; accepted April 24, 2012
Keywords: Profit-Sharing; Endogenous Timing; Observable Delay Game
ABSTRACT
Whether firms move sequentially or simultaneously is one of the most important questions in the oligopoly theory. Forms of firms and/or their remuneration systems influence the decisions. This paper analyzes the effect of profit-sharing on the endogenous order of moves in a wage-setting stage of a unionized duopoly where one adopts profit-sharing while the other does not. It is shown that the two firms do not move simultaneously. In addition, if a fraction of profits going to the union is large, the Stackelberg equilibrium with the profit sharing firm moving first emerges endogenously.
1. Introduction
Whether firms move sequentially or simultaneously has been one of the main issues in the oligopoly theory since the seminal work by Cournot (1838) and Stakelberg (1934). When the identical firms compete using the same strategic variable (quantity or price) under deterministic environment, there is no doubt that all the firms have the same preference in the order of moves: in general, trying to be a leader in a quantity-setting oligopoly and a follower in a price-setting one. Even in a quantity-setting oligopoly of homogenous products, however, as Amir and Grilo [1] demonstrate, the endogenous move can emerge under certainty when the firms have different cost functions. Also, Normann [2] shows that the endogenous sequential moves can be verified by incomeplete information.1 Differences in forms of firms and/or remuneration systems are another source for the endogenous order of moves. For example, Pal [4], Barcena-Ruiz and Sedano [5] and others analyze the endogenous timing in a mixed oligopoly where welfare-maximizing firms interact with profit-maximizing private firms, and derive strikingly different results from those obtained in a corresponding oligopoly with all profit-maximizing firms. The present paper tries to constitute another addition to this line of study, focusing endogenous timing of wage decisions in a unionized oligopoly.
In a monopoly union model, the unions determine wages and the firms choose the output so as to maximize their owners’ objectives subject to the determined wages. The paper analyzes a unionized duopoly where one firm adopts profit-sharing while the other does not. Instead of assuming a simultaneous or sequential move, the order of wage decisions is determined endogenously by the unions.2 The rest of the paper is organized as follows. Section 2 sets up the model of duopoly and presents the game structure. Section 3 derives the subgame perfect equilibria and the main proposition. Section 4 provides some concluding remarks.
2. The Model
Consider a duopoly with a profit-sharing firm and a conventional non-profit-sharing firm. Each firm faces its labor union that sets the wage rate. After observing the wage rates, each firm determines the output so as to maximize its owners’ objective. Therefore, the model presented in this paper falls into what has been called a monopoly union model (see e.g. Kaufman [7]).3 The firms produce homogenous goods according to the same production function:
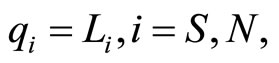 (1)
(1)
where 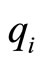 is output and
is output and  is employment in firm
is employment in firm , and
, and 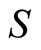 stands for the profit-sharing and
stands for the profit-sharing and 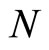 the conventional non-profit-sharing. Assuming that labor is an only input, the profits of firm i are:
the conventional non-profit-sharing. Assuming that labor is an only input, the profits of firm i are:
 (2)
(2)
where 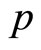 is the output price and
is the output price and 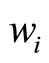 is the wage rate in firm
is the wage rate in firm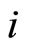 .
.
The objective of the owners of firm S is to maximize their income:
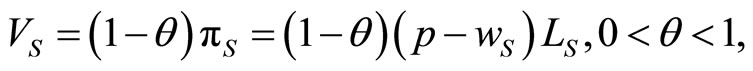 (3)
(3)
where  is a sharing parameter which represents a fraction of profits going to the union. Similarly, the objective function of firm N’s owners is their income, which is equal to the firm’ s profits:
is a sharing parameter which represents a fraction of profits going to the union. Similarly, the objective function of firm N’s owners is their income, which is equal to the firm’ s profits:
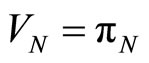 . (4)
. (4)
The objectives of the unions are assumed to maximize the sum of their members’ rents. For Union S, i.e., firm S’s union, the objective function is:
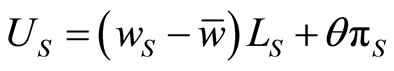 , (5)
, (5)
and for the Union N, i.e., firm N’s union:
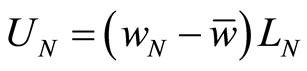 , (6)
, (6)
where  is the alternative wage that the workers can obtain elsewhere (or the unemployment benefit).
is the alternative wage that the workers can obtain elsewhere (or the unemployment benefit).
To simplify the analysis, the following linear demand curve for their products is employed:
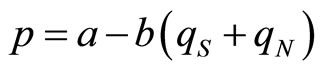 , (7)
, (7)
where 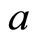 and
and 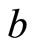 are positive constants.
are positive constants.
The game structure of the model is specified as follows. There are assumed to be three stages. The observable delay game of Hamilton and Slutsky [9] is considered in the context of a wage setting duopoly where the labor unions first choose the timing of wage rate determination.4 There are two periods for it, and each union may determine the wage rate in one of the two periods. In stage 1, the unions simultaneously announce in which period they determine the wage rates and are committed to this choice. In stage 2, each union determines the wage rate knowing when the other union will make a decision. If both unions decide to determine the wage rates in the same period, a simultaneous move game occurs, whereas if the two unions decide to determine the wage rates in different periods, a sequential move game arises. In stage 3, the firms produce. In the model of a homogenous product duopoly with a linear demand function and a linear cost (or production) function, there is no follower’s advantage in the Cournot competition under certainty.5 Therefore, the order of moves is not investigated in the output determination stage.
3. Endogenous Orders of Moves
To obtain subgame perfect equilibria, the model is solved backward: stage 3 is solved first, stage 2 second and finally stage 1.
3.1. Employment Determination (Stage 3)
Firm 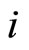 maximizes
maximizes  with respect to
with respect to 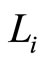 subject to the production function (1), the demand function (7), and the wage rates
subject to the production function (1), the demand function (7), and the wage rates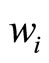 ’s set by the unions. The first order conditions give the best-response functions of the firms. Solving the best-response functions, we have each firm’s labor demand function in the Cournot-Nash equilibrium:
’s set by the unions. The first order conditions give the best-response functions of the firms. Solving the best-response functions, we have each firm’s labor demand function in the Cournot-Nash equilibrium:
 , (8a)
, (8a)
 . (8b)
. (8b)
3.2. Wage Determination (Stage 2)
The objective function of Union S is expressed as:
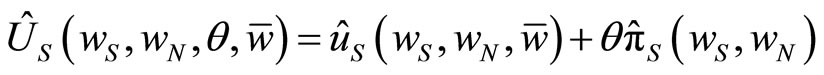 , (9)
, (9)
where:
 , (10a)
, (10a)
 (10b)
(10b)
The union maximizes the above with respect to , taking
, taking 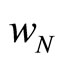 as given. From the first order condition:
as given. From the first order condition:
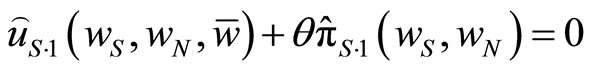 , (11)
, (11)
where 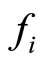 indicates the partial derivative of
indicates the partial derivative of 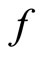 with respect to ith argument, we have the best-response function:
with respect to ith argument, we have the best-response function:
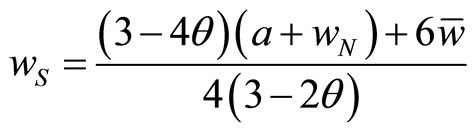 . (12)
. (12)
Similarly, Union N maximizes:
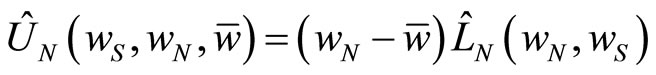 , (13)
, (13)
with respect to , taking
, taking 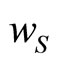 as given to obtain the following best-response function:
as given to obtain the following best-response function:
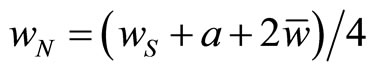 . (14)
. (14)
There are four possible combinations of orders of moves: (Union S, Union N) = (Leader, Leader), (Leader, Follower), (Follower, Leader) and (Follower, Follower). Among them, (Leader, Leader) and (Follower, Follower) are the same in implying the simultaneous move. In the simultaneous move, the wage rates and the employment levels are determined by the above best-response and labor demand functions, as follows:
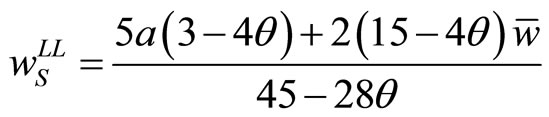 , (15a)
, (15a)
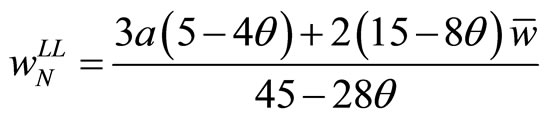 , (15b)
, (15b)
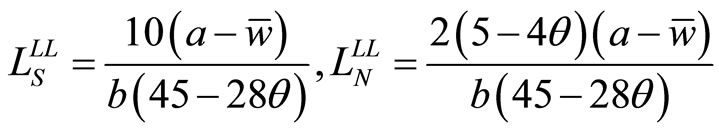 , (15c)
, (15c)
where the superscript LL stands for the simultaneous move, or (Leader, Leader).6 If Union S is the leader and Union N is the follower, Union S determines the wage rate so as to maximize 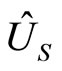 subject to (14), the reaction function of Union N. After observing the wage rate of Union S, Union N determines the wage rate according to its best-response function. The wage rates and the employment levels in the Stackelberg equilibrium are:
subject to (14), the reaction function of Union N. After observing the wage rate of Union S, Union N determines the wage rate according to its best-response function. The wage rates and the employment levels in the Stackelberg equilibrium are:
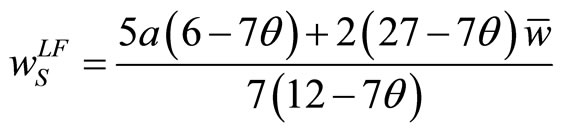 , (16a)
, (16a)
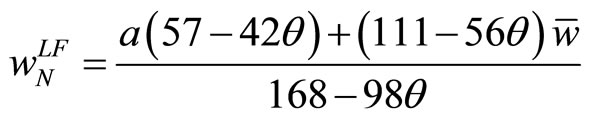 , (16b)
, (16b)
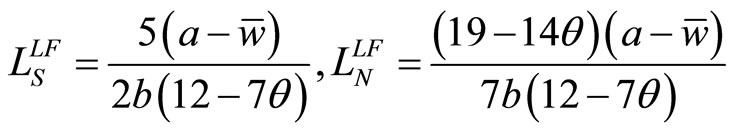 , (16c)
, (16c)
where the superscript LF stands for the Stackelberg equilibrium in which Union S is the leader and Union N is the follower, or (Leader, Follower).
Similarly, the wage rates and the employment levels in the Stackelberg equilibrium with Union N moving first are obtained as follows:
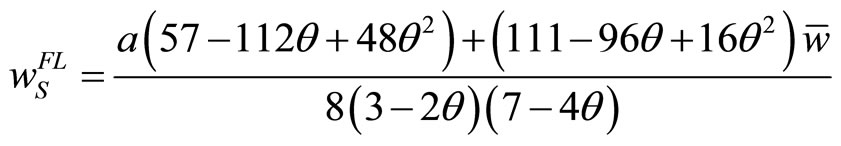 , (17a)
, (17a)
 , (17b)
, (17b)
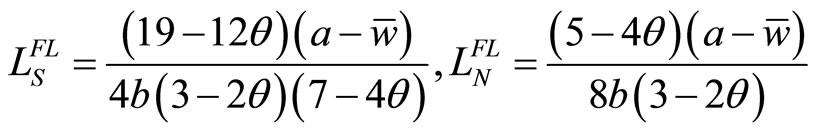 , (17c)
, (17c)
where the superscript FL stands for the Stackelberg equilibrium in which Union S is the follower and Union N is the leader, or (Follower, Leader).
3.3. Timing Determination (Stage 1)
 ,
,
 ,
,
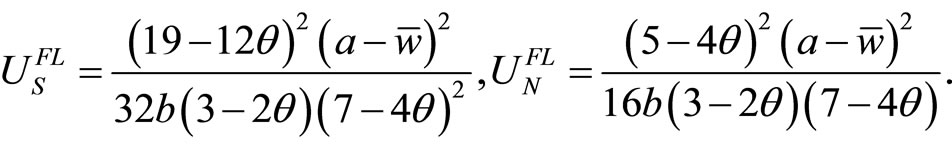
Using the results in the previous subsection, let us construct the unions’ payoff matrix, which is presented in Table 1.
The following relationships are easily verified:
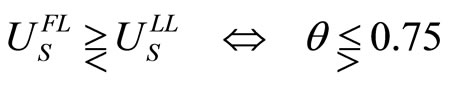 , (18a)
, (18a)
 . (18b)
. (18b)
If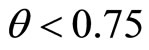 , both unions prefer their Stackelberg follower’s payoffs to the simultaneous play payoffs. Therefore, by Theorem III in Hamilton and Slutsky [9], both types of sequential play subgames, one is Union S being the leader and the other is Union N being the leader, are the Nash equilibria of the extended game with observable delays. If
, both unions prefer their Stackelberg follower’s payoffs to the simultaneous play payoffs. Therefore, by Theorem III in Hamilton and Slutsky [9], both types of sequential play subgames, one is Union S being the leader and the other is Union N being the leader, are the Nash equilibria of the extended game with observable delays. If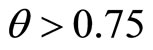 , on the contrary, Union S moving first and Union N delaying is an outcome which Pareto dominates the simultaneous play game and the reverse order is an outcome which does not. Hence, by Theorem IV in Hamilton and Slutsky [9], the sequential play, where Union S moves first and Union N second, is the unique subgame perfect equilibrium of the extended game with observable delays.
, on the contrary, Union S moving first and Union N delaying is an outcome which Pareto dominates the simultaneous play game and the reverse order is an outcome which does not. Hence, by Theorem IV in Hamilton and Slutsky [9], the sequential play, where Union S moves first and Union N second, is the unique subgame perfect equilibrium of the extended game with observable delays.
Proposition. In the extended game of observable delays, only Stackelberg equilibria, with either the profitsharing firm’s union or the conventional non-sharing firm’s union moving first, emerge endogenously. However, the profit-sharing firm’s union is always the leader when a sharing parameter, which represents a fraction of profits going to the union, is large.

Table 1. Payoff matrix in wage-setting stage.
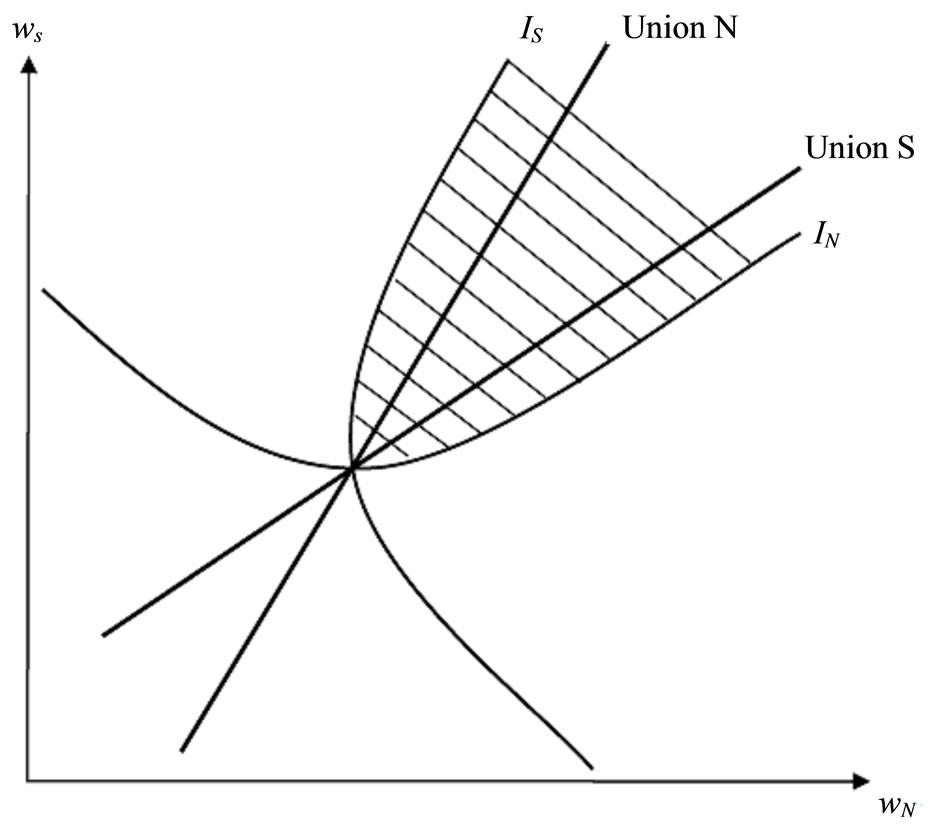
The above proposition can be illustrated graphically. In Figure 1, two possible combinations of best-response functions are depicted in the two panels. The best-response function of Union S is upward-sloping when 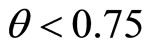 and downward-sloping when
and downward-sloping when , while the best-response of Union N is always upward-sloping.
, while the best-response of Union N is always upward-sloping.
In Figure 1(a), each best-response function is upward-sloping like a symmetric Bertrand equilibrium with differentiated products (see Cheng [11]) and a portion of both best-response functions lies in the set of Pareto superior outcomes. Therefore, the follower has the advantage of being able to undercut the leader’s wage and thus does better than the leader. The leader in turn can do at least as well in the sequential move game as in the simultaneous play game since the Nash equilibrium of simultaneous play is feasible for the leader (Lemma 1 in Hamilton and Slutsky [9]). Hence, the Stackelberg equilibria, with either the profit-sharing union or the conventional non-profit-sharing union moving first, emerge endogenously.
In Figure 1(b), the best-response curve of Union S is downward-sloping and only the Union N’s best-response curve is passing through the Pareto superior set. In this case, Union N still has the follower’s advantage while union S prefers the leader. Therefore, only the Stackelberg equilibrium with Union S moving first emerges endogenously.
To see why the Union S’s best-response curve is downward-sloping when  is large, let us derive the slope from (11):
is large, let us derive the slope from (11):
 , (19)
, (19)
where  indicates the second partial derivative of
indicates the second partial derivative of 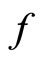 with respect to
with respect to 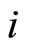 th and
th and 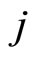 th arguments. While the denominator of RHS in (19) must be negative by the second order condition, the numerator can be either positive or negative since
th arguments. While the denominator of RHS in (19) must be negative by the second order condition, the numerator can be either positive or negative since 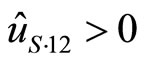 and
and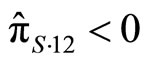 . In the non-profit-sharing case (
. In the non-profit-sharing case ( ), the slope is always positive just like union N’s best-response curve. In the profit-sharing case, on the contrary, the slope depends on
), the slope is always positive just like union N’s best-response curve. In the profit-sharing case, on the contrary, the slope depends on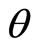 : positive if it is small while negative if it is large. When
: positive if it is small while negative if it is large. When 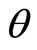 is large, the effect of the firm’s profits
is large, the effect of the firm’s profits  dominates that of the union’s utility (
dominates that of the union’s utility (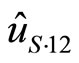 ). In the model presented in this paper, 0.75 is the critical value of
). In the model presented in this paper, 0.75 is the critical value of 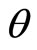 for the sign of the slope: negative if
for the sign of the slope: negative if 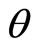 is above it while positive if below it.
is above it while positive if below it.
Since the simple and concrete production and demand functions are employed in the presented model, one can pin down the critical value. As for more general cases, in principle, it can be obtained from (19) as follows:
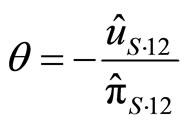 (20)
(20)
 (a)
(a)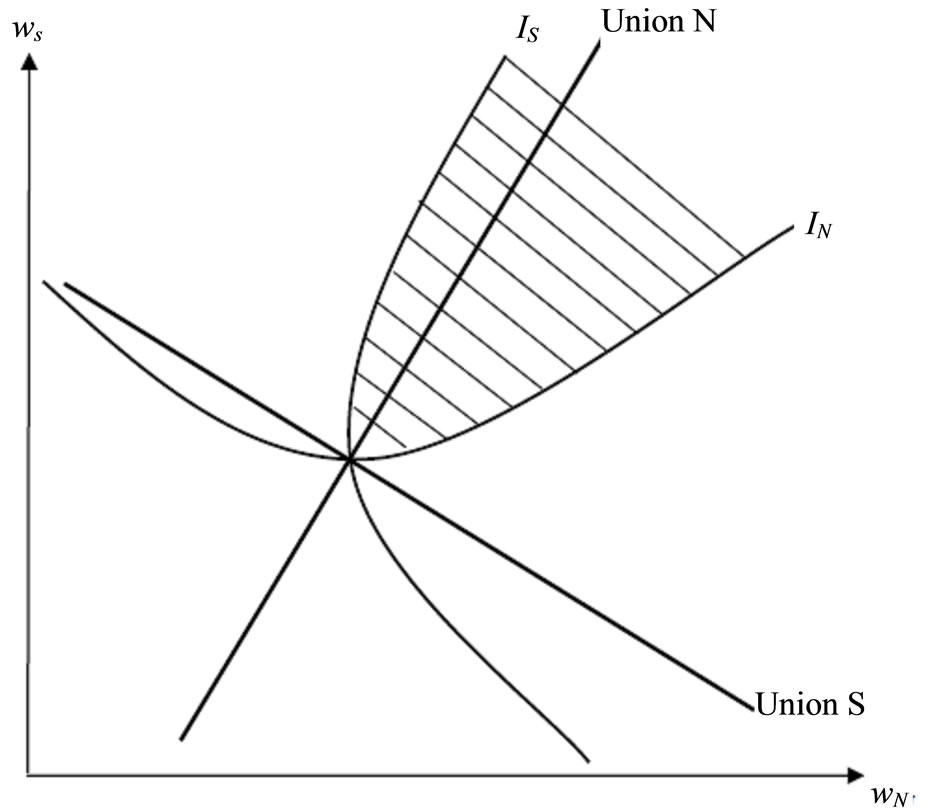 (b)
(b)
Figure 1. Reaction functions and Pareto superior sets. IS is Union S’s indifference curve, IN is Union N’s indifference curve, straight lines indicated by Union S and Union N are the best-response functions, and the shaded regions show Pareto superior sets. (a) θ < 0.75; (b) θ > 0.75.
In other words, the critical value could be smaller or larger than 0.75 depending on 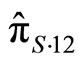 and
and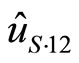 .
.
4. Concluding Remarks
This paper analyzes the endogenous order of wage decision in a unionized duopoly model with a profit-sharing and a conventional non-profit-sharing firm, adopting the observable delay game of Hamilton and Slutsky [9]. As a result, it is shown that the two firms do not move simultaneously. In addition, if a fraction of profits going to the union is large, only the Stackelberg equilibrium with the profit sharing firm moving first emerges endogenously. In this paper, a rather specific model is employed to simplify the demonstration. Undoubtedly, the critical value of the sharing parameter, above which only the profitsharing union’s leadership emerges, depends on the specific assumptions. It deserves future study to investigate the relationship between the critical value and market and production structures. It is also important to examine what happens if the sharing parameter is endogenously determined as an outcome of the bargaining between firms and their unions.
5. Acknowledgements
The authors would like to thank an anonymous referee, and seminar participants at the Kwansei Gakuin University, the Oita University, and the Osaka University of Economics, for their valuable comments. The Grantsin-Aid for Scientific Research (C) (No. 23530325 and 22530180) from the Japanese Society for the Promotion of Science is gratefully acknowledged. The second author thanks the Kobe University 21st Century COE Program, the research grant from the Japanese Ministry of Education and Science, for financial support. Part of this research is also financially supported by the Japan Economic Research Foundation. The usual disclaimer applies.
REFERENCES
- R. Amir and I. Grilo, “Stackelberg versus Cournot Equilibrium,” Games and Economic Behavior, Vol. 26, No. 1, 1999, pp. 1-21. doi:10.1006/game.1998.0650
- H.-T. Normann, “Endogenous Stackelberg Equilibria with Incomplete Information,” Journal of Economics, Vol. 66, No. 2, 1997, pp. 177-187.
- B. von Stengel, “Follower Payoffs in Symmetric Duopoly Games,” Games and Economic Behavior, Vol. 69, No. 2, 2010, pp. 512-516. doi:10.1016/j.geb.2009.10.012
- D. Pal, “Endogenous Timing in a Mixed Oligopoly,” Economics Letters, Vol. 61, No. 2, 1998, pp. 181-185. doi:10.1016/S0165-1765(98)00115-3
- J. C. Barcena-Ruiz and M. Sedano “Weighted Welfare and Price Competition,” Japanese Economic Review, Vol. 62, No. 4, 2011, pp. 485-503.
- C.-Y. Liu and J.-J. Chang, “Macroeconomic Implications of a Sharing Compensation Scheme in a Model of Endogenous Growth,” Journal of Economics, Vol. 102, No. 1, 2011, pp. 57-75. doi:10.1007/s00712-010-0163-y
- B. E. Kaufman, “Models of Union Wage Determination: What Have We Learned Since Dunlop and Ross?” Industrial Relations, Vol. 41, No. 1, 2002, pp. 110-158. doi:10.1111/1468-232X.00238
- J. R. Sørensen, “Profit-Sharing in a Unionized Cournot Duopoly,” Journal of Economics, Vol. 55, No. 2, 1992, pp. 151-167. doi:10.1007/BF01227418
- J. H. Hamilton and S. T. Slutsky, “Endogenous Timing in Duopoly Games: Stackelberg or Cournot Equilibria,” Games and Economic Behavior, Vol. 2, No. 1, 1990, pp. 29-46. doi:10.1016/0899-8256(90)90012-J
- M. A. Fonseca, W. Müller and H.-T. Normann, “Endogenous Timing in Duopoly: Experimental Evidence,” International Journal of Game Theory, Vol. 34, No. 3, 2006, pp. 443-456. doi:10.1007/s00182-006-0027-4
- L. Cheng, “Comparing Bertrand and Cournot Equilibria: A Geometric Approach,” Rand Journal of Economics, Vol. 16, No. 1, 1985, pp. 146-151. doi:10.2307/2555596
NOTES
1Another example is von Stengel [3], which examines the endogenous timing in symmetric duopoly games.
2Profit-sharing is analyzed not only in the microeconomics but in the macroeconomics literature. For example, Liu and Chang [6] investigate the macroeconomic implications of a sharing system in an endogenous growth model.
3The basic structure of the model is the same as Sørensen’s [8] unionized duopoly. He analyzes bargaining between firms and their unions to shed light on the conditions for the introduction of profit-sharing while this paper does not consider the bargaining to focus on the endogenous order of moves in the wage-setting.
4Base upon actual experiments, Fonseca, Müller and Normann [10] develop an insightful discussion on the applicability and validity of observable delay games in duopoly.
5In contrast, the seminal work by Hamilton and Slutsky [9] shows that a firm has an incentive to be a follower in a differentiated duopoly.
6It should be noticed that the wage of Union S’s member is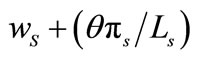 . Throughout the paper, the equilibrium wage is always larger than the reservation wage
. Throughout the paper, the equilibrium wage is always larger than the reservation wage 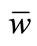 although there is the possibility that
although there is the possibility that . Of course, it also holds that
. Of course, it also holds that  in any possible equilibrium.
in any possible equilibrium.

