American Journal of Operations Research
Vol.3 No.2(2013), Article ID:29239,10 pages DOI:10.4236/ajor.2013.32025
Optimal Approximation Algorithms for Reoptimization of Constraint Satisfaction Problems
V.M. Glushkov Institute of Cybernetics, National Academy of Sciences of Ukraine, Kyiv, Ukraine
Email: mikhailyukvictor2@gmail.com
Received November 23, 2012; revised December 25, 2012; accepted January 8, 2013
Keywords: C-Approximation Algorithm; Reoptimization; Approximation Resistant Predicates; Integrality Gap; Unique Games Conjecture (UGC)
ABSTRACT
The purpose of reoptimization using approximation methods—application of knowledge about the solution of the initial instance I, provided to achieve a better quality of approximation (approximation ratio) of an algorithm for determining optimal or close to it solutions of some “minor” changes of instance I. To solve the problem Ins-Max-EkCSP-P (reoptimization of Max-EkCSP-P with the addition of one constraint) with approximation resistant predicate P exists a polynomial threshold (optimal) 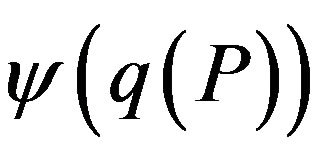 -approximation algorithm, where
-approximation algorithm, where  (
(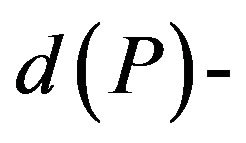 the threshold “random” approximation ratio of P). When the unique games conjecture (UGC) is hold there exists a polynomial threshold (optimal)
the threshold “random” approximation ratio of P). When the unique games conjecture (UGC) is hold there exists a polynomial threshold (optimal)  -approximation algorithm (where
-approximation algorithm (where 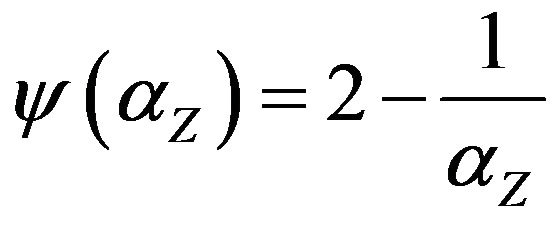 and
and 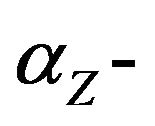 the integrality gap of semidefinite relaxation of Max-EkCSP-P problem Z) to solve the problem Ins-Max-EkCSP-P.
the integrality gap of semidefinite relaxation of Max-EkCSP-P problem Z) to solve the problem Ins-Max-EkCSP-P.
1. Introduction
In the constraint satisfaction problems (or CSP problems), there are many variables and a set of constraints (defined by predicates), each of which depends on a number of variables, and the goal is to find such assigning values to variables that satisfy the maximum number of constraints.
More formally, CSP problem Q is defined by a set of predicates over a finite domain . Each instance of problem Q consists of a set of variables V and a set of constraints on it. The goal is to find the assignment to variables that satisfies the maximum number of constraints. In general, the predicates can be replaced with actual payoff functions, and the goal is to maximize the total payment. A large number of fundamental optimization problems, such as Max Cut and Max k-Sat, there are examples of CSP problems.
. Each instance of problem Q consists of a set of variables V and a set of constraints on it. The goal is to find the assignment to variables that satisfies the maximum number of constraints. In general, the predicates can be replaced with actual payoff functions, and the goal is to maximize the total payment. A large number of fundamental optimization problems, such as Max Cut and Max k-Sat, there are examples of CSP problems.
Most of the CSP problems are NP-hard and so to solve them exactly in a reasonable time is hardly possible. Therefore we considered an effective approximation algorithm for solving such problems. For the maximization problem saying that the algorithm is the C-approximation algorithm, if for any instance gives a solution with objective function value no less than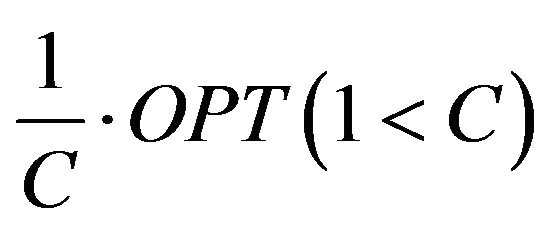 , where OPT—the global optimum. In this C is called the approximation ratio. Such a definition can be given to minimization problems.
, where OPT—the global optimum. In this C is called the approximation ratio. Such a definition can be given to minimization problems.
For the problem Q an upper bound of approximation ratio is established, if there exists a polynomial C-approximation algorithm for solving Q. For the problem Q the lower bound of approximation ratio c is established, if for any 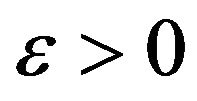 there is no polynomial approximation algorithm for Q where the approximation ratio
there is no polynomial approximation algorithm for Q where the approximation ratio 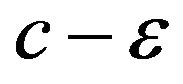 (or strictly less than c) is achieved. If C = c, then, for the problem Q the threshold of approximation ratio is established (is equal to C = c). The corresponding algorithm is called the threshold or optimal (and the approximation ratio-optimal).
(or strictly less than c) is achieved. If C = c, then, for the problem Q the threshold of approximation ratio is established (is equal to C = c). The corresponding algorithm is called the threshold or optimal (and the approximation ratio-optimal).
A fundamental question for a given NP-hard problem is to determine for which values you can rely on efficient (polynomial) C-approximation algorithm. This is a large research area in theoretical computer science with its positive and negative results.
The problem of establishing lower bounds for the approximation ratio (like any problem of obtaining lower bounds for the complexity) is a very difficult task. For this problem there is the name of inapproximability or the hardness of approximation. Great influence on the development of methods for obtaining lower bounds the famous PCP theorem [1] and discrete Fourier analysis to test the properties of problems (property testing) are provided [2,3].
Beginning with Goemans and Williamson [4,5] for Max Cut, semidefinite programming (SDP) has become the main tool in the construction of approximation algorithms for the CSP problems. For many of the problems are built SDP relaxations and apply appropriate procedures for the probabilistic rounding the solutions were obtained.
As already noted, the problem of inapproximability has been solved successfully for many of the problems due to PCP theorem. In particular, Hastad [6-8] showed that Max-E3-Lin-2 and Max 3-Sat are NP-hard to approximate with ratios 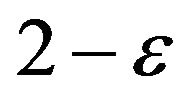 and
and 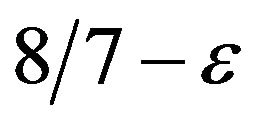 respectively. This means that a simple random algorithm for assigning is the best (optimal) for these problems, if
respectively. This means that a simple random algorithm for assigning is the best (optimal) for these problems, if 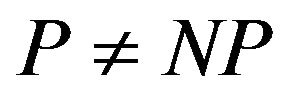 or that ratios 2 and 8/7 are the threshold. In [9] is showed (also involving PCP theorem) that the set covering problem has a threshold approximation ratio equal to
or that ratios 2 and 8/7 are the threshold. In [9] is showed (also involving PCP theorem) that the set covering problem has a threshold approximation ratio equal to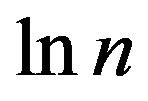 .
.
In studying the problem of inapproximability for general constraints satisfaction problems (in particular with the predicates of arity 2), such progress was not achieved. The most promising approach to obtaining strong results (thresholds of approximation ratios)—the so called Unique Games Conjecture (UGC), introduced by S. Khot [11-14]. Unique games conjecture (UGC) is one of the most important open problems in modern theoretical computer science because of the large number of strong results in inapproximability that follow from the UGC. For example, —the hardness of approximating Vertex Cover [12], Max Independent Set [15], Multi Cut [16].
—the hardness of approximating Vertex Cover [12], Max Independent Set [15], Multi Cut [16].
Recently, a close relationship between the concepts of the approximation ratio, the inapproximability ratio and integrality gap of simple SDP relaxation (defined as the maximum ratio of the SDP solution to the real optimum) has been established. From the truth of UGC, it follows that the simple SDP relaxation gives the optimal approximation ratio for CSP. For the first time link between the SDP rounding schemes for relaxation and results in innapproximability based on the UGC, was noticed in [13] for Boolean CSP of two variables. In general, in [17-19] proposed the rounding schemes by which the optimal approximation ratio for each CSP problem, assuming the true UGC, is achieved.
The concept of reoptimization [20-26] is as follows. Let Q-some NP-hard (perhaps NP-complete) problem, I-the initial problem instance of Q, the optimal solution of which is known. We propose a new instance 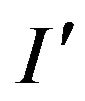 of the problem Q, received some “minor” changes of instance I.
of the problem Q, received some “minor” changes of instance I.
The question arises: how can we effectively utilize the knowledge of the optimal solution of I for the calculation of exact or approximate solution of the instance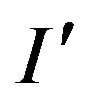 ? The purpose of reoptimization using approximation methods - application of knowledge about the solution of the initial instance I, provided either to achieve a better quality of approximation (approximation ratio), or a more efficient (in time) algorithm for determining optimal or close to it solutions, or execution of the first and second points.
? The purpose of reoptimization using approximation methods - application of knowledge about the solution of the initial instance I, provided either to achieve a better quality of approximation (approximation ratio), or a more efficient (in time) algorithm for determining optimal or close to it solutions, or execution of the first and second points.
Such results for the reoptimization of discrete optimization problems are known. When an elementary disjunction is inserted reoptimization of Max Weighted Sat (weighted satisfiability problem for maximum) approximated with the ratio of 0.81, while Max Weighted Sat - approximable with ratio 0.77 [25]. When inserting a vertex in the graph reoptimization of Min Vertex Cover (minimum vertex cover of a graph) can be approximated with the ratio of 1.5, Min Vertex Cover-with the ratio of 2 [25]. When inserting a vertex (terminal or not) reoptimization of Min Steiner Tree (minimum Steiner tree) can be approximated with the ratio of 1.5, Min Steiner Treeapproximated by the ratio 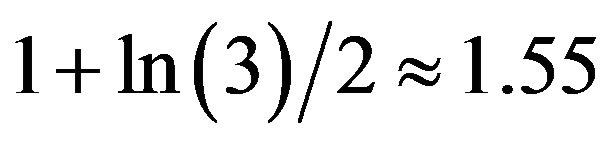 [21].When you insert or delete an item from a set, the set covering problem is approximable with ratio
[21].When you insert or delete an item from a set, the set covering problem is approximable with ratio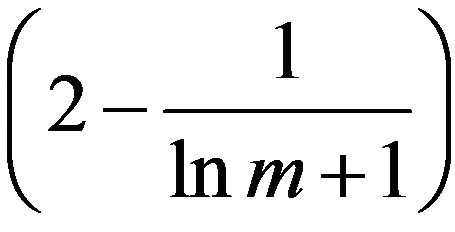 , where m—the number of elements. A similar result occurs when you insert or delete an arbitrary number of
, where m—the number of elements. A similar result occurs when you insert or delete an arbitrary number of 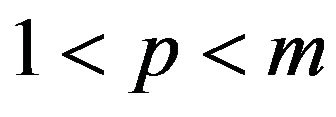 elements of the set [26]. It should be noted a series of papers on the problem of reoptimization of traveling salesman problem (TSP-Travelling Salesman Problem) [20-22,24]. For example, the problem of Minimum Metric TSP (Min TSP—the traveling salesman problem with the minimum metric distances) approximable with ratio 1.5, its reoptimization when inserting a new unit—with ratio of 1.34, reoptimization of this problem when you change the distance—with ratio of 1.4 [25]. For the general traveling salesman problem (Min TSP) are unknown estimates of approximation ratio as for herself, and for different versions of reoptimization.
elements of the set [26]. It should be noted a series of papers on the problem of reoptimization of traveling salesman problem (TSP-Travelling Salesman Problem) [20-22,24]. For example, the problem of Minimum Metric TSP (Min TSP—the traveling salesman problem with the minimum metric distances) approximable with ratio 1.5, its reoptimization when inserting a new unit—with ratio of 1.34, reoptimization of this problem when you change the distance—with ratio of 1.4 [25]. For the general traveling salesman problem (Min TSP) are unknown estimates of approximation ratio as for herself, and for different versions of reoptimization.
The main results of this paper are as follows. We investigated the reoptimization versions of constraint satisfaction problems with predicates of arity k (Ins-MaxEkCSP-P) by adding of any constraint. To solve the problem Ins-Max-EkCSP-P (reoptimization Max-EkCSPP) with approximation resistant predicates there exists a polynomial threshold (optimal)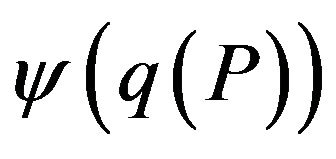 —approximation algorithm, where
—approximation algorithm, where
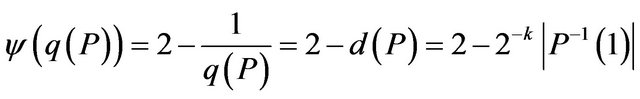
(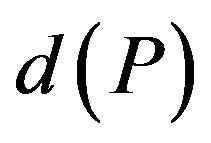 —the threshold “random” approximation ratio).
—the threshold “random” approximation ratio).
When the unique games conjecture (UGC) is hold there exists a polynomial threshold (optimal)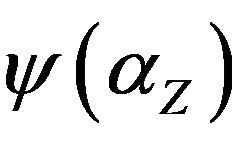 —approximation algorithm (where
—approximation algorithm (where  and
and —
—
the integrality gap of semidefinite relaxation of MaxEkCSP-P problem Z) to solve the problem Ins-MaxEkCSP-P.
2. Preliminaries
Present the necessary notations and definitions [6,28,31]. Under the predicate P of arity k we mean the map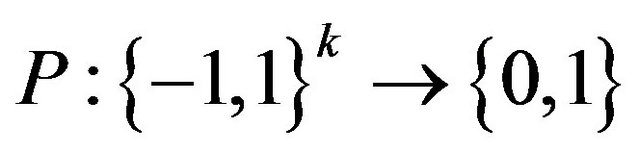 . For notational convenience, the input data with a value of −1 is interpreted as “true”, value of 1-as “false”. If the predicate P accepts an input value y then
. For notational convenience, the input data with a value of −1 is interpreted as “true”, value of 1-as “false”. If the predicate P accepts an input value y then , else
, else . Thus, the set of values accepted by the predicate P, is denoted as
. Thus, the set of values accepted by the predicate P, is denoted as . Logic AND, OR and XOR with two variables is denoted as
. Logic AND, OR and XOR with two variables is denoted as  and
and , respectively. For integer k denote predicates kOR, kAND and kXOR as a logical OR, AND and XOR of the k variables, respectively. If
, respectively. For integer k denote predicates kOR, kAND and kXOR as a logical OR, AND and XOR of the k variables, respectively. If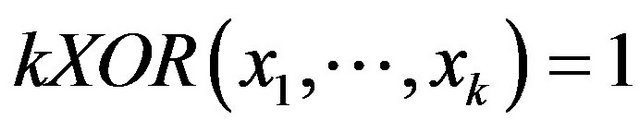 , then
, then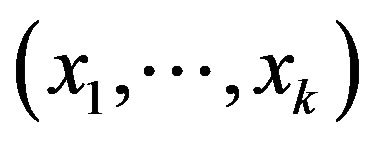 has odd parity, else even parity. Literal—a Boolean variable or its negation.
has odd parity, else even parity. Literal—a Boolean variable or its negation.
Definition 1. Suppose there is a predicate
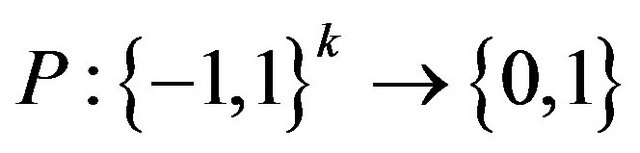 . An instance of the problem MaxCSP-P consists of
. An instance of the problem MaxCSP-P consists of 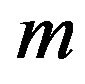 weighted constraints, each of them is a k-tuple of literals
weighted constraints, each of them is a k-tuple of literals 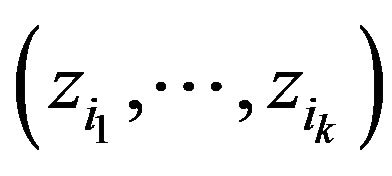 drawn from the set
drawn from the set . All variables in the tuple are different. Constraint is satisfied if and only if P accepts a tuple. The solution is the assignment of truth values to
. All variables in the tuple are different. Constraint is satisfied if and only if P accepts a tuple. The solution is the assignment of truth values to
 . Value of the solution is
. Value of the solution is where
where 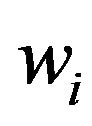 is (not negative) weight of i-th constraint. The goal is to maximize this value. When P depends on no more than k literal Max-CSP-P will be called MaxkCSP-P, if in P exactly k literals-then Max-EkCSP-P.
is (not negative) weight of i-th constraint. The goal is to maximize this value. When P depends on no more than k literal Max-CSP-P will be called MaxkCSP-P, if in P exactly k literals-then Max-EkCSP-P.
Along with the problems of the type Max-CSP-P discussed problems such as CSP-P, where the goal is to find such assignment, that all constraints are satisfied (kCSP-P and EkCSP-P similarly defined).
Definition 2. Two k-arity predicates P and 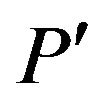 have the same type if and only if there exists a permutation
have the same type if and only if there exists a permutation  on
on  and
and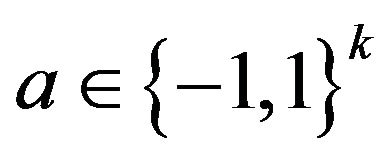 , such that
, such that
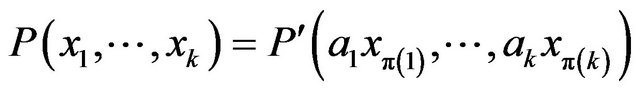 for all
for all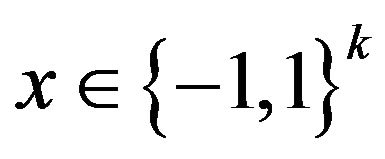 .
.
If P and 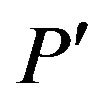 have the same type, then an instance Max-CSP-P can be expressed as an instance Max-CSP-P', rearranging the tuples according to the mask, i.e., these problems are equivalent.
have the same type, then an instance Max-CSP-P can be expressed as an instance Max-CSP-P', rearranging the tuples according to the mask, i.e., these problems are equivalent.
Definition 3. Problem Max-kCSP-P, where each constraint is disjunction of no more than k literals is a problem Max-k-SAT. If each constraint contains exactly k literals, that is the problem Max-Ek-SAT.
Definition 4. Problem Max-kCSP-P, where each constraint is a product of no more than k literals equal to a constant, is the problem Max-k-LIN. If each constraint contains exactly k literals, that is the problem Max-EkLIN.
Let  is the value of the optimal solution of instance
is the value of the optimal solution of instance .
.
Definition 5. The algorithm A is C-approximation algorithm for the maximization problem if for all instances I of the problem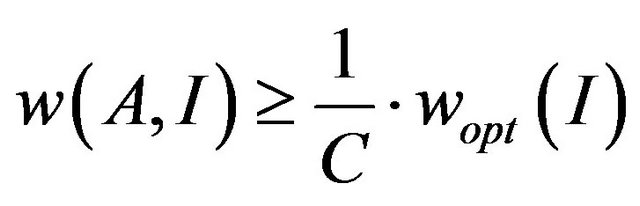 , where
, where 
the value of the solution of algorithm A for the input I. In this talk, that A has the approximation ratio C. For probabilistic algorithms 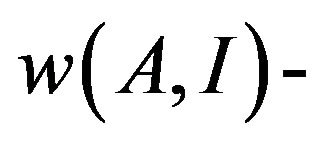 the expected value of random elections of algorithm A.
the expected value of random elections of algorithm A.
The predicate P is approximation resistant (and the corresponding problem Max-CSP-P), if to find a solution Max-CSP-P, that is much better than expected value of random assignment, is NP-hard. Because of random assignment accept any P-constraint with probability  , we have the following definition.
, we have the following definition.
Definition 6. The predicate 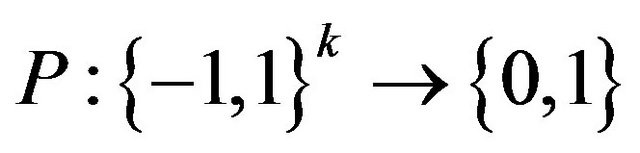 is called approximation resistant if for any constant
is called approximation resistant if for any constant 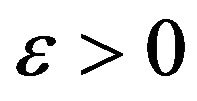 to find a solution x of instance I of the problem MaxCSP-P such, that the value x no more than
to find a solution x of instance I of the problem MaxCSP-P such, that the value x no more than
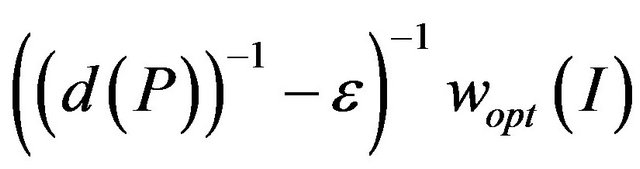 , is
, is -hard.
-hard.
Definition 7. The problem Max-CSP-P is always approximable, if for any 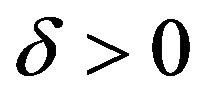 there exists
there exists  and an efficient algorithm, which is based on an instance, where some
and an efficient algorithm, which is based on an instance, where some  -part of constraints may be simultaneously accepted, find the assignment, that accept no more than
-part of constraints may be simultaneously accepted, find the assignment, that accept no more than 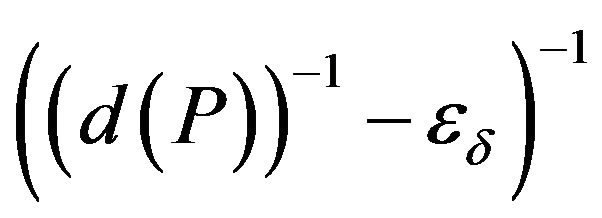 -part of the constraints.
-part of the constraints.
Definition 8. The predicate  is called hereditary approximation resistant if all the predicates
is called hereditary approximation resistant if all the predicates which are consequences of P (i.e.
which are consequences of P (i.e. 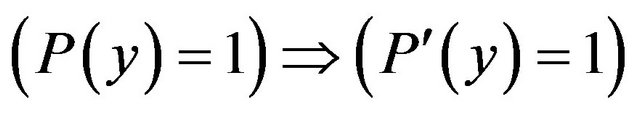 , for all y) are approximation resistant.
, for all y) are approximation resistant.
Theorem 1 [8]. The problem Max-CSP-P admits a polynomial approximation algorithm with approximation ratio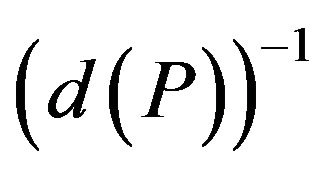 .
.
Proof. Let us have an instance with m constraints. Random assignment accepted any given constraint with a probability  and, thus, accepted
and, thus, accepted 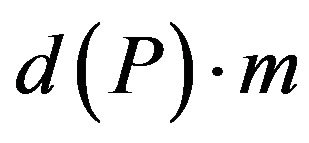 constraints on average. Since the optimal assignment accepted no more than m constraints, we have the random
constraints on average. Since the optimal assignment accepted no more than m constraints, we have the random  approximation algorithm. That random algorithm may be derandomized dy the method of conditional expectation.
approximation algorithm. That random algorithm may be derandomized dy the method of conditional expectation.
Remark 1. For approximation resistant predicates P threshold approximation ratio of the problem Max-CSP-P is attained (Theorem 1) and equals
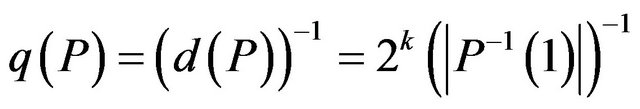 .
.
This value is called the threshold “random” approximation ratio.
We have the following results on approximation resistant predicates of Max-EkCSP-P problems. There is no predicate of arity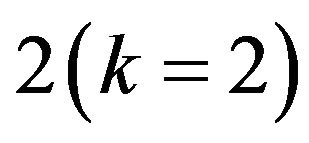 , which are approximation resistant [8]. If
, which are approximation resistant [8]. If  the problem Max-E3-LIN is hereditary approximation resistant [6], and it exhausts all of approximation resistant predicates of arity 3 [29]. Approximation resistant predicates of arity
the problem Max-E3-LIN is hereditary approximation resistant [6], and it exhausts all of approximation resistant predicates of arity 3 [29]. Approximation resistant predicates of arity 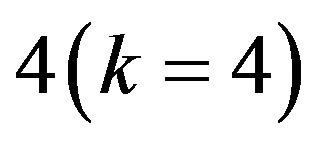 are studied in [28]. There are 400 different predicates (up to permutations of variables and their negations). Among them, 79 were identified as approximation resistant, 275- not as approximation resistant, the status of the remaining 46 predicates could not be determined.
are studied in [28]. There are 400 different predicates (up to permutations of variables and their negations). Among them, 79 were identified as approximation resistant, 275- not as approximation resistant, the status of the remaining 46 predicates could not be determined.
Present the main results for approximation resistant predicates of arity 3 (Max-E3CSP-P).
Theorem 2 [6]. For an arbitrary 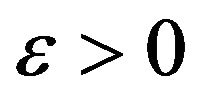 it is
it is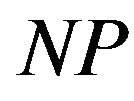 -hard to approximate Max-E3-LIN with ratio
-hard to approximate Max-E3-LIN with ratio . In other words
. In other words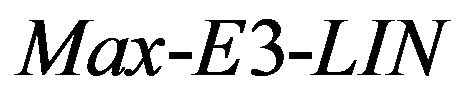 is approximation resistant.
is approximation resistant.
Theorem 3 [6]. For an arbitrary  it is
it is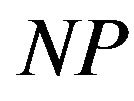 -hard to approximate Max-E3-LIN with ratio
-hard to approximate Max-E3-LIN with ratio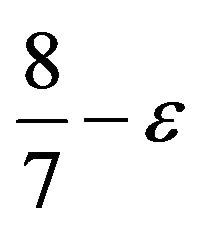 . In other words Max-E3-LIN is approximation resistant.
. In other words Max-E3-LIN is approximation resistant.
Theorem 4 [6]. Let P the predicate of arity 3 such, that 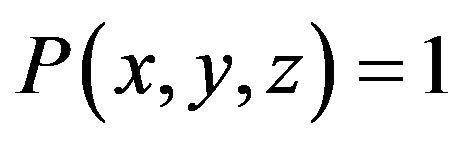 for any x, y, z, satisfying the equation xyz = 1, then CSP, determined by P, is approximation resistant.
for any x, y, z, satisfying the equation xyz = 1, then CSP, determined by P, is approximation resistant.
Theorem 4 remains true if we replace the equation xyz = 1 by xyz = −1. Generalization of Theorem 4 is the following theorem.
Theorem 5 [8]. Predicate P of arity 3 is approximation resistant, if and only if it is a consequence of the odd parity or even parity.
Consider the following predicates of arity 3:

The above results can be summarized in the following assertion.
Theorem 6. Predicates XOR, NTW, OXR, OR are approximation resistant predicates. Among them XOR, NTW, OXR-hereditary approximation resistant predicates.
Following [30,31] we introduce a generalization of the CSP problem (GCSP problems), where instead of predicates with values from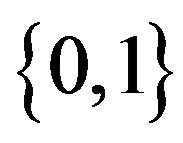 , payoff functions with values from
, payoff functions with values from  to be used.
to be used.
Definition 9 (Λ-GCSP problem). Λ-GCSP problem is defined as 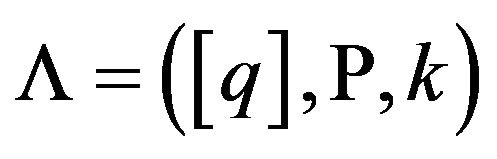 where
where 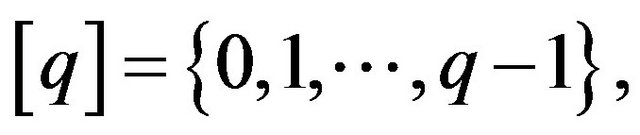
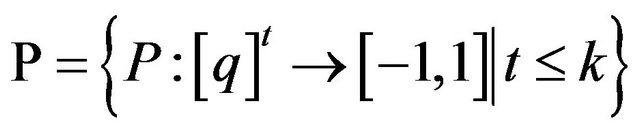 , a lot of payoff functions.
, a lot of payoff functions.
The maximum number of inputs of the payoff function  is the dimension of the problem
is the dimension of the problem .
.
Definition 10. An instance 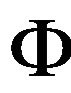 of the problem Λ-GCSP is defined as
of the problem Λ-GCSP is defined as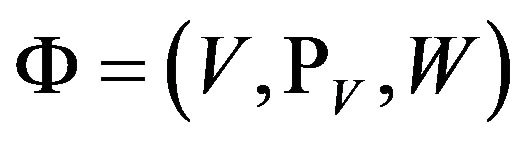 , where
, where
• 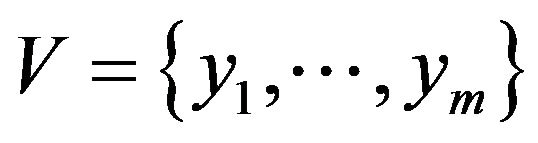 : variables taking values from
: variables taking values from ;
;
•  consists of the payoff functions that are applied to subsets S of variables V of size no more than k. More precisely, for a subset
consists of the payoff functions that are applied to subsets S of variables V of size no more than k. More precisely, for a subset 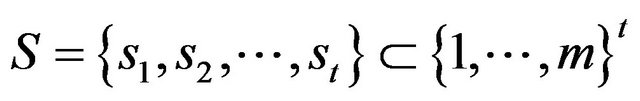 payoff function
payoff function 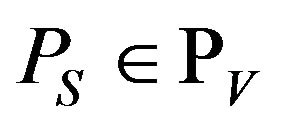 is applied to the variables
is applied to the variables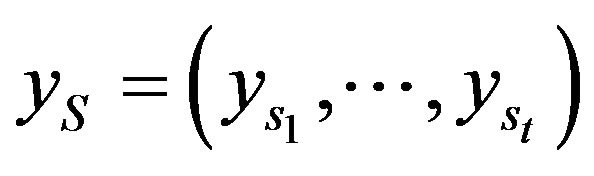 ;
;
• positive weights 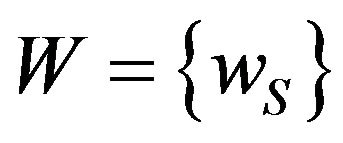 satisfy
satisfy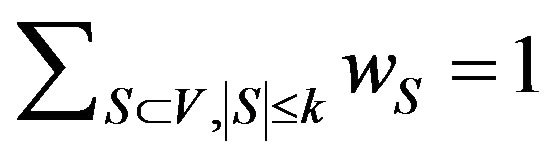 ,
,  denote the set S, chosen according to probability distribution W.
denote the set S, chosen according to probability distribution W.
The goal is to find the assignment of variables that maximize the expected total weight or total weight, i.e.
maximize 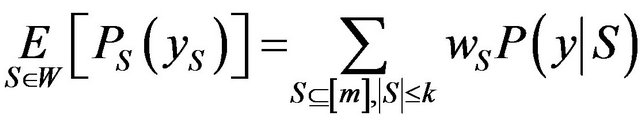 (denote this maximum as
(denote this maximum as ).
).
Note, that if the payoff functions P are predicates, and the problem Λ-GCSP is unweighted , then
, then 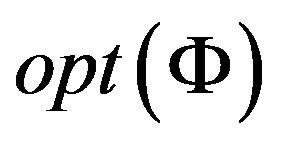 will be just the maximum number of accepted constraints.
will be just the maximum number of accepted constraints.
We introduce the predicate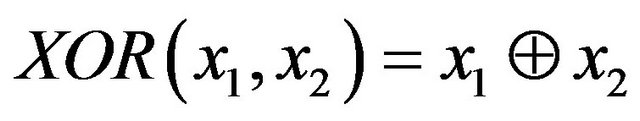 . In the future, as an example, we consider the problem Max Cut.
. In the future, as an example, we consider the problem Max Cut.
Definition 11 (Max Cut). For a given undirected graph 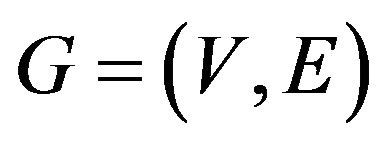 with set vertices V and edges E of Max Cut is the problem of finding a partition
with set vertices V and edges E of Max Cut is the problem of finding a partition 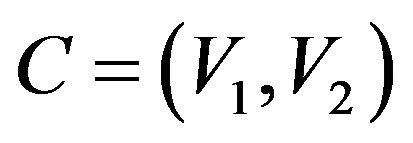 of the vertices
of the vertices , that maximizes the size of the set
, that maximizes the size of the set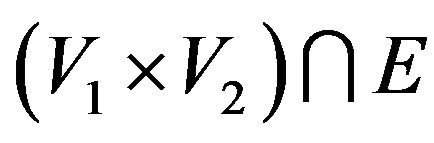 . For a given weight function
. For a given weight function , weighted Max Cut problem is to maximize
, weighted Max Cut problem is to maximize
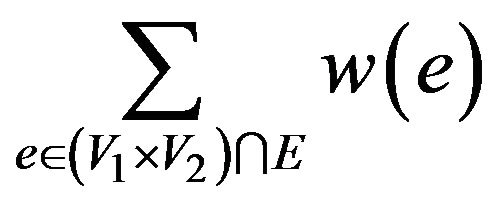 .
.
Let us consider in more detail the problem Max Cut. For a graph 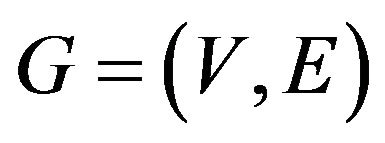 with set vertices V and edges E this problem (the maximum cut in the graph) is defined as follows: find a partition V on
with set vertices V and edges E this problem (the maximum cut in the graph) is defined as follows: find a partition V on  and
and 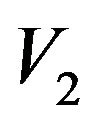 to maximize the number of edges, that form a cut, i.e. lies between the two parts. If each vertex i associate a Boolean variable
to maximize the number of edges, that form a cut, i.e. lies between the two parts. If each vertex i associate a Boolean variable , then the problem can be viewed as Max-E2CSP-XOR or Max-E2-LIN with the equations of the form
, then the problem can be viewed as Max-E2CSP-XOR or Max-E2-LIN with the equations of the form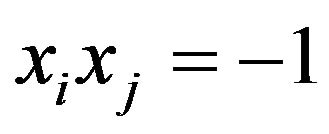 .
.
3. On Computational Complexity of Reoptimization
Consider an arbitrary unweighted Max-EkCSP-P problem Z (Definition 1). Let  the set of variables, E-the set of constraints. The constraint
the set of variables, E-the set of constraints. The constraint 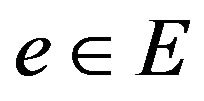 is denoted as
is denoted as 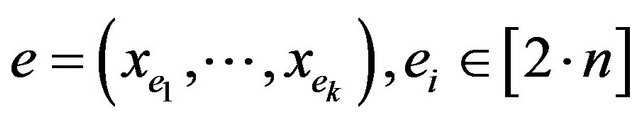 with a special order of the variables (relative to V). The assignment is a map
with a special order of the variables (relative to V). The assignment is a map , the assignment
, the assignment 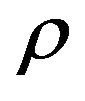 accepted constraint e, if
accepted constraint e, if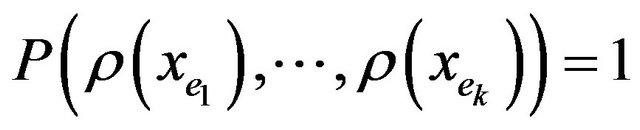 . We denote by
. We denote by 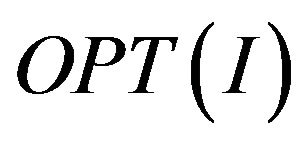 the maximum part of the constraints accepted by any assigning an arbitrary instance I of the problem Z.
the maximum part of the constraints accepted by any assigning an arbitrary instance I of the problem Z.
Let an instance I of the problem Z such, that
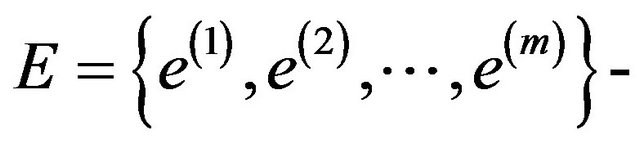 the set of m constraints. The constraint
the set of m constraints. The constraint 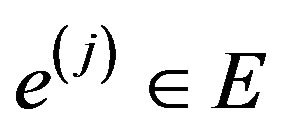 is denoted as
is denoted as ,
,
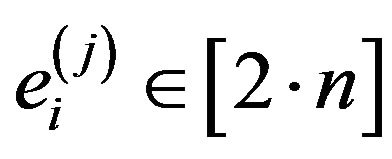 ,
, 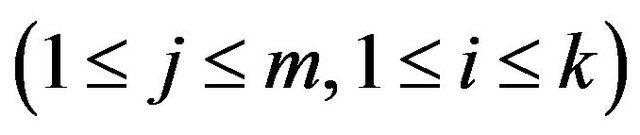 with a special order of the variables (relative to V). An instance
with a special order of the variables (relative to V). An instance 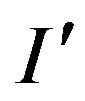 of the problem is obtained from I by adding an arbitrary
of the problem is obtained from I by adding an arbitrary 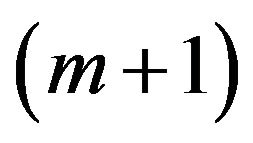 -th constraint
-th constraint 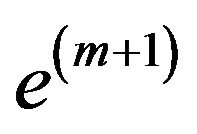 (the same structure, as
(the same structure, as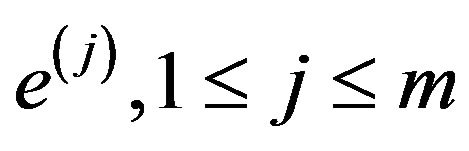 ). Define reoptimization version of the problem MaxEkCSP-P.
). Define reoptimization version of the problem MaxEkCSP-P.
Problem Ins-Max-EkCSP-P. Input. Arbitrary instance I of the problem Max-EkCSP-P,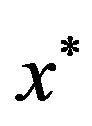 —the optimal solution of instance I.
—the optimal solution of instance I.
Result. Find the optimal solution of instance  (obtained on the basis of I, as described above) of the problem Max-EkCSP-P, using
(obtained on the basis of I, as described above) of the problem Max-EkCSP-P, using .
.
Purpose. Find x, that maximizes the number of accepted constraints of instance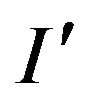 .
.
Useful and interesting are challenges to establishing of 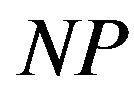 -hardness of reoptimization versions of optimization problems. Using the results of [27] (in particular Theorem 2), we propose a criterion for determining of NP-hardness of reoptimization. The essence of the criterion for the most of NP-hard problems is that in order to show NPhardness of reoptimization versions suggestions are based on polynomial Turing reducibility of the original problem to its reoptimization version.
-hardness of reoptimization versions of optimization problems. Using the results of [27] (in particular Theorem 2), we propose a criterion for determining of NP-hardness of reoptimization. The essence of the criterion for the most of NP-hard problems is that in order to show NPhardness of reoptimization versions suggestions are based on polynomial Turing reducibility of the original problem to its reoptimization version.
Lemma 1. Let P-NP-hard problem and mod-P-some local modification to P. If there exists a polynomial algorithm A, which for any instance I of the problem P computes:
1) instance 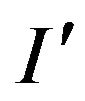 for
for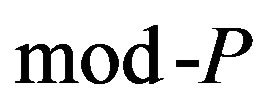 ;
;
2) the optimal solution  for
for ;
;
3) a sequence of local modifications of the type mod (no more than a polynomial), that transforms 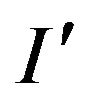 into I, then the problem mod-P is NP-hard.
into I, then the problem mod-P is NP-hard.
Proof. Reduce P to mod-P using a polynomial Turing reducibility. Because of P is NP-hard, and that such (i.e., NP-hard) will be mod-P.
Let q—the number of local modifications of the type mod for A that 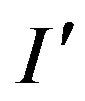 is converted into an instance I. Suppose that there exists a polynomial algorithm A1 (with complexity p) for mod-P. Then, using A1 exactly q times since with
is converted into an instance I. Suppose that there exists a polynomial algorithm A1 (with complexity p) for mod-P. Then, using A1 exactly q times since with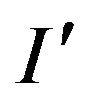 , we find the optimal solution for I. At the same time as the number of calculations
, we find the optimal solution for I. At the same time as the number of calculations 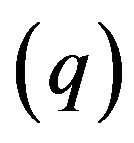 and time of each calculation
and time of each calculation , polynomial in the size of P, we obtained polynomial reducibility (with the complexity
, polynomial in the size of P, we obtained polynomial reducibility (with the complexity ). Lemma is proved.
). Lemma is proved.
Using Lemma 1, it is possible for specific predicates P from NP-hardness of Max-EkCSP-P (at ) set NPhardness of Ins-Max-EkCSP-P. For example, we show how to do it for Max-Ek-Lin.
) set NPhardness of Ins-Max-EkCSP-P. For example, we show how to do it for Max-Ek-Lin.
Theorem 7. The problem Ins-Max-Ek-Lin is NP-hard.
Proof. We use Lemma 1. As P we take a NP-hard problem Max-Ek-Lin [8], but as a mod-P-problem InsMax-Ek-Lin. Let I—an arbitrary instance of the problem Max-Ek-Lin (it corresponds to a system L of m linear equations). Let  -one of these equations (we take it as
-one of these equations (we take it as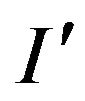 ). Construct in polynomial time an assignment of values to vector
). Construct in polynomial time an assignment of values to vector , which makes this equation acceptable. We assign the set of
, which makes this equation acceptable. We assign the set of 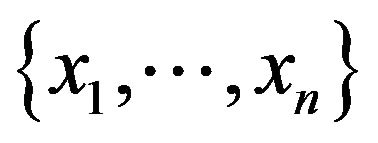 arbitrary values of truth. If
arbitrary values of truth. If 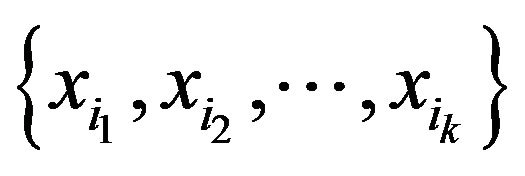 satisfies equation
satisfies equation 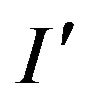 then the build is completed, otherwise any value
then the build is completed, otherwise any value is reversed, resulting in the equation
is reversed, resulting in the equation 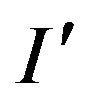 will be accepted in polynomial time, i.e. point 1) and 2) of Lemma 1 are satisfied. As
will be accepted in polynomial time, i.e. point 1) and 2) of Lemma 1 are satisfied. As 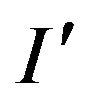 can be transformed into I no more than m modifications mod-P (i.e., add no more than m equations), point 3) of Lemma 1 is also fulfilled and the theorem is proved.
can be transformed into I no more than m modifications mod-P (i.e., add no more than m equations), point 3) of Lemma 1 is also fulfilled and the theorem is proved.
4. Reoptimization of Constraint Satisfaction Problems with Approximation Resistant Predicates
Theorem 8. If 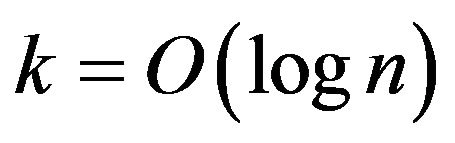 and for the problem MaxEkCSP-P exists a polynomial
and for the problem MaxEkCSP-P exists a polynomial 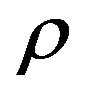 -approximation algorithm, then for the problem Ins-Max-EkCSP-P (reoptimization Max-EkCSP-P) exists a polynomial
-approximation algorithm, then for the problem Ins-Max-EkCSP-P (reoptimization Max-EkCSP-P) exists a polynomial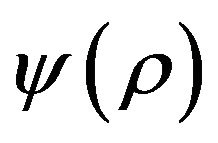 —
—
approximation algorithm, where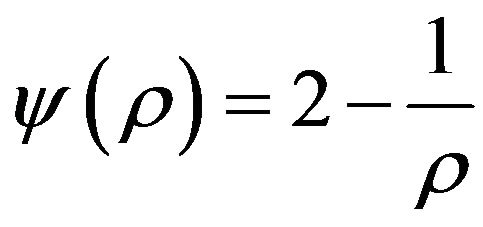 .
.
Proof. We apply the approach discussed in [25,26]. Let Ian instance of the problem Max-EkCSP-P, which consists of a system of constraints 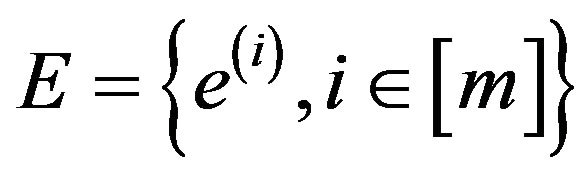 and optimal solution
and optimal solution 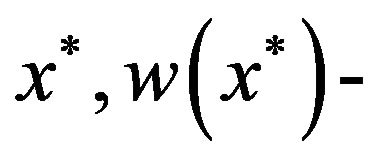 the number of accepted constraints in the system E by solution
the number of accepted constraints in the system E by solution . Adds a constraint
. Adds a constraint  to the system, the result is an instance
to the system, the result is an instance 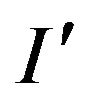 of the problem Max-EkCSP-P, let
of the problem Max-EkCSP-P, let  - the best solution of it. If
- the best solution of it. If 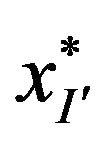 does not accepted constraint
does not accepted constraint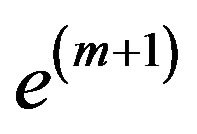 , then
, then  is the optimal solution of instance
is the optimal solution of instance 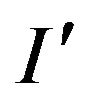 of the problem Ins-MaxE2CSP-P, then
of the problem Ins-MaxE2CSP-P, then
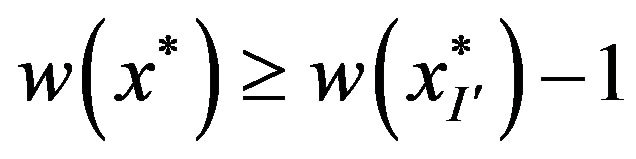 (1)
(1)
(on the left side write down the condition, that 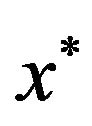 - the best solution, and the right, that the optimal solution does not accepted constraint
- the best solution, and the right, that the optimal solution does not accepted constraint ). Suppose
). Suppose 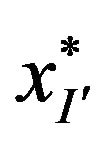 is accepted the constraint
is accepted the constraint 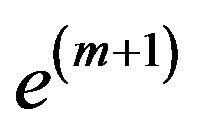 and there are l ways in which the constraint is satisfied (obviously,
and there are l ways in which the constraint is satisfied (obviously,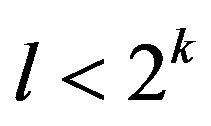 ).
).
We construct l approximate solutions 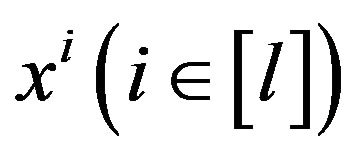 as follows. Take i-th assignment, which accepted
as follows. Take i-th assignment, which accepted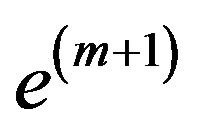 . From the constraint system we remove
. From the constraint system we remove  and for the constraints, that remain (including the result of assignment) use a polynomial
and for the constraints, that remain (including the result of assignment) use a polynomial 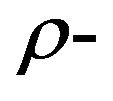 approximation algorithm, we obtain an approximate solution
approximation algorithm, we obtain an approximate solution . The result is
. The result is
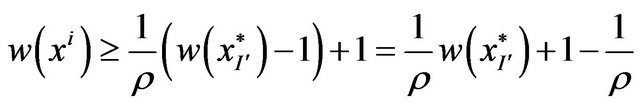 (2)
(2)
Multiplying (1) on 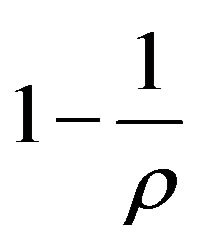 and adding with (2) we obtain
and adding with (2) we obtain
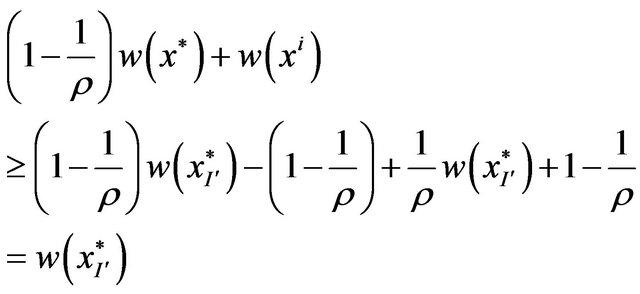
Among the solutions 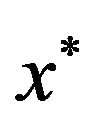 and
and 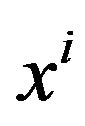 choose the best (i.e., with the largest value of the objective function w) and is denoted by
choose the best (i.e., with the largest value of the objective function w) and is denoted by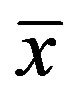 . We have
. We have
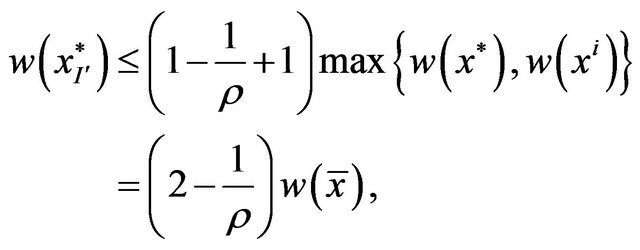
and . To the algorithm is polynomial was sufficient to require that
. To the algorithm is polynomial was sufficient to require that 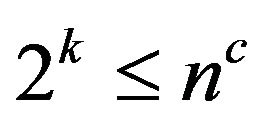 (n-the total number of variables, c = const), which means
(n-the total number of variables, c = const), which means
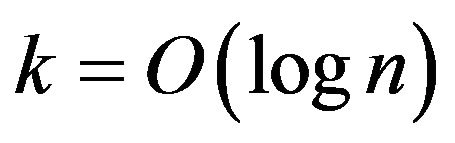 in the theorem. Thus, as a result of this algorithm, an approximate solution
in the theorem. Thus, as a result of this algorithm, an approximate solution 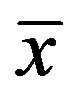 of the instance
of the instance 
with approximation ratio  is obtained. It is clear that at all times
is obtained. It is clear that at all times .
.
Theorem 9. If for a problem Max-EkCSP-P exists a polynomial threshold (optimal) 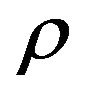 -approximation algorithm, and for the problem Ins-Max-EkCSP-P (reoptimization Max-EkCSP-P), there exists a polynomial
-approximation algorithm, and for the problem Ins-Max-EkCSP-P (reoptimization Max-EkCSP-P), there exists a polynomial  -approximation algorithm, then
-approximation algorithm, then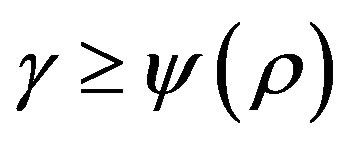 .
.
Proof. Let Ian instance of the problem Max-EkCSP-Pwhich consists of a system of constraints 
and optimal solution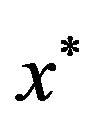 . Adds a constraint
. Adds a constraint 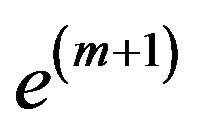 to the system, the result is an instance
to the system, the result is an instance 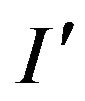 of the problem InsMax-EkCSP-P. Let
of the problem InsMax-EkCSP-P. Let 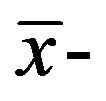 the solution of Ins-Max-EkCSPP, obtained by the algorithm of Theorem 6. The solution
the solution of Ins-Max-EkCSPP, obtained by the algorithm of Theorem 6. The solution  is the best (more on the value of the objective function) of the solutions
is the best (more on the value of the objective function) of the solutions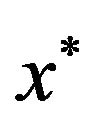 , and
, and , it is obtained by a polynomial approximation algorithm with approximation ratio
, it is obtained by a polynomial approximation algorithm with approximation ratio . The proof is by contradiction. Let
. The proof is by contradiction. Let 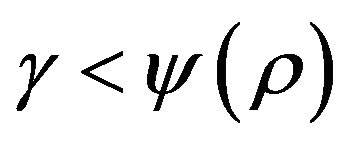 and
and  such, that
such, that . Since the function
. Since the function 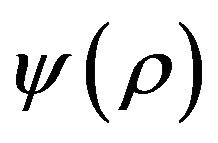 is increasing in
is increasing in 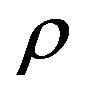 and
and 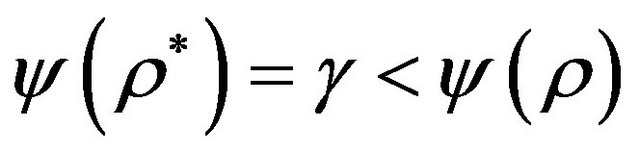 , it follows, that
, it follows, that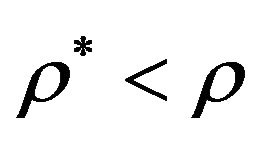 . But this contradicts the fact, that for the problem Max-EkCSP-P exists a polynomial threshold (optimal)
. But this contradicts the fact, that for the problem Max-EkCSP-P exists a polynomial threshold (optimal) 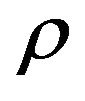 -approximation algorithm (i.e., for solutions
-approximation algorithm (i.e., for solutions 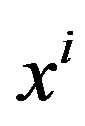 to be applied polynomial-time algorithm with approximation ratio
to be applied polynomial-time algorithm with approximation ratio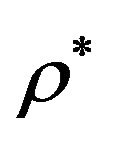 , less than
, less than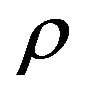 , that is impossible).
, that is impossible).
Theorem 10. If for a problem Max-EkCSP-P exists a polynomial threshold (optimal) 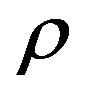 -approximation algorithm and
-approximation algorithm and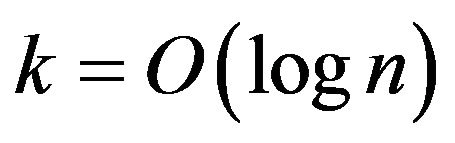 , then for the problem Ins-MaxEkCSP-P (reoptimization Max-EkCSP-P), there exists a polynomial threshold (optimal)
, then for the problem Ins-MaxEkCSP-P (reoptimization Max-EkCSP-P), there exists a polynomial threshold (optimal)  -approximation algorithm, where
-approximation algorithm, where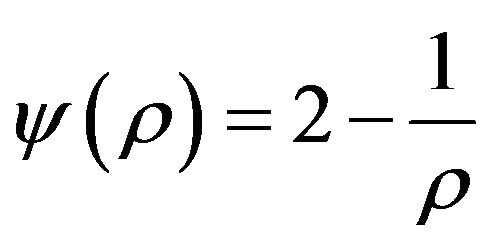 .
.
The proof follows from Theorems 8 and 9 Corollary 1. If  and the predicate P approximation resistant, then for the problem Ins-MaxEkCSP-P (reoptimization of Max-EkCSP-P), there exists a polynomial optimal
and the predicate P approximation resistant, then for the problem Ins-MaxEkCSP-P (reoptimization of Max-EkCSP-P), there exists a polynomial optimal 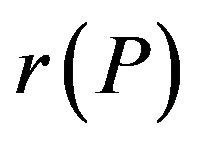 -approximation algorithmwhere
-approximation algorithmwhere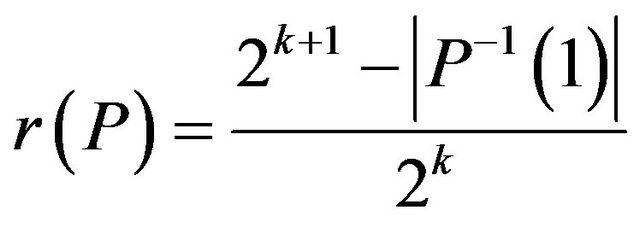 .
.
Proof. Since the predicate P is approximation resistant, according to Remark 1, the algorithm of Theorem 1 for Max-EkCSP-P is optimal 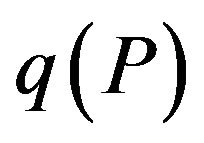 -approximation algorithm, where
-approximation algorithm, where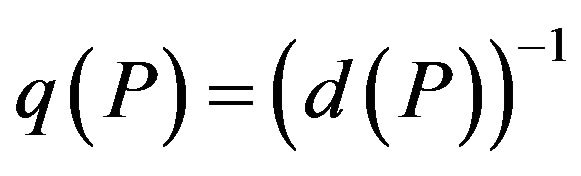 ,
,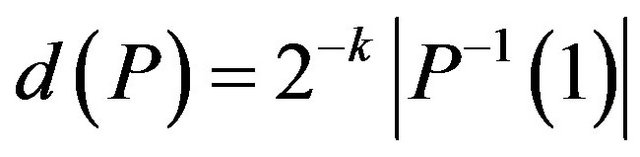 . Hence, by Theorem 10 for Ins-Max-EkCSP-P there exists a polynomial threshold (optimal)
. Hence, by Theorem 10 for Ins-Max-EkCSP-P there exists a polynomial threshold (optimal) 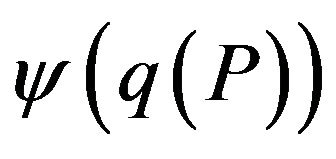 -approximation algorithm, where
-approximation algorithm, where
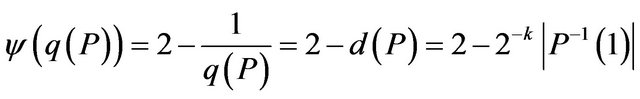 .
.
Example 1. Consider the problem Max-E3CSP-XOR with the appropriate reoptimization version Ins-MaxE3CSP-XOR. By Theorem 6, the predicate XORis hereditary approximation resistant (there is proof of this fact in [28]). We apply Theorem 10 (or more precisely, Corollary 1) 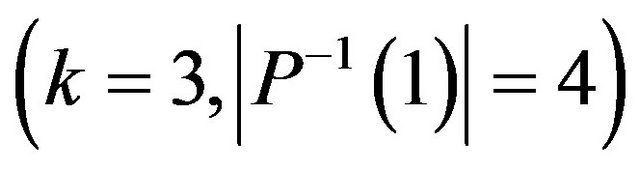 and obtain proposition.
and obtain proposition.
Proposition 1. For the problem Ins-Max-E3CSP-XOR (reoptimization of Max-E3CSP-XOR) there exists a polynomial optimal approximation algorithm with an approximation ratio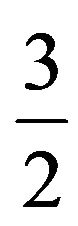 .
.
5. Integrality Gaps of Semidefinite Relaxation
For each instance  (Definition 10) is constructed semidefinite (SDP) relaxation [30] (which is not presented here). Let
(Definition 10) is constructed semidefinite (SDP) relaxation [30] (which is not presented here). Let 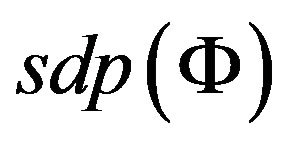 -solution of SDP relaxation (clearly,
-solution of SDP relaxation (clearly, ). We introduce the notion of integrality gap for semidefinite relaxation of the constraint satisfaction problems.
). We introduce the notion of integrality gap for semidefinite relaxation of the constraint satisfaction problems.
Definition 12. Integrality gap of Λ-GCSP problem is defined as 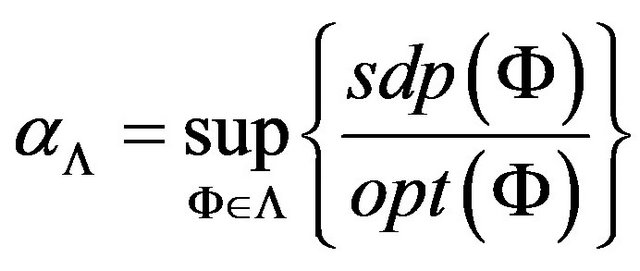
The notion of integrality gap for some relaxation (not only semidefinite) is important, because it allows to design approximation algorithms for solving discrete optimization problems with a given approximation ratio. The following theorem holds.
Theorem 11 [31]. For the problem Λ-GCSP with nonnegative payoff functions there exists a polynomial approximation algorithm with approximation ratio no more than integrality gap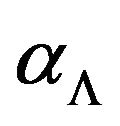 .
.
This theorem can comment on such arguments. First, we solve the problem 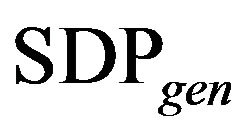 (general SDP relaxation of the problem Λ-GCSP), let
(general SDP relaxation of the problem Λ-GCSP), let 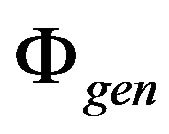 the solution of it. Applying some probabilistic scheme of rounding, from solution
the solution of it. Applying some probabilistic scheme of rounding, from solution 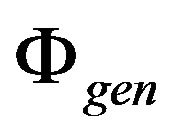 we obtain an approximate solution
we obtain an approximate solution  of the original problem Λ. By Definition 12 we obtain
of the original problem Λ. By Definition 12 we obtain  (where
(where  denotes the weight of the solution), then
denotes the weight of the solution), then
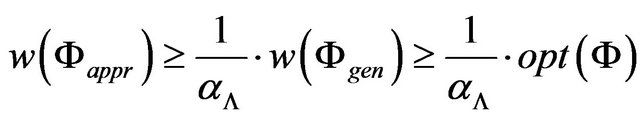
and, by definition 5, we received an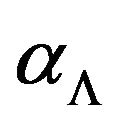 —approximation algorithm.
—approximation algorithm.
Note, that the calculation (estimation) of integrality gaps of relaxations is in itself a difficult research task. For many problems it is still unsolvable. However, even without knowing the specific values of the integrality gaps of relaxations, one can argue about the existence of threshold (optimal) approximation algorithms for optimization problems (which will be noted later).
To illustrate, consider the Max Cut problem. Let 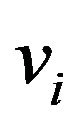 -a unit vector in Euclidean space, which corresponds to a Boolean variable
-a unit vector in Euclidean space, which corresponds to a Boolean variable . We have the following SDP relaxation of Max Cut:
. We have the following SDP relaxation of Max Cut:
 where
where  the scalar product
the scalar product 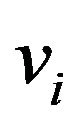 and
and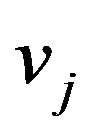 . We define an integrality gap
. We define an integrality gap  of this relaxation:
of this relaxation:
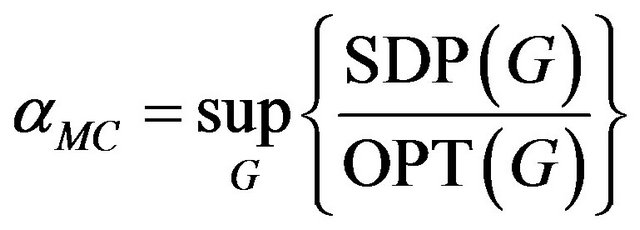 , where
, where —the optimum of relaxation.
—the optimum of relaxation.
Theorem 12 [5].
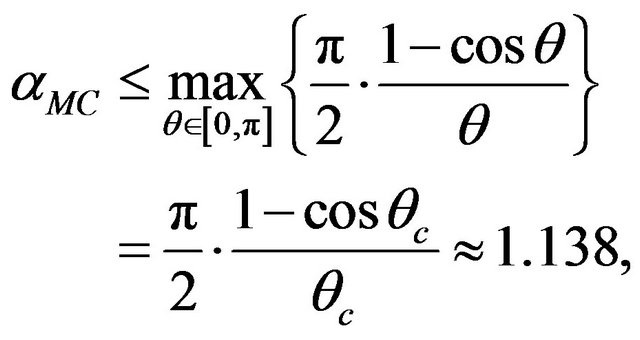
where 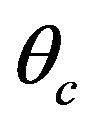 is the “critical angle” at which the maximum is attained.
is the “critical angle” at which the maximum is attained.
Goemans and Williamson give random rounding algorithm (now known as the random hyperplane rounding algorithm) that for any solution of SDP relaxation find a cut in a graph with a value no less, than 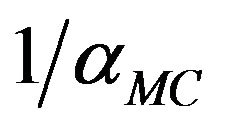 times once expected SDP solution (note that
times once expected SDP solution (note that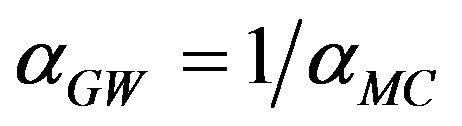 , where
, where 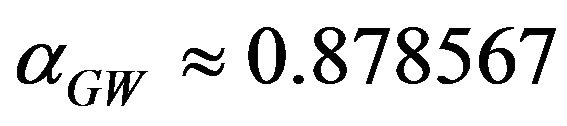 a known Goemans-Williamson constant). Thus, the approximation algorithm not only finds an approximate optimum value, but also gives an approximate cut. This feature is characteristic of most algorithms based on SDP and LP (linear) relaxation.
a known Goemans-Williamson constant). Thus, the approximation algorithm not only finds an approximate optimum value, but also gives an approximate cut. This feature is characteristic of most algorithms based on SDP and LP (linear) relaxation.
Theorem 13 [10]. For any 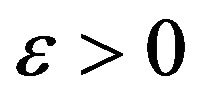 there exists a graph
there exists a graph  such, that
such, that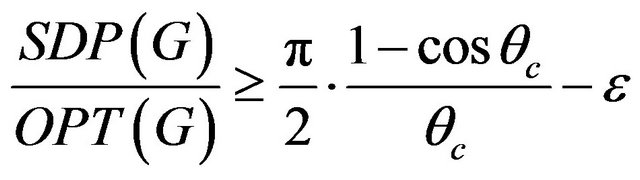 . Thus
. Thus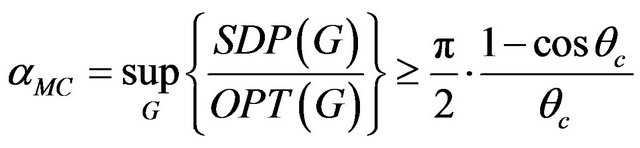 , combining with Theorem 12, we obtain
, combining with Theorem 12, we obtain .
.
A lower bound for integrality gap is a graph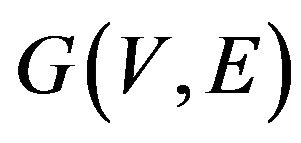 , where the bound is attained. Corresponding instance of the problem is Integrality Gap Instance (IGI).
, where the bound is attained. Corresponding instance of the problem is Integrality Gap Instance (IGI).
So, for Max Cut managed to find the exact value of the integrality gap of SDP relaxation.
6. Unique Games Conjecture and Reoptimization
Unique Games Conjecture (UGC) was introduced by Khot [11] as a possible way to obtain new results on strong innapproximability. We formulate the UGC in terms of Unique Game Problem.
Definition 13. A Unique Game Problem is a constraint satisfaction problem, which is defined as follows. There is a directed graph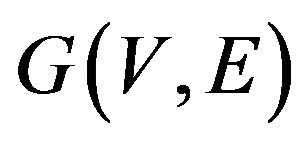 , whose vertices represent variables and edges-constraints. The purpose is to assigning a label to each vertex from the set [n]. Constraint on the edge
, whose vertices represent variables and edges-constraints. The purpose is to assigning a label to each vertex from the set [n]. Constraint on the edge 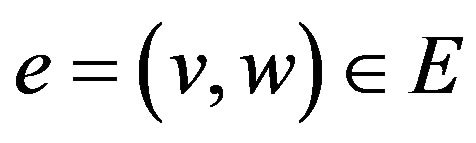 is described by a bijection
is described by a bijection . Labeling the vertices
. Labeling the vertices 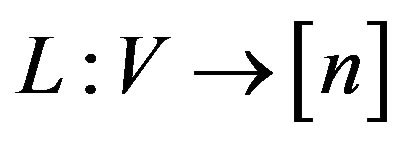 satisfies (accepts) a constraint on the edge
satisfies (accepts) a constraint on the edge , iff
, iff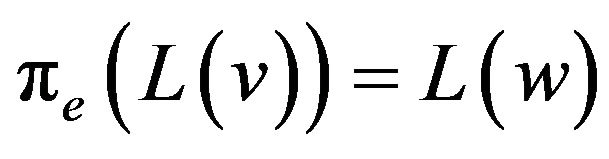 . Let
. Let 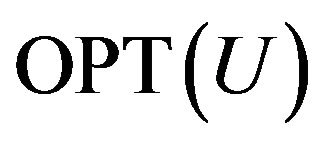 denote the maximum part of constraints, which may be satisfied by any labeling:
denote the maximum part of constraints, which may be satisfied by any labeling:
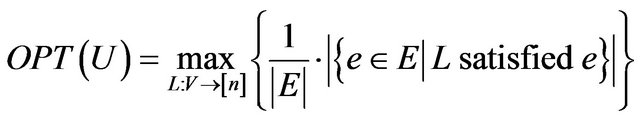 .
.
Unique Games Conjecture (UGC) [11]. For any 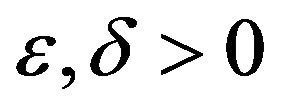 there exists a constant
there exists a constant 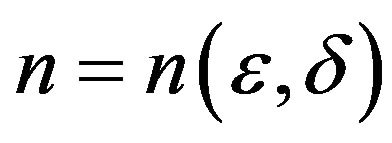 such that, for this instance of unique game problem
such that, for this instance of unique game problem  is NP-hard to distinguish between two cases:
is NP-hard to distinguish between two cases:
• YES case: 
• NO case: .
.
A typical technique to obtain the results on innapproximability can be described as follows. The source is the following argument. Suppose Pan arbitrary optimization (to be specific to a maximum of) problem. Under the  version of the problem P (notation
version of the problem P (notation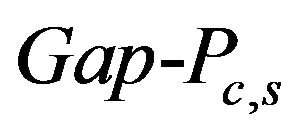 ) we understand the problem, for which either
) we understand the problem, for which either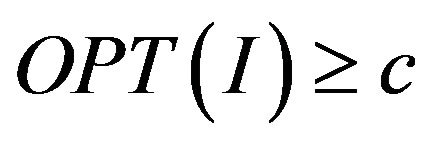 , or
, or 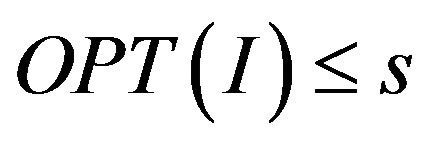 for any instance
for any instance . Consider the NP-complete problem 3-Sat (3-Satisfiability). Arbitrary 3-Sat formula (E3-CNF formula) is the conjunction of a set of clauses, where each clause is the disjunction of three Boolean variables or their negations. The goal is to determine the assignment of a Boolean variable, such that the formula is logically true (acceptable). Suppose that there exists a polynomial reducibility of
. Consider the NP-complete problem 3-Sat (3-Satisfiability). Arbitrary 3-Sat formula (E3-CNF formula) is the conjunction of a set of clauses, where each clause is the disjunction of three Boolean variables or their negations. The goal is to determine the assignment of a Boolean variable, such that the formula is logically true (acceptable). Suppose that there exists a polynomial reducibility of  to
to  for some
for some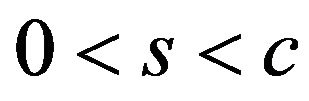 , that is, reducibility, which displays a 3-Sat formula
, that is, reducibility, which displays a 3-Sat formula 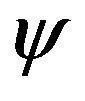 to an instance I of the problem P such that:
to an instance I of the problem P such that:
(YES case): If  has an assignment, that makes it acceptable, then
has an assignment, that makes it acceptable, then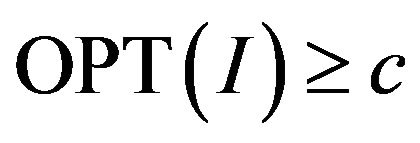 ;
;
(NO case): If 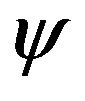 has no assignments, that make it acceptable, then
has no assignments, that make it acceptable, then .
.
This reducibility implies that if there exists a polynomial algorithm with approximation ratio strictly less than
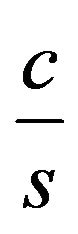 for the problem P, then it is possible to efficiently determine whether a 3SAT formula is satisfiable, and hence
for the problem P, then it is possible to efficiently determine whether a 3SAT formula is satisfiable, and hence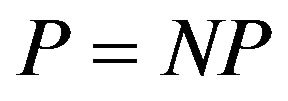 . Thus, under the standard assumption, that
. Thus, under the standard assumption, that 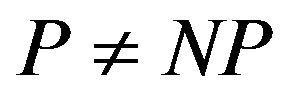 this reducibility—the source of results on inapproximability of the problem P. We start from the PCP (Prababilistically Checkable Proof) Theorem [1] in one form or another for some NP-complete language (for example, 3-Sat). We construct a reducibility to the problem (language), which inapproximability to install (for example,
this reducibility—the source of results on inapproximability of the problem P. We start from the PCP (Prababilistically Checkable Proof) Theorem [1] in one form or another for some NP-complete language (for example, 3-Sat). We construct a reducibility to the problem (language), which inapproximability to install (for example,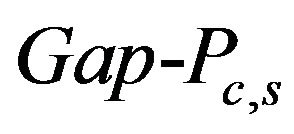 ). Constructed PCP verifier for the problem
). Constructed PCP verifier for the problem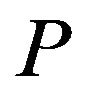 , which is in the form of a test (dictatorship) to the Boolean function that is responsible to P. Using the elements and some of the results of Fourier analysis of Boolean functions, estimated completeness c of the verifier (the lower bound of the probability of accepting the test, that a Boolean function-dictatorship or YES case) and soundness s of verifier (the upper bound of the probability of not accepting the test, that Boolean function is far from dictatorship or NO case). It follows that P NPhard to approximate with a ratio smaller than c/s. This is a common inapproximability.
, which is in the form of a test (dictatorship) to the Boolean function that is responsible to P. Using the elements and some of the results of Fourier analysis of Boolean functions, estimated completeness c of the verifier (the lower bound of the probability of accepting the test, that a Boolean function-dictatorship or YES case) and soundness s of verifier (the upper bound of the probability of not accepting the test, that Boolean function is far from dictatorship or NO case). It follows that P NPhard to approximate with a ratio smaller than c/s. This is a common inapproximability.
If not proceed from the PCP theorem, but from the unique game conjecture (UGC) in the above reducibility, we receive inapproximability based on UGC or conditional inapproximability.
Let  the solution of SDP relaxation of instance
the solution of SDP relaxation of instance  of GCSP problem
of GCSP problem . In [30] to get closer to the optimal solution proposed scheme of rounding (Rounding Scheme, RS). In this paper, studies are being conducted in the language of integrality gap curve and unique games hardness curve. We describe the result with an integrality gap coefficient
. In [30] to get closer to the optimal solution proposed scheme of rounding (Rounding Scheme, RS). In this paper, studies are being conducted in the language of integrality gap curve and unique games hardness curve. We describe the result with an integrality gap coefficient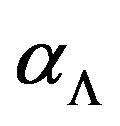 . We will assume that
. We will assume that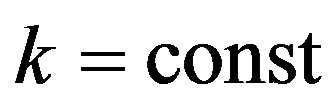 .
.
Theorem 14 [30]. Assuming the UGC, for any GCSP problem  and any
and any 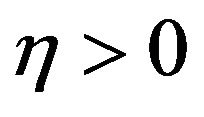 it is NP-hard to approximate
it is NP-hard to approximate  with approximation ratio
with approximation ratio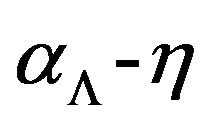 .
.
Using Theorems 11 and 14, we get a result.
Corollary 2 [30]. Assuming the UGC for any GCSP and any 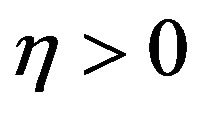 rounding scheme RS determines the approximation ratio in the range
rounding scheme RS determines the approximation ratio in the range  of optimal polynomial algorithm, i.e. for any GCSP problem
of optimal polynomial algorithm, i.e. for any GCSP problem  there exists a polynomial threshold (optimal)
there exists a polynomial threshold (optimal) 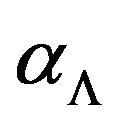 -approximation algorithm.
-approximation algorithm.
Consider an arbitrary unweighted Max-EkCSP-P problem Z (definition 1). Let  the set of variables, E—the set of constraints. The constraint
the set of variables, E—the set of constraints. The constraint  is denoted as
is denoted as 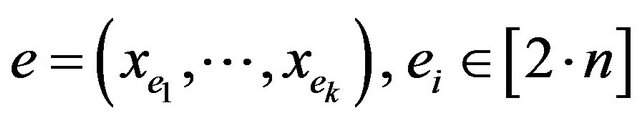 with special order on the variables (relative to V). Assignment is a map
with special order on the variables (relative to V). Assignment is a map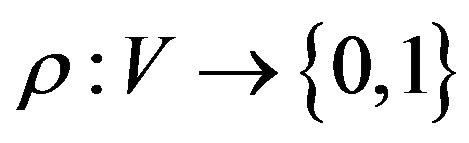 , assignment
, assignment 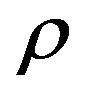 accepts constraint e, if.
accepts constraint e, if.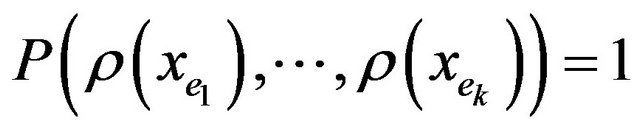 . We denote by
. We denote by 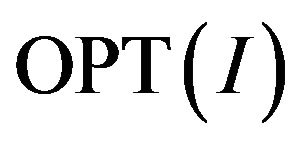 the maximum part of constraints accepted by an arbitrary assigning for instance
the maximum part of constraints accepted by an arbitrary assigning for instance 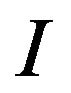 of the problem
of the problem . Let
. Let 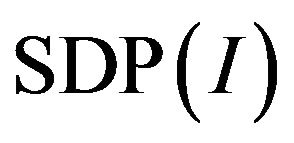 denote the optimum SDP relaxation of Raghavendra [30], we define an integrality gap
denote the optimum SDP relaxation of Raghavendra [30], we define an integrality gap
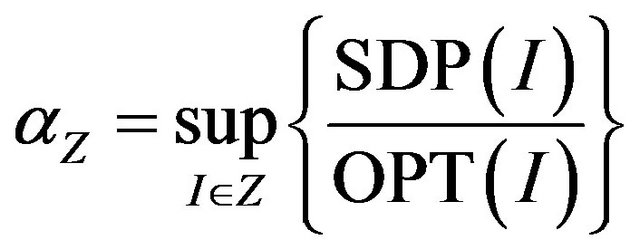 . In [31] showed how to round a solution and find assignment with the approximation ratio close to
. In [31] showed how to round a solution and find assignment with the approximation ratio close to 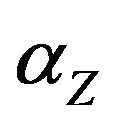 (theorem 11). Let
(theorem 11). Let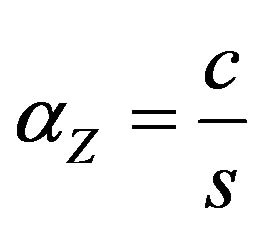 , then the result of Raghavendra [30] in this case can be presented as a theorem.
, then the result of Raghavendra [30] in this case can be presented as a theorem.
Theorem 15 [14]. Suppose there is an instance 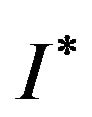 of Max-EkCSP-P problem Z such, that
of Max-EkCSP-P problem Z such, that  and
and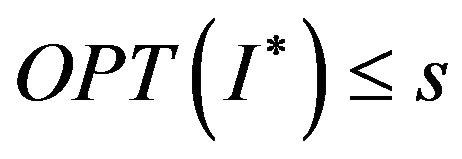 . Then for any
. Then for any 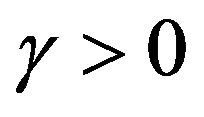 there exist
there exist 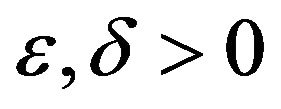 and polynomial reducibility from the instance of unique game problem to the instance I of problem Z such, that:
and polynomial reducibility from the instance of unique game problem to the instance I of problem Z such, that:
• (YES case): If , then
, then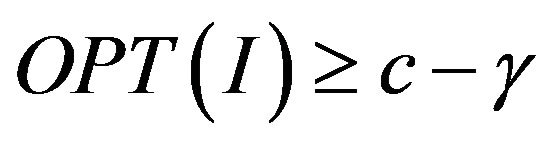 ;
;
• (NO case): If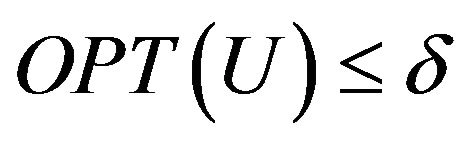 , then
, then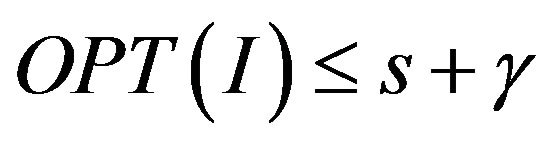 .
.
In particular, assuming the UGC, it is NP-hard to approximate Z with ratio strictly less than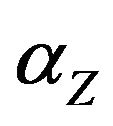 .
.
Corollary 3. Assuming the UGC, for every MaxEkCSP-P problem Z there exists a polynomial threshold (optimal)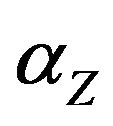 —approximation algorithm.
—approximation algorithm.
The proof follows from theorems 11, 14 and 15.
Note that theorem 15 converts the integrality gap into inapproximability gap. Roughly speaking the idea is to use integrality gap instance (IGI) of SDP relaxation for the construction of a dictatorship test and combining it with an instance of unique game problem. The value of the result of Raghavendra is that even without knowing explicitly the exact value of integrality gap, you can set an optimality of corresponding polynomial approximation algorithm (using IGI). For example, in [32] showed that although for Grothendieck’s Problem integrality gap  (the famous Grothendieck’s constant) are still unknown, based on the UGC it is NP-hard to approximate the problem of Grothendieck with an arbitrary ratio less than
(the famous Grothendieck’s constant) are still unknown, based on the UGC it is NP-hard to approximate the problem of Grothendieck with an arbitrary ratio less than 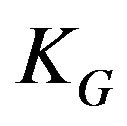 (
( -approximation algorithm is optimal). Constant
-approximation algorithm is optimal). Constant 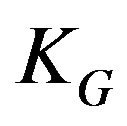 can be calculated with some error
can be calculated with some error 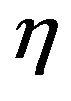 in the time dependent only on
in the time dependent only on .
.
Theorem 16. Suppose that a unique game conjecture (UGC) is hold. Let Z is any unweighted Max-EkCSP-P problem with integrality gap 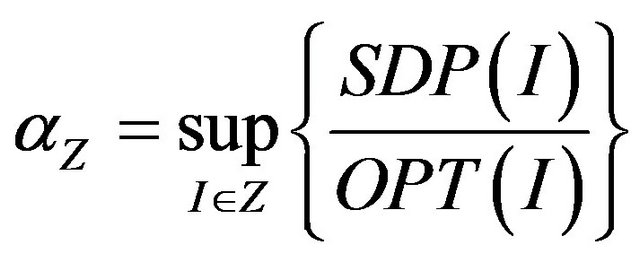 and k = const, then for the problem Ins-Max-EkCSP-P (reoptimization of Max-EkCSP-P) there exists a polynomial threshold (optimal)
and k = const, then for the problem Ins-Max-EkCSP-P (reoptimization of Max-EkCSP-P) there exists a polynomial threshold (optimal)  -approximation algorithmwhere
-approximation algorithmwhere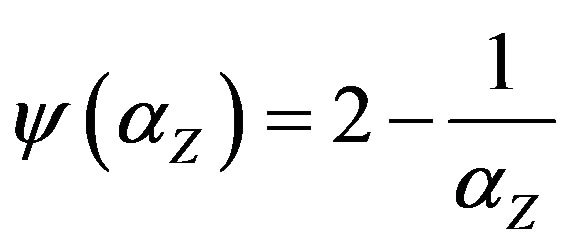 .
.
The proof follows by applying corollary 3 to theorem 10.
Example 2. Consider the problem Max Cut. In our notation, this is a problem Max-E2CSP-XOR, and reoptimization version—the problem Ins-Max-E2CSP-XOR, obtained by adding an arbitrary edge to Max Cut. By theorems 12 and 13 integrality gap of SDP relaxation of problem Max Cut is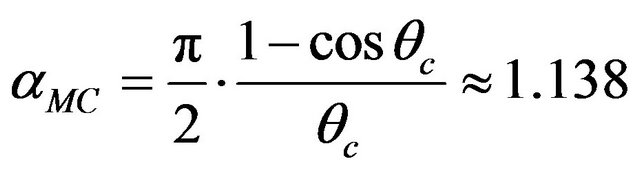 . Then from theorem 16 follows proposition 2.
. Then from theorem 16 follows proposition 2.
Proposition 2. Suppose that a unique games conjecture (UGC) is hold. Then for the problem Ins-Max-E2CSPXOR (reoptimization of Max Cut) there exists a polynomial threshold (optimal) 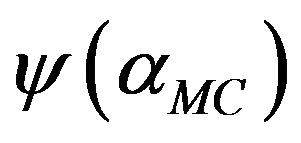 -approximation algorithm, where
-approximation algorithm, where .
.
7. Conclusions
To solve the problem Ins-Max-EkCSP-P (reoptimization of Max-EkCSP-P) with approximation resistant predicates there exists a polynomial threshold (optimal)  - approximation algorithm, where
- approximation algorithm, where
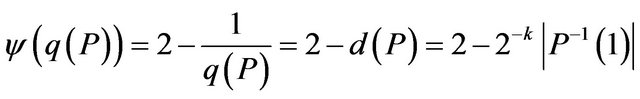
(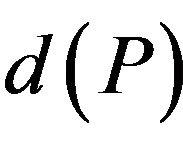 —the threshold “random” approximation ratio of P). Note that the property of the approximation resistance may be stronger than the property of NP-completeness of corresponding decision problem. Since in this case the effective computation can not gives anything more than a random assignment of truth values to variables.
—the threshold “random” approximation ratio of P). Note that the property of the approximation resistance may be stronger than the property of NP-completeness of corresponding decision problem. Since in this case the effective computation can not gives anything more than a random assignment of truth values to variables.
Using the results of [30,31] it can be argued, that if the unique games conjecture (UGC) is hold, then there exists a polynomial threshold (optimal)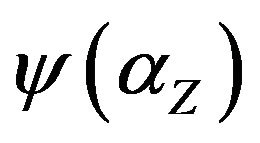 —approximation algorithm to solve the problem Ins-Max-EkCSP-P (reoptimization of Max-EkCSP-P), where
—approximation algorithm to solve the problem Ins-Max-EkCSP-P (reoptimization of Max-EkCSP-P), where —the integrality gap of SDP relaxation of Max-EkCSP-P problem.
—the integrality gap of SDP relaxation of Max-EkCSP-P problem.
The results of this work greatly depend on the truth of the unique game conjecture (UGC). Note that if Uthe unique games problem, the UGC can be formulated as follows: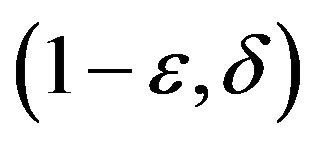 —gap version of the unique games problem
—gap version of the unique games problem  is NP-hard problem. Along with the problems of complexity class relationships with respect to inclusion (for example,
is NP-hard problem. Along with the problems of complexity class relationships with respect to inclusion (for example, ) it is one of the major open problems of modern theoretical computer science. Even if the UGC is false, you may find that
) it is one of the major open problems of modern theoretical computer science. Even if the UGC is false, you may find that 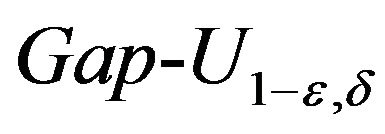 is hard in the sense of undecidability in polynomial time, and such (a weak) hardness can be applied to all problems, where the hardness show up on the basis of UGC.
is hard in the sense of undecidability in polynomial time, and such (a weak) hardness can be applied to all problems, where the hardness show up on the basis of UGC.
REFERENCES
- S. Arora, C. Lund, R. Motwani, M. Sudan and M. Szegedy, “Proof Verification and Intractability of Approximation Problems,” Journal of the ACM, Vol. 45, No. 3, 1998, pp. 501-555. doi:10.1145/278298.278306
- O. Goldreich, S. Goldwasser and D. Ron, “Property Testing and Its Connection to Learning and Approximation Abstract,” Journal of the ACM, Vol. 45, No. 4, 1998, pp. 653-750. doi:10.1145/285055.285060
- O. Goldreich and M. Sudan, “Locally Testable Codes and PCPs of Almost-Linear Length,” Journal of the ACM, Vol. 53, No. 4, 2006, pp. 558-655. doi:10.1145/1162349.1162351
- M. X. Goemans and D. P. Williamson, “Improved Approximation Algorithms for Maximum Cut and Satisfiability Problems Using Semidefinite Programming,” Journal of the ACM, Vol. 42, No. 6, 1995, pp. 1115-1145. doi:10.1145/227683.227684
- M. X. Goemans and D. P. Williamson, “0.878 Approximation Algorithms for MAX-CUT and MAX-2SAT,” In: Proceedings of the 26th Annual ACM Symposium on the Theory of Computing (STOC), ACM, Montreal, 1994, pp. 422-431.
- J. Hastad, “Some Optimal Inapproximability Results,” Journal of the ACM, Vol. 48, No. 4, 2001, pp. 798-859. doi:10.1145/502090.502098
- J. Hastad, “Complexity Theory, Proofs and Approximation,” European Congress of Mathematics, Stockholm, 2005.
- J. Hastad, “On the Efficient Approximability of Constraint Satisfaction Problems,” In: A. Hilton and J. Talbot, Eds., Surveys in Combinatorics 2007, London Mathematical Society Lecture Notes Series (No. 346), Cambridge University Press, Cambridge, 2007, pp. 201-222. doi:10.1017/CBO9780511666209.008
- U. Feige, “A Threshold of lnn for Approximating Set Cover,” Journal of the ACM, Vol. 45, No. 4, 1998, pp. 634-652. doi:10.1145/285055.285059
- U. Feige and G. Schechtman, “On the Integrality Ratio of Semidefinite Relaxations of MAX CUT,” In: Proceedings of the 23rd Annual ACM Symposium on Theory of Computing, ACM, New York, 2001, pp. 433-442.
- S. Khot, “On the Power of Unique 2-Prover 1-Round Games,” In: Proceedings of the 34th Annual ACM Symposium on Theory of Computing, ACM, New York, 2002, pp. 767-775.
- S. Khot and O. Regev, “Vertex Cover Might be Hard to Approximate to within 2 − ε,” Journal of Computer and System Sciences, Vol. 74, No. 3, 2008, pp. 335-349. doi:10.1016/j.jcss.2007.06.019
- S. Khot, G. Klendler, E. Mossel and R. O’Donnell, “Optimal Inapproximability Results for Max-Cut and Other 2-Variable CSPs?” Proceedings of 45th Annual IEEE Symposium on Foundations of Computer Science (FOCS), Rome, 17-19 October 2004, pp. 146-154. doi:10.1109/FOCS.2004.49
- S. Khot, “On the Unique Games Conjecture,” Proceedings of the 25th Annual IEEE Conference on Computational Complexity, Cambridge, 9-12 June 2010, pp. 99- 121.
- A. Samorodnitsky and L. Trevisan, “Gowers Uniformity, Influence of Variables, and PCPs,” In: Proceedings of the 38th Annual ACM Symposium on Theory of Computing, ACM, New York, 2006, pp. 11-20.
- S. Chawla, R. Krauhgamer, R. Kumar, Y. Rabani and D. Sivakumar, “On the Hardness of Approximating Multicut and Sparsest-Cut,” Proceedings of the 20th Annual IEEE Conference on Computational Complexity, San Jose, 11- 15 June 2005, pp. 144-153. doi:10.1109/CCC.2005.20
- P. Austrin, “Balanced Max 2-Sat Might Not be the Hardest,” Proceedings of the 39th Annual ACM Symposium on Theory of Computing, San Diego, 11-13 June 2007, pp. 189-197.
- P. Austrin, “Towards Sharp Inapproximability for Any 2- CSP,” In: Proceedings of the 48th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society, Washington DC, 2007, pp. 307-317.
- M. Lewin, D. Livnat and U. Zwick, “Improved Rounding Techniques for the MAX 2-SAT and MAX DI-CUT Problems,” Proceedings of 9th International Integer Programming and Combinatorial Optimization Conference (IPCO), Lecture Notes in Computer Science, Vol. 2337, Cambridge, 27-29 May 2002, pp. 67-82. doi:10.1007/3-540-47867-1_6
- G. Ausiello, B. Escoffier, J. Monnot and V. Th. Paschos, “Reoptimization of Minimum and Maximum Traveling Salesman’s Tours,” Journal of Discrete Algorithms, Vol. 7, No. 4, 2009, pp. 453-463. doi:10.1007/11785293_20
- H. J. Bockenhauer, L. Forlizzi, J. Hromkovic, et al., “On the Approximability of TSP on Local Modifications of Optimal Solved Instances,” Algorithmic Operations Research, Vol. 2, No. 2, 2007, pp. 83-93.
- H.-J. Bockenhauer, J. Hromkovic, T. Momke and P. Widmayer, “On the Hardness of Reoptimization,” In: V. Geffert et al., Eds., SOFSEM, Lecture Notes in Computer Science, Vol. 4910, Springer, Berlin, 2008, pp. 50-65.
- B. Escoffier, M. Milanic and V. Th. Paschos, “Simple and fast Reoptimizations for the Steiner Tree Problem,” Algorithmic Operations Research, Vol. 4, No. 2, 2009, pp. 86- 94.
- C. Archetti, L. Bertazzi and M. G. Speranza, “Reoptimizing the Travelling Salesman Problem,” Networks, Vol. 42, No. 3, 2003, pp. 154-159. doi:10.1002/net.10091
- G. Ausiello, V. Bonifacci and B. Escoffier, “Complexity and Approximation in Reoptimization,” In: S. B. Cooper and A. Sorbi, Eds., Computability in Context: Computation and Logic in the Real World, Imperial College Press, London, 2011, pp. 101-130.
- V. A. Mikhailyuk, “Reoptimization of Set Covering Problems,” Cybernetics and Systems Analysis, Vol. 46, No. 6, 2010, pp. 879-883. doi:10.1007/s10559-010-9269-z
- V. A. Mikhailyuk, “General Approach to Estimating the Complexity of Postoptimality Analysis for Discrete Optimization Problems,” Cybernetics and Systems Analysis, Vol. 46, No. 2, 2010, pp. 290-295. doi:10.1007/s10559-010-9206-1
- G. Hast, “Beating a Random Assignment,” Doctoral Thesis, Royal Institute of Technology, Stockholm, 2005.
- U. Zwick, “Approximation Algorithms for Constraint Satisfaction Problems Involving at Most Three Variables per Constraint,” In: Proceedings of the 9th Annual ACMSIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, 1998, pp. 551-560.
- P. Raghavendra, “Optimal Algorithms and Inapproximability Results for Every CSP?” In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, ACM, New York, 2008, pp. 245-254.
- P. Raghavendra and D. Steurer, “How to Round Any CSP?” In: Proceedings of the 50th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society, Washington DC, 2009, pp. 586-594.
- P. Raghavendra and D. Steurer, “Towards Computing the Grothendieck Constant,” Proceedings of the 20th Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, 2009, pp. 525-534.

