Journal of Biophysical Chemistry
Vol.1 No.2(2010), Article ID:2554,10 pages DOI:10.4236/jbpc.2010.12011
Curvature-driven lipid sorting: coarse-grained dynamics simulations of a membrane mimicking a hemifusion intermediate
Department of Laboratory Medicine, Teikyo University School of Medical Technology, Tokyo, Japan; *Corresponding Author: kazunet@med.teikyo-u.ac.jp
Received 26 May 2010; revised 29 June 2010; accepted 5 July 2010.
Keywords: Membrane Fusion; Raft; Membrane Domain; Cholesterol; Lipid Phase Separation
ABSTRACT
How membrane curvature influences lipid distribution is under intensive research. In this short report, after a brief review of recent studies, the results of our coarse-grained (CG) molecular dynamics simulations of membranes with “hemifused ribbons” geometry are discussed. When membranes of a binary mixture of (dipalmitoyl-phosphatidylcholine (DPPC) / diol- eoyl-phosphatidylethanolamine (DOPE) were used, DOPE accumulated in the negatively curved region of the monolayer that formed as the proximal monolayers fused (i.e., cis leaflets). However, the enrichment was dependent on the presence of tethering molecules which kept the curvature high (the curvature radius of ~1 nm), placing the cis monolayers ~2-2.5 nm from each other. Simulations in which DOPE was replaced with dioleoyl-phosphatidylcholine (DOPC) sh- owed an insignificant degree of DOPC accumulation, suggesting the importance of lateral interaction among DOPE molecules for the curvature sorting. The above composition was not close to a demixing point and our radial distribution function analysis suggested that the DOPE accumulation was not assisted by the lipid phase separation which has been shown to promote curvature-driven lipid sorting. Relevance of curvature-driven lipid sorting to biological membrane fusion is discussed.
1. INTRODUCTION
Inhomogeneous distribution of lipids within a lipid bilayer has been implicated in many biological activities. Lipid composition is different among organelles and membranous structures, implying the presence of mechanisms for lipid sorting (e.g., [1-3]). Several studies utilizing lipid-like dyes provide direct evidence for nonhomogenous intracellular lipid distribution. Mukherjee et al. [4] analyzed intracelluar distribution of three different DiI (dialkylindocarbocyanine) molecules that have the same headgroup but different acyl chains (in length or unsaturation) and showed that these display remarkably different sorting in cells. In several studies, the regions in which lipid inhomogeneity was observed often corresponded to highly curved membrane regions, suggesting that lipids are sorted primarily by curvature of the membrane. For example, when a membrane buds off during secretory and endocytic vesicle formation, some lipids are incorporated into vesicles while others are excluded [5]. In a study of Tetrahymena membrane [6], enrichment in cone-shaped 2-aminoethylphospholipids was shown in pore-containing membrane regions during mating when the regions become highly negatively curved. One possible mechanism for the inhomogeneous distribution is curvature-driven lipid sorting, where the lipids with intrinsic (spontaneous) curvature (due to the imbalanced size of the polar headgroups relative to the hydrophobic tail) are sorted laterally in the membrane such that the spontaneous curvature of each lipid fits better to the local membrane curvature. If the curvaturesorting works, cone-shaped lipid molecules like phosphatidylethanolamine (PE) and phosphatidylglycerol (PG) accumulate in the negatively curved region. In general, theoretical studies have suggested the possibility of lateral segregation of lipids based on the local curvature. On the other hand, the lipid accumulation at curved membrane regions is often associated with accumulation of specific proteins in the cellular environment. For example, the yeast vertex microdomain, which occurs around the periphery of the two apposed membranes on vacuole docking, is enriched in Rab GTPase and the fusion protein as well as ergosterol, diacylglycerol and 3- and 4-phosphoinositides (e.g., [7]). This implies the difficulty in evaluating the relative importance of curvature-sorting and protein-mediated sorting of molecules in a physiological environment.
After Helfrich formulated curvature energy [8], theoretical frameworks for lateral segregation based on the lipid spontaneous curvature were proposed [9-11]. Markin [9] considered the composition dependence of spontaneous curvature and the bending stiffness of membranes. Kozlov and Helfrich [10] developed a framework for thermodynamic analyses of lipid distribution, bending stiffness and curvature. Curvature-induced phase segregation was also analyzed in a phenomenological continuum theory [11]. Curvature-driven lateral segregation of lipid was also computed in more recent works such as [12,13].
Experimental studies have significantly advanced the understanding of the curvature sorting of lipids. Using giant unilamellar vesicles (GUVs) formed from a ternary mixture of sphingomyelin, dioleoylphosphatidylcholine (DOPC) and cholesterol, in which Lo (liquid-ordered) and Ld (liquid-disordered) phases coexist, Baumgart et al [14] showed a correlation between domain composition and local membrane curvature. (At temperatures where single component PC bilayers would be in the fluid Lα phase, cholesterol gives rise to an intermediate degree of organization in PC membranes known as the Lo phase (e.g., [15]). Using microfabricated surfaces, Parthasarathy et al. [16] showed that the Lo domains formed in DOPC/DPPC/cholesterol membranes are preferentially localized at regions of low curvature. Several recent studies adopted a well-studied approach; tubepulling from vesicles. With this method, very thin membrane tubes with a diameter of several tens of nanometers are formed by pulling a small portion of the membrane from GUVs (e.g., [17]). When applied to vesicles prepared from sphingomyelin, PC and cholesterol, this method showed that the tubes are essentially composed of membranes in the Ld phase enriched in DOPC, whereas GM1, which is known to segregate into the Lo phase, was excluded from tubes [18]. Lipid sorting by membrane curvature in these studies was therefore associated with phase separation (Lo and Ld), which is a collective behavior of lipids.
In both experiments and simulations, however, curvature sorting of lipids based on spontaneous curvature (of individual lipid molecule) has exhibited only a weak effect, not leading to strong segregation of lipids. A fluorescent-labeled lipid was used in the tube-pulling system [19], showing that spontaneous curvature is not a strong factor influencing partition of the fluorescent lipid. Intriguingly, in the same system, the Cholera toxin subunit B, a protein that interacts with several lipid molecules, showed a significant effect on curvature sorting, suggesting the importance of a collective behavior of lipids. Using fluorescence-labeled lipids and quenchers, the distribution of the lipids between the outer and inner monolayers of vesicles of various sizes was compared [20]. The difference in lipid density between the monolayers was present but small, indicating that the curvature sorting is weak [20]. In a simulation study using a CG representation of lipid (three beads for one lipid) [21], no significant sorting by curvature was observed. Theoretical consideration [13] has also suggested the weak effect of spontaneous curvature of individual lipids on curvature sorting.
Collectively, these studies have led to the consensus that lipid segregation is not significant when lipid sorting is driven only by spontaneous curvature of individual lipids. In most of the experimental settings, not only the curvature, but also the propensity toward phase separation is important for curvature sorting. That is, for curvature to induce strong lipid sorting, the lipid composition must be close to the demixing point. Thus, the enthalpy related to curvature fitness is not likely to be enough to overcome the entropic penalty that prefers good mixing.
One of the current models for membrane fusion proposes formation of a stalk (Figures 1(a) and (b)) (i.e., an hourglass-shaped structure) and subsequently hemifusion intermediates (Figures 1(c) and (d)), leading to fusion pore formation (Figure 1(e)) [22-24]. The hemifusion intermediate is a state where contacting (proximal) monolayers are fused but the distal monolayers stay intact and therefore there is no content mixing. The model suggests that, for membrane fusion, properties of the monolayer are also important. The intrinsic curvature of lipid monolayers as well as bilayers has been studied [25,26]. However, the potential usefulness of their data has not been fully explored possibly because it is difficult to study biologically relevant “monolayers”. With interest in hemifusion, we applied molecular dynamics simulation to a system mimicking a hemifusion intermediate. In this system, the curvature of a monolayer could be higher than physiologically relevant curvatures formed by bilayers. However, note that our system (i.e., hemifused ribbon or ‘l’-system) has not yet been applied to membranes containing cholesterol. Therefore, more analyses are necessary in order to consider the behavior of physiological membranes in fusion intermediates.
2. SIMULATION DETAILS—HEMIFUSED MEMBRANE SYSTEM
In the present study, CG simulations of membranes con-
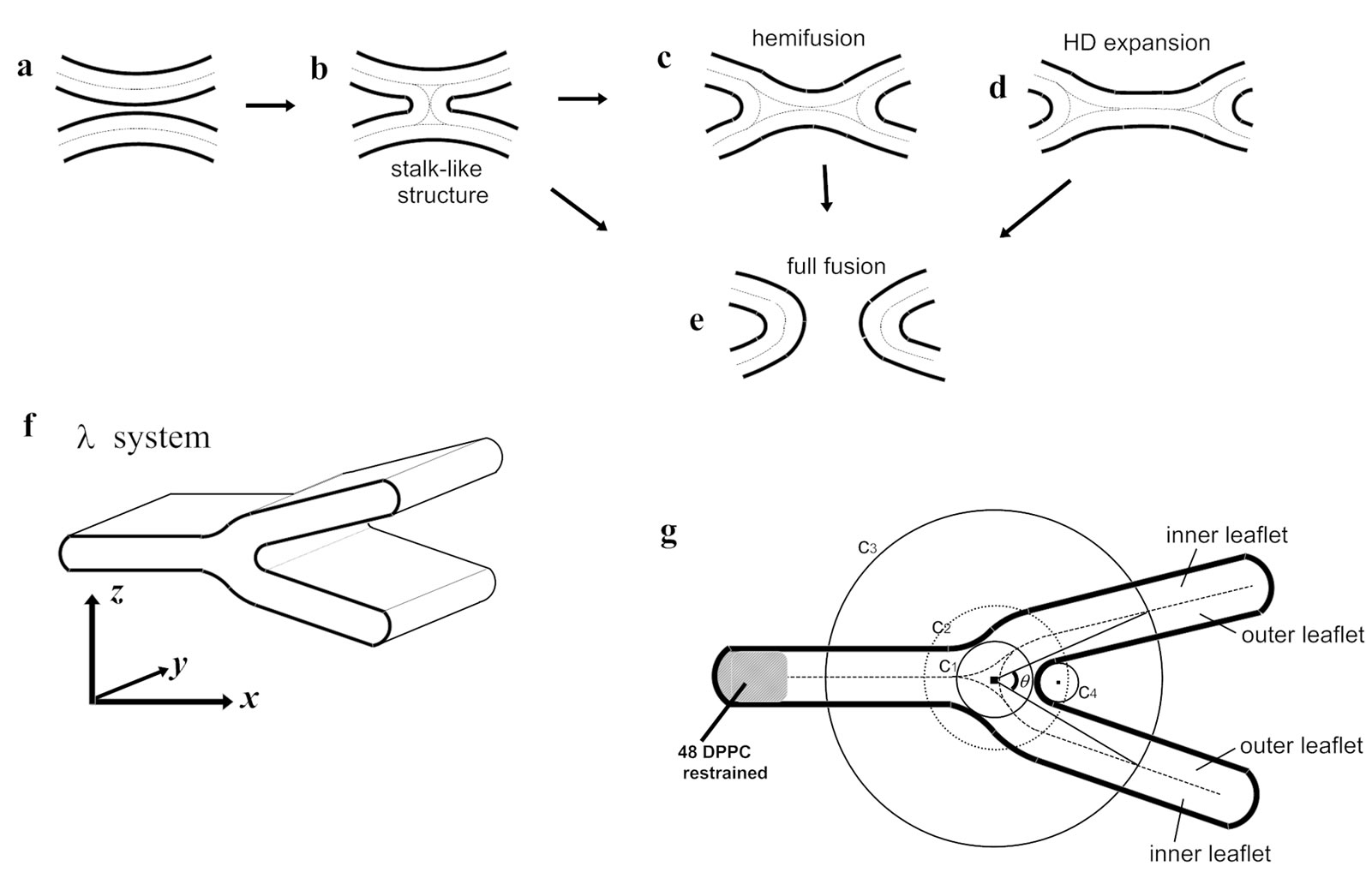
Figure 1.The stalk-hemifusion model (a-e) and the l-system (f,g). In the stalk-hemifusion model [24], two apposed bilayers (a) initially form a stalk (b) and subsequently leads to hemifusion (c), which undergoes the hemifusion rupture (d) and finally ends with the full fusion (e). The arrow from (b) to (e) indicates a direct transition from the stalk-like structure to fusion pore formation, which has been observed in the CG-simulation studies [27,28]. (f) The l-system. The periodic boundary condition allows the l-shaped (hemifused) bilayer ribbons to have an infinite length in the y-direction. For clarity, water is hidden. The definition of the x,y and z directions is also shown. (g) The definition of the curvature strength. Shown are the angle between the two outer leaflets and the zone boundaries. To determine them, first, C1, the circle that has the longest radius located inside the phosphorus atoms of any lipid monolayers, is found. Two circles C2 and C3, which have the same center as that of C1 are drawn (in this study, the radius of C2 and C3 was set at 4 nm and 10 nm, respectively). C2 defines the curved region of the outer leaflet. The planar regions of the outer leaflet are defined as the regions located between the two circles whose sizes are 8nm and 12nm (radius) and the center is the same as C1. The com of each lipid molecule was used for reference. The points of intersection between C3 and the midplanes are used to define the angle q. C4, the circle that best fits the phosphorus atoms belonging to the outer leaflet and located inside of C2, is determined. The radius of C4 represents the curvature of the outer leaflet.
taining bend(s) were carried out. We mainly used “l-shaped” membranes (Figure 1(f)). This structure consists of two bilayer ribbons that are partly fused such that the cross section of the ribbon has a l-like shape (Figures 1(f) and (g)). This structure has 2D-curvature; i.e., the membranes projected onto the xz-plane are curved whereas they are basically flat along the y-axis (Figure 1(f)). For l membranes, the “outer” leaflet refers to the monolayer which is highly negatively curved in Figure 1(g), mimicking the fused cis monolayers. For the outer leaflet, the planar and the curved regions are defined as described in the legend for Figure 1. CG simulations were performed using the MARTINI forcefield (version 2.0) as in Marrink et al [29]. For example, for DPPC, the choline is represented as Qo particle and the phosphate group as Qa, whereas the glycerol ester, which has intermediate hydrophilicity, is represented by two Na particles. (Figure 2(a)). Each of the lipid tails are modeled by four C1 particles. For DOPE, the topology provided by Marrink et al. (http://md.chem.rug.nl/~marrink/coarse-grain.html) was used (Figure 2(b)). l membranes consisting of 350 DPPC and 184 (or DOPC molecules) were used making the nominal DOPE (or DOPC) fraction was 34.5%, but the higher density of DPPC at the membrane edges augmented the effective fraction of DOPC (DOPC) in the planar and curved regions. The leftmost part of the membrane was capped with additional 48 DPPC molecules (Figure 1(g)), the GL1 particles of which were harmonically restrained (with the coefficient of 100 kJ/nm2/mol) so as to avoid the gross drift and deformation of the

Figure 2. The CG model of lipids and representative snapshots of the simulations. (a) The CG model of DPPC; (b) The CG model of DOPE; (c) The CG model of the tethering molecule. Shown here is LK3 along with DPPC. For (a)-(c), particle name (e.g., NC3) and type (e.g., Qo) used are indicated; (d)-(g) Representative snapshots obtained from the simulations. (d) Set 1, the simulations of DPPC/DOPE membrane without the tethering molecule; (e) Set 2, the DPPC/DOPE membrane simulated with the tethering molecules restrained at 12nm from the center of the circle C1 defined in Figure 1; (f) Set 3, the DPPC/DOPE with the tethering molecules used at three different positions; (g) Set 4, the DOPC/DPPC with the tethering molecules at the same positions as in (f). For (d)-(g) the leftmost part of the l membrnae is hidden; this part consists of the DPPC molecules whose com was restrained to reduce the large drift of membranes. The representation scheme for (d)-(g): blue spheres, DPPC headgroup particles (from NC3 to GL2); light blue spheres, DPPC hydrophobic tail particles; orange spheres, DOPE (or DOPC) headgroup particles; yellow spheres, DOPE hydrophobic tail particles; gray spheres, particles representing the tethering molecules.
membrane. For the initial structure, a membrane of DPPC was prepared and, subsequently, an appropriate number of DPPC chosen randomly were replaced with DOPE. Four water molecules were modeled by one particle as in [29]. For all l simulations 11423 water particles were used. A typical size of the simulation box was 31, 4.5, 16 (nm) in x-, y-, and z-direction respectively. The artificial tethering (crosslinking) molecules that tether the cis monolayers were CG-modeled peptides consisting of three (“LK3”) or six (“LK6”) Ser residues (Figure 2(c)). As in [30,31], the peptide backbone was represented by the P1 particle while the Ser sidechain was represented by P5. Each tethering molecule was attached to the PO4 particle of two DPPC molecules each contained in each of the cis (fused) monolayers (Figure 2(c)). When the tethering molecules were used (i.e., set 2-4 in Table 1), their center of mass (com) positions were harmonically restrained; for example, for sets 3 and 4, the four LK3 were restrained at a position 4 nm (along the x-direction) from the center of the circle C1 (see Figure 1(g)), whereas the two LK6 were restrained at 6nm and two more LK6 were restrained at 8nm from
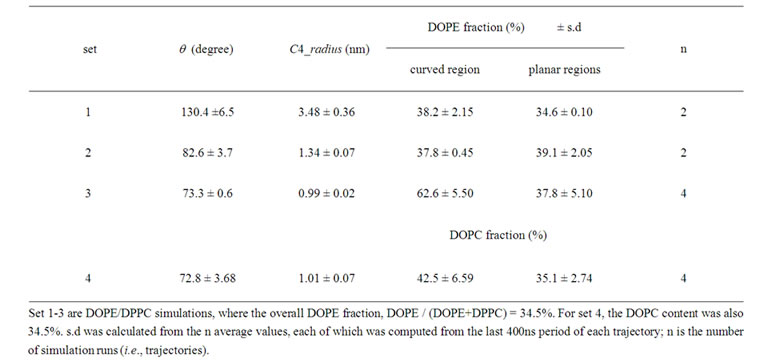
Table 1. Outer leaflet curvature and DOPE (DOPC) distribution in the curved and planar regions.
the C1 center. For the remaining part of the l-membrane, a harmonic restraint was applied to the com of each tethering molecule.
Nonbonded interactions are described by a LennardJones potential [29]. In addition, the charged particles interact via a Coulombic energy function with a relative dielectric constant = 15, which represents screening effect. The cut-off lengths and the switching function were set as in [29]. Gromacs (ver 3.3) was used [32] for 500 ns simulations performed at 323 K with the time step of 20 fs and with semi-isotropic pressure coupling at 1bar. Due to the increased diffusion rate of molecules with the CG system [29], in the following we show the time after the 4-fold multiplication. The pressure coupling time constant was 0.2 ps and the compressibility set at 3 × 10-5 bar-1.
3. RESULTS
Four sets of simulations, each consisting of two to five independent 2000ns simulations, were performed (Table 1). For sets 1-3, the DOPE/DPPC membranes were used, whereas for set 4 the DOPC/DPPC membrane was used. Table 1 shows the average (+ s.d.) of the mean values (each obtained from the final 400 ns of each trajectory) of θ, the C4 radius and the DOPE (or DOPC) density in the curved region and planar regions. For all these results the s.d. was small, which was not surprising because the 1600 ns pre-run allowed sufficient equilibration time. When no tethering molecule was used (set 1), the three bilayers quickly became equivalent (at ~400 ns); the angle between any two bilayers equally approached 120 degree (Figure 2(d)). The DOPE density relative to DPPC became similar between the curved and the planar regions (Table 1, set 1). Note that the enrichment of DPPC at the edge, generally increased the DOPE fraction above the nominal 34.5%.
When two LK3 molecules were used for tethering at 12nm from the C1 center, and the C4 radius decreased, indicating negative curvature. However, the outer leaflet had horseshoe-like roundness (Figure 2(e)). In this case, the DOPE accumulation in the negatively curved region was not significant (Table 1).
When the number of tethering molecules was increased and some positioned close to the junction (as described in the above section), the higher curvature was maintained (Figure 2(f)). Then, the significant enrichment in DOPE was observed for the negatively curved region compared to the planar region (set 3) (p < 0.01; t-test). In contrast, when the DOPE molecules of the DOPE/DPPC membrane (set 3) were all replaced with DOPC (set 4, Figure 2(g)), the DOPC density in the negatively curved region was lower than the density of DOPE of set 3 simulations (p < 0.05).
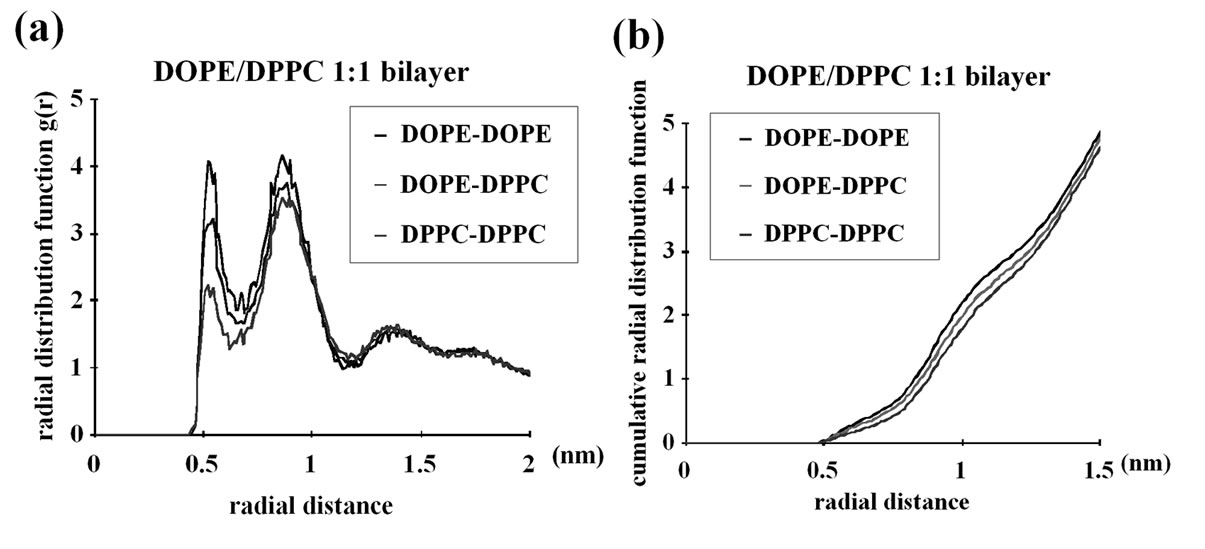
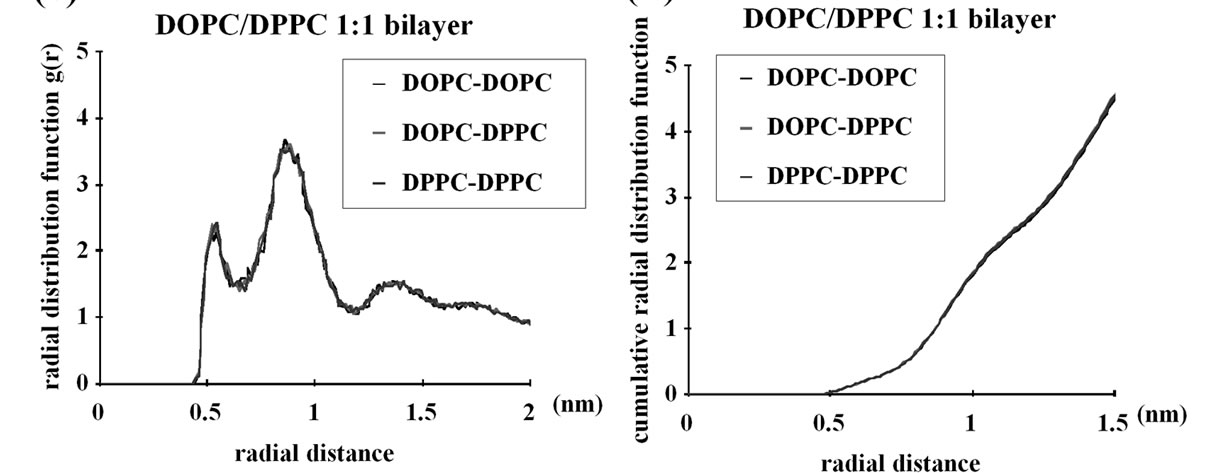
6000 ns simulations of simple planar bilayers of the same compositions as above were performed as a pilot analysis and, for the final 400ns, the radial distribution function (rdf) of the lipids were examined. The planar bilayers made up of 512 lipid molecules in total were used. The DOPE density in the proximity (~0.5-1 nm) of each DOPE molecule was high, indicating that the DOPE-DOPE interaction was stronger than DOPEDPPC interaction, which, in turn was slightly stronger than DPPC-DPPC interaction (Figures 3(a) and (b)). The DOPC-DOPC interaction was as weak as the DOPC-
 (c) (d)
(c) (d)
Figure 3. Radial distribution function (rdf) analyses of the CG lipids used in this study. 6000ns pilot simulations with planar bilayers composed of 512 lipid molecules were performed and the last 400ns data were used for this analysis. (a) DOPE/DPPC 1:1 membrane; (b) Same as (a) but the cumulative rdf is shown; (c) DOPC/DPPC 1:1 membrane; (d) Same as (c) but the cumulative rdf is shown. For example, the “DOPE-DOPE” curve shows the density (relative to the density over the whole system) of the DOPE NH3 particle at the indicated distance from each DOPE NH3 particle. Similarly, the DOPE-DPPC curve shows the density of DPPC NC3 around DOPE NH3, whereas DOPC-DPPC shows the DPPC NC3 density around DOPC NC3.
DPPC interaction and the DPPC-DPPC interaction (Figures 3(c) and (d)). Therefore, for the CG model used, the between-headgroups interaction determines the lateral distribution in planar bilayers, whereas the between-acyl chains interaction is not important. We also note that the DOPE-DOPE interaction is very local and there is no lipid clustering on scales greater than ~1 nm; in fact, at >2 nm from each DOPE molecule the density of DOPE is the same as that of DPPC (Figure 3(a)). Therefore, the DOPE and DPPC membrane is not demixed; only subtle enrichment in DOPE occurs in the close proximity (~0.5-1 nm) of each DOPE molecule. While we cannot rule out the possibility that further demixing of DOPE from DPPC could take place in longer simulations, there was no significant difference in the rdf results between the ~1000 ns and ~5600 ns data (details not shown), suggesting that the DOPE/DPPC planar bilayer was equilibrated earlier than 5600 ns.
4. DISCUSSION AND PERSPECTIVES
Above we showed that with the use of tethering molecules that maintain highly negative curvature, DOPE accumulates in the negatively curved monolayer region of the DOPE/DPPC membranes. Accumulation was significantly less when DOPC molecules were used in place of DOPE. Radial distribution function of a pilot analysis using a planar bilayer showed a modest level (~1.3 fold compared with DPPC) of enrichment in DOPE ~0.5 nm from each DOPE molecule (Figure 3(a)), which represents the direct contact of DOPE headgroups with each other. No phase separation was observed in the planar DOPE/DPPC membrane until the end of the simulation (6000 ns).
While these results may be of physicochemical relevance, several questions remain in terms of membrane physiology. First, biological relevance of the tethering molecules is unclear; in the real fusion, proteins are generally large, likely making the curvature of the fused monolayers lower than our setting (e.g., [33,34]; and references cited therein). However, in a cell fusion study using SNARE proteins expressed on the cell surface, it has been shown that GPI (glycerophosphatidylinositol)-anchored EYFP (Enhanced Yellow Fluorescent Protein consisting of 239 amino acid residues) does not diffuse between hemifused cells whereas GPI-anchored short peptide (named GPI-AU1) does (Figure 7 of [35]). In the latter case, the negative curvature between the fused monolayers may be so high that membrane proteins with a large ectodomain are excluded from the between-cell diffusion.
Second, results with the 2D-curvature system have to be carefully interpreted; our 2D-curvature system is obviously different from a small hemifusion diaphragm having a saddle-like (i.e., high Gaussian) curvature between the fused monolayers [24]. It should also be remembered that, while a large hemifusion diaphragm is observed especially with a high PE fraction, it is possible that the hemifusion diaphragm may not be a major intermediate in the fusion pathway of physiologic membranes [36,37].
It still seems relevant to ask why theoretical and in vitro experimental studies show only a weak degree of curvature sorting of lipids, despite in vivo evidence arguing for the curvature sorting effects that support cellular activities [5,6,38]. As several authors have suggested, the lateral interaction between lipids may have a profound impact on the efficacy of curvature sorting. The question arises then, how such lipid-lipid interactions modulate the lipid partitioning into differently curved membrane portions. This question may be considered based on two scenarios. First, a strong lipid-lipid interaction increases the effective area of the lipid molecule. For example, if DOPE favors interaction with DOPE, but not with DPPC, this leads to lipid sorting and can be regarded as an increase in the effective molecule area of both DOPE and DPPC. The second scenario is that the sorting can be based on the bending stiffness [19,39]. Once the curvature facilitates phase segregation in the membrane close to a demixing point, relatively soft and rigid domains may be generated. While soft domains can move into highly curved regions, rigid domains favor locations in the relatively flat regions.
Consider the first scenario. How does the increase in molecule area (surface area per molecule) influence curvature sorting. In the study employing tube pulling, a model considering individual molecule curvature sorting based on spontaneous curvature has been proposed [19,39]. For a membrane consisting of lipids α and β, based on the assumption of equal chemical potentials of molecule α (and β), on tether and vesicle, the authors have derived the following relationship:
kc a (C – Cst + Csv) (Cb – Ca)
= kT ln (faov/ faot) + kT ln (fbot / fbov), (1)
where, kc is the bending stiffness, a is the molecule area, C = 1/Rt is the tube curvature (with Rt being the tube radius), Cst and Csv are the spontaneous curvature of the outer monolayer of the tube and the vesicle, respectively, k is the Bolzmann constant, faov, for example, is the mole fraction of molecule in the outer leaflet of the vesicle. Eq.1 is derived via the partial differentiation of the total energy function by Naot, which is the number of molecule in the outer monolayer of the tube. The left side of Eq.1 corresponds to the potential regarding the bending energy, whereas the right side corresponds to the entropy term. The weighted average spontaneous curvature is assumed to be Cst = (CaNaot + CβNβot) / Not, where Ca is the spontaneous curvature of molecule α. Our λ system can be considered similarly; the curved region corresponds to the tube, while the planar regions correspond to the vesicle. Let α represent DOPE and β represent DPPC. Let faov = 0.38, faot = 0.63 (set 3), Ca = – 0.3 nm-1 [25]. The remaining terms may be approximated as: kc = 4 × 10-20 J [25]; C = – 1.0 nm-1; Cst = – 0.19 nm-1; Csv = – 0.11 nm-1; Cb = ~0 nm-1; kT = ~4 × 10-21 J. These values lead to a = ~0.4 nm2, smaller than the real value for the CG system (0.64 nm2 and 0.66 nm2 for DPPC and DOPE respectively). This may be because Ca and Cβ for the CG-model of DOPE and DPPC are not known and also our definition of C and the curved region may not be suitable.
The above relationship helps to infer the impact of molecule area. For example, if the DOPE-DOPE interaction and the DPPC-DPPC interaction are greater than the DOPE-DPPC interaction so that DOPE and DPPC behave, on average, as a particle with a 1.5-fold effective molecular area, then this would increase the fraction of DOPE in the curved region from 0.63 to ~0.75. (Here, Nov >> Not was assumed.) The reality should be far more complex, yet this notion supports the view [20] that individual lipids have a small molecular area compared with transmembrane proteins or lipid clusters, and therefore, although some lipids have high spontaneous curvatures, the membrane curvature preference of these lipids is weak.
In the second scenario, where lipid sorting is based on rigidity or bending stiffness, the effect of cholesterol on membrane properties is likely to be important. After the detergent resistant membrane domains known as rafts were identified as important membrane structural components in signal transduction and in the sorting of proteins and lipids [40,41], the effects of cholesterol on the phase properties of phospholipid bilayers were studied [42]. The cholesterol/saturated/unsaturated lipid mixture has a dramatically strong tendency toward phase separation compared with the binary mixture lacking cholesterol [15]. In addition, different fluid phases may have different bending stiffness. The Ld region (consisting of sphingomyelin and cholesterol) has a higher bending stiffness kc value compared with the Lo phase [14]. While our analyses do not take into account the kc difference between the membrane regions, this difference may be important in the case of cholesterol-containing mixtures as considered in [19,39]. Another intriguing finding regarding cholesterol segregation is that cholesterol accumulates in high curvature regions in a membrane composed of brominated di18:0 PC/cholesterol 2:1 [43].
Characterization of cholesterol-containing membranes is a topic of computational research. Several groups conducted atomistic simulations and showed several features such as hydrogen bond formation between cholesterol and phospholipids, which are consistent with experimental findings [44,45]. In general, the simulations supported the consensus that cholesterol interacts with phospholipid molecules and gives rise to the intermediate level of organization in lipid membranes, Lo [46]. (In the Lo phase, lipid hydrocarbon chains are ordered as in a Lc gel state, but phospholipid molecules are nearly as mobile as in a La fluid phase [47], for review see [41]). In terms of domain formation, Vattulainen and coworkers used a coarse-grained model and showed the formation of cholesterol-rich and cholesterol-poor domains at intermediate cholesterol concentrations [48,49]. Recently, Risselada and Marrink [50] showed that the CG model can reproduce the experimental findings on the formation of distinct phases (Lo and Ld (liquid-disordered) phase). The lateral organization of cholesterol of the raft-like structure in [50] resembles that derived from the atomistic preassembled raft-like mixtures [51]. The necessity of cholesterol for the phase separation has also been shown in [50]; in the absence of cholesterol, the DPPC/diC18:2-PC 3:1 mixture exhibited nonrandom (nonideal) mixing, yet macroscopic phase separation did not occur. From this finding, and also considering the choice of 323K in our system, it seems unlikely that the phase separation occurs in our DOPE/DPPC planar bilayer even when the simulation is extended longer than 6000ns. Future simulation analyses could focus on the phase separation in curved regions, especially those containing the stalk or the rim of the hemifusion diaphragm. As stated above, curvature sorting is significant only when the lipid mixture is close to the demixing point and therefore the ternary complex (cholesterol/ saturated lipid/unsaturated lipid) may well be examined.
Computational lipid sorting analyses also have implications in peptide-lipid interaction. Although our atomistic simulations have recently shown that an influenza virus HA2 fusion peptide enhances the rate of stalk formation [52], it is yet unknown whether such fusion peptides associate with and stabilize a particular lipid domain or, more positively, draw particular types of lipid, creating a domain in the proximity of the peptide, thereby modulating the fusion rate. (The fusion peptide was also studied in recent atomistic simulations of vesicle fusion [53]). One difficulty is the limitation in the simulation time; atomistic simulations typically cover 10-100ns and therefore very subtle lipid sorting cannot be studied with this approach.. This problem may be partially remedied by using initial structures based on the ones obtained from well equilibrated CG simulations. Phase separation simulation in [50] may provide an important framework for analyses of interactions between peptides and lipid domains.
Another interesting problem in membrane fusion is the mechanism by which transmembrane (TM) peptide domains control the fusion. Findings from Langosch and other researchers ([54] and references cited therein) generally argue that, while the ectodomains (hydrophilic domains located between the cis membranes) of fusion proteins are important in stalk formation and/or in the hemifusion intermediate, TM domains play a crucial role in later steps of fusion, such as, the rupture of the hemifusion diaphragm and/or pore formation. Considering the practical difficulties in computation (i.e., system size and simulation time), it is hoped that 2D-curved membrane systems such as ours will provide a useful starting point for such peptide analyses.
5. CONCLUSIONS
DOPE enrichment in a negatively curved region was observed in the CG models of the DOPE/DPPC monolayer mimicking the monolayer that would occur upon the fusion of the proximal monolayers. Enrichment was insignificant for DOPC in the DOPC/DPPC monolayer simulated similarly, suggesting the promoting effect of headgroup interaction between DOPE molecules on curvature sorting. Artificial tethering molecules that kept the negative curvature high (R = ~1 nm) were necessary for significant accumulation of DOPE. No phase separation was observed in the DOPE/DPPC membrane simulated as a planar bilayer. It is envisaged that, in a more physiological environment in which cholesterol is contained and is close to a demixing point, the membrane curvature could exert more pronounced lipid sorting than the one shown in this study.
6. ACKNOWLEDGEMENTS
This work was supported by Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science, and Technology of Japan.
REFERENCES
- Holthuis, J.C. and Levine, T.P. (2005) Lipid traffic: Floppy drives and a superhighway. Nature Reviews Molecular Cell Biology, 6(3), 209-220.
- Van Meer, G., Voelker, D.R. and Feigenson, G.W. (2008) Membrane lipids: Where they are and how they behave. Nature Reviews Molecular Cell Biology, 9(2), 112-124.
- De Matteis, M.A. and Luini, A. (2008) Exiting the Golgi complex. Nature Reviews Molecular Cell Biology, 9(4), 273-284.
- Mukherjee, S., Soe, T.T. and Maxfield, F.R. (1999) Endocytic sorting of lipid analogues differing solely in the chemistry of their hydrophobic tails. Journal of Cell Biology, 144(6), 1271-1284.
- Van Meer, G. and Lisman, Q. (2002) Sphingolipid transport: Rafts and translocators. Journal of Biological Chemistry, 277(29), 25855-25858.
- Ostrowski, S.G., Van Bell, C.T., Winograd, N. and Ewing, A.G. (2004) Mass spectrometric imaging of highly curved membranes during Tetrahymena mating. Science, 305(5680), 71-73.
- Fratti, R.A., Jun, Y., Merz, A.J., Margolis, N. and Wickner, W. (2004) Interdependent assembly of specific regulatory lipids and membrane fusion proteins into the vertex ring domain of docked vacuoles. Journal of Cell Biology, 167(6), 1087-1098.
- Helfrich, W. (1973) Elastic properties of lipid bilayers: Theory and possible experiments. Zeitschrift fur Naturforschung C, 28(11), 693-703.
- Markin, V.S. (1981) Lateral organization of membranes and cell shapes. Biophysical Journal, 36(1), 1-19.
- Kozlov, M.M. and Helfrich, W. (1992) Effects of a cosurfactant on the stretching and bending elasticities of a surfactant monolayer. Langmuir, 8(11), 2792-2797.
- Seifert, U. (1993) Curvature-induced lateral phase segregation in two-component vesicles. Physical Review Letters, 7(9), 1335-1338.
- Iglic, A., Hägerstrand, H., Veranic, P., Plemenitas, A. and Kralj-Iglic, V. (2006) Curvature-induced accumulation of anisotropic membrane components and raft formation in cylindrical membrane protrusions. Journal of Theoretical Biology, 240(3), 368-373.
- Derganc, J. (2007) Curvature-driven lateral segregation of membrane constituents in Golgi cisternae. Physical Biology, 4(4), 317-324.
- Baumgart, T., Hess, S.T. and Webb, W.W. (2003) Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature, 425(6960), 821-824.
- Radhakrishnan, A. and McConnell, H. (2005) Condensed complexes in vesicles containing cholesterol and phospholipids. Proceedings of the National Academy of Sciences of the United States of America, 102(36), 12662- 12666.
- Parthasarathy, R., Yu, C.H. and Groves, J.T. (2006) Curvature-modulated phase separation in lipid bilayer membranes. Langmuir, 22(11), 5095-5099.
- Bo, L. and Waugh, R.E. (1989) Determination of bilayer membrane bending stiffness by tether formation from giant, thin-walled vesicles. Biophysical Journal, 55(3), 509-517.
- Roux, A., Cuvelier, D., Nassoy, P., Prost, J., Bassereau, P. and Goud, B. (2005) Role of curvature and phase transition in lipid sorting and fission of membrane tubules. European Molecular Biology Organization Journal, 24(8), 1537-1545.
- Tian, A. and Baumgart, T. (2009) Sorting of lipids and proteins in membrane curvature gradients. Biophysical Journal, 96(7), 2676-2688.
- Kamal, M.M., Mills, D., Grzybek, M. and Howard, J. (2009) Measurement of the membrane curvature preference of phospholipids reveals only weak coupling between lipid shape and leaflet curvature. Proceedings of the National Academy of Sciences of the United States of America, 106(52), 22245-22250.
- Cooke, I.R. and Deserno, M. (2006) Coupling between lipid shape and membrane curvature. Biophysical Journal, 91(2), 487-495.
- Chernomordik, L.V., Melikyan, G.B. and Chizmadzhev, Y.A. (1987) Biomembrane fusion: A new concept derived from model studies using two interacting planar lipid bilayers. Biochimica et Biophysica Acta, 906(3), 309- 352.
- Tamm, L.K., Crane, J. and Kiessling, V. (2003) Membrane fusion: A structural perspective on the interplay of lipids and proteins. Current Opinion in Structural Biology, 13(4), 453-466.
- Chernomordik, L.V. and Kozlov, M.M. (2008) Mechanics of membrane fusion. Nature Structural & Molecular Biology, 15(7), 675-683.
- Marsh, D. (2006) Elastic curvature constants of lipid monolayers and bilayers. Chemistry and Physics of Lipids, 144(2), 146-159.
- Fuller, N. and Rand, R.P. (2001) The influence of lysolipids on the spontaneous curvature and bending elasticity of phospholipid membranes. Biophysical Journal, 81(1), 243-254.
- Marrink, S.J. and Mark, A.E. (2003) The mechanism of vesicle fusion as revealed by molecular dynamics simulations. Journal of American Chemical Society, 125(37), 11144-11145.
- Kasson, P.M., Kelley, N.W., Singhal, N., Vrljic, M., Brunger, A.T. and Pande, V.S. (2006) Ensemble molecular dynamics yields submillisecond kinetics and intermediates of membrane fusion. Proceedings of the National Academy of Sciences of the United States of America, 103(32), 11916-11921.
- Marrink, S.J., Risselada, H.J., Yefimov, S., Tieleman, D.P. and De Vries, A.H. (2007) The MARTINI force field: Coarse grained model for biomolecular simulations. Journal of Physical Chemistry B, 111(27), 7812-7824.
- Bond, P.J. and Sansom, M.S.P. (2006) Insertion and assembly of membrane proteins via simulation. Journal of the American Chemical Society, 128(8), 2697-2704.
- Bond, P.J., Holyoake, J., Ivetac, A., Khalid, S. and Sansom, M.S.P. (2007) Coarse-grained molecular dynamics simulations of membrane proteins and peptides. Journal of Structural Biology, 157(3), 593-605.
- Lindahl, E., Hess, B. and Van der Spoel, D. (2001) GROMACS 3.0: A package for molecular simulation and trajectory analysis. Journal of Molecular Modeling, 7(8), 306-317.
- Weissenhorn, W., Hinz, A. and Gaudin, Y. (2007) Virus membrane fusion. FEBS Letters, 581(11), 2150-2155.
- Wickner, W. and Schekman, R. (2008) Membrane fusion. Nature Structural & Molecular Biology, 15(7), 658-664.
- Giraudo, C.G., Hu, C., You, D., Slovic, A.M., Mosharov, E.V., Sulzer, D., Melia, T.J. and Rothman, J.E. (2005) SNAREs can promote complete fusion and hemifusion as alternative outcomes. Journal of Cell Biology, 170(2), 249- 260.
- Liu, T., Wang, T., Chapman, E.R. and Weisshaar, J.C. (2008) Productive hemifusion intermediates in fast vesicle fusion driven by neuronal SNAREs. Biophysical Journal, 94(4), 1303-1314.
- Kasson, P.M. and Pande, V.S. (2007) Control of membrane fusion mechanism by lipid composition: Predictions from ensemble molecular dynamics. PLoS Computational Biology, 3(11), 2228-2238.
- Van Meer, G. and Sprong, H. (2004) Membrane lipids and vesicular traffic. Current Opinion in Cell Biology, 16(4), 373-378.
- Tian, A., Capraro, B.R., Esposito, C. and Baumgart, T. (2009) Bending stiffness depends on curvature of ternary lipid mixture tubular membranes. Biophysical Journal, 97(6), 1636-1646.
- Edidin, M. (2003) The state of lipid rafts: From model membranes to cells. Annual Review of Biophysics and Biomolecular Structure, 32(1), 257-283.
- Jacobson, K., Mouritsen, O.G. and Anderson, R.G. (2007) Lipid rafts: At a crossroad between cell biology and physics. Nature Cell Biology, 9(1), 7-14.
- Mannock, D.A., Lewis, R.N., McMullen, T.P. and McElhaney, R.N. (2010) The effect of variations in phospholipid and sterol structure on the nature of lipid-sterol interactions in lipid bilayer model membranes. Chemistry and Physics of Lipids, 163(6), 403-448.
- Wang, W., Yang, L. and Huang, H.W. (2007) Evidence of cholesterol accumulated in high curvature regions: Implication to the curvature elastic energy for lipid mixtures. Biophysical Journal, 92(8), 2819-2830.
- Chiu, S.W., Jakobsson, E., Mashl, R.J. and Scott, H.L. (2002) Cholesterol-induced modifications in lipid bilayers: A simulation study. Biophysical Journal, 83(4), 1842- 1853.
- Hofsäss, C., Lindahl, E. and Edholm, O. (2003) Molecular dynamics simulations of phospholipid bilayers with cholesterol. Biophysical Journal, 84(4), 2192-2206.
- Pandit, S.A., Khelashvili, G., Jakobsson, E., Grama, A. and Scott, H.L. (2007) Lateral organization in lipid-cholesterol mixed bilayers. Biophysical Journal, 92(2), 440- 447.
- McMullen, T.P. and McElhaney, R.N. (1995) New aspects of the interaction of cholesterol with dipalmitoylphosphatidylcholine bilayers as revealed by high-sensitivity differential scanning calorimetry. Biochimica et Biophysica Acta, 1234(1), 90-98.
- Murtola, T., Falck, E., Patra, M., Karttunen, M. and Vattulainen, I. (2004) Coarse-grained model for phospholipid/ cholesterol bilayer. Journal of Chemical Physics, 121(18), 9156-9165.
- Murtola, T., Karttunen, M. and Vattulainen, I. (2009) Systematic coarse graining from structure using internal states: Application to phospholipid/cholesterol bilayer. Journal of Chemical Physics, 131(5), (055101)1-15.
- Risselada, H.J. and Marrink, S.J. (2008) The molecular face of lipid rafts in model membranes. Proceedings of the National Academy of Sciences of the United States of America, 105(45), 17367-17372.
- Niemelä, P.S., Ollila, S., Hyvönen, M.T., Karttunen, M. and Vattulainen, I. (2007) Assessing the nature of lipid raft membranes. PLoS Computational Biology, 3(2), 304- 312.
- Nishizawa, M. and Nishizawa, K. (2010) Molecular dynamics simulation analyses of viral fusion peptides in membranes prone to phase transition: Effects on membrane curvature, phase behavior and lipid-water interface destabilization Journal of Biophysical Chemistry, 1(1), 19-32.
- Kasson, P.M., Lindahl, E. and Pande, V.S. (2010) Atomicresolution simulations predict a transition state for vesicle fusion defined by contact of a few lipid tails. PLoS Computational Biology, 6(6), e1000829.
- Langosch, D., Hofmann, M. and Ungermann, C. (2007) The role of transmembrane domain in membrane fusion. Cellular and Molecular Life Sciences, 64(7-8), 850-864.

