Int'l J. of Communications, Network and System Sciences
Vol.1 No.3(2008), Article ID:109,13 pages DOI:10.4236/ijcns.2008.13026
Distributed Relay Diversity Systems forOFDM-Based Networks
1Ericsson Research, Stockholm, Sweden
3Royal Institute of Technology (KTH), Stockholm, Sweden
E-mail: 1Afif.Osseiran@ericsson.com, 3slimane@radio.kth.se
Received on April 3, 2008; revised and accepted on August 21, 2008
Keywords: Coherent Combining, Cooperative Communication, Cyclic Delay Diversity, Multi-User Diversity, OFDM, Relay Node, Selection Diversity, Space Time Transmit Diversity, System Performance
Abstract
In this paper, distributed relay diversity systems are analyzed, modeled and evaluated in an Orthogonal Frequency Division Multiplexing (OFDM) based networks. The investigated distributed relay diversity schemes extend the ideas of a single hop transmit antenna schemes such as Cyclic Delay Diversity (CDD), Space Time Transmit Diversity (STTD), transmit Coherent Combining (CC) and Selection Diversity (SD) to distributed diversity systems. In contrast to the classical single hop system, the antennas in the distributed systems belongs to distributed relays instead of being co-located at the transmitter. The distributed relay diversity methods considered in this paper: Relay CDD (RCDD), Relay Alamouti (i.e.STTD), Relay CC (RCC) and Relay SD (RSD) are compared to the traditional 1-hop system. Analytical expressions for the received Signal to Interference Noise Ratio (SINR) are derived and used in a dynamic multi-cell multi-user simulator. Results show considerable SINR gains for both Round Robin and Max-SINR schedulers. The SINR gains translate into substantial cell throughput gains, up to 200%, compared to 1-hop systems. Despite its low complexity, the RCDD scheme has similar performance to that of other more sophisticated 2-hop schemes such as Relay Alamouti and Relay Coherent Combining. Marginally better results are observed for the Relay Selection Diversity scheme.
1. Introduction
The main driving force in the development of wireless communication networks and systems is to provide, among other aspects, increased coverage and/or support for higher data rates. At the same time, the cost of building and maintaining the system is of great importance and is expected to become even more so in the future, as data rates and/or communication distances are increased. The problem of increased battery consumption is another area of concern. Until recently the main topology of wireless communication systems has been fairly unchanged, for the three existing generations of cellular networks. The topology of existing wireless communication systems is characterized by the cellular architecture, which consists of fixed radio Base Stations (BSs) and User Terminals (UTs) as the only transmitting and receiving entities in the network. Several radio access transmission technologies have been proposed to increase capacity, flexibility and/or coverage in communication systems. Orthogonal Frequency Division Multiplexing (OFDM) is an example of such technologies. The OFDM receiver is relatively simple, since the multiple data streams are transmitted over a number of parallel flat fading channels, and equalization is done in the frequency domain involving a single tap filter per frequency tone. Despite the simplicity of the OFDM receiver, un-coded OFDM lacks diversity which is required to combat the fast fading.
One way to introduce diversity in the received signal is to utilize multiple antennas at the transmitter and possibly also at the receiver. The use of Multiple InputMultiple Output (MIMO) channels offers significant diversity and multiplexing gains relative to single antenna systems [1,2]. Spatial diversity offered by MIMO can thus improve the link reliability and the spectral efficiency relative to Single-Input Single-Output (SISO) channels. An alternative approach is to introduce macro-diversity utilizing cooperative relaying. A relaying system is based on a conventional radio network complemented with Relay Nodes (RNs). The RNs communicate wirelessly with other network elements (e.g. BS, another RN or a UT). A cooperative relaying system is a relaying system where the information sent to an intended destination is conveyed through various routes and combined at the destination. Each route can consist of one or more hops utilizing the RNs. In addition, the destination may receive the direct signal from the source. Such systems offer the possibility to reduce path loss between communicating (relay) entities, which may benefit the end users. Cooperative relaying systems are typically limited to only two (or a few) hops. In the literature, several names are in use, such as cooperative diversity [3] cooperative coding [4], and virtual antenna arrays [5].
Cooperative relaying systems are generally divided into two categories. A signal may be decoded, re-modulated and re-transmitted, or alternatively simply amplified and re-transmitted. The former is known as decode-and-forward or regenerative relaying, whereas the latter is known as amplify-and-forward, or non-regenerative relaying.
The introduction of cooperative relaying systems will increase macro-diversity gains. There are at least two well-known schemes that offer diversity gain: Alamouti diversity based cooperative relaying [6] and coherent combining based relaying, which in addition offers a beamforming gain as described in [7]. Alamouti diversity based cooperative relaying requires a receiver to perform signal processing in accordance with the Alamouti code. Besides that, the Alamouti diversity order is limited to two and has shown little system capacity gain in a WCDMA system [8]. This is also true for other space-time codes similar to Alamouti diversity. Higher order space-time codes cannot be constructed without reducing the code rate. Coherent combining based cooperative relaying requires some sort of feedback to estimate channel phase and amplitude. This increases the control signaling in the system, which in turn may reduce the user data rate. Additionally the feedback channel can be erroneous hence may reduce rather increase the system performance as intended. In the amplify-and-forward schemes the desired signal is amplified at the Relay Nodes (RN) at the expense of amplifying the interference. However, in the coherent combining case, the signal of interest is coherently added whereas noise and interferers are added non-coherently. In the decode-and-forward schemes if the signal is erroneously decoded, the error will propagate to the destination.
Inducing multi-path diversity by means of cooperative communications nodes have already been proposed for a single carrier system [6,9–11]. At the destination the signal consists of several delayed copies due to either the introduced delay at the nodes or asynchronous operation, or due to the propagation delay or the processing delay. The diversity is exploited either by increasing the data symbol length [9] in order to avoid ISI or by using a complex equalizer such a generalized decision feedback equalizer [10] or by introduction Cyclic Prefix (CP) in conjunction with Frequency Domain Equalization (FDE) [11].
In this paper several distributed diversity schemes are investigated. One of these schemes is a new cooperative relaying scheme for future wireless communication systems referred to as Relay Cyclic Delay Diversity (RCDD) [12]. The idea is to use a set of distributed RNs each associated with a different cyclic shift. This cyclic shift can be pre-determined or random. Besides the improved link gain usually obtained from a cooperative relaying system, the proposed scheme introduces frequency selectivity and macro-diversity in OFDM based systems. RCDD scheme, relay Alamouti, relay coherent combining and relay selection diversity are investigated and evaluated in a multi-cell (radio network) scenario. Moreover the received SINR at the mobile unit is derived analytically. To the authors best knowledge, no system level (i.e. multi-user in a multi-cell radio network) investigation that tackles distributed diversity schemes has been reported in the open literature. This comprehensive study is the main objective of the contribution.
The paper is organized as follows. In Section 2, the principle of 2-hop distributed RCDD is introduced and its relation to conventional CDD is explained. Relay communication in combination with the Alamouti scheme is discussed in Section 5. Signal representation for different 2-hop relaying schemes are given in Section 6. SINR derivation is exposed in Section 7. The system modeling and simulation assumptions are given in Section 8. Finally simulation results are presented in Section 9.
2. Distributed Relay Cyclic Delay Diversity
As an alternative to the conventional diversity methods, an artificial diversity, which mimics the effects of spatial diversity, can be introduced in wireless communication systems by the use of artificial Delays. The idea is to transmit the same information modulated symbols from separate antennas with different time delays, thereby causing multipath replicas even when the channel is flat. With the help of an equalizer the receiver can extract these paths and achieve a Delay Diversity (DD) gain [13]. For communication systems that employ the IFFT/FFT operators such as OFDM and Single Carrier with Frequency Domain Equalization (SC-FDE), DD can be achieved through the use of a cyclic delay. Cyclic Delay Diversity (CDD) has been used in combination with OFDM in [14,15] and has been used with SC-FDE systems with no additional complexity at the receiver in [11]. In this context, cyclic delay increases the selectivity of the fading channel which in the presence of channel coding can increase the diversity gain of the system.
The use of distributed CDD (i.e. located in different BSs) to exploit macro-diversity has been presented in [16]. The drawback of this scheme is that the wireless infrastructure must rely on Radio Network Controler to deliver in a timely fashion the data to multiple BS. Obviously, the control and data signalling in the backhaul will be very high. To avoid this complexity, distributed RNs should be used instead.
In analogy to CDD and in order to provide frequency selectivity and spatial diversity in a cooperative relaying wireless communication system, a set of distributed RNs is treated as a single entity composed of multiple antennas where at each RN transmit antenna a cyclic shift is applied to the OFDM symbol that is forwarded between the BS and the UT. An example of a cooperative relaying network is shown in Figure 1. The figure shows one cell of a wireless network comprising of a BS, several RNs and a UT.
The transmission is made in two phases as illustrated in Figure 2. In the first transmission phase as it is shown in Figure 2(a), the BS transmits the desired data to the scheduled UTs and to the active RNs in a specific cell. In the second transmission phase (see Figure 2(b)), the active RNs or/and the BS retransmit the same data sent by the BS to the scheduled users in the first transmission phase.
According to the proposed method artificial frequency selectivity and spatial diversity is provided in a cooperative relaying wireless communication system. The artificial frequency selectivity is exploited in conjunction with forward error correction coding (FEC) to provide a coding diversity gain. The BS transmits to K RNs and possibly also directly to the UT. The RNs1 forward the information received from the BS to the UT using cyclic delay diversity. Each RN applies an individual cyclic shift and adds the cyclic prefix (CP) to solve the problem of Inter Symbol Interference (ISI) and preserve the orthogonality between the OFDM sub-carriers in a fading multi-path environment. The signals are then up-converted from base-band into the RF-band and transmitted. The receiver and transmitter of one specific RN is illustrated in Figure 3 where we have assumed that decode-and-forward is employed.
It is interesting to mention that the UT does not need any information about the number of RNs. The UT receives the multiple access signals and decodes the data that may be combined with the signal directly received from the BS. The combined signal as experienced by the UT will in a sense be similar to the signal from a transmitter with multiple antennas, utilizing CDD, but with the added benefits with regards to gain and coverage associated with cooperative relaying.
3. Relay Selection Diversity
Relay selection diversity (RSD) is similar to antenna selection diversity. In RSD the BS will select one RN out of a set of RNs belonging to the BS. In the second transmission phase, the selected RN will forward the information from the BS to the UT. Contrary to the classical antenna selection where the selected antenna for transmission is based on the short term statistics (e.g. fast fading), the selection criterion for RSD is done on a slow basis and consists of the distance and shadow fading gain. In particular the BS station will calculate the channel gains between the UT of interest and all the RNs belonging to that BS based on distance and shadow fading maps. Consequently, the BS will select the RN which has the highest channel gain to the UT of interest.
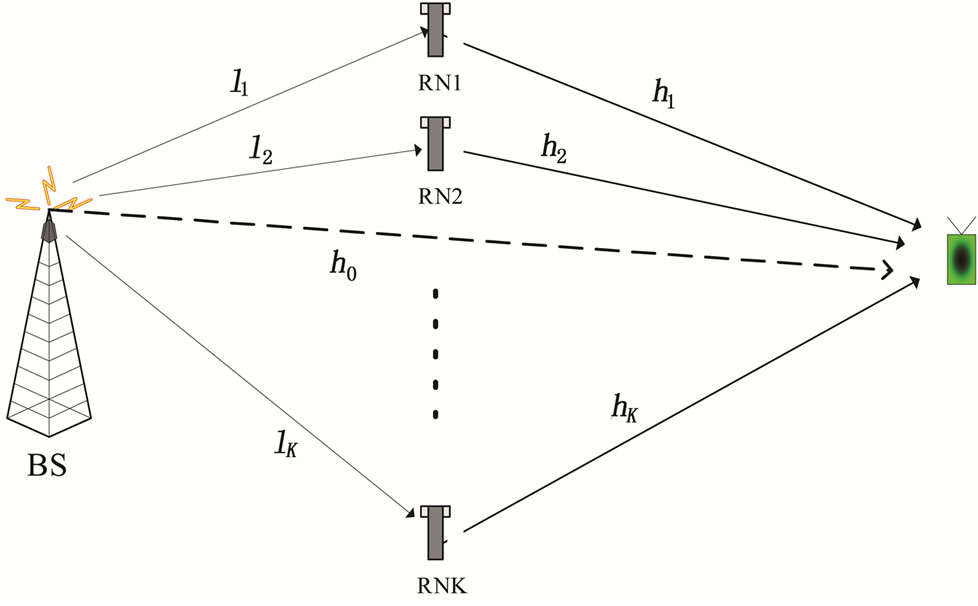
Figure 1. The channel impulse responses of a simple 2-hop cooperative system: One BS, K RNs and a UT.
 (a) Phase I.
(a) Phase I.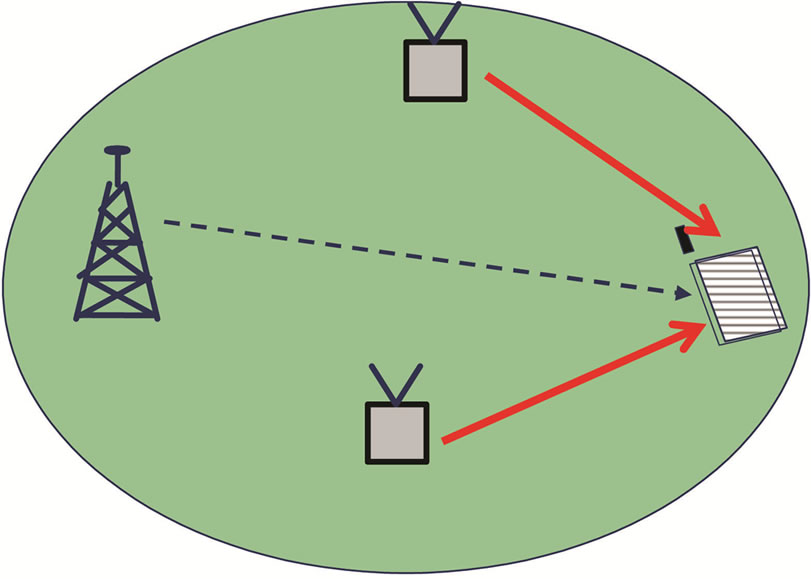 (b) Phase II.
(b) Phase II.
Figure 2. Transmission phases in a 2-hop relay network.
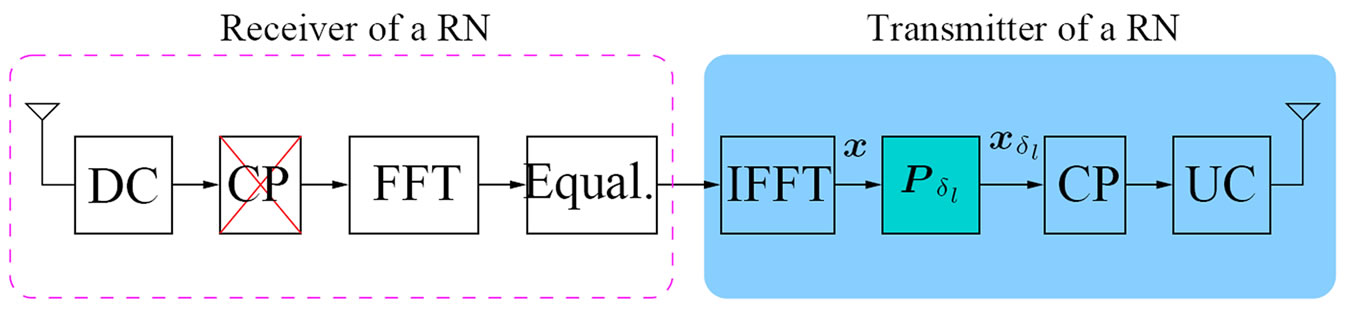
Figure 3. The receiver and transmitter structure of a RN for RCDD.
4. Relay Coherent Combining
Relay coherent combining was first proposed in [7]. It consists of multiplying the transmitted signal at each RN by a phase that compensates the one introduced by the channel. In fact the effective channel at the UT will be a constructive summation of all the RN signals transmitting to the desired UT.
5. Relay Alamouti Diversity
Relay Alamouti diversity consists of two distributed relays that are used to mimic conventional STTD. For instance, the BS will transmit an even number of OFDM symbols in the first transmission phase then the RN will re-transmit these symbols during the second transmission phase. For simplicity let us assume that the duration of the transmission phases is two OFDM symbols, e.g. 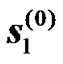 and
and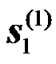 . For the second transmission phase (of equal duration to the first transmission phase), two RNs attached to the BS are selected. Each of these RNs is equipped with a single antenna as shown in Figure 4. The two antennas of the RNs will act jointly as in the case of two transmitting antennas for a conventional STTD. The only difference is that each of the antenna is attached to a different antenna system instead of being controlled by the same radio unit. After demodulating the two received symbols the RNs will act jointly as a STTD encoder. While the first RN will resent the same symbols i.e
. For the second transmission phase (of equal duration to the first transmission phase), two RNs attached to the BS are selected. Each of these RNs is equipped with a single antenna as shown in Figure 4. The two antennas of the RNs will act jointly as in the case of two transmitting antennas for a conventional STTD. The only difference is that each of the antenna is attached to a different antenna system instead of being controlled by the same radio unit. After demodulating the two received symbols the RNs will act jointly as a STTD encoder. While the first RN will resent the same symbols i.e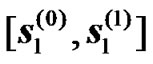 , the second RN will swap the order of the received symbols in addition to conjugating them as it is done in the second antenna of a conventional STTD encoder, i.e.
, the second RN will swap the order of the received symbols in addition to conjugating them as it is done in the second antenna of a conventional STTD encoder, i.e.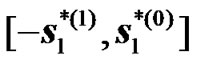 .
.
6. Mathematical Models
To illustrate the evaluated concepts we consider K RN nodes and one BS as shown in Figure 1, where the BS and each RN is equipped with one transmit and one receive antenna. Let x be the OFDM symbol at a given symbol interval and 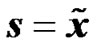 its corresponding modulated data vector. Let us assume a slowly varying fading multi-path channel, and let hk denote the channel impulse response between the transmit antenna of RN k and the receive antenna of the UT. It is assumed that the CP is greater than the maximum delay of the channel.
its corresponding modulated data vector. Let us assume a slowly varying fading multi-path channel, and let hk denote the channel impulse response between the transmit antenna of RN k and the receive antenna of the UT. It is assumed that the CP is greater than the maximum delay of the channel.
6.1. Relay Cyclic Delay Diversity
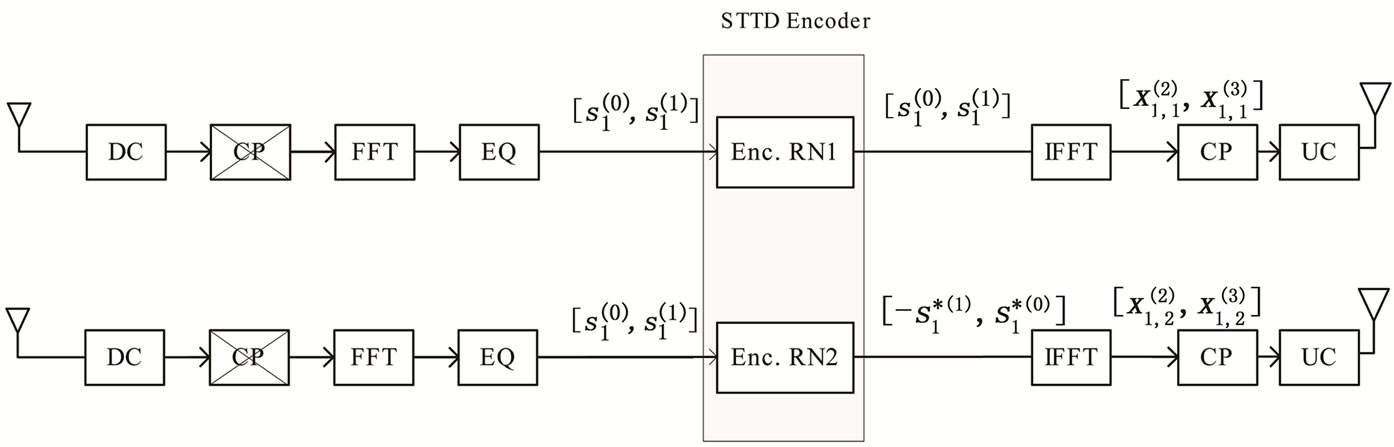
Figure 4. The receiver and transmitter structure of Relay Alamouti.
Let x denote the [N×1] post IFFT data vector, where N is the number of sub-carriers. At each RN, the data vector x will then undergo a cyclic shift of length , yielding:
, yielding:
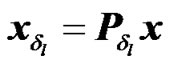 , with
, with  (1)
(1)
where Pl is a permutation matrix that applies a delay of length l to a vector x, Pl is a right circulant matrix with  as the first row i.e.
as the first row i.e.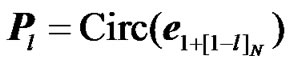 , ek is column vector with all elements equal to zero except the element at position k which is equal to one. [a]b, denoted as a modulo b, is the remainder of the division a by b. It is well known that a cyclic shift of length l in (1), is equivalent to a phase shift in the frequency domain. Hence, the noise free received OFDM symbol with cyclic shift can be written as
, ek is column vector with all elements equal to zero except the element at position k which is equal to one. [a]b, denoted as a modulo b, is the remainder of the division a by b. It is well known that a cyclic shift of length l in (1), is equivalent to a phase shift in the frequency domain. Hence, the noise free received OFDM symbol with cyclic shift can be written as
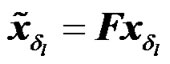 , with
, with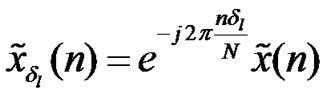 where
where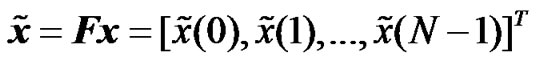 , and F is the unitary discrete Fourier transform matrix of size N×N, its (n,m)th element for
, and F is the unitary discrete Fourier transform matrix of size N×N, its (n,m)th element for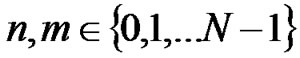 , is given by
, is given by
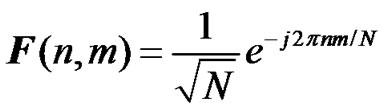 (2)
(2)
Hence, 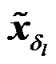 can be expressed as a function of the original modulated data vector
can be expressed as a function of the original modulated data vector 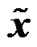 as
as
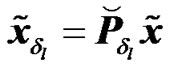 (3)
(3)
where
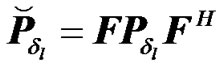
 .
.
Combined with the transfer function of the channels between the RN transmit antennas and the receive antenna, this permutation matrix will increase the frequency selectivity of the channel seen at the UT receiver.
In the case of relay CDD, a cyclic shift of length 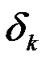 is applied to the signal at the antenna of the
is applied to the signal at the antenna of the 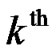 RN before transmission. Let
RN before transmission. Let  and
and 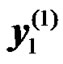 be the received symbols at the UT from the BS and RNs for the first and second transmission phases, respectively. They can be expressed as:
be the received symbols at the UT from the BS and RNs for the first and second transmission phases, respectively. They can be expressed as:
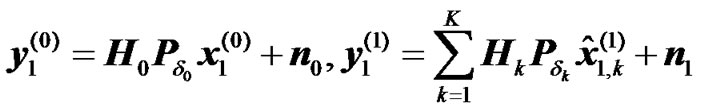 , (4)
, (4)
where 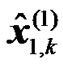 is the estimate of the symbol
is the estimate of the symbol  at RN k, n0 and n1 represent the thermal noise at the UT from the first and second transmission phases, respectively.
at RN k, n0 and n1 represent the thermal noise at the UT from the first and second transmission phases, respectively.
The matrix 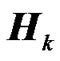 represents the channel matrix from the kth RN transmit antenna to the receive antenna of the UT. Since
represents the channel matrix from the kth RN transmit antenna to the receive antenna of the UT. Since  is a circulant matrix, the channel matrix can be diagonalized as follows:
is a circulant matrix, the channel matrix can be diagonalized as follows:
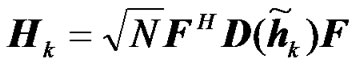 , (5)
, (5)
where2
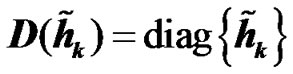
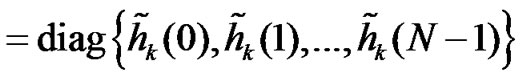 .
.
Since 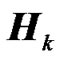 and
and 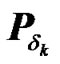 are circulant matrices then
are circulant matrices then  is also a circulant matrix [17] and can be decomposed as
is also a circulant matrix [17] and can be decomposed as 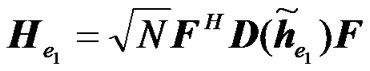 where
where  can be called the effective channel impulse response from the relays, where its FFT is given by:
can be called the effective channel impulse response from the relays, where its FFT is given by:
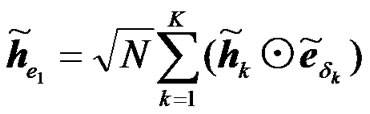 , (6)
, (6)
where ⊙ denotes the Hadamard product. Taking the FFT of the received signals in (4) yields:
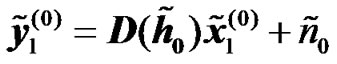 ,
, 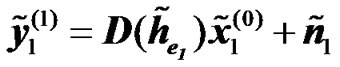 , (7)
, (7)
where it is assumed that the modulated data is correctly decoded at the different RNs, i.e.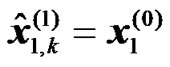 ,
,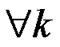 .
.
The signals can be combined using the MRC method. Note that the channels from each antenna do not need to be explicitly estimated. The effective channel impulse response and the channel response from the BS can be estimated using a common time-frequency pilot pattern, which is not antenna specific. The same conclusion is reached when multiple transmit antennas are used at the BS and/or the RNs.
6.2. Relay Coherent Combining
The expression of received signals at the UT for the coherent combining is similar to the RCDD case (see (7)). The only difference resides in the expression of the effective channel which for the coherent combining case is simply given by:
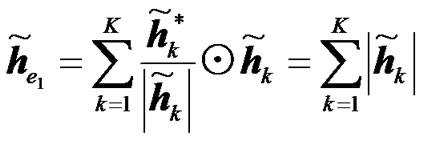 , (8)
, (8)
where ⊙ is the Hadamard product.
6.3. Relay Alamouti Diversity
Let 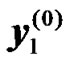 and
and 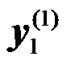 denote the received signals at the UT corresponding to modulated transmitted symbols
denote the received signals at the UT corresponding to modulated transmitted symbols 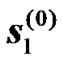 and
and 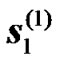 from the BS, respectively. Let
from the BS, respectively. Let 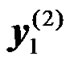 and
and  the received signals from the RNs during the second transmission phase. The received signals at the UT can be expressed as:
the received signals from the RNs during the second transmission phase. The received signals at the UT can be expressed as:
 (9)
(9)
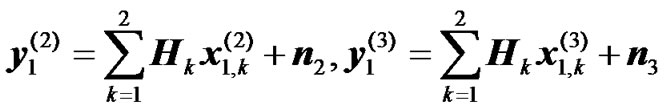 , (10)
, (10)
where 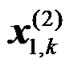 and
and 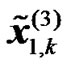 are the transmitted OFDM symbols from the
are the transmitted OFDM symbols from the 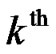 RN during the second transmission phase. Assuming a perfect detection at the RNs of the transmitted symbols from the BS during the first phase then:
RN during the second transmission phase. Assuming a perfect detection at the RNs of the transmitted symbols from the BS during the first phase then:
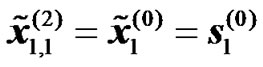 ,
, 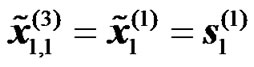 (11)
(11)
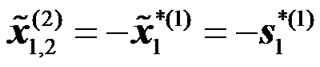 ,
,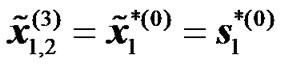 (12)
(12)
Taking the FFT of the received signals in (9) and (10) during the two transmission phases, diagonalizing the channel matrices Hj for , and using (11) and (12), we obtain:
, and using (11) and (12), we obtain:
 (13)
(13)
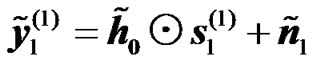 (14)
(14)
 (15)
(15)
 (16)
(16)
At the UT, the symbols 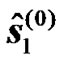 and
and 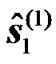 are estimated during the first phase by simply equalizing the received signals defined in (9). Further, a second estimate of the transmitted symbol
are estimated during the first phase by simply equalizing the received signals defined in (9). Further, a second estimate of the transmitted symbol 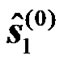 is obtained at the end of the second phase by applying simply the STTD decoding operations as follows:
is obtained at the end of the second phase by applying simply the STTD decoding operations as follows:
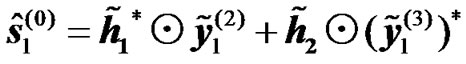 (17)
(17)
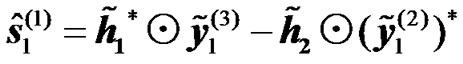 (18)
(18)
7. SINR Derivation
7.1. Received Signal & Combining
In this section the received signals at the UT for RCDD, Relay Alamouti, Relay coherent combining and Relay Selection Diversity schemes are derived.
1) Relay Cyclic Delay Diversity: In the previous section, the received signal at the UT was derived by ignoring the intra-cell and inter cell interference. Assuming that Nu radio elements (BS or RN), are transmitting on the same frequency band, then the received signal at the UT of interest during the second transmission phase can be expressed as
 (19)
(19)
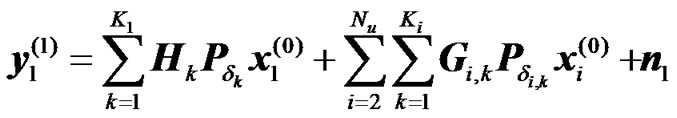 (20)
(20)
where Gi is the channel matrix between the interfering ith radio element and the UT of interest (here UT = 1) during the first transmission phase, xi is the transmitted data sequence by the ith radio element, Ki is the number of active RNs in cell i, and Nu is the number of co-channel links. Assuming that the Gi are circulant, hence these matrices can be diagonalized using the FFT decomposition. Otherwise the interference is counted as a part of the noise term. Taking the FFT of the two vectors in (19) and (20) we obtain
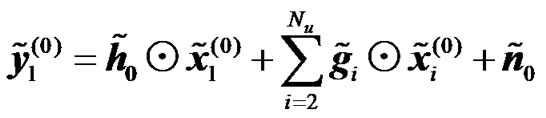 (21)
(21)
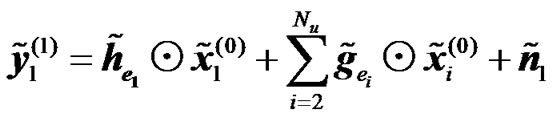 , (22)
, (22)
where 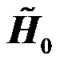 and
and 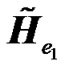 are as defined earlier, and
are as defined earlier, and 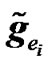 is the effective frequency channel response between the ith radio element and the UT of interest and is given by:
is the effective frequency channel response between the ith radio element and the UT of interest and is given by:
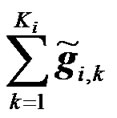
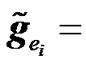 . (23)
. (23)
2) Relay Selection Diversity: The expression of the received signals for relay selection diversity method is similar to the RCDD expressions given in (21) and (22). The only difference is that only one RN instead of several is transmitting in the second phase. The RN is selected out of K RNs based on the slow term channel statistics. Then the channel frequency response between radio element 1 and the UT of interest is given by

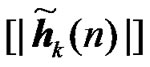
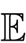
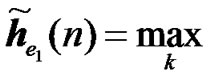 ,
, 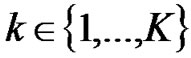 , (24)
, (24)
where 
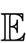 is the expectation function. Further, the effective channel frequency response between the ith interfering element and the UT of interest is given by
is the expectation function. Further, the effective channel frequency response between the ith interfering element and the UT of interest is given by
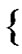
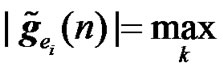
![]()
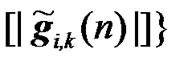 ,
, .(25)
.(25)
3) Relay Coherent Combining: The expression of the received signals for relay coherent combining method is identical to the RCDD expressions given in (21) and (22). The effective channel frequency response between radio element 1 and the UT of interest is as given by (8). Further, the effective channel frequency response between the ith interfering element and the UT of interest can be easily shown to be equal to
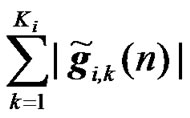
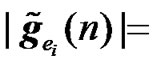 (26)
(26)
4) Relay Alamouti Diversity: As in subsection 1 of section 7.1., taking into account co-channel interference into the expression of the received signals for relay Alamouti scheme at the UT for the two transmission phases, equations (13) to (16) become
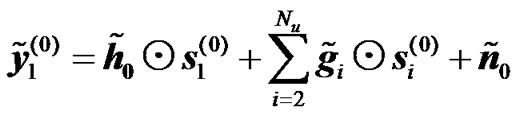 (27)
(27)
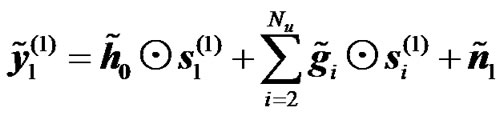 (28)
(28)
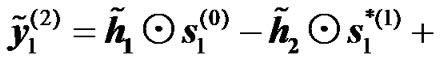
 (29)
(29)
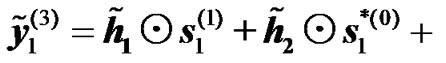
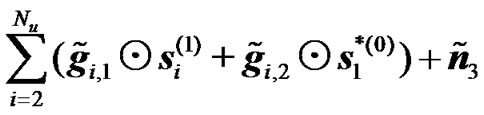 (30)
(30)
It is interesting to mention that the received signals of interest 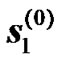 and
and  will be amplified by the combined channel from the transmitting RNs,
will be amplified by the combined channel from the transmitting RNs,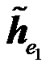 . Replacing the received signals in (17) and (18) by its expression given by (29) and (30), it can be easily shown that the combined signal of the 2-hop signal takes the form given in (22) with
. Replacing the received signals in (17) and (18) by its expression given by (29) and (30), it can be easily shown that the combined signal of the 2-hop signal takes the form given in (22) with
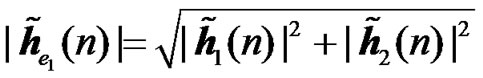 , (31)
, (31)
and
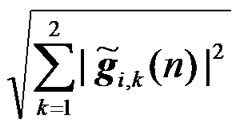
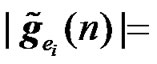 . (32)
. (32)
7.2. SINR Expression
A generic expression of the received SINR for the two communication phases for the evaluated schemes can be derived from section 7.1. The received SINR for RCDD, relay selection diversity and relay coherent combining can be simply derived from (21) and (22). The SINR of relay Alamouti can be derived from (27), (29) and (30). Assuming that the elements of , l
, l 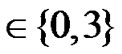 are independent variables with zero mean and having pi as variance, the thermal noise is AWGN (with zero mean and variance
are independent variables with zero mean and having pi as variance, the thermal noise is AWGN (with zero mean and variance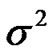 ) then the received SINR on the nth tone from the first and second hop can be shown to be given by
) then the received SINR on the nth tone from the first and second hop can be shown to be given by
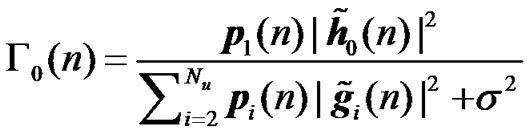 (33)
(33)
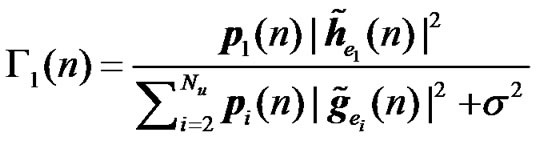 (34)
(34)
Applying maximum ratio combining, the received SINR of the combined signal on the nth tone becomes
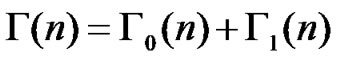 . (35)
. (35)
The expressions of the effective channel IR 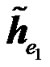 for RCDD, relay Alamouti (RALA) and relay coherent combining (RCC) are given in equations (6), (31) and (8), respectively. The channel IR of the interfering BS for RCDD, relay Alamouti, and relay coherent combining are given in (23), (32), and (26), respectively.
for RCDD, relay Alamouti (RALA) and relay coherent combining (RCC) are given in equations (6), (31) and (8), respectively. The channel IR of the interfering BS for RCDD, relay Alamouti, and relay coherent combining are given in (23), (32), and (26), respectively.
It can be clearly seen from (34), that the performance of the different schemes is dictated by the effective channel impulse responses of the useful part and interfering part of the received signal (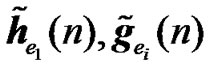 ).
).
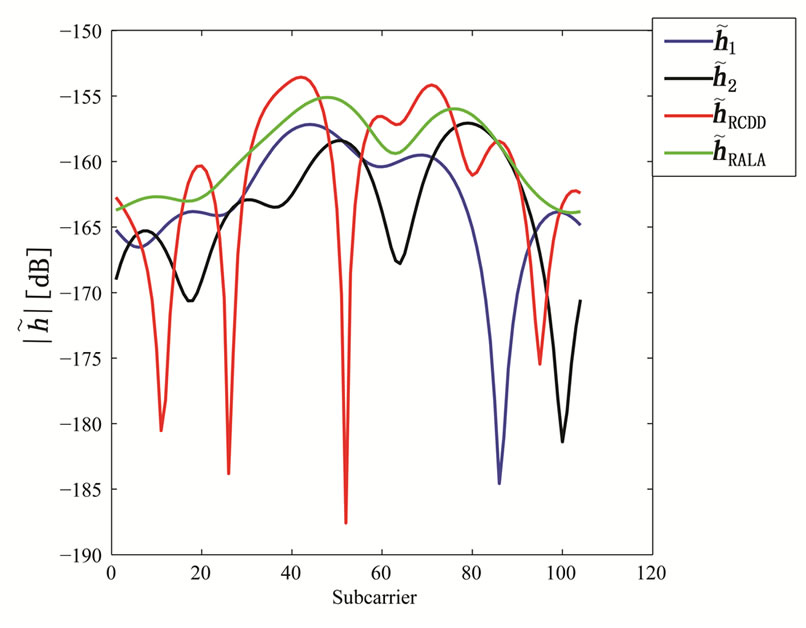
An example is shown in Figure 5 where 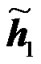 and
and  are the channel IRs seen at the UT from two RNs. The amplitude of the effective channel of the useful signal for the RCDD scheme as given in (6), with random cyclic shifting in the two RNs, is shown and compared to that of the RALA scheme as given in (31). It is observed that the applied cyclic shift on the two RNs impacts hugely the form of the effective channel. For instance, as illustrated in Figure 5(b), the RCDD effective channel has a greater amplitude for most of the subcarriers as compared to that of the RALA scheme, up to 5 dB greater for some of the subcarriers. In general, the cyclic shifts introduced at the different relays produce more selective channel (big variance in terms of its amplitude, see Figure 5(a)). The effective channel shown in Figure 5(a) exhibits considerable selectivity, thus having substantially lower amplitude for some sub-carrier and higher for others. In fine, the BS may greatly benefit from this large scale variance in terms of the channel amplitude by choosing to transmit to the desired users on those subcarriers with favorable channel conditions that was produced artificially by the cyclic shift. For RALA and RCC schemes, the channels from the different relays are coherently combined at the UT. Hence their effective channels exhibit less frequency selectivity but a higher power average is observed.
are the channel IRs seen at the UT from two RNs. The amplitude of the effective channel of the useful signal for the RCDD scheme as given in (6), with random cyclic shifting in the two RNs, is shown and compared to that of the RALA scheme as given in (31). It is observed that the applied cyclic shift on the two RNs impacts hugely the form of the effective channel. For instance, as illustrated in Figure 5(b), the RCDD effective channel has a greater amplitude for most of the subcarriers as compared to that of the RALA scheme, up to 5 dB greater for some of the subcarriers. In general, the cyclic shifts introduced at the different relays produce more selective channel (big variance in terms of its amplitude, see Figure 5(a)). The effective channel shown in Figure 5(a) exhibits considerable selectivity, thus having substantially lower amplitude for some sub-carrier and higher for others. In fine, the BS may greatly benefit from this large scale variance in terms of the channel amplitude by choosing to transmit to the desired users on those subcarriers with favorable channel conditions that was produced artificially by the cyclic shift. For RALA and RCC schemes, the channels from the different relays are coherently combined at the UT. Hence their effective channels exhibit less frequency selectivity but a higher power average is observed.
8. System Modeling and Assumptions
In this section the air interface characteristics, the system assumptions for the evaluation of the relaying schemes are described. The evaluation is made via a dynamic system simulator that focuses on the physical layer, radio network deployment and algorithms (such as link adaptation and scheduling), utilizing the extended spatial channel model proposed in [18]. The relaying schemes will be evaluated in a 2-hop radio network and compared to a 1-hop system. The most relevant parameters that characterizes the air interface are summarized in Table3 1. Note that only the downlink connection (when the UT is receiving) is considered. An average number of 10 UT per sector is generated. A simple data traffic model is used since the interest is in the relative performance of the simulated schemes and not in the traffic modelling
 (a)
(a) (b)
(b)
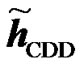 is very selective.(b)
is very selective.(b) 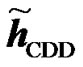 is the best.
is the best.Figures 5. Effective channel impulse response samples of the useful signal for the different relaying schemes. Comparison of Channel Impulse responses of two RNs 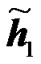 and
and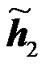 , the RCDD
, the RCDD  and the RALA
and the RALA .
.
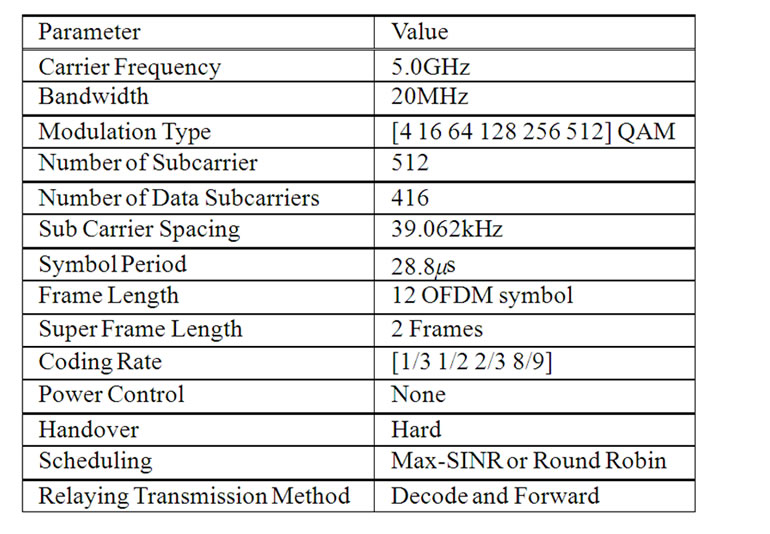
Table 1. Air interface parameters.
performance per se. Generated users have full buffers, ready to transmit when they are scheduled.
8.1. BS and RN Deployment
The simulated cell plan consists of 7 sites, each site with three sectors, with a regular hexagonal deployment topology as shown in Figure 6. The BSs are represented by red circles and are placed at the intersection of three hexagons. The RNs are placed on a circular arc with a BS as an origin. As seen from Figure 6, three RNs per sector, represented by the star signs were assumed. The distanceof the RNs to their associated BSs is set to half of the cell radius. No attempt has been made to optimize the locations of the RNs within the network. Clearly, this optimization must be addressed and will be considered in future studies.
8.2. Path Loss and Channel
The radio propagation channel and distance path model is an extension of the one proposed in the SCM [19] and developed by the Winner project4 [18,20,21]. Similar radio propagation conditions between the UT the BS and RN are assumed. Further, as indicated in Section 4, the radio communication between the BS and the active RNs is assumed error free.
8.3. Link to System Interface
The model used for the link to system interface is based on the mutual-information metric which accounts for the modulation alphabet [22], called the Mutual Information Effective SINR Metric (MIESM). In fact this method has been shown to be an efficient link quality model for predicting the Packet Error Rate (PER) in system simulations involving low complexity. In order to calculate the PER or BLock Error Rate (BLER) the method follows the following steps:
• The user SINR of a specific resource element (according to SINR sampling period in time and frequency in an OFDM system) is calculated after receiver processing.
• For each resource element, the average mutual information per bit ( ) is calculated (depending on the modulation used).
) is calculated (depending on the modulation used).
• The  is mapped to a PER depending on the channel coding type and rate.
is mapped to a PER depending on the channel coding type and rate.
8.4. Antenna Arrangement
The BS is equipped with a 3-Sector site antenna with maximum antenna gain of 14 dBi as defined in [19], while an omnidirectional antenna of 10dBi was assumed at the RNs.
8.5. Radio Network Algorithms
The most relevant Radio Network Algorithm (RNA) used to evaluate the relaying schemes are described in this section.
Handover: Only hard handover is considered. In order to avoid ping-pong effect a handover margin of 3 dB is used.
Power Control & Link Adaptation: No power control is applied. Modulation and channel coding were adapted to the channel conditions, which can be considered as an alternative and preferred method to power control.
Scheduling: Two types of scheduler are investigated. The first one is round robin where the scheduler assigns time slot for transmission to each user in equal portions and order. The second investigated scheduler is Max-SINR, unfair compared to the round robin. The Max-SINR scheduler allows to fully exploit the RCDD concept. The frequency bandwidth is divided into several sub-bands (consisting of more than one sub-carrier each), the user having the highest (i.e. maximum) SINR on each sub-band is scheduled. For instance, if the bandwidth is divided into 10 sub-bands then up to 10 users can be scheduled (i.e. one user is scheduled in each sub-band) for the whole available bandwidth. Note that the SINR or an equivalent measure per sub-band of the UTs connected to an BS is considered to be available at the BS. When using the Max-SINR scheduler the MAC objective is to maximize the system throughput. The update rate of the scheduler is equal to the super-frame length (i.e. the duration of 24 OFDM symbols).
Radio Node Selection: The BS selection is based on the path loss and shadow fading. The active RNs in a cell are chosen based on the path loss. During the second transmission phase, only two out of six RNs will retransmit data to the scheduled users.
8.6. Environment Description and Evaluations Criteria
The simulations were carried out using a dynamic system level simulator. The radio network cell plan is simulated over a certain number of snapshots. Each snapshot consists of a large number of super-frames which itself is composed of a certain number of radio frames. Each radio frame consists of a number of OFDM symbols. A set of new users is generated at the start of each super-frame, placed in the cell plan and associated to a
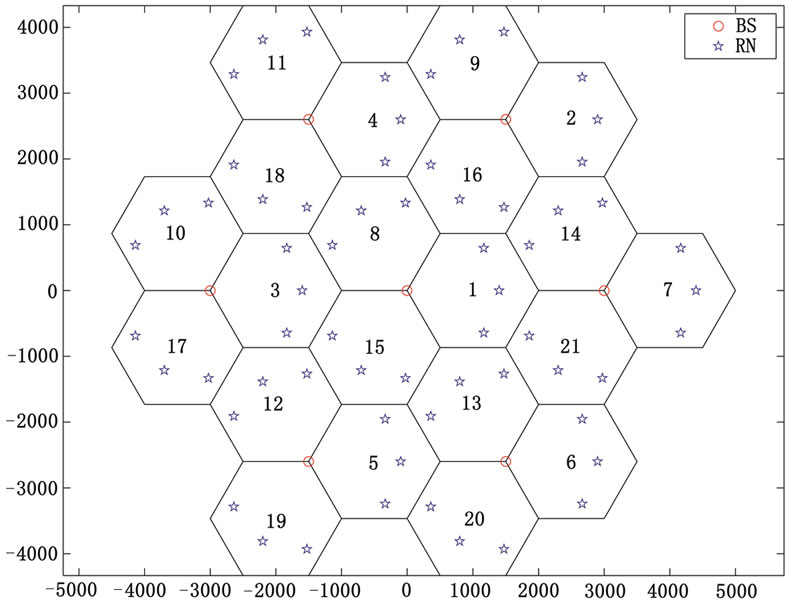
Figure 6. Cell Plan of 21 sectors where each sector is equipped with 3 RNs.
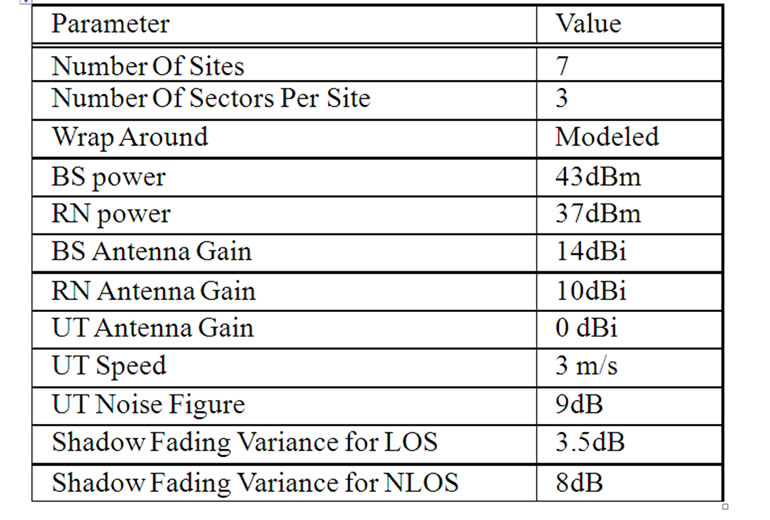
Table 2. Simulation Parameters.
BS according to their path loss and shadow fading. On the frame level, first the users will move5 and then the propagation channel conditions will be generated (i.e. path loss, slow and fast fading). Thereafter the traffic model will generate the data packets for all active users. Then, the scheduler will decide which users will be scheduled. The users’ modulation and coding schemes will be decided by the link adaption algorithm. The link to system interface derives the block error rate taking into account the interference of all BSs and RNs. This process will be repeated until the desired number of snapshots is reached. The most relevant simulation parameters are described in Table 2.
Cell throughput is used as a measure to compare the performance of the investigated concepts. The cell throughput is the average number of correctly received bits over the entire simulation time divided by the simulation time and the number of cells.
9. Simulation Results
In this section we provide numerical results for the performance of distributed relay diversity schemes such as RCDD, relay Alamouti, relay coherent combining and relay selection diversity and compare it to that of the classical 1-hop system. We look at the cumulative distribution function (cdf) of the received SINR at the UT and the cell throughput. The investigated schemes are:
• The reference case, i.e. a single hop system and is designated in the figures by “1-hop”.
• The relay cyclic delay diversity is denoted “RCDD”.
• The relay selection diversity is denoted “RSD”.
• The relay Alamouti method is denoted “RALA”.
• The relay coherent combining is designated by “RCC” in the figures label.
For all the 2-hop methods, the signal from the first transmission (i.e. BS to UT) is combined with the signal from the second transmission (RN to UT) at the UT using maximum ratio combining.
9.1. Performance with Round Robin Scheduling
With Round Robin scheduling, all users are allocated the same share of bandwidth. The cdf of the received SINR at the mobile unit of the 1-hop and 2-hop systems for a cell radius of 1 km is illustrated in Figure 7. We notice that the 2-hop schemes outperform the 1-hop scheme by about 10 dB. However, the performance difference between the various 2-hop schemes is quite small (less than 1 dB). The cdf of the received interference is shown in Figure 8 and that of the received useful signal is shown in Figure 9 for the same cell radius of 1 km. While the experienced interference in the 2-hop schemes is larger than that in the 1-hop scheme, the received power of the useful signal improves due to the gain in terms of path and the additional diversity provided by the fading multi-path channel.
One way to reduce interference within the system is to allow only one relay to be active at a time. This is denoted by “RSD” in the figures. It is observed that such a scheme reduces the experienced interference with reduction in received power.
The SINR gain for the 2-hop schemes translates into a good cell throughput gain as shown in Figure 10. For a cell size ranging from 1 km to 3 km, the relay cyclic delay diversity scheme “RCDD” yields 1.7 to 2.6 times cell throughput gain compared to a single hop system. We also notice that Relay Alamouti “RALA” yields no additional cell throughput gain while requiring additional overheard and higher complexity compared to the case “RCDD”. Although the case “RCC” gives the highest cell throughout, its relative gain compared to the case “RCDD” remains marginal in the order of 10% at the expense of higher overhead, feedback signalling and complexity. Furthermore, feedback errors in the channel state information are expected to degrade substantially the performance of the “RCC” scheme.
9.2. Performance with Max-SINR Scheduling
With Max-SINR scheduling (see section 8.-8.5.), the system can take full advantage of the channel variation of the different users as only the best subcarriers are allocated to the user. The cdf of the received SINR of the 1-hop and 2-hop systems is illustrated in Figure 11 where we notice a much higher received SINR in comparison with that obtained with Round Robin scheduling. We also notice that the 2-hop schemes outperform the 1-hop scheme and the “RSD” provides the best performance. The “RSD” scheme experiences less interference in comparison with the other 2-hop schemes and hence, can take better advantage of the variation of the fading multipath channel. This improvement in the received SINR will translate in a better system cell throughput. Figure 12 shows the cell throughput gain with respect to the 1-hop case for different cell radii and a demodulatingloss of 3 dB. It is observed that the gain is moderate, only 1.2-1.35 times. This is a result of the limited modulation levels used where, with a high received SINR as shown in Figure 11, the 2-hop relaying system becomes modulation limited and the SINR improvement provided by the 2-hop relaying schemes cannot be reflected in the system cell throughput.
In the case of more pronounced demodulation loss (10 dB), the cell throughput gain is evident as illustrated in Figure 13. A cell throughput gain of about 2 times is obtained with the different 2-hop relaying schemes in comparison with the 1-hop scheme.
It can be noticed from Figures 12 & 13 that for small to medium cell radii (i.e. smaller or equal to 2km) the relative cell throughput gain of the 2-hop schemes is roughly constant, whereas for larger cell radii (only shown for the round robin case in Figure 10) the cell throughput and by product the spectral efficiency increases further more.
10. Conclusions
Distributed relay diversity methods such as Relay Cyclic Delay Diversity (RCDD), Relay Alamouti, Relay Coherent Combining and Relay Selection Diversity that introduce frequency and macro diversity in a cooperative communication OFDM system were proposed, modeled, and evaluated in a dynamic multi-cell multi-user simulator. Further, analytical expressions for the received Signal to Interference Noise Ratio (SINR) were derived. The results were compared to the traditional 1-hop system. Simulation results showed considerable SINR gains, for both Round Robin and Max-SINR schedulers. As expected, SINR gains translated into substantial cell throughput gains. Finally some interesting observations were made:
• The investigated distributed diversity schemes outperforms the classical 1-hop scheme for both Round Robin scheduling and Max-SINR scheduling. These schemes yield up to a factor of 3 times performance gain.
• RCDD scheme provides up to 2.7 performance gain compared to a 1-hop system.
• Relay Alamouti yields no additional cell throughput gain compared to RCDD.
• Relay coherent combining method gives marginal gain compared to RCDD, in the order of 10%, at the expense of higher overhead, feedback signaling and complexity.
• Relay selection diversity yields the highest system throughput gain, slightly higher than the other investigated distributed diversity schemes. In fact, selecting a single relay to transmit during the second hop, reduces the experienced interference within the system quite considerably.
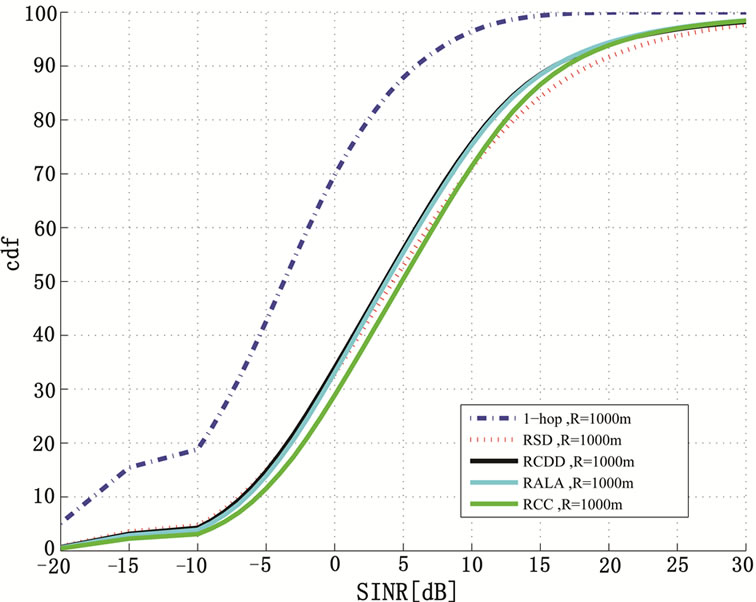
Figure 7. cdf of the SINR for 1-hop, RCDD, RSD, RCC and RALA for Round Robin Scheduling assuming 3 dB demodulating loss and a cell radius of 1 km.
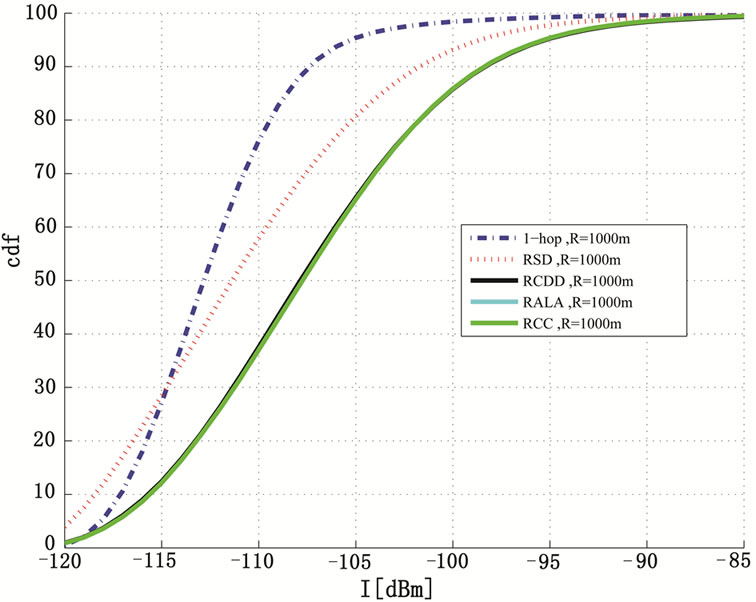
Figure 8. cdf of the interference for 1-hop, RCDD, RSD and RALA for Round Robin Scheduling assuming 3 dB demodulating loss and a cell radius of 1 km.

Figure 9. cdf of the signal for 1-hop, RCDD, RSD, RCC and RALA for Round Robin Scheduling assuming 3 dB demodulating loss and a cell radius of 1 km.

Figure 10. Normalized cell throughput versus the cell radius for 1-hop, RCDD, RSD, RCC and RALA for Round Robin Scheduling and 3 dB demodulating loss.
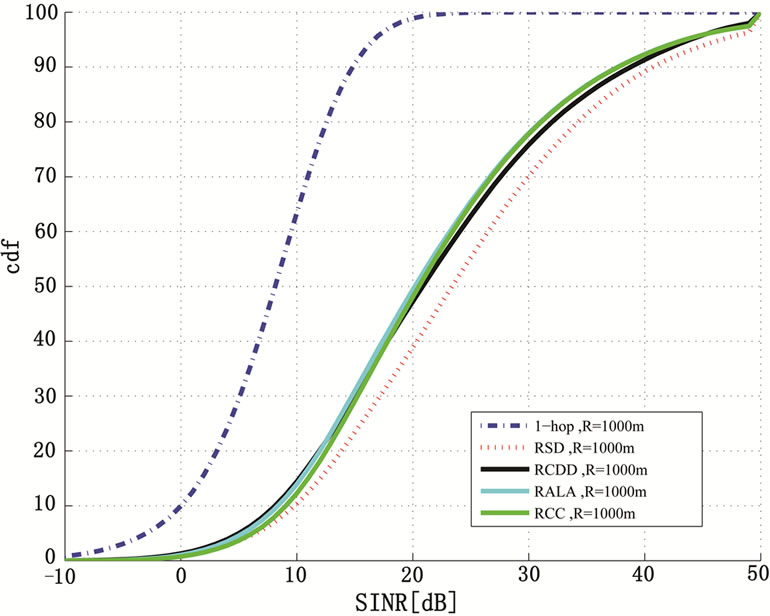
Figure 11. cdf of the SINR for 1-hop, RCDD, RSD, RCC and RALA for Max-SINR scheduling and 3 dB demodulating loss and a cell radius of 1 km.
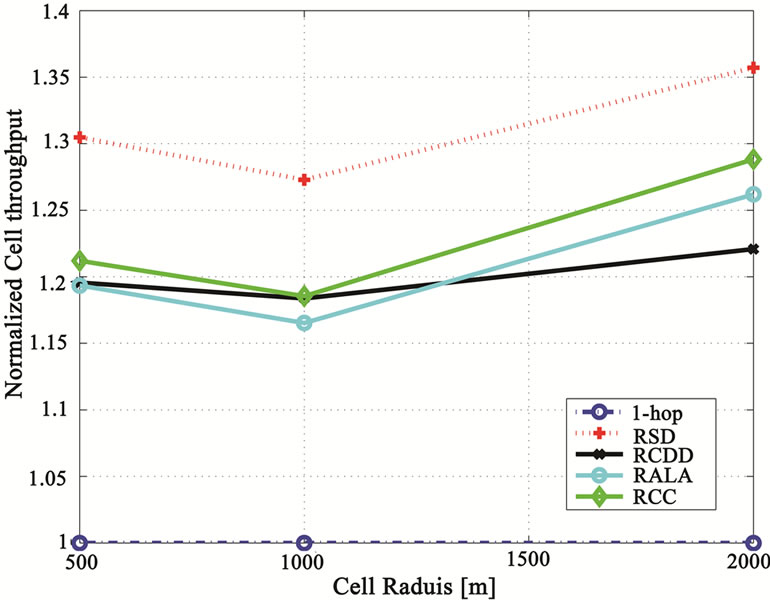
Figure 12. Normalized cell throughput versus the cell radius for 1-hop, RCDD, RSD, RCC and RALA for Max-SINR scheduling and 3 dB demodulating loss.
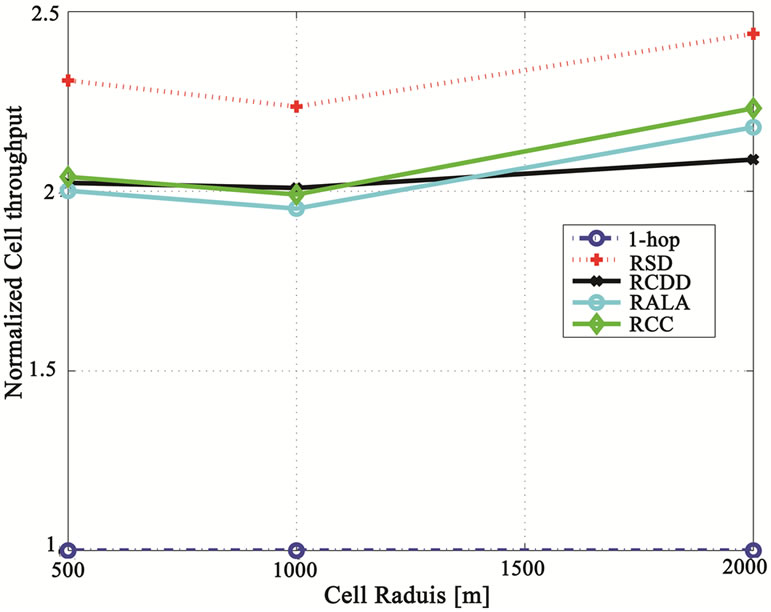
Figure 13. Normalized cell throughput versus the cell radius for 1-hop, RCDD, RSD, RCC and RALA for Max-SINR scheduling and 10 dB demodulating loss.
11. References
[1] S. M. Alamouti, “A simple transmit diversity technique for wireless communication,” IEEE J. Select. Areas Commun., Vol. 16, pp. 1451–1458, October 1998.
[2] V. Tarokh, N. Seshadri, and A. Calderbank, “Space-time codes for high data rate wireless communication: Performance criterion and code construction,” IEEE Transactions on Information Theory, Vol. 44, No. 2, pp. 744–765, March 1998.
[3] J. N. Laneman, “Cooperative diversity in wireless networks: Algorithms and architectures,” Ph.D. dissertation, Massachusetts Institute of Technology, Cambridge, MA, August 2002.
[4] A. Stefanov and E. Erkip, “Cooperative coding for wireless networks,” IEEE Transactions on Communications, Vol. 52, No. 9, pp. 1470–1476, September 2004.
[5] M. Dohler, E. Lefranc, and H. Aghvami, “Virtual antenna arrays for future wireless mobile communication systems,” in ICT 2002, Beijing, China, June 2002.
[6] P. Anghel and M. Kaveh, “On the performance of distributed space-time coding systems with one and two non-regenerative relays,” IEEE Transactions on Wireless Communications, Vol. 5, No. 2, pp. 682–692, March 2006.
[7] P. Larsson, “Large-scale cooperative relay network with optimal coherent combining under aggregate relay power constraints,” in Proceedings Future Telecommunications Conference, Beijing, China, pp. 166–170, December 2003.
[8] H. Rong, Z. Zhang, and P. Larsson, “Cooperative relaying based on Alamouti diversity under aggregate relay power constraints,” in Proceedings IEEE Vehicular Technology Conference, Spring, Melbroune, Australia, May 2006.
[9] A. Scaglione and Y. Hong, “Opportunistic large arrays: Cooperative transmission in wireless multihop ad hoc networks to reach far distances,” IEEE Transactions SP ’03, Vol. 51, No. 8, pp. 2082–2092, August 2003.
[10] S. Wei, D. Goeckel, and M. Valenti, “Asynchronous cooperative diversity,” in Conference on Information Sciences and Systems, 2004.
[11] S. B. Simane and A. Osseiran, “Relay communication with delay diversity for future communication systems,” in Proceedings IEEE Vehicular Technology Conference, Fall, Montreal, Canada, September 2006.
[12] A. Osseiran, “Advanced antennas in wireless communications: Co-located & distributed,” Ph.D. dissertation, Royal Institute of Technology, Stockholm, Sweden, May 2006.
[13] A. Wittneben, “A new bandwidth efficient transmit antenna modulation diversity scheme for linear digital modulation,” in IEEE International Conference on Communications, pp. 1630–1634, May 1993.
[14] K. Witrisal et al., “Antenna diversity for OFDM using cyclic delays,” in 8th Symposium on Communications and Vehicular Technology, Benelux, pp. 13–17, October 2001.
[15] M. Bossert et al., “On cyclic delay diversity in OFDM based transmission schemes,” in 7th International OFDM-Workshop, Hamburg, Germany, pp. 1–5, September 2002.
[16] O. Hyunseok et al., “Novel transmit diversity techniques for broadcast services in cellular networks,” in Proceedings IEEE Vehicular Technology Conference, Spring, vol. 2, Stockholm, Sweden, pp. 896–900, 2005.
[17] P. J. Davis, Circulant Matrices, 2nd Edition, New York: Chelsea, 1994.
[18] D. S. Baum, J. Salo, G. D. Galdo, M. Milojevic, P. Kyösti, and J. Hansen, “An interim channel model for beyond-3G systems,” in Proceedings IEEE Vehicular Technology Conference, Spring, Stockholm, Sweden, May 2005.
[19] 3GPP, “Spatial channel model for multiple input multiple output (mimo) simulations,” Technical Report 3GPP TR 25.996 V6.1.0, September 2003http://www.3gpp.org/ftp/Specs/html-info/25996.htm.
[20] J. Meinilä, Ed., IST-2003-507581 WINNER I, D5.4, Final report on link level and system level channel models, 2005, No. v1.
[21] -----, IST-2003-507581 WINNER I, D5.2, Determination of Propagation Scenario, 2005, No. v1.
[22] K. Brueninghaus et al., “Link performance models for system level simulations of broadband radio access systems,” in IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Berlin, Germany, September 2005.
Notes
1All nodes are assumed to be OFDM symbol synchronized in the downlink.
2D(x) is a diagonal matrix with x on its main diagonal.
2Airspan Networks, previously with Ericsson Research.
3The terms LOS and NLOS designate Line Of Sight and none LOS, respectively.
4Winner is a part of the European Union’s 6th Framework Programme.
5The users are uniformly distributed in the cells which are of hexagonal shapes. They are slowly moving in the cell plan with an average speed of 3 m/s and a small acceleration.

