Journal of Global Positioning Systems (2004)
Vol. 3, No. 1-2: 290-295
Convergence of Block Decorrelation Method for the Integer
Ambiguity Fix
Samsung Lim* & Binh Quoc Tran**
*School of Surveying & Spatial Information Systems, UNSW, Sydney NSW 2052, Australia
**Department of Geography, Hanoi University of Sciences, VNU, 332 Nguyen Trai, Thanh Xuan, Hanoi, Vietnam
Received: 15 Nov 2004 / Accepted: 3 Feb 2005
Abstract. Because of the integer-valued nature of carrier
phase ambiguities, it is essential to fix the float estimates
into integer values in order for high precision DGPS
positioning. A decorrelation process is necessary to solve
the problem since double-differenced ambiguities are
highly correlated in general. In this paper, Block
Decorrelation Method (BDM) is presented and tested for
its convergence. BDM divides the variance-covariance
matrix into four blocks and decorrelates them
simultaneously. A number of randomly selected examples
show that BDM is comparable to the existing
decorrelation algorithm, however its speed of
convergence is relatively faster due to the computations
performed on small blocks.
Key words: Carrier Phase, Decorrelation, Double-
Differenced, Integer Ambiguity, Variance-Covariance
1 Introduction
A float estimate for an initial ambiguity of GPS carrier
phase measurements can be obtained by the ordinary least
squares technique. However, it is essential to fix the
integer value in order to achieve high precision
positioning. The problem of integer ambiguities is
equivalent to the minimization of the following objective
function (Teunissen, 1998):
n
Zaaa
a
Q
T
aaaS ∈−
−
−= with )(
1
)()(min



(1)
where a

is a vector of n float values of double-
differenced ambiguities, which is obtained by the least
squares estimation with respect to the corresponding
variance-covariance matrix a
Q, a is a vector of n
unknown integer values of ambiguities, and n
Z
is the n-
dimensional integer space.
Searching for the minimum for )(aS is difficult because
it involves the discrete parameter a. In practice, Equation
(1) is usually solved by a discrete search strategy. The
idea is that the search space n
Z
can be replaced by a
small subset or ambiguity search space bounded by
hyper-ellipsoid:
)()(21 χ ≤−− −aaQaa a
T


 (2)
where 2 χ is a suitably chosen constant which ensures
that the ellipsoid contains at least one integer vector a.
The variance-covariance matrix a Q affects overall the
geometry of elongation and rotation of the search
ellipsoid and 2 χ determines its size. Consequently, a Q
directly affects the effectiveness of the search process. In
an ideal case, a Q is diagonal and hence a can be obtained
simply by rounding the float solution a

to nearest integer
values.
Double-differenced ambiguities are highly correlated, and
consequently, a Q is far from diagonal. It means that the
search ellipsoid is greatly elongated and its principal axes
are misaligned with the grids axes (Teunissen 1998, De
Jonge 1996). To speed up the search process, a Q needs
to be “decorrelated”. This can be done by using the linear
transformation aZz T = (Teunissen 1998). Equation (1)
is now equivalent to:
ZQZQaZzaZz
zzQzzS(z)
a
T
z
TT
z
T
 

 


===
−−= −
, ,with
)()(n 1
mi (3)

Lim et al: Convergence of Block Decorrelation Method for the Integer Ambiguity Fix 291
In order to preserve the nature of a in z, the
transformation matrix Z must satisfy two conditions:
 C1: Elements of Z must be integers;
 C2: Elements of 1−
Z
must be integers too. It is
equivalent to 1]det[±
=
Z.
Any permutation matrix or triangular integer matrix with
1± in its diagonal meets both conditions C1 and C2. The
transformation matrix T
Z
will be chosen so that z Q
become near-diagonal and its condition number c become
near 1. In general, a diagonal matrix z
Q with condition
number c=1 is impossible because of the two conditions
C1 and C2 above.
There may exist several methods of devising T
Z
. A
group of methods based on Gauss transformation
algorithm (Strang 1997, Teunissen 1998, Xu 2000) is at
hand. To decorrelate the element ()
ij
a
Q, T
k
Z can be
constructed as an identity matrix except one nonzero
element at row i and column j:
()
()
()
int
,
,1,11,0 11
/
, , ....
T
kzkzk
jj
ij
ij
TTTTT
zkkzkkzah h
ZQQ
QZQZQQZZZZ
−−− −
=−
===



(4)
where the operator
[]
int
⋅ denotes rounding to the nearest
integer. The procedure consists of many steps until the
last matrix T
k
Z becomes an identity matrix. The
transformation matrix T
Z
is a product of matrices
,
T
k
Z),...,1( hk =. Although Gauss transformation
algorithm usually decorrelates z Q well, its convergence
is slow because each element of a Q should be
decorrelated separately.
Another group of methods are based on the factorization
of the original matrix a Q:
DKKQ T
a=
 (5)
where D is a diagonal or a “near diagonal” matrix.
Processing float-valued T
K
properly, one can obtain
integer-valued transformation matrix T
Z
satisfying C1
and C2 so that
ZQZQa
T
z
= (6)
where z
Q is an almost diagonal matrix. The most popular
method for factorizing a Q is Cholesky’s factorization
(De Jonge 1996, Xu 2000):
DUUQLDLQ T
a
T
a==  or (7)
where L and U are lower- and upper-triangular matrices
with diagonal elements 1, respectively, and D is a
diagonal matrix. Note that D is an ideal form of a Q.
The simplest way to construct T
Z
is to round each
element of L or T Uto nearest integers, that is,
1
int
1,
int
1
int
21
1][...][
...............
001][
0001 −
−













=
nnn
T
LL
L
Zor
T
nnn
T
UU
U
Z
−
−













=
1][...][
...............
001][
0001
int
1,
int
1
int
21 (8)
For the factorization of a Q, one can also use Gram-
Schmidt orthogonalization process (Grapharend 2000, Xu
2000):
11 −−−− === ZQZOZOZVVQ Z TTTT
a
 (9)
where O is an almost orthogonal matrix, and
consequently, z Q is almost diagonal.
Methods based on factorizations are usually faster than
methods based on the Gauss transformation. However,
due to the fact that they deal with the original matrix a Q
indirectly via T
K
, their results may be relatively worse.
Also, some of the methods still experience difficulty with
convergence of iteration process (Xu, 2000).
In this paper, a new method for integer decorrelation of
variance-covariance matrix a Q, which is faster than the
method based on the Gauss transformation, will be
presented. This method deals with the original matrix a Q
directly, but unlike the Gauss transformation, it divides
a
Q into 4 small blocks and decorrelates elements in each
block simultaneously. Therefore, the new method will be
named as “Block Decorrelation Method” (BDM)
hereafter.
2 Block Decorrelation Method
Consider the following matrix multiplication:

292 Journal of Global Positioning Systems










=
−− 1
00
01
00
kn
T
k
k
ka
T
k
I
x
I
ZQZ




















−− 1
332313
232212
131211
00
010
0
**
kn
k
k
TT
T
I
xI
qqq
qqq
qqq










=
3313
1311
qtq
tps
qsq
k
T
T
kk
T
k
k
(10)
1211qxqskk +=,
TT
kqxqt 2313 += ,
11 1212221222
()
TT TTT
kk kkkkk
pxqqxxqqsxxqq=+++=++
where m
I
is an identity matrix of size m; the symmetric
positive-definite matrix a Q of size n*n is divided into 3
by 3 blocks because of the pre-multiplication by T
k
Z and
post-multiplication by k
Z
. Note that pk is a scalar, but
kk ts , are vectors. In Equation (10), it is clear that:
If the elements of k
xare integers, then T
k
Zis an
admissible transformation matrix that satisfies C1 and
C2.
The upper-left 11 q and lower-right 33 q are intact after the
multiplications. The blocks 13
q and T q13 do not change
too.
Since a Q is symmetric positive-definite, 11 q is invertible.
Consequently the off-diagonal blocks k s and T
k
s will be
zero if xk satisfies the following.
12
1
111211or 0qqxqxqs kkk
−
−==+=


(11)
Due to the condition C1, k x cannot be a float solution of
(11) and T
kkss ,cannot be set to zero. But one can expect
that T
kkss , will be “nearly zero” if k
x is rounded to the
nearest integers:
[]
int
kk xx

= (12)
Assume that index k increases monotonically from 1 to
(m-1) with a step size 1. By using Equations (10) to (12),
the elements of k
s and T
k
s can become close to zero.
After the recursive process up to (m-1) step, the (m*m)
upper-left block of the last matrix in Equation (10) will
have “decorrelated” elements all over the off-diagonal
area.
If another form T
h
Zof transformation matrix is taken,
Equations (10) to (12) will become Equation (13) to (15),
respectively:










=
−−1
00
10
00
hn
T
h
h
ha
T
h
I
x
I
ZQZ 




















−− 1
332313
232212
131211
0
010
00
**
hn
h
h
TT
T
Ix
I
qqq
qqq
qqq










=
3313
1311
qsq
spt
qtq
h
T
T
hh
T
h
h
(13)
T
hh qxqs 2333 +=, 1213 qxqt hh += ,
33 2323 2223 22
()
TTTTTT
hh hhhhh
pxqqxxqqsxxqq=+++=++
T
h
T
hh qqxqxqs 23
1
332333 or 0−
−==+=


(14)
[
]
int
hhxx

= (15)
Comparing with Equation (10), positions of s and t are
exchanged and the role of 11
q is now given to 33 q in
Equation (13). If the index h decreases from (n-2) to m
with the step size -1, the block 33 q will augment from
(1*1) to (n-m-1)*(n-m-1) matrix in the recursive process
of Equations (13), (14) and (15). In addition to that, there
is another useful block matrix multiplication:
11 12
12 22
11
0**
0
gg
Tg
gagTng Tng
g
g
T
gg
Iqq
I
y
ZQZ yI qq I
qs
sp
−−
 

= 

 



=


(16)
1211 qyqs gg
+
=
,
111212 221222
()
TT TTT
gg ggggg
pyqqyyqqsyyqq=+++=++
Again, the upper-left block 11 q does not change after
transformation. The off-diagonal blocks T
gg ss , will be
zero if g y

is a solution of:
12
1
111211 or 0qqyqyqgg
−
−==+


(17)
Because of the conditions C1, C2 imposed to T
g
Z, it is
only possible to set T
gg ss , to near zero by rounding the
solution of (17) to nearest integers:

Lim et al: Convergence of Block Decorrelation Method for the Integer Ambiguity Fix 293
[]
int
yyg

= (18)
Equations (10) to (18) provide an idea of decorrelating
a
Q. Dividing a Q into four blocks of nearly equal size
(see Figure 1), the upper-left block A can be decorrelated
using Equations (10) to (12). Equations (16) to (18) can
be used to make lower-left T
B and upper-right B near
zero, and then the lower right block C will be
decorrelated by Equations (13) to (15). Instead of full-
size matrix a Q, this process deals with smaller (or half-
size) blocks A, B, and C. Thus it will speed up the
decorrelation process of a Q.
a1 a2
a1 A
a2
a)
b b b
A B
b
b B
T
b
b)
A B
c2
B
T C c1
c2 c1
c)
Figure 1. Graphical visualization of block decorrelation
method for a 6*6 variance-covariance matrix: (a) - matrix
A
Q; (b) - AB Q; (c) - ABCZQQ =; a1, a2, c1, c2 show the
order of substeps in the corresponding step; elements
with gray color have near zero values.
Assume that there are n ambiguities in Equation (1),
m=n/2 if n is even, and m=(n+1)/2 if n is odd number.
BDM suggests decorrelating a
Q within a few numbers of
iteration; each consists of the following steps:
Step 1: Permute matrix a Q to obtain a Q
G
so that its first
m diagonal elements are minimal and stay in increasing
order, i.e.,
)( ][][...][][2211 njmQQQQ jjammaaa ≤<≤≤≤≤ 
G
G
G
G
This step is necessary to achieve a better decorrelation of
block A (Figure 1a). Assume that the minimal diagonal
element of a Q currently stays at row r. To make it the
first diagonal element, one can use the permutation:
11 A
H
a
Q
T
A
H
a
Q
G
= (19)
where T
A
H1 is a permutation matrix, obtained from the
identity matrix by exchanging rows 1 and r. Repeating
the procedure above for the second, third, … and mth-
diagonal elements, it yields to:
...... ...
11 (1)(1)
TT T
QHHHQHHH
aa
A
mAA Am Am Am
T
HQH
a AA
=−−
=
G


(20)
Note that T
Aj
H and T
A
H satisfy conditions C1 and C2 and
are admissible transformation matrices.
Step 2: Apply the decorrelation process to the upper-left
block A of a
Q
G
using Equations (10), (11) and (12) with
index k increasing from 1 to (m-1). The upper-left
diagonal block 11 q in Equation (10) will be gradually
augmented by T
kkss , and k
p to fill up A as shown in
Figure 1a. To speed up the process, the following formula
can be used for inverting the augmented matrix k q11,
based on the inverted matrix 11
11 ][−−k
q in previous substep
k-1:
[]






=






=
−
−−
−
−
−
2212
1211
1
11
1
1
11
1
11 GG
GG
ps
sq
qT
k
T
k
k
k
k
[
]
1
1
111
−
−
−
=kT
kqsR
(21)
1
1122 )(− −− −= kkRspG ,
2212 GRG T
−= ,
[
]
RGqGk
12
1
1
1111 −=−
−
Thus the process of Step 2 is recursive. It produces a
partially decorrelated matrix A
Q:
(1)2112(1)
[...] [...]
TTT
AAaAAAaAA
TTTT
AmAAAaAAAAm
QZQZZHQHZ
ZZZHQHZZZ
−−
==
=


G
(22)

294 Journal of Global Positioning Systems
Step 3: Decorrelate blocks B and T B of A Q (Figure 1b)
using Equations (16) to (18). The size of the block 11
q in
Equation (16) is m*m. To get its inverse, Equations (21)
and 11
11 ][ −−m
q from Step 2 can be used. As a result, AB Q is
obtained by:
BA
T
BAB ZQZQ = (23)
Step 4: Permute AB Q to yield AB Q
H
so that the diagonal
elements of its lower-right block C (Figure 1c) stays in
decreasing order, i.e.,
)1)(1()1)(1( ][...][][ ++−− ≤≤≤mmABnnABnnAB QQQ
H
H
H
.
Analogous to the Step 1, this procedure can be done by
the matrix T
C
H:
CAB
T
CABHQHQ =
H
(24)
The upper-left block A remains unchanged in this step.
Step 5: Decorrelate the last block C in AB Q
H
using
Equations (13) to (15) with index h decreasing from (n-2)
to m. The lower-right block 33 q in Equation (13) will be
gradually augmented by T
hh ss, and h
p to fill up C as
shown in Figure 1. The formula for inverting the
augmented matrix is similar to Equation (21):
[]






=






=
−
−
−
−−
−
2212
1211
1
1
331
11
1
33 GG
GG
qs
sp
qT
h
h
T
hh
h
[]
1
1
1
33 −
−
−
=h
hsqR
(25)
1
1111 )( − −− −= RspG T hh ,
T
RGG 1112 −= ,
[]
12
1
1
3322 RGqG h−=−
−
The first m elements of the vector 12 q and the first m
rows of 13
q in Equation (13) are near zero because the
block B is already decorrelated in Step 3. Thus the first
m elements of the vector 1213 qxqt hh += in Equation
(13) also become near zero. Hence, elements of T B and
B remain near-zero, even though they can change at Step
5. It provides a decorrelated matrix iz Q:
CAB
T
CABCiz ZQZQQ
H
== (26)
Combining Equations (20), (22), (23), (24) and (26)
yields:
(2)(1)1
1(1) (2)
[ ......]
[...... ] *
T TTT T
ziCCBAAaAA BCC
TTTTTTT
CmC nCBA mAAa
AAAmB CCnCm
QZHZZHQHZZHZ
Z
ZHZZ ZHQ
HZ ZZHZZ
−−
−−
=
=
 

(27)
The transformation matrix T
i
Zin current ith-iteration is
obtained by Equation (27):
T
A
T
A
T
mA
T
B
T
C
T
nC
T
Cm
T
iHZZZHZZZ1)1()2( ...... −−
= (28)
Since ,
T
Ch
Z ,
T
B
ZT
Ak
Z ;,...,2(mnh −
=
)1,...,0
−
=mk and
T
C
T
AHH ,satisfy conditions C1 and C2, it is readily seen
that T
i
Z satisfies these conditions too.
The procedure described in steps 1 to 5 can be repeated
until T
i
Z becomes an identity matrix i.e., until no further
decorrelation of a
Q can be obtained. The final
transformation matrix T
Z
is then computed by:
∏
=
−== 1 11...
Mi
T
i
TT
M
T
M
TZZZZZ (29)
where M denotes the number of iteration. An estimation
shows that each iteration without explicit calculation of
T
i
Zrequires about 7n3/8 multiplication. Therefore, the
decorrelation process requires about 7Mn3/8
multiplication.
3 Numerical Example
In this section, BDM is used for decorrelating two sets of
ambiguities. Ambiguities of these numerical examples are
highly correlated. To quantify the decorrelation of a Q,
two kinds of measures are used:
 The correlation coefficients;
 The condition number c which is the ratio of the
largest and the smallest singular value of
variance-covariance matrix.
If e denotes the elongation of the ellipsoid in Equation (2)
then:
2
min
2
max
2/RRec == (30)
where max R and min R are the largest and smallest axes of
the ellipsoid, respectively.
Table 1 shows the main characteristics of the
decorrelation process: the condition numbers ca and cz,
the smallest min
ρ
and the largest max
ρ
correlation
coefficients of original matrix a
Q and decorrelated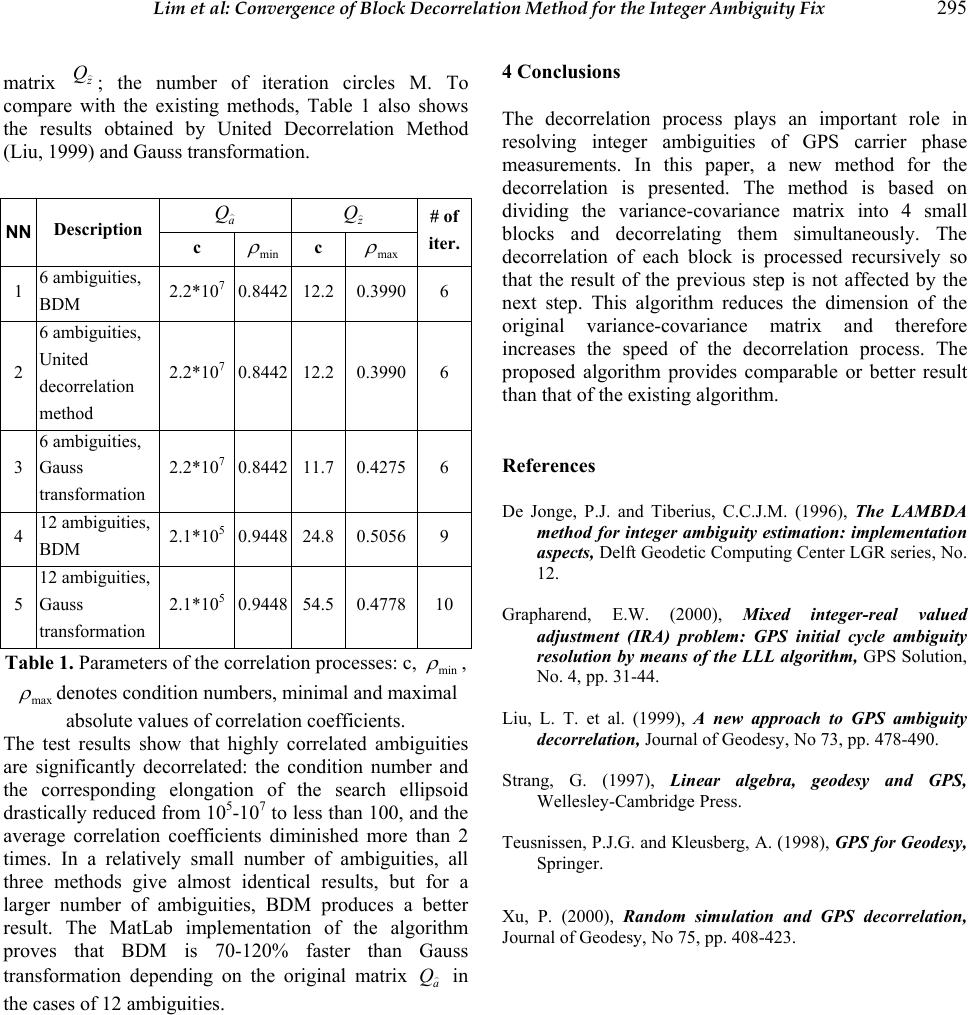

Lim et al: Convergence of Block Decorrelation Method for the Integer Ambiguity Fix 295
matrix z
Q; the number of iteration circles M. To
compare with the existing methods, Table 1 also shows
the results obtained by United Decorrelation Method
(Liu, 1999) and Gauss transformation.
a
Q z Q
NN Description
c min
ρ
c max
ρ
# of
iter.
1 6 ambiguities,
BDM 2.2*107 0.8442 12.2 0.3990 6
2
6 ambiguities,
United
decorrelation
method
2.2*107 0.8442 12.2 0.3990 6
3
6 ambiguities,
Gauss
transformation
2.2*107 0.8442 11.7 0.4275 6
4 12 ambiguities,
BDM 2.1*105 0.9448 24.8 0.5056 9
5
12 ambiguities,
Gauss
transformation
2.1*105 0.9448 54.5 0.4778 10
Table 1. Parameters of the correlation processes: c, min
ρ
,
max
ρ
denotes condition numbers, minimal and maximal
absolute values of correlation coefficients.
The test results show that highly correlated ambiguities
are significantly decorrelated: the condition number and
the corresponding elongation of the search ellipsoid
drastically reduced from 105-107 to less than 100, and the
average correlation coefficients diminished more than 2
times. In a relatively small number of ambiguities, all
three methods give almost identical results, but for a
larger number of ambiguities, BDM produces a better
result. The MatLab implementation of the algorithm
proves that BDM is 70-120% faster than Gauss
transformation depending on the original matrix a Q in
the cases of 12 ambiguities.
4 Conclusions
The decorrelation process plays an important role in
resolving integer ambiguities of GPS carrier phase
measurements. In this paper, a new method for the
decorrelation is presented. The method is based on
dividing the variance-covariance matrix into 4 small
blocks and decorrelating them simultaneously. The
decorrelation of each block is processed recursively so
that the result of the previous step is not affected by the
next step. This algorithm reduces the dimension of the
original variance-covariance matrix and therefore
increases the speed of the decorrelation process. The
proposed algorithm provides comparable or better result
than that of the existing algorithm.
References
De Jonge, P.J. and Tiberius, C.C.J.M. (1996), The LAMBDA
method for integer ambiguity estimation: implementation
aspects, Delft Geodetic Computing Center LGR series, No.
12.
Grapharend, E.W. (2000), Mixed integer-real valued
adjustment (IRA) problem: GPS initial cycle ambiguity
resolution by means of the LLL algorithm, GPS Solution,
No. 4, pp. 31-44.
Liu, L. T. et al. (1999), A new approach to GPS ambiguity
decorrelation, Journal of Geodesy, No 73, pp. 478-490.
Strang, G. (1997), Linear algebra, geodesy and GPS,
Wellesley-Cambridge Press.
Teusnissen, P.J.G. and Kleusberg, A. (1998), GPS for Geodesy,
Springer.
Xu, P. (2000), Random simulation and GPS decorrelation,
Journal of Geodesy, No 75, pp. 408-423.