 J. Biomedical Science and Engineering, 2013, 6, 165-174 JBiSE http://dx.doi.org/10.4236/jbise.2013.62020 Published Online February 2013 (http://www.scirp.org/journal/jbise/) Novel algorithms for accurate DNA base-calling Omniyah G. Mohammed1, Khaled T. Assaleh1, Ghaleb A. Husseini2, Amin F. Majdalawieh3, Scott R. Woodward4 1Department of Electrical Engineering, American University of Sharjah, Sharjah, UAE 2Department of Chemical Engineering, American University of Sharjah, Sharjah, UAE 3Department of Biology, Chemistry and Environmental Sciences, American University of Sharjah, Sharjah, UAE 4Sorenson Molecular Genealogy Foundation, Salt Lake City, USA Email: kassaleh@aus.edu Received 5 October 2012; revised 6 November 2012; accepted 17 November 2012 ABSTRACT The ability to decipher the genetic code of different species would lead to significant future scientific achi- evements in important areas, including medicine and agriculture. The importance of DNA sequencing ne- cessitated a need for efficient automation of identi- fication of base sequences from traces generated by existing sequencing machines, a process referred to as DNA base-calling. In this pap er, a pattern recognition technique was adopted to minimize the inaccuracy in DNA base-calling. Two new frameworks using Artifi- cial Neural Networks and Polynomial Classifiers are proposed to model electropherogram traces belonging to Homo sapiens, Saccharomyces mikatae and Dro- sophila melanogaster. De-correlation, de-convolution and normalization were implemented as part of the pre-processing stage employed to minimize data im- perfections attributed to the nature of the chemical reactions involved in DNA sequencing. Discriminative features that characterize each chromatogram trace were subsequently extracted and subjected to the chosen classifiers to categorize the events to their re- spective base classes. The models are trained such that they are not restricted to a specific species or to a specific chemical procedure of sequencing. The base- calling accuracy achieved is compared with the exist- ing standards, PHRED (Phil’s Read Editor) and ABI (Applied Biosystems, version 2.1.1) KB base-callers in terms of deletion, insertion and substitution errors. Experimental evidence indicates that the proposed models achieve a higher base-calling accuracy when compared to PHRED and a comparable performance when compared to ABI. The results obtained demon- strate the potential of the proposed models for effi- cient and accurate DNA base-calling. Keywords: Artificial Neural Network (ANN); Base-Calling; Electropherogram; Polynomial Classifier (PC); Sequencing 1. INTRODUCTION Until the last decade, the complete human genome se- quence was not identified. However, a massive research effort resulted in deciphering nearly three billion con- stituents of the human genome. The human genome re- fers to the heredity information encoded in the DNA of Homo sapiens stored in 23 pairs of chromosomes located in the cell nucleus. A DNA, or deoxyribonucleic acid, strand consists of four nucleotide bases: Adenine (A), Cytosine (C), Thymine (T) and Guanine (G). A DNA molecule has a double helical structure consisting of two intertwined chains made up of complementary nucleotide strands in which A bonds with T and C pairs up with G [1]. The process of determining the ordered sequence of these nucleotide bases in a DNA molecule is referred to as DNA sequencing. Information derived from the ge- nomic sequence is likely to contribute enormously to medical advances such as more accurate diagnosis of genetic diseases, improved drug design to target specific genes causing certain diseases and gene therapy by re- placement of defective genes. The ability to decode the genetic material is also very important to researchers trying to improve the resistance of crops to parasites, detect bacteria that may pollute air or water, determine pedigree for seed or livestock breeds, explore species origin and ancestry, and determine the cause of migration of different populations and various other evolutionary studies. DNA sequencing also has potential benefits in applied fields such as DNA forensics in which crime suspects can be identified by matching their DNA with evidence left at crime scenes, establishing paternity and identifying crime and catastrophe victims. One of the first DNA sequencing techniques was de- veloped in 1976 by Maxam and Gilbert based on chemi- cal modification of the DNA molecule which breaks a terminally labeled DNA template partially at each base. The reaction of dimethyl sulphate, piperidine, formic acid, hydrazine and sodium chloride, individually or in combinations, causes the cleavage of the four bases. The OPEN ACCESS 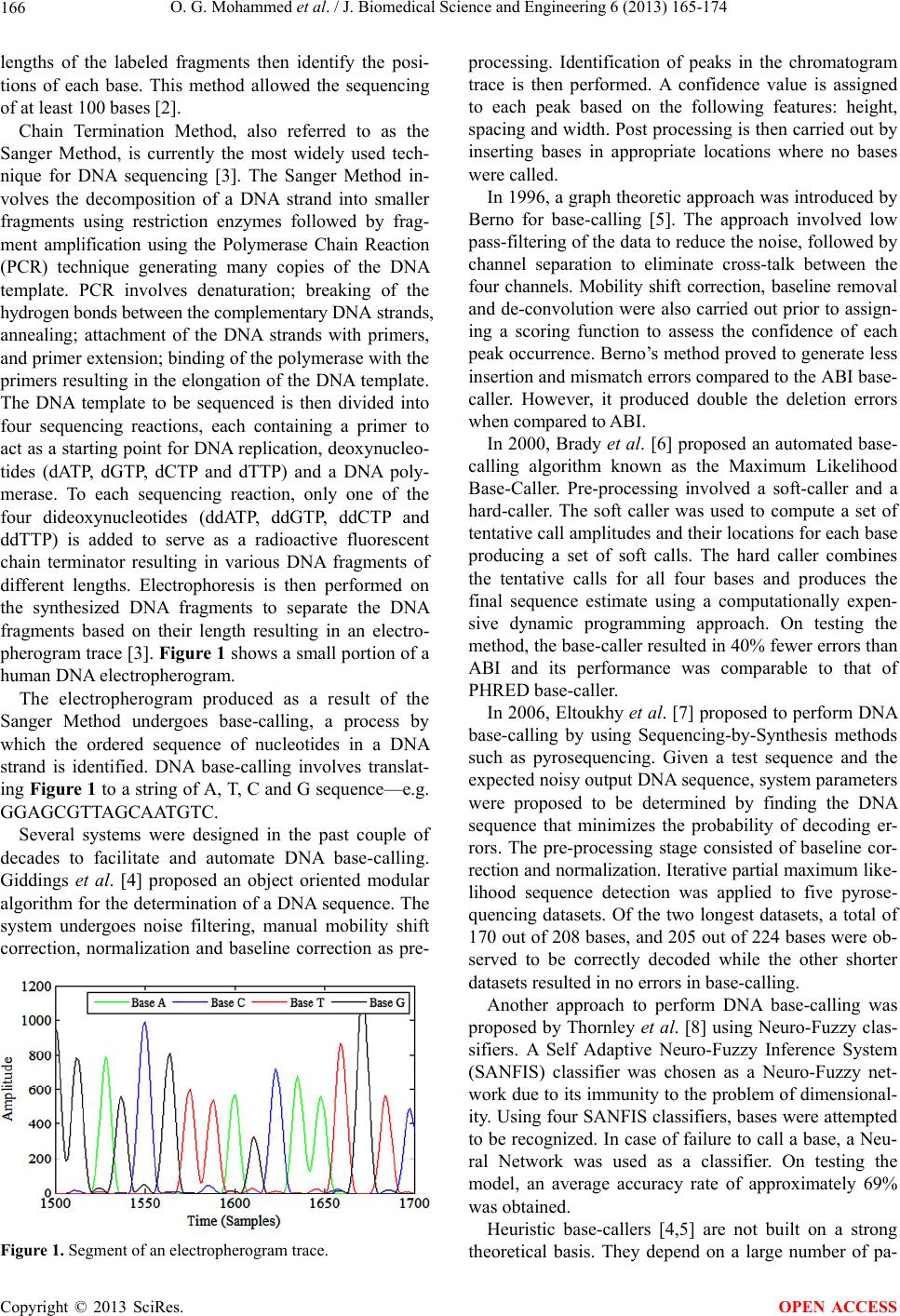 O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 166 lengths of the labeled fragments then identify the posi- tions of each base. This method allowed the sequencing of at least 100 bases [2]. Chain Termination Method, also referred to as the Sanger Method, is currently the most widely used tech- nique for DNA sequencing [3]. The Sanger Method in- volves the decomposition of a DNA strand into smaller fragments using restriction enzymes followed by frag- ment amplification using the Polymerase Chain Reaction (PCR) technique generating many copies of the DNA template. PCR involves denaturation; breaking of the hydrogen bonds between the complementary DNA strands, annealing; attachment of the DNA strands with primers, and primer extension; binding of the polymerase with the primers resulting in the elongation of the DNA template. The DNA template to be sequenced is then divided into four sequencing reactions, each containing a primer to act as a starting point for DNA replication, deoxynucleo- tides (dATP, dGTP, dCTP and dTTP) and a DNA poly- merase. To each sequencing reaction, only one of the four dideoxynucleotides (ddATP, ddGTP, ddCTP and ddTTP) is added to serve as a radioactive fluorescent chain terminator resulting in various DNA fragments of different lengths. Electrophoresis is then performed on the synthesized DNA fragments to separate the DNA fragments based on their length resulting in an electro- pherogram trace [3]. Figure 1 shows a small portion of a human DNA electropherogram. The electropherogram produced as a result of the Sanger Method undergoes base-calling, a process by which the ordered sequence of nucleotides in a DNA strand is identified. DNA base-calling involves translat- ing Figure 1 to a string of A, T, C and G sequence—e.g. GGAGCGTTAGCAATGTC. Several systems were designed in the past couple of decades to facilitate and automate DNA base-calling. Giddings et al. [4] proposed an object oriented modular algorithm for the determination of a DNA sequence. The system undergoes noise filtering, manual mobility shift correction, normalization and baseline correction as pre- Figure 1. Segment of an electropherogram trace. processing. Identification of peaks in the chromatogram trace is then performed. A confidence value is assigned to each peak based on the following features: height, spacing and width. Post processing is then carried out by inserting bases in appropriate locations where no bases were called. In 1996, a graph theoretic approach was introduced by Berno for base-calling [5]. The approach involved low pass-filtering of the data to reduce the noise, followed by channel separation to eliminate cross-talk between the four channels. Mobility shift correction, baseline removal and de-convolution were also carried out prior to assign- ing a scoring function to assess the confidence of each peak occurrence. Berno’s method proved to generate less insertion and mismatch errors compared to the ABI base- caller. However, it produced double the deletion errors when compared to ABI. In 2000, Brady et al. [6] proposed an automated base- calling algorithm known as the Maximum Likelihood Base-Caller. Pre-processing involved a soft-caller and a hard-caller. The soft caller was used to compute a set of tentative call amplitudes and their locations for each base producing a set of soft calls. The hard caller combines the tentative calls for all four bases and produces the final sequence estimate using a computationally expen- sive dynamic programming approach. On testing the method, the base-caller resulted in 40% fewer errors than ABI and its performance was comparable to that of PHRED base-caller. In 2006, Eltoukhy et al. [7] proposed to perform DNA base-calling by using Sequencing-by-Synthesis methods such as pyrosequencing. Given a test sequence and the expected noisy output DNA sequence, system parameters were proposed to be determined by finding the DNA sequence that minimizes the probability of decoding er- rors. The pre-processing stage consisted of baseline cor- rection and normalization. Iterative partial maximum like- lihood sequence detection was applied to five pyrose- quencing datasets. Of the two longest datasets, a total of 170 out of 208 bases, and 205 out of 224 bases were ob- served to be correctly decoded while the other shorter datasets resulted in no errors in base-calling. Another approach to perform DNA base-calling was proposed by Thornley et al. [8] using Neuro-Fuzzy clas- sifiers. A Self Adaptive Neuro-Fuzzy Inference System (SANFIS) classifier was chosen as a Neuro-Fuzzy net- work due to its immunity to the problem of dimensional- ity. Using four SANFIS classifiers, bases were attempted to be recognized. In case of failure to call a base, a Neu- ral Network was used as a classifier. On testing the model, an average accuracy rate of approximately 69% was obtained. Heuristic base-callers [4,5] are not built on a strong theoretical basis. They depend on a large number of pa- Copyright © 2013 SciRes. OPEN ACCESS  O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 Copyright © 2013 SciRes. 167 OPEN ACCESS rameters that needs to be optimized to a specific type of chemistry or to a certain type of sequencing technology. Statistical base-callers [6] are either poorly tested or slow, due to the high computational complexity of the imple- mented algorithms. In this paper, a well-established pat- tern recognition framework is used to build our base- caller. Artificial Neural Networks (ANN) and Polynomial Classifiers (PC) are proposed as base-calling classifiers such that the base-caller designed is not restricted to a specific chemistry or sequencing machine. Success achie- ved in our approach indicates the potential of our models. The rest of the paper is organized as follows. In section II, we briefly describe the method adopted for data acquisi- tion, pre-processing and feature extraction. In section III, we describe the proposed system models: Artificial Neu- ral Network (ANN) and Polynomial Classifier (PC), fol- lowed by a brief description of the testing results ob- tained using the trained models in Section 4. Finally, Section 5 summarizes our conclusions. 2. DATA ACQUISITION, PREPROCESSING AND FEATURE EXTRACTION The approach adopted in this paper to solve the problem of base-calling is based on designing a pattern recogni- tion classifier. The data to be classified are acquired from sequencing machines; hence a pre-processing stage is needed to achieve noise removal prior to feature extrac- tion. The success in the implementation of any approach depends on the effectiveness of the features extracted to represent a DNA pattern. In this section, the main com- ponents of any pattern recognition model are: data ac- quisition (or sensing), pre-processing and feature extrac- tion, are discussed. 2.1. Data Acquisition/Sensing One of the main considerations in designing a pattern recognition classifier is the presence of an adequate size of data to train and test the model. Performance of the classifier model increases as the amount of data used increases. The training data are chosen such that every possible case scenario is seen and learnt by the model. However, over-fitting needs to be prevented so that the generalization of the classifier model to novel data is not affected. The needed chromatogram traces for training and test- ing the classifier models were obtained from the Sorenson Molecular Genealogy Foundation (SMGF) along with their respective consensus sequences, i.e. DNA sequences obtained from the sequencing of overlapping fragments of a gene several times. Moreover, data obtained from the National Center for Biotechnology Information (NCBI) trace archive [9] were labeled using commercially avail- able PHRED base-calling software, CodonCode Aligner. PHRED is used since it demonstrates high accuracy when tested over a wide variety of sequencing methods and has proven to have a higher system performance compared to other existing base-callers [10]. The NCBI Basic Local Alignment Search Tool (BLAST) is then run on each PHRED generated sequence to locate the corre- sponding consensus sequence for each DNA fragment being tested. The determined consensus sequences were used to label the chromatogram traces for accurate train- ing of the classifier. To evaluate the performance of the designed classifier models based on noise contamination, chromatogram source and read length of the electropherograms, the traces obtained from the SMGF and from the NCBI trace archive were categorized into three main data sets as shown in Table 1. For the analysis of classifier performance, the DNA sequence obtained using PHRED and ABI base-callers on the above three data sets are needed. CodonCode Aligner and Bioedit were used to obtain the DNA se- quence called by PHRED and ABI base-callers. 2.2. Pre-Processing Electropherograms obtained after the implementation of electrophoresis may be contaminated by noise introduced at various stages of DNA sequencing. Noise contamina- tion occurs as a result of the imperfections in the chemis- try involved and the electronics of electrophoresis. Noise superimposed on a DNA trace may appear in the form of overlapping spectra, presence of one or more large peaks at the beginning of the trace, a drift in the DC value of the signal, variations in the dynamic range, or low peak resolution. The data chosen for both training and testing the designed models are hence subjected to several stages Table 1. Distribution of data acquired into three data sets. Data Set No. Data Source No. of Traces Specie Characteristics 1 NCBI 6 Homo sapiens chromosome: 5, 6, 11, 12, 13. Noisy trace, belongs to one species, consists of 600 - 700 bases. 2 NCBI & SMGF 11 Homo sapiens mitochondrian D-loop, Saccharomyces mikatae, Drosophila melanogaster. Noisy trace, belongs to three species, consists of 675 - 775 bases. 3 SMGF 5 Homo sapiens mitochondrian D-loop. Lower noise level, trace belongs to only one species, consists of 800 - 900 bases. 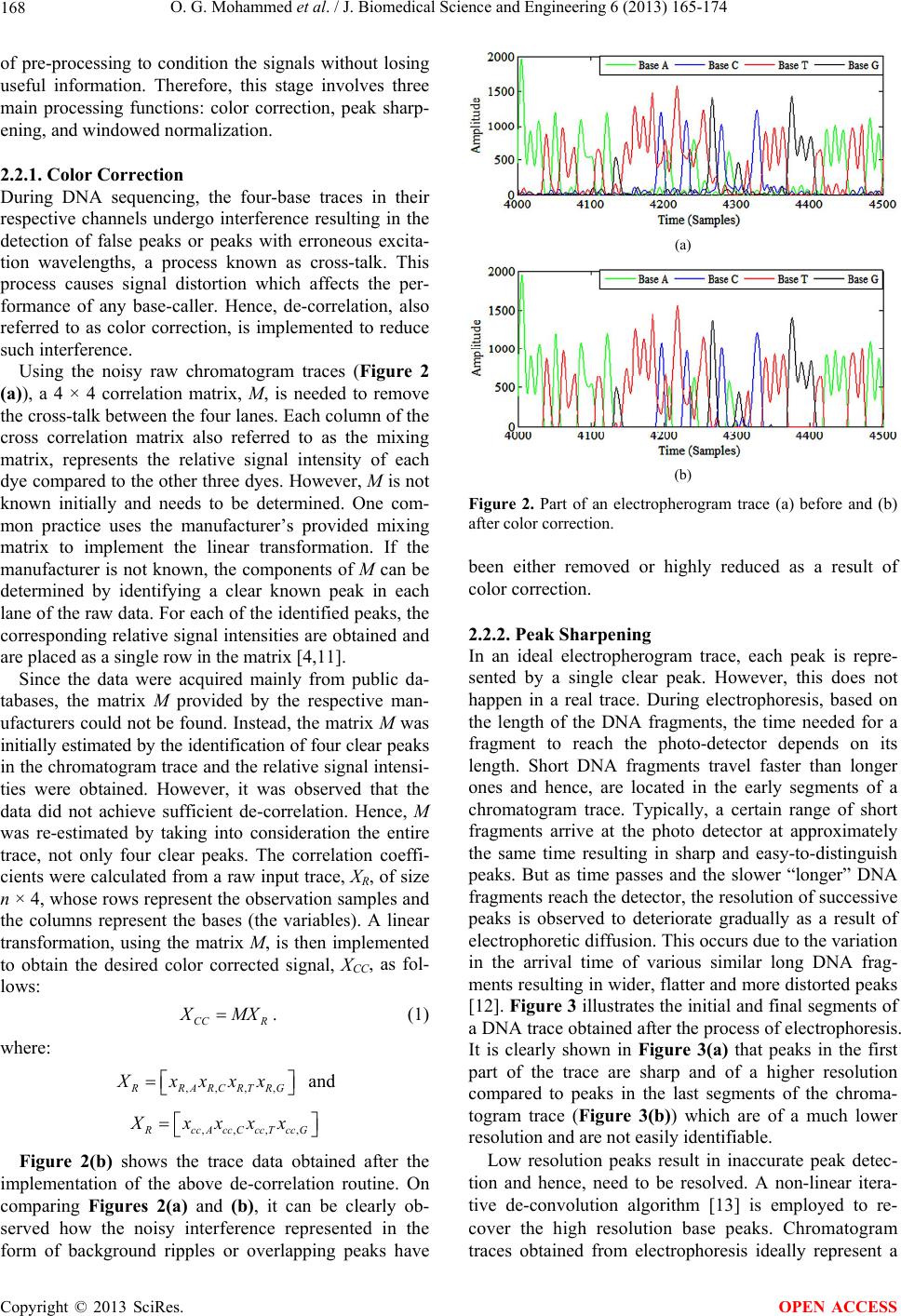 O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 168 of pre-processing to condition the signals without losing useful information. Therefore, this stage involves three main processing functions: color correction, peak sharp- ening, and windowed normalization. 2.2.1. Color Correction During DNA sequencing, the four-base traces in their respective channels undergo interference resulting in the detection of false peaks or peaks with erroneous excita- tion wavelengths, a process known as cross-talk. This process causes signal distortion which affects the per- formance of any base-caller. Hence, de-correlation, also referred to as color correction, is implemented to reduce such interference. Using the noisy raw chromatogram traces (Figure 2 (a)), a 4 × 4 correlation matrix, M, is needed to remove the cross-talk between the four lanes. Each column of the cross correlation matrix also referred to as the mixing matrix, represents the relative signal intensity of each dye compared to the other three dyes. However, M is not known initially and needs to be determined. One com- mon practice uses the manufacturer’s provided mixing matrix to implement the linear transformation. If the manufacturer is not known, the components of M can be determined by identifying a clear known peak in each lane of the raw data. For each of the identified peaks, the corresponding relative signal intensities are obtained and are placed as a single row in the matrix [4,11]. Since the data were acquired mainly from public da- tabases, the matrix M provided by the respective man- ufacturers could not be found. Instead, the matrix M was initially estimated by the identification of four clear peaks in the chromatogram trace and the relative signal intensi- ties were obtained. However, it was observed that the data did not achieve sufficient de-correlation. Hence, M was re-estimated by taking into consideration the entire trace, not only four clear peaks. The correlation coeffi- cients were calculated from a raw input trace, XR, of size n × 4, whose rows represent the observation samples and the columns represent the bases (the variables). A linear transformation, using the matrix M, is then implemented to obtain the desired color corrected signal, XCC, as fol- lows: CC R MX. (1) where: ,,,,RRARCRTRG Xxxxx and ,,,,RccAcc Ccc Tcc G Xxxxx Figure 2(b) shows the trace data obtained after the implementation of the above de-correlation routine. On comparing Figures 2(a) and (b), it can be clearly ob- served how the noisy interference represented in the form of background ripples or overlapping peaks have (a) (b) Figure 2. Part of an electropherogram trace (a) before and (b) after color correction. been either removed or highly reduced as a result of color correction. 2.2.2. Pe ak Sharpeni ng In an ideal electropherogram trace, each peak is repre- sented by a single clear peak. However, this does not happen in a real trace. During electrophoresis, based on the length of the DNA fragments, the time needed for a fragment to reach the photo-detector depends on its length. Short DNA fragments travel faster than longer ones and hence, are located in the early segments of a chromatogram trace. Typically, a certain range of short fragments arrive at the photo detector at approximately the same time resulting in sharp and easy-to-distinguish peaks. But as time passes and the slower “longer” DNA fragments reach the detector, the resolution of successive peaks is observed to deteriorate gradually as a result of electrophoretic diffusion. This occurs due to the variation in the arrival time of various similar long DNA frag- ments resulting in wider, flatter and more distorted peaks [12]. Figure 3 illustrates the initial and final segments of a DNA trace obtained after the process of electrophoresis. It is clearly shown in Figure 3(a) that peaks in the first part of the trace are sharp and of a higher resolution compared to peaks in the last segments of the chroma- togram trace (Figure 3(b)) which are of a much lower resolution and are not easily identifiable. Low resolution peaks result in inaccurate peak detec- tion and hence, need to be resolved. A non-linear itera- tive de-convolution algorithm [13] is employed to re- cover the high resolution base peaks. Chromatogram traces obtained from electrophoresis ideally represent a Copyright © 2013 SciRes. OPEN ACCESS 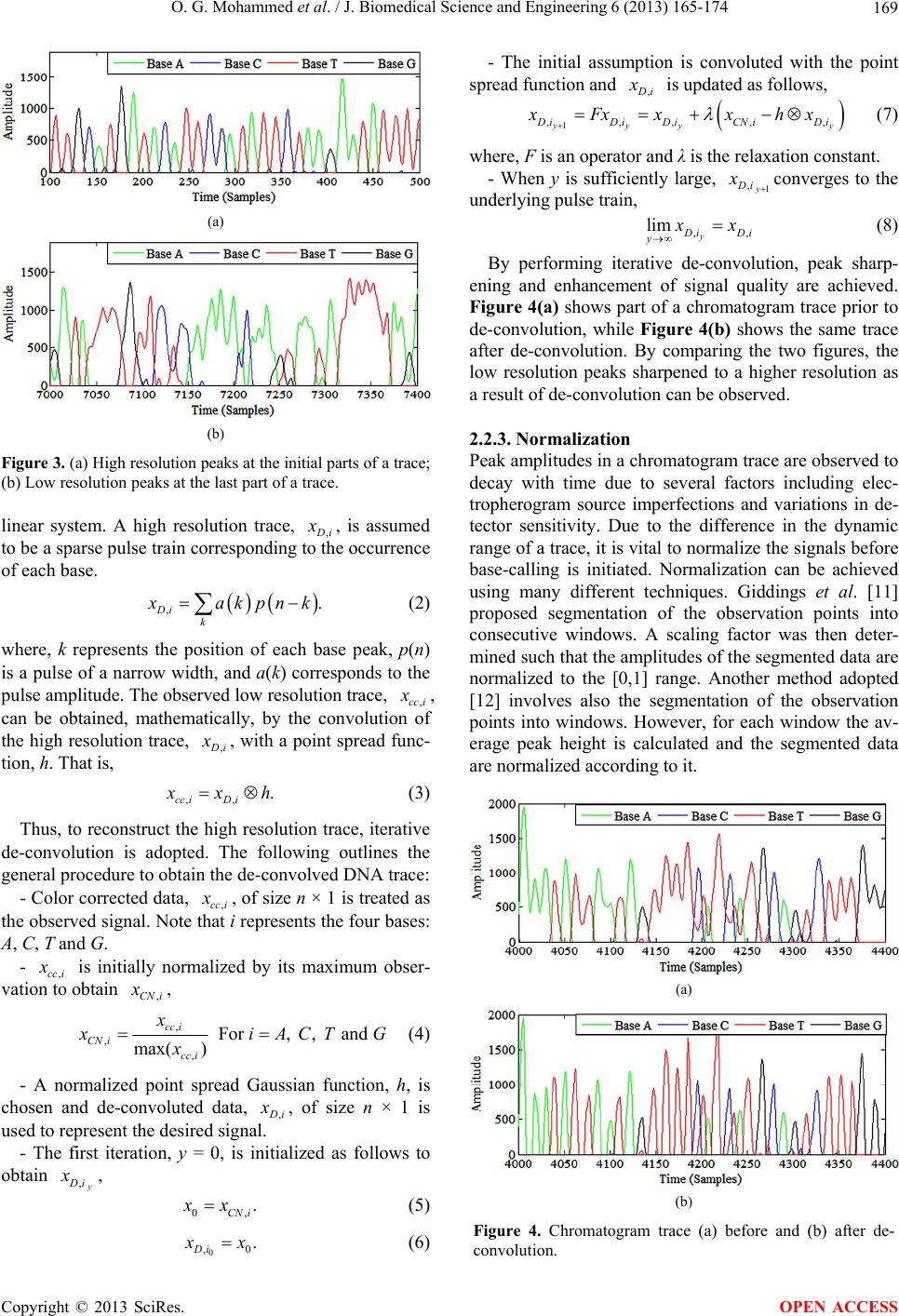 O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 169 (a) (b) Figure 3. (a) High resolution peaks at the initial parts of a trace; (b) Low resolution peaks at the last part of a trace. linear system. A high resolution trace, , i , is assumed to be a sparse pulse train corresponding to the occurrence of each base. ,. Di k ak pnk (2) where, k represents the position of each base peak, p(n) is a pulse of a narrow width, and a(k) corresponds to the pulse amplitude. The observed low resolution trace, ,cc i , can be obtained, mathematically, by the convolution of the high resolution trace, , i , with a point spread func- tion, h. That is, ,, . cc iD i xh (3) Thus, to reconstruct the high resolution trace, iterative de-convolution is adopted. The following outlines the general procedure to obtain the de-convolved DNA trace: - Color corrected data, ,cc i , of size n × 1 is treated as the observed signal. Note that i represents the four bases: A, C, T and G. - ,cci is initially normalized by its maximum obser- vation to obtain ,CN i , , , , For , , and max( ) cc i CN i cc i x iACT G x (4) - A normalized point spread Gaussian function, h, is chosen and de-convoluted data, , i , of size n × 1 is used to represent the desired signal. - The first iteration, y = 0, is initialized as follows to obtain ,y i , 0. CN i xx, 0 (5) 0 ,. Di x (6) - The initial assumption is convoluted with the point spread function and , i is updated as follows, 1 ,,, , yyy DiDi DiCNiDi xFxxxhx , y , (7) where, F is an operator and λ is the relaxation constant. - When y is sufficiently large, converges to the underlying pulse train, 1 ,y Di x , lim y iD yi x (8) By performing iterative de-convolution, peak sharp- ening and enhancement of signal quality are achieved. Figure 4(a) shows part of a chromatogram trace prior to de-convolution, while Figure 4(b) shows the same trace after de-convolution. By comparing the two figures, the low resolution peaks sharpened to a higher resolution as a result of de-convolution can be observed. 2.2.3. N ormaliz ation Peak amplitudes in a chromatogram trace are observed to decay with time due to several factors including elec- tropherogram source imperfections and variations in de- tector sensitivity. Due to the difference in the dynamic range of a trace, it is vital to normalize the signals before base-calling is initiated. Normalization can be achieved using many different techniques. Giddings et al. [11] proposed segmentation of the observation points into consecutive windows. A scaling factor was then deter- mined such that the amplitudes of the segmented data are normalized to the [0,1] range. Another method adopted [12] involves also the segmentation of the observation points into windows. However, for each window the av- erage peak height is calculated and the segmented data are normalized according to it. (a) (b) Figure 4. Chromatogram trace (a) before and (b) after de- convolution. Copyright © 2013 SciRes. OPEN ACCESS  O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 170 In this paper, a simple windowed normalization tech- nique is adopted to obtain a normalized chromatogram trace. The pre-processed trace obtained from the previous stage is initially divided into non-overlapping consecu- tive windows. Each segment is then normalized by its maximum amplitude. Figure 5(a) illustrates the trace signal prior to normalization while Figure 5(b) illus- trates the same trace after normalization. The decay in the amplitude is evident in Figure 5(a) while the uni- formity of the signal height after normalization is seen in Figure 5(b). 2.3. Feature Extraction Feature extraction is the main stage which has a direct effect on the performance of a pattern recognition model. Feature extraction can be thought of as a form of dimen- sionality reduction. It is the process in which the pre- processed input data is transformed into a set of repre- sentative, discriminative and unique set of features to characterize each chromatogram trace. These features are then used to train and test the proposed classifier model in a much more efficient way. In our approach, the features chosen to represent each observation point in a chromatogram trace are as fol- lows: ACT G FFFF (9) where for ,, and i gxgiACT G (10) and, - F1 represents the set of feature vectors of base i. It is a matrix of size n × 3 where, n is the number of sample (a) (b) Figure 5. Part of an electropherogram trace (a) before and (b) after normalization. points in the chromatogram trace. - x is a vector of size n × 1. It represents the signal strength of base i at each observation point, 12 ,, , n xx x (11) - is a vector of size n × 1. It consists of the gra- dient values for each observation point calculated using the signal strength of the prior three sample points for each observation. 12 ,,, n gg g (12) where 3for 4, 5n3 3 zz z xx gz (13) - is a vector of size n × 1. It consists of the gra- dient values for each observation point calculated using the signal strength of the subsequent three sample points for each observation. 12 ,,, n gg g (14) where 3for 4, 5n3 3 zz z xx gz (15) From the chromatogram trace, it is observed that the positive ascent of a peak to the apex and the negative descent of a peak to the subsequent valley are defined by using a minimum of three sample points respectively. Hence, for the calculation of positive (Eq. 15) and ne- gative (Eq. 13) gradient values, three samples are adop- ted. 3. SYSTEM MODELS Using features extracted in the previous section, the DNA base-calling problem can now be tackled. In this paper, two pattern recognition models are used to solve the problem of base-calling: Artificial Neural Networks (ANNs) and Polynomial Classifiers (PCs). 3.1. Artificial Neural Network Artificial Neural Network (ANN) is a computational approach conceived as an imitation of the human’s brain neural network. Based on the training data, ANNs are capable of adapting its structure accordingly. The basic building block of an ANN is an information processing unit, referred to as neuron, consisting mainly of weights equal to the size of the data set, an adder to sum up the weighted inputs, and an activation function for limiting the output of the neuron [14]. ANN’s quality as universal function estimators renders them attractive as pattern classifiers. ANN’s ability to model both linear and non- linear data is another advantage. However, this property Copyright © 2013 SciRes. OPEN ACCESS  O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 171 makes an ANN prone to over-fitting, the tendency of a model to adapt itself to the minute details of a training data set. Figure 6 illustrates a single hidden layer feed forward neural network consisting of an input layer, a hidden layer, and an output layer. Multiple neurons group to- gether to form a layer and are connected to the neurons in the preceding and subsequent layers through biases and weights. The features extracted from the acquired data, represented as the input layer, constitute the input signals applied to the neurons comprised in the first hid- den layer. Hence, the number of neurons in the input layer is equal to the dimensionality of the input feature vector, i.e. 12 (three features for each of the four bases). As a rule of thumb, a neural network with one hidden layer has the same expressive power as a network built from several hidden layers. Moreover, as a practice, the number of neurons in a hidden layer is twice that of the input layer [15]. The outputs of the hidden layer are then used as inputs to the output layer. The number of neurons in the output layer represents the number of classes the input data can be classified into [16]. For the proposed base-calling problem, classification involves recognition of the four bases, A, C, T and G, referred to as classes. Hence, five neurons are used to form the output layer: four of which represent the presence of each of the four nucleotides, while the fifth neuron represents the absence of all the four bases, represented as N. In the learning stage, a target matrix, T, is needed for labeling the ANN input data classes. 1,1,1,1, 1, 1 2,2,2,2, 2, 2 ,,,,, ACT GN ACT GN n nAnCnTnG nN ttttt t ttttt t T tttttt (16) Bias Z 1 Z m Input La er d features Hidden Layer Output Layer M classes X (1) X (2) X (d) Figure 6. A single hidden layer feedforward neural network. The values assigned to the elements of T are as fol- lows: - ,1 ziB t while ,, , zi BzN tt 0 for sample point z and ,,,CTBAG, if base i has a positive feature , indicating a positive slope for the three sample points prior to z, and a negative feature , indicating a negative slope for the three sample points subsequent to z. - ,0.05 zN t while ,0 zi t for sample point z and G,,,BACT if the above condition is not satis- fied. The prior probabilities indicating presence and ab- sence of a base are imbalanced due to the large availabil- ity of class N in a chromatogram trace compared to the other bases. Since it is difficult to balance the amount of data belonging to each class, the weight given for class N is reduced by assigning it a target value of 0.05 [17]. Using the MATLAB R2009b Neural Network toolbox, the neural network model was trained and tested using a single hidden layer, an output layer consisting of five neurons to represent each of the five previously men- tioned classes, and hyperbolic tangent sigmoid transfer functions. To avoid the problem of over-fitting, a valida- tion data set is used in addition to the training and testing data sets. The validation data ensures that the training process is terminated prior to over-fitting the training data to the model. 3.2. Polynomial Classifier Polynomial Classifiers (PCs) [18] represent non-linear system identifications providing an efficient method to describe non-linear input/output relationships. PCs are a single layer neural network that adopts the polynomial terms of the pattern features as inputs. A PC uses k:d-dimensional feature vectors, X, which can be catego- rized into non-linearly separable classes. A mapping function between each input and its respective class then needs to be determined. A Kth order polynomial classifier uses a Kth order polynomial expansion function to map a d-dimensional feature vector, x, to a higher dimensional vector space, p(x) For example, if x is a 2-dimensional feature vector represented as 12 xx, the mapping of x to a higher dimensional space of K = 2 produces, 22 121212 1pxxxxxxx (17) Similarly, the sequence of N:d-dimensional feature vectors, 12 ,, , n xx x is expanded into their Kth order polynomial expansion, M, where, 12 N Mpxpx px (18) Using the expanded feature vectors, M, the polynomial classifier is trained to determine the optimum set of weights, , that minimizes the difference between the opt w Copyright © 2013 SciRes. OPEN ACCESS  O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 Copyright © 2013 SciRes. 172 model output and the desired targets, tx such that, itself k times. The trained models were tested by comparing the re- sults obtained in terms of bases called to the consensus sequence of each chromatogram trace and to the DNA sequences obtained from ABI and PHRED base-callers. The performance of the neural network model and the polynomial classifier model in terms of correct bases obtained was measured based upon three types of errors that can occur in DNA base-calling: deletion errors, in- sertion errors, and substitution errors. A deletion error represents the loss of one or more bases by the base- caller. For example, when the base sequence of a DNA template is TACGGT and the base-caller calls TCGGT, a deletion error has occurred. An insertion error, on the other hand, involves the addition of one or more bases by the base-caller. For example, when the base sequence of a DNA template is TACGGT and the base-caller calls TATCGGT, an insertion error has occurred. A substitu- tion error occurs when the base-called replaces the actual base. For example, when the base sequence of a DNA template is TACGGT and the base-caller calls TACCGT, a substitution error has occurred. 2 arg min opt x w wMWt T (19) m T opt X MwM t (20) Using the parameters obtained from the training stage, an unknown feature vector, z, is expanded to its polyno- mial terms, p(z), to test the trained model. The target vector, tz, is obtained as follows, z opt twpz (21) On employing a 2nd order polynomial expansion on the features extracted from the data acquired, the data are still observed to be non-linearly separable. Hence, a 3rd order polynomial classifier using a 3rd order polynomial expansion function is implemented in this work to train the PC. The trained model is then tested using novel data from the three data sets and a set of scores are obtained, followed by post-processing to attain the final DNA se- quence. 4. MODEL TESTING AND RESULTS The performance of the trained model is shown in Ta- bles 2-4 for the three data sets. In the three cases shown, an overall base-calling average of 98.4% and 98.64% are achieved by ANN and PC, respectively, indicating the flexibility of the designed topologies [19,20]. Moreover, in comparison to ABI and PHRED, the currently most widely used base-calling software, in terms of deletion, insertion and substitution errors, both proposed models achieved a higher accuracy than PHRED and a compara- ble performance to that of ABI. However, ABI and PHRED base-callers were designed using thousands of chromatogram traces while the models designed in this paper used a discrete number of traces for its training and testing. This indicates the high potential of the proposed classifiers as more efficient alternative base-callers. Data acquired were divided into three sets based on the extent of noise contamination, source of the data, the organism the trace belongs to, and the read length. In light of the limitation in the number of bases, round robin strategy is used in training and testing the proposed models to increase the statistical significance of the results. The available traces are divided into k disjoint sets, such that k models are trained using the data in the (k − 1) sets and tested on the remaining non-trained data set. In the case where k is equal to the number of traces in the data set, i.e. k = 6, leave-one-out method is implemented, i.e. out of the six available traces, traces 2 to 6 are used for training while the first trace is used for testing. The next round uses traces 1, 3 to 6 for training and the second trace is spared for testing, and the cycle repeats Table 2. Performance measure of trained ANN and PC compared to PHRED and ABI for data set 1. Correct Recognition (%) Deletion Errors (%) Insertion Errors (%) Substitution Errors (%) Chromatogram Traces ANN PC PHRED ABI ANNPCPHREDABIANNPCPHREDABI ANN PC PHREDABI Trace 1—639 Bases97.65 98.6 61.19 99.21 1.560.6318.47 0.160.160 0.78 0.63 0.63 0.78 19.560 Trace 2—623 Bases96.15 95.83 71.43 97.75 1.120.644.01 0.161.611.120.32 0.16 1.12 2.41 24.241.93 Trace 3—632 Bases97.63 98.1 97.63 99.68 0.790.790.16 0 0.950.320.16 0 0.63 0.79 2.060.32 Trace 4—632 Bases97.47 98.26 98.73 99.37 1.110.470 0.160.160.320 0.32 1.27 0.95 1.270.16 Trace 5—722 Bases97.23 98.06 97.51 98.75 0.830.830.14 0.550.830.420.69 0.14 1.11 0.69 1.660.55 Trace 6—722 Bases98.20 98.34 88.92 99.45 0.280.288.73 0.140.830.550.69 0.28 0.69 0.83 1.660.14 OPEN ACCESS 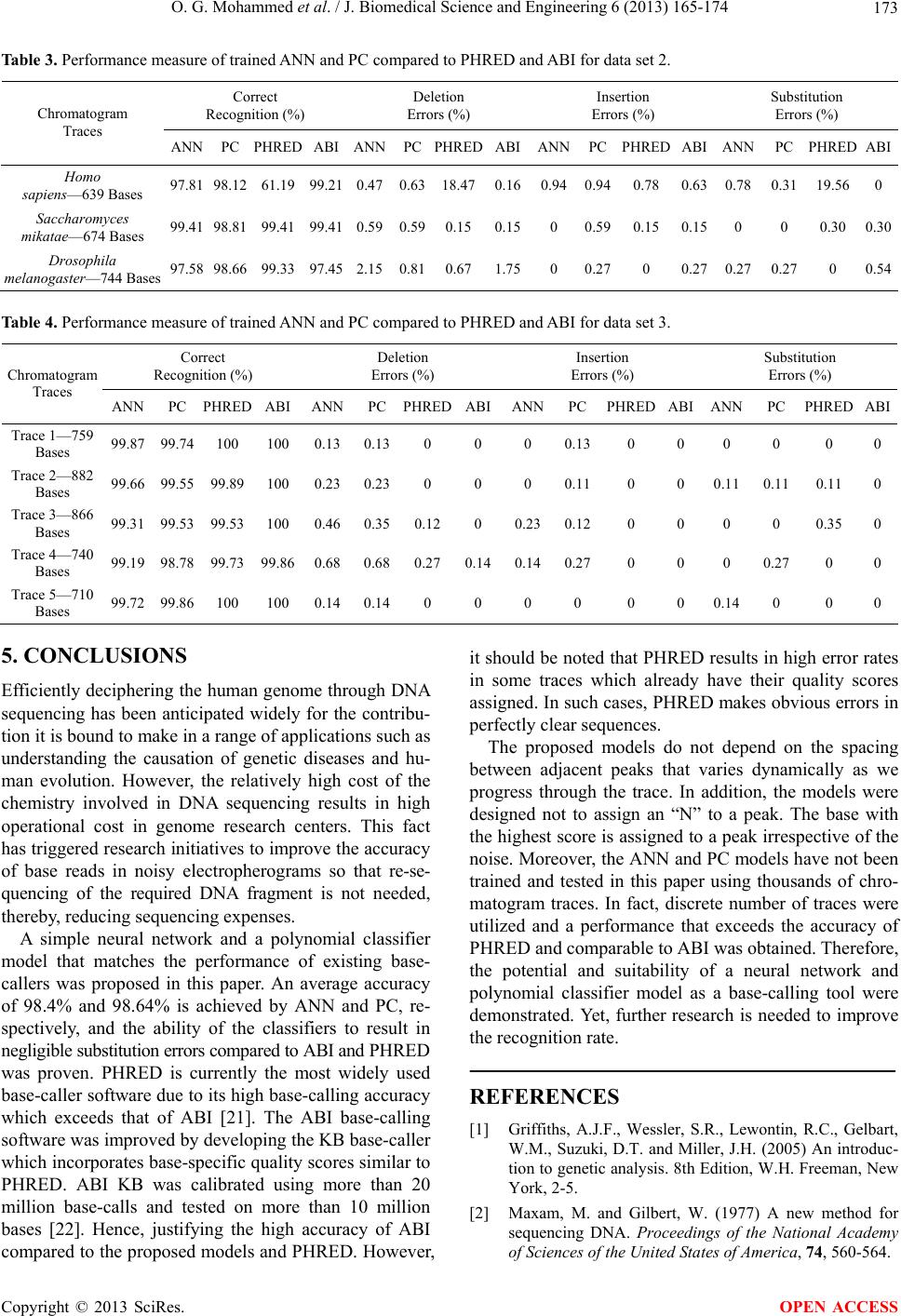 O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 173 Table 3. Performance measure of trained ANN and PC compared to PHRED and ABI for data set 2. Correct Recognition (%) Deletion Errors (%) Insertion Errors (%) Substitution Errors (%) Chromatogram Traces ANN PC PHRED ABI ANNPCPHREDABIANNPCPHREDABI ANN PC PHREDABI Homo sapiens—639 Bases 97.81 98.12 61.19 99.21 0.470.6318.470.160.940.940.780.63 0.78 0.31 19.560 Saccharomyces mikatae—674 Bases 99.41 98.81 99.41 99.41 0.590.590.150.150 0.590.150.15 0 0 0.300.30 Drosophila melanogaster—744 Bases 97.58 98.66 99.33 97.45 2.150.810.671.750 0.270 0.27 0.27 0.27 0 0.54 Table 4. Performance measure of trained ANN and PC compared to PHRED and ABI for data set 3. Correct Recognition (%) Deletion Errors (%) Insertion Errors (%) Substitution Errors (%) Chromatogram Traces ANN PC PHRED ABI ANN PC PHREDABIANNPC PHREDABI ANN PC PHREDABI Trace 1—759 Bases 99.87 99.74 100100 0.13 0.130 0 0 0.130 0 0 0 0 0 Trace 2—882 Bases 99.66 99.55 99.89 100 0.23 0.230 0 0 0.110 0 0.11 0.11 0.11 0 Trace 3—866 Bases 99.31 99.53 99.53 100 0.46 0.350.120 0.230.120 0 0 0 0.35 0 Trace 4—740 Bases 99.19 98.78 99.73 99.86 0.68 0.680.270.140.140.270 0 0 0.27 0 0 Trace 5—710 Bases 99.72 99.86 100100 0.14 0.140 0 0 0 0 0 0.14 0 0 0 5. CONCLUSIONS Efficiently deciphering the human genome through DNA sequencing has been anticipated widely for the contribu- tion it is bound to make in a range of applications such as understanding the causation of genetic diseases and hu- man evolution. However, the relatively high cost of the chemistry involved in DNA sequencing results in high operational cost in genome research centers. This fact has triggered research initiatives to improve the accuracy of base reads in noisy electropherograms so that re-se- quencing of the required DNA fragment is not needed, thereby, reducing sequencing expenses. A simple neural network and a polynomial classifier model that matches the performance of existing base- callers was proposed in this paper. An average accuracy of 98.4% and 98.64% is achieved by ANN and PC, re- spectively, and the ability of the classifiers to result in negligible substitution errors compared to ABI and PHRED was proven. PHRED is currently the most widely used base-caller software due to its high base-calling accuracy which exceeds that of ABI [21]. The ABI base-calling software was improved by developing the KB base-caller which incorporates base-specific quality scores similar to PHRED. ABI KB was calibrated using more than 20 million base-calls and tested on more than 10 million bases [22]. Hence, justifying the high accuracy of ABI compared to the proposed models and PHRED. However, it should be noted that PHRED results in high error rates in some traces which already have their quality scores assigned. In such cases, PHRED makes obvious errors in perfectly clear sequences. The proposed models do not depend on the spacing between adjacent peaks that varies dynamically as we progress through the trace. In addition, the models were designed not to assign an “N” to a peak. The base with the highest score is assigned to a peak irrespective of the noise. Moreover, the ANN and PC models have not been trained and tested in this paper using thousands of chro- matogram traces. In fact, discrete number of traces were utilized and a performance that exceeds the accuracy of PHRED and comparable to ABI was obtained. Therefore, the potential and suitability of a neural network and polynomial classifier model as a base-calling tool were demonstrated. Yet, further research is needed to improve the recognition rate. REFERENCES [1] Griffiths, A.J.F., Wessler, S.R., Lewontin, R.C., Gelbart, W.M., Suzuki, D.T. and Miller, J.H. (2005) An introduc- tion to genetic analysis. 8th Edition, W.H. Freeman, New York, 2-5. [2] Maxam, M. and Gilbert, W. (1977) A new method for sequencing DNA. Proceedings of the National Academy of Sciences of the United States of America, 74, 560-564. Copyright © 2013 SciRes. OPEN ACCESS  O. G. Mohammed et al. / J. Biomedical Science and Engineering 6 (2013) 165-174 174 doi:10.1073/pnas.74.2.560 [3] Sanger, F., Nicklen, S. and Coulson, A. (1977) DNA sequencing with chain terminating inhibitors. Proceed- ings of the National Academy of Science, 74, 5463-5467. doi:10.1073/pnas.74.12.5463 [4] Giddings, M., Brumley, R., Haker, M. and Smith, L. (1993) An adaptive, object oriented strategy for base-calling in DNA sequence analysis. Nucleic Acids Research, 21, 4530- 4540. doi:10.1093/nar/21.19.4530 [5] Berno, A. (1996) A graph theoretic approach to the analysis of DNA sequencing data. Genome Research, 6, 80-91. doi:10.1101/gr.6.2.80 [6] Brady, D., Kocic, M., Miller, A. and Karger, B. (2000) Maximum likelihood base-calling for DNA sequencing. IEEE Journal of Biomedical Engineering, 47, 1271-1280. doi:10.1109/10.867962 [7] Eltoukhy, H. and Gamal, A. (2006) Modeling and base- calling for DNA sequencing-by-synthesis. IEEE Interna- tional Conference on Acoustics, Speech and Signal Proc- essing, 2, 2. [8] Thornley, D. and Petridis, S. (2007) Decoding trace peak behavior—A neuro-fuzzy approach. IEEE International Fuzzy Systems Conference, London, July 2007, 1-6. [9] Trace Archive. National center for biotechnology infor- mation. http://www.ncbi.nlm.nih.gov/Traces/trace.cgi# [10] Richterich, P. (1998) Estimation of errors in raw DNA sequences: A validation study. Letter in Genome Research, 8, 251-259. [11] Berno, A. (1996) A graph theoretic approach to the ana- lysis of DNA sequencing data. Genome Research, 6, 80- 91. doi:10.1101/gr.6.2.80 [12] El-Difrawy, S.A. (2003) A soft computing system for ac- curate DNA base-calling. Ph.D. Dissertation, Northeast- ern University, Boston. [13] Zhang, X.-P. and Allison D. (2002) Iterative deconvolu- tion for automatic base-calling of the DNA electrophore- sis time series. Workshop on Genomic Signal Processing and Statistics, Raleigh. [14] Priddy, K.L. and Keller, P.E. (2005) Artificial neural net- works: An introduction. The International Society for Op- tical Engineering, Washington, 11. doi:10.1117/3.633187 [15] Duda, R.O., Hart, P.E. and Stork, D.G. (2000) Pattern classification. 2nd Edition, John Wiley and Sons, New York. [16] Haykin, S.S. (2009) Neural networks and learning ma- chines. 3rd Edition, Prentice Hall, New Jersey, 10-22. [17] Farrell, K.R., Mammone, R.J. and Assaleh, K.T. (1994) Speaker recognition using neural networks and conven- tional classifiers. IEEE Transactions on Speech and Au- dio Processing, 2, 194-205. doi:10.1109/89.260362 [18] Campbell, W.M., Assaleh, K. and Broun, C.C. (2004) Speaker recognition with polynomial classifiers. IEEE Transactions in Speech and Audio Processing, 10, 205- 212. doi:10.1109/TSA.2002.1011533 [19] Mohammed, O.G., Assaleh, K.T., Husseini, G.A., Ma- jdalawieh, A.F. and Woodward, S.R. (2010) DNA base- calling using polynomial classifiers. Proceedings of In- ternational Joint Conference on Neural Networks, 18-23 July 2010, Barcelona, 1-5. [20] Khan, O.G.M., Assaleh, K.T., Husseini, G.A., Majda- lawieh, A.F. and Woodward, S.R. (2011) DNA base-cal- ling using artificial neural networks. Middle East Con- ference on Biomedical Engineering, Sharjah, February 2011, 96-99. [21] Ewing, B., Hillier, L., Wendle, M.C. and Green, P. (1998) Base-calling of automated sequencer traces using phred. I. Accuracy assessment. Genome Research, 8, 175-185. [22] Brockman, W., Alvarez, P., Young, S., Garber, M., Gian- noukos, G., Lee, W.L., Russ, C., Lander, E.S., Nusbaum, C. and Jaffe, D.B. (2008) Quality scores and SNP detec- tion in sequencing-by-synthesis systems. Genome Re- search, 18, 763-770. doi:10.1101/gr.070227.107 Copyright © 2013 SciRes. OPEN ACCESS
|