Graphene, 2013, 2, 49-54
http://dx.doi.org/10.4236/graphene.2013.21007 Published Online January 2013 (http://www.scirp.org/journal/graphene)
General Scattering Mechanism and Transport in Graphene
Musah Rabiu1, Samuel Y. Mensah2, Sulemana S. Abukari2
1Department of Applied Physics, Faculty of Applied Science, University for Development Studies, Navrongo, Ghana
2Center for Laser and Fiber Optics, Physics Department, University of Cape Coast, Cape Coast, Ghana
Received November 14, 2012; revised December 19, 2012; accepted January 17, 2013
ABSTRACT
Using quasi-time dependent semi-classical transport theory, within relaxation time approximation, we obtained coupled
electronic current equations in the presence of time varying field, and based on general scattering mechanism, ε

 .
In the vicinity of Dirac points, we find that a characteristic exponent 2


 corresponds to acoustic phonon scatter-
ing, 1

 long-range Coulomb scattering mechanism and 1


 is short-range (delta or contact potential) scat-
tering in which the conductivity is constant of temperature. The 0


case is the ballistic regime. In the low-energy
dynamics of Dirac electrons in graphene, the effect of the time-dependent electric field is to alter just the electron
charge by

0
1Ωee i

 making electronic conductivity non-linear. The effect of constant magnetic field at finite
temperature is also considered.
Keywords: Boltzmann Transport Equation; Relaxation Time Approximation; Graphene Energy Spectrum; Electronic
Conductivity; Scattering
1. Introduction
Quite recently, semiconductor nanostructures have be-
come the model of choice for investigation of electrical
conduction. The unique two-dimensional material gra-
phene which was first thought to be an academic material
is not an exception. This 2D nanomaterial is fast becom-
ing better candidate for electronic devices. Not only be-
cause of its noble electronic transport properties [1], but
it also promises a good future in graphene based elec-
tronics industry. Graphene has received a wide academic
attention and serve as a bridge between condensed matter
physics and high energy physics [2]. The advantage of
this planner material is that, one can easily change its
electronic properties by introducing tunable gap in the
sample or changing the number of graphene planes [3]. It
is also possible to fabricate free standing graphene sheets
[4]. Intrinsic superconducting states can also be realized
in graphene [5]. These among other things, means that
the electronic properties of graphene can easily be tai-
lored to fit device conditions.
The crystal structure of graphene is made up of mono-
layer of carbon atoms arranged in hexagonal lattice. The
low energy dynamics of fermions in graphene is charac-
terized by linear dispersion,


F
kv|p∽
graphene, a relevant scattering potential (mechanism) is
essential. However, as we shall see in this report, one
does not need to consider any explicit form of scattering
potential. It was shown in [6] that Boltzmann theory with
long-range coulomb scattering can account for all ex-
perimental findings. Especially, when the electronic den-
sity around Dirac points are normalized. Also, within the
Boltzmann theory using random phase approximation,
coulomb scattering has been predicted to be the dominant
scattering mechanism [7]. Several theories including
Boltzmann Transport Equation (BTE) suggest a non-
universal behavior of minimal conductivity which none-
theless coincides with experimentally observed value
times, i.e. π,π
thory exp



 [8,9]. The same BTE pre-
dict other transport coefficients which agree well with
experiment [9-11].
In this brief report, we reproduce transport properties
of graphene. Within the BTE formalism and with energy
dependent relaxation time depending on power law, we
showed dependence of graphene’s transport coefficients
on applied field frequency. The remaining of this paper is
organized as follows: Section 2 formulates BTE and pro-
vides arguments leading to a quasi-time dependent (t-
BTE) solution. In Section 3 we used the t-BTE to derive
coupled current equations from which we derived con-
ductivity and other transport quantities. The conductivity
tensor is re-derived in the presence of magnetic. The last
|. In a clean-
ed sample, the conduction and valence bands touch at
two inequivalent Dirac points located at the corners of
Brillouin zone. To understand the low energy transport in
C
opyright © 2013 SciRes. Graphene

M. RABIU ET AL. 50
Section 4 contains discussion, conclusion and some
recommendations.
2. BTE and Quasi-Time Dependent Solution
A time time-dependent linearized BTE has the following
form [12]
 



trr
f
p
fp vpTe
Te
fp
 


 

 

 





, (1)
where

f
p depends on and , i.e. t,r p


f
t,r,p
The group velocity, is constant of time, v


f
p is
the scattering term and is the lattice temperature. The
applied electric field has the form
T



0cos ΩE tEt,
0 is the static electric field. Exact analytical solution of
(1) is very difficult to obtain. Especially, the non-linear-
ity of the scattering term and the fact that velocity can
generally depend on time. In view of this, we adopt some
approximations including relaxation time approximation
where
E
 


0
Γ
f
pfpf   p. (2)
Γ is inverse of relaxation time

.
f
and are 0
f
the
time-dependent (equilibrium) and time-independent (non-
equilibrium) Fermi-Dirac distribution functions. Moti-
vated by [13] in the absence of magnetic field (B0

),
we consider a picture where the only time dependent
quantity in (1) is the electric field. Note that Mensah so-
lution considered the space term as perturbation. Under
the above simplified assumptions together with the steady
state solution [12,14], the quasi solution is
 
 
ΓΓ
0
00
Γd ed e
ε
ε
tt
rr
fptf petvp
f
p
TEt
eT e






 
 
 

 





(3)
so that it can easily reduce back to [13] when Ω0

.
2.1. Coupled Currents and Transport
Coefficients
The sheet current for electron and energy flux in gra-
phene are defined by the formulas

sv
ev
gge
J
vpfp
A
 (4)
and

ε
sv p
gge
J
pfp
A

. (5)
Where
s
g
, v
g
are spin and valley degeneracies and
A
is graphene sheet area. We convert the sums in (4)
and (5) to integrals following

π
2π0
dd
2π- p
App





.
Substituting (2) in to (3), (4) and simplifying using an
energy dependent relaxation time of the form


Λε

 , (6)
where
A
is constant of energy with dimensions of
s
J

and

is characteristic exponent which deter-
mines the specific type of scattering mechanism involved.
One easily obtains coupled current equations






ΩΦ
err
J
ST  
(7a)


Φ
r

r
J
TSK T

. (7b)
Where the measured electrochemical potential gradient,


ΦreE 

 . The coefficients in (5) are
  
22
11
2
0
π1
6
Ω
1ΩΛ
B
min kT
i
u










(8)
  
22
2
0
π
Ω1
3
min B
SkT
eT u




 (9)
 
221
2
0
π
Ω
3
min B
KkT
eT
u





 (10)
2
2
min eh
  is the minimal conductivity in graphene
and the constant 0 is defined through u2
0Λu. It
has dimension of energy square.
Now, to derive a particular type of scattering mecha-
nism, we consider specific cases when 2

 ,



,
1



and constant


which correspond to

=
+2, +1, −1, 0 respectively. Because the electronic con-
ductivity,

is the only coefficient depending on fre-
quency, we specifically study this quantity for various

values. For 1


, the conductivity in (8) assumes
the form
 
12
0
1
Ω
1ΩΛ
min
u


2

. (11)
This is characterized by short-range potential that has
the form of contact (or delta) potential and may be due to
localized impurity (defect) in the sample [9,10,15]. For
0


, we get
 
02
0
Ω
1ΩΛ
min
u


2

, (12)
which corresponds to coherent [9] or random Dirac mass
scattering, and describes the ballistic scattering for elec-
tronic conductivity in graphene. Behavior of the elec-
tronic conductivity, 0

resulting from these processes

M. RABIU ET AL. 51
Figure 1. 0

: Normalized conductivity is plotted against
c
ΩΩ at fixed values of doping; μ = 1.0 eV, 0.8 eV, 0.5 eV
with and . .0 1 e
B
KT V21 23m Vs. 

1
is shown in Figure 1 at fixed values of chemical poten-
tial (doping). Finally, for 1

 , the electronic conduc-
tivity becomes
 

22
2
12
0
π
3
Ω
1ΩΛ
B
min kT
u





2
. (13)
This is an important and dominant scattering mecha-
nism in graphene [16]. It is characterized by unscreened
long-range Coulomb (charged impurity) scattering [7].
The second term in (13) is inevitable at finite tempera-
tures. This extra term was missing in [9]. It is the contri-
bution due to scattering by phonons. From (13) conduc-
tivity departs slightly from linearity behavior at low fre-
quencies. Figure 2 depicts this situation.
The conductivity for acoustic phonon scattering is
identified with 2

 ,
 

2
32
22
0
π
Ω
1ΩΛ
B
min kT
u2





. (14)
2.2. Resistivity, Thermal Conductivity and
Thermopower
In this section we turn to (7) to compute other transport
properties of graphene. Specifically, we will calculate the
resistivity

, thermal conductivity, and thermo-
power, 0 for

S1

 We will drop the

subscript
in the following equations. By inverting (7), one can find
these quantities that experimentalist usually like working
with. We will write our equations similar to the format in
[9]. The resistivity is,




2
2
0
22
2
1ΩΛ
Ω
π
3
min B
u
kT





, (15)
thermal conductivity
Figure 2. 2


: Normalized conductivity is plotted against
c
ΩΩ at fixed values of doping; μ = 1.0 eV, 0.8 eV, 0.5 eV
with and .
B
KT V.01e
21
23mVs. 

1
 
 

222
2
44
2
2
2
2π
Ω
3
1ΩΛ
8π
9π
13
B
B
B
kT
hT
KT
hT kT







(16)
and thermoelectric power
  

22
2
02
2
2
1ΩΛ
2π
Ω
3π
13
B
B
KT
SeT kT






. (17)
The new physics emerging from these equations is the
linear dependence of these quantities on . Note that
electron density dependence in our equations is self
manifest, since one can easily incorporate it through [9]
2
Ω
n
2
n

 at zero temperature or
  
22
2
2
11 π
π3BT
F
nT K
v






(18)
for finite temperatures.
2.3. Magnetoconductivity
The BTE for non-zero magnetic field is realized from (1)
by making the transformation or adding
the term
EEvH




vH gp in the linearized BTE. This
simple replacement will not yield a general solution, be-
cause of the cross product. It ensures that .
To find the general solution, one usually obtains separate
solutions for magnetic and electric fields and superim-
pose them [12]. Here, we obtained the solution as follows;
if the lattice temperature is constant of space, (1) be-
comes

0H vv

M. RABIU ET AL. 52


 
0Φ
ε
e
p
p
fp
fev
f
pvHf








p.
(19)
The electrochemical potential is now defined as

Φee' e'E    

, with

1ΩΛe' ei

 . We
have assumed time independent magnetic field. The right
hand side of (19) can be seen as an expansion of


f
p' ,
where

F ev
p'pp H
p

 

, (20)
so that

0Φ
ε
f
f
evf p' 


 


 . (21)
We need to invert (20) and put it in (19). To do this, we
make the subject as p

22
1
1
ppp
H






H

, (22)
where F ev| p|

 . Equation (21) now becomes
 
022 Φ Φ
1
f
fp fpH
H





 



(23)
after dropping the prime. Notice the energy dependence
of

through

, i.e. 1




. Where 2 Λ
F
ev   is
identified as the mobility in units of centimeter square
per volts per second. Now, to compute the electric cur-
rent, (23) is used in (4) with 1

 to get

22
Ω
Φ Φ
1
e
J
H



H. (24)
The presence of magnetic field vector has created off
diagonal elements in the electric current density tensor.
To compute the components of the new tensor we write
(24) in an indicial notation as


22
Ω
Φ
1
e
iiijk
JH
H



Φ
jk
. (25)
The longitudinal and transverse components of the
magnetoconductivity tensors are


22
Ω
1
xx
H


, (26a)

22
Ω
1
xy
H
H



. (26b)
The rest of the components are determined through the
relations
x
xyy

  and
x
yyx



. In terms of mag-
netoresistivities, (26a) and (26b) are usually written as
22
xx
xx
x
xxy




 (27a)
22
xy
xy
x
xxy




 (27b)
with the resistivity 1
xx



and the Hall resistivity
xy H



. In terms of electron concentration
xy
n,H ne


, where 1
H
ne R

and
H
R is the Hall
coefficient. In general,

is complex. For this reason,
we make the replacement



2
11 1
H
1 iH  
So that both longitudinal and transverse electronic con-
ductivities, in the presence of constant magnetic field, for
1


 take the form
 
 
22
1ΛΩ
Ω0
1ΩΛ 1
xx
H
H

 



 


 
(28)
and


  
2
ΩΛΩ
01ΩΛ1
xy H
H



2

 


 
. (29)
Where the temperature dependent zero frequency con-
ductivity is
 
22
2
2
0
π
03
min B
kT
u








.
We now observe the effect of crossed magnetic and
electric field on graphene by plotting longitudinal con-
ductivity with frequency and magnetic fields in Figures
3 and 4.
3. Discussion and Conclusions
The advantage of our approach is that, one does not need
to go through rigorous process of calculating the specific
scattering rate


Γ

. For instance, unlike in [9], finite
temperature conductivity was found by separately calcu-
lating phonon and normal relaxation times. Quite re-
Figure 3. Normalized longitudinal conductivity with c ΩΩ
and αH at fixed values of doping; Top: μ = 0.5 eV, Middle: μ
= 0.3 eV, Bottom: μ = 0.2 eV, μ ≥ 2 KBT and α = 2.3
21
mVs
1



.

M. RABIU ET AL. 53
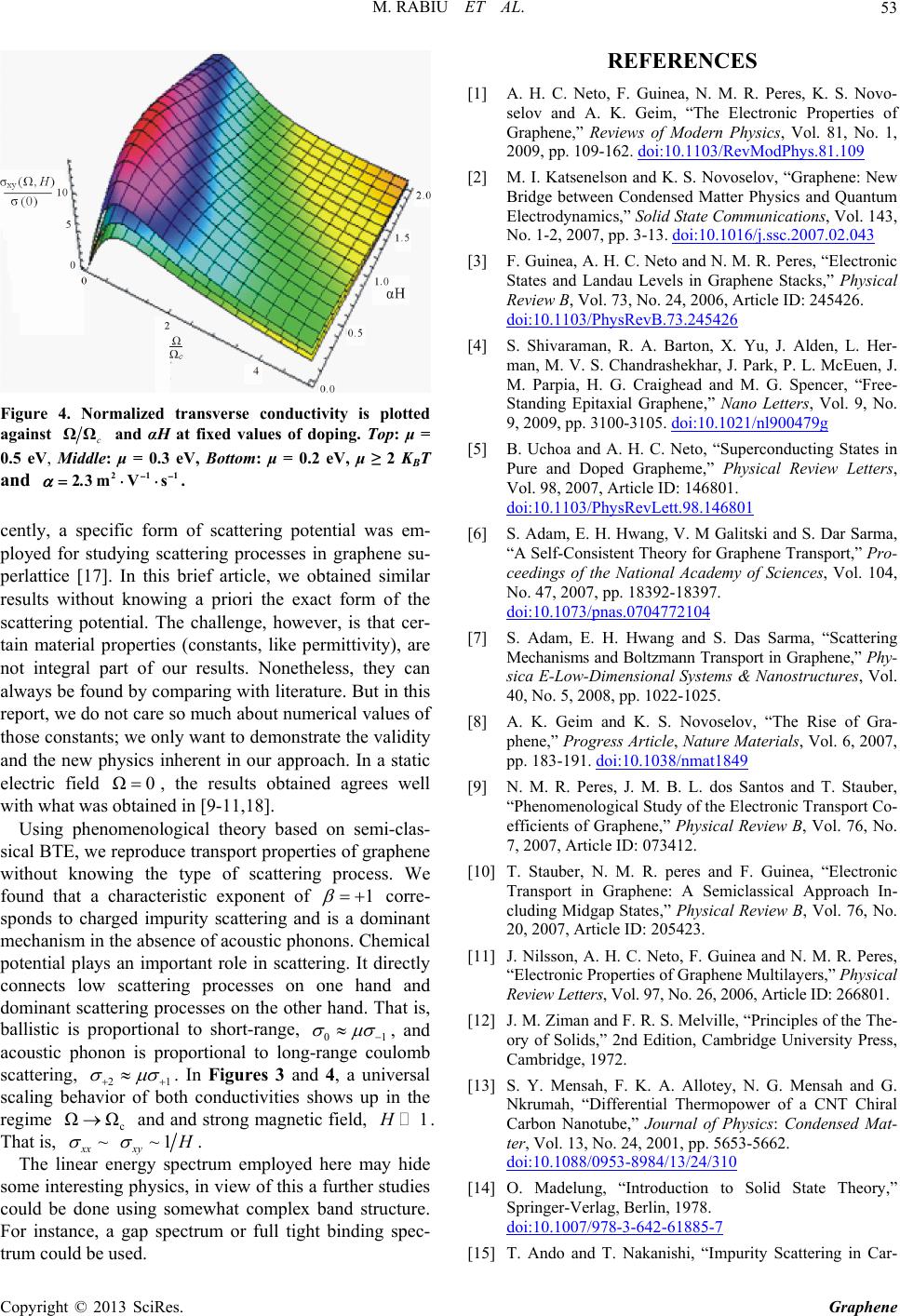
Figure 4. Normalized transverse conductivity is plotted
against c ΩΩ and αH at fixed values of doping. Top: μ =
0.5 eV, Middle: μ = 0.3 eV, Bottom: μ = 0.2 eV, μ ≥ 2 KBT
and 211 23mVs. 

.
cently, a specific form of scattering potential was em
ain
ased on semi-clas-
si
-
ployed for studying scattering processes in graphene su-
perlattice [17]. In this brief article, we obtained similar
results without knowing a priori the exact form of the
scattering potential. The challenge, however, is that cer-
tain material properties (constants, like permittivity), are
not integral part of our results. Nonetheless, they can
always be found by comparing with literature. But in this
report, we do not care so much about numerical values of
those constants; we only want to demonstrate the validity
and the new physics inherent in our approach. In a static
electric field Ω0, the results obtained agrees well
with what was obted in [9-11,18].
Using phenomenological theory b
cal BTE, we reproduce transport properties of graphene
without knowing the type of scattering process. We
found that a characteristic exponent of 1

 corre-
sponds to charged impurity scattering and minant
mechanism in the absence of acoustic phonons. Chemical
potential plays an important role in scattering. It directly
connects low scattering processes on one hand and
dominant scattering processes on the other hand. That is,
ballistic is proportional to short-range, 01
is a do



, and
acoustic phonon is proportional to long-lomb
scattering, 21
range cou



. In Figures 3 and 4, a universal
scaling behth conductivities shows up in the
regime c ΩΩ and and strong magnetic field, 1
avior of bo
H

.
That is, 1
xy ~H xx ~


near ene
.
The litrurgy specm employ
so
trum could be used.
. Guinea, N. M. R. Peres, K. S. Novo-
selov and A. K. Geim, “The Electronic Properties of
Graphene,” Re, Vol. 81, No. 1,
2009, pp. 109-dPhys.81.109
ed yhere ma hide
me interesting physics, in view of this a further studies
could be done using somewhat complex band structure.
For instance, a gap spectrum or full tight binding spec-
REFERENCES
[1] A. H. C. Neto, F
views of Modern Physics
162. doi:10.1103/RevMo
[2] M. I. Katsenelson and K. S. Novoselov, “Graphene: New
Bridge between Condensed Matter Physics and Quantum
Electrodynamics,” Solid State Communications, Vol. 143,
No. 1-2, 2007, pp. 3-13. doi:10.1016/j.ssc.2007.02.043
[3] F. Guinea, A. H. C. Neto and N. M. R. Peres, “Electronic
States and Landau Levels in Graphene Stacks,” Physical
Review B, Vol. 73, No. 24, 2006, Article ID: 245426.
doi:10.1103/PhysRevB.73.245426
[4] S. Shivaraman, R. A. Barton, X. Yu, J. Alden, L. Her-
man, M. V. S. Chandrashekhar, J. Park, P. L. McEuen, J.
M. Parpia, H. G. Craighead and M. G. Spencer, “F
Standing Epitaxial Graphene,” Nan ree- o Letters, Vol. 9, No.
9, 2009, pp. 3100-3105. doi:10.1021/nl900479g
[5] B. Uchoa and A. H. C. Neto, “Superconducting States in
Pure and Doped Grapheme,” Physical Review Letters,
Vol. 98, 2007, Article ID: 146801.
doi:10.1103/PhysRevLett.98.146801
[6] S. Adam, E. H. Hwang, V. M Galitski and S. Dar Sarma,
“A Self-Consistent Theory for Graphene Transport,” Pro-
ceedings of the National Academy of
No. 47, 2007, pp. 18392-18397.
Sciences, Vol. 104,
doi:10.1073/pnas.0704772104
[7] S. Adam, E. H. Hwang and S. Das Sarma, “Scattering
Mechanisms and Boltzmann Transport in Graphene,” Phy-
sica E-Low-Dimensional Systems
40, No. 5, 2008, pp. 1022-1025.
& Nanostructures, Vol.
[8] A. K. Geim and K. S. Novoselov, “The Rise of Gra-
phene,” Progress Article, Nature Materials, Vol. 6, 2007,
pp. 183-191. doi:10.1038/nmat1849
[9] N. M. R. Peres, J. M. B. L. dos Santos and T. Stauber,
“Phenomenological Study of the Electronic Transport Co-
efficients of Graphene,” Physical Review B, Vol. 76, No.
7, 2007, Article ID: 073412.
[10] T. Stauber, N. M. R. peres and F. Guinea, “Electronic
Transport in Graphene: A Semiclassical Approach In-
cluding Midgap States,” Physical Review B, Vol. 76, No.
20, 2007, Article ID: 205423.
[11] J. Nilsson, A. H. C. Neto, F. Guinea and N. M. R. Peres,
“Electronic Properties of Graphene Multilayers,” Physical
Review Letters, Vol. 97, No. 26, 2006, Article ID: 266801.
[12] J. M. Ziman and F. R. S. Melville, “Principles of the The-
ory of Solids,” 2nd Edition, Cambridge University Press,
Cambridge, 1972.
S. Y. Mensah, F. K. A. Allotey, N. G. Mensah and G.[13]
Nkrumah, “Differential Thermopower of a CNT Chiral
Carbon Nanotube,” Journal of Physics: Condensed Mat-
ter, Vol. 13, No. 24, 2001, pp. 5653-5662.
doi:10.1088/0953-8984/13/24/310
[14] O. Madelung, “Introduction to Solid State Theory,”
Springer-Verlag, Berlin, 1978.
doi:10.1007/978-3-642-61885-7
[15] T. Ando and T. Nakanishi, “Impurity Scattering in Car-

M. RABIU ET AL. 54
, pp. 1704-
bon Nanotubes-Absence of Back Scattering,” Journal of
the Physical Society of Japan, Vol. 67, 1998
1713. doi:10.1143/JPSJ.67.1704
[16] J.-H. Chen, C. Jang, S. Adam, M. S. Fuhrer, E. D. Wil-
liams and M. Ishigami, “Charged-Impurity Scattering in
Graphene,” Nature Physics, Vol. 4, 2008, pp. 377-381.
doi:10.1038/nphys935
[17] S. V. Kryuchkov and E. I. Kukhar, “Influence of the
Magnetic Field onthe G raphene Conductivity,” Journal of
raphene,” Physical Review Letters, Vol.
Modern Physics: Scientific Research, Vol. 3, No. 9, 2012,
pp. 994-1001.
[18] K. Namura and A. H. McDonald, “Quantum Hall Ferro-
magnetism in G
96, No. 25, 2006, Article ID: 256602.