Journal of Modern Physics
Vol.3 No.9A(2012), Article ID:23124,22 pages DOI:10.4236/jmp.2012.329170
Geometrical Models of the Locally Anisotropic Space-Time
1University Politehnica of Bucharest, Bucharest, Romania
2Skobeltsyn Institute of Nuclear Physics, Moscow State University, Moscow, Russia
3Institute of Hypercomplex Systems in Geometry and Physics, Fryazino, Russia
4State University of Civil Aviation, St. Petersburg, Russia
5“Transilvania” University of Braşov, Braşov, Romania
Email: *bogoslov@theory.sinp.msu.ru
Received June 16, 2012; revised July 23, 2012; accepted August 3, 2012
Keywords: Lorentz-, Poincareand Gauge Symmetry; Spontaneous Symmetry Breaking; Alternative Gravity Theories; Space-Time Anisotropy; Finsler Differential Geometry
ABSTRACT
Along with the construction of non-Lorentz-invariant effective field theories, recent studies which are based on geometric models of Finsler space-time become more and more popular. In this respect, the Finslerian approach to the problem of Lorentz symmetry violation is characterized by the fact that the violation of Lorentz symmetry is not accompanied by a violation of relativistic symmetry. That means, in particular, that preservation of relativistic symmetry can be considered as a rigorous criterion of the viability for any non-Lorentz-invariant effective field theory. Although this paper has a review character, it contains (with few exceptions) only those results on Finsler extensions of relativity theory, that were obtained by the authors.
1. Introduction
Nowadays, the program of geometrization and algebraization of the fundamental laws of nature which was formulated at the early stage of GR development is still not fulfilled. Every step in realization of this program suggests partial or complete reconsideration of the common notions and of the properties of the corresponding to them physical objects. Many basic concepts of the modern physics and mathematics are expressed in terms of the notion of manifold, which allows possibility of universal arythmetization of the events of the physical world and of the relations between them; the notion of manifold is also a symbiosis of geometric and algebraic ideas.
Despite the abstract character of the manifolds studied in modern physics and mathematics and of a lot of additional structures which geometrically describe the laws of nature, some of these structures still remain rather conservative. First of all, we mention the manifolds endowed with metrics, while the majority of modern geometrical models deal with the metric tensor as a function on the tangent bundle. In every coordinate chart, the metric tensor field depends on the coordinates of the base in an arbitrary smooth way, and it depends bi-linearly on the coordinates of the fiber. Despite the fact that the most natural generalization of this construction is known to the mathematicians for a very long time within Finsler geometry [1-3] which describes the locally anisotropic spaces, the first viable model of Finsler space-time [4] and the based on it special relativistic theory of locally anisotropic space-time [5-7] were promoted not long ago. These works were motivated by the suggested at that time and now popular idea [8,9] of Lorentz symmetry violation, which means that the “true” metric of the flat space-time deviates from the Minkowski metric.
Generally speaking, the discussion on space-time anisotropy needs to clarify first two issues: 1) why this should be done, i.e. what are its physical premises and 2) what does the suggested anisotropy mean. The second question implies that geometry in mathematics corresponds to the theory of measurements in physics, that is, when we speak of, say, space-time curvature, we presume that it will show itself in measurements. If we have in mind the physical applications of the geometrical constructions, the same must be true for anisotropy. Notice that to speak of the curvature or anisotropy of the empty space is possible only when we don’t deal with experimental science at all, and if we do deal with it, the characteristic scale for the possible applications of the theoretical speculations must be provided. The last means that when the necessity to study the space-time anisotropy occurs, one should suggest its local source.
The answer to the first question is less obvious and is rather vast from the point of view of the analysis of the situation in physics (see [10-15] and additional reasoning below). The result of this analysis has both general and concrete aspects. The general conclusion is that the gravitation theory, i.e. GR, was developed for and successfully applied at the scale of planetary systems. When applied to cosmological (galactic) scales in the way in which this is done now, it demands the introduction of corrections that are 25 times larger than the value of mass of the observable Universe and which are related to the existence of the new (still unknown) substances—dark matter and dark energy, which were not supposed to be present in the initial theory. Obviously, alongside with their tracking, one should make sure that the theoretical models are valid. These models are: the so called simplest scalar used in the expression for the Hilbert-Einstein action, i.e. scalar curvature; the geometry used for the space-time description, i.e. Riemann geometry; and the 4D space-time used for the description of the physical reality itself.
Important observations that make simple sense, have sufficient value and statistical validity, but contradict classical GR, are the rotation curves of spiral galaxies. The attempts to modify the theory in order to describe them in an adequate way based on increase of complexity [16,17] or change [18] of the simplest scalar, or on the modification of the metric [19], appeared to be either not consistent enough—f(R)-theories, or imposed as well to introduce a new unknown scalar field or some new unknown interaction. The phenomenological MOND theory [20] required either an arbitrary change of the dynamics law, or an arbitrary change of the expression of the gravitation force, in order to provide an acceptable description of the phenomena observed at galactic scales. Its covariant generalization [21] also leads to the introduction of the new scalar field.
The concrete consequence of the analysis is that there is a necessity to make the next step and to study the possibility to use a new geometry to interpret the observations. The natural generalizations of Riemann geometry are Finsler and Lagrange geometries, both taking into account the dependence of the metric tensor on direction at the given point. This direction can be global—which corresponds to one of the geometries constructed on the commutative-associative algebra, namely, to Berwald-Moor geometry. If we use the Berwald-Moor metric to interpret the gravitation theory, there appear a fixed number of stationary global sources of gravitation whose nature is unclear. This direction could be local—and then the interpretation might correspond to the motion of the local sources of curvature. The last one seems well-grounded, since the common features of the gravitation theory and of electrodynamics from the point of view of Lorentz invariance and of the inverse square law were long ago noticed. The corresponding attempts to generalize the theory with the help of the notion of mass currents were undertaken in [22,23], and the common geometrical background of both theories was discussed in [12]. Nevertheless, the gravito-electromagnetism [23] doesn’t seem to be self-consistent enough, because one cannot deal with the gravitation charges in the same way as with electric charges: the first are sources of curvature, while the second are not. Instead of the introduction of Lorentz force according to a formal analogy, one should require that, in the case of gravitation, the metric becomes anisotropic. This would lead to the gravitational force dependence on the velocity of the test particle and on the vector field corresponding to the motion of the sources of curvature. The literal meaning of the equivalence principle suggests the same: the inertial forces might depend on velocities and have large values, while the usual relativistic corrections interpreted as the force dependence on velocities, are small. In this case the application of the Schwarzschild type solutions to the problems stated at galaxy scale is not appropriate, and cannot be used to describe the spiral galaxies dynamics which is revealed by observations.
Turning back to the motivation of the research which deals with Finsler geometric structures of space-time, one should notice that the whole variety of astrophysical data including the anisotropy of the acceleration of the Universe expansion and the anisotropy of relic radiation, points at the anisotropy of space-time only in an indirect way. The same can be said about the baryonic asymmetry problem, a breaking of the discrete space-time symmetries in weak interactions, the problem of anomalous magnetic moment of muon, etc. This emphasizes the significance of new results obtained in the two independent experiments which show directly the existence of the space-time anisotropy.
In the first of them [24], the precise atomic interfereometer was used to measure the phase shifts of the freely falling atoms. The local Lorentz symmetry break larger than 2 standard errors was found, which means that there exists an anisotropic condensate of unknown nature, and that, this interacts with the gravitation field in such a way, that the central symmetry of the gravitational potential is broken. Consider now the second experiment.
Recently, at Large Hadronic Collider (LHC) there was found a new phenomenon [25] which is now known as Ridge/CMS-effect (CMS stands for Compact Muon Solenoid which is both the detector and the name of the corresponding research collaboration). One of the features of the effect consists in the following. If the proton-proton collisions with the full energy 7 TeV produce more than 100 particles, the planes corresponding to the tracks of every pair of the produced charged particles are oriented in such a way that a significant part of them has a common cross-line coinciding with the initial protons collision axis. This resembles the situation with the elastic scattering of a moving particle on a particle at rest: due to the momentum conservation (the momentum is equal to the flying particle momentum), all the planes to which the tracks of the two particles belong after scattering, have the common crossline which coincides with the track of the initial flying particle. But contrary to the elastic scattering on the particle at rest, the total momentum of the colliding protons at LHC is equal to zero. This fact and also the fact that the Ridge/CMS-effect is characteristic only to the high multiplicity events are hard to explain by regular considerations: the physical origin of the appearance of the preferred direction coinciding with the protons collision axis when a hundred or more particles are emitted, remains unclear.
High multiplicity events take place in case of the central collision of the initial protons. Then the energy density at the moment of the collision is comparable to the energy density shortly after the Big Bang, when instead of hadrons there was quark-gluon plasma. It is clear that dealing with the high multiplicity events in the proton-proton collisions, one should account for the phase transitions corresponding to the high gauge symmetries violations that are accompanied by the vacuum rearrangement. The condensate appearing during such rearrangement is locally isotropic (Higgs type) only in frames of the usual relativistic theory. In the relativistic theory with Lorentz symmetry violation, or, in other words, in the anisotropic theory of relativity, which will be discussed below, the role of the Higgs condensate is played by the axially symmetric anisotropic fermion-antifermion condensate. Besides, when rapid cooling and hadronization of quarkgluon plasma takes place, an entirely anisotropic threegluon condensate can appear. On the one hand, quantumfield vacuum, that includes the anisotropic condensate, is the physical carrier of the local anisotropy of space-time, and it can be regarded as an anisotropic quintessence, on the other—it imparts all the particles the properties of quasi-particles in the crystalline environment. In particular, apart from the rest energy, the particles obtain a rest momentum. With regard to the Ridge/CMS-effect, this means that in the reference frame coinciding with the center of masses of the colliding protons, (relative to the laboratory), the total momentum of the appearing primordial plasma differs from zero and lies on the collision axis (this is due to the anisotropy of the condensate, which arises spontaneously along the collision axis). This is why the correlation of paired tracks in the CMS experiment has turned out such that the planes to which the tracks belong cross mostly on the axis of proton collisions.
Thus, the Ridge/CMS-effect directly demonstrates that in the early Universe there spontaneously emerged the axially symmetric local anisotropy of space-time with a group DISIMb(2) as an inhomogeneous group of local relativistic symmetry and the corresponding Finsler metric. As for the possibility of spontaneous emergence of the complete local anisotropy of space-time with the Abelian homogeneous group of local relativistic symmetry and the corresponding generalized Finslerian Berwald-Moor metric, the answer to this question will depend on the threeparticle correlation function, whose measurement is already planned by the CMS collaboration.
In Section 2, we consider the relativistic Finslerian DISIMb(2)-invariant model of a flat space-time with partially broken isotropy in the 3D space. It will be shown that in this model the physical carrier of the anisotropy of flat space-time is axially symmetric neutrino-antineutrino condensate, and the model itself underlies the anisotropic special theory of relativity and admits a natural generalization to the case of curved space-time and the Finslerian extension of GR. The mentioned above Finsler extensions of general relativity necessarily leads to the existence of, at least, one gauge vector field and of its interaction with the conserved current of the rest mass.
A number of astrophysical effects of this interaction were studied in detail in the framework of the approach proposed by S. V. Siparov. It is suggested to model the physical real world by the 8-dimensional phase spacetime, one of the coordinates of which appears to have a constant value. The discussion of this approach, of its origination and of the corresponding calculated and observed effects is given in Section 3 of this review.
As to Section 2, in addition to the flat space-time with partially broken isotropy of the 3D space, it contains a brief review of a three-parameter family of flat Finsler spaces with entirely broken 3D isotropy and with Abelian three-parametric group of relativistic symmetry. The Abelian group structure of the relativistic symmetry was the starting point for a deeper study of Finsler Berwald-Moor space, which for the four-dimensional case belongs to the specified family.
In Section 4 we consider the geometric, algebraic, and physical aspects of the commutative associative algebras and Berwald-Moor geometries of various dimensions associated with them. In recent years, studies of this kind were also conducted within the framework of international cooperation between the Romanian Academy and the Academy of Sciences of the Russian Federation. In particular, thanks to the work of Romanian geometers led by V. Balan, the results concerning the algebraic side of the theory of Berwald-Moor metrics for various dimensions were complemented by the specific results originnating from the modern differential geometry of Finsler spaces. Their description in a concentrate form can be found in Section 5 of this review.
2. Relativistically Invariant Finslerian Spaces with Local Lorentz Symmetry Violation
As it is known, space-time is Riemannian within the framework of GR, and the distribution and motion of matter only determines the local curvature of space-time without affecting the geometry of the tangent spaces. In other words, regardless of the properties of the material medium which fills the Riemannian space-time, any flat tangent space-time remains the space of events of SR, i.e. the Minkowski space with its Lorentz symmetry, which is usually identified with the relativistic symmetry.
However, in recent literature there is an increasing interest in the problem of violation of Lorentz symmetry. Particularly, the string-motivated approach to this problem is widely discussed.
The point is that even if the original unified theory of interactions possesses Lorentz symmetry up to the most fundamental level, this symmetry can be spontaneously broken due to the emergence of the condensate of vector or tensor field. The appearance of such a condensate, or of a constant classical field on the background of Minkowski space, implies that it can affect the dynamics of the fundamental fields and thereby modify the Standard Model of strong, weak and electromagnetic interactions. Since the constant classical field is transformed by the passive Lorentz transformations as a Lorentz vector or tensor, its influence on the dynamics of fundamental fields of the Standard Model is described by the introduction of the additional terms representing all possible Lorentz-covariant convolutions of the condensate with the Standard fundamental fields into the Standard Lagrangian. The phenomenological theory, based on such a Lorentz-covariant modification of the Standard model is called the Standard Model Extension (SME) [26-32].
By design, the phenomenological SME theory is not Lorentz-invariant, since its Lagrangian is not invariant under active Lorentz transformations of the fundamental fields against the background of fixed condensate. In addition, in the context of SME, a violation of Lorentz symmetry also involves the violation of relativistic symmetry, since the presence of non-invariant condensate breaks the physical equivalence of the different inertial reference systems.
It should be added that in the low-energy limit of gravitation theories with broken Lorentz and relativistic symmetries, there appears an unlimited number of possibilities to build a variety of effective field theories, each of which could potentially explain at least some of the recently discovered astrophysical phenomena (see, e.g., [33]).
The very existence of the Finsler geometric models of space-time within which a violation of Lorentz symmetry occurs without the violation of relativistic symmetry strongly constrains the possible effective field theories with broken Lorentz symmetry: in order to be viable, such theories, in spite of the presence of Lorentz violation, should have the property of relativistic invariance.
Since only two types of Finsler spaces with broken Lorentz symmetry are relativistic invariant [34], we first consider the Finsler spaces of the first type.
2.1. The Relativistically Invariant Finslerian Spaces with Partially Broken 3D Isotropy
The metric of such spaces suggested in [4] has the following form
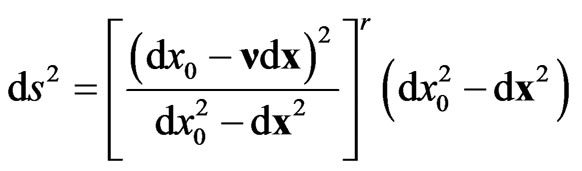 (1)
(1)
This metric depends on two constant parameters r and 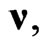 and generalizes the Minkowski metric, where r determines the spatial anisotropy, characterizing, thus, the degree of deviation of (1) from the Minkowski metric. Instead of the 3-parametric group of rotations of Minkowski space, Finsler spaces (1) can have only an 1-parametric group of rotations around the unit vector
and generalizes the Minkowski metric, where r determines the spatial anisotropy, characterizing, thus, the degree of deviation of (1) from the Minkowski metric. Instead of the 3-parametric group of rotations of Minkowski space, Finsler spaces (1) can have only an 1-parametric group of rotations around the unit vector 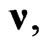 which presents a physically preferred direction in the 3D space. The translational symmetry suffers no change: space-time translations preserve metric (1) invariant (in this sense, it is natural to consider the family of spaces (1) as a family of flat Finsler spaces. With regard to the transformations connecting different inertial reference frames, the usual Lorentz boosts conformally modify metric (1). Therefore, they do not belong to a group of isometries of this metric. However, by using them, we can construct such transformations [5] which belong to the group of isometries of metric (1). The corresponding generalized Lorentz transformations (generalized Lorentz boosts) are as follows
which presents a physically preferred direction in the 3D space. The translational symmetry suffers no change: space-time translations preserve metric (1) invariant (in this sense, it is natural to consider the family of spaces (1) as a family of flat Finsler spaces. With regard to the transformations connecting different inertial reference frames, the usual Lorentz boosts conformally modify metric (1). Therefore, they do not belong to a group of isometries of this metric. However, by using them, we can construct such transformations [5] which belong to the group of isometries of metric (1). The corresponding generalized Lorentz transformations (generalized Lorentz boosts) are as follows
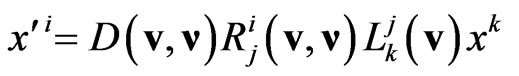 (2)
(2)
where 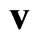 stands for the velocities of the moving (primed) reference frames, the matrices
stands for the velocities of the moving (primed) reference frames, the matrices 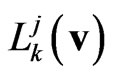 are the usual Lorentz boosts, the matrices
are the usual Lorentz boosts, the matrices 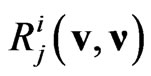 are the additional rotations of the spatial axes of the moving systems around vectors
are the additional rotations of the spatial axes of the moving systems around vectors  at angles
at angles
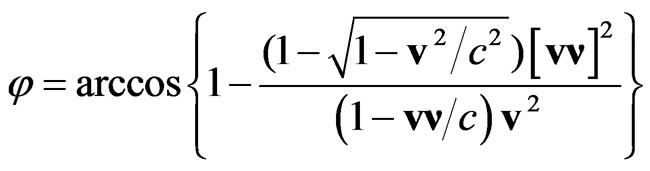
corresponding to the relativistic aberration of vector 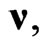 and, finally, the diagonal matrices
and, finally, the diagonal matrices
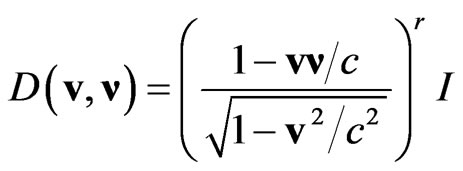
present the additional dilatational transformations of the coordinates of events.
In contrast to the usual Lorentz boosts, the generalized boosts (2) determine a 3-parametric non-compact group with generators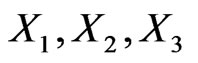 . Thus, with inclusion of 1- parameter group of rotations around the preferred direction
. Thus, with inclusion of 1- parameter group of rotations around the preferred direction 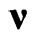 and 4-parameter translation group, the inhomogeneous group of isometries, or in other words, inhomogeneous group of relativistic symmetry of flat Finsler spaces (1) appears to have 8-parameters. To obtain the simplest representation for its generators, it is enough to send the third spatial axis along
and 4-parameter translation group, the inhomogeneous group of isometries, or in other words, inhomogeneous group of relativistic symmetry of flat Finsler spaces (1) appears to have 8-parameters. To obtain the simplest representation for its generators, it is enough to send the third spatial axis along 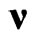 and rewrite the transformation (2) in the infinitesimal form. As a result, we come to the following eight generators
and rewrite the transformation (2) in the infinitesimal form. As a result, we come to the following eight generators
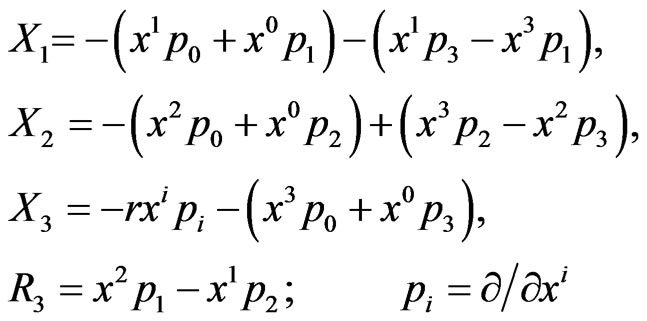 (3)
(3)
According to [5], these generators satisfy the commutation relations
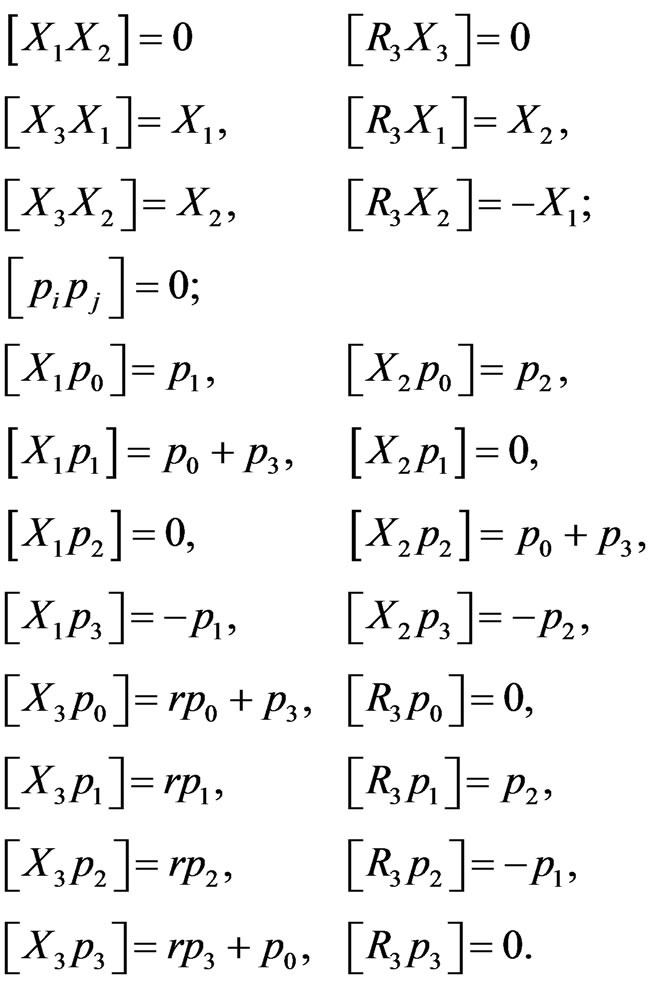 (4)
(4)
This shows that the homogeneous isometry group of flat Finsler spaces with partially broken 3D isotropy contains four parameters (generators 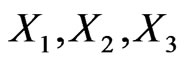 and
and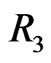 ). It is a subgroup of the 11-parametric Weyl group [35], and it is isomorphic to the corresponding 4-parametric subgroup (with generators
). It is a subgroup of the 11-parametric Weyl group [35], and it is isomorphic to the corresponding 4-parametric subgroup (with generators 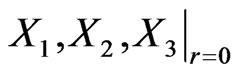 and
and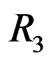 ) of the homogeneous Lorentz group. Since the 6-parametric homogeneous Lorentz group does not have any 5-parametric subgroup, while its 4-parametric subgroup is unique up to isomorphisms [36], the passage from Minkowski space to Finsler spaces (1) implies a minimum possible violation of Lorentz symmetry. With this, the relativistic symmetry represented now by the generalized Lorentz boosts (2) remains valid [37].
) of the homogeneous Lorentz group. Since the 6-parametric homogeneous Lorentz group does not have any 5-parametric subgroup, while its 4-parametric subgroup is unique up to isomorphisms [36], the passage from Minkowski space to Finsler spaces (1) implies a minimum possible violation of Lorentz symmetry. With this, the relativistic symmetry represented now by the generalized Lorentz boosts (2) remains valid [37].
Here it is worth noting the following. Despite the fact that at 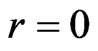 the Finsler metric (1) reduces to Minkowski metric
the Finsler metric (1) reduces to Minkowski metric 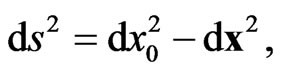 the 3-parametric non-compact transformations (2) that serve as the homogeneous relativistic symmetry transformations for Finsler metric (1) don’t reduce to the usual Lorentz boosts
the 3-parametric non-compact transformations (2) that serve as the homogeneous relativistic symmetry transformations for Finsler metric (1) don’t reduce to the usual Lorentz boosts 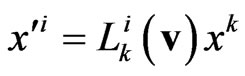 but reduce to the transformations
but reduce to the transformations
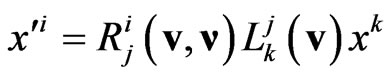 (5)
(5)
that differ by additional rotations 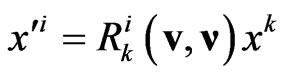 of the space axes. These rotations are designed so that if a light-beam in one inertial frame has the direction of
of the space axes. These rotations are designed so that if a light-beam in one inertial frame has the direction of 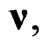 then it will have the same direction in all inertial frames.
then it will have the same direction in all inertial frames.
Thus, at 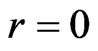 i.e. in frames of the usual SR, the transformations (5) are the alternative to the Lorentz boosts, however, in contrast to the Lorentz boosts, for any value of
i.e. in frames of the usual SR, the transformations (5) are the alternative to the Lorentz boosts, however, in contrast to the Lorentz boosts, for any value of 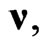 they present a 3-parameter non-compact subgroup of the 6-parametric homogeneous Lorentz group. As it was noted in [37], in order to realize these transformations physically, it is enough to choose
they present a 3-parameter non-compact subgroup of the 6-parametric homogeneous Lorentz group. As it was noted in [37], in order to realize these transformations physically, it is enough to choose 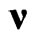 as a direction at any star and then perform an arbitrary Lorentz boost, supplementing it with such rotation of spatial axes that in the new reference system, the direction at the star does not change. Taken together, these transformations form the specified subgroup (5) of the 6-parametric homogeneous Lorentz group. As a result, we can say that within the framework of SR,
as a direction at any star and then perform an arbitrary Lorentz boost, supplementing it with such rotation of spatial axes that in the new reference system, the direction at the star does not change. Taken together, these transformations form the specified subgroup (5) of the 6-parametric homogeneous Lorentz group. As a result, we can say that within the framework of SR, 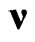 has no physical meaning and serves to the relativistically invariant calibration of the directions of spatial axes of inertial frames.
has no physical meaning and serves to the relativistically invariant calibration of the directions of spatial axes of inertial frames.
In connection with the last statement, it is necessary to make another important remark concerning the 3-parametric non-compact group of homogeneous transformations (5). If one complements this group by the 1-parametric group of rotations around 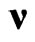 and 4-parametric translation group, the result is an 8-parameter subgroup of the Poincare group, whose generators and Lie algebra have in our basis the forms (3) and (4) assuming that
and 4-parametric translation group, the result is an 8-parameter subgroup of the Poincare group, whose generators and Lie algebra have in our basis the forms (3) and (4) assuming that 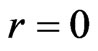 For such a group the name ISIM(2) is now used, and its homogeneous 4-parametric subgroup SIM(2), which includes (5) and the rotations around
For such a group the name ISIM(2) is now used, and its homogeneous 4-parametric subgroup SIM(2), which includes (5) and the rotations around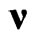 , is the basis for the so-called Very Special Relativity (VSR) [38]. According to VSR, SIM(2) symmetry suggests a more fundamental local space-time symmetry than the local Lorentz symmetry. In particular, the requirement of SIM(2) symmetry was sufficient to show [39] that neutrinos may have mass along with the lepton number conservation, and it is important that this result can not be obtained within the framework of Lorentz-invariant approach without introducing sterile neutrinos. However, a significant drawback of the VSR is that
, is the basis for the so-called Very Special Relativity (VSR) [38]. According to VSR, SIM(2) symmetry suggests a more fundamental local space-time symmetry than the local Lorentz symmetry. In particular, the requirement of SIM(2) symmetry was sufficient to show [39] that neutrinos may have mass along with the lepton number conservation, and it is important that this result can not be obtained within the framework of Lorentz-invariant approach without introducing sterile neutrinos. However, a significant drawback of the VSR is that 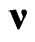 is regarded only as a phenomenological parameter and VSR can not say anything of its physical nature.
is regarded only as a phenomenological parameter and VSR can not say anything of its physical nature.
Much more meaningful from the physical point of view is the special relativistic theory of the locally anisotropic space-time [5-7], based on Finsler metric (1), which describes a family of flat relativistically invariant spaces of events with partially broken 3D isotropy, and hence with broken Lorentz symmetry. Most of the results obtained under such a theory have been reproduced in [40] using alternative methods (see also [41]). In particular, the inhomogeneous 8-parametric group of relativistic symmetry of metric (1) with its Lie algebra (4) were obtained using the method of continuous deformations of algebra ISIM(2). As a result, the corresponding symmetry is more frequently called DISIMb(2) symmetry (where b is the new designation of the parameter r), and the theory itself [5-7] is more frequently called General Very Special Relativity (GVSR).
2.1.1. The Rest Momentum in Addition to the Rest Energy
In order to modify the usual relativistic mechanics in accordance with the requirement of invariance with respect to DISIMb(2) it is enough to replace the Minkowski line element 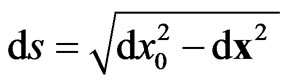 in the integral of action
in the integral of action
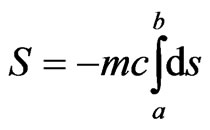 (6)
(6)
by the Finsler line element (1). As a result, the Lagrange function corresponding to a relativistic particle in a locally anisotropic space (1), is the following
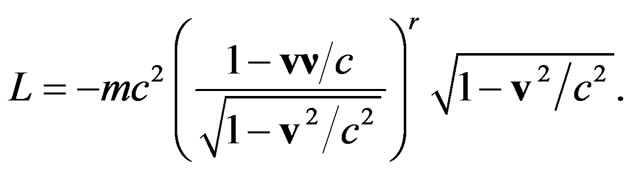 (7)
(7)
With this, one can get the expression for the energy 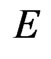 and momentum
and momentum 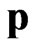 of the relativistic particle [6]:
of the relativistic particle [6]:
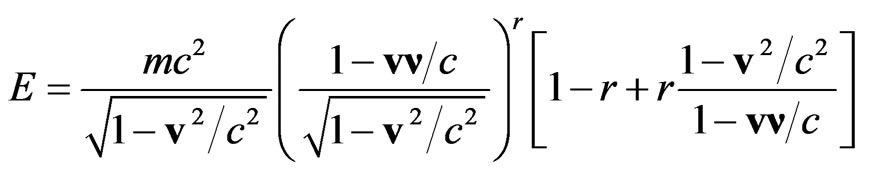 (8)
(8)
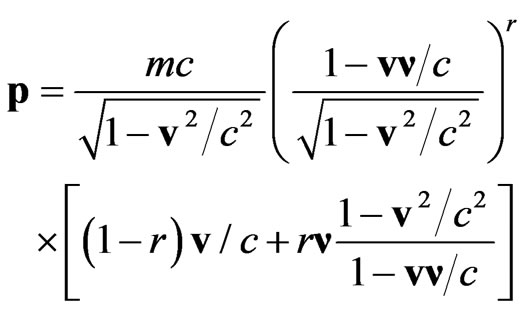 (9)
(9)
According to (8), the particle energy E reaches its absolute minimum 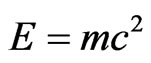 at
at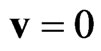 . As for the momentum
. As for the momentum 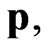 then according to (9), at
then according to (9), at  it takes the value
it takes the value 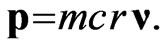 Thus, in the anisotropic space with metric (1), in addition to the rest energy
Thus, in the anisotropic space with metric (1), in addition to the rest energy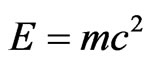 , any massive particle obtains another observable parameter—the rest momentum
, any massive particle obtains another observable parameter—the rest momentum 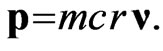 Note also that as shown in [6], the 4-momentum
Note also that as shown in [6], the 4-momentum 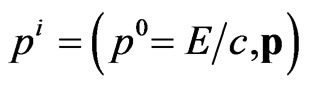 satisfies the DISIMb(2) -invariant dispersion relation, which we give here in the form:
satisfies the DISIMb(2) -invariant dispersion relation, which we give here in the form:
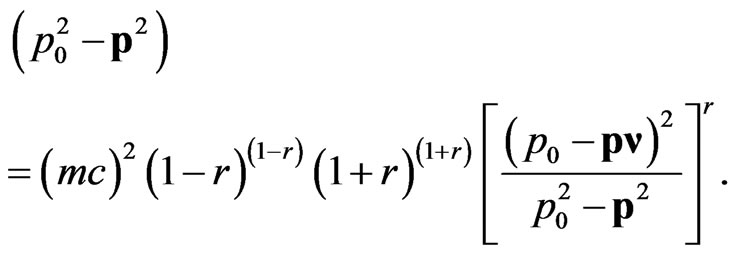 (10)
(10)
In the non-relativistic limit, the Lagrange function (7) has the following form
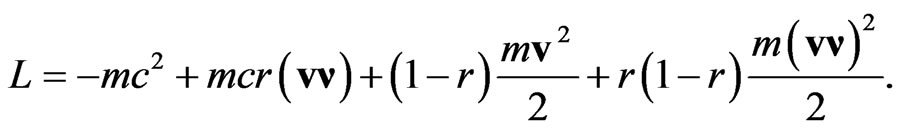
Since this expression 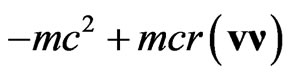 which is present here is the total derivative over time, it can be omitted. As a result, we see that the kinetic energy and momentum
which is present here is the total derivative over time, it can be omitted. As a result, we see that the kinetic energy and momentum
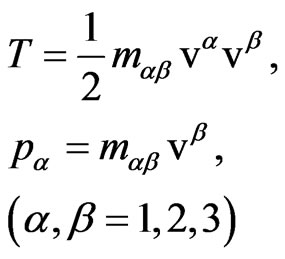
of the non-relativistic particle in the anisotropic space (1) are determined by the tensor of the inertial mass [34]:
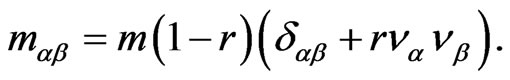 (11)
(11)
Let us now rewrite the Finsler metric (1) so that it is expressed through the four-dimensional quantities:
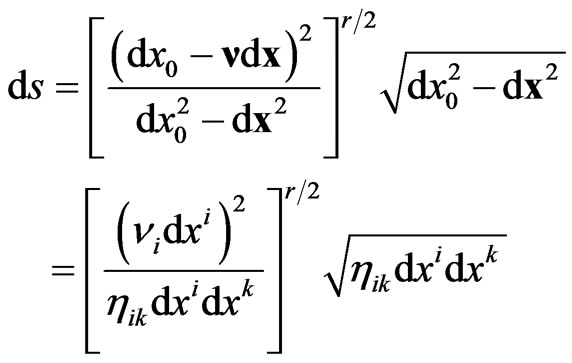 (12)
(12)
Since 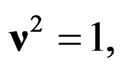 it is clear that here we have
it is clear that here we have
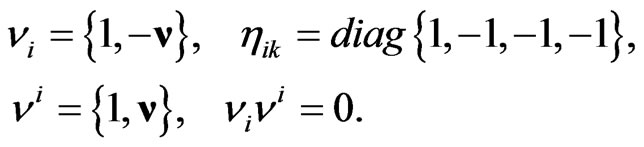
Finally, we present the physical carrier of the anisotropy of the flat space of events (12) and outline a plan for the further development of the theory. In order to do this, we first turn our attention to the unique property of Finsler metric (12). On the one hand, for 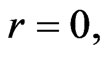 this turns into Minkowski metric, on the other, at
this turns into Minkowski metric, on the other, at 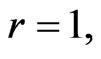 it transforms into the total differential
it transforms into the total differential 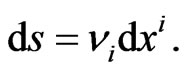 The latter means that in this case the action (6) does not depend on the shape of the world line connecting the points a and b In other words, the space-time loses such a physical characteristics as spatial extension, and only a temporal duration which represents the absolute time interval
The latter means that in this case the action (6) does not depend on the shape of the world line connecting the points a and b In other words, the space-time loses such a physical characteristics as spatial extension, and only a temporal duration which represents the absolute time interval 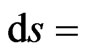
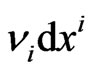 is left. Moreover, according to (11), the inertial masses of all particles also vanish, and
is left. Moreover, according to (11), the inertial masses of all particles also vanish, and 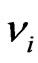 becomes not the spurionic vector field but is transformed into a covariant constant vector field defined on this degenerate (from the metric point of view) space-time manifold. Incidentally, we note that it is on the space-time manifold, and not on the Minkowski space-time, that the massless fundamental fields (for example, those of the Standard Model) are introduced before spontaneous violation of the initial gauge symmetry and before the appearance of masses of the initially massless particles. It is clear due to the fact that in the massless world there are no inertial reference systems, with their mandatory attribute—the reference stick.
becomes not the spurionic vector field but is transformed into a covariant constant vector field defined on this degenerate (from the metric point of view) space-time manifold. Incidentally, we note that it is on the space-time manifold, and not on the Minkowski space-time, that the massless fundamental fields (for example, those of the Standard Model) are introduced before spontaneous violation of the initial gauge symmetry and before the appearance of masses of the initially massless particles. It is clear due to the fact that in the massless world there are no inertial reference systems, with their mandatory attribute—the reference stick.
In accordance with (6) and (12), a constant non-zero field r defines the specific inseparable interaction of the constant spurionic field 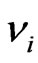 with massive particles. The effect of this interaction is that the particles obtain—according to (11), the properties of quasi-particles in an axially symmetric crystalline medium. The complex of constant fields containing the scalar field r and the spurionic field
with massive particles. The effect of this interaction is that the particles obtain—according to (11), the properties of quasi-particles in an axially symmetric crystalline medium. The complex of constant fields containing the scalar field r and the spurionic field 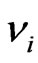 is, thus, the physical carrier of the anisotropy of the flat space of events (12). As it turned out, the null-vector spurionic field
is, thus, the physical carrier of the anisotropy of the flat space of events (12). As it turned out, the null-vector spurionic field 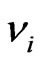 presents a neutrino-antineutrino condensate constructed out of constant Weyl spinors. Such spinors are an exact solution of the DISIMb(2) -invariant generalized massive Dirac equation [42], whose Lagrangian has the form
presents a neutrino-antineutrino condensate constructed out of constant Weyl spinors. Such spinors are an exact solution of the DISIMb(2) -invariant generalized massive Dirac equation [42], whose Lagrangian has the form
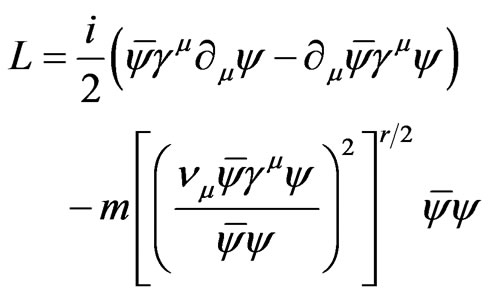 (13)
(13)
If the constant scalar field r is set to zero, the DISIMb(2)-invariant generalized massive Dirac equation becomes the standard massive Dirac equation, which does not have any solution in the form of constant spinors. However, the Weyl equations, arising from the standard massless Dirac equation have solutions in the form of constant spinors, and they provide the possibility to build a constant null-vector spurionic field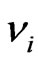 . But physically, it would be unobservable, since at
. But physically, it would be unobservable, since at 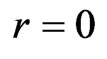 we come back to the framework of SR: the Finsler metric (12) becomes the Minkowski metric, the rest momentum
we come back to the framework of SR: the Finsler metric (12) becomes the Minkowski metric, the rest momentum 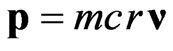 disappears, the tensor of inertial mass (11) ceases to be a tensor and becomes a scalar m. Accordingly, all the other effects of spatial anisotropy discussed in [43] will be lost.
disappears, the tensor of inertial mass (11) ceases to be a tensor and becomes a scalar m. Accordingly, all the other effects of spatial anisotropy discussed in [43] will be lost.
2.1.2. On the Problem of Construction of the Finslerian GR Based on the Group DISIMb(2)
As noted in the Introduction, the Ridge/CMS-effect which was observed at the LHC, directly suggests that in the early Universe the axially symmetric anisotropy of spacetime spontaneously arose, and it had the DISIMb(2) group as an inhomogeneous group of local relativistic symmetry and the respective Finsler metric (12). This is the first and most important reason to regard the problem of constructing a Finslerian general relativity based on the group DISIMb(2) Needless to speak about the complexity of such a problem, especially because it involves the answers to the questions concerning the nature of the dark matter and dark energy. Despite some advances in this direction, this problem is still not completely solved. So, in the end of Section 2.1, we suggest a possible way the progress on which is likely to lead to the planned purpose.
The key point in the generalization of the flat DISIMb(2)- invariant Finsler metric (12) to a Finsler metric, which describes the corresponding curved locally anisotropic space-time is the following. If the constant values on which the metric (12) depends, namely a scalar 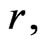 the spurion null-vector vi and the spurion tensor
the spurion null-vector vi and the spurion tensor 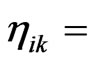
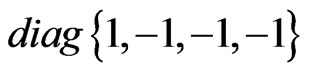 are replaced by the corresponding conventional fields defined on the space-time manifold, i.e. in the metric (12) the substitutions
are replaced by the corresponding conventional fields defined on the space-time manifold, i.e. in the metric (12) the substitutions 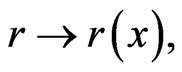
 are performed, then the result will be the curved Finsler metric of the following form (see [44,45])
are performed, then the result will be the curved Finsler metric of the following form (see [44,45])
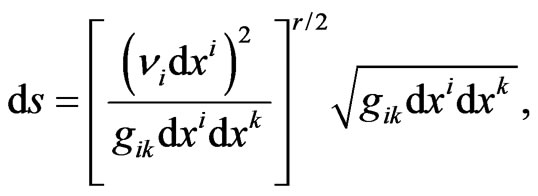 (14)
(14)
where 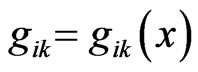 is the Riemannian metric tensor associated with the gravitational field,
is the Riemannian metric tensor associated with the gravitational field, 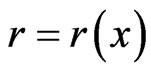 is a scalar field, which characterizes the magnitude of the local space-time anisotropy and
is a scalar field, which characterizes the magnitude of the local space-time anisotropy and 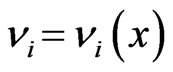 is a null-vector field that indicates the locally preferred directions in the space-time.
is a null-vector field that indicates the locally preferred directions in the space-time.
At any point of the curved Finsler space (14), the corresponding flat tangent Finsler space (12) has its own values of the parameters r and 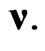 These values are nothing but the values of the fields
These values are nothing but the values of the fields 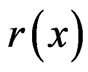 and
and 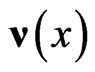 at the point of tangency.
at the point of tangency.
Obviously, the dynamics of a Finsler space (14) is completely determined by the dynamics of the interacting fields 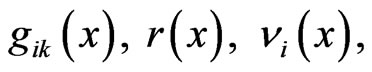 and these fields together with fields of matter form a unified dynamic system. Therefore, in contrast to the existing purely geometric approaches to the Finsler generalization of Einstein’s equations, our approach [44,45] to this problem is based on the use of methods of the conventional theory of interacting fields.
and these fields together with fields of matter form a unified dynamic system. Therefore, in contrast to the existing purely geometric approaches to the Finsler generalization of Einstein’s equations, our approach [44,45] to this problem is based on the use of methods of the conventional theory of interacting fields.
The fact that during the transition from a flat DISIMb(2)-invariant Finsler metric (12) to a curved Finsler metric (14), we replaced the spurion tensor 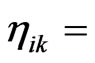
 and the spurion null-vector
and the spurion null-vector 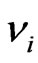 by the conventional fields, became the property of metric (14) invariance with regard to the following local transformations
by the conventional fields, became the property of metric (14) invariance with regard to the following local transformations
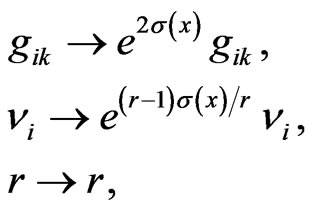 (15)
(15)
where 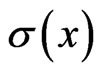 is an arbitrary function.
is an arbitrary function.
In addition to metric (14), the local transformations (15) leave invariant all the observables. Therefore, in the theory of gravitation based on the group DISIMb(2) the transformations (15) have the meaning of local gauge transformations. For example, the action
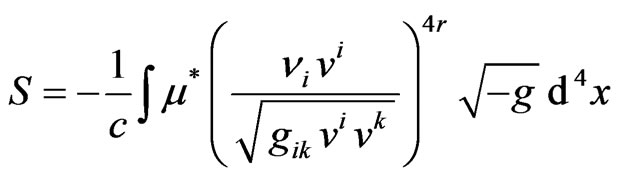
for a compressible fluid in a Finsler space (14) is gauge invariant. In this formula, 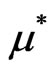 is the invariant energy density of the liquid,
is the invariant energy density of the liquid, 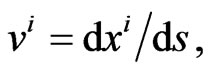 and ds is metric (14).
and ds is metric (14).
In connection with the above-mentioned local gauge invariance, the dynamical system consisting of the fields 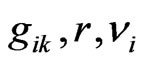 and a compressible fluid must be supplemented by two vector gauge fields
and a compressible fluid must be supplemented by two vector gauge fields 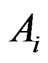 and
and 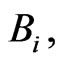 that under local transformations (15) are transformed in the corresponding gradient manner. The
that under local transformations (15) are transformed in the corresponding gradient manner. The 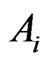 field for a certain class of problems is a pure gauge field, and the
field for a certain class of problems is a pure gauge field, and the 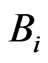 field, whose gauge transformation has the form
field, whose gauge transformation has the form
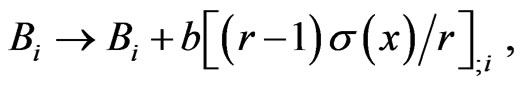
where b is a constant with the dimensionality of length, interacts with the conserved rest mass current 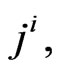 adding the term proportional to
adding the term proportional to 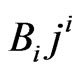 to the full gauge invariant Lagrangian.
to the full gauge invariant Lagrangian.
2.2. The Relativistically Invariant Finslerian Spaces with Entirely Broken 3D Isotropy
In general case, the metric of relativistically invariant Finslerian spaces with entirely broken 3D isotropy [46,47] is:
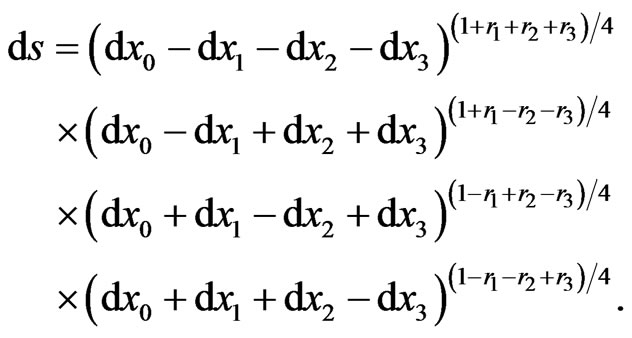 (16)
(16)
The three parameters (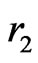
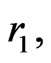 and
and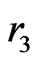 ) characterize the anisotropy of spaces (16) and have the following restrictions
) characterize the anisotropy of spaces (16) and have the following restrictions
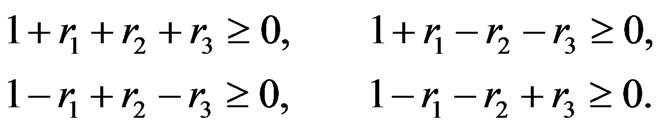
It should be noted that if 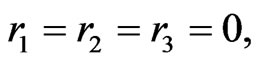 then the metric (16) becomes the fourth power root of the product of four 1-forms
then the metric (16) becomes the fourth power root of the product of four 1-forms
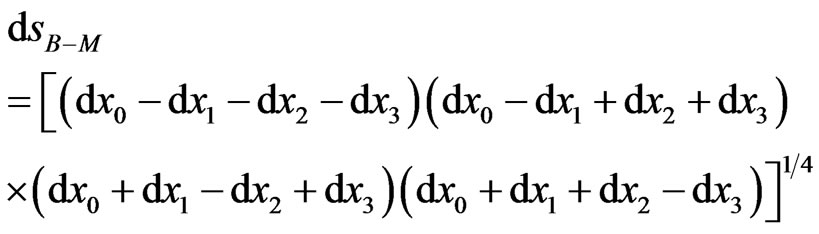
Thus, in this particular case, we obtain the well-known Berwald-Moor metric, but written in the basis, which was introduced in [46].
Now consider the group of isometries of flat Finsler space (16). The homogeneous 3-parametric non-compact group of isometries, i.e. the group of the relativistic symmetry of space-time (16) appears to be Abelian, and the transformations belonging to such a group have the same meaning as the ordinary Lorentz boosts. The explicit form of these transformations is
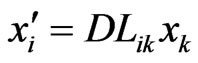 (17)
(17)
where
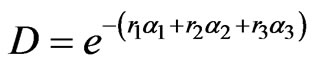
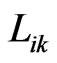 are the unimodular matrices that are given by the formulas
are the unimodular matrices that are given by the formulas
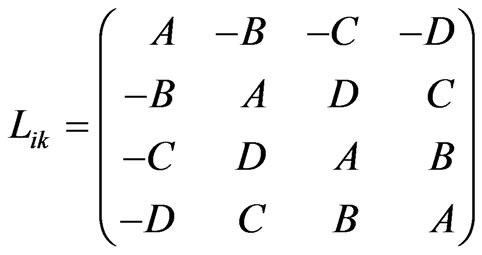 (18)
(18)
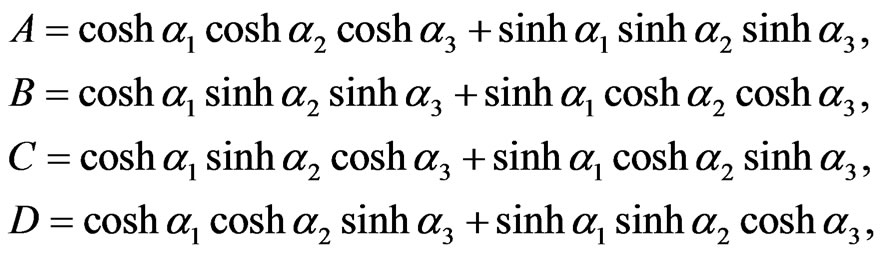
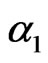 ,
, 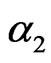 ,
, 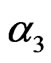 are the parameters of the group. Along with the parameters
are the parameters of the group. Along with the parameters 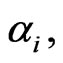 the components
the components 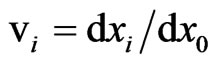 of the coordinate velocity of the primed reference frame can also be used as group parameters. The parameters
of the coordinate velocity of the primed reference frame can also be used as group parameters. The parameters 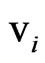 and
and 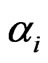 are related by
are related by
 (19)
(19)
The reverse relations have the form
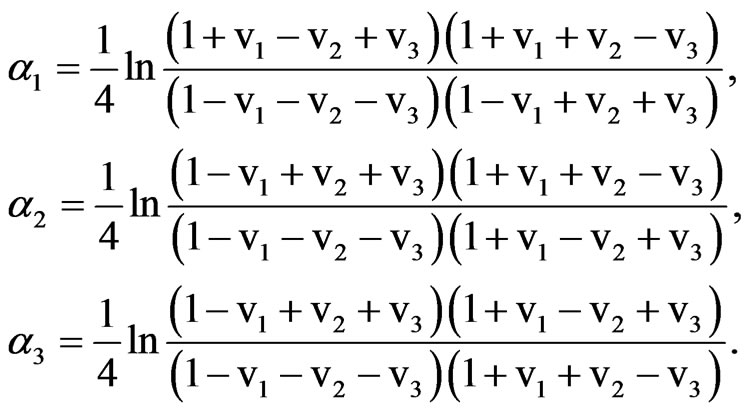 (20)
(20)
As for the generators 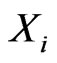 of the homogeneous 3-parametric group of isometries (17) of the space-time (16), they can be represented as follows
of the homogeneous 3-parametric group of isometries (17) of the space-time (16), they can be represented as follows
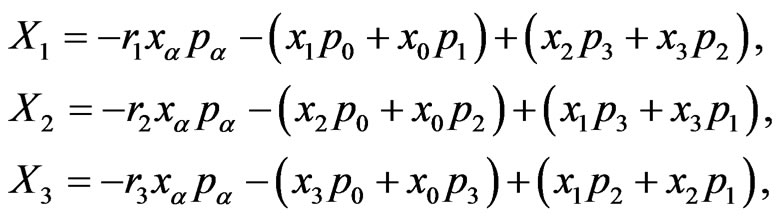
where 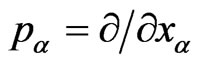 are the generators of the 4-parametric group of translations. Thus, with inclusion of the latter, a inhomogeneous group of isometries of the entirely anisotropic Finsler space of events (16) is a 7-parametric group. As to its generators, they satisfy the commutation relations
are the generators of the 4-parametric group of translations. Thus, with inclusion of the latter, a inhomogeneous group of isometries of the entirely anisotropic Finsler space of events (16) is a 7-parametric group. As to its generators, they satisfy the commutation relations
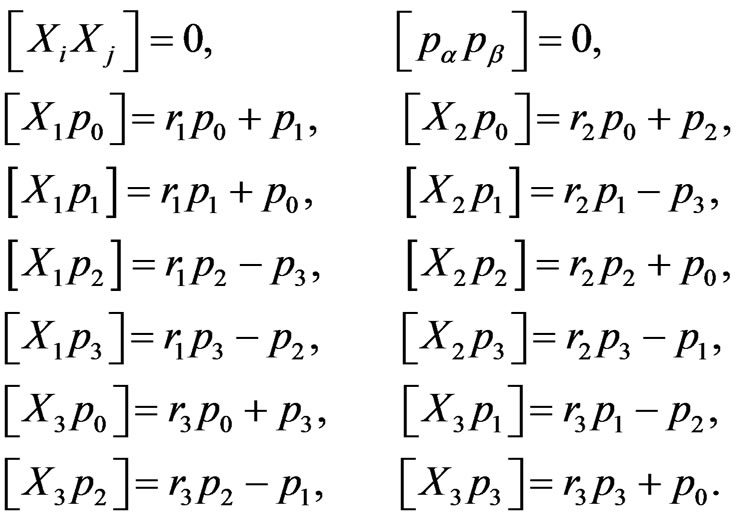
3. Modeling Real World by the Phase Space-Time and Physical Results Obtained on This Way
The theory and results briefly given below are discussed in detail in the monograph [83].
Let 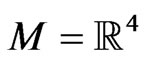 be a differentiable 4-dimensional manifold of class
be a differentiable 4-dimensional manifold of class 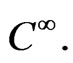 Let TM be its tangent bundle with coordinates
Let TM be its tangent bundle with coordinates 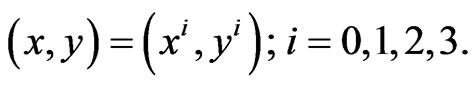 If c is a parametrizable curve on M,
If c is a parametrizable curve on M, 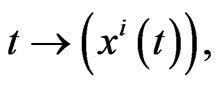
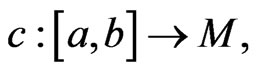 then its natural extension on TM is
then its natural extension on TM is 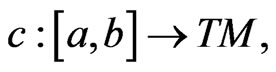
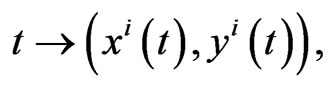 where
where 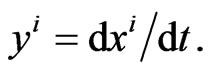 The arc length s, usually chosen as the natural parameter on the curve is thus equal to
The arc length s, usually chosen as the natural parameter on the curve is thus equal to 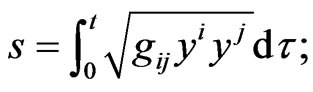
 Suppose that the metric introduced above depends on y, i.e.
Suppose that the metric introduced above depends on y, i.e. 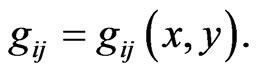 In general, this metric corresponds to the generalized Lagrange geometry,
In general, this metric corresponds to the generalized Lagrange geometry, 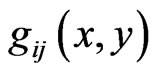 is a twice covariant symmetric tensor on TM with the only restrictions: a)
is a twice covariant symmetric tensor on TM with the only restrictions: a) 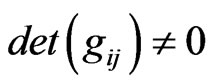 for any
for any 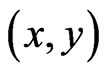 on TM and b) when the coordinates on TM change in the way corresponding to the change of coordinates on M, the components of the metric vary in the same way as the components of the (0,2)-tensor on the main manifold M. This means that TM is an 8-dimensional Riemannian manifold, analogous to the 6-dimensional phase space well-known in physics. Its geometry is quite complicated and uses such concepts as nonlinear connection (Ehresmann). But if we limit ourselves to the case of linear coordinate transformations with constant coefficients and of weak gravitational field, i.e.
on TM and b) when the coordinates on TM change in the way corresponding to the change of coordinates on M, the components of the metric vary in the same way as the components of the (0,2)-tensor on the main manifold M. This means that TM is an 8-dimensional Riemannian manifold, analogous to the 6-dimensional phase space well-known in physics. Its geometry is quite complicated and uses such concepts as nonlinear connection (Ehresmann). But if we limit ourselves to the case of linear coordinate transformations with constant coefficients and of weak gravitational field, i.e.
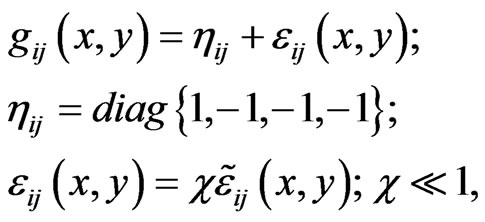
the geometry essentially simplifies, and the definition of 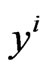 makes it possible to use the Sasaki lift for raising and lowering indices on the vertical and horizontal components of the bundle, that is use the same metric tensor. The tensor
makes it possible to use the Sasaki lift for raising and lowering indices on the vertical and horizontal components of the bundle, that is use the same metric tensor. The tensor 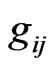 is a zero-order homogeneous in y tensor, i.e. the metric depends only on the direction of y, but not on its value. This is expressed by the relation
is a zero-order homogeneous in y tensor, i.e. the metric depends only on the direction of y, but not on its value. This is expressed by the relation
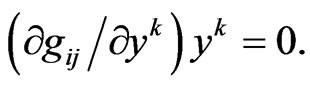 If there also holds the condition
If there also holds the condition
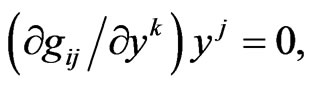 then this metric becomes the usual Finsler one [1], but in this approach this is not assumed.
then this metric becomes the usual Finsler one [1], but in this approach this is not assumed.
The described formalism means that alongside with the use of a new geometry for the modeling of phenomena in the physical world, instead of the space and time of Newton or of the Minkowski space-time, the 8-dimensional phase space-time is introduced. The character of its extra dimensions is not formal, but they have clear physical meaning, due to the used approach. Clearly, the correspondence between the Lagrangian and Hamiltonian formalism now obtains a new dimension. It should be noted that similarly to the situation when the transition from Newton’s time and space to the Minkowski spacetime took place and the fundamental constant c with the dimension of speed was demanded, the transition from Minkowski space-time to the 8-dimensional phase spacetime demands another fundamental constant, l, this time with the dimension of length. One can associate it with the fundamental speed and take 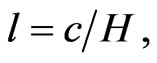 then H will be a new constant which has the dimension
then H will be a new constant which has the dimension 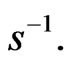 This suggests that in the interpretations, the following correspondence
This suggests that in the interpretations, the following correspondence
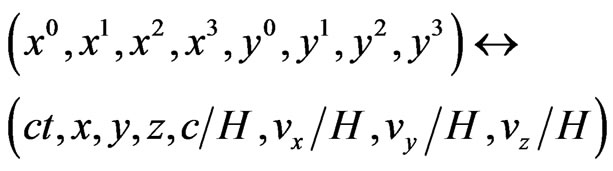
should be borne in mind. One should also pay attention to the fact that all the events would take place in the 7- dimensional subspace of the 8-dimensional phase spacetime, one of the coordinates of which is constant according to construction. The symmetry groups corresponding to this space will be the generalized Lorentz group and de Sitter group. The last can be contracted and be used in the Carroll space and in the Newton-Hooke space that are of interest for the astronomical applications. The possibility of separating the resulting space into such parts as 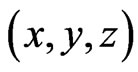 and
and 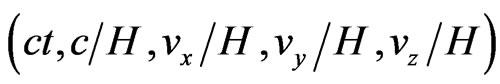 allows the use of Lobachevsky geometry to describe the space of velocities, this geometry was previously used only in the theory of high-energy particles.
allows the use of Lobachevsky geometry to describe the space of velocities, this geometry was previously used only in the theory of high-energy particles.
Preserving only linear terms proportional to 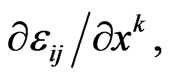
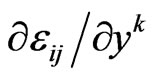 and
and 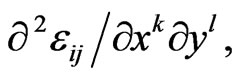 one can obtain the generalized geodesics similarly to [48-50] in the following form
one can obtain the generalized geodesics similarly to [48-50] in the following form
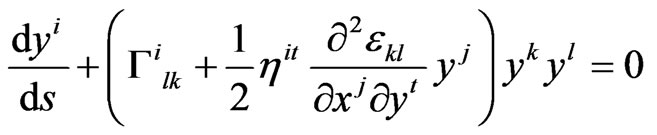 (21)
(21)
where 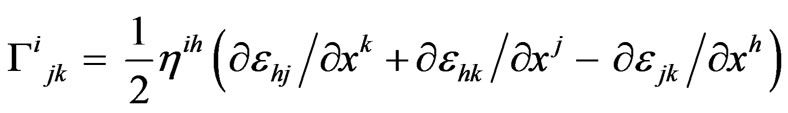 is the Christoffel symbol depending on y. Thus, in order to obtain the equations of motion (dynamic equations) in the weak field limit in the anisotropic space, one should use (21), but not geodesic equation
is the Christoffel symbol depending on y. Thus, in order to obtain the equations of motion (dynamic equations) in the weak field limit in the anisotropic space, one should use (21), but not geodesic equation 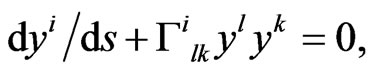 which is appropriate in the same approximation only in a space with Riemann geometry. As a result, after certain simplifications and extraction of the anti-symmetric part of the auxiliary tensor introduced in [10-15], the equation of motion obtained from the geodesic (21) and applied to the spatial cross-section of the space takes the form
which is appropriate in the same approximation only in a space with Riemann geometry. As a result, after certain simplifications and extraction of the anti-symmetric part of the auxiliary tensor introduced in [10-15], the equation of motion obtained from the geodesic (21) and applied to the spatial cross-section of the space takes the form
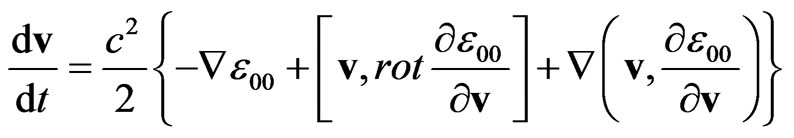 (22)
(22)
where 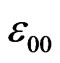 is the only (temporal) component of the metric tensor, which remains in the equation of motion in the approximation of the weak field. Regarding (22) as the equation of dynamics, we obtain the expression for the generalized gravitational force depending on velocities [10-15]
is the only (temporal) component of the metric tensor, which remains in the equation of motion in the approximation of the weak field. Regarding (22) as the equation of dynamics, we obtain the expression for the generalized gravitational force depending on velocities [10-15]
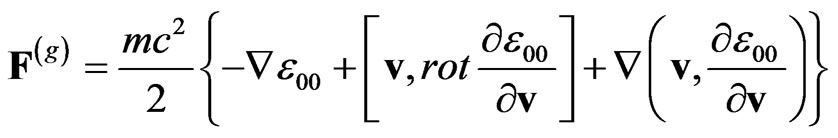 (23)
(23)
The last two equations are obtained from the geodesics corresponding to the field equations for an anisotropic metric. They do not require a special choice of the energymomentum tensor, and any additional a priori assumptions. The field equations in the anisotropic space in the linear approximation for weak fields retain their form [51], although their terms may now depend on y.
To study the dynamics of spiral galaxies, one could choose
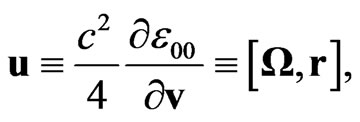
where
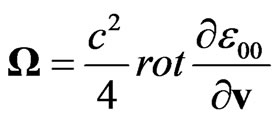
and
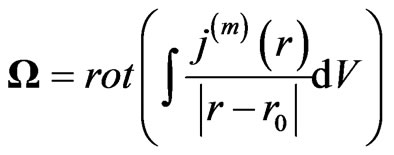
where 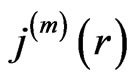 is the mass current density, and r0 corresponds to the observer. Then the equation for the gravitational force obtains the form
is the mass current density, and r0 corresponds to the observer. Then the equation for the gravitational force obtains the form
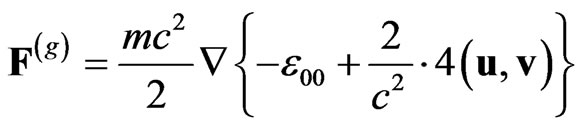 (24)
(24)
If we demand the existence of limit transition to the usual GRT, then
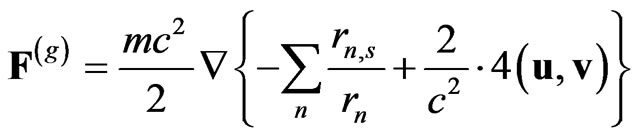 (25)
(25)
and it can be shown that the second term under the gradient has the same order of magnitude as the first one at distances of the order of a galaxy radius. It is this that prevents the vanishing of orbital velocity required by the general relativity. At the same time, the motion in the galactic plane and perpendicular to this plane is now described by the different laws, which removes the wellknown paradox [52] in the observations of motion of stellar globular clusters.
In the framework of the suggested approach—anisotropic geometrodynamics (AGD)—the notion of a point mass is not sufficient to model the elementary (effective) source of gravitation, and one should use a system of “center plus current” which represents a gravitational analogue of the circular coil with current around the central charge. The use of such a system for simulation of a spiral galaxy, leads to the expression 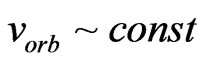 for the orbital velocity corresponding to the observed flat rotation curve, and to the empirical Tully-Fisher law
for the orbital velocity corresponding to the observed flat rotation curve, and to the empirical Tully-Fisher law 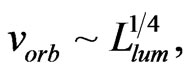 which has no explanation in general relativity. The same model can explain the observed substantial excess of deflection in some gravitational lenses over the theoretical calculations, which appears to be due to the internal motions of the masses in the galaxy-lens. It has been also shown that in addition to the known convex gravitational lenses, in the AGD there exist concave gravitational lenses. This can lead to the incorrect determination of distances to the sources compared to “standard candles”. And this can account for another interpretation of the data which led to the idea of the acceleration of the Universe expansion and to the notion of dark energy.
which has no explanation in general relativity. The same model can explain the observed substantial excess of deflection in some gravitational lenses over the theoretical calculations, which appears to be due to the internal motions of the masses in the galaxy-lens. It has been also shown that in addition to the known convex gravitational lenses, in the AGD there exist concave gravitational lenses. This can lead to the incorrect determination of distances to the sources compared to “standard candles”. And this can account for another interpretation of the data which led to the idea of the acceleration of the Universe expansion and to the notion of dark energy.
Calculation of the explosion of the central body in the “center plus current” model, resulting in the release of the two equal masses in opposite directions in the plane of the coil leads to trajectories that resemble the well-known observations obtained by the HUBBLE telescope (compare Figures 1(a) and (b)).
Besides, there are also the images received recently by the space observatory HERSCHEL [84] (compare Figure 1(b) and Figure 2) when photographing the center of our galaxy. Thus, there could be a new approach to the study of the origins of the arms and bars, characteristic of most spiral galaxies.
The theory presented in this section is based on the new notion, which serves the basis for the description of physical reality—the phase space-time admitting the use
 (a)
(a)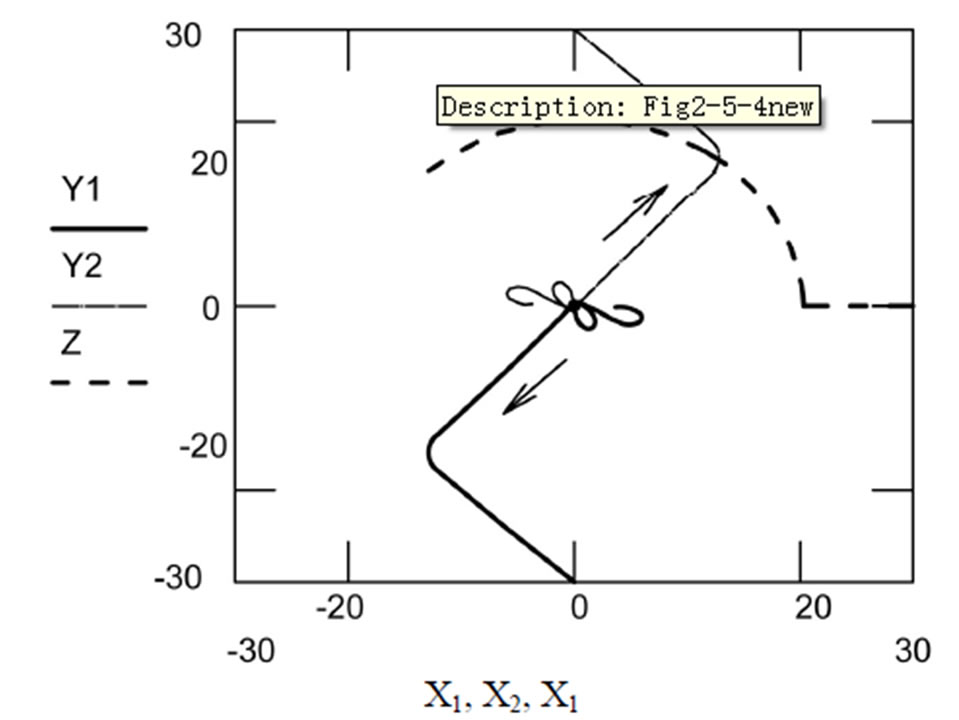 (b)
(b)
Figure 1. (a) Galaxy NGC-1365 (Hubble telescope image, NASA/ESA); (b) Numerical calculation based on the “center plus current” model in the framework of AGD (the exact view of the central details depends on the step of the calculation but they remain always present).

Figure 2. Details discovered by Herschel orbital observatory in the center of milky way.
of various geometries to describe its subspaces. The AGD approach is consistent with observations at the galactic scale, and does not require the introduction of dark matter. Besides, it includes a new (or additional) interpretation of the Hubble law, which takes into account not the radial expansion of the Universe but the various tangential motions of its distant parts. The last being regarded in the framework of AGD leads to a linear decrease of frequency with distance to the radiation sources explained by the gravitational red shift. The observations of extremely high tangent velocities of the distant quasars present an indirect evidence supporting this idea.
4. Mathematical, Physical and Geometric Aspects of Hyper-Complex Numbers Algebra
The natural basis for Finsler geometries of special type (the so-called Berwald-Moor spaces 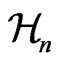 with metric
with metric
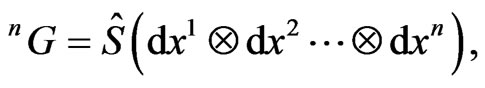 (26)
(26)
where 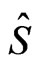 is the symmetrization operator (without the numerical factor)) represent the well-known associativecommutative algebras
is the symmetrization operator (without the numerical factor)) represent the well-known associativecommutative algebras 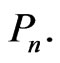
This section of the review is devoted to presenting the geometrical, algebraic and physical results obtained in the study of poly-numbers associative-commutative algebras and Berwald-Moor geometries of various dimensions related to them.
4.1. Conformal Gauges and Non-Linear Symmetries
It is well known that the Finslerian Berwald-Moor space  have a rich (infinite) group of conformal symmetries
have a rich (infinite) group of conformal symmetries 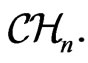 We denote by
We denote by 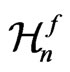 the Berwald-Moor manifold in a special conformal gauge, which can be obtained from
the Berwald-Moor manifold in a special conformal gauge, which can be obtained from 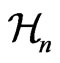 by the action of some
by the action of some 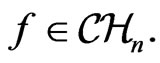 Instead of the transformations of the manifold
Instead of the transformations of the manifold 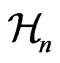 belonging to the group
belonging to the group 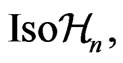 we now have the transformations of the manifold
we now have the transformations of the manifold 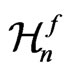 belonging to the group
belonging to the group 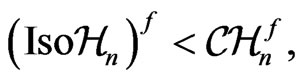 whose elements
whose elements 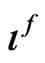 are defined by the formula
are defined by the formula 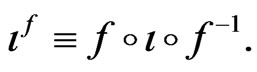 The action of the group
The action of the group 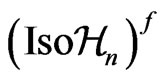 in the coordinate space of the manifold
in the coordinate space of the manifold 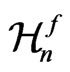 in general case is described by nonlinear functions, so this group is naturally called the nonlinear
in general case is described by nonlinear functions, so this group is naturally called the nonlinear 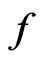 -representation of the group
-representation of the group 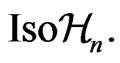 In general, the group
In general, the group 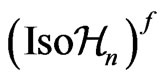 can always be regarded as a (generally nonlinear) group of isometries
can always be regarded as a (generally nonlinear) group of isometries 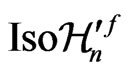 of a manifold
of a manifold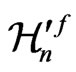 , which differs from
, which differs from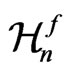 , only by its metric. The form of this metric depends on the type of the gauge function
, only by its metric. The form of this metric depends on the type of the gauge function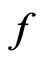 .
.
In [53,54] there are concrete examples that illustrate the fact that the isometry group and the group of conformal symmetries of the Berwald-Moor metric can interact with each other in a non-trivial way leading to nonlinear symmetries of the known geometries.
4.2. Osculating Riemannian Metrics
With the disposal of the metric (26) and vector fields of Lie algebras of the groups 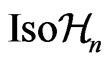 (and
(and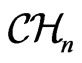 ), one can naturally obtain an infinite number of Riemannian metrics out of the metric (26) with the help of the following general technique. Consider the “incomplete” scalar polyproduct of the form:
), one can naturally obtain an infinite number of Riemannian metrics out of the metric (26) with the help of the following general technique. Consider the “incomplete” scalar polyproduct of the form:
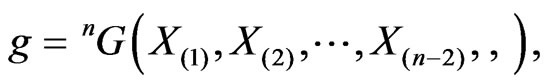
where 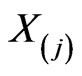 are the elements of Lie algebras of the groups
are the elements of Lie algebras of the groups  and (or)
and (or) 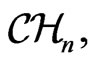 that are for convenience numbered by the indices corresponding to their places as the arguments of the Berwald-Moor metric. It is obvious that
that are for convenience numbered by the indices corresponding to their places as the arguments of the Berwald-Moor metric. It is obvious that  is a (pseudo-) Riemannian metric, depending on the chosen fields
is a (pseudo-) Riemannian metric, depending on the chosen fields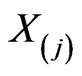 . The described method leads to a generalization of the concept of “Riemannian metric osculating to a given Finslerian metric”, discussed in [1].
. The described method leads to a generalization of the concept of “Riemannian metric osculating to a given Finslerian metric”, discussed in [1].
Consider as a reference vector field a common element of the Lie algebra of the subgroup of the uni-modular dilations 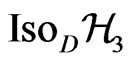 of the complete group
of the complete group 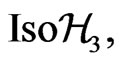 which has the form:
which has the form:
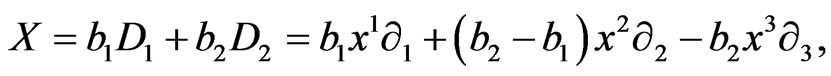
where  are arbitrary real parameters. The Riemannian metric osculating along this field has the form:
are arbitrary real parameters. The Riemannian metric osculating along this field has the form:
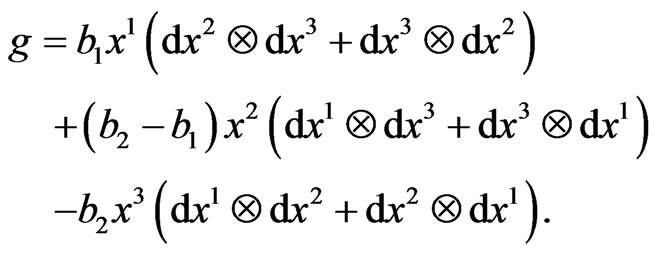 (27)
(27)
This metric is generally not flat. Its determinant defining a local volume element is given by:
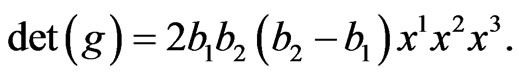
One can see that the metric (27) is nonsingular only if all of the conditions: 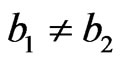
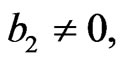
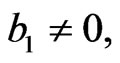 are fulfilled simultaneously. The standard study of isometries and conformal symmetries of this metric reveals the fact that this metric has a 3-dimensional algebra of isometries and 10-dimensional algebra of conformal symmetries. Such a rich algebra of conformal symmetries is a residual “track” of the infinite-dimensional algebra of conformal symmetries of the original Berwald-Moor metric (26) for
are fulfilled simultaneously. The standard study of isometries and conformal symmetries of this metric reveals the fact that this metric has a 3-dimensional algebra of isometries and 10-dimensional algebra of conformal symmetries. Such a rich algebra of conformal symmetries is a residual “track” of the infinite-dimensional algebra of conformal symmetries of the original Berwald-Moor metric (26) for 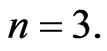
The study of residual symmetries of the Riemannian metrics osculating to the Berwald-Moor metrics admits a more general setting in which we obtain the following basic relations:
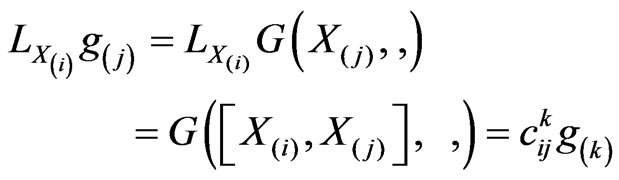 (28)
(28)
and
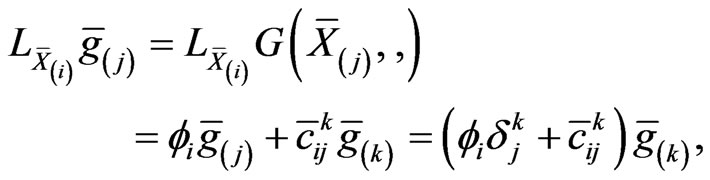 (29)
(29)
where 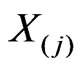 is an element of the Lie algebra of the group
is an element of the Lie algebra of the group 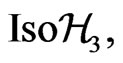
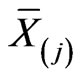 is an element of the Lie algebra of the conformal group
is an element of the Lie algebra of the conformal group 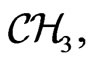
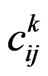 and
and 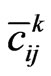 are the structural constants or the structural functions of the Lie algebra of the groups
are the structural constants or the structural functions of the Lie algebra of the groups 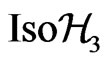 and
and 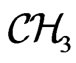 respectively.
respectively.
Thus, the families of metrics 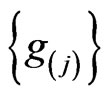 and
and 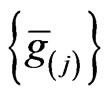 form differential ideals with respect to their Lie differentiation along the families of fields
form differential ideals with respect to their Lie differentiation along the families of fields 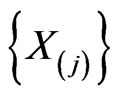 and
and 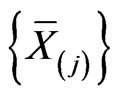 respectively. This is a general property and it allows us to formulate some general theorems concerning the symmetry of Riemannian metrics
respectively. This is a general property and it allows us to formulate some general theorems concerning the symmetry of Riemannian metrics 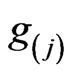 and
and 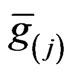 [55].
[55].
4.3. Metric Bingles in 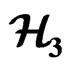
Studying the properties of angles in Finsler geometry is of particular interest for its physical applications. One of the approaches to the problem of constructing of additive poly-angles (e.g. bingles and tringles) is to formulate and solve the corresponding functional equations that satisfy the additivity condition [56]. Instead of solving the functional differential equations in the space of basic conformal invariants of B-M geometry, one can from the very beginning relate all the types of poly-angles with notions additive by their definition, such as lengths, areas or volumes, calculated on the unit sphere (indicatrix) of the B-M geometry.
It turns out that for any pair of non-isotropic vectors A and B one can introduce two types of bingles—mutual and relative. The expression for the mutual bingle has the following form:
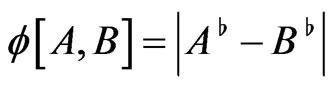 (30)
(30)
where 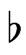 is a bi-projection operation in
is a bi-projection operation in 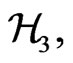 which acts on an arbitrary element
which acts on an arbitrary element 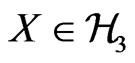 according to the rule:
according to the rule:
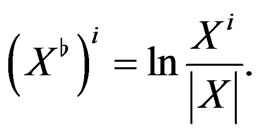
The norm in (30) is calculated with the help of the standard Berwald-Moor metric in the isotropic coordinates. The bingle defined by (30) is additive by definition, i.e. for any triplet of the “coplanar” vectors 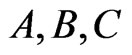 there is a condition which is analogous to the Euclidean one:
there is a condition which is analogous to the Euclidean one:
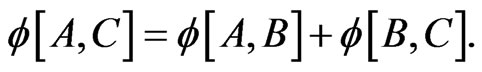 (31)
(31)
The condition of coplanarity of the vectors 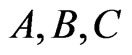 has the form of the condition of collinearity of the corresponding
has the form of the condition of collinearity of the corresponding  -images:
-images:
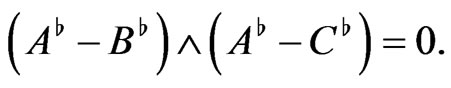 (32)
(32)
Expressions for the second (mutual) bingle (there may be three types of it, depending on the mutual orientation of vectors A and B) have the form:
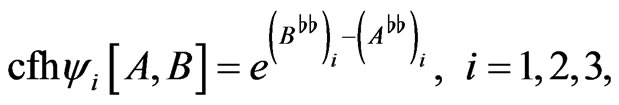 (33)
(33)
and the function, which is inverse to the Finsler-hyperbolic cosine 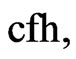 is defined by the integral:
is defined by the integral:
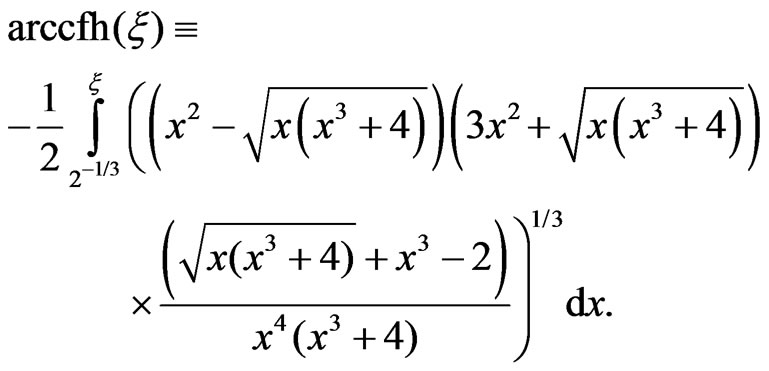 (34)
(34)
Finally, the expression for the value analogous to the solid angle on the vectors A, B and C is given by the following integral:
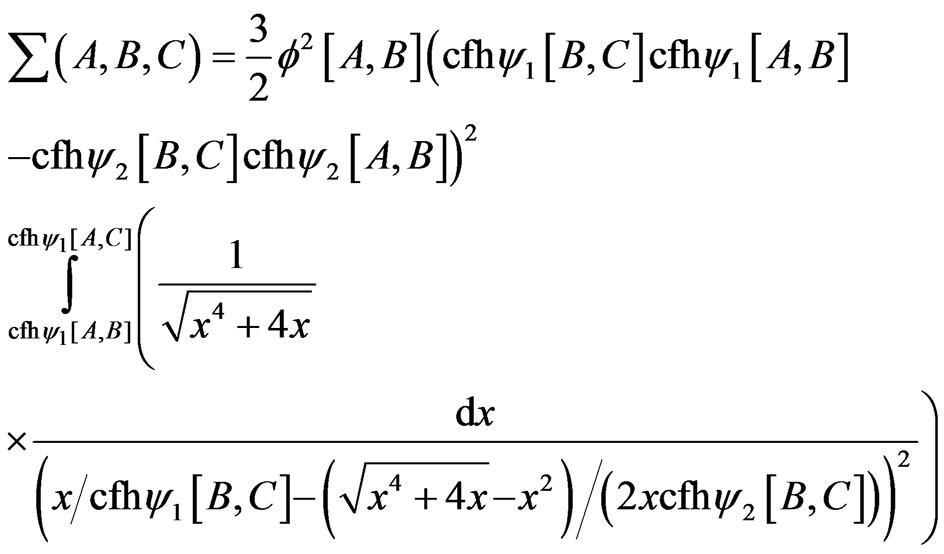
(35)
The exact formulations, proofs and illustrations can be found in [57].
4.4. Classification of Homogeneous Cubic Metrics
Symmetry analysis of geometric objects is a key means of study of their internal invariant properties (i.e. being independent on the coordinates). In order to understand the place of Berwald-Moor metric among other related cubic metrics, the study of the isometry group of the general homogeneous cubic form
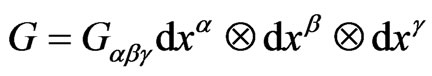 (36)
(36)
was undertaken. Here 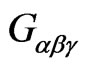 are the constant real components of the cubic form. The results of the study are summarized in Table 1.
are the constant real components of the cubic form. The results of the study are summarized in Table 1.
This proves that the symmetry analysis reveals 6 different symmetry classes (7th class is empty, and the 6th coincides with the 5th), the previously known 13 projective classes [58] are distributed amongst them. The Berwald-Moor metric falls into the 1st symmetry class. One of the important findings of this study is the conclusion on the incompleteness of the classification of cubic homogeneous metrics according to their isometry algebras [59].
4.5. h-Holomorphic Functions of a Double Variable
For the interpretation of  as a plane of a double variable
as a plane of a double variable  it is natural to consider only the maps that preserve the hyperbolic complex structure of the plane, i.e. by the maps
it is natural to consider only the maps that preserve the hyperbolic complex structure of the plane, i.e. by the maps  of the form:
of the form: 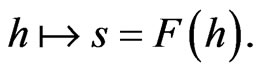 The differentiable functions
The differentiable functions 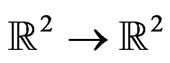 which satisfy the condition:
which satisfy the condition: 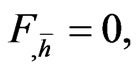 are called
are called 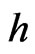 -holomorphic functions of double variable h.
-holomorphic functions of double variable h.
Let us formulate some important properties of the hholomorphic functions as theorems.
Theorem 1. Any 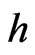 -holomorphic function maps zero divisors into zero divisors.
-holomorphic function maps zero divisors into zero divisors.
Theorem 2. The components 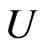 and
and 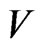 of the
of the 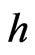 - holomorphic function
- holomorphic function 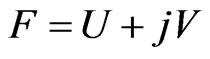 satisfy the hyperbolic Cauchy-Riemann conditions:
satisfy the hyperbolic Cauchy-Riemann conditions: 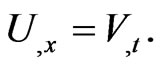
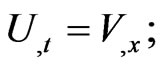
Theorem 3. For any 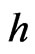 -holomorphic function
-holomorphic function 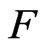 in
in 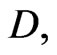 there holds the integral Cauchy Theorem:
there holds the integral Cauchy Theorem:
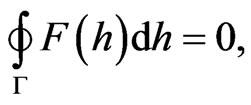 where
where 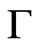 is a simple closed piecewise smooth contour which has no isotropic elements and lies entirely in
is a simple closed piecewise smooth contour which has no isotropic elements and lies entirely in 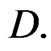
Theorem 4. For any 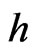 -holomorphic function
-holomorphic function 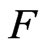 in D, there holds true the integral Cauchy formula:
in D, there holds true the integral Cauchy formula:
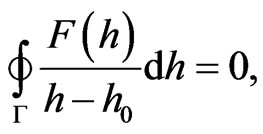
where 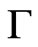 is a simple closed piecewise smooth contour which has no isotropic elements, lies entirely in
is a simple closed piecewise smooth contour which has no isotropic elements, lies entirely in 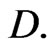 and encloses the point
and encloses the point 
Other versions of Cauchy’s integral formula are given in [60].
Theorem 5. For a simple closed piecewise smooth contour 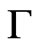 that has no isotropic elements and encloses the point
that has no isotropic elements and encloses the point 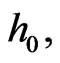 we have the formula:
we have the formula:
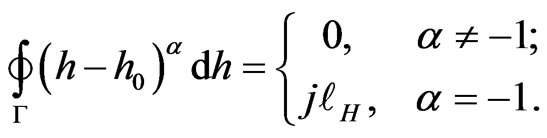 (37)
(37)

Table 1. Projective and symmetry classes of 3D cubic metrics.
where  is any real number,
is any real number, 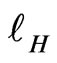 is the improper “fundamental constant” in the plane of double variable that determines the amount of space of the hyperbolic angles (analogous to the constant
is the improper “fundamental constant” in the plane of double variable that determines the amount of space of the hyperbolic angles (analogous to the constant 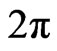 in the complex plane).
in the complex plane).
Theorem 6. The pseudo-Euclidean metric 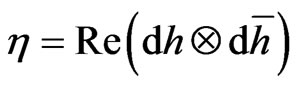 is conformal relative to an arbitrary h-holomorphic mapping of the plane of the double variable.
is conformal relative to an arbitrary h-holomorphic mapping of the plane of the double variable.
In [60] the properties of the basic elementary h-holomorphic functions of the double variable were studied in detail.
4.6. Hyperbolic Field Theory on the 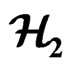 Plane
Plane
We consider an arbitrary h-holomorphic function 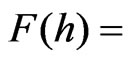
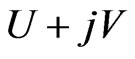 as complex h-potential of a certain 2-dimensional vector field (h-field) in the plane of double variable. The real part
as complex h-potential of a certain 2-dimensional vector field (h-field) in the plane of double variable. The real part 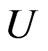 of this function we associate with the potential of the field (
of this function we associate with the potential of the field (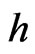 -potential function) and the imaginary part V we associate with the strength function of this field. We define the strength,
-potential function) and the imaginary part V we associate with the strength function of this field. We define the strength, 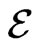 of the
of the 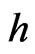 -field by the formula:
-field by the formula:
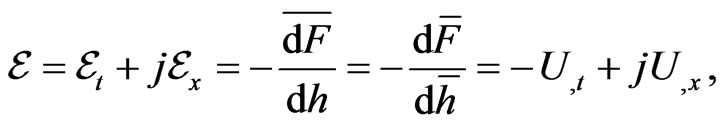 (38)
(38)
which can be regarded as a double form of representation for the vector field of the gradient of the function U with respect to the pseudo-Euclidean metric. Equation (38) is obtained taking into account the hyperbolic CauchyRiemann conditions.
In view of the relation 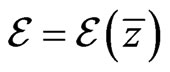 (antiholomorphicity of strength), arising from the definition (38), we obtain the following identity:
(antiholomorphicity of strength), arising from the definition (38), we obtain the following identity:
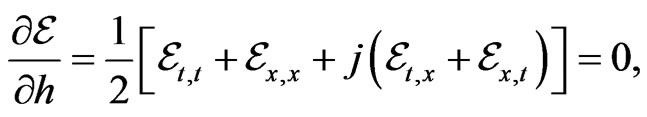 (39)
(39)
which is equivalent to two identities:
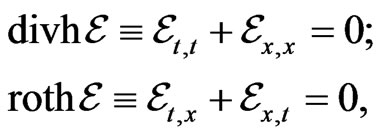 (40)
(40)
expressing, respectively, the solenoidal and  -potential properties of the electrostatic field1.
-potential properties of the electrostatic field1.
As an example, consider the  -potential of the form
-potential of the form
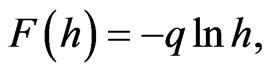 (41)
(41)
which is obviously the hyperbolic generalization of the Coulomb potential. The corresponding field strength is given by (38) and has the form:
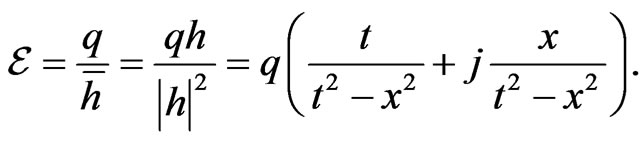 (42)
(42)
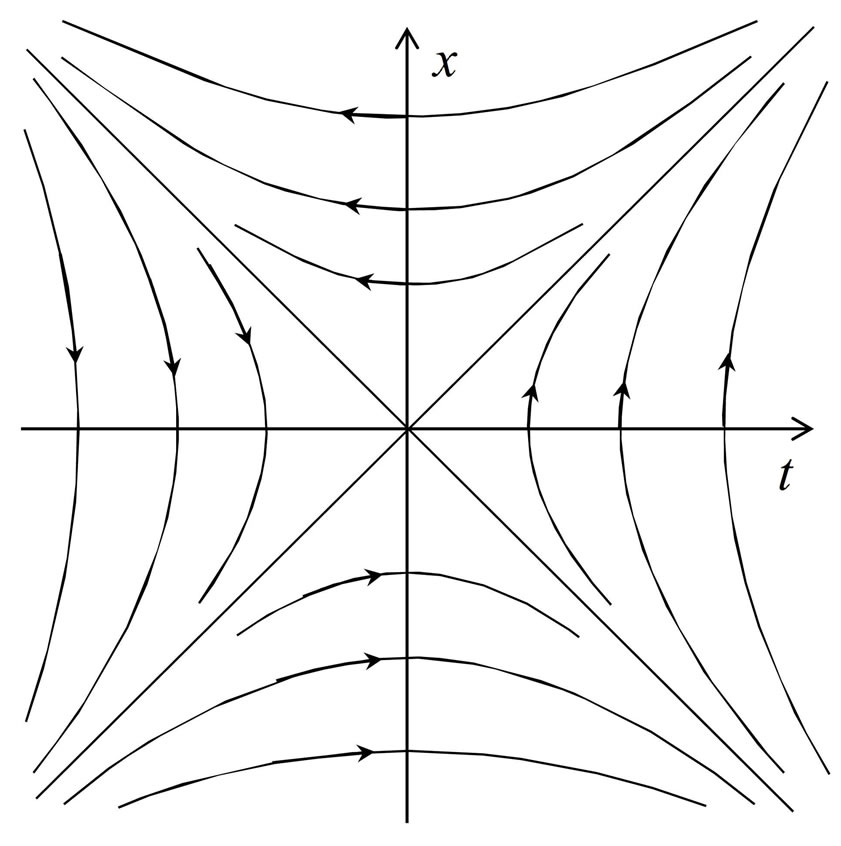
The field lines of a hyperbolic point source are the radial lines with 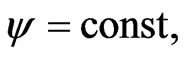 and the equipotential lines are the hyperbolas
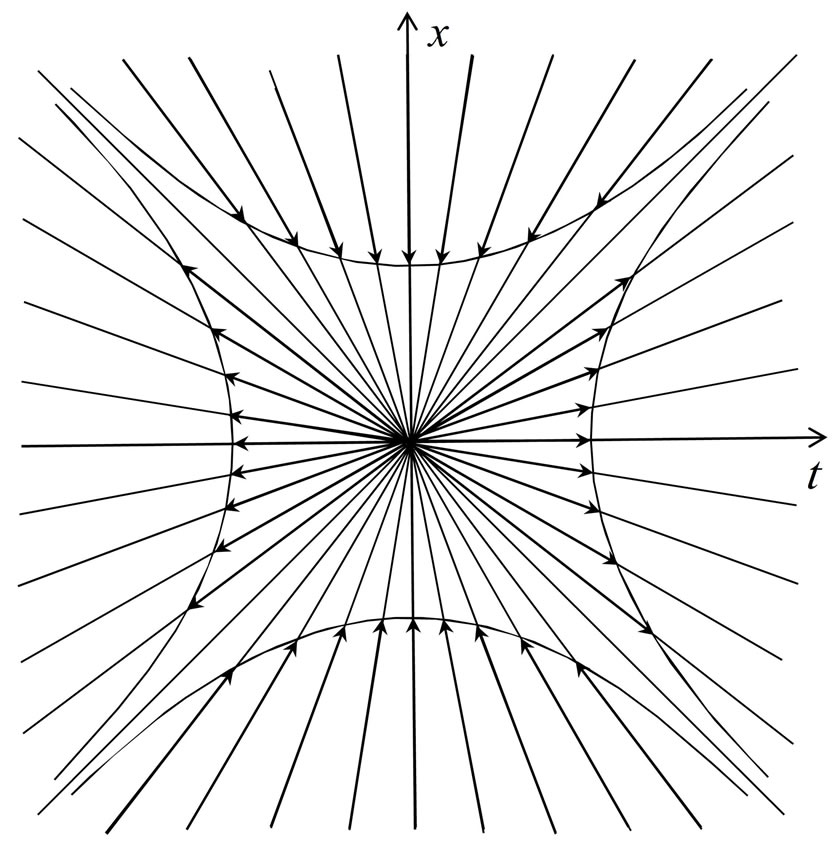
and the equipotential lines are the hyperbolas 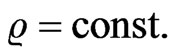 The picture of the field lines in all 4 wedges is shown on the figure:
The picture of the field lines in all 4 wedges is shown on the figure:
The dual interpretation of the hyperbolic point source is obtained by passing from the potential 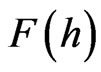 in (41) to the potential
in (41) to the potential 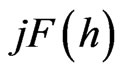 At the same time for a new dual field
At the same time for a new dual field 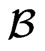 we get the following expression:
we get the following expression:
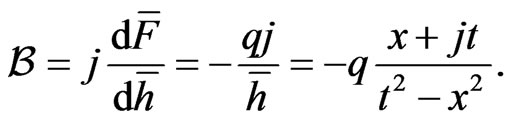 (43)
(43)
Field  is a hyperbolic analogue of a point vortex. Its lines of force are shown in the picture and present the hyperbolas:
is a hyperbolic analogue of a point vortex. Its lines of force are shown in the picture and present the hyperbolas:
By analogy with the complex case, it is possible to combine the above two situations into one introducing the concept of hyperbolic vortex-source with the complex charge 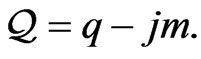 Then the potential takes the form:
Then the potential takes the form:
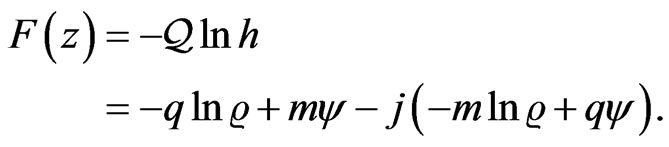 (44)
(44)
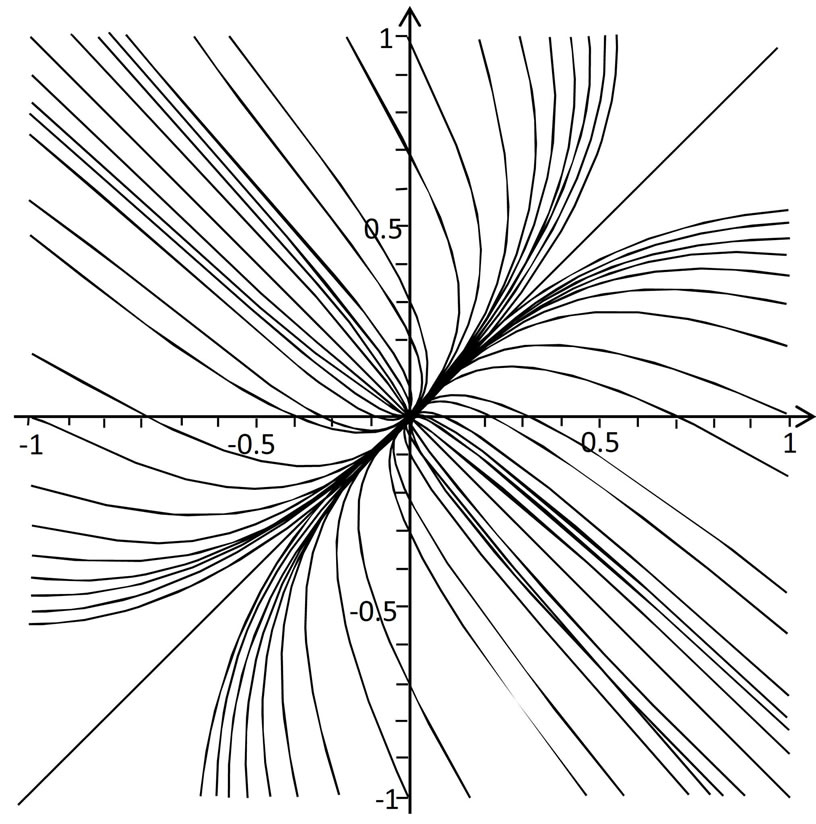
Such a potential can be most naturally interpreted in the framework of dual-symmetric hyperbolic field theory in which the hyperbolic electric and magnetic charges and currents are present on “equal footing”. The equation for the field lines of such field is obtained from (44) by equating the imaginary part to a constant:
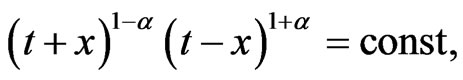 (45)
(45)
where 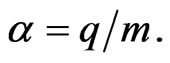 The picture of the field lines for
The picture of the field lines for 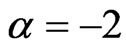 is shown on the figure:
is shown on the figure:
For physical applications it is necessary to generalize the concept of the h-field for the case of commutative and associative algebras of higher dimensions. In what follows we illustrate the idea of such a generalization by the example of the algebra of 3-numbers 
We start with an isotropic basis in the  in which the h -holomorphic function has the following representation:
in which the h -holomorphic function has the following representation:
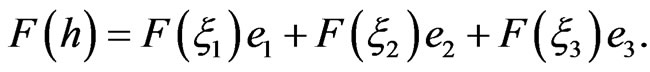 (46)
(46)
The operators of differentiation with respect to the independent variables 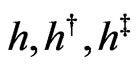 have the following form:
have the following form:
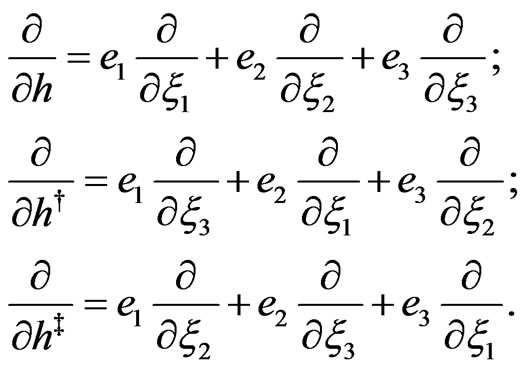 (47)
(47)
With the help of (47), one can easily verify the validity of equations for function 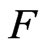 in the form of (46) by the direct calculation in components
in the form of (46) by the direct calculation in components
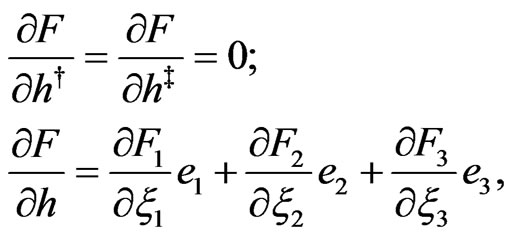 (48)
(48)
where here and further 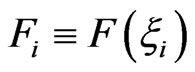 is the same function of various isotropic variables.
is the same function of various isotropic variables.
The conditions of holomorphicity (multidimensional analogue of the standard Cauchy-Riemann conditions), in symmetric non-isotropic basis 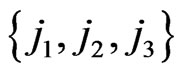 which is defined by:
which is defined by:
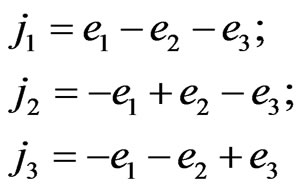 (49)
(49)
and by the rules of multiplication:
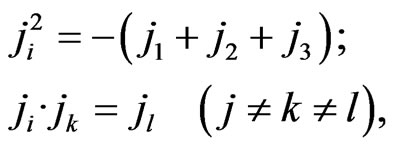 (50)
(50)
have the form of matrix differential equations:
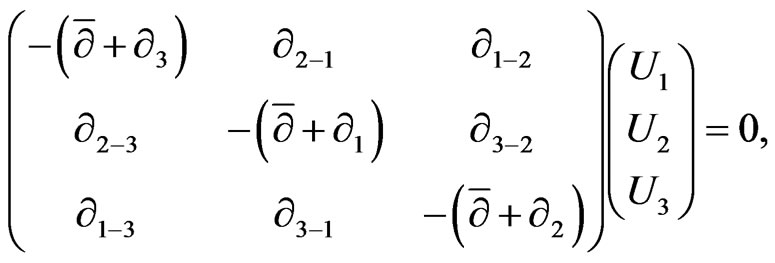 (51)
(51)
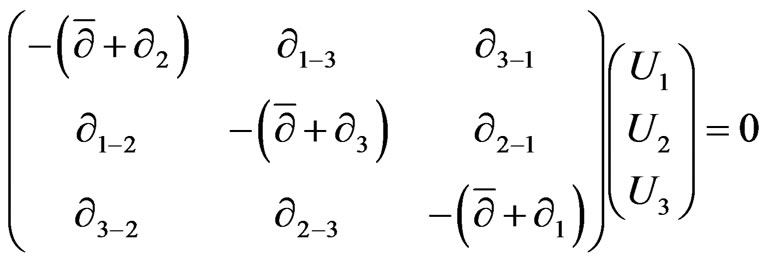 (52)
(52)
for every h-holomorphic function 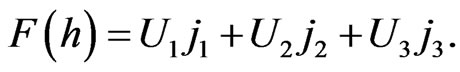 Here
Here 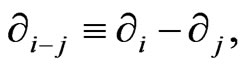
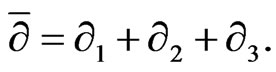 Due to the invariance properties of the h-holomorphy with respect to the choice of the algebra basis, we can say that the general solution of (51) and (52) is written by representing
Due to the invariance properties of the h-holomorphy with respect to the choice of the algebra basis, we can say that the general solution of (51) and (52) is written by representing 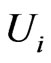 in terms of
in terms of 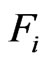 (components in the isotropic basis) expressed in terms of x-coordinates:
(components in the isotropic basis) expressed in terms of x-coordinates:
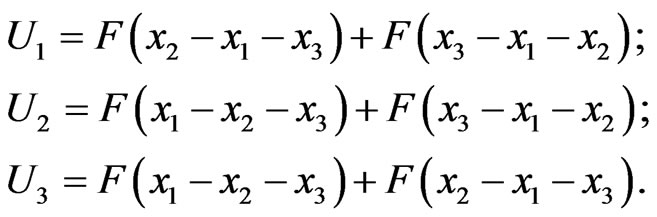 (53)
(53)
This fact can be verified by direct substitution of (53) into (51) and (52). The combinations of coordinates in the arguments of F present the higher analogues of retarded and advanced arguments in the double plane.
The third-order operator
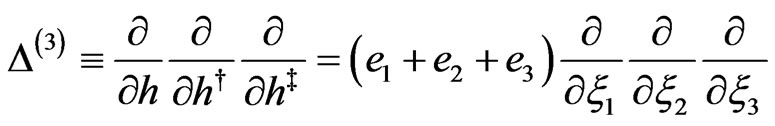 (54)
(54)
is proportional to the algebraic unity, so for every smooth function 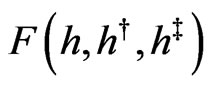
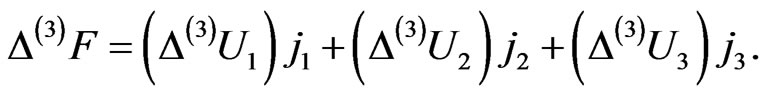 (55)
(55)
If the function F is h-holomorphic, then because the operator 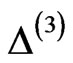 contains differentiation with respect to
contains differentiation with respect to 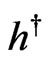 and
and 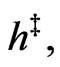 there holds the relation
there holds the relation 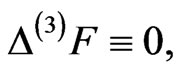 which is equivalent to its three components:
which is equivalent to its three components:
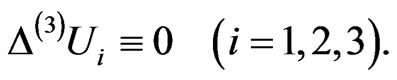 (56)
(56)
Equation (56) is a 3-dimensional analogue of the harmonicity conditions or the hyperbolic harmonicity conditions which are identically satisfied by holomorphic functions of complex or of double variable, respectively.
The discussion and development of these ideas can be found in [61].
4.7. Conformal Two-Dimensional Theory of Relativity We extend the Poincare group acting on the two-dimensional space-time  to a group of arbitrary h-holomorphic transformations that operate on points-events of space-time as on the elements of
to a group of arbitrary h-holomorphic transformations that operate on points-events of space-time as on the elements of  Using the exponential representation for the derivative of
Using the exponential representation for the derivative of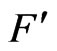 :
:
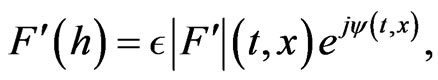 (57)
(57)
we conclude that locally h-holomorphic transformations implement not only reflections and boosts known in the theory of relativity but also the extension of lengths of the vectors (scalar factor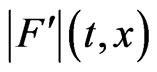 ). Let us consider the function
). Let us consider the function 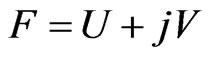 as the complex potential of the reference vector field of the 2-velocity or the reference field of the proper time. The field of 2-velocity u is determined by the formula:
as the complex potential of the reference vector field of the 2-velocity or the reference field of the proper time. The field of 2-velocity u is determined by the formula:
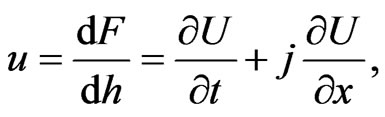 (58)
(58)
which uses the definition of the operator of complex differentiation and the hyperbolic Cauchy-Riemann conditions. The square of the modulus of the 2-velocity is
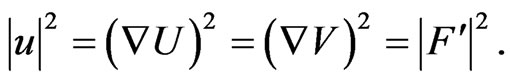 (59)
(59)
“The velocity field” of the proper time for any integral curve  of this field is given by:
of this field is given by:
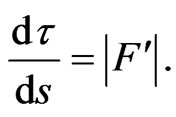 (60)
(60)
Now in the h-holomorphic theory of relativity under consideration, the intervals of the pseudo-Euclidean length and time become different and the relationship between them at each point is governed by the hyper-complex potential 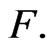
The integral curves of the field 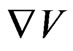 are spatial sections of 2-dimensional space-time, orthogonal to the lines of time at every point. Thus, the scale factor “governs” both the course of the proper time and spatial distances.
are spatial sections of 2-dimensional space-time, orthogonal to the lines of time at every point. Thus, the scale factor “governs” both the course of the proper time and spatial distances.
For arbitrary motions of test particles, the length and time intervals are calculated as:
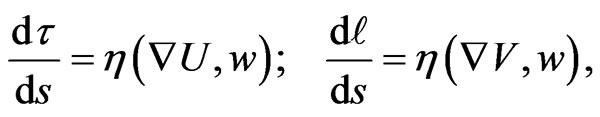 (61)
(61)
where 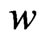 is the standard vector of the 2-velocity of the test particle
is the standard vector of the 2-velocity of the test particle 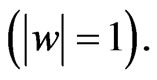
The simplest version of the variational principle of the dynamics theory of the hyperbolic field that takes into account the non-holomorphy of the hyperbolic potential inside the sources is determined by the action of the form:
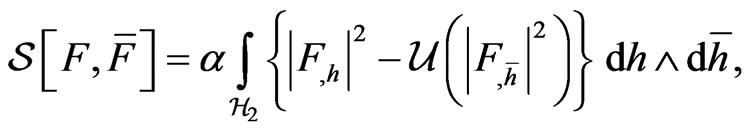 (62)
(62)
where the first term under the integral is a hyperbolic “kinetic term”. It is responsible for the dynamics of the hyperbolic potential in vacuum. The second term represents a hyperbolic “potential term” and is responsible for the properties and for the contribution of sources. This last term depends only on the hyperbolic modulus of the magnitude of non-holomorphy, and in the region outside the sources, where the non-holomorphy becomes equal to zero, it defines (in the action) a certain “full divergence” that does not give any contribution to the equations of motion. The standard procedure of varying the action (62) over the field variables  leads to the following field equations:
leads to the following field equations:
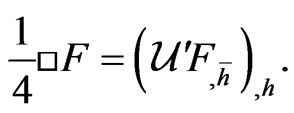 (63)
(63)
This expression is the inhomogeneous wave equation with a source on the right-hand side, depending only on the non-holomorphy of  As expected, the field equations are nonlinear, since the field
As expected, the field equations are nonlinear, since the field  as follows from the principles of the theory, describes its own sources through effective self-interaction. In this sense the developed theory is adjacent to the versions of the unified field theory by Mie.
as follows from the principles of the theory, describes its own sources through effective self-interaction. In this sense the developed theory is adjacent to the versions of the unified field theory by Mie.
A remarkable feature of Equation (63) is the existence (regardless of the specific form of the potential function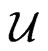 ) of the first integral
) of the first integral
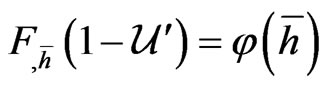 (64)
(64)
containing an arbitrary function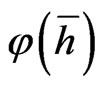 .
.
The explicit expressions for the energy density of the algebraidized matter 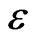 and its pressure p, obtained using the standard formalism of the field theory (Noether’s theorem), have the form:
and its pressure p, obtained using the standard formalism of the field theory (Noether’s theorem), have the form:
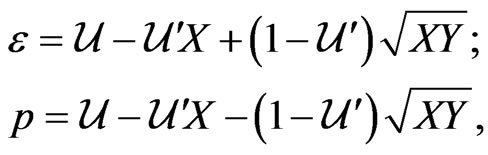 (65)
(65)
where 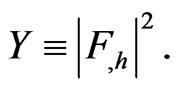
With the help of the super-variational principle introduced in [62], it appears possible to calculate the general form of the potential  in the theory presented here
in the theory presented here
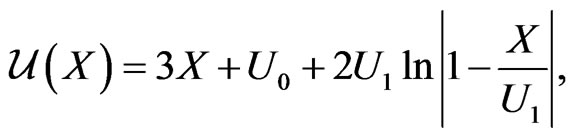 (66)
(66)
where  and
and  are two fundamental constants of the theory.
are two fundamental constants of the theory.
5. Differential-Geometric Aspects of the Theory of Berwald-Moor Type Finsler Spaces of Various Dimensions
In order to find out the fundamental relations between the scalar poly-product and geometric objects induced by it, as a continuation of research on these interrelations (which started by the works of M.Matsumoto, H. Shimada, S.Numata, K.Okubo and of Romanian geometers [70, refs. [29-32] and [43]] and [75, refs.[3,4]]), new correlations were obtained between the Berwald-Moor m-th root pseudo-norms and geometric objects from the classical Finslerian context ([75, §2 and 5-7]). Such relations were investigated in [72] and [74]. Their role is a methodological one: they enhance the process of deriving properties of certain structures (e.g., projective ones, [75]), or passing from algebraic aspects of m-th root metric theory to differential geometry specific aspects from the theory of Finsler spaces.
Description of the Obtained Results
The study of connections which are compatible with remarkable geometric structures was performed in [72], where, for specific connections from Finsler geometry (e.g., for Cartan, Barthel and Miron connections), the authors point out the properties of induced connections on hypersurfaces, as a necessary step in the study of mean Y-curvature within the N-extremality framework. In this study, the authors propose an original software for the calculation and the use of Finslerian geometric objects specific to the study of y-minimal submanifolds. With the help of Maple symbolic calculations, they determine the coefficients of these geometric objects for low-dimensional manifolds equipped with 3-rd and 4-th root metrics and with Berwald-Moor conformal metrics. The underlying algorithm of this Maple software, was introduced by M. Matsumoto ([72, refs. [39,40]]) and is likely to provide a wide range of applications in the study of anisotropic media.
Moreover, in the paper [75,§3], there are indicated the essential connections to be used in determining whether an m-th root metric space is of Berwald or of Douglas type, and are derived original results concerning spaces with Berwald-Moor type metrics.
On the other side, in [68], Landsberg spaces are characterized by means of classical connections (Vasiman and Levi-Civita) and the connections which are subsequently induced into the structural and transversal fibers of the bundle, are indicated.
The work [63,§2-3] performs a preliminary study of the cotangent bundle of spaces endowed with Berwald-Moor metric; in the cited paper, one defines the v-curvature tensors and the T-tensor of the Berwald-Moor space, for the case of Shimada-type m-th root metrics; the results are specialized for the case of dual m-th root metric spaces having the indicatrix given by the product of the momentum components. In this case, the classical results regarding the vanishing of the torsion tensor and of the T -tensor, obtained by M. Matsumoto and H. Shimada ([63, refs.[5,11]]) and also the property of  -likeness for the Berwald-Moor space, were obtained for the first time for the dual case.
-likeness for the Berwald-Moor space, were obtained for the first time for the dual case.
The determining of connections and of induced geometric objects on submanifolds of m-th root metric spaces was carried out in the paper [72], by summing up known results and by original implementation of their construction into Maple code, using macros and supplementary procedures which simplify the use of the code and allows to extend the results specific to the study of the indicatrix.
The procedure for obtaining the mean curvature and minimal (Y-extremal) surfaces/hypersurfaces and corresponding computer simulation are presented in [72], which embeds two addenda devoted to the 4-dimensional case. Here, the mean curvature and the equations of Y - extremal (hyper-)surfaces are explicitly obtained by the use of symbolic software, and the calculation of the explicit form of the normal field to a submanifold (theoretically described in [72, ref. [40]]), represents a concrete application of software procedures in solving nonlinear equations. Also, the mean curvature – depending on the energy of a space-like or light-like normal vector field, is obtained by using specific procedures of the relativistic pseudo-Finslerian approach. This approach imposes restrictions on the submanifolds for the indicated practical applications, aiming to find solutions of the equations of Y-extremal submanifolds.
Another aim of an earlier planned research ([68, ref. [2]]) relates to determining specific types of cohomology in mth root metric spaces ([68,77]), including the cohomologies of certain Berwald-Moor Finslerian spaces. These papers present new results concerning fibered structures of Finsler type: in [77], it is proved the existence of a diffeomorphism between the 2-jet vertical bundle induced by the canonical bundle and the product of the horizontal, vertical and mixed subbundles of 2-jets induced by the second order tangent bundle. In [68], it is introduced the Vaisman connection and it is proven that the pair LeviCivita connection—Vaisman connection induces a pair of connections of the same type as the initial ones in the structural bundle, only if the base manifold M is a Landsberg space, and that the slit tangent bundle (the tangent bundle without the image of its null section, denoted as ) is a Reinhart space if and only if the base manifold is Riemannian. Further, the 2-leaf jets on
) is a Reinhart space if and only if the base manifold is Riemannian. Further, the 2-leaf jets on 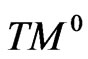 are studied, it is obtained a decomposition of this space, and the 1-dimenional Cech cohomology group with coefficients from the sheaf of basic functions is constructed in terms of fields on leaves of 2-jets. It is defined the Mastrogiacomo coholology group with respect to the connection on the structure sheaf induced by a connection on the manifold
are studied, it is obtained a decomposition of this space, and the 1-dimenional Cech cohomology group with coefficients from the sheaf of basic functions is constructed in terms of fields on leaves of 2-jets. It is defined the Mastrogiacomo coholology group with respect to the connection on the structure sheaf induced by a connection on the manifold 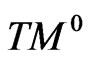 and it is proven that the associated cohomology group is isomorphic to the 1-dimensional Cech cohomology group on the manifold
and it is proven that the associated cohomology group is isomorphic to the 1-dimensional Cech cohomology group on the manifold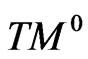 , having as coefficients germs of functions on
, having as coefficients germs of functions on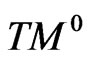 , which are related to the induced connection; in particular, for 4-dimensional m-th root spaces, it is proven that this sheaf is isomorphic to the sheaf of basic functions on
, which are related to the induced connection; in particular, for 4-dimensional m-th root spaces, it is proven that this sheaf is isomorphic to the sheaf of basic functions on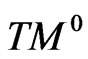 .
.
In [78,79], the 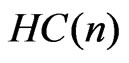 Halphen-Castelnuovo problem for smooth curves is split into two parts: the study of the lacunary and of the non-lacunary domain. The latter one is studied: existence obstructions are determined and examples of curves on rational surfaces and irrational scrolls are built. There are studied for the first time the existence of smooth irreducible non-degenerate curves of degree d and genus g from the projective space (the HalphenCastelnuovo
Halphen-Castelnuovo problem for smooth curves is split into two parts: the study of the lacunary and of the non-lacunary domain. The latter one is studied: existence obstructions are determined and examples of curves on rational surfaces and irrational scrolls are built. There are studied for the first time the existence of smooth irreducible non-degenerate curves of degree d and genus g from the projective space (the HalphenCastelnuovo 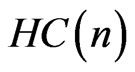 problem). For the domains
problem). For the domains 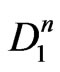 and
and 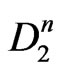 , built in the plane (
, built in the plane ( ), it is shown that
), it is shown that 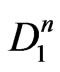 is simply connected, by using curves which are displaced on rational surfaces related to hyper-elliptic type sections, and are presented well known theorems of Ciliberto, Sernesi and Pasarescu. As well, using results of Horrowitz, Ciliberto, Harris and Eisenbud, it is conjectured that
is simply connected, by using curves which are displaced on rational surfaces related to hyper-elliptic type sections, and are presented well known theorems of Ciliberto, Sernesi and Pasarescu. As well, using results of Horrowitz, Ciliberto, Harris and Eisenbud, it is conjectured that 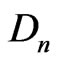 is exactly the targeted lacunary domain.
is exactly the targeted lacunary domain.
Geodesics and Jacobi fields are investigated in [75,§2] and [74,§3], where geodesic equations and spray coefficients are introduced and studied for conformal flag metrics. In [75], the hv-curvature tensor is determined for arbitrary m-th root structures; this result is further used in determining the specific characterizations of Landsberg and Berwald-type m-th root metric spaces. Relations between the coefficients of two sprays for non-decomposable metrics are obtained in an explicit form, for cubic metrics in [74,§6]. All these results complete known results obtained for m-th root metric spaces by M. Matsumoto and H. Shimada. It is emphasized the role of flag curvature, which is a key one in describing the behavior of geodesics. This is continued in [73], where there are described the geodesic equations perturbed by the presence of an electromagnetic field. In Finsler spaces, the 4-potential 1-form is anisotropic, and represents a horizontal 1-form on the tangent bundle, having specific properties.
Relativistic models based on 4-dimensional m-th root metric are subject of intensive research. In [48], original results were obtained for the OMPR (optic-metrical parametric resonance) effect, with applications to relativity theory and to experimental physics (detection of gravitational waves). This work has been carried out in collaboration with the Russian physicist S. Siparov. The influence of a weak deformation of a flat pseudo-Finslerian metric upon the electromagnetic field tensor is studied in [73] and, in particular—for the case of m-th root metrics of Berwald-Moor type. The generalized geometric models are obtained and the physical meaning of such a generalization, together with its role in the equations of electromagnetism in Finsler spaces is pointed out. Geodesics and Jacobi fields are also studied in [70,§1-2] in the context of structural stability of second order differential equations, where the authors obtain original results for sheaves of curves and for the forces which deviate trajectories from geodesics in the case of conformal deformations of m-th root structures or locally Minkowski metrics. With the help of supplementary software designed to determine geodesics by means of the computer, original procedures for defining the invariants which characterize the stability of structures were derived.
In [75,§3-6], there are studied m-th root Berwald and Landsberg spaces and projectively flat spaces and, in the work [74,§4]—cubic spaces. In [75, Th.17 and Th.18], there are investigated m-th root projective spaces and, in particular, Riemann-projective spaces with m-th root metrics [75, Th.19, 20 and Prop.22]. All these results are original and they complete, in the case of m-th root metrics, known results obtained by S. Bacso, Zs.Szabo, L. Tamassy and Cs. Vincze.
In [70], the authors present the basic notions from the theory of structural stability (KCC—Kosambi-CartanChern)—created and developed by P. L.Antonelli, I. Bucataru and S. Sabau [70, refs. [1-8, 48-49]] and carried out by V. Balan and I. R. Nicola for biological and ecological models ([70, refs. [10-13]]). The five KCC-invariants are described and in the Appendix, original Maple programs for determining the invariants describing Jacobi stability of dynamical systems associated with the Finslerian approach, are presented. Sections 4 and 5 contain original results for the case of conformal deformations of m-th root metrics and describe the properties of the associated deformation algebras.
The papers [64,66] extend known results for symmetric positive definite tensors for Z, H and E-spectra of Berwald-Moor and Chernov tensors in 4-dimensional spaces. The algebraic properties of these tensors induce geometrical properties: by spectral techniques it is shown that the indicatrices of the associated Finsler metric are not ruled and compact, and that the problem of the minimal distance between the origin of the frame and the indicatrix has a solution depending on the Z-eigenvalue with maximal absolute value and with the corresponding direction given by the generating Z-eigenvector. The problem of asymptotic behavior of the indicatrix is solved by means of spectral properties of the symmetric tensor associated to the fundamental Finsler function. There are defined: recession vectors, degenerate vectors, singular points of the indicatrix and the best first-order approximation. The qualitative description of the three types of eigenvalues is obtained in [71] with the help of the theory of resolvents for the cubic Berwald-Moor metric.
Hamilton equations, Legendre duality and physical models associated with m-th root metric spaces on the tangent or on the cotangent bundle are studied in [67], where it is indicated an essential parallelism between different transformations with physical meaning, and it is emphasized a Legendre-type relation between the Lagrangian formalism and the Hamiltonian one. It is investigated the alternative given by the use of the Rashevskii transformation commonly used in mechanics and its degenerate nature. The hyperbolic character of the Finsler and Cartan functions is emphasized and the correspondence between the basic geometric objects and their duals given by Legendre-Finsler duality for general Berwald-Moor metrics of arbitrary dimension is described.
In [51,80-82], the authors build models for the gravitational and for the electromagnetic fields, based on generalized Lagrange metrics and in particular, on the locally Minkowskian Berwald-Moor metric.
In [65], it is studied the geometry of submanifolds in m-th root metric spaces and in [67] the hyperbolic character of the Berwald-Moor metric is emphasized; in [65], the author proposes a pseudo-Finslerian formalism for Finsler metrics of locally Minkowski type, including the Berwald-Moor metric; a special attention is paid to the objects which allow to characterize minimal surfaces. Linear and nonlinear Cartan connections are studied and Gauss-Weingarten, Gauss-Codazzi, Peterson-Mainardi and Ricci-Kuhn equations are obtained. In [64,66], geometric properties of the Berwald-Moor indicatrix are obtained by means of spectral theory associated to a supersymmetric tensor; the spectra are obtained with the help of the Maple software.
The study of cohomology classes for m-th root metric spaces and the study of associated bundles extend known results by addressing to the initial context of Finsler spaces (in particular, for locally Minkowskian metrics). The results include an explicit description of the Vaisman connection for a vertical fiber with respect to the verical bundle and a proof of the fact that its leaves are Reinhart spaces [76]. Further, in [77], in a vertical fiber of a Finsler manifold it is defined an adapted basis to the Liouville fibration, the vertical bundle of 2-jets and the leaves of vertical bundles of 2-jets of transversal and mixed types. It is proven that there exists a canonical diffeomorphism between the total space of the vertical bundle of 2-jets and one of the product bundles of vertical, transversal and mixed leaves of 2-jets.
Specific variational features of the energy in m-th root metric spaces and the behavior of geodesics is studied in [81,82]; the authors investigate extensions of Lorentz geodesics to generalized Lagrange relativistic models obtained for small deformations of Berwald-Moor and locally Minkowski metrics. In [82], it is described a class of solutions of the Einstein field equations for such models. In [69], a system of second order differential equations is considered as an extension of geodesic equations and it is investigated by means of the KCC approach.
The study of constant scalar curvature and constant flag curvature is continued in [65]; there, it is investigated the horizontal curvature of a pseudo-Finsler manifold. It is proven that, in the Berwald-Moor case, the horizontal and the flag curvature of the space vanish, while the induced curvatures on submanifolds are generally nontrivial.
The investigation of rheonomic KCC models is continued in the work [69]; the autonomous case is extended to the rheonomic one by means of a geometrization of classical KCC theory on first order jet spaces. Here, the authors study the relations between spatial and time semisprays and define a nonlinear connection on the 1-jet space. They find the five invariants of the theory and point out the differences between the rheonomic case and the autonomous one, considering the geometric objects related to induced connections and KCC invariants.
6. Acknowledgements
The last author was partially supported by the Sectorial Operational Program Human Resources Development (SOP HRD), financed from the European Social Fund and by the Romanian Government under the Project number POSDRU/89/1.5/S/59323.
REFERENCES
- H. Rund, “Differential Geometry of Finsler Spaces,” Springer, Berlin, 1959.
- D. Bao, S. S. Chern and Z. Shen, “An Introduction to Finsler Geometry,” Springer-Verlag, New York, 2000. HUdoi:10.1007/978-1-4612-1268-3U
- G. I. Garas’ko, “Elements of Finsler Geometry for Physicists,” Tetru, Moscow, 2009.
- G. Yu. Bogoslovsky, “On a Special Relativistic Theory of Anisotropic Space-Time,” Doklady Akademii Nauk SSSR, Vol. 213, No. 5, 1973, pp. 1055-1058.
- G. Yu. Bogoslovsky, “A Special Relativistic Theory of the Locally Anisotropic Space-Time, Part I. The Metric and Group of Motions of the Anisotropic Space of Events,” Nuovo Cimento B, Vol. 40, No. 1, 1977, pp. 99- 115. HUdoi:10.1007/BF02739183UH
- G. Yu. Bogoslovsky, “A Special Relativistic Theory of the Locally Anisotropic Space-Time, Part II. Mechanics and Electrodynamics in the Anisotropic Space,” Nuovo Cimento B, Vol. 40, No. 1, 1977, pp. 116-134. HUdoi:10.1007/BF02739184U
- G. Yu. Bogoslovsky, “Theory of Locally Anisotropic Space-Time,” Moscow State University Press, Moscow, 1992.
- D. A. Kirzhnits and V. A. Chechin, “Ultra-High Energy Cosmic Rays and Possible Generalization of the Relativistic Theory,” Yadernaya Fizika, Vol. 15, No. 5, 1972, pp. 1051-1059.
- T. G. Pavlopoulos, “Breakdown of Lorentz Invariance,” Physical Review, Vol. 159, No. 5, 1967, pp. 1106-1110. HUdoi:10.1103/PhysRev.159.1106U
- S. V. Siparov, “Theory of Zero Order Effect That Can Be Used to Investigate the Space-Time Geometrical Properties,” Hypercomplex Numbers in Geometry and Physics, Vol. 3, No. 2, 2006, pp. 155-173.
- S. V. Siparov, “Theory of Zero Order Effect Suitable to Investigate the Space-Time Geometrical Properties,” Acta Mathematica APN, Vol. 24, No. 1, 2008, pp. 135-144.
- S. V. Siparov, “On the Problem of Anisotropy in Geometrodynamics,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 64-74.
- S. V. Siparov, “Gravitation Law and Source Model in the Anisotropic Geometrodynamics,” Hypercomplex Numbers in Geometry and Physics, Vol. 6, No. 2, 2009, pp. 140-161.
- S. V. Siparov, “Anisotropic Metric for the Gravitation Theory: New Ways to Interpret the Classical GRT Tests,” In: S. V. Siparov, Ed., BSG Proceedings, Geometry Balkan Press, Bucharest, 2010, pp. 205-218.
- S. V. Siparov, “Anisotropic Geometrodynamics in Cosmological Problems,” In: S. V. Siparov, Ed., AIP Conference Proceedings, Melville, New York, 2010, pp. 222- 231.
- B. S. DeWitt, “Relativity, Groups and Topology,” Gordon and Breach, New York, 1964.
- C. Brans and R. H. Dicke, “Mach’s Principle and a Relativistic Theory of Gravitation,” Physical Review, Vol. 124, No. 3, 1961, pp. 925-935. HUdoi:10.1103/PhysRev.124.925U
- P. D. Mannheim and D. Kazanas, “Newtonian Limit of Conformal Gravity and the Lack of Necessity of the Second Order Poisson Equation,” General Relativity and Gravitation, Vol. 26, No. 4, 1994, pp. 337-345. HUdoi:10.1007/BF02105226U
- J. W. Moffat, “Nonsymmetric Gravitational Theory,” Physics Review Letters B, Vol. 355, No. 3-4, 1995, pp. 447-452. HUdoi:10.1016/0370-2693(95)00670-GU
- M. Milgrom, “A Modification of the Newtonian Dynamics as a Possible Alternative to the Hidden Mass Hypothesis,” Astrophysical Journal, Vol. 270, 1983, pp. 365- 370. HUdoi:10.1086/161130U
- J. D. Bekenstein, “Relativistic Gravitation Theory for the Modified Newtonian Dynamics Paradigm,” Physics Review D, Vol. 70, No. 8, 2004, pp. 1-28.
- J. Lense and H. Thirring, “On the Influence of the Proper Rotation of Central Bodies on the Motions of Planets and Moons According to Einstein’s Theory of Gravitation,” Physikalische Zeitschrift/Physical Journal, Vol. 19, 1918, pp. 156-163.
- M. L. Ruggiero and A. Tartaglia, “Gravitomagnetic Effects,” Preprint, 2002. arXiv:gr-qc/0207065v2
- H. Muller, S. W. Chiow, S. Herrmann, S. Chu and K. Y. Chung, “Atom Interferometry Tests of the Isotropy of PostNewtonian Gravity,” Physics Review Letters, Vol. 100, No. 3, 2008, pp. 1-4.
- The CMS Collaboration, “Observation of Long-Range Near-Side Angular Correlations in Proton-Proton Collisions at the LHC,” JHEP, Vol. 9, 2010, pp. 1-37.
- D. Colladay and V. A. Kostelecky, “Lorentz-Violating Extension of the Standard Model,” Physics Review D, Vol. 58, No. 11, 1998, pp. 1-23.
- Q. G. Bailey and A. Kostelecky, “Signals for Lorentz Violation in Post-Newtonian Gravity,” Physics Review D, Vol. 74, No. 4, 2006, pp. 1-46.
- V. A. Kostelecky, “CPT and Lorentz Symmetry,” World Scientific, Singapore, 1999.
- V. A. Kostelecky, “CPT and Lorentz Symmetry II,” World Scientific, Singapore, 2002.
- V. A. Kostelecky, “CPT and Lorentz Symmetry III,” World Scientific, Singapore, 2005.
- V. A. Kostelecky, “CPT and Lorentz Symmetry IV,” World Scientific, Singapore, 2008.
- V. A. Kostelecky, “CPT and Lorentz Symmetry V,” World Scientific, Singapore, 2011.
- D. Blas and S. Sibiryakov, “Technically Natural Dark Energy from Lorentz Breaking,” Preprint, 2011. arXiv:1104.3579v1 [hep-th]
- G. Yu. Bogoslovsky and H. F. Goenner, “Finslerian Spaces Possessing Local Relativistic Symmetry,” General Relativity and Gravitation, Vol. 31, No. 10, 1999, pp. 1565- 1603. HUdoi:10.1023/A:1026786505326U
- J. Patera, P. Winternitz and H. Zassenhaus, “Continuous Subgroups of the Fundamental Groups of Physics. II. The Similitude Group,” Journal of Mathematical Physics, Vol. 16, No. 8, 1975, pp. 1615-1624. HUdoi:10.1063/1.522730U
- P. Winternitz and I. Fris, “Invariant Expansions of Relativistic Amplitudes and Subgroups of the Proper Lorentz Group,” Yadernaya Fizika, Vol. 1, No. 5, 1965, pp. 889- 901.
- G. Yu. Bogoslovsky, “Lorentz Symmetry Violation without Violation of Relativistic Symmetry,” Physics Letters A, Vol. 350, No. 1-2, 2006, pp. 5-10. HUdoi:10.1016/j.physleta.2005.11.007U
- A. G. Cohen and S. L. Glashow, “Very Special Relativity,” Physics Review Letters, Vol. 97, No. 2, 2006, pp. 1- 3.
- A. G. Cohen and S. L. Glashow, “A Lorentz-Violating Origin of Neutrino Mass?” Preprint, 2006. arXiv:hep-ph/0605036v1.
- G. W. Gibbons, J. Gomis and C. N. Pope, “General Very Special Relativity is Finsler Geometry,” Physics Review D, Vol. 76, No. 8, 2007, pp. 1-5.
- G. W. Gibbons, J. Gomis and C. N. Pope, “Deforming the Maxwell-Sim Algebra,” Physics Review D, Vol. 82, No. 6, 2010, pp. 1-15.
- G. Yu. Bogoslovsky and H. F. Goenner, “Concerning the Generalized Lorentz Symmetry and the Generalization of the Dirac Equation,” Physics Letters A, Vol. 323, No. 1-2, 2004, pp. 40-47. HUdoi:10.1016/j.physleta.2004.01.040U
- G. Yu. Bogoslovsky, “Some Physical Displays of the Space Anisotropy Relevant to the Feasibility of Its Being Detected at a Laboratory,” Preprint, 2007. arXiv:0706.2621v1 [gr-qc]
- G. Yu. Bogoslovsky, “Finsler Model of Space-Time,” Physics of Particles and Nuclei, Vol. 24, No. 3, 1993, pp. 354-379.
- G. Yu. Bogoslovsky, “A Viable Model of Locally Anisotropic Space-Time and the Finslerian Generalization of the Relativity Theory,” Fortschritte der Physik/Progress of Physics, Vol. 42, No. 2, 1994, pp. 143-193. HUdoi:10.1002/prop.2190420203U
- G. Yu. Bogoslovsky and H. F. Goenner, “On the Possibility of Phase Transitions in the Geometric Structure of Space-Time,” Physics Letters A, Vol. 244, 1998, pp. 222- 228.
- G. Yu. Bogoslovsky, “Dynamic Rearrangement of Vacuum and the Phase Transitions in the Geometric Structure of Space-Time,” International Journal of Geometric Methods in Modern Physics, Vol. 9, No. 1, 2012, pp. 1-20. doi:10.1142/S0219887812500077
- S. V. Siparov and N. Brinzei, “Space-Time Anisotropy: Theoretical Issues and the Possibility of an Observational Test,” Preprint, 2008. arXiv:0806.3066 [gr-qc]
- N. Brinzei and S. V. Siparov, “On the Possibility of the OMPR Effect in Spaces with Finsler Geometry, Part I,” Hypercomplex Numbers in Geometry and Physics, Vol. 4, No. 2, 2007, pp. 41-53.
- S. V. Siparov and N. Brinzei, “On the Possibility of the OMPR Effect in Spaces with Finsler Geometry, Part II,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 56-64.
- N. Voicu, “New Considerations on Einstein Equations in Anisotropic Spaces,” In: N. Voicu, Ed., AIP Conference Proceedings, Melville, New York, 2010, pp. 249-258.
- A. Aguirre, C. P. Burgess, A. Friedland and D. Nolte, “Astrophysical Constraints on Modifying Gravity at Large Distances,” Classical and Quantum Gravity, Vol. 18, No. 23, 2001, pp. R223-R232.
- D. G. Pavlov and S. S. Kokarev, “Conformal Gauges of the Berwald-Moor Geometry and Nonlinear Symmetries Induced by Them,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 3-14.
- S. S. Kokarev, “Is It Really That Different Geometries Are Different?” In: M. C. Duffy, V. O. Gladyshev, A. N. Morozov and P. Rowlands, Eds., Proceedings of XV International Meeting PIRT-2009, BMSTU Press, Moscow, 2009, pp. 116-123.
- D. G. Pavlov and S. S. Kokarev, “Riemannian Metrics Osculating to the 3-Dimentional Berwald-Moor Finsler metric,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 15-24.
- D. G. Pavlov and S. S. Kokarev, “Additive Angles in H3,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 25-43.
- D. G. Pavlov and S. S. Kokarev, “Polyangles and Their Symmetries in H3,” Hypercomplex Numbers in Geometry and Physics, Vol. 6, No. 1, 2009, pp. 42-67.
- N. P. Sokolov, “Spatial Matrices and Their Applications,” GIFML, Moscow, 1960 (in Russian).
- S. S. Kokarev, “Isometry Classification of Cubic Homogeneous 3-Dimensional Forms,” Symmetry: Culture and Science, Symmetry Festival, Vol. 20, No. 1-4, 2009, pp. 371-391.
- D. G. Pavlov and S. S. Kokarev, “h-Holomorphic Functions of Double Variable and Their Applications,” Hypercomplex Numbers in Geometry and Physics, Vol. 7, No. 1, 2010, pp. 44-77.
- D. G. Pavlov and S. S. Kokarev, “Hyperbolic Theory of Field on the Plane of Double Variable,” Hypercomplex Numbers in Geometry and Physics, Vol. 7, No. 1, 2010, pp. 78-126.
- D. G. Pavlov and S. S. Kokarev, “Algebraic Unified Theory of Space-Time and Matter on the Plane of Double Variable,” Hypercomplex Numbers in Geometry and Physics, Vol. 7, No. 2, 2010, pp. 11-37.
- Gh. Atanasiu and M. Neagu, “On Cartan Spaces with the m-th Root Metric
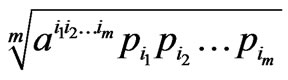 ,” Hypercomplex Numbers in Geometry and Physics, Vol. 6, No. 2, 2009, pp. 67-73.
,” Hypercomplex Numbers in Geometry and Physics, Vol. 6, No. 2, 2009, pp. 67-73. - V. Balan, “Spectral Properties and Applications of Numerical Multilinear Algebra of m-Root Structures,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 101-108.
- V. Balan, “Notable Submanifolds in Berwald-Moor Spaces,” BSG Proceedings of 17th (ISI Proceedings), Geometry Balkan Press, Bucharest, 2010, pp. 21-30.
- V. Balan, “Numerical Multilinear Algebra of Symmetric m-Root Structures. Spectral Properties and Applications,” Symmetry: Culture and Science, Symmetry Festival 2009, Symmetry in the History of Science, Art and Technology. Part 2. Geometric Approaches to Symmetry, Vol. 21, No. 1-3, 2010, pp. 119-131.
- V. Balan and S. Lebedev, “On the Legendre Transform and Hamiltonian Formalism in Berwald-Moor Geometry,” Differential Geometry-Dynamical Systems, Vol. 12, No. 1, 2010, pp. 4-11.
- V. Balan and A. Manea, “Leafwise 2-Jet Cohomology on Foliated Finsler Manifolds,” BSG Proceedings 16 (ISI Proceedings), Geometry Balkan Press, Bucharest, 2009, pp. 28-41.
- V. Balan and M. Neagu, “Jet Geometrical Extension of the KCC-Invariants,” Balkan Journal of Geometry and Its Applications, Vol. 15, No. 1, 2009, pp. 8-16.
- V. Balan and I.-R. Nicola, “Berwald-Moor Metrics and Structural Stability of Conformally-Deformed Geodesic SODE,” Differential Geometry-Dynamical Systems, Vol. 11, 2009, pp. 19-34.
- V. Balan and N. Perminov, “Applications of Resultants in the Spectral m-Root Framework,” Applied Science, Vol. 12, 2010, pp. 20-29.
- V. Balan and A. Pitea, “Symbolic Software for Y-Energy Extremal Finsler Submanifolds,” Applied Science, Vol. 1, 2009, pp. 41-53.
- N. Brinzei (Voicu) and S. V. Siparov, “Equations of Electromagnetism in Some Special Anisotropic Spaces,” Hypercomplex Numbers in Geometry and Physics, Vol. 5, No. 2, 2008, pp. 45-55.
- N. Brinzei (Voicu), “On Cubic Berwald Spaces,” Bulletin of the Calcutta Mathematical Society, Vol. 17, No. 1-2, 2009, pp. 75-84.
- N. Brinzei (Voicu), “Projective Relations for m-th Root Metric Spaces,” Journal of the Calcutta Mathematical Society, Vol. 5, No. 1-2, 2009, pp. 21-35.
- A. Manea, “The Vaisman Connection of the Vertical Bundle of a Finsler Manifold,” Bulletin of the Transilvania University of Brasov, Series III, Vol. 2, No. 51, 2009, pp. 199-206.
- A. Manea, “Some New Types of Vertical 2-Jets on the Tangent Bundle of a Finsler Manifold,” Scientific Bulletin—University Politehnica of Bucharest, Series A, Vol. 172, No. 1, 2010, pp. 177-194.
- O. Pasarescu, “Curves on Some Irrational Scrolls,” Romanian Academy of Sciences, GAR 4/2009.
- O. Pasarescu, “Curves on Rational Surfaces with Hyperelliptic Hyperplane Sections,” in press. arXiv:1101.0577v1 [math.AG].
- N. Voicu (Brinzei), “Anisotropy and Analogies between Gravity and Electromagnetism,” In: M. C. Duffy, V. O. Gladyshev, A. N. Morozov and P. Rowlands, Eds., Proceedings of XV International Meeting PIRT-2009, BMSTU Press, Moscow, 2009, pp. 124-132.
- N. Voicu-Brinzei and S. Siparov, “A New Approach to Electromagnetism in Anisotropic Spaces,” BSG Proceedinds 17th International Conference on Differential Geometry and Dynamical Systems, Bucharest, 2009, pp. 235-245.
- N. Voicu-Brinzei and S. Siparov, “Space-Time Anisotropy—Mathematical Formalism and the Possibility of an Experimental Test,” AIP Proceedings of 4th Gamow International Conference on Astrophysics and Cosmology after Gamow: Recent Progress and New Horizons, Odessa, 2009, pp. 152-162.
- S. Siparov, “Introduction to the Anisotropic Geometrodynamics,” World Scientific, Singapore, 2011.
- S. Molinari, et al., “A 100-Parsec Elliptical and Twisted Ring of Cold and Dense Molecular Clouds Revealed by HERSCHEL around the Galactic Center,” Preprint, 2011. arXiv:1105.5486v1, [astro-ph.GA].
NOTES
*Corresponding author.
1Notice that the divergence of the vector field is defined in the same way in the complex and hyperbolic cases, as opposed to the operation of the curl of a vector field, which includes the symmetric combination of partial derivatives in the hyperbolic case.

