A Journal of Software Engineering and Applications, 2012, 5, 59-65
doi:10.4236/jsea.2012.512b013 Published Online December 2012 (http://www.scirp.org/journal/jsea)
Random Search Algorit hm f or t he G eneral ized Weber
Problem
Lev Kazakovtsev
Department of In formation Technologies, S ib erian State Aerospace U niversit y, Krasnoyarsk, Rus sian Federation.
Received 2012.
ABSTRACT
In this paper, we consider the planar multi-facility Weber problem with restricted zones and non-Euclidean distances,
propose an algorithm based on the probability changing method (special kind of genetic algorithms) and prove its effi-
ciency for approximate solving this problem by replacing the continuous coordinate values b y discrete ones. Ver sion of
the al gorithm for multiprocessor systems is proposed. Experimental results for a high-perfor mance cluster are given.
Keywords: Discrete Optimization; Weber Problem; Random Search; Gen eti c A lg or ith ms ; Parallel Algorithm
1. Introduction
Location problems are a special class of optimization
problems [1]. A single-facility Weber problem is a prob-
lem of searching for a point X that the sum of weighted
distances from X to some existing points A1, A2... ,AN is
minimum [2].
( )() min.AX,Lw=XF
i
N
=i i
→
∑
1
(1)
Here, wi is a weight of the i'th point, L(A,B) is the
distance between A=(a1,b1) and B=(b1,b2). In the Euc-
lidean metrics l2,
()() () .
2
22
2
11 ba+ba=BA,L−−
(2)
But, ot her t ypes of distances have been exploited. A
review of exploited metrics is presented in [3]. Distance
functions based on altered norms are investigated in [4,
5]. Problems with weighted one-infinity norms are
solved in [6]. Asymptotic distances [7] and weighted
sums of order p [8] are also.
Also, the rectangle [4] (or Manhattan) metrics l1 is
well investigated. Here,
() || ||
.
2211 ba+ba=BA,L−− (3)
Manhattan metric can be used for fast approximate
solution instead of Euclidean metric.
Weber (or Fermat-Weber) problem is a generali-
zation of a simple Fermat problem and has series of ge-
neralized formulations.
Multi-facility problem (Multi-Weber problem) is a
gener alization o f the sin gle -fac ility problem [9]:
( ) ( ) min.A,XLw=X,XF
ij
N
=i
M
=j iM
→
∑∑
1 1
1
...,
(4)
The problem is searching for M additional places
for new facilities
M.j,X
j
≤≤1
Or, in other case [9], the objective function is de-
fined as (minsum problem):
( ) ( )
min.A,XLw=X,XF
ij
n i mMjj,
N
=i iM
→
≤≤
∑1
1
1,
...,
(5)
Also, the problem can include the restricted areas,
barriers etc. In case of restricted zones, the optimization
problem, in general, includes constraints:
Zj
RX ∉
(6)
where RZ is a set of restricted coor d inates.
In case of barriers, the distance between 2 po ints is,
in genera l , non-Euclidean (Fig.1)
Figure 1 . Distance with a barrier.

Random Search Algorithm for the Gen er alized Weber Problem
Copyright © 2012 S ciRes. JSEA
60
Here, the distance between points A and B is the
sum of di st ances d1 and d2 (piano movers distance [10]).
Continuous (regional) Weber problem deals with
finding a median for a continuum of demand points. In
particular, we consider versions of the ''continuous
k-median (Fermat-Weber) problem'' where the goal is to
select one or more center points that minimize the
weighted distance to a set of points in a demand region
[11]. If the existing facilities are distributed in some
compact area
n
RΩ∈
then t he si ngle -facility contin uous
Weber problem [12] is to find X so that
( )()() min.AdμAX,Lw=XFii
Ω
N
=i i→
∫
∑
1
(7)
where
( )
i
Aμ
is the expectation of the fact that the i'th
customer is placed in some area. If this expectation is
equal among some area, i.e., if i'th cust omer is uni for ml y
(equably) distributed in the ar ea i Ωthen
()()() ,
1
mindAAAX,L w=XF
i
i
Ω
N
=i i
→
∫
∑
ρ
(8)
( )



∉
∈
i
i
iΩA
ΩA
=A ,0
,1
ρ . (9)
In case of continuous (regional) multi-Weber prob-
lem,
( )
( ) ( ) min.dAAA,XLw=
=X,,XF
ij
i
Ω
n i mMjj,
N
=i i
M
→
∫
∑
≤≤
ρ
1
1
1
...
(10)
In this paper, we propose an algorithm for approx-
imate solving the problem (10) with constraints (6)
where the distance function L() is an arbitrary monotone
function. In the example given this function is the well
known path loss function implemented to calculate the
radio-prop agation features of the area (media).
2. Related Works, Existing Methods
The Weber problem locates medians (facilities) at
continuous set of locations in the Euclidean plane (or
plane with an arbitrary metrics in generalized case). Ha-
kimi proposed similar problem statement for finding me-
dians on a network or graph [13, 14], proved that an op-
timal absolute median is always located at a vertex of the
graph, thus providing a discrete representation of a con-
tinuous problem and generalized the absolute median to
find p medians. Solutions consisting of p vertices are
called p-medians of the graph.
In the case of discrete coordinates, considering all
cells of discrete rectangular coord inate system as feasible
poi nts, we have p-median problem. But the dimension of
such prob lem is ver y large if the discretization i s pre cise
enough. In general, p-median problem is NP-hard, the
polynomial ti me algorith m is available o n trees onl y [15]
In [16], authors utilized a network flow procedure (an
algorithm for p-median problem) to solve the mul-
ti-facility location problem with rectilinear distances . In
case of the Weber problem (except one with Manhattan
or similar metric) [17], the sum of the edges weights is
not equal to distance in the problem with the discrete
coordinate grid.
Drezner and Wesolowsky [18] researched the con-
tinuous problem under an arbitrary lp distance metric.;
and, in [6], authors formulated the well-known
“block-norm” for the distances involved.
The unconstrained problem with the mixed coordi-
nates (discrete and continuous) is considered in [17].
For generalized multi-Weber problem with re-
stricted zones and barriers, only some special cases are
considered. Bischoff et al. [18] provided two heuristics
for the multi-Weber problem with barriers, and reported
that their algorithms can attain solutions of reasonably
sized multifacility location problems with barriers, both
with r egard to computation ti me and solutio n quality.
Having tra nsfor med our co ntinuous W eber pr oblem
into problem with discrete coordinate grid, we have a
combinatorial discrete optimization problem.
Most exact solution approaches to the problem of
discrete (combinatorial) optimization are based on
branch-and-bound method (tree search) [19, 20, 21],
most them are in the complexity class NP-hard and re-
quire searching a tree of the exponential size and even
parallelized versions of such algorithms do not allow us
to solve some large-scale pseudo-Boolean optimization
problems in acceptable time.
The heuristic random search methods do not guar-
antee any exact solution but they statistically optimal. I. e .
the percent of the problems solved “almost optimal”
grows with the increas e of the problem dimension [19].
Being initially designed to solve the unconstrained
pseudo-Boolean optimization problems, the probability
changing method (MIVER) is a random search method
organize d by the followi ng commo n s cheme [19 , 20, 22].
Algorithm 1
1. k=0, the start ing values o f the prob abilities Pk={pk1,
pk2, ... , pkN} are assigned where pkj=P{xj=1}. Correct
setting of the the starting probabilities is a very signifi-
cant question for the constrained optimization problems.
.
2. With probability distributions defined by the vector
Pk, we ge nerate a set of the rando m Boolean vectors Xk.
3. The functi on values are calculated: F(Xki).
4. Some function values from the set F(Xk) and cor-
responding points Xki are picked out (for example, point
with ma x i mu m and mini mu m va lues) .
5. On the basis of results in item 4, vector Pk is mod-
ified .
6. k=k+1, if k<R then go to 2. This stop conditio n may
diffe r.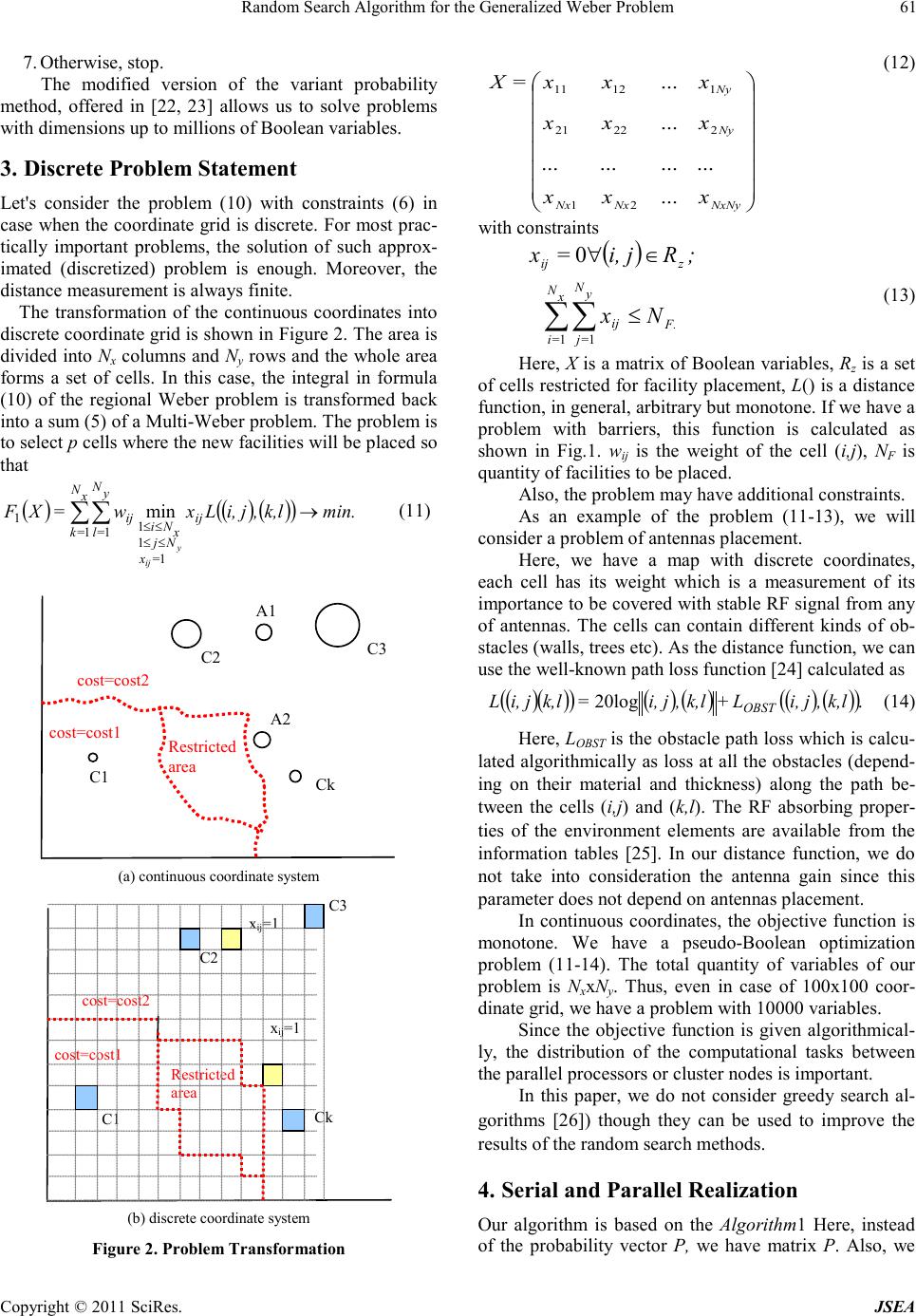

Random Search Algorithm for the Gen er alized Weber Problem
61
7. Otherwise, stop .
The modified version of the variant probability
method, offered in [22, 23] allows us to solve problems
with dimensions up to millions of Boolean variables.
3. Discrete Problem Statement
Let's consider the problem (10) with constraints (6) in
case when the coordinate grid is discrete. For most prac-
tically important problems, the solution of such approx-
imated (discretized) problem is enough. Moreover, the
distance measurement is always fi ni te.
The transformation of the continuous coordinates into
discrete co ordinate grid is sho wn in Fig ure 2 . T he a rea is
divided into Nx columns and Ny ro ws and the whole area
forms a set of cells. In this case, the integral in formula
(10) of the regional Weber problem is transformed back
into a sum (5) of a Multi-Weber problem. The problem is
to select p cells where the new facilitie s will be plac ed so
that
()()()() min.lk,,ji,Lxw=XF ij
=x Nj x
Ni
x
N
=k
y
N
=lij
ij
y
→
≤≤
≤≤
∑∑
1
1
1
1 1
1min (11)
C1
C2
C3
Ck
cost=cost1
cost=cost2
Restricted
area
A1
A2
(a) continuous coordina te system
C1
C2
C3
Ck
cost=cost1
cost=cost2
Restricted
area
xij=1
xij=1
(b) disc r ete c o ordinate system
Figure 2. Problem Transformation
















NxNyNxNx
Ny
Ny
xxx
xxx
xxx=X
...
............
...
...
21
22221
11211
(12)
with constrain ts
( )
F.
x
N
=i
y
N
=jij
zij
Nx
;Rji,=x
≤
∈∀
∑∑
1 1
0
(13)
Here, X is a matrix of Boolean variables, Rz is a set
of cells restricted for fac ility place ment, L() is a dista nce
functio n, in general, ar bitra r y but monotone. I f we have a
problem with barriers, this function is calculated as
shown in Fig.1. wij is the weight of the cell (i,j), NF is
quantity of facilities to be placed.
Also, the pro blem may have additio nal constraints.
As an example of the problem (11-13), we will
consider a problem of antennas placement.
Here, we have a map with discrete coordinates,
each cell has its weight which is a measurement of its
importance to be covered with stable RF signal from any
of antennas. The cells can contain different kinds of ob-
stacles (walls, trees etc). As the distance function, we can
use the well-known path loss function [24] calculated as
( )()()( )( )()()() .20loglk,,ji,L+lk,,ji,=lk,ji,L
OBST
(14)
Here, LOBST is the obstac le path loss which is calcu-
lated algorith mica lly as loss a t all the obstacles (depend-
ing on their material and thickness) along the path be-
tween the cells (i,j) and (k,l). The RF absorbing proper-
ties of the environment elements are available from the
information tables [25]. In our distance function, we do
not take into consideration the antenna gain since this
parameter does not depend on antennas placement.
In continuous coordinates, the objective function is
monotone. We have a pseudo-Boolean optimization
problem (11-14). The total quantity of variables of our
problem is NxxNy. Thus, even in case of 100x100 coor-
dinate grid, we have a problem with 10000 variables.
Since the objective function is given algorithmical-
ly, the distribution of the computational tasks between
the parallel processors or cluster nodes is important.
In this paper, we do not consider greedy search al-
gorithms [26]) though they can be used to improve the
results of the random searc h methods.
4. Serial and Parallel Realization
Our algorithm is based on the Algorithm1 Here, instead
of the probability vector P, we have matrix P. Also, we

Random Search Algorithm for the Gen er alized Weber Problem
Copyright © 2012 S ciRes. JSEA
62
have matrix of Boolean variables X instead of a vector. It
doe s not cha nge t he ge neral s cheme of our a lgor ithm b ut
simplifies the further description.
At the step of initializatio n (Step 1 of the Algorith m
1), all the variables p (components of the probability
matrix P) are set to their initial values (0<pi<1 ∀
Pp
i
∈
). Then (Step 2), we generate the matrices X of
optimized boolean variables. In our case of constrained
problem, the large values of mat r ix P co mpo nents ge ner-
ate the values of X which are out of the feasible solutions
area due to the constraints (13). Due to the constraints
(13), the optimal initial values of the matrix P compo-
nents do not exceed NF/(Nx Ny) [30].
Instead of maximum number of steps R (Step 6), we
can use the maximum run time as the stop condition. In
some cases, it is reasonable to use t he maximum number
of steps which do not improve the result achieved.
In the cycle (i=1,N), we generate the set of N ma-
trices Xki in accordance with the probability matrix P.
Then, the objective functio n is calculated for each Xki.
To take into consideration the constraints (13), we
modify the step of X exemplars generatio n.
Algorithm 2
∑=
Y
N
jijip=S1
.
1. XSET =Ø; n=0;
2 . while n<NF do
2.1. for each i in (1,Nx): ;
2.2. rx=Random();
2.3.
∑ =i
N
ixx
Sr=S
Y
1
;
2.4. select minimum i so that
xi
i
k
SS ≥
∑ =1
;
2.5. ry=Rando m();
2.6.
iyy
Sr=S
:
2.7. select minimum j so that
yil
j
l
Sp ≥
∑ =1
;
2.8. if
Z
Rji ∈) ,(
then goto 2.2
2.9. else,
( )
ji,X=XSETSET ∪
; n=n+1; goto 2;
Here, XSET is a set of coordinates (numbers of col-
umns and rows) of the resulting matrix X which are equal
to 1, NF is quantity of the facilities plac ed, Rando m() is a
function with r andom value in r ange [0, 1).
The solution of different practical problems [22]
shows the best result if we use the multiplicative adapta-
tion of eleme nts of matrix P with rollback procedure [27].
In thi s c ase , the c ompo ne nt s o f t he matr ix P are never set
to the value of 0 or 1 which may cause that all the further
generations of the X matrix very similar.
In Algo rith m 1, all Boolean variables are considered
as independent and the value of an element pij of the ma-
trix P at the k'th step can be calculated as
( )
( )
( )
∑∑
∑∑
−
−
−
⋅
⋅x
N
=l
y
N
=m ji,,k
ji,k,
x
N
=l
y
N
=m ji,,k
ji,k,ji,,k
ji,k, p
dp
dp
p
1 11
1 11
1
=
. (15)
Here, dk,i,j is the adaptation coefficient,
max
kj,i,
x
and
min
kj,i,
x
are the exemplars of the matrix X giving the max-
imum and the minimum values of the objective function
(11). In case of multiplicative adaptation, dk,i,j does not
depend on the step number k. In this case, the absolute
value of adaptation step depends on the corresponding
value of pkj.
In case of Weber problem, we consider the va-
riables xij as dep endent from each other. As follows from
the common sense (and proved experimentally), if the
obj ective functi on has maxi mum value with Xworst so tha t
1=x
min
kj,i,
then, with some probability, the results at the
next steps will be better if
1=x
min
kj,i,
or in some sur-
roundin g area:
SS
SS
kj,i
N+jjNj
,+NiiNi
x
**
*
max
,
*
*
*
1,
≤≤−
≤≤−
=
(16)
where NS is the width and height of the surr ounding area.
The value of the coefficient d must be bigger for the
points close to (i,j) for farther points, it must tend to 0.
We used the foll owing for mulas :
w*
/
ji,k,ji,k,ji,k,
dd=d
; (17)
( ) ( ) ( )()







±∉∨
∨±∉
±∈
∧±∈
][
][
,1
][^
][
,1/1
*
*
*
*
*
**
0
*
S
S
ji,k,
S
S
ji,k,
Njj
Nji
=d
Njj
Nji
ji,,j,iL+d+
=d
(18)
( ) ( ) ( )()







±∉∨
∨±∉
±∈∧
∧±∈
][
][
1,
][
]
[
,1/1
w
ww
0
S
w
S
w
ji,k,
S
w
S
w
wji,k,
Njj
Nji
=d
Njj
Nji
ji,,j,iL+d+
=d
.
(19)
Here, (i*,j*) and (iw,jw) are the closest points so that
1
min
,
*
*
=x
kj,i
and
1
,
w
w
=x
worst
kj,i
correspondingly, Xworst is
an exemplar of the X matrix with minimum objective
functi on among the generated set .
After several steps, the values of P matrix element s
are close to 0 or 1 and X generated are close t o so me lo-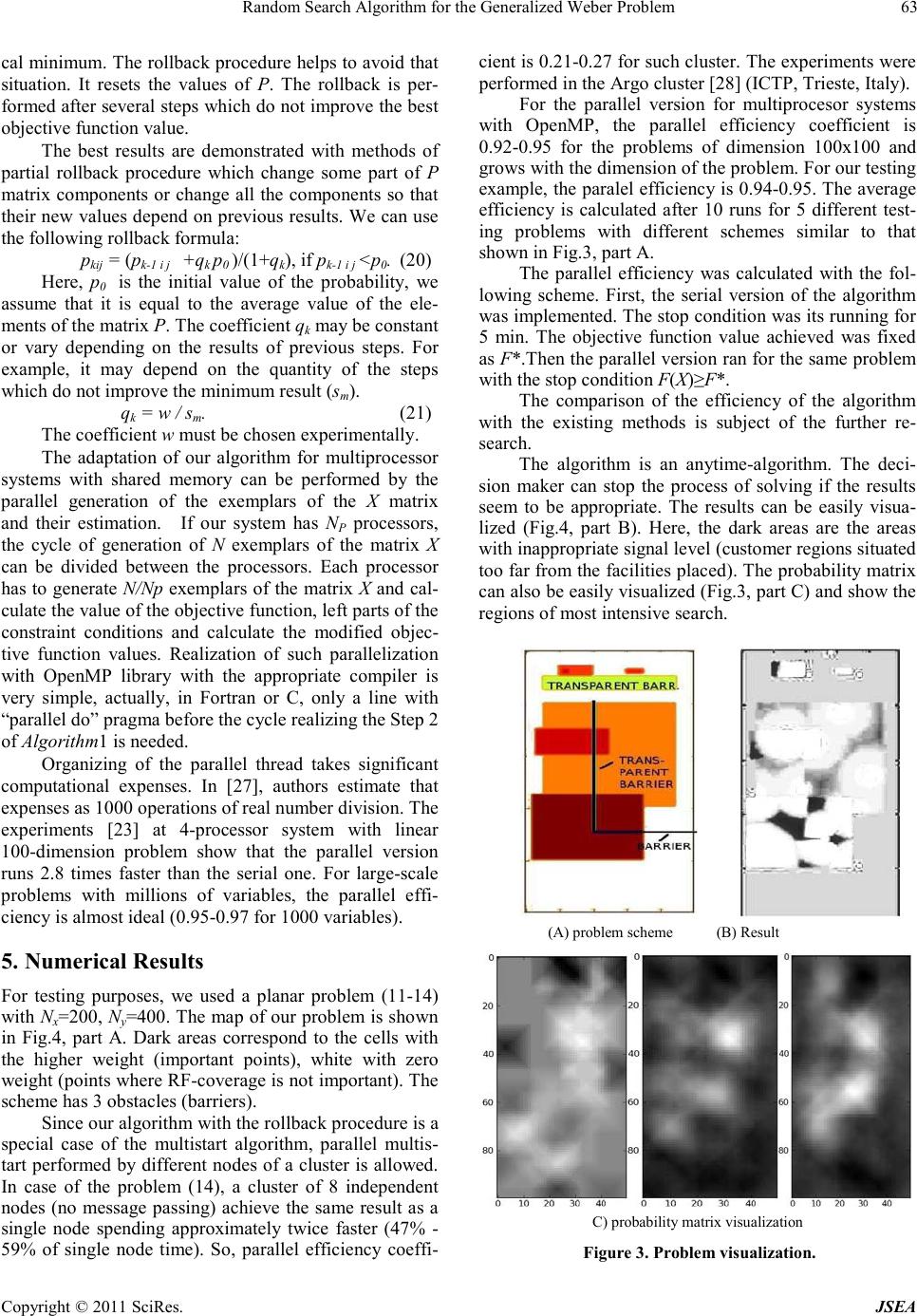

Random Search Algorithm for the Gen er alized Weber Problem
63
cal minimum. The rollback procedure helps to avoid that
situation. It re sets the values of P. The rollback is per-
formed after several steps which do not improve the best
objective functi on value.
The best results are demonstrated with methods of
partial rollback procedure which change some part of P
matri x compone nts or change all the co mponent s so that
their new values depend on previous results. We can use
the followin g rollback formula:
pkij = (pk-1 i j +qk p0 )/(1+qk), if pk-1 i j <p0. (20)
Here, p0 is the initial value of the probability, we
assume that it is equal to the average value of the ele-
ments of the matr ix P. The coefficient qk may be constant
or vary depending on the results of previous steps. For
example, it may depend on the quantity of the steps
which do not improve the minimum result (sm).
qk = w / sm. (21)
The coefficient w must be chosen experimentally.
The adaptation of our algorithm for multiprocessor
systems with shared memory can be performed by the
parallel generation of the exemplars of the X matrix
and their estimation. If our system has NP processors,
the cycle of generation of N exemplars of the matrix X
can be divided between the processors. Each processor
has to generate N/Np exemplars of the matrix X and cal-
culate the value of the obj ective function, left parts of the
constraint conditions and calculate the modified objec-
tive function values. Realization of such parallelization
with OpenMP library with the appropriate compiler is
very simple, actually, in Fortran or C, only a line with
“pa rallel do” pragma before the cycle realizing the Step 2
of Alg o rith m 1 is needed.
Organizing of the parallel thread takes significant
computational expenses. In [27], authors estimate that
expense s as 1000 operations of real number division. The
experiments [23] at 4-processor system with linear
100-dimension problem show that the parallel version
runs 2.8 times faster than the serial one. For large-scale
problems with millions of variables, the parallel effi-
ciency is almo st ideal (0.95-0.97 for 1000 variables).
5. Numerical Results
For testing purposes, we used a planar problem (11-14)
with Nx=200, Ny=400. The map of our problem is shown
in Fig.4, part A. Dark areas correspond to the cells with
the higher weight (important points), white with zero
weight (points where RF-cove rage is no t impor tant) . T he
scheme has 3 obstacles (barriers).
Since our algorith m with the rollback procedure is a
special case of the multistart algorithm, parallel multis-
tart performed by different nodes of a cluster is allowed.
In case of the problem (14), a cluster of 8 independent
nodes (no message passing) achieve the sa me result as a
single node spending approximately twice faster (47% -
59% of single node time). So, parallel efficiency coeffi-
cient is 0.21-0.27 for such cluster. The experiments were
performed in the Ar go cluster [28] (ICTP, Trieste, Italy).
For the parallel version for multiprocesor systems
with OpenMP, the parallel efficiency coefficient is
0.92-0.95 for the problems of dimension 100x100 and
grows with the dimension of the problem. For our testing
example, the paralel efficiency is 0.94-0.95. The average
efficiency is calculated after 10 runs for 5 different test-
ing problems with different schemes similar to that
shown in Fi g.3, part A.
The parallel efficiency was calculated with the fol-
lowing scheme. First, the serial version of the algorithm
was i mplemented. The stop condition was its running for
5 min. The objective function value achieved was fixed
as F*.T hen the parallel version ran for the same problem
with the stop co nd ition F(X)≥F*.
The comparison of the efficiency of the algorithm
with the existing methods is subject of the further re-
search.
The algorithm is an anytime-algorithm. The deci-
sion maker can stop the process of solving if the results
seem to be appropriate. The results can be easily visua-
lized (Fig.4, part B). Here, the dark areas are the areas
with inapprop riate signal le vel ( custo mer regions situated
too far fro m the facil ities place d). The probab ility matrix
can also be easily visualized (Fig.3 , part C) and show the
regions of most intensive sea rch.
(A) problem scheme (B) Result
C) probability matrix visualization
Figure 3 . Problem visualization.

Random Search Algorithm for the Gen er alized Weber Problem
Copyright © 2012 S ciRes. JSEA
64
6. Conclusion
Modified random search algorithm based on probability
changing method can be used for approximate solving
planar generalized multi-Weber problem with non- Euc-
lidean monotone distance function. Modern computing
facilities (multiprocessor systems, low-cost clusters) al-
low solving problems with appropriate precision. In the
case of the MPI cluster for random search problems, ex-
pensive high-performance network is not needed because
of absence of any data tra ffic.
REFERENCES
[1] G. Wesolowsky, ''The Weber Problem: History and
Perspectives'', Location Science, 1,1993, pp. 5–23.
[2] R.Chen, ''Locatio n Problems wit h Costs Being Sums
of Powers of Euclidean Distances'', Computers &
Ops. Res., 11, 1984, pp.285–294
[3] Z. Drezner and H. Hawacher, ''Facility Location:
Applications and Theory'', Berlin,, Springer-Verlag,
2004.
[4] R.F. Love and J.G. Morris, ''Computation Procedure
for the Exact Solution of Location-Allocation Prob-
lems with Rectangular Distances'', Naval Research
Logistics Quarterly, 22, 1975, pp.441–453. doi:
10.1002/nav.3800220304
[6] J.E. Ward and R.E. Wenll, ''Using Block Norms for
Location Modeling'', Operations Research, 33, 1985,
pp.1074–1090. doi: 10.1287/opre.33.5.1074
[5] R.F. Love, W.G.
[12] M. Gugat and B. Pfeiffer, ''Weber Problems with
Mixed Distanc es and Regiona l Dema nd'', Math Meth
Oper Res, issue 66, 2007, pp.419–449.
doi:10.1007/s00186-007-0165-x
[13] S.L. Hakimi, ''Optimum Locations of Switching
Centers and the Absolute Centers and Medians of a
Graph'', Operations Research, 12(3), 1964,
pp.450–459. doi: 10.1287/opre.12.3.450
[14] S.L. Hakimi, ''Optimum Distribution of Switching
Centers in a Communication Network and Some Re-
lated Graph Theoretic Problems'', Operations Re-
search, 13(3), 1965, pp.462–475. doi:
10.1287/opre.13.3.462
[15] O. Kariv and S.L. Hakimi, ''An algorithmic ap-
proach to network location problems. II. The
p-medians'', SIAM Journal on Applied Mathematics,
37(3), 1979, pp. 5 39 –560. oi: 10.1137/0137041
[16] A.V. Cabot, R.L. Francis and M.A. Stary, ''A Net-
work Flo w Solutio n to a Recti linear Di stance Fa cil it y
Location Problem'', American Institute of Industrial
Engineers Transactions 2, 1970, pp. 132–141.
[17] S. Stanimirovic, M. Ciric, ''Single-facility Weber
Location Problem Based On The Lift Metric''.
http://arxiv.or g/abs/11 0 5 . 0 75 7
[18] M. Bischoff, T. Fleischmann and K . Klamroth, ''The
Multi-Facility Location-Allocation Problem with
Polyhedral Barriers'', Computers and Operations Re-
search, 36, 2009, pp.1376–1392. doi:
10.1016/j.cor.2008.02.014
[19] A.N. Antamoshkin, ''Optimizatsiya Funktsionalo v s
Bulevymi Peremennymi'' (''Optimization of Func-
tionals with Boolean Variables''), TGU, Tomsk, 1987
[20] A.Antamoshkin, H.P. Schwefel, A. Toern, G. Yin
and A.Zhilin skas, ''System Anal ysis, Desin g and Op-
timization. An Introduction'', Ofset, Krasnoyarsk,
1993
[21] Yu. Finkelstein et al. ''Diskretnaya Optimzatsiya''
(''Discrete Optimization''), Metody Optimizatsii v
Ekonomiko-Matematicheskom Modelirovanii, Nauka,
Moscow, 1991, pp. 350-367
[22] L.Kazakovtsev, “Adaptive Model of Static Routing
for Traffic Balance between Multiple Telecommuni-
cation channels to different ISPs”,
http://citeseer x.ist.psu.edu/vie wdo c/d ownload?doi= 1
0.1.1.102.9445&rep=rep1&type=pdf (accessed
01.08.2012)
[23] L.A.Kazakovtsev and A.A.Stupina, ''Parallelnaya
Realizatsiya Metoda Izmenyayushikhsya
Veroyatnostey'' (''Parallel Realization of the Proba-
bility Changing Method''), Sovremennye problemy
nauki i obrazovaniya, №4, 2012,
http://www.science-education.ru/104-6810
[24] T.S. Rappaport, ''Wireless Communications: Prin-
ciples and Practice'', 2nd ed.–IEEE Press, 2002
[25] J.Hu and E. Goodman, ''Wireless Access Point
Configuration by Genetic Programming'', in Evolu-
tionary Computation, 2004. CEC2004. Congress on,
vol.1, 2004,pp. 1178- 1184
Truscott and J. Walker, ''Terminal
Location Problem: A Case Study Supporting the
Status Quo'', J. Opl Res. Soc., 36,1985, pp.131-136.
doi:10.1057/jors.1985.26
[7]. M.J. Hodgson, R.T. Wong and J.Honsaker, ''The
P-Centroid Problem on an Inclined Plane'', Opera-
tions Research, Issue 35,1987, pp. 221–233. doi:
10.1287/opre.35.2.221
[8] J. Brimberg and R.F.Love, ''Properties of Ordinary
and Weighted Sums of Order p Used for Distance
Estimation'', Recherche Operationnelle, Issue
29,1995, pp. 59–72.
[9] L. Cooper, ''An extension of the generalized Weber
problem'', Journal of Regional Science, Vol.8, Issue
2, 1968, pp. 181–197l. doi:
10.1111/j.1467-9787.1968.tb01323.x
[10] M.M. Deza and E. Deza, ''Encyclopedia of
Distances'', Springer Verlag, 2009. doi:
10.1007/978-3-642-00234-2_19
[11] S.P. Fekete, ''On the Continuous Fermat-Weber
Problem'', Operations Research, Vol. 53 1
2005,61–76 . doi: 10.1287/opre.1040.0137

Random Search Algorithm for the Gen er alized Weber Problem
65
[26] P.M. Pardalos, L.Pitsoulis, T. Mavridou and M.G.C.
Resende, ''Parallel Search for Combinatorial Optimi-
zation: Genetic Algorithms, Simulated Annealing,
Tabu Search and GRASP '', in Parallel A lgorithm s for
Irregularly Structured Problems: Lecture Notes in
Computer Science, issue 980, 1995, pp 317- 331.
doi: 10.1007/3-540-60321-2_26
[27] L.Dagum, R.Menon, ''OpenMP: An Indus-
try-Standard API for Shared-Memory Programming'',
IEEE Computational Science and Engineering (IEEE
Computer Society Press), Vol. 5, Issue 1, 1998,
p.46–55.
[28] A.Messina, “Meet Argo”, http://argo.ictp.