Journal of Software Engineering and Applications, 20 12, 5, 26-29
doi:10.4236/jsea.2012.512b006 Published Online December 2012 (http://www.SciRP.org/journal/jsea)
Copyright © 2012 Sci R es. JSEA
Periodic Solution of n-Species Gilpin-Ayala Competition
System with Impulsive Perturbations
Kaihua Wang, Zhanji Gui*
Scho ol of Mathematics and S tatistics, Hainan N ormal University, Haiko u, Hainan, China.
Received 2012
ABSTRACT
The principle aim of this paper is to explore the existence of periodic solution of n-Species Gilpin-Ayala competition
system with impulsive perturbations. Sufficient and realistic conditions are obtained by using Mawhin's continuation
theorem of the coincidence degree. Further, some numerical simulations show that our model can occur in many forms
of complexities includin g p e r iodic oscilla tion and chaotic s trange attractor .
Keywords: Periodic Solution; Impulsive Perturba tions; Ma whin’s Continuation The orem
1. Introduction
The dynamics of Ayala-Gilpin competitive system,
which was first introduced by Ayala et al. [1], has been
widely studied by many authors [2-6]. However, the
corresponding problems with periodic coefficients and
impulsive perturbations were studied far less often [7]. In
this paper, we will study the following impulsive Gil-
pin-Ayala s ystem:
1,
()() ()
()
()
1() ,
() ()
()() ()(),,
i
i ii
nj
iij
j ji
ij
i
ikik ikkikk
zt rtzt
zt
zt t
Kt Kt
ztztztpztt t
θ
α
= ≠
+− −
= ⋅



−−




∆= − ==


∑

(1.1)
where
)(tzi
represents the density of the
thi
species
at time
t
;
)(tr
i
deno tes the intr insi c gr owth r ate of the
thi
species;
)(tKi
means the environment carrying
capacity of species
i
in the absence of competition;
)(t
ij
α
(
ji ≠
) measures the amount of competition be-
tween the species i x and
j
x
; i θ is a positive con-
stant and provide a nonlinear measure of intra-specific
interference; i
k
p are constants.
In system (1.1), we give two hypotheses as follows.
(H1)
)(),( tKtrii
and
)(t
ij
α
(
jinji ≠= ,,,1, 
)
are all nonnegative
T
- periodic functions defined
on
R
.
(H2)
01 >+
i
k
p
and there exists a positive inte-
ger
q
such that
Ttt
kqk+= +,
i
k
iqk
pp =
+
.
2. Existence of Positive Solutions
To prove our result s, we need the noti on of t he Ma whi n’s
continuation theorem formulated in [8].
Lemma 1 ([8]) Let
X
and
Y
be two Banach spaces.
Consider an operator equation
NxLx λ =
where
:L
Dom
YXL →
is a Fredholm operator of index zero
and
]1,0[∈ λ
is a parameter, then there exist two projectors
XXP →:
and
YYQ →:
such t hat
=PIm
Ker
L
and
=LIm
Ker
Q
. Assume that
YN →Ω:
is
L
-
compact on
Ω
, where
Ω
is open bounded in
X
. Fur-
thermore, assume that
a) for each
)1,0(∈ λ
,
Ω∂∈x
Dom L,
NxLx λ ≠
;
b) for each
Ω∂∈x
Ker
L
,
0≠QNx
;
c)
{ Ω,degJQN
Ker
} 00, ≠L
, where
→QJ Im:
Ker
L
is an isomorphism and deg{*} represents
the Brouwer degree.
Then the equatio n
NxLx =
has at least one solution
in
Ω
Dom
L
.
For the sake of convenience, we shall make some
preparation. Let
RI ⊂
. Denote by
),(
n
RIPC
the
space of functions
n
RItx →:)(
which are conti-
nuous at
It∈
,k tt≠ , and are left continuous for
*Corresponding author.

Periodi c Solution of n-Species Gilpin-Ayala Competition System with Impulsive Perturbations
27
Itt
k∈= . Let
)}({min
0
tuu
Tt
L
≤≤
=
,
)}({max
0
tuu
Tt
M
≤≤
=
,
∫
=
T
dttu
T
u
0
)(
1
,
∫
=Tdttvtu
T
uv 0)()(
1
,
where
)(tu
,
)(tv
are
T
periodi c functions.
Theorem 1. Suppose (H1) and (H2) hold, furthermore,
the following co nditions are satisfied.
(H1)
∑∑
≠==
>++
n
ijj
C
iji
L
j
i
q
k
i
k
j
Ter
K
Trp
,11
1
)1ln( α
,
where
1
11
1
ln 1ln(1)ln
2
ln(1 )|ln(1 )|.
qjM
kj
k
j
jj
j
qq
jj
kk
kk
pK
rT
C rT
pp
θ
=
= =

+ ++



= +
+ +++
∑
∑∑
Then system (1.1) has at least one positive
T
- periodic
solution.
Proof. Let
)(
)( tx
ii
etz = (
ni ,,1 =
) (2.1)
then the s ystem (1.1) becomes
()
()
1,
()() 1()
() ()
( )ln(1)
j
ii
i
xt
xt n
i iijk
j ji
ij
i
ikk k
ee
xtrttt t
K tKt
xtpt t
θ
θ
α
= ≠

=−− ≠

 
∆=+ =

∑

(2.2)
In order to use Lemma 1, we set
T
n
txtxx))(,),((
1
=
,
)}()(|),({ txTtxRRPCxX n=+∈=
,
nq
RXY ×=
,
then it is standard to show that both
X
and
Y
are
Banach space when they are endowed with the norm
|)(|sup|||| ],0[txx Tt
c∈
=
and
2/122
1
2
1
)||||||(||||),,,(||
qcq
ccxccx +++=
.
Set
:DomLLX Y⊂→
as
))(,),(),(())((
1q
txtxtxtLx ∆∆= 

,
where Dom{|'()(,)}
n
LxXxtPC R R
=∈∈
,





=+∈=
∑
∫
=
0)(|),,,(Im
1
0
1
q
ii
T
q
cdttyYccyL 
and Ker
Ker n LR=
.
At the same time, we denote
YXN →:
as
)))((,)),(()),( ,(())((
11 qq
txtxtxtftNx ΦΦ =
,
where ()
()
1, 1
(,)
() 1()()
()
j
ii
i
xt
xt n
i ij
j jij
in
ftx
ee
rt tKt
Kt
θ
θ
α
= ≠×


= −−
 




∑,
( )
T
n
kkkk
pptx )1ln(,),1ln())((
1
++=Φ 
,
where
ni ,,1=
,
qk ,,2,1 =
.
Define two projectors
P
and
Q
as
LXP ker:→
,
∫
=Tdttx
T
Px 0)(
1
;
YYQ →:
,





+= ∑
∫=
0,,0,)(
1
),,,(
1
0
1
q
kk
T
qcdssy
T
ccyQ
.
It can be easily proved that
L
is a Fredholm
operator of index zero, that
P
,
Q
are projectors,
and that
N
is
L
- compact on
Ω
for any given
open and bound subset
Ω
in
X
.
Now we are in a position to search for an appro-
priate open bounded subset
Ω
for the application
of Lemma 1 correspo nding to operator equation
NxLx λ =
,
)1,0(∈ λ
(2.3)
Suppose that
T
ntxtxtx))(,),(()( 1=
is a periodic
solution of (2.3) for certain
)1,0(∈ λ
. By integrating
(2.3) over the interval
],0[ T
, we get
()
0
1
()
0
1,
()
ln(1)()
() ()()
ii
i
j
qTxt
ii
ik
ki
xt
nT
i ij
j jij
rt
rTpe dt
Kt
e
r ttdt
Kt
θ
θ
α
=
= ≠
=− ++
+
∑∫
∑∫
(2.4)
From (2.3), (2.4), we can obtain
i
q
k
i
ki
T
iApTrdttx ≡++≤
∑
∫
=1
0)1ln(2|)(| 
(2.5)
Since )],,0([)(
RTPCtx
i∈, there exist
},,,{],0[,
21+++
∈
qii
tttT  ηξ
, such that
)(inf)(
],0[
txx
i
Tt
ii∈
= ξ
,
)(sup)(],0[ txx i
Tt
ii ∈
=
η
,
It follows fro m (2.4) that
( )()
0
1
() 1
()
ln(1)
ii iii
i
T
x xt
i
i
M
ii
qi
ik
k
rt
rTee dt
K Kt
rT p
θξ θ
θ
=
≤
≤+ +
∫
∑
which implies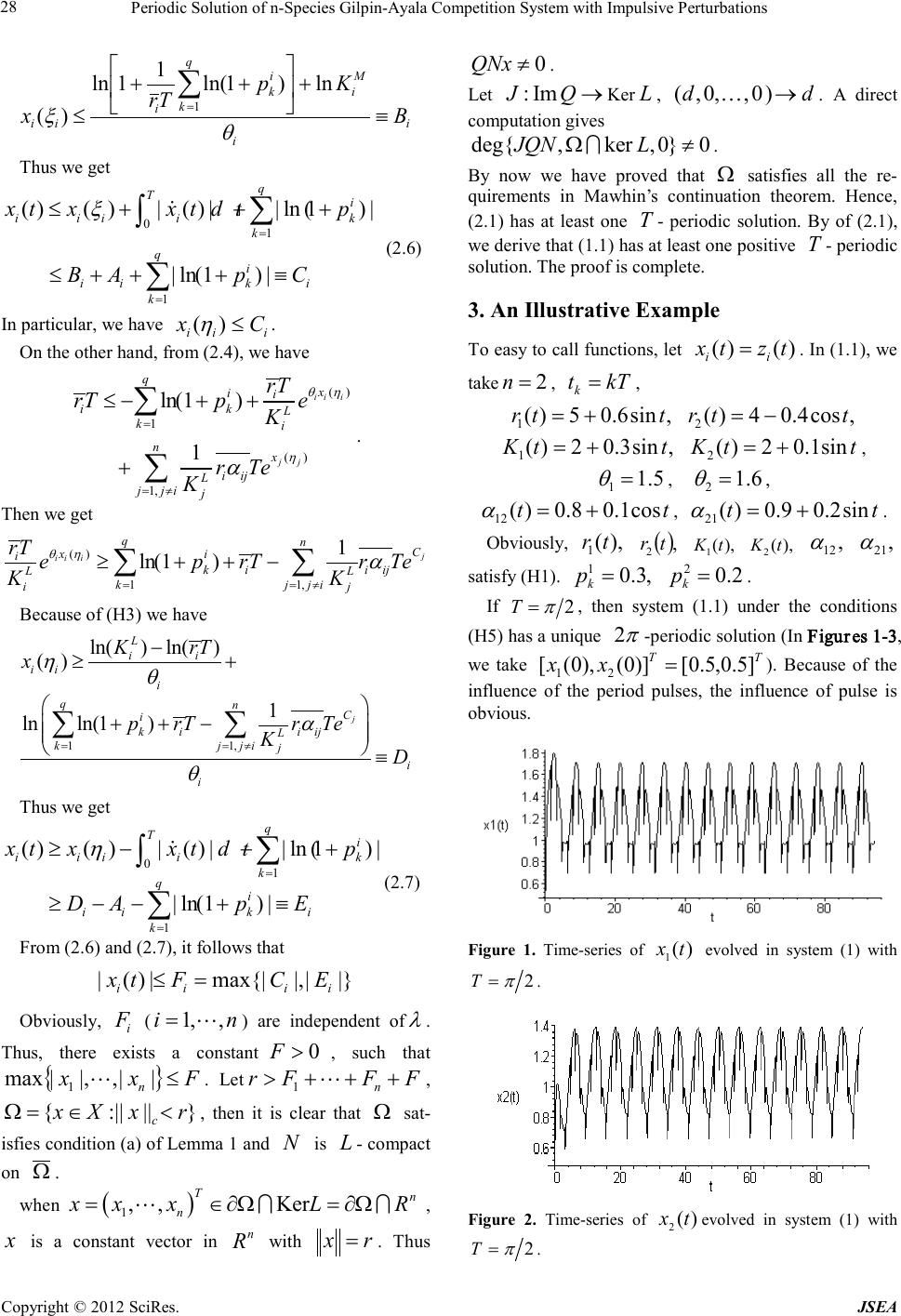

Periodi c Solution of n-Species Gilpin-Ayala Competition System with Impulsive Perturbations
28
i
i
M
i
q
k
i
k
i
ii
B
Kp
Tr
x≡
+





++
≤
∑
=
θ
ξ
ln)1ln(
1
1ln
)(
1
Thus we get
01
1
( )()|( )||ln(1)|
| ln(1) |
q
Ti
i iiik
k
qi
iik i
k
xt xxtdtp
BAp C
ξ
=
=
≤+++
≤+++ ≡
∑
∫
∑

(2.6)
In particular, we have
iii Cx ≤)(
η
.
On the other hand, from (2. 4 ), we have
()
1
()
1,
ln(1)
1
ii i
jj
qx
ii
ik
L
ki
nx
i ij
L
j jij
rT
rTp e
K
r Te
K
θη
η
α
=
= ≠
≤−++
+
∑
∑
.
The n we get
()
1 1,
1
ln(1 )
j
ii i
qnC
xi
ikii ij
LL
kj ji
ij
rT eprTr Te
KK
θη
α
== ≠
≥+ +−
∑∑
Because of (H3) we have
1 1,
ln() ln()
()
1
ln ln(1 )
j
L
ii
ii
i
qnC
i
kiiij
L
kjjij
i
i
K rT
x
prTr Te
KD
ηθ
α
θ
== ≠
−
≥+

+ +−



≡
∑∑
Thus we get
01
1
( )()|( )||ln(1)|
| ln(1) |
q
Ti
i iiik
k
qi
iik i
k
xtxxt dtp
DAp E
η
=
=
≥−− +
≥ −−+≡
∑
∫
∑

(2.7)
From (2.6 ) and (2.7) , it follows that
|}||,max{||)(| iiiiECFtx =≤
Obviously,
i
F
(
ni ,,1=
) are independent of
λ
.
Thus, there exists a constant
0>F
, such that
{ } Fxx n≤||,|,|max 1
. Let
FFFr n+++>
1
,
}||:||{ rxXx
c
<∈=Ω
, then it is clear that
Ω
sat-
isfies condition (a) of Lemma 1 and
N
is
L
- compact
on
Ω
.
when
( )
1
, ,Ker
Tn
n
xx xLR=∈∂Ω=∂Ω
,
x
is a constant vector in n
R
with
xr=
. Thus
0QNx ≠
.
Let
: ImJQ→
Ker
L
,
( ,0,,0)dd→
. A direct
computatio n gives
deg{,ker,0}0JQN LΩ≠
.
By now we have proved that
Ω
satisfies all the re-
quirements in Mawhin’s continuation theorem. Hence,
(2.1) has at least one
T
- periodic solution. By of (2.1),
we derive that (1.1) has at least one positive
T
- periodic
solution. The proof is complete.
3. An Illustrative Example
To e asy to call functio ns, let () ()
ii
xt zt=. In (1.1), we
take
2n=
,
kTtk=
,
,sin6.05)(
1ttr+=
,cos4.04)(
2ttr −=
,sin3.02)(
1ttK +=
ttK sin1.02)(
2
+=
,
5.1
1=
θ
,
6.1
2
= θ
,
tt cos1.08.0)(
12 +=
α
,
tt sin2.09.0)(
21 +=
α
.
Obviously,
),(
1tr
( ) ,
2
tr
),(
1tK
),(
2
tK
,
12
α
,
21
α
satisfy (H1).
,3.0
1=
k
p
2.0
2
=
k
p
.
If
2 π =T
, then system (1.1) under the conditions
(H5 ) ha s a uni q ue
π 2
-periodic so lution (In Figures 1-3,
we take
TT
xx ]5.0,5 .0[)]0(),0([
21
=
). Because of the
influence of the period pulses, the influence of pulse is
obvious.
Figure 1. Time-series of
)(
1
tx
evolved in system (1) with
2 π =T
.
Figure 2. Time-series of
)(
2
tx
evolved in system (1) with
2 π =T
.

Periodi c Solution of n-Species Gilpin-Ayala Competition System with Impulsive Perturbations
29
But if
2=T
, then (H2 ) is not satisfied. Periodic os-
cillation of system (1.1) under the conditions (H5) will
be destroyed by impulsive effect. Numeric results show
that system (1.1) under the conditions (H5) has gui cha-
otic strange attractor (see Figure 4) [9]. In Figure 4, we
take
TT
xx ]5.0,5.0[)]0(),0([
21
=
.
Figure 3. Phase portrait of periodic solutions of system (1)
with
2 π =T
.
Fig ure 4. P ha se p ortrait of ch a ot ic st range a tt ract or of sys-
tem (1) with
2=T
.
4. Acknowledgement s
This work is supported jointly by the Natural Sciences
Foundation of China under Grant No. 60963025, Natural
Scienc es Fo undat ion of Ha ina n Pro vince und er Gr ant No.
110007 and the Start-up fund of Hainan Nor mal Uni ver-
sity under Project No. 00203020201.
REFERENCES
[1] Ayala F J, Gilpin M E and Eherenfeld J G “Competition
between species: Theoretical models and experimental
tests,” The or e t. Popul. Bi ol . 4 (1973) 331-56.
[2] Gilpin M E and Ayala F J “Global models of growth and
competition,” Proc. Natl. Acad. Sci. USA. 70 (1973)
3590-93.
[3] Liao X X and Li J “Stability in Gilpin-Ayala competition
models with diffusion,” Nonlinear Anal. 2 8 19971751-58
[4] Ahmad S and Lazer A C “Average conditions for global
asymptotic stability in a nonautonomous Lotka-Volterra
s yst em,” Nonlinear Anal. 40 (2000) 37-49.
[5] Chen F D “Average conditions for permanence and ex-
tinction in nonautonomous Gilpin-Ayala competition
model,” Nonlinear Anal. 4 (2006) 895-915.
[6] Xi a Y H, Han M A and Huang Z K “Global attractivity of
an almost periodic N-Species nonlinear ecological com-
petitive model,” J. Math. Anal. Appl. 337 (2008) 144-168.
[7] Wang Q, Ding M M, Wang Z J and Zhang H Y “Exis-
tence and attractivity of a periodic solution for an
N-species Gilpin-Ayala impulsive competition system”
Nonlinear Ana: Real World Applications 11 (2010)
2675-85
[8] Gaines R E and Mawhin J L “Coincidence degree and
nonlinear diferential equations ” Springer-Verlag, Berlin,
1977.
[9] Zhang J and Gui Z J “Periodic solutions of nonautonom-
ous cellular neural networks with impulses and delays,”
Nonlinear Analysis: Real World Applications. 10 (2009)
1891-1903.