Journal of Modern Physics
Vol.06 No.13(2015), Article ID:60800,10 pages
10.4236/jmp.2015.613201
A Chart of Conversion Supporting EPR Paradox vs. Bell’s Inequalities Violation
Olivier Serret
Cugnaux, France
Email: o.serret@free.fr
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 September 2015; accepted 25 October 2015; published 30 October 2015
ABSTRACT
Quantum Mechanics formalism remains difficult to understand and sometimes is confusing, especially in the explanation of ERP paradox and of Bell’s inequalities with entanglement photons. So a chart of conversion, in which elements are named differently, is proposed. Next, experiment about Bell’s inequalities violation is described in another way, and we hope a clearer one. Main result is Bell’s inequalities would not be violated! The explanation would come from confusion between the definition of the correlation function S1, and a property S2. And consequently, Einstein, Podolski and Rosen would be right on the local “hidden” variable.
Keywords:
Quantum Mechanics, Correlation Function, Correlation Coefficient, Total Correlation, EPR, Einstein-Podolski-Rosen Paradox, Bell Inequality Violation, Entanglement, Local Hidden Variable

1. Introduction
“God does not play dice” Einstein wrote. Where there appears to be random, there is only a cause we have not yet found or discriminated. EPR paradox [1] was formulated in 1935 by Einstein, Podolski, and Rosen to define a determinist theory, including local hidden variables which Quantum Mechanics would have missed. Then, in 1964, the physician Bell demonstrated that this determinist theory obeyed the mathematical Bell’s in- equalities [2] . In the 1980s, some scientists’ teams showed Bell’s inequalities would be violated. Because Quantum Mechanics formalism is difficult to read, the purpose of this article is to propose another notation for some elements, and then to discuss this EPR paradox and the proofs of the Bell’s inequalities violation. The guide line of this article is a critical reading of Alexandre Moatti’s chapter about Quantum Physics [3] , by using the proposed conversion chart.
2. Proposed Formalism
2.1. Quantum Mechanics Formalism
Quantum Mechanics Formalism is difficult to understand [4] ; it is also confusing. Some parameters can have two different meanings, and the same meaning can be called by different parameters. For example:
・ A (or B) can mean Photon and/or Separator
・ x (or y) can mean Photon and/or Axis
・ Alice (or Bob) can mean a detector and/or its complementary detector
・ The same axis can be called either (Ox’) or (Oa)
Also some parameters are not precise enough, or are surprising. For example:
・ |x,x> symbolizes the polarization status of a photon pair. The first x is for the first photon, the second x is for the second photon. But there are twodifferent photons. So the idea will be to distinguish the two photons with the letters X and Y.
・ When a photon is detected, the value of the measure is +1. When it is not detected, it value of the no- measure is −1, which is quite surprising. Usually, when we cannot detect an object or a phenome, the value is 0. To avoid disturbing to much our reader, we will have here the convention to keep the convention −1 when a photon is not detected.
2.2. A Conversion Chart
To correct the confusing term, we will use in this article the conversion Chart 1 hereafter.
3. Bell’s Inequality
3.1. The Wave Function
Quantum mechanics introduces a wave function
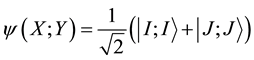 (1)
(1)
with:
- I,J: axes;
- X,Y: photons;
|I> characterizes the polarity of the photon X according to the axis I.
3.2. The Polarization Status on a Single Side
Let us have a simple set up with a single separator, as seen in Figure 1:
1) First, separator A is adjusted with an angle
 (which mean parallel to I).
(which mean parallel to I).
When we measure these photons on the detector DA, we will find {+} each time (and on the detector \DA, we will find nothing, i.e. {−})
So each time
 and
and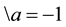 . This will occur to each photon polarized |I>.
. This will occur to each photon polarized |I>.
It is said in QM the polarization (of this photon) parallel to I is exactly defined.
2) Then, separator A is adjusted with an angle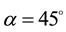 ,
,
And let us call L the axis which has an angle of 45˚ with the axis I
These photons still have a polarity according to I (to simplify, we can say these are the same photons again)
When we measure these photons on the detector DA (with the new value of angle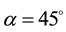 ), we will find
), we will find
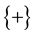 in 50% of the cases and
in 50% of the cases and
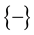 in the other 50% cases (and on \DA we will find
in the other 50% cases (and on \DA we will find
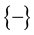 in 50% of the cases and
in 50% of the cases and
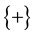 in 50% of the cases).
in 50% of the cases).
It is the said in QM the polarization (of the photons) parallel to L is not defined.
Remark: it is “not” the polarization of the photons X which has changed; it is only the angle α to measure them which has changed. More generally, we can say that, except with the particular case of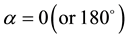 , the polarization of these photons would not be (exactly) defined according to QM!
, the polarization of these photons would not be (exactly) defined according to QM!
3.3. The Experiment
Let us now use the proposed formalism to check the experimental set up used to prove Bell’s inequalities violation
Chart 1. Chart of conversion.
(Figure 2):
with
- a source which emits entangled pairs of photons (X,Y) in green;
- two channels separators A and B which direct photons according their polarization toward the detectors;
- detectors DA and DB which detect photons polarized according to α and β;
Figure 1. A single separator.
Figure 2. Experimental principle.
- detectors \DA and \DB which detect photons polarized according to \α and \β;
- a the measure done on DA;
- \a the measure done on \DA;
- b the measure done on DB;
- \b the measure done on \DB;
3.4. A Property of the Correlation Function
As a consequence of the wave function, there is a property associated
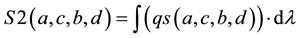 (2)
(2)
where
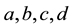 are the measures of the experiment;
are the measures of the experiment;
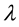 is a local “hidden” variable.
is a local “hidden” variable.

Another author [5] explains “making measurements on a large number of pairs, it can measure the average value of”:

A mathematical integral is nothing less than a sum (or an average sum).
This sum (or this average sum) S2 is called by Quantum mechanics theory: a correlation function property!
3.5. The Quantum Sum
What is

Remark: it is a bit confusing to call “sum” an operation with a subtraction (minus “−”) in the formula. But we keep this QMdesignation of “sum”, adding the term “quantum”.
On the Chart 2 hereafter, we can check all the possible value for the quantum sum qs:
The quantum sum

In practice, c is the complementary measure of a. In other word,





3.6. Bell’s Inequalities
We have seen on the previous paragraph on the quantum sum (§3.5) that


By mathematical construction, S2 cannot be greater than 2.
This property is called Bell’s inequalities
4. The Correlation Function
4.1. Definition of the Correlation Function S1
The correlation function S1 is defined as

with

E(α,β) the correlation coefficient.
We have to note that the correlation function is different of the correlation coefficient (and of the total corre- lation). To define the correlation coefficient, we first need to explain what the probabilities in Quantum Mecha- nics are.
4.2. Entanglement
Entanglement means the 2 photons of the pair emitted by the source have the same polarization.
Because produced by the same source, photons pairs are entangled photons.
4.3. Total Correlation
1) Let us have a single photon pair (X, Y).
Chart 2. Possible values of the quantum sum qs.
It is supposed they have the polarity |I,I>. Because they have the same polarity (I = I), they are entangled photons. They would also be entangled photons when they have the polarity |J,J>.
When we measure these photon pairson DA (with the value of angle

2) Using a photons source, each pair of photons will have a different polarization (but the two photons of each pair have the same polarization). Because there is no preferential polarization at the source, 50% of these photons will be received on DA and 50% of these photons will be received on \DA. Please check Chart 4.
It is the said in QM there is total correlation between the measures on DA and on DB.
3) Then, when we measure these X photons on DA (with the new value of angle α = 45˚), we will find {+} in 50% of the cases and {−} in the other 50% cases (and on \DA we will find {−} in 50% of the cases and {+} in 50% of the cases). On the same time, when we measure these Y photons on DB (with the new value of angle β = 45˚), we will find {+} in 50% of the cases and {−} in the other 50% cases (and on \DB we will find {−} in 50% of the cases and {+} in 50% of the cases). So we will find on DA and DB: 25% of [+1, +1], 25% of [+1, −1], 25% of [−1, +1] and 25% of [−1, −1].
It is the said in QM there is total decorrelation between the measures on DA and on DB.
It has been transcribed in Chart 5 the results with the same 8 photon pairs.
Chart 3. Measure of a single pair.
Chart 4. Measures with α = 0˚ and β = 0˚.
Chart 5. Measures with α = 45˚ and β = 45˚.
Remark: we can do the same remark than this of the previous paragraph: it is not the polarization of the photons (X, Y) which has changed; it is only the angle α to measure them which has changed. More generally, we can say that, except with the particular case of α = 0 (or 180˚) and β = 0˚ (or 180˚), there would be between the measures on DA and DB decorrelation according to QM!
4.4. Probability
1) Let us first remind the definition of the probability of an event happening: it is the number of ways it can happen out of the total number of outcomes. In Quantum Mechanics,

2) If we take again the previous example of §4.3.b with 8 photon pairs, with the separators angles: α = 0˚ and β = 0˚




3) If we take again the previous example of §4.3.b with 8 photon pairs, but with the separators angles: α = 45˚ and β = 45˚

And then we cancheck that:



That means that with exactly the same 8 pairs of photons, probabilities will be different according we take a separator angle or another separator angle. The event the probability measure here is not the photons polarization, but it is the effect on photons detector by the separator angle.
4.5. Correlation Coefficient
In QM, it is defined a quantum correlation coefficient E(α;β) such as:

Remark: E(α,β) is different of the (mathematical) statistical correlation. E(α,β) can take any value in the interval [−1; +1]

When we apply this coefficient to:
- the first example (cf §4.4.b) with the 8 photons pairs:

it is said there is total “correlation” in QM.
- the second example (cf §4.4.c) with the “same” 8 photons pairs

it is said there is total “decorrelation” in QM.
With the examples (b) and (c), it is the same 8 photons pairs, but QM says on one hand there is total correlation and on the other hand there is total decorrelation about photons. In fact, it is depending of the angles of the separators. The quantum correlation coefficient E(α;β) does not measure the polarization of the photon, but the effect of the separators angles (α;β) on polarized photons.
4.6. Property of the Correlation Coefficient
1) Probability property
A property found in QM is

Results are shown in Figure 3.
2) Correlation coefficient property
Due to the random sequence:

So

And due to mathematical property on the angle:

And due to the randomsequence (remind −1 means no detection); by symmetry:

So

By definition of the Quantum correlation coefficient
Figure 3. Probability to get (+1; +1) in function of

Due to mathematical property on the angles

Results are shown in Figure 4.
Application: When α = β or when α = β + 180˚, E(α,β) = 1; it is said in QMthere is correlation.
Until here, all the results are determined; there is no uncertainty, no chance, no probabilities in the results.
3) Consequence on the correlation function S1:
Because,



4.7. Particular Angles of the Experiment
Let us have the angles for the separator A which can take either the value 0˚, or the value 45˚. To clearly distinguish them, we will call the first possible value α = 0˚ and the second possible value γ = 45˚. Idem for the separator B with the angles: β = 22.5˚ or δ = 67.5˚. Please have a look on Figure 5 & Chart 6.
If we use the property of Equation (25):

Figure 4. Quantum correlation coefficient E in function of
Figure 5. Angles of the separators.
Chart 6. Values of the quantum correlation coefficient E.



So,

4.8. The Combination
Definition of


It is only the QM theory which postulates that:

where (please check again the Conversion chart of §2.2)
-

-

This Equation (31) is not argued, not justified, and so it appears for us to be wrong!
Let us remind
- Equation (30) : S1 can reach the value 2.8
- Equations (2) and (4) called Bell’s inequality: S2 is equal or lower than 2
Then, due to the unjustified Equality (31) where

5. Conclusions
It is here proposed a conversion chart in order to better distinguish elements when necessary.
The main result of this paper is to distinguish the correlation function: the definition itself S1(α,γ,β,δ) on one side, and a property S2(a,c,b,d) on the other side. The equality between S1 and S2 is not obvious, not argued and maybe wrong.
The demonstration of the Bell’s inequalities violation could come from confusion between the definition S1 and a property S2 of the correlation function. And so it would mean that Bell’s inequalities violation is not strictly justified. Consequently, Albert Einstein, Boris Podolsky and Nathan Rosen with the ERP paradox could be right on the local hidden variable.
Acknowledgements
I would like to thank people who did the proofreading.
Cite this paper
OlivierSerret, (2015) A Chart of Conversion Supporting EPR Paradox vs. Bell’s Inequalities Violation. Journal of Modern Physics,06,1950-1960. doi: 10.4236/jmp.2015.613201
References
- 1. Einstein, A., Podolsky, B. and Rosen, N. (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?
http://www.drchinese.com/David/EPR.pdf - 2. Bell, J.S. (1964) On the Einstein Podolsky Rosen Paradox.
https://www.bibnum.education.fr/sites/default/files/texte-bell-epr.pdf - 3. Moatti, A. (2011) Les indispensables mathématiques et physiques pour tous. Editions Odile Jacob, 208-217.
- 4. Gribbin, J. (2010) Le chat de Schrödinger. Editions Flammarion, Paris.
- 5. Scarani, V. (2006) Initiation à la Physique Quantique. Editions Vuibert, Paris.
- 6. Aspect, A. (1983) Thèse de doctorat” 27 to 36.
http://tel.archives-ouvertes.fr/tel-00011844/ - 7. Serret, O. (2014) And If Bell’s Inequality Were Not Violated. Journal of Modern Physics, 5, 1360-1369.
http://dx.doi.org/10.4236/jmp.2014.514137






