Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

doi:10.4236/jsea.2012.510089

Paper Menu >>

Journal Menu >>

Journal of Software Engineering and Applications, 2012, 5, 764-776

http://dx.doi.org/10.4236/jsea.2012.510089 Published Online October 2012 (http://www.SciRP.org/journal/jsea)

Java Simulation of Au Diffusion in Si Affected by

Vacancies and Self-Interstitials: Partial Differential

Equations

Masami Morooka

Department of Electrical Engineering, Fukuoka Institute of Technology, Fukuoka, Japan.

Email: morooka@ee.fit.ac.jp

Received July 25th, 2012; revised August 28th, 2012; accepted September 10th, 2012

ABSTRACT

A Java program in a GUI environment has been developed for the numerical solution of basic partial differential equa-

tions and applied to Au diffusion in Si affected by vacancies and self-interstitials. Text fields of selected parameters for

the calculation are set on the display, and the calculation starts by checking the start button after putting values on the

text fields. The calculated results are plotted immediately after the finish of the calculation as the concentration profiles

of substitutional Au, interstitial Au, vacancies and self-interstitials, and their diffusion can be presented immediately,

resulting in the identification of the diffusion mechanism. By changing the values of the text fields, new results can be

represented immediately. The diffusion of Au in Si can be simulated correctly and easily by this program. Results from

the program for one set of conditions are shown, including images produced on the display.

Keywords: Numerical Solution; Partial Differential Equations; Simulation of Impurity Diffusion; Java; Simulation of

Partial Differential Equations

1. Introduction

Au atoms in Si occupy interstitial and substitutional sites,

and the substitutional Au exists in three states depending

on the heat treatment history [1]: high-temperature sub-

stitutional Au, low-temperature substitutional Au, and ag-

glomerations of substitutional Au. During the heat treat-

ment, high-temperature substitutional Au diffuses very

slowly itself and the change in its concentration is domi-

nated by an interchange mechanism with interstitial Au

and substitutional Au associated with vacancies [2] and

self-interstitials [3]. In this case, the concentrations of

substitutional Au, interstitial Au, vacancies and self-in-

terstitials can be obtained from four partial differential

equations [4,5]. The concentration of substitutional Au

exhibits a diffusion profile depending on the relative

contributions of vacancies and interstitial Si atoms [6].

The author has previously investigated Au diffusion us-

ing Java programming by obtaining a numerical solution

to a single partial differential equation obtained from the

above four differential equations under several approxi-

mations. This approach was adopted because of the dif-

ficulty of directly numerically solving the above four

partial differential equations due to the limitation in the

capacity of personal computers [7]. However, recently

the capacity of personal computers has been progressing

rapidly, and the author has been able to directly solve the

four partial differential equations involved in Au diffu-

sion by Java programming. As a result, the diffusion of

Au in Si can be simulated correctly and easily using Java

in a GUI (Graphical User Interface) environment.

2. Basic Partial Differential Equations for

Au Diffusion in Si

The basic diffusion equations for substitutional impuri-

ties, interstitial impurities, vacancies and self-interstitials

in the interchange mechanism of interstitial and substitu-

tional impurities associated with vacancies and self-in-

terstitials are given as



Vr iVVe sIe i SiIrI s,



NNKNKNNK NN



(1)





Vr iVVe sIe i SiIr I s

iiSSi0i

NNKNK NNK NN

DKNN



 

 

(2)





Vri VVe sFe SiFrV I

VVSSV0V

NNKNKNKN N

DKNN



 



(3)

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations 765





IeiSiIrIs FeSiFrVI

IISSI0I

NN KNNKN KNN

DKNN







SiLssV .NNNN (5)

Here, the terms caused by the internal sink-sources

such as dislocations in Equations (2)-(5) based on the site

conservation are added to the equations given in refer-

ence [4]. In above equations, N, t, x, K and D are concen-

tration, time, distance from surface, chemical reaction

constant and diffusion constant. The subscripts s, i, V, I, Si,

Vr, Ve, Ir, Ie, Ls, Fr, Fe, iSS, VSS, and

0 stand for substitutional

impurity, interstitial impurity, vacancy, self-interstitial,

Si atom at a lattice site, vacancy recombination, vacancy

emission, self-interstitial recombination, self-interstitial

emission, lattice site, recombination of Frenkel pair,

emission of Frenkel pair, emission and annihilation of

interstitial impurity at internal sink-sources, emission and

annihilation of vacancy at internal sink-sources, emission

and annihilation of self-interstitial at internal sink-sources,

and thermal equilibrium value. Each concentration is

normalized by its thermal equilibrium concentration and

the distance, x, is normalized by the specimen thickness,

L, for easier numerical calculation.



s1 iVVess3iSis4Is ,

CaCCK CaCCaCC







(6)

 



i1 iVi2si3iSii4Is

i5iSS i

21,

CaCC aCaCCaCC

aKC





 



(7)





V1 iVV2sV3SiV4VI

V5VSS V

21,

CaCC aCaCaCC

aKC





 



(8)





I1iSiI2IsI3SiI4VI

I5ISS I

21,

CaCCaCCaC aCC

aKC









(9)

SiSi1Si2sSi3V.CaaCaC  (10)

Here, C is the normalized concentration and ξ is x/L.

The coefficients are given as follows.

Vr i0 V0

KNN

 (11)

Ie i0 Si0

KNN

 (12)

s4IrI0,aKN



(13)

i1VrV0 ,aKN



(14)

Ve s0

 (15)

i3IeSi0 ,aKN



(16)

IrI0 s0

KNN

 (17)

i5 2,

 (18)

V1Vri0 ,aKN



(19)

Ve s0

 (20)

Fe Si0

 (21)

V4FrI0,aKN



(22)

V5 2,

 (23)

Ie i0 Si0

KNN

 (24)

I2Irs0 ,aKN



(25)

Fe Si0

 (26)

I4FrV0 ,aKN



(27)

I5 2,

 (28)

Si1

Si0

 (29)

Si2

Si0

 (30)

Si3

Si0

 (31)

3. Crank-Nicolson’s Implicit Method and

Gauss-Seidel’s Iteration Method

The partial differential terms in the equations are approxi-

mated to the difference equations by Crank-Nicolson’s

implicit method. Namely, an advanced differential-dif-

ference approximation is used for the partial differential

by time, ∂C/∂t, and a neutral differential-difference ap-

proximation is used for the partial differential by distance,

∂2C/∂ξ2.

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

766

neutral value for the function of C, f(C), according to

Crank-Nicolson.

 



i,j+1 i,j

CCC







(32)







 





i,ji,j i-1,j

i,j+1i,j+1i-1,j+1

CCCC

CCC









(33)











 





siVISi

s i,ji(i,jV i,jI i,jSi i,j

s i,j+1ii,j+1V i,j+1Ii,j+1Sii,j+1

,, ,,

1,,,,

,, ,,

fCCC CC

fC CCC C

fCC CC C



.

(34)

Here, k and h are the differences of t and ξ, respec-

tively. We define









i,j

,i, jCtChkC



, where i =

0, 1, 2, 3, ···, imax and j = 0, 1, 2, 3, ···, jmax. We use the

We obtain the value of Cs at



si,j1

j1 ,tkC



 , by

applying Equations (32)-(34) to Equation (6).



 



  



s1s2 s34

i i,j+1V i,j+1i i,jVi,js i,ji i,j+1Sii,j+1i i,jSi i,jI i,js i,js i,j

si,j+1

s2 s4s2 s4

Ii,j+1 Ii,j+1

()()

bCCCCbCbCCC CbCCC

CbbC bbC

 



 (35)

Here, s1s1 2bka, s2Ve 2bkK, s3s3 2bka and s4s4 2bka



. We obtain



ii,j1



, and



Vi,j 1

C





Ii,j 1



applying Equations (32)-(34) to Equations (7)-(9), respectively.



 



 

 

i1i(i,j)V(i,j) i2s(i,j)i3i(i,j)Si(i,j) i4I(i,j)s(i,j)

s i,j+1I i,j+1si,j+1

ii,j+1

i1 i3i5i6i1 i3i5i6

V i,j+1Si i,j+1V i,j+1Si i,j+1

i5 i i+1,ji i,ji i-1,ji

(+) ()

1++2 1++2

{(2) (

bCCbCCbCCb CCCC

CbCbCb bbCbCb b

bCCCC



 



 



 

 



i+1,j+1i i,j+1i i-1,j+1i i,ji i,j

i1 i3i5i6i1i3i5i6

V i,j+1Si i,j+1V i,j+1Si i,j+1

2)}(2)

1+ +21+ +2

CC bCC

bC bCbbbC bCbb

 





(36)



 

 

 

 

 

V1 V2V3V4

i i,jV i,jsi,j+1s i,jSii,j+1Si i,jVi,jI i,j

Vi,j+1

V1V4V5 V6V1V4V5V6

i i,j+1I i,j+1i i,j+1I i,j+1

V5 V i+1,jV i,jV i-1,jVi+1,j+1V i,j+1V i-1,j+1

(+)( )

1++21++2

{(2) (2)

bC Cb CCb CCbCC

CbCbC bbbCbC bb

bCC CCCC



 



 



 

V6 Vi,j Vi,j

V1 V4V5V6V1 V4V5V6

i i,j+1Ii,j+1i i,j+1Ii,j+1

}(2),

1++21+ +2

bC C

bC bCbbbC bCbb







(37)



  

 

 

 

 

I1I2 I3I4

i i,j+1Si i,j+1ii,jSi i,jIi,js i,jSi i,j+1Si i,jV i,jI i,j

Ii,j+1

I2I4I5I6I2I4I5 I6

s i,j+1V i,j+1s i,j+1V i,j+1

I5 Ii+1,jIi,j Ii-1,jIi+1,j+1Ii,j

()()

1++2 1++2

{(2) (2

bCCCCbCCbC CbCC

CbCbCbbbCbCbb

bCC CCC

 





 



 

 

+1Ii-1,j+1Ii,jIi,j

I2I4I5I6I2I4I5I6

s i,j+1V i,j+1s i,j+1V i,j+1

)}(2 ).

1++2 1++2

CbCC

bCbCb bbCbCb b







(38)

initial values, for example C(i+1,j+1) = . The cal-

C(i+1, j+1)

(1)

Here, i1i1 2bka, i2i2 2bka, i3i32bka,

i4i4 2bka,



i5i5 2bka h, i6iSS 2bkK,

V1V1 2bka, V2V2 2bka, V3V3 2bka,

V4V4 2bka,



V5V5 2bka h, V6VSS 2bkK,

I1I1 2bka, I2I2 2bka, I3I3 2bka, I4I4 2bka





culation is iterated until



 



i,j+1 i,j+1

i,j+1

, where e is



I5I5 2bka h and I6ISS 2bkK. We obtain a criterion value for the convergence, and



i,j+1



is then

 

Si1Si2Si3

Si i,j+1si,j+1V i,j+1 .CaaCaC  (39) used as an approximate value of .



i,j 1

C

from Equation (10). 4. Constants

Calculating the new value of a variable, such as



i,j 1



involves using unknown values of variables such as



i1,j1 in Equations (35)-(38). Here, we use Gauss-

Seidel iteration method, in which the previously calcu-

lated value is used as the initial value in the first calcula-

tion of from i = 0 to i = imax, for example,

. We note the value obtained from the

C



i1,j1





i,j 1

C



i1,j





The chemical reaction constants for the recombination

reactions based on random diffusion to sinks are given by

Damask and Dienes [8].



VriV iV

4π,KrDD



(40)





IrsI sI

4π,

rD D

(41)



first calculation as . For the second calculation of





i,j+1



FrVI VI

4π.



rD D (42)



i,j 1

C, , the first calculated values are used as



i,j+1

CHere, riV, rsI, and rVI are recombination distances be-

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations 767

tween interstitial impurity and vacancy, substitutional

impurity and self-interstitial, and vacancy and self-inter-

stitial. The chemical reaction constants for the creation

reactions are given from thermal equilibrium conditions

as follows,

Vr i0 V0

KNN

 (43)

Ir s0 I0

i0 Si0

KNN

 (44)

Fr I0 V0

Si0

KNN

 (45)

The chemical reaction constants of the internal sink-

sources, are given also by Damask and Dienes,

iSSc ic

4π,

rDN (46)

VSSc Vc

4π,

rD N (47)

ISSc I c

4π,

rDN (48)

for spherical internal sink-sources with a capture radius

of rc and a concentration of Nc, and as

iSSd i

2πln ,

KnD











(49)

VSSd V

2πln ,

KnD











(50)

ISSd I

2πln ,

KnD











(51)

for cylindrical internal sink-sources with a density of nd.

We used a single atomic distance of 0.234 nm for the

recombination distances and the capture radius, by as-

suming that the recombination and the capture occur for

the nearest neighbours. The thermal equilibrium concen-

tration of substitutional Au in Si is given by Collins,

Carlson and Gallagher [9]



22 3

1.76

8.15 10expcm,NkT









 (52)

and the diffusion constant and thermal equilibrium con-

centration of interstitial Au in Si is given by Willcox and

LaChapelle [10]



24 3

2.52

5.95 10expcm,NkT





 



 (53)



0.386

2.4410expcms.DkT



 







(54)

Values of the thermal equilibrium concentrations and

diffusion constants of vacancies and self-interstitials dif-

fer greatly between different authors, by as much as 6

orders of magnitude [11]. Therefore, it is difficult to

choose particular values. On the other hand, compara-

tively consistent products of the equilibrium concentra-

tion and the diffusion constant are available [12]. The

self-diffusion of host atoms is given by summing two

vacancy and self-interstitial terms [11]. In our case [6],

Si0 selfVV0II0

0.50.7273 ,ND DNDN



 (55)

take into account the correlation factors. Here, Dself is the

self-diffusion constant of Si atom, whose value does not

differ much among the authors [13], and we use aD times

value of the equation by Demond et al. [14],



self D

0.45

25expcms ,Da kT



 







(56)

where 0.1 ≤ aD ≤ 10. We chose the contribution rate of

self-interstitials, dIsd, as a constant related to the concen-

trations of vacancies and self-interstitials,

II I0

Isd

self Si0

fDN

dDN

 (57)

where, fI is the correlation factor of the self-interstitials.

Then the contribution rate of vacancies, dVsd, is obtained as

VVV0

Vsd I

self Si0

fDN

  (58)

where, fV is the correlation factor of the vacancies. In our

case, fI = 0.7273 and fV = 0.5. A value of either one of the

equilibrium concentrations or a diffusion constant is nec-

essary in order to fix both of them from Equations (57)

and (58). It is better to use a diffusion constant as it has a

true physical nature, whereas fixing a equilibrium con-

centration at some arbitrary value can cause difficulties,

such as unrealistically small diffusion constant if that con-

tribution is in reality very small. We use aV times value of



1.47

10 expcms,Da kT











(59)

by Masters and Gorey [15], and aI times value of



0.4

10expcms,Da kT



 







(60)

by Tan and Gösele [16], where 0.1 ≤ aV ≤ 10 and 0.1 ≤ aI ≤

10. NSi0 is obtained by Equations (6) and (58),

Ls s0

Si0

Vsd self

NdD











(61)

NI0 and NV0 are obtained by Equations (57) and (58),

respectively.

Isd selfSi0

dD N

NfD

 (62)

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

768

Vsd selfSi0

dDN

NfD

 (63)

5. Selection of Parameters

The calculated results can be presented immediately as

figures by changing the value of the text fields. We select

T, L, dIsd, cr and jmax as the values of the text fields, where

cr indicates the ratio of k to h, and

k (64)

Here, cr = 1 is the condition of convergence in the ex-

plicit method. Such a limitation for the convergence is

not necessary in the implicit method, but the calculation

does not converge in the Gauss-Seidel iteration if we use

too large a value of cr. It is better to use a larger value of

cr to provide a shorter computing time until a required

diffusion time is achieved and then it is better to choose a

larger convergence value after a tentative calculation with

a small jmax using several cr values.

6. Boundary and Initial Conditions

The surface concentration of impurities during heat treat-

ment for impurity diffusion differs depending on the sur-

face conditions [17]. Therefore, we adopt a surface con-

dition with sufficient impurities to put the boundary con-

ditions of the surface into their equilibrium concentra-

tions, and the surface concentrations of vacancies and

self-interstitials should be at their equilibrium concentra-

tions due to the presence of sufficient sink-sources of the

surface. The boundary conditions at the other back sur-

face are the same as the top surface mentioned above,

and we put i = imax at x = L/2 and the concentrations at

max is equal to those at max . We use the

boundary conditions such as the thermal equilibrium con-

centration at i = 0 and the same concentration at

and ii .

ii 1

ii 1

max max

The initial concentrations of impurities contributing to

impurity indiffusion depend on the quality of the as-

grown crystal, and we used 5 × 1010 cm–3 as the initial

concentration of substitutional impurities assuming the

quality as 99.9999999999%. We used 5.0 × 1010 × Ni0/Ns0

cm–3 as the initial concentration of interstitial impurities.

The initial concentration of substitutional impurities con-

tributing to out-diffusion can be set to the measured value

after the pre-indiffusion of the impurities and that of in-

terstitial impurities is set to the equilibrium concentration

at the pre-indiffusion temperature. The initial concentra-

tions of vacancies and self-interstitials in impurity indif-

fusion depend on the growth rate and on the longitudinal

temperature gradient near the crystallization front [18],

and we used NV ≤ 7.3 × 1012 cm–3, NI ≤ 2.6 × 1013 cm–3

[11]. We used NV = a × 7.3 × 1012 cm–3 and NI = b × 2.6 ×

1013 cm–3 as the initial concentrations for impurity indif-

fusion, here, a ≤ 1 and b ≤ 1. Those for impurity

out-diffusion can be set as the thermal equilibrium con-

centrations at the temperature for the pre-indiffusion heat-

treatment.

1

7. Java Simulation

One example of the program used here is shown below.

The function of the main part of program is written as a

comment line. Five text fields for temperature T, thick-

ness L, fraction of interstitial mechanism dIsd, the ratio of

k to h, cr, and number of calculations (to determine the

time) jmax are set on the display, and the calculation starts

by checking the start button after putting the value in the

text fields. The results are shown immediately as figures

on the display after the end of the calculation, and the

calculated results can be identified immediately. By

changing the values of the text fields, the new results can

be again be identified immediately. The distributions of

the logarithmic concentrations of Cs, Ci, CV, CI and CSi

are plotted on the display automatically in the range from

(xxmini,yymi ni) to (xxmax,yymax ). Six distributions at j = 0, j

= jmax/5, j = 2 × jmax/5, j = 3 × jmax/5, j = 4 × jmax/5 and j =

jmax for each concentration are plotted in our case. One of

the computed results for the indiffusion process is shown

in Figure 1 as an image on the display, and that for the

annealing is shown in Figure 2. The diffusion mecha-

nism based on the simulations will be investigated in

another paper.

/* Numerical solution (Implicit and Gauss-Sedel method)

of basic partial differential equations for Au diffusion in

Si and graphics by Java (2012.05.25 M.Morooka) */

/*<applet code="DiffAuSi200JSEA.class" width=901

height=800></applet>*/

import java.applet.Applet;

import java.awt.*;

import java.awt.event.*;

public class DiffAuSi200JSEA extends Applet imple-

ments ActionListener {

TextField txt1,txt2,txt3,txt4,txt5;

Button btn1,btn2,btn3;

Label lb1,lb2,lb3,lb4,lb5;

String moji;

double temp,dIsd,xL,cr; int jmax;

public void init() {

lb1 = new Label("temperature (C) temp =");

add(lb1);

txt1 = new TextField(8);

add(txt1);

lb2 = new Label("fraction of Interstitial mechanism

dIsd =");

add(lb2);

txt2 = new TextField(8);

add(txt2);

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations 769

lb3 = new Label("thickness (cm) xL =");

add(lb3);

txt3 = new TextField(8);

add(txt3);

lb4 = new Label("increment ratio of t (dt=0.5*cr*dx*dx),

cr =");

add(lb4);

txt4 = new TextField(8);

add(txt4);

lb5 = new Label("No. of calculation t, jmax =");

add(lb5);

txt5 = new TextField(8);

add(txt5);

btn1 = new Button("start");

btn1.addActionListener(this);

add(btn1);

btn2 = new Button("clear");

btn2.addActionListener(this);

add(btn2);

btn3 = new Button("end");

btn3.addActionListener(this);

add(btn3);

}

public void actionPerformed(ActionEvent e) {

moji = e.getActionCommand();

repaint();

}

public void paint(Graphics g) {

if (moji=="start") {

lb1.setText("temperature (C) temp =");

lb2.setText("fraction of Interstitial mechanism dIsd

=");

lb3.setText(" thickness (cm) xL =");

lb4.setText("increment ratio of t (dt=0.5*cr*dx*dx), cr

=");

lb5.setText("No. of calculation t, jmax =");

try {

temp = Double.parseDouble(txt1.getText());

dIsd = Double.parseDouble(txt2.getText());

xL = Double.parseDouble(txt3.getText());

cr = Double.parseDouble(txt4.getText());

jmax = Integer.parseInt(txt5.getText());

}

catch (NumberFormatException ex) {

lb1.setText("input error");

}

int i,j;

// INPUT imax, i=0 at x=0, i=imax at x =0.5

(0-----imax)

int imax; imax = 50;

double[] cs0 = new double[imax+2];

double[] cs1 = new double[imax+2];

double[] cs1Old = new double[imax+2];

double[] cAi0 = new double[imax+2];

double[] cAi1 = new double[imax+2];

double[] cAi1Old = new double[imax+2];

double[] cV0 = new double[imax+2];

double[] cV1 = new double[imax+2];

double[] cV1Old = new double[imax+2];

double[] cI0 = new double[imax+2];

double[] cI1 = new double[imax+2];

double[] cI1Old = new double[imax+2];

double[] cSi0 = new double[imax+2];

double[] cSi1 = new double[imax+2];

double[] cSi1Old = new double[imax+2];

// INPUT print out number between j=1 and jmax

int jpn,jpm;

jpn = 5;

jpm = jmax/jpn;//interval of print out j=1 - jmax

double[][] csOut = new double[imax+2][jpn+2];

double[][] cAiOut = new double[imax+2][jpn+2];

double[][] cVOut = new double[imax+2][jpn+2];

double[][] cIOut = new double[imax+2][jpn+2];

double[][] cSiOut = new double[imax+2][jpn+2];

double[] diftime = new double[jpn+2]; //diffusion time

// INPUT constants cs0,dself,dV,aD

double cN0,k,kT,csN0,cAiN0,dAi,dself,dVsd,dV,fV,

cVN0,fI,dI,cIN0,cSiN0;

cN0 = 4.9968e22; //density of site in Si

k=8.617386e-5; kT=k*(temp+273.15);

// INPUT surface concentration

dVsd=1.0-dIsd;

csN0=8.15e22*Math.exp(-1.76/kT); //Ns0 by Collins

cAiN0=5.95e24*Math.exp(-2.52/kT); //Ni0 by Willcox

dAi=2.44e-4*Math.exp(-0.386/kT); //Di by Willcox

double aD; aD=10.0;

dself=aD*25.0*Math.exp(-4.50/kT); //Dself by Demond

fV=0.5; fI=0.7273;

double aV,aI; aV=10.0; aI = 1.0;

dV=aV*10.0*Math.exp(-1.47/kT); // DV by Masters

dI=aI*1.0e-5*Math.exp(-0.4/kT); // DI by Tan

cSiN0=(cN0-csN0)/(1.0+dVsd*dself/(fV*dV)); //NSi0

cVN0=dVsd*dself*cSiN0/(fV*dV); // NV0

cIN0=dIsd*dself*cSiN0/(fI*dI); // NI0

// INPUT initial value of cs,cAi,cV,cI,cSi at t=0

double csNi,cAiNi,cVNi,cINi,cSiNi;

double cs0i,cAi0i,cV0i,cI0i,cSi0i;

double ai,abi,aVi,aIi;

ai=0.5;

csNi=7.5e16;//experimental varue at annealing

csNi=ai*5.0e10;//at indiffusion

cs0i = csNi/csN0;

abi=0.5;

cAiNi=5.95e24*Math.exp(-2.52e0/(k*(1150+273.15)));

// at annealing (solid solubility at pre-indiffusion 1150C)

cAiNi=abi*csNi*cAiN0/csN0;// at indiffusion

cAi0i = cAiNi/cAiN0;

aVi=1.0;

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

770

cVNi=4.2e12;//at annealing (NV0 at pre-indiffusion)

cVNi=aVi*7.3e12;//at indiffusion

cV0i = cVNi/cVN0;

aIi=1.0;

cINi=5.2e14;//at annealing (NI0 at pre-indiffusion)

cINi=aIi*2.6e13;//at indiffusion

cI0i = cINi/cIN0;

cSi0i = (cN0-csNi-cVNi)/cSiN0;

// INPUT boundary values of cs,cAi,cV,cI,cSi at x=0

double c00,cs00,cAi00,cV00,cI00,cSi00;

c00 = 1.0;

cs00 = c00; cAi00 = c00;

cV00 = c00; cI00 = c00;

cSi00 = (cN0-cs00*csN0-cV00*cVN0)/cSiN0;

double h,r,kk,tmax;

h = 0.5/(double)imax; //increment of x/xL

r=0.5*cr; kk=r*h*h; //increment of t, dt=kk

tmax=kk*(double)jmax; //j=0 at t=0, j=jmax at t=tmax

double arcAi,aNc,aKAiSS,aNd,arcV,aKVSS,arcI,

aKISS,arAiV,aKVr,aKVe,arsI,aKIr,aKIe,arVI,aKFr,a

KFe;

// emission and anihiration of int.Au into/from sink-

sources

arcAi=2.34e-8; //capture radius of int.Au

// INPUT sink-source density aNc

aNc=0.0; aKAiSS=4.0*Math.PI*arcAi*aNc*dAi;

// emission and anihiration of vacancy and int.Si

into/from sink-sources

// INPUT dislocation density aNd (cm-2)

aNd=20000.0;

arcV=2.34e-8; //capture distance of vacancy

aKVSS=2.0*Math.PI*aNd*dV*Math.log(1.0/(arcV*

Math.sqrt(Math.PI*aNd)));

if(aNd<=0.1){

aKVSS=0.0;

}

arcI=2.34e-8; //capture radius of int.Si

aKISS=2.0*Math.PI*aNd*dI*Math.log(1.0/(arcI*Math.

sqrt(Math.PI*aNd)));

if(aNd<=0.1){

aKISS=0.0;

}

// recombination rate of int.Au and vacancy

arAiV=2.34e-8; //recombination distance

aKVr=4.0*Math.PI*arAiV*(dAi+dV);

aKVe=aKVr*cAiN0*cVN0/csN0;

// recombination rate of subt.Au and int.Si

arsI=2.34e-8; //recombination distance

aKIr=4.0*Math.PI*arsI*dI;

aKIe=aKIr*cIN0*csN0/(cAiN0*cSiN0);

// recombination rate of vacancy and int.Si

arVI=2.34e-8; //recombination distance

aKFr=4.0*Math.PI*arVI*(dV+dI);

aKFe=aKFr*cIN0*cVN0/cSiN0;

// symplify of the constants

double as1,as3,as4,aAi1,aAi2,aAi3,aAi4,aAi5;

as1=aKVr*cAiN0*cVN0/csN0;

as3=aKIe*cAiN0*cSiN0/csN0;

as4=aKIr*cIN0;

aAi1=aKVr*cVN0; aAi2=aKVe*csN0/cAiN0;

aAi3=aKIe*cSiN0;

aAi4=aKIr*cIN0*csN0/cAiN0; aAi5=dAi/(xL*xL);

double aV1,aV2,aV3,aV4,aV5,aI1,aI2,aI3,aI4,aI5;

aV1=aKVr*cAiN0; aV2=aKVe*csN0/cVN0;

aV3=aKFe*cSiN0/cVN0;

aV4=aKFr*cIN0; aV5=dV/(xL*xL);

aI1=aKIe*cAiN0*cSiN0/cIN0; aI2=aKIr*csN0;

aI3=aKFe*cSiN0/cIN0;

aI4=aKFr*cVN0; aI5=dI/(xL*xL);

double a05,a06,a07;

a05 = cN0/cSiN0; a06 = csN0/cSiN0;

a07 = cVN0/cSiN0;

// symplify of the constants 2

double bs1,bs2,bs3,bs4,bAi1,bAi2,bAi3,bAi4,bAi5,

bAi6;

bs1=kk*as1/2.0; bs2=kk*aKVe/2.0; bs3=kk*as3/2.0;

bs4=kk*as4/2.0;

bAi1=kk*aAi1/2.0; bAi2=kk*aAi2/2.0;

bAi3=kk*aAi3/2.0;

bAi4=kk*aAi4/2.0; bAi5=kk*aAi5/(2.0*h*h);

bAi6=kk*aKAiSS/2.0;

double bV1,bV2,bV3,bV4,bV5,bV6,bI1,bI2,bI3,bI4,

bI5,bI6;

bV1=kk*aV1/2.0; bV2=kk*aV2/2.0; bV3=kk*aV3/2.0;

bV4=kk*aV4/2.0; bV5=kk*aV5/(2.0*h*h);

bV6=kk*aKVSS/2.0;

bI1=kk*aI1/2.0; bI2=kk*aI2/2.0; bI3=kk*aI3/2.0;

bI4=kk*aI4/2.0; bI5=kk*aI5/(2.0*h*h);

bI6=kk*aKISS/2.0;

// boundary conditions

cs0[0] = cs00; cs1[0] = cs00;

cAi0[0] = cAi00; cAi1[0] = cAi00;

cV0[0] = cV00; cV1[0] = cV00;

cI0[0] = cI00; cI1[0] = cI00;

cSi0[0] = cSi00; cSi1[0] = cSi00;

for (j=0;j<=jpn;++j) {

csOut[0][j]=cs00;

cAiOut[0][j]=cAi00;

cVOut[0][j]=cV00;

cIOut[0][j]=cI00;

cSiOut[0][j]=cSi00;

}

// initial conditions

for (i=1;i<=imax+1;++i) {

cs0[i] = cs0i; cs1[i] = cs0i; csOut[i][0] = cs0i;

cAi0[i] = cAi0i; cAi1[i] = cAi0i;

cAiOut[i][0] = cAi0i;

cV0[i] = cV0i; cV1[i] = cV0i; cVOut[i][0] = cV0i;

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations 771

cI0[i] = cI0i; cI1[i] = cI0i; cIOut[i][0] = cI0i;

cSi0[i] = cSi0i; cSi1[i] = cSi0i; cSiOut[i][0] = cSi0i;

}

diftime[0] = 0.0;

// Crank Nicolson implicit method

int jpd,jp; jpd = 0; jp = 0;

// INPUT maximum of iteration in Gauss-Sedel

int mgs; mgs=100;

// INPUT convergence value in Gauss-Sedel

double egs; egs=1.0e-10;

int igs;

double

fs1,fs2,gs,fAi1,fAi2,fAi3,fAi4,gAi,fV1,fV2,fV3,

fV4,gV,fI1,fI2,fI3,fI4,gI;

double ecm,ecs,ecsm,ecAi,ecAim,ecV,ecVm,ecI,ecIm,

ecSi,ecSim;

ecm = 0.0;

for (j=0;j<=jmax;j++) {

// Gauu-Seidel iteration

igs=0;

do {

igs=igs+1;

if(igs>=mgs){

System.out.println("Gauss-Seidel dosn't converge, mgs

= "+mgs+"egs = "+egs+"ecm = "+ecm);

System.exit(0);

}

ecsm=0.0; ecAim=0.0; ecVm=0.0; ecIm=0.0;

ecSim=0.0;

for (i=1;i<=imax;i++) {

cs1Old[i]=cs1[i];

cAi1Old[i]=cAi1[i];

cV1Old[i]=cV1[i];

cI1Old[i]=cI1[i];

cSi1Old[i]=cSi1[i];

if(i==imax) {

cs1[imax+1]=cs1[imax-1];

cAi1[imax+1]=cAi1[imax-1];

cV1[imax+1]=cV1[imax-1];

cI1[imax+1]=cI1[imax-1];

cSi1[imax+1]=cSi1[imax-1];

cs1Old[imax+1]=cs1Old[imax-1];

cAi1Old[imax+1]=cAi1Old[imax-1];

cV1Old[imax+1]=cV1Old[imax-1];

cI1Old[imax+1]=cI1Old[imax-1];

cSi1Old[imax+1]=cSi1Old[imax-1];

}

fs1=bs1*(cAi1[i]*cV1[i]+cAi0[i]*cV0[i])-bs2*

cs0[i];

fs2=bs3*(cAi1[i]*cSi1[i]+cAi0[i]*cSi0[i])-bs4*

cI0[i]*cs0[i];

gs=1.0+bs2+bs4*cI1[i];

cs1[i]=(fs1+fs2+cs0[i])/gs;

fAi1=-bAi1*cAi0[i]*cV0[i]+bAi2*(cs1[i]+

cs0[i]);

fAi2=-bAi3*cAi0[i]*cSi0[i]+bAi4*(cI1[i]*

cs1[i]+cI0[i]*cs0[i]);

fAi3=bAi5*(cAi0[i+1]-2.0*cAi0[i]+cAi0[i-1]+

cAi1[i+1]+cAi1[i-1]);

fAi4=bAi6*(2.0-cAi0[i]);

gAi=1.0+bAi1*cV1[i]+bAi3*cSi1[i]+2.0*bAi5

+bAi6;

cAi1[i]=(fAi1+fAi2+fAi3+fAi4+cAi0[i])/gAi;

fV1=-bV1*cAi0[i]*cV0[i]+bV2*(cs1[i]+cs0[i]);

fV2=bV3*(cSi1[i]+cSi0[i])-bV4*cV0[i]*cI0[i];

fV3=bV5*(cV0[i+1]-2.0*cV0[i]+cV0[i-1]+

cV1[i+1]+cV1[i-1]);

fV4=bV6*(2.0-cV0[i]);

gV=1.0+bV1*cAi1[i]+bV4*cI1[i]+2.0*bV5+

bV6;

cV1[i]=(fV1+fV2+fV3+fV4+cV0[i])/gV;

fI1=bI1*(cAi1[i]*cSi1[i]+cAi0[i]*cSi0[i])-bI2*

cI0[i]*cs0[i];

fI2=bI3*(cSi1[i]+cSi0[i])-bI4*cV0[i]*cI0[i];

fI3=bI5*(cI0[i+1]-2.0*cI0[i]+cI0[i-1]+cI1[i+1]+

cI1[i-1]);

fI4=bI6*(2.0-cI0[i]);

gI=1.0+bI2*cs1[i]+bI4*cV1[i]+2.0*bI5+bI6;

cI1[i]=(fI1+fI2+fI3+fI4+cI0[i])/gI;

cSi1[i] = a05-a06*cs1[i]-a07*cV1[i];

ecs=Math.abs((cs1[i]-cs1Old[i])/cs1Old[i]);

ecsm=Math.max(ecs,ecsm);

ecAi=Math.abs((cAi1[i]-cAi1Old[i])/

cAi1Old[i]);

ecAim=Math.max(ecAi,ecAim);

ecV=Math.abs((cV1[i]-cV1Old[i])/cV1Old[i]);

ecVm=Math.max(ecV,ecVm);

ecI=Math.abs((cI1[i]-cI1Old[i])/cI1Old[i]);

ecIm=Math.max(ecI,ecIm);

ecSi=Math.abs((cSi1[i]-cSi1Old[i])/cSi1Old[i]);

ecSim=Math.max(ecSi,ecSim);

ecm=Math.max(ecsm,ecAim);

ecm=Math.max(ecm,ecVm);

ecm=Math.max(ecm,ecIm);

ecm=Math.max(ecm,ecSim);

}

if(ecm<egs) {

for (i=1;i<=imax+1;i++) {

cs0[i]=cs1[i];

cAi0[i]=cAi1[i];

cV0[i]=cV1[i];

cI0[i]=cI1[i];

cSi0[i]=cSi1[i];

}

}while(ecm>=egs);

// Gauss Seidel iteration end

// print out values between j=0 (t=0) and j=jmax

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

772

jpd=jpd+1;

if(jpd>=jpm){

jpd=0;

jp=jp+1;

for (i=0;i<=imax;i++) {

csOut[i][jp]=cs1[i];

cAiOut[i][jp]=cAi1[i];

cVOut[i][jp]=cV1[i];

cIOut[i][jp]=cI1[i];

cSiOut[i][jp]=cSi1[i];

}

diftime[jp]=jp*jpm*kk;

}

// Crank Nicolson end

// graphics

// maxmum and minimum values

double xmini,xmax,y1mini,y1max,y2mini,y2max,

y3mini,y3max,y4mini,y4max,y5mini,y5max,ymini,ym

ax;

xmini = 0.0; xmax = 0.5;

y1mini = csOut[0][0]; y1max = csOut[0][0];

y2mini = cAiOut[0][0]; y2max = cAiOut[0][0];

y3mini = cVOut[0][0]; y3max = cVOut[0][0];

y4mini = cIOut[0][0]; y4max = cIOut[0][0];

y5mini = cSiOut[0][0]; y5max = cSiOut[0][0];

for (j=0;j<=jpn;j++) {

for (i=0;i<=imax; i++) {

y1max = Math.max(csOut[i][j],y1max);

y1mini = Math.min(csOut[i][j],y1mini);

y2max = Math.max(cAiOut[i][j],y2max);

y2mini = Math.min(cAiOut[i][j],y2mini);

y3max = Math.max(cVOut[i][j],y3max);

y3mini = Math.min(cVOut[i][j],y3mini);

y4max = Math.max(cIOut[i][j],y4max);

y4mini = Math.min(cIOut[i][j],y4mini);

y5max = Math.max(cSiOut[i][j],y5max);

y5mini =Math.min(cSiOut[i][j],y5mini);

}

ymini = Math.min(y1mini,y2mini);

ymini = Math.min(ymini,y3mini);

ymini = Math.min(ymini,y4mini);

ymini = Math.min(ymini,y5mini);

ymax = Math.max(y1max,y2max);

ymax = Math.max(ymax,y3max);

ymax = Math.max(ymax,y4max);

ymax = Math.max(ymax,y5max);

// Log(csOut),,,,,,

double[][] csOutLog = new double[imax+2][jpn+2];

double[][] cAiOutLog = new double[imax+2][jpn+2];

double[][] cVOutLog = new double[imax+2][jpn+2];

double[][] cIOutLog = new double[imax+2][jpn+2];

double[][] cSiOutLog = new double[imax+2][jpn+2];

for (j=0;j<=jpn;j++) {

for (i=0;i<=imax;i++) {

csOutLog[i][j]=Math.log(csOut[i][j])/Math.

log(1.0e1);

cAiOutLog[i][j]=Math.log(cAiOut[i][j])/Math.

log(1.0e1);

cVOutLog[i][j]=Math.log(cVOut[i][j])/Math.

log(1.0e1);

cIOutLog[i][j]=Math.log(cIOut[i][j])/Math.

log(1.0e1);

cSiOutLog[i][j]=Math.log(cSiOut[i][j])/Math.

log(1.0e1);

}

double y1miniLog,y1maxLog,y2miniLog,y2maxLog,

y3miniLog,y3maxLog ,y4miniLog,y4maxLog,y5 miniL

og,

y5maxLog,yminiLog,ymaxLog;

y1miniLog = Math.log(y1mini)/Math.log(1.0e1);

y1maxLog = Math.log(y1max)/Math.log(1.0e1);

y2miniLog = Math.log(y2mini)/Math.log(1.0e1);

y2maxLog = Math.log(y2max)/Math.log(1.0e1);

y3miniLog = Math.log(y3mini)/Math.log(1.0e1);

y3maxLog = Math.log(y3max)/Math.log(1.0e1);

y4miniLog = Math.log(y4mini)/Math.log(1.0e1);

y4maxLog = Math.log(y4max)/Math.log(1.0e1);

y5miniLog = Math.log(y5mini)/Math.log(1.0e1);

y5maxLog = Math.log(y5max)/Math.log(1.0e1);

yminiLog = Math.log(ymini)/Math.log(1.0e1);

ymaxLog = Math.log(ymax)/Math.log(1.0e1);

// painting boundary

int xxmini,xxmax,yymini,yymax;

xxmini = 100; xxmax = 850;

yymini = 100; yymax = 700;

// painting place

int[] xx = new int[imax+2];

int[][]yy1 = new int[imax+2][jpn+2];

int[][] yy2 = new int[imax+2][jpn+2];

int[][] yy3 = new int[imax+2][jpn+2];

int[][] yy4 = new int[imax+2][jpn+2];

int[][] yy5 = new int[imax+2][jpn+2];

double[] xt = new double[imax+2];

for (i=0;i<=imax;i++) {

xt[i] = xmini+(xmax-xmini)*(double)i/(double)imax;

}

double xxa,yy1a,yy2a,yy3a,yy4a,yy5a;

for (i=0;i<=imax;i++) {

xxa = (double)xxmini + (xt[i]-xmini)/(xmax-xmini)*(

(double)xxmax-(double)xxmini);

xx[i] = (int)xxa;

}

for (j=0;j<=jpn;j++) {

for (i=0;i<=imax;i++) {

yy1a =(double)yymax - (csOutLog[i][j]-yminiLog)

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations 773

/(ymaxLog-yminiLog)*(double)(yymax-yymini);

yy2a=(double)yymax- (cAiOutLog[i][j]-yminiLog)

/(ymaxLog-yminiLog)*(double)(yymax-yymini);

yy3a =(double)yymax- (cVOutLog[i][j]-yminiLog)

/(ymaxLog-yminiLog)*(double)(yymax-yymini);

yy4a =(double)yymax - (cIOutLog[i][j]-yminiLog)

/(ymaxLog-yminiLog)*(double)(yymax-yymini);

yy5a=(double)yymax- (cSiOutLog[i][j]-yminiLog)

/(ymaxLog-yminiLog)*(double)(yymax-yymini);

yy1[i][j] = (int)yy1a;

yy2[i][j] = (int)yy2a;

yy3[i][j] = (int)yy3a;

yy4[i][j] = (int)yy4a;

yy5[i][j] = (int)yy5a;

}

// painting

g.drawLine(xxmini,yymini,xxmini,yymax);

g.drawLine(xxmini,yymax,xxmax,yymax);

g.drawLine(xxmax,yymax,xxmax,yymini);

g.drawLine(xxmax,yymini,xxmini,yymini);

for (j=0;j<=jpn;j++) {

for (i=0;i<=imax-1; ++i) {

try {

g.setColor(Color.darkGray);

g.drawLine(xx[i],yy3[i][j],xx[i+1],yy3[i+1][j]);

g.setColor(Color.magenta);

g.drawLine(xx[i],yy4[i][j],xx[i+1],yy4[i+1][j]);

g.setColor(Color.black);

g.drawLine(xx[i],yy5[i][j],xx[i+1],yy5[i+1][j]);

g.setColor(Color.blue);

g.drawLine(xx[i],yy2[i][j],xx[i+1],yy2[i+1][j]);

g.setColor(Color.red);

g.drawLine(xx[i],yy1[i][j],xx[i+1],yy1[i+1][j]);

}

catch (ArrayIndexOutOfBoundsException ex) {}

}

int[] sdiftime = new int[jpn+1]; //diffusion time for

String[] s = new String[jpn+1];

for (j=0;j<=jpn;j++) {

sdiftime[j] = (int)diftime[j];

s[j] = Integer.toString(sdiftime[j]);

g.drawString("time("+j+") = "+s[j]+" (s)",xxmax-100,

yymax-15-15-15*j);

}

String s1; s1 = Double.toString(kk);

g.drawString("increment of time kk = "+s1+" (s)",

xxmax-200, yymax-15);

String scsmax,scsmini,scAimax,scAimini,scVmax,

scVmini,scImax,scImini,scSimax,scSimini;

float y1miniP,y1maxP,y2miniP,y2maxP,y3miniP,

y3maxP,y4miniP,y4maxP,y5miniP,y5maxP;

y1miniP = (float)y1mini; y1maxP = (float)y1max;

y2miniP = (float)y2mini; y2maxP = (float)y2max;

y3miniP = (float)y3mini; y3maxP = (float)y3max;

y4miniP = (float)y4mini; y4maxP = (float)y4max;

y5miniP = (float)y5mini; y5maxP = (float)y5max;

scsmax = Float.toString(y1maxP);

scsmini = Float.toString(y1miniP);

scAimax = Float.toString(y2maxP);

scAimini = Float.toString(y2miniP);

scVmax = Float.toString(y3maxP);

scVmini = Float.toString(y3miniP);

scImax = Float.toString(y4maxP);

scImini = Float.toString(y4miniP);

scSimax = Float.toString(y5maxP);

scSimini = Float.toString(y5miniP);

g.setColor(Color.darkGray);

g.drawString("cVmax = "+scVmax+"cVmini =

"+scVmini, xxmax-300, yymini+80);

g.setColor(Color.magenta);

g.drawString("cImax= "+scImax+"cImini = "+scImini,

xxmax-300, yymini+95);

g.setColor(Color.black);

g.drawString("cSimax = "+scSimax+"cSimini =

"+scSimini, xxmax-300, yymini+110);

g.setColor(Color.blue);

g.drawString("cAimax = "+scAimax+"cAimini =

"+scAimini, xxmax-300, yymini+65);

g.setColor(Color.red);

g.drawString("csmax = "+scsmax+" csmini

= "+scsmini, xxmax-300, yymini+50);

g.setColor(Color.black);

String s21,s22,s23,s24,s25;

double csimaxjp,cAiimaxjp,cVimaxjp,cIimaxjp,

cSiimaxjp;

csimaxjp = csN0*csOut[imax][jpn];

cAiimaxjp = cAiN0*cAiOut[imax][jpn];

cVimaxjp = cVN0*cVOut[imax][jpn];

cIimaxjp = cIN0*cIOut[imax][jpn];

cSiimaxjp = cSiN0*cSiOut[imax][jpn];

float csimaxjpP,cAiimaxjpP,cVimaxjpP,cIimaxjpP,

cSiimaxjpP;

csimaxjpP = (float)csimaxjp;

cAiimaxjpP = (float)cAiimaxjp;

cVimaxjpP = (float)cVimaxjp;

cIimaxjpP = (float)cIimaxjp;

cSiimaxjpP = (float)cSiimaxjp;

s21 = Float.toString(csimaxjpP);

g.drawString("csNat 0.5*xL and "+s[jpn]+" (s) =

"+s21, xxmax-290, yymax-180);

s22 = Float.toString(cAiimaxjpP);

g.drawString("cAiN at 0.5*xL and "+s[jpn]+" (s)=

"+s22, xxmax-290, yymax-165);

s23 = Float.toString(cVimaxjpP);

g.drawString("cVN at 0.5*xL and "+s[jpn]+" (s)=

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

774

"+s23, xxmax-290, yymax-150);

s24 = Float.toString(cIimaxjpP);

g.drawString("cIN at 0.5*xL and "+s[jpn]+" (s)=

"+s24, xxmax-290, yymax-135);

s25 = Float.toString(cSiimaxjpP);

g.drawString("cSi at 0.5*xL and "+s[jpn]+" (s)= "+s25,

xxmax-290, yymax-120);

String s31,s32,s33,s34,s35,s36,s37,s38;

float csN0P,cAiN0P,dAiP,cVN0P,dVP,cIN0P,dIP,

dselfP;

csN0P = (float)csN0;

cAiN0P = (float)cAiN0;

dAiP = (float)dAi;

cVN0P = (float)cVN0;

dVP = (float)dV;

cIN0P = (float)cIN0;

dIP = (float)dI;

dselfP = (float)dself;

String s31i,s32i,s34i,s36i;

float csNiP,cAiNiP,cVNiP,cINiP;

csNiP = (float)csNi;

cAiNiP = (float)cAiNi;

cVNiP = (float)cVNi;

cINiP = (float)cINi;

s31 = Float.toString(csN0P);

g.drawString("csN0 = "+s31+" (/cc)", xxmax-290,

yymax-375);

s31i = Float.toString(csNiP);

g.drawString("csNi= "+s31i+" (/cc)", xxmax-290, yy-

max-360);

s32 = Float.toString(cAiN0P);

g.drawString("cAiN0 = "+s32+" (/cc)", xxmax-290,

yymax-345);

s32i = Float.toString(cAiNiP);

g.drawString("cAiNi = "+s32i+" (/cc)", xxmax-290,

yymax-330);

s33 = Float.toString(dAiP);

g.drawString("dAi= "+s33+" (cm^2/s)", xxmax-290,

yymax-315);

s34 = Float.toString(cVN0P);

g.drawString("cVN0 = "+s34+" (/cc)", xxmax-290,

yymax-300);

s34i = Float.toString(cVNiP);

g.drawString("cVNi = "+s34i+" (/cc)", xxmax-290,

yymax-285);

s35 = Float.toString(dVP);

g.drawString("dV = "+s35+" (cm^2/s)", xxmax-290,

yymax-270);

s36 = Float.toString(cIN0P);

g.drawString("cIN0 = "+s36+" (/cc)", xxmax-290,

yymax-255);

s36i = Float.toString(cINiP);

g.drawString("cINi = "+s36i+" (/cc)", xxmax-290,

yymax-240);

s37 = Float.toString(dIP);

g.drawString("dI = "+s37+" (cm^2/s)", xxmax-290,

yymax-225);

s38 = Float.toString(dselfP);

g.drawString("dself = "+s38+" (cm^2/s)", xxmax-290,

yymax-210);

// scale and label

int xxp;

double xxpd;

xxpd = (xxmax-xxmini)/(xmax - xmini)*0.1;

xxp = (int)xxpd;

g.drawLine(xxmini,yymax,xxmini,yymax-10);

g.drawString("0.0", xxmini-10, yymax+20);

g.drawLine(xxmini+xxp,yymax,xxmini+xxp,yymax-

10);

g.drawString("0.1", xxmini+xxp-10, yymax+20);

g.drawLine(xxmini+xxp*2,yymax,xxmini+xxp*2,

yymax-10);

g.drawString("0.2", xxmini+xxp*2-10, yymax+20);

g.drawLine(xxmini+xxp*3,yymax,xxmini+xxp*3,

yymax-10);

g.drawString("0.3", xxmini+xxp*3-10, yymax+20);

g.drawLine(xxmini+xxp*4,yymax,xxmini+xxp*4,

yymax-10);

g.drawString("0.4", xxmini+xxp*4-10, yymax+20);

g.drawLine(xxmini+xxp*5,yymax,xxmini+xxp*5,

yymax-10);

g.drawString("0.5", xxmini+xxp*5-10, yymax+20);

int symini,symax,syy,yyp;

symini = (int)yminiLog; symax = (int)ymaxLog; syy =

symax - symini;

double yypd,yypa;

yypd = (yymax - yymini)/(ymaxLog - yminiLog);

yyp = (int)yypd;

int[] ly = new int[syy+2];

int[] yypp = new int[syy+2];

String[] sy = new String[syy+2];

for (i=0;i<=syy;i++) {

ly[i] =symini+i;

sy[i] = Integer.toString(ly[i]);

yypa =(double)yymax - ((double)ly[i]-yminiLog)/

(ymaxLog-yminiLog)*(double)(yymax-yymini);

yypp[i] = (int)yypa;

g.drawLine(xxmini,yypp[i],xxmini+10,yypp[i]);

g.drawString(sy[i], xxmini-25, yypp[i]+5);

g.drawString("10", xxmini-40, yypp[i]+15);

}

else if (moji=="end"){System.exit(0);}

if (moji=="clear") {

g.clearRect(0,0,901,800);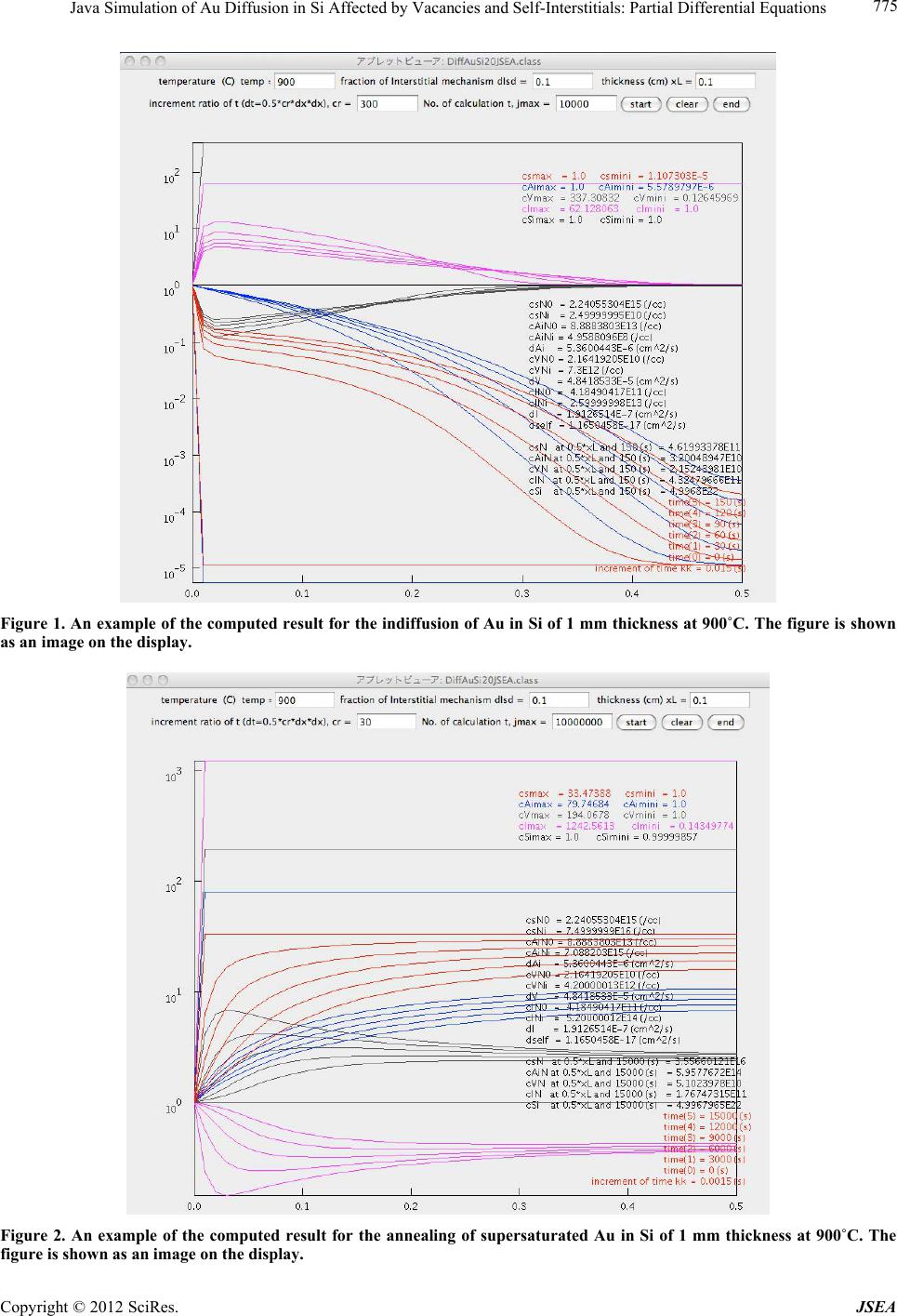

}

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

775

Figure 1. An example of the computed result for the indiffusion of Au in Si of 1 mm thickness at 900˚C. The figure is shown

as an image on the display.

Figure 2. An example of the computed result for the annealing of supersaturated Au in Si of 1 mm thickness at 900˚C. The

figure is shown as an image on the display.

Java Simulation of Au Diffusion in Si Affected by Vacancies and Self-Interstitials: Partial Differential Equations

776

8. Discussion and Results

The author has numerically solved Equations (6)-(10) by

Java programming and the distribution of each concen-

tration can be simulated correctly and easily using a usual

personal computer employing the GUI method of Java.

Namely, simultaneous partial different equations can be

calculated numerically under known boundary and initial

conditions by this program, and the distribution of each

unknown can be easily simulated. The time for the com-

putation until the required diffusion time depends on cr,

the ratio of k to h, and its maximum value for the con-

vergence depends on the constants in the equations. In

our case (dIsd = 0.1 and xL = 0.1 cm), the maximum value

is about 300 for the indiffusion at 900˚C and about 40 at

1160˚C. It is better to choose the largest cr value by ten-

tative calculations with small jmax values.

REFERENCES

[1] M. Morooka, H. Tomokage, H. Kitagawa and M. Yoshida,

“Three States of Substitutional Gold in Silicon,” Japa-

nese Journal of Applied Physics, Vol. 24, No. 2, 1985, pp.

133-136. doi:10.1143/JJAP.24.133

[2] W. C. Dash, “Gold-Induced Climb of Dislocations in Sili-

con,” Journal of Applied Physics, Vol. 31, No. 12, 1960,

pp. 2275-2283. doi:10.1063/1.1735538

[3] U. Gösele, W. Frank and A. Seeger, “Mechanism and

Kinetics of the Diffusion of Gold in Silicon,” Applied

Physics, Vol. 23, No. 4, 1980, pp. 361-368.

doi:10.1007/BF00903217

[4] M. Morooka and M. Yoshida, “Boundary and Initial

Conditions of Approximate Diffusion Equation for Gold

in Silicon,” Japanese Journal of Applied Physics, Vol. 28,

No. 3, 1989, pp. 457-463. doi:10.1143/JJAP.28.457

[5] H. Mehrer, “Diffusion in Solids,” Springer-Verlag, Berlin,

2007.

[6] M. Morooka and T. Kajiwara, “Indiffusion and Out-Dif-

fusion Profiles of Substitutional Au in Si Affected by

Self-Interstitials and Vacancies,” Japanese Journal of Ap-

plied Physics, Vol. 42, No. 6, 2003, pp. 3311-3315.

doi:10.1143/JJAP.42.3311

[7] M. Morooka, “Java Programming for Numerical Solution

of Nonlinear Diffusion Equation (Dissociative and Kick-

Out Mechanisms), Research Bulletin of Fukuoka Institute

of Technology, Vol. 35, No. 1, 2002, pp. 1-11.

[8] A. C. Damask and G. J. Dienes, “Point Defects in Metals,”

Gordon and Breach, London, 1963.

[9] C. B. Collins, R. O. Carlson and C. J. Gallagher, “Proper-

ties of Gold-Doped Silicon,” Physical Review, Vol. 105,

No. 4, 1957, pp. 1168-1173.

doi:10.1103/PhysRev.105.1168

[10] W. R. Willcox and T. J. LaChapelle, “Mechanism of Gold

Diffusion into Silicon,” Journal of Applied Physics, Vol.

35, No. 1, 1964, pp. 240-246. doi:10.1063/1.1713077

[11] W. Zulehner, “Oxygen-Related Defects and Microde-

fects,” In: M. Schulz, Ed., Impurities and Defects in

Group IV Elements and III-V Compounds, Spring-Verlag,

Berlin, 1989, pp. 391-396.

[12] W. Frank, U. Gösele, H. Mehrer and A. Seeger, “Diffu-

sion in Silicon and Germanium,” In: G. E. Murch and A.

S. Nowick, Eds., Diffusion in Crystaline Solids, Aca-

demic Press Inc., Orlando, 1984, pp. 129-134.

[13] M. Schulz, “Diffusion of Impurities,” In: M. Schulz, Ed.,

Impurities and Defects in Group IV Elements and III-V

Compounds, Spring-Verlag, Berlin, 1989, pp. 250-262.

[14] F. J. Demond, S. Kalbitzer, H. Mannsperger and H.

Damjantschitsch, “Study of Si Self-Diffusion by Nuclear

Techniques,” Physics Letters A, Vol. 93, No. 9, 1983, pp.

503-506. doi:10.1016/0375-9601(83)90641-2

[15] B. J. Masters and E. F. Gorey, “Photon-Enhanced Diffu-

sion and Vacancy Migration in Silicon,” Journal of Ap-

plied Physics, Vol. 49, No. 5, 1978, pp. 2717-2724.

doi:10.1063/1.325193

[16] T. Y. Tan and U. Gösele, “Point Defects, Diffusion Proc-

esses, and Swirl Defect Formation in Silicon,” Physics

and Astronomy, Vol. 37, No. 1, 1985, pp. 1-17.

[17] M. Morooka, Y. Nakabayashi and S. Matsumoto, “Effect

of Surface Condition on the Solid Solubility of Substitu-

tional Gold in the Out-Diffusion of Supersaturated Gold

in Silicon,” Defect and Diffusion Forum, Vol. 194-199,

2001, pp. 623-628.

[18] V. V. Voronkov, “The Mechanism of Swirl Defects For-

mation in Silicon,” Journal of Crystal Growth, Vol. 59,

No. 3, 1982, pp. 625-643.

doi:10.1016/0022-0248(82)90386-4