Journal of Quantum Information Science, 2012, 2, 90-101
http://dx.doi.org/10.4236/jqis.2012.23015 Published Online September 2012 (http://www.SciRP.org/journal/jqis)
A Comparative Study on Correlation Measures of Pure
Bipartite States through Incomparability
Amit Bhar1, Indrani Chattopadhyay2, Debasis Sarkar2
1Department of Mathematics, Jogesh Chandra Chaudhuri College, Kolkata, India
2Department of Applied Mathematic s, University of Calcut ta, Kolkata, India
Received July 20, 2012; revised July 30, 2012; accepted August 16, 2012
ABSTRACT
The entanglement of a pure bipartite state is uniquely measured by the von-Neumann entropy of its reduced density
matrices. Though it cannot specify all the non-local characteristics of pure entangled states. It was proven th at for every
possible value of entanglement of a bipartite system, there exists an infinite number of equally entangled pure states, not
comparable (satisfies Nielsen’s criteria) to each other. In this work, we investigate other correlation measures of pure
bipartite states that are able to differentiate the quantum correlations of the states with entropy of entanglement. In
Schmidt rank 3, we consider the whole set of states having same entanglement and compare how minutely such states
can be distinguished by other correlation measures. Then for different values of entanglement we compare the sets of
states belonging to the same entanglement and also investigate the graphs of different correlation measures. We extend
our search to Schmidt rank 4 and 5 also.
Keywords: LOCC; Entanglement; Incomparability
1. Introduction
Non-local features of quantum mechanics distinguishes it
from classical systems [1,2] and entanglement plays as a
non-local resource to perform various computational
tasks [3]. For this type of correlation between different
subsystems of a composite system, we require a well
defined process to quantify the amount of entanglement
of a state. In asymptotic sens e, both th e quantities needed
to prepare a pure bipartite state and distill pure entan-
glement from it [4,5], are equal with the von-Neumann
entropy of the reduced density matrices of the pure bi-
partite state and is usually called as the entanglement of
the state. Under stochastic local operations along with
classical communications (in short, LOCC) this reversi-
bility character and corresponding uniqueness of the
measure of entanglement of pure bipartite systems are
established [6]. It is found that the measures, not equiva-
lent in asymptotic sense, with von-Neumann entropy of
reduced density matrices for a pure system, are unable to
impose consistent ordering on the set of all quantum sys-
tems [7,8]. However the nature of evolution of composite
systems in case of pure bipartite states under determinis-
tic LOCC [9], are not very much clear to us. From the
quantification procedures one may conclude that entan-
glement is monotonic under LOCC [5,10,11]. Though it
does not help us to identify a unique measure of entan-
glement of pure bipartite systems. In case of mixed bi-
partite systems the situation is more complex; e.g. the
non-monotonicity of relative entropy of entanglement
with negativity and concurrence [12]. We proceed here to
find the existence of such ordering on different correla-
tion measures for lower rank pure bipartite states. For
this reason we critically observed the behaviour of pure
bipartite systems under deterministic LOCC. The possi-
bility of transforming one pure bipartite state to another
is determined by the majorization relation between the
Schmidt coefficients of the states specified by Nielsen’s
criteria [13]. It immediately suggests us that it could not
be always possible to transform a pure bipartite state to
every other pure bipartite state having a lower amount of
entanglement under deterministic LOCC. There are dif-
ferent measures of entanglement, that are not equivalent
with the von-Neumann entropy of reduced density ma-
trices for pure bipartite states, depend directly on coeffi-
cients of Schmidt decomposition of the state. Those
measures could generate some ordering on the systems
regarding possibility of its evolution under LOCC [14 ]. It
is established that considering only single copy of the
state, there are infinitely many measures generating dif-
ferent ordering on the Schmidt form of the state [15].
This work is directed to characterize and compare the
different correlation measures of entanglement under
preservation of entanglement. We begin with the study
C
opyright © 2012 SciRes. JQIS

A. BHAR ET AL. 91
from 3 × 3 pure bipartite system, then 2 concentrating on
4 × 4 system ended with an example of 5 × 5 system. For
higher and higher Schmidt rank, the behavior of lower
rank systems indicate chaotic behavior.
The brief outline of our work is as follows: in Section
2 we first recall the notion of entanglement of pure bipar-
tite states shared between two distant parties. Then we
discuss (Section 3) about the transformation of a pure
bipartite system under deterministic LOCC governed by
the majorization rule [16]. This is a nice ordering be-
tween Schmidt vectors of the associated states. This pro-
vides us the existence of pair of states, for which a higher
entangled state could not be always transformed to a
lower entangled one with certainty. In other words, their
entanglement are not comparable (precisely, comparabil-
ity means those states which would satisfy Nielsen’s cri-
teria). This concept of incomparability (i.e. violets Niel-
sen’s criteria, or in other words, the states are not con-
vertible under deterministic LOCC) indicate a non-local
feature not incorporated in the unique quantification
scheme of entanglement for pure bipartite systems. Con-
servation of entanglement under deterministic LOCC
necessarily produced a class of states of same Schmidt
rank, all mutually incomparable to each other (if not lo-
cally unitarily connected). We mention here this class of
states as equi-entangled. This work is mainly intended to
study different measures of correlations in equi-entan-
gled class. In Section 4, we recall the notions of such
correlations measures [17] of pure states and some of
their properties; e.g. Concurrence, Logarithmic Negativ-
ity, Linear Entropy, Rényi Entropy, Concurrence Hier-
archy, Maximum Fidelity, Robustness and some Dis-
tance measures that depend only on the largest Schmidt
coefficient of the state. In Section 5, we present all the
graphs of the measures against the largest Schmidt coef-
ficient and numerical tables for the correlation measures.
We concentrate on studying pure bipartite system where
the features of incomparability will be reflected neglect-
ing the effect of entanglement via preservation of entan-
glement under LOCC. In our whole work as we are
mainly concerned about pure bipartite states, we will use
occasionally the terms entanglement and entanglement of
formation, as they have the same value and later is more
operationally meaningful. In the appendix, we discuss
about some other effects of incomparability. We prepare
equal mixture of states from one equi-entangled class
with maximally mixed states of same rank. The resulting
mixed states sometimes preserve positivity under partial
transpose operation, i.e. the states are PPT [18,19].
Whereas in equal mixture with some other states from
the same class will generate NPT (negative under partial
transposition) states. Also, we show that the o ptimal tele-
portation fidelity, differ for different states of an equi-
entangled class.
2. Pure State Entanglement
The amount of entanglement of any pure bipartite state is
uniquely described by the von-Neumann entropy of the
reduced density matrices of the state and usually it is
known as entropy of entanglement or simply entangle-
ment of a pure bipartite state. It is established [20] that
any measure of entanglement for a bipartite state (pure or
mixed) is bounded by the limits defined by the two as-
ymptotic measures, entanglement of formation and dis-
tillable entanglement. For pure states both the measures
coincide with the quantity entropy of entanglement. It is
thus intuitive to con clude th at the non-local correlation of
any pure bipartite state is uniquely characterized by the
entropy of entanglement. However, recent observations
in bipartite pure states compel us to rethink about the
structure of state space with respect to the other measures
of correlations [21].
To understand the nature of pure state entanglement
we concentrate here on preservation of entanglement
under LOCC. It has been found that for every possible
amount of entanglement of non-maximally-entangled
bipartite state of Schmidt rank d, there exists infinite
number of equi-entangled pure bipartite states of same
Schmidt rank [21]. This is quite understandable from the
functional form of von-Neumann entropy, but what is
much more physically significant that all such states are
incomparable with each other. This is the key feature of
investigating further the pure state entanglement and its
evolution under local physical operations. We first recall
the concept of comparability and in comparability of pure
bipartite states.
3. Deterministic LOCC and Incomparability
Any pure bipartite state

of the joint Hilbert space
=AB
H
HH

have the Schmidt representation:
1
=d
iA B
i
ii 


 (1)
where


A
i and


B
i are orthonormal bases of the
local Hilbert spaces A
H
and
B
H
respectively. The set
of real numbers


i

, for , known as
Schmidt coefficients of the state, are just the square-root
of the eigenvalues of the reduced density matrices of the
state, satisfying i
=1
1,i
,2, ,id
0


 and 1
d
i

1
i

. The
number of Schmidt coefficients




min dim,dim
AB
dHH
known as the Schmidt rank of the pure bipartite state.
The Schmidt coefficients remain invariant under any
local unitary transformations on the pure bipartite state.
Thus they are expected to serve well as ingredients of
any good measure of entanglement.
The notion of incomparability is a direct consequence

A. BHAR ET AL.
92
of non-interconvertibility of pure bipartite states under
deterministic LOCC. Given a pure bipartite state

shared between two distant parties, suppose we want to
convert it into another pure bipartite state

under
deterministic LOCC. The Schmid t vectors corresponding
to the states ,


are


12
,, n


   and


12
,, m


   respectively(where 1ii0



0
for , =1,2, ,1in1jj




nm
for
=1,2, ,1jm and =1 =1
=1=
i
ij j


). Then from
Nielsen’s criterion [13],

can be converted to

with certainty under LOCC, denoted by

 , if
and only if


is majorized by


(denoted by



) and describe as
=1=1 , =1,2,,
kk
ii
ii
kd  

where we consider without loss of generality .
Now, if the above criteria fails for at least one , then
we usually denote it by
==dmn
k

 
, i.e.

is not
convertible to

under deterministic LOCC. Though
it may happen that

 . For some pair


,


whenever both

 
 and

  occur, then
we denote it by

 
 and call 
,


as a
pair of incomparable states. For system there
exists no incomparable pair of pure en tangled states. The
explicit form of incomparability criteria for a pair of pure
entangled states
22

,

in , with Schmidt
vectors 33


123
=, ,



and


12
=, 3 ,



is given
by:

 
 whenever either of the following pair of
relations
11223
1122 3
>>>
>> >
3
3









(2)
must hold. It is due to the fact that all incomparable pair
of states in are strongly incomparable. The
incomparability of pair of pure bipartite states could be
used as a detector of many unphysical operations [22].
This aspect motivates us to investigate the effect of
incomparability on different measures of correlations. In
[23] it has been established that there is pair of in-
comparable pure bipartite states for which entanglement
of formation is not in general monotone with
concurrence. Now, keeping in mind the criteria of deter-
ministic local transformation of pure bipartite systems,
one may ask about the effect on amount entanglement of
the states involved. The consequence of Nielsen’s result
is that if
33
of LOCC for this purpose. However, the mathematical
form of von-Neumann entropy could not suggest us in
either way. Interestingly it has been found that such
states must be incomparable with each other [21]. Any
pair of states, with different Schmidt vectors, from a
class of equally entangled states cannot be deter-
ministically converted to one another by LOCC. In other
words, pure bipartite states with equal amount of en-
tanglement, either they are locally unitarily connected or
incomparable to each other. In the next section, we recall
the notions of some correlation measures.
4. Correlation Measures
Firstly, we consider some well-known correlation mea-
sures, like, concurrence, linear entropy, logarithmic
negativity, etc.
Concurrence is one of the most important measure to
quantify entanglement, functionally related to entangle-
ment of formation [24] in systems (this is due to
the wonderful invention of Wootters ). For any pure
bipartite state
22
=

 in the Hilbert space
AB
H
H

of two subsystems ,
A
B it is in general
defined by


2
=21 A C    , where A

is the
reduced density matrix of

, after tracing out the
subsystem . For mixed bipartite states, it is just the
convex roof extension. The entanglement of formation
for any state of the two-qubit system could be expressed
as [25],
B
 
2
11
=2
F
C
E







where the function

is defined as






22
=11 log log
x
xx xx 

 
d
. For higher dimen-
sional pure bipartite state (say, ), concurrence is
given by [26] d

d2
<=
=4 =21
ij i
ij i
C1

 







 (3)
which varies sm oothly from for product states to
0

21d
d

for maximally entangled pure states of Schmidt rank .
d

  under LOCC with certainty, then




EE

  where


.E equals to the
von-Neumann entropy of the reduced density matrices of
the subsystems and usually known as the entropy of
entanglement. Again, if someone search for what kind of
deterministic LOCC, the amount of entanglement of the
states could be preserved. All the local unitary operations
preserve entanglement, so one must search for other kind
Logarithmic Negativity is a computable measure of
entanglement. It has functional relation with another
important quantification scheme, known as negativity.
Negativity is defined from the Peres-Horodecki criteria
[18,19] by,

11
2
A
T
N



 (4)

A. BHAR ET AL. 93
where 1 denote the trace norms of
A
T

A
T

, partial
transpose of the bipartite mixed state

with respect to
the subsystem A, which corresponds to the absolute value
of the sum of the negative eigenvalues of A
T

and
vanishes for separable states. For a pure state

negativity is


2
11
2i
i
N 




.
Now, Logarithmic Negativity, is defined by
  
22
1=2
log log
A
T
LN N   1
It is an entanglement monotone[27], related to the PPT
(positive under partial transposition) entanglement cost,






PPT 2
= log EN  1 of the state

, known as
the cost of exact preparing under PPT preserving
operations. For pure bipartite states this measure is
calculated by

d
2=1
=2 log i
i
LN







(5)
An interesting observation is that Negativity is a
convex function [28] of the state, though Logarithmic
Negativity is not.
A series of correlation measures known as Rényi
Entropy [29] or Alpha-Entropy ( S

), are proposed by
generalizing the concept of von-Neumann entropy;
1
1
=ln
1
d
i
i
S













All the Rényi entropy measures (naturally excluding
the von-Neumann Entropy function itself) are suitable to
discriminate between any class of incomparable states
with same entanglement. Here we only consider the
Linear Entropy and for
2
S=3

i.e. .
3
Linear Entropy for the pure bipartite state in the form
(1) is given by
S

2
22
=log i
i
S








(6)
Giampaolo et al. [30] showed that for all non-maxi-
mally entangled states of 3d

system, there exists a
range of values of linear entropy with same entangle-
ment.
Rényi entropy for =3

i.e. of the state (1) is
computed by the fo rmula, 3
S

3
32
=log i
i
S







(7)
Now, we will provide notions of some other measure
of correlations. Concurrence Hierarchy [31] is a series of
correlation measures generalized from the concept of
concurrence, in finite dimensional bipartite pure states.
For a general bipartite pure state of rank d in the
Schmidt form (1), the precise definition of the concur-
rence hierarchy is given by:


12
112
; 1,,
kiii
k
iii d
k
Ck 
  
d

(8)
For 33

system, there is only one concurrence
hierarchy for , i.e.
=3k

31
=C23


.
The Maximum fidelity for a pure state of the form (1),
is given by,

=1
max
exp 2ln
=d
d
i
i
F






(9)
The maximum fidelity is a convex function of the
generalized entropy,
 
max1 2
=exp
F
H  d where
12
H
is the Renyi entropy for 1 =2  .
The correlation measure robustness of entanglement
[32], denoted by


R

examines how much mixing can
take place between an entangled state and any other state,
so that the convex combination of these two states is
separable. In the characterization of the state space in
terms of entangled and separable states, we observe some
interesting properties of this measure. Robustness


R

,
is convex functio n of

, i.e. for any two states 1

and
2

we have the following inequality





 
121
1ttR 2 1tRRt
 
 
 
=
. Robustness
of entanglement remains unchanged under unitary
transformation of state, i.e.

L
L where RR
 UU 
L
U
L
is a local unitary transformation of the form
12
=UUU

. Now for the pure state (1), we could
define Robustness of entanglement as follows,

1
2
1
=exp2ln1
d
i
i
R 










(10)
Next we consider some of the distance measures of
quantum correlationm [33], proposed from the view of
measuring the distance of the state from its closest
separable state [10]. For any two pure states

and

,
the Fubini-Study distance is defined as,
 
,=
FS
dTr

 .
It is bounded by,

0,
2
FS
d 


.
Fubini-Study distance is related to information theoretic
measures of statistical distance between two probability
distributions. From the concept of this distance between
two states, a measure of correlation of a pure bipartite
state is proposed as the minimum of Fubini-Study
distance of the given state with all separable states and is
obtained by the formula,



max 1
= arccos=arccos
min FS
SEP
FS d


 
 


(11)

A. BHAR ET AL.
94
The Hilbert-Schmidt distance is another distance
measure [34]. For two states

and

, this distance is
given by,
 
2
,=
HS
dTr

  
. Taking minimum
over all separable states, a correlation measure of
entanglement of any pure state is proposed by,


  
max 1
=21 =21
min HS
SEP
HS d

 
(12)
The trace distance


,D


between two arbitrary
statistical operators

and

represents a good
measure to quantify the closeness of such states [33,35].
The relation



,Tr PTrPD






holds for any projection operator P, where the ex-
pressions


Tr P

and Tr P


 
represent the proba-
bility for the occurrence of the measurement outcome
associated with P when the system is in the state

and

Then the correlation measure is defined by the
minim um distanc e bet wee n the giv en stat e and the se para ble
state. For pure bi partite states i t has the form ,


max 1
=2 1=2 1
min fs
SEP d








(13)
All the distance measures are found to be monotone in
nature with 1
lnH


 , where 1

is the the largest
Schmidt coefficient.
5. Correlation Measures and
Incomparability
We now consider sets of pure bipartite states incompara-
ble to each other, with same amount of entanglement and
study their behavior with other correlation measures.
Under deterministic LOCC, we cannot conclude a single
measure of entanglement for pure bipartite states is suffi-
cient to probe the correlated structure of the system. We
show that the existence of different pure states with the
same value of entanglement, is not only a mathematical
property of the en tropy operator. We start with the 33

system, where the notion of genuine pair of incomparable
states begin. As shown in a previous work [20], the
structure of classes of incomparable states with same
ent ang le ment i n h igh er Schmidt ranks (greater than three)
follows the same pattern as of Schmidt rank 3 states. In
higher Schmidt ranks, states with same entropy of entan-
glement, should differ in at least three Schmidt coeffi-
cients. Therefore, although we have restricted our study
on lower Schmidt rank states only, however, the results
could be extended for higher ranks also.
5.1. Geometry of Equally Entangled States of
Different System
For every value of entanglement for a non-maximally
entangled state in Schmidt rank 3, one may easily gener-
ate a curve representing the states having that fixed value
of the entanglement of formation. In Figure 1, we con-
sider the class of states of rank 3 having entanglement of
formation 1.521985 e-bit and to represent the curve we
plot the three Schmidt coefficients along the X, Y, Z axes
respectively.
Similarly, for every value of non-maximal entangle-
ment in Schmidt rank 4 system, there is a surface in
three-dimensional space generated by the states of that
system. In Figure 2, we consider the surface generated
by the states having entanglement of formation 1.846439
e-bit, by plotting the first three Schmidt coefficients of
those states along the three rectangular coordinate axes.
The figure has some regular geometrical pattern. From a
distant view it appears to be a continuous curve formed
by semi-circular rings.
Figure 1. States of Schmidt rank 3 with entanglement of
formation = 1.521985 where three axes represent values of
the three Schmidt coefficients.
Figure 2. Surface generated by Schmidt rank 4 states hav-
ing entanglement of formation 1.846439 against three larg-
est coefficient where axes X, Y, Z represents three Largest
Schmidt coefficients in decre asing orde r.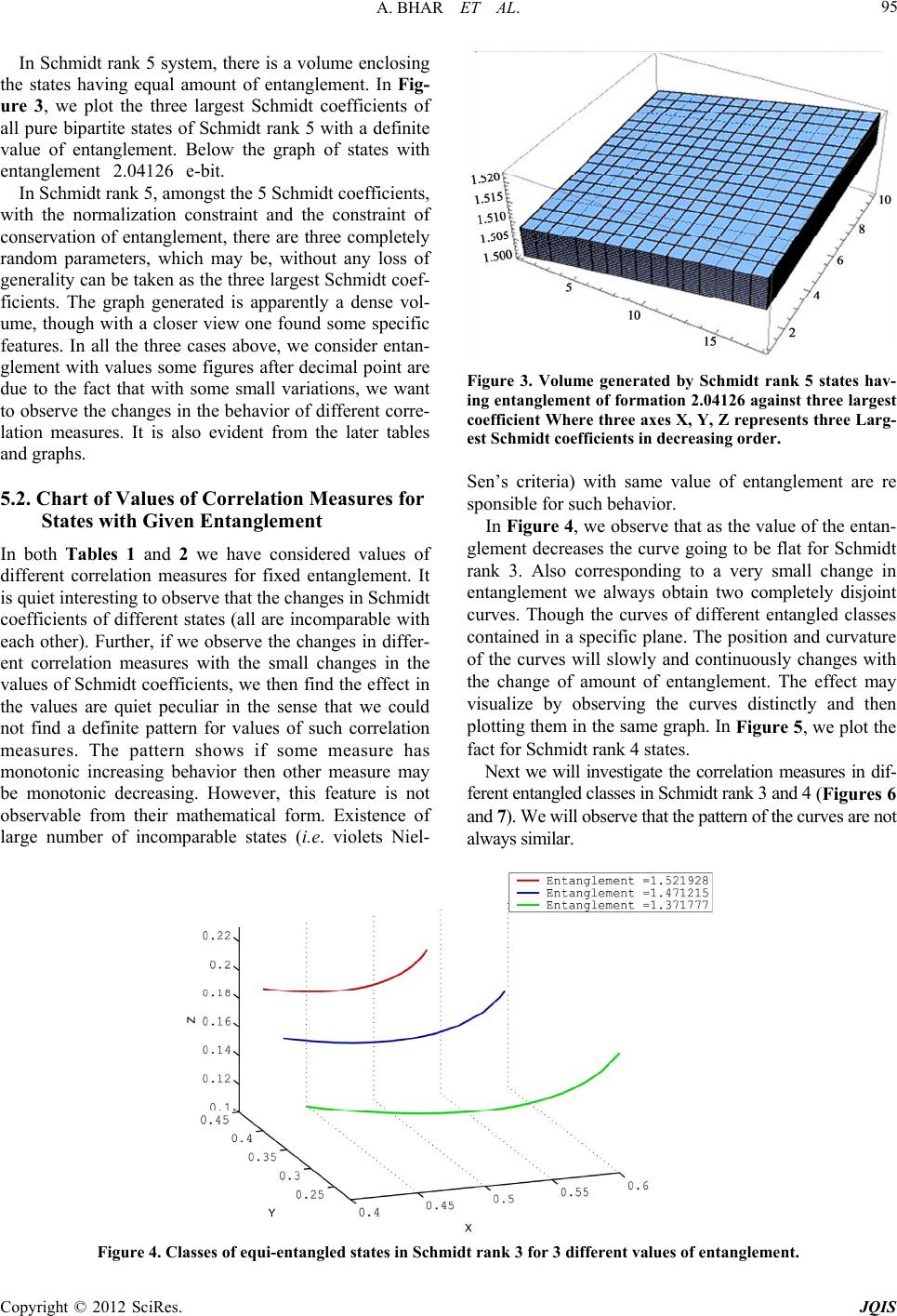

A. BHAR ET AL.
95
In Schmidt rank 5 system, there is a volume enclosing
the states having equal amount of entanglement. In Fig-
ure 3, we plot the three largest Schmidt coefficients of
all pure bipartite states of Schmidt rank 5 with a definite
value of entanglement. Below the graph of states with
entanglement e-bit. 2.04126
In Schmidt rank 5, amongst the 5 Schmidt coefficients,
with the normalization constraint and the constraint of
conservation of entanglement, there are three completely
random parameters, which may be, without any loss of
generality can be taken as the three largest Schmidt coef-
ficients. The graph generated is apparently a dense vol-
ume, though with a closer view one found some specific
features. In all the three cases above, we consider entan-
glement with values some figures after decimal point are
due to the fact that with some small variations, we want
to observe the changes in the behavior of different corre-
lation measures. It is also evident from the later tables
and graphs.
Figure 3. Volume generated by Schmidt rank 5 states hav-
ing entanglement of formation 2.04126 against three largest
coefficient Where three axes X, Y, Z represents three Larg-
est Schmidt coefficients in decreasing order.
Sen’s criteria) with same value of entanglement are re
sponsible for such behavior.
5.2. Chart of Values of Correlation Measures for
States with Given Entanglement In Figure 4, we observe that as the value of the entan-
glement decreases the curve going to be flat for Schmidt
rank 3. Also corresponding to a very small change in
entanglement we always obtain two completely disjoint
curves. Though the curves of different entangled classes
contained in a specific plane. The position and curvature
of the curves will slowly and continuously changes with
the change of amount of entanglement. The effect may
visualize by observing the curves distinctly and then
plotting them in the same graph. In Figure 5, we plot the
fact for Schmidt rank 4 states.
In both Tables 1 and 2 we have considered values of
different correlation measures for fixed entanglement. It
is quiet interesting to observe that the changes in Schmidt
coefficients of different states (all are incomparable with
each other). Further, if we observe the changes in differ-
ent correlation measures with the small changes in the
values of Schmidt coefficients, we then find the effect in
the values are quiet peculiar in the sense that we could
not find a definite pattern for values of such correlation
measures. The pattern shows if some measure has
monotonic increasing behavior then other measure may
be monotonic decreasing. However, this feature is not
observable from their mathematical form. Existence of
large number of incomparable states (i.e. violets Niel-
Next we will investigate the correlation measures in dif-
ferent e nta n gle d cl as ses in Schm idt rank 3 and 4 (Figures 6
and 7). We will observe that the patt ern of the curves are not
always similar.
Figure 4. Classes of equi-entangled states in Schmidt rank 3 for 3 different values of entanglement.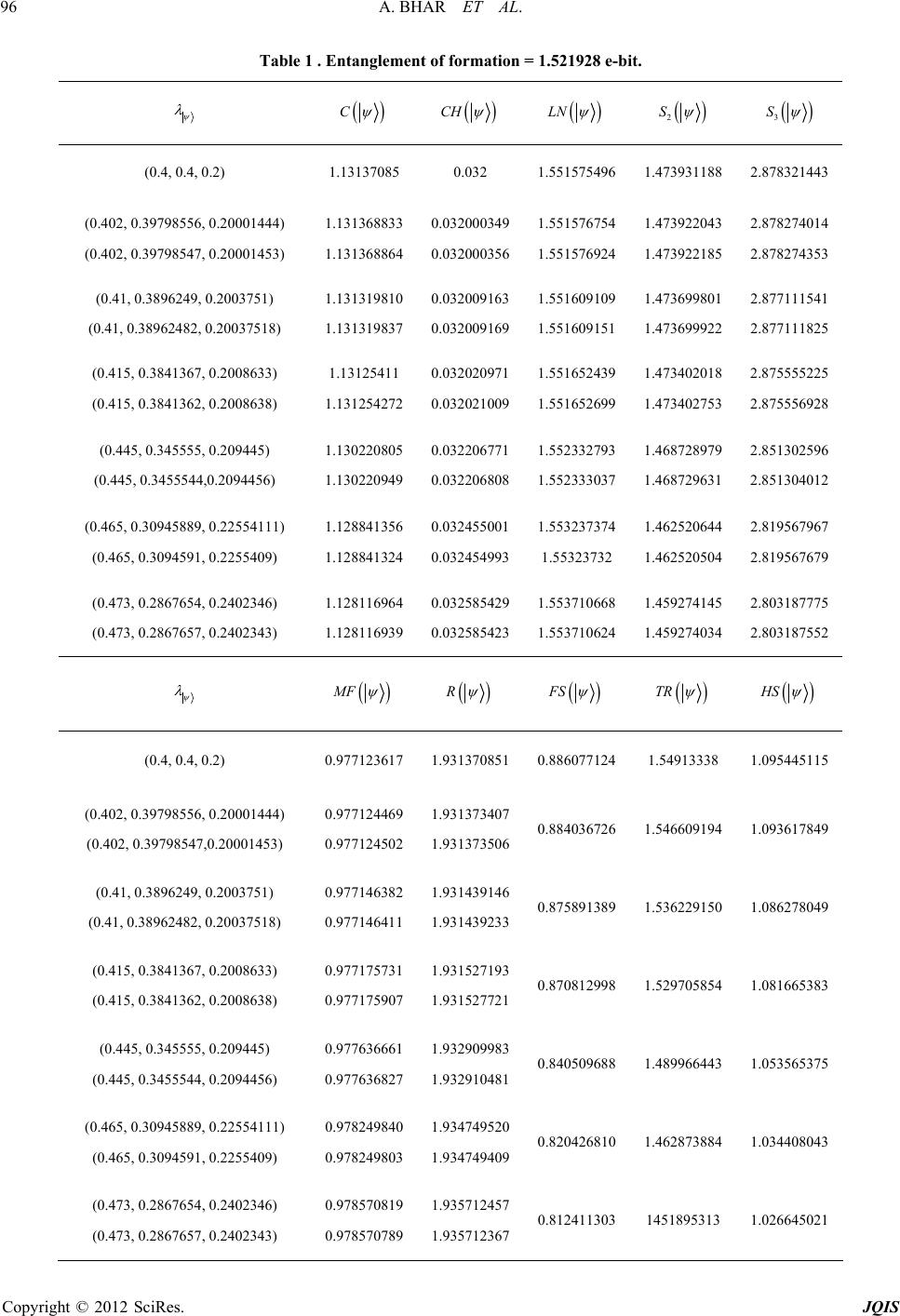

A. BHAR ET AL.
96
Table 1 . Entanglement of formation = 1.521928 e-bit.


C


CH



LN





2
S


3
S

(0.4, 0.4, 0.2) 1.13137085 0.032 1.5515754961.473931188 2.878321443
(0.402, 0.39798556, 0.20001444)
(0.402, 0.39798547, 0.20001453)
1.131368833
1.131368864
0.032000349
0.032000356
1.551576754
1.551576924
1.473922043
1.473922185
2.878274014
2.878274353
(0.41, 0.3896249, 0.2003751)
(0.41, 0.38962482, 0.20037518)
1.131319810
1.131319837
0.032009163
0.032009169
1.551609109
1.551609151
1.473699801
1.473699922
2.877111541
2.877111825
(0.415, 0.3841367, 0.2008633)
(0.415, 0.3841362, 0.2008638)
1.13125411
1.131254272
0.032020971
0.032021009
1.551652439
1.551652699
1.473402018
1.473402753
2.875555225
2.875556928
(0.445, 0.345555, 0.209445)
(0.445, 0.3455544,0.2094456)
1.130220805
1.130220949
0.032206771
0.032206808
1.552332793
1.552333037
1.468728979
1.468729631
2.851302596
2.851304012
(0.465, 0.30945889, 0.22554111)
(0.465, 0.3094591, 0.2255409)
1.128841356
1.128841324
0.032455001
0.032454993
1.553237374
1.55323732
1.462520644
1.462520504
2.819567967
2.819567679
(0.473, 0.2867654, 0.2402346)
(0.473, 0.2867657, 0.2402343)
1.128116964
1.128116939
0.032585429
0.032585423
1.553710668
1.553710624
1.459274145
1.459274034
2.803187775
2.803187552


MF



R



FS



TR



HS


(0.4, 0.4, 0.2) 0.9771236171.9313708510.8860771241.54913338 1.095445115
(0.402, 0.39798556, 0.20001444)
(0.402, 0.39798547,0.20001453)
0.977124469
0.977124502
1.931373407
1.931373506 0.8840367261.546609194 1.093617849
(0.41, 0.3896249, 0.2003751)
(0.41, 0.38962482, 0.20037518)
0.977146382
0.977146411
1.931439146
1.931439233 0.8758913891.536229150 1.086278049
(0.415, 0.3841367, 0.2008633)
(0.415, 0.3841362, 0.2008638)
0.977175731
0.977175907
1.931527193
1.931527721 0.8708129981.529705854 1.081665383
(0.445, 0.345555, 0.209445)
(0.445, 0.3455544, 0.2094456)
0.977636661
0.977636827
1.932909983
1.932910481 0.8405096881.489966443 1.053565375
(0.465, 0.30945889, 0.22554111)
(0.465, 0.3094591, 0.2255409)
0.978249840
0.978249803
1.934749520
1.934749409 0.8204268101.462873884 1.034408043
(0.473, 0.2867654, 0.2402346)
(0.473, 0.2867657, 0.2402343)
0.978570819
0.978570789
1.935712457
1.935712367 0.8124113031451895313 1.026645021

A. BHAR ET AL. 97
Table 2. Entanglement = 1.4712154 e-bit.


C


CH



LN




2
S



3
S

(0.45, 0.39, 0.16) 1.113373253 0.02808 1.523115558 1.395169563 2.693947792
(0.46, 0.37804914,0.16195086)
(0.46, 0.37804916, 0.16195084)
1.112879838
1.112879830
0.028163676
0.028163674
1.523457634
1.52345762
1.393086963
1.393086930
2.683948086
2.683948021
(0.47, 0.36532505, 0.16467495)
(0.47, 0.36532508, 0.16467492)
1.112222791
1.112222780
0.028275146
0.028275143
1.523912199
1.523912178
1.390319798
1.390319752
2.670742795
2.670742882
(0.48, 0.35165453, 0.16834547)
(0.48, 0.35165456, 0.16834544)
1.111394524
1.111394514
0.028415735
0.028415732
1.524483684
1.524483665
1.386841400
1.386841358
2.654273336
2.654273258
(0.49, 0.33676025, 0.17323975)
(0.49, 0.33676030, 0.17323970)
1.110387791
1.110387776
0.028586728
0.028586724
1.525176047
1.525176018
1.382628248
1.382628187
2.634514394
2.634514282
|


 MF


R



FS



TR


HS



(0.45, 0.39, 0.16) 0.958036852 1.874110556 0.835481874 1.483239679 1.048808848
(0.46, 0.37804914, 0.16195086)
(0.46, 0.37804916, 0.16195084)
0.958264038
0.958264029
1.874792114
1.874792087 0.825440953 1.469693846 1.039230485
(0.47, 0.36532505, 0.16467495)
(0.47, 0.36532508, 0.16467492)
0.958566002
0.958566016
1.875698006
1.875698048 0.815416193 1.456021978 1.029563014
(0.48, 0.35165453, 0.16834547)
(0.48, 0.35165456, 0.16834544)
0.958945801
0.958945789
1.876837403
1.876837367 0.805403501 1.442220510 1.019803903
(0.49, 0.33676025, 0.17323975)
(0.49, 0.33676030, 0.17323970)
0.959406119
0.959406100
1.878218357
1.8782183 0.795398830 1.428285686 1.009950494
0.65
Figure 5. Surface generated by equi-entangled states for different values of entangled states of Schmidt rank 4 where axes X,
Y represents largest two Schmidt coefficients.

A. BHAR ET AL.
98
Figure 6. Graphs of different correlation measures of equi-entangled states in Schmidt rank 3.
Figure 7. Graphs of different correlation measures of equi-entangled state with entanglement of formation 2.04126 in
Schmidt rank 4 considering three largest Schmidt coefficients.

A. BHAR ET AL.
99
6. Observations
The behavior of different correlation measures observed
by plotting curves and by providing numerical figures.
The nature of the curves show non-monotonic behavior
of the measures in general with respect to the entangle-
ment, e.g. concurrence [23]. This is observed due to only
incomparability of a large number of states with same
entanglement. For comparable states it would not be pos-
sible to observe such behavior. This feature of state
spaces has some other consequences, e.g. the behavior
under partial transposition of mixtures of incomparable
states from equi-entangled class with the maximally
mixed state. We discuss this feature as distinguishing
factor of the states belonging to any equi-entangled class
in appendix.
In conclusion, the work is intended to find the differ-
ences by some known correlation measures of pure states
through incomparability. As the Schmidt rank increases
gradually only the measures depending on Schmidt coef-
ficients would be able to differentiate the states of equal
entanglement but incomparable with each other. For
Schmidt rank 4 system, the behavior of the measures like,
Concurrence, Linear Entropy and Rényi Entropy are
similar in nature irrespective of some phase differences.
Whereas the behavior of the measures like, Logarithmic
Negativity, Concurrence Hierarchy, Maximum Fidelity
and Robustness are quite opposite to that of the previous
measures. Distance measures depending only on the
largest Schmidt coefficient generate a straight line only
indicating the variation of the largest Schmidt coefficient
for preservation of entanglement under LOCC. The
measure showing the largest variation for a fixed value of
entanglement, for all most all values of entanglement in
rank 4 system, is Concurrence Hierarchy and the next
largest variation of values for constant entanglement is
seen in the Rényi entropy for =3

. With the increase
of entanglement, curvature of the surface as well as the
area traced out by the states of an equi-entangled class
will gradually shrinking down and tends to a line parallel
to the X-axis, from a curved surface.
REFERENCES
[1] J. S. Bell, “On the Einstein Podolsky Rosen Paradox,”
Physics, Vol. 1, No. 3, 1964, pp. 195-200.
[2] C. H. Bennett and G. Brassard, “Quantum Cryptography:
Public Key Distribution and Coin Tossing,”Proceedings
of IEEE International Conference on Computers, Systems
and Signal Processing, Bangalore, 10-12 December 1984,
pp.175-179.
[3] C. H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A.
Peres and W. K. Wootters, “Teleporting an Unknown
Quantum State via Dual Classical and Einstein-Podolsky-
Rosen Channels,” Physical Review Letters, Vol. 70, No.
13, 1993, p. 1895. doi:10.1103/PhysRevLett.70.1895
[4] C. H. Bennett, G. Brassard, S. Popescu, B. Schumacher, J.
A. Smolin and W. K. Wootters, “Purification of Noisy
Entanglement and Faithful Teleportation via Noisy
Channels,” Physical Review Letters, Vol. 76, No. 5, 1996,
pp. 722-755. doi:10.1103/PhysRevLett.76.722
[5] C. H. Bennett, H. J. Bernstein, S. Popescu and B.
Schumacher, “Concentrating Partial Entanglement by
Local Operations,” Physical Review A, Vol. 53, No. 4,
1996, pp. 2046-2052. doi:10.1103/PhysRevA.53.2046
[6] S. Popescu and D. Rohrlich, “Thermodynamics and the
Measure of Entanglement,” Physical Review A (R), Vol.
56, No. 5, 1997, pp. 3319-3322.
[7] S. Virmani and M. B. Plenio, “Ordering States with En-
tanglement Measures,” Physical Revi ew Letters, Vol. 268,
No. 1-2, 2000, pp. 31-34.
doi:10.1016/S0375-9601(00)00157-2
[8] F. Verstraete, K. Audenaert, J. Dehaene and B. D. Moor,
“A Comparison of the Entanglement Measures Negativity
and Concurrence,” Journal of Physics A: Mathematical
and General, Vol. 34, No. 47, 2001, p. 10327.
doi:10.1088/0305-4470/34/47/329
[9] H. K. Lo and S. Popescu, “Concentrating Entanglement
by Local Actions: Beyond Mean Values,” Physical Re-
view A, Vol. 63, No. 2, 2001.
doi:10.1103/PhysRevA.63.022301
[10] V. Vedral and M. B. Plenio, “Entanglement Measures and
Purification Procedures,” Physical Review A, Vol. 57, No.
3, 1998, pp. 1619-1633.
doi:10.1103/PhysRevA.57.1619
[11] V. Vedral, M. B. Plenio, M. A. Rippin and P. L. Night,
“Quantifying Entanglement,” Physical Review Letters,
Vol. 78, No. 12, 1997, p. 2275.
doi:10.1103/PhysRevLett.78.2275
[12] A. Miranowicz and A. Grudka, “Ordering Two-Qubit
States with Concurrence and Negativity,” Physical Re-
view A, Vol. 70, No. 3, 2004, Article ID: 032326.
doi:10.1103/PhysRevA.70.032326
[13] M. A. Nielsen, “Conditions for a Class of Entanglement
Transformations,” Physical Review Letters, Vol. 83, No.
2, 1999, pp. 436-439. doi:10.1103/PhysRevLett.83.436
[14] K. Zyczkowski, “Volume of the Set of Separable States
II,” Physical Review A, Vol. 60, No. 5, 1999, pp. 3496-
3507. doi:10.1103/PhysRevA.60.3496
[15] G. Vidal, “Entanglement Monotones,” Journal of Modern
Optics, Vol. 47, No. 2-3, 2000, pp. 355-376.
[16] M. A. Nielsen, “Lecture Notes,” Department of Physics,
Univesity of Queensland, Queensland, 2002.
[17] M. B. Plenio and S. Virmani, “An Introduction to Entan-
glement Measures,” Quantum Information & Computa-
tion, Vol. 7, No. 1, 2007, pp. 1-51.
[18] A. Peres, “Seperability Criteria for Density Matrices,”
Physical Review Letters, Vol. 77, No. 8, 1996, pp. 1413-
1415. doi:10.1103/PhysRevLett.77.1413
[19] M. Horodecki, P. Horodecki and R. Horodecki, “Separa-
bility of Mixed States: Necessary and Sufficient Condi-
tions,” Physical Review A, Vol. 223, No. 1-2, 1996, pp.

A. BHAR ET AL.
100
1-8. doi:10.1103/PhysRevLett.84.2014
[20] M. Horodecki, P. Horodecki and R. Horodecki, “Limits
for Entanglement Measures,” Physical Review Letters,
Vol. 84, No. 9, 2000, pp. 2014-2017.
doi:10.1103/PhysRevLett.84.2014
[21] I. Chattopadhyay and D. Sarkar, “Character of Locally
Inequivalent Classes of States and Entropy of Entangle-
ment,” Physical Review A (R), Vol. 77, No. 5, 2008, Arti-
cle ID: 050305.
[22] I. Chattopadhyay and D. Sarkar, “General Classes of
Impossible Operations through the Existence of Incom-
parable states,” Quantum Information and Computation,
Vol. 7, No. 4, 2007, pp. 392-400.
doi:10.1103/PhysRevA.73.044303
[23] I. Chattopadhyay and D. Sarkar, “Entanglement of For-
mation Is Non-Monotonic with Concurrence: A Simple
Proof,” Quantum Information Processing, Vol. 7, No. 6,
2008, pp. 243-249. doi:10.1007/s11128-008-0085-6
[24] W. K. Wootters, “Entanglement of Formation of an Arbi-
trary State of Two Qubits” Physical Review Letters, Vol.
80, No. 10, 1998, pp. 2245-2248.
doi:10.1103/PhysRevLett.80.2245
[25] W. K. Wootters, “Entanglement of Formation and Con-
currence,” Quantum Information & Computation, Vol. 1,
No. 1, 2001, pp. 27-44.
[26] K. Chen, S. Albeverio and S. M. Fei, “Concurrence of
Arbitrary Dimensional Bipartite Quantum States,” Phy-
sical Review Letters, Vol. 95, No. 4, 2005, Article ID:
040504. doi:10.1103/PhysRevLett.95.040504
[27] M. B. Plenio, “Logarithmic Negativity: A Full Entangle-
ment Monotone That Is Not Convex,” Physical Review
Letters, Vol. 95, No. 9, 2005, Article ID: 090503.
doi:10.1103/PhysRevLett.95.090503
[28] G. Vidal and R. F. Werner, “Computable Measure of
Entanglement,” Physical Review A, Vol. 65, No. 3, 2002,
Article ID: 032314. doi:10.1103/PhysRevA.65.032314
[29] A. Rényi, “On the Notion of Entropy and Its Role in
Probability Theory,” Proceedings of the 4th Berkeley
Symposium on Mathematical Statistics and Probability,
University of California Press, Berkeley, Vol. 1, 1961, pp.
547-561.
[30] S. M. Giampaolo and F. Elluminati, “Characterization of
Separability and Entanglement in (2 × D)- and (3 ×
D)-Dimensional Systems by Single-Qubit and Single-
Qutrit Unitary Transformations,” Physical Review A, Vol.
76, No. 4, 2007, Article ID: 042301.
doi:10.1103/PhysRevA.76.042301
[31] H. Fan, K. Matsumoto and H. Imai, “Quantify Entangle-
ment by Concurrence Hierarchy,” Journal of Physics A:
Mathematical and General, Vol. 36, No. 14, 2003, p.
4407. doi:10.1088/0305-4470/36/14/316
[32] G. Vidal and R. Tarrach, “Robustness of Entanglement,”
Physical Review A, Vol. 59, No. 1, 1999, pp. 141-155.
doi:10.1103/PhysRevA.59.141
[33] K. Zyczkowski and I. Bengtsson, “Relativity of Pure
States Entanglement,” Annals of Physics, Vol. 295, No. 2,
2002, pp. 115-135. doi:10.1006/aphy.2001.6201
[34] C. Writte and M. Trucks, “A New Entanglement Measure
Induced by the Hilbert-Schmidt Norms,” Physics Letters
A, Vol. 14, No. 1-2, 1999, pp.14-20.
[35] G. Vidal, D. Jonathan and M. A. Nielsen, “Approximate
Transformations and Robust Manipulation of Bipartite
Pure-State Entanglement,” Physical Review A, Vol. 62,
No. 1, 2000, Article ID: 012304.
doi:10.1103/PhysRevA.62.012304

A. BHAR ET AL. 101
Appendix
Behavior of Mixture with Maximally Mixed State:
Our observation is the signature of partial transpose on
the mixture of states from a class of equally entangled
states with the maximally mixed state through the PPT
(positive under partial transpose) criteria [17,24]. Sup-
pose

12
,,,
d


 be the Schmidt vector in decreas-
ing order of the pure bipartite state

of dd

sys-
tem. We prepare the mixture

2
1Ip
dp


 

for each state

. Taking partial transpose over the
subsystem B of the state, we find eigenvalues of the
transpose matrix as,
2
1 ; =1,2,,d
i
pi
dp
 
 and
2
1 ; =1,2,,1 ; =1,2,,
ij
pidjii
dp
 
d.
Therefore, all the eigenvalues are non-negative when-
ever,
2
<
<
<
12
1
{}
min
{1} 0
min
{}
max
1
ij
ij
ij
ij
ij
ij
p
dp
p
p
p









Let

be any pure bipartite state of system,
having same entanglement but not local unitary equiva-
lent with
dd

, i.e. both the states ,

 are incom-
parable with each other. Let the Schmidt vector in de-
creasing order of

be


12
,,,
d

 .
When 12 12



, choosing the value of as p
12 12
11
<p




we find


is a PPT state and the state


is NPT
(negative under partial transpose). So for any pair of in-
comparable states with same amount of entanglement if
the product of two largest Schmidt coefficients are not
equal, then we could always prepare equi-mixture of the
two pure states with maximally mixed state in the same
dimension( 2
1dd
I
d

), such that one is PPT and another is
a NPT state. The above feature undoubtedly probe the
differences exist in different states of equi-entangled
states, but not reflected by the unique quantification
scheme for pure bipartite states through the von-Neu-
mann entropy of the red uce d density mat ri c es.
0
1

(14)