Int. J. Communications, Network and System Sciences, 2012, 5, 513-519
http://dx.doi.org/10.4236/ijcns.2012.59062 Published Online September 2012 (http://www.SciRP.org/journal/ijcns)
Primality Testing Using Complex Integers and
Pythagor ean Triplets
Boris S. Verkhovsky
Computer Science Department, New Jersey Institute of Technology, Newark, USA
Received July 23, 2012; revised August 16, 2012; accepted August 31, 2012
“Mathematicians have tried in vain to this day to discover some ord er in the sequence of
prime numbers, and we have reason to believe that it is a mystery, into which the human
mind will never penetrate.” Leonard Euler
ABSTRACT
Prime integers and their generalizations play important roles in protocols for secure transmission of information via open
channels of telecommunication networks. Generation of multidigit large primes in the design stage of a cryptographic
system is a formidable task. Fermat primality checking is one of the simplest of all tests. Unfortunately, there are
composite integers (called Carmichael numbers) that are not detectable by the Fermat test. In this paper we consider
modular arithmetic based on complex integers; and provide several tests that verify the primality of real integers.
Although the n ew t e st s det ect most Carmichael numbers, there are a small percentage of them that escape these tests.
Keywords: Cryptosystem Design; Primality Testing; Fermat Test; Pythagorean Triplet; Strong Carmichael Number;
Quaternions
1. Introduction
Large prime numbers are at the core of every modern
cryptographic protocol. These protocols rely on multidigit
large primes to ensure that the cryptanalysis of an encrypted
message is too complicated to break in any relevant time.
Therefore, the efficiency of primality tests is important
[1].
Primality testing has a long history. Paul Erdös, re-
phrasing Einstein’s famous statement, expressed his view
as “God may not play dice with the Universe, but something
strange is going on with the prime numbers”, [2]. I be-
slieve that maybe the following proposition explains the
views of L. Euler and P. Erdös:
Conjecture: If there exists an algorithm that describes
an order in the sequence of primes smaller than n, it has
complexity

f
n


11 p
a

, where f(n) is a monotone non-
decreasing function of n, [3].
There are many ways to test an integer for primality.
The Sieve of Eratosthenes, although able to detect all
primes, has a time complexity in the order of n, [4]. Fer-
mat’s Little Theorem (FLT) can be used to test for pri-
mality. Although the Fermat test is very simple, there
exists an infinite set of composite integers, {called Car-
michael numbers or CMNs, for short}, that are not de-
tectable by the Fermat test, [5].
2. Basic Properties of Primes
Euclid Lemma: If p is a prime number and p divides a
product ab of integers, then p divides a or p divides b.
This is used in some proofs of the uniqueness of prime
factorizations.
Fermat Little Theorem (FLT): If p is a prime that
does not divide an integer a, then is divisible
by p,


p
aa

mod p = 1. (2.1) otherwise
Wilson Theorem: provides a necessary and sufficient
condition for primality testing: an integer is a
prime if and only if 2p


1! 1p is divisible by p. (2.2)


However, since the Wilson Theorem has complexity
O(p), it is not computationally efficient.
Prime Number Theorem: The number of primes smal-
ler than x is asymptotic to

Oln
x
x
,,2,.., ,..aa qaqa kq
[6]. (2.3)
Dirichlet Theorem: In every arithmetic progression


1q where the positive integers a and are relatively prime, there are infinitely many
C
opyright © 2012 SciRes. IJCNS

B. VERKHOVSKY
514
primes. This property can be applied to generate large
primes (greater than 10100), which are important com-
ponents in public-key cryptography.
Existence of Generator: For every prime p there ex-
ists an integer 1
g
p
11bp
,mod
d
bg p

, called a generator, such that
every integer can be expressed as
. (2.4)
Here d is called a discrete logarithm of b modulo p.
This property plays an important role in the ElGamal
cryptographic algorithm [7] and in elliptic-curve cryp-
tography, [8].
3. Generalizations
The concept of prime numbers is so important that it has
been generalized in different ways in various branches of
mathematics. For example, we can define complex primes.
Notice that 5 is not a complex prime, because it is the
product of two complex integers and

12i


12i.
Another observation:


 
1212i i 
mod 43
n
Rcdi
)dim wi 
wadbc
(cab;Sbd
52 2ii ;
which means that complex factorization is not unique.
However, integer 3 is a co mplex prime. In general, every
real prime n that satisfies n (called Blum
prime) is also a complex prime. Yet, every real prime n
that satisfies is the complex composite, [9].
A public key cryptographic algorithm based on complex
moduli is described in [10].
mod4 1
4. Arithmetic Operations on Complex
Integers
Modular arithmetic with modulus n, unlike the “school-
grade” arithmetic, operates on a finite set of integers in
the interval [0, n – 1].
4.1. Multiplications of Complex Numbers
Let ; and ; consider
Labi
()(LRabi c ;
where and . Hence, the com-
putation of m and w requires four multiplications of real
numbers, where integers in a cryptographic scheme might
be of size 10100 or larger. However, [11] describes an al-
gorithm that computes LR using only three multiplica-
tions. Indeed, let ;Qand
macbd
()Pab )d

then and . mQS wPQ
abi mwi
 
bbqab
2wq
S 
Consider now the squaring of a complex integer:

222
2abia b ;
and , , and . ra
mpa r
Then ; and , where the latter can be
performed by left shift, if integers are in binary form.
Therefore, squaring is done using two multiplications and
two additions.
p
If each integer A and B has s decimal digits, then alge-
braic addition
A
B

requires ()
s
 digital operations
and multiplication AB has complexity 2 ()
s

mod 1bd n
.
4.2. Modular Multiplicative Inverse of Complex
Integer
Definition4.1: Let b and d be complex integers, where

; then b and d are called mutually multipli-
cative inverse modulo n.
bcfidghi and Let



22
; (4.1)
compute
s
cf1 s

 and t. (4.2)

If gcd(s,n) = 1, then the inverse of s can be computed
using either the extended Euclid algorithm, [12] or the al-
gorithms in [2,13,14].
Finally,
g
ct

and . (4.3)

hnft
22
pu w
4.3. Complex Primes
It is known that for every prime p congruent to 1 modulo
4 (non-Blum prime) there exists two real integers u and
w such that
. (4.4)


Thus, every such prime can be presented as two prod-
ucts of two factors each:



  
puwiuwi wuiwui . (4.5)
Therefore, there are no complex primes among non-
Blum integers.
However, every Blum prime is also a complex prime,
since it cannot be presented as a product of two complex
integers except as


ppii, [6].

In the following consideration we are using the notation:


,:ababi. (4.6)


5. Fundamental Identity
Proposition 5.1: If p is a real prime, then for every com-
plex integer (a,b),


22
gcd,1abp where


 
21
,mod1,01
p
ab p

(,) (0,0)ab 
; (5.1)
the following identity holds
. (5.2)
Proof: First of all, if ; then





 
,, ,,modab uvabxyp; (5.3)





implies that

,,moduv xyp
 
. (5.4)
Indeed, there exists a complex integer



1
122
,, modabap b abp

  (5.5)

B. VERKHOVSKY
Cop IJCNS
515
 
mod1,0p

1
,ab
such that .

1
,,ab ab
6. Major Results
By multiplying both parts of (5.3) with

we
prove (5.4). Proposition 6.1: Let (a,b) be a complex integer, satis-
fying (5.1), and p be a Blum prime {pmod4=3}; then
Proposition5.1 implies the follow ing identity for every a,
b and p:
Let’s consider a product A of all complex numbers (j,k)
with components
0, 0jk

1,mod
1jk p and , (5.6)
yright © 2012 SciRes.
i.e., at least one of the components is strictly positive:

0,
,0
:
jk p
jk
A
jk p


21
,mod
p
kabp



,mod
,mod
jk p
k p








mod


. (5.7)
Consider now


0, 1
,0
:,
jk p
jk
Bj
 

; (5.8)
then
. (5.9)




21
0, 1
,0
0, 1
,0
:,
=,
p
jk p
jk
jk p
jk
Bab
abj







Since every (j,k) satisfying (5.6) is an element of a cy-
clic group, then all (a,b) (j,k) are a permutation of the
elements of the same group.
Hence,

0, 1
,0
:,
jk p
jk
A
jk



p B
21
,mod1p


od1,0.p

. (5.10)
Therefore, (5.7), (5.8) and (5.10) imply that

p
ab . Q.E.D. (5.11)
Remark5.1: If p is not a prime, then there exists (a,b),
for which neither (5.1) holds, nor (5.3) implies (5.4). If
p=qr, then


22
11
,m
qr
ab  (5.12)
Proposition 5.2: For every real prime p there exists a
complex integer G, called a complex generator, such that
every complex integer (a,b), where (5.1) holds, can be
expressed as


,modb p



12
,mod,
p
abpde

0.de
; (6.1)
where either d = 0 or e = 0, but


22
modab p exists, then Furthermore, if


22
moddea bp; (6.2)
otherwise


22
moddea bp . (6.3)
22
ab
11qp
222
abc
Remark6.1: is the absolute value of (a,b).
The alternative in (6.3) is based on the following obser-
vation: if p is a Blum prime, and ; then from
the Euler criterion of quadratic residuosity either q or p –
q, but not both, is a quadrat i c resi d ue m odulo p [6].
The identity (6.1) in the following text is called the
BV-3 primality test. Thousands of computer experiments
have demonstrated that this test detects the overwhelm-
ing majority of CMNs {see Section 7 for details}.
Definition 6.1: A triplet {a, b, c} of positive integers
where a and b are co-prime and satisfy
; (6.4)




is called a Pythagorean triplet.
Proposition 6.2: For every Pythagorean triplet {a,b,c},
and every Blum prime p the following identity holds

12
,mod
p
abc p


1006
5,12 13mod2011

22 2
51213
. (6.5)
Example 6.1: Let p = 2011; a = 5 and b = 12; then
; where . More
examples are provided in Table 2.
7. Carmichael Numbers
Carmichael numbers {CMNs} are composite integers
that nevertheless satisfy Fermat’s Little Theorem [15].
Carmichael found that 561 is the smallest integer that
escapes the primality test of Fermat’s Little Theorem [5].
Indeed, for every 0 < a < 561, co-prime with 561, holds: d
Ga; (5.13)


561 mod561 0aa


here d is called a discrete logarithm of (a,b) modul o p.
Table 1. Classification of integers and Fermat Test (FT).
n nmod4=1 nmod4=3
Primes Pass the Fermat test Pass the Fermat and BV-3 tests
Ordinary composites Detectable by FT Detectable by FT
Carmichael numbers Non-detectabl e by FT; Highly likely detectable by the BV-1 testNon-detectable by FT; Highly likely detectable by the BV-3 test

B. VERKHOVSKY
516
Table 2. BV-3 test with primes and Pythagorean triplets (3,4); (5,12) (8,15) and (21,20) as testing seeds.
Primes (3,4) (5,12) (8,15) (21,20) Primes (3,4) (5,12) (8,15) (21,20)
499 (5,0) (13,0) (–17,0) (29,0) 827 (5,0) (13,0) (-17,0) (29,0)
503 (5,0) (13,0) (17,0) (29,0) 863 (5,0) (13,0) (17,0) (29,0)
563 (5,0) (13,0) (–17,0) (29,0) 1031 (5,0) (13,0) (17,0) (29,0)
647 (5,0) (13,0) (17,0) (29,0) 1051 (5,0) (13,0) (–17,0) (29,0)
727 (5,0) (13,0) (17,0) (29,0) 1063 (5,0) (13,0) (17,0) (29,0)
739 (5,0) (13,0) (–17,0) (29,0) 1999 (5,0) (13,0) (17,0) (29,0)
823 (5,0) (13,0) (17,0) (29,0) 2011 (5,0) (13,0) (–17,0) (29,0)
According to Richard Pinch, there are 585,355 CMNs
smaller than 1017. Moreover, there are 8241 CMNs smaller
than 1012; 19,279 smaller than 1013; 44,706 smaller than
1014; 105,212 smaller than 1015; and 246,683 smaller
than 1016.
For the experimen ts pro vid ed in th is p aper, CMNs nu m-
bers smaller than 1016 [16] are used. An algorithm that
generates large CMNs is provided in [17].
Proposition 7.1: Since every CMN is a product of at
least three primes, i.e., 123 CMN ppp

, therefore at least
one of these factors is smaller than the cubic root of the
this CMN:
3CMN
k
p. (7.1)
Therefore, (2.3) and (7.1) imply that the co mplexity to
find the smallest factor f of a CMN is of order

33
/lnfnn (7.2)
The smaller factors of each CMN are shown in the
left-most column of Table 5.
Example 7.1: If n = 612816751 {see Table 3} is a
CMN, then in order to find its smallest factor it is suffi-
cient to check whether n is divisible by at most one of the
first 140 primes. It is easy to verify that f = 251.
Computer experiments indicate that for numerous CMNs
the smallest factor of a CMN does not exceed 4CMN
0an 0bn n

{see Tables 5 and Table A.1 in the Appendix}.
8. Primality Tests
BV-3 test: If n is a Blu m prime, a an d b are distinct posi-
tive integers , , and ab, then
for every complex (a, b) holds that
 
12 , ncd 
0an bnabn
,modnab ; (8.1)
where either c or d, but not both, are equal zero.
BV-1 test: If n is a non-Blum prime, a and b are dis-
tinct positiv e integers ,0,and

,
then for every complex (a,b) holds t hat



,n cd
12
, mod
n
ab 

280
2,3mod561 16,459
222
1;
;;;
;; .
ijk
ijkjki kij
jikkjiikj


; (8.2)
where either c or d, but not both, are equal zero.
Example 8.1: Let n=561 and (2,3); then
.
Therefore, 561 is not a prime, because (8.2) does not
hold.
For more numeric examples see Table 5.
9. Primality Testing with Quaternions
For integers congruent to 1 modulo 4 we introduce a pri-
mality test based on quaternions
(a,b,c,d): = a + bi + cj + dk; (9.1)
where


 
1
,, ,mod,0,0,0
n
abcdnh

222 2
cd h
(9.2)
Conjecture 10.1: If n is a prime, then for every seed
(a,b,c,d) holds
, (9.3)
w here ab

 
1
2mod
pp 1od pp 
222
abc
. (9.4)
10. Computer Experiments
The goal of the experiments is to verify the correctness
of the primality tests.
The inputs for the experiments included all 246,683
Carmichael numbers smaller than 1016. For other inputs
we only considered complex primes to verify the tests,
see Proposition 5.1. Table 1 provides the classification
of integers.
In parallel we tested various types of inputs using the
Fermat test: in the two right-most columns of Ta ble s 3-5
are computed and 5m .
Table 2 displays results of Pythagorean triplets, {see
Proposition 6.2}. Each seed represents (a,b) and the re-
sult is c of the Pythagorean triplet
. (10.1)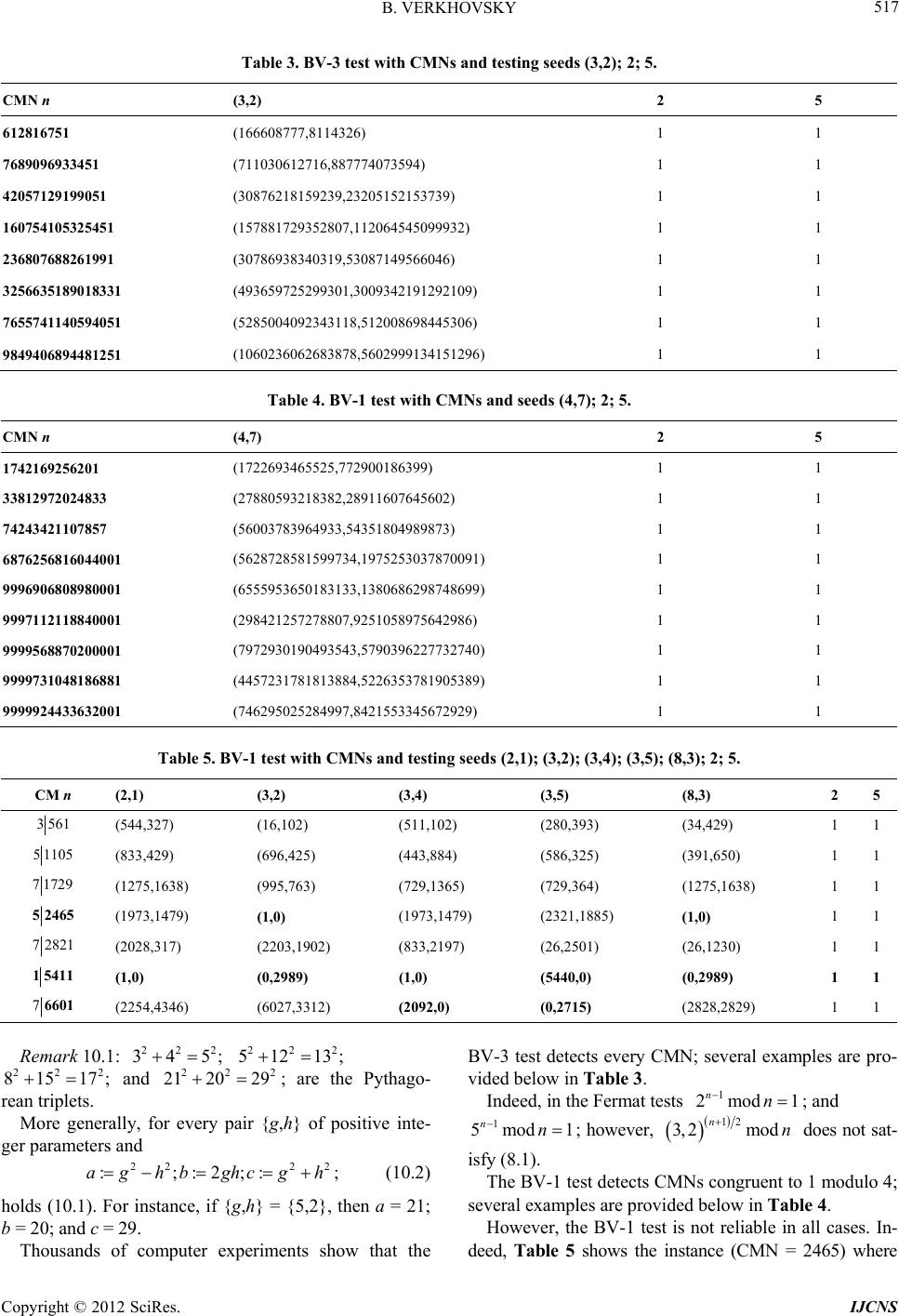



B. VERKHOVSKY 517
Table 3. BV-3 test with CMNs and testing seeds (3,2); 2; 5.
CMN n (3,2) 2 5
612816751 (166608777,8114326) 1 1
7689096933451 (711030612716,887774073594) 1 1
42057129199051 (30876218159239,23205152153739) 1 1
160754105325451 (157881729352807,112064545099932) 1 1
236807688261991 (30786938340319,53087149566046) 1 1
3256635189018331 (493659725299301,3009342191292109) 1 1
7655741140594051 (5285004092343118,512008698445306) 1 1
9849406894481251 (1060236062683878,5602999134151296) 1 1
Table 4. BV-1 test with CMNs and seeds (4,7); 2; 5.
CMN n (4,7) 2 5
1742169256201 (1722693465525,772900186399) 1 1
33812972024833 (27880593218382,28911607645602) 1 1
74243421107857 (56003783964933,54351804989873) 1 1
6876256816044001 (5628728581599734,1975253037870091) 1 1
9996906808980001 (6555953650183133,1380686298748699) 1 1
9997112118840001 (298421257278807,9251058975642986) 1 1
9999568870200001 (7972930190493543,5790396227732740) 1 1
9999731048186881 (4457231781813884,5226353781905389) 1 1
9999924433632001 (746295025284997,8421553345672929) 1 1
Table 5. BV-1 test with CMNs and testing seeds (2,1); (3,2); (3,4); (3,5); (8,3); 2; 5.
CM n (2,1) (3,2) (3,4) (3,5) (8,3) 2 5
3561 (544,327) (16,102) (511,102) (280,393) (34,429) 1 1
51105 (833,429) (696,425) (443,884) (586,325) (391,650) 1 1
71729 (1275,1638) (995,763) (729,1365) (729,364) (1275,1638) 1 1
52465 (1973,1479) (1,0) (1973,1479) (2321,1885) (1,0) 1 1
72821 (2028,317) (2203,1902) (833,2197) (26,2501) (26,1230) 1 1
15411 (1,0) (0,2989) (1,0) (5440,0) (0,2989) 1 1
76601 (2254,4346) (6027,3312) (2092,0) (0,2715) (2828,2829) 1 1
Remark 10.1:
and ; are the Pythago-
rean triplets.
222
345;222 51213;
2
29
22 22
2;:ghcg h
1
2mod 1
nn 
1mod 15nn 
22 2
81517; 22 21 20
More generally, for every pair {g,h} of positive inte-
ger parameters and
:;:aghb; (10.2)
holds (10.1). For instance, if {g,h} = {5,2}, then a = 21;
b = 20; and c = 29 .
Thousands of computer experiments show that the
BV-3 test detects every CMN; several examples are pro-
vided below in Table 3.
Indeed, in the Fermat tests ; and


12
3,2 mod
nn 
; however, does not sat-

isfy (8.1).
The BV-1 test detects CMNs congruent to 1 modulo 4;
several examples are provided below in Table 4.
However, the BV-1 test is not reliable in all cases. In-
deed, Table 5 shows the instance (CMN = 2465) where

B. VERKHOVSKY
518
the BV-1 test fails. Numerous computer experiments de-
tected CMNs in 95% of cases with the BV-1 test; more
details on the experiments are provided in [18].
Remark 10.2: Table 3 shows the cases where every
CMN is detected by the BV-3 test using one seed (3,2)
only.
Remark 10.3: Table 4 shows the cases where every
CMN is detected by BV-1 with one complex seed (4,7)
only.
Remark10.4: n = 2465 in Table 5 is a strong CMN
since it escapes the BV-1 test with seeds (3,2) and (8,3);
n = 6601 is another strong CMN since it escapes this test
with seeds (3,4) and (3,5). Yet, n = 5441 is a prime; these
cases are shown in bold in Table 5.
11. Acknowledgements
Several graduate and undergraduate students of New
Jersey Institute of Technology have participated in thou-
sands of computer experiments. I express my special ap-
preciations to A. Mutovic, D. Rodik, K. Sauraj and S.
Naredla. I also deeply appreciate insightful comments of
C. Pomerance and R. Rubino.
REFERENCES
[1] L. M. Adleman, C. Pomerance and R. S. Rumley, “On Dis-
tinguishing Prime Numbers from Composite Numbers”,
The Annals of Mathematics, Vol. 117, No. 1, 1983, pp.
173-206. doi:10.2307/2006975
[2] C. Pomerance, “Paul Erdös, Number Theorist Extraordi-
naire”, The Notices of the American Mathematical Soci-
ety, Vol. 45, 1998, pp. 19-23.
[3] B. Verkhovsky, “Multiplicative Inverse Algorithm and Its
Space Complexity”, Annals of European Academy of Sci-
ences, Vol. 2, 2004, pp. 110-124.
[4] M. Agrawal, N. Kayal and N. Saxena, “PRIMES Is in P” ,
The Annals of Mathematics, Vol. 160, No. 2, 2002, pp.
781-793.
[5] W. R. Alford, A. Granville and C. Pomerance, “There
Are Infinitely Many Carmichael Numbers”, The Annals of
Mathematics, Vol. 140, No. 3, 1994, pp. 703-722.
[6] C. F. Gauss, “Disquisitiones Arithmeticae”, Yale Univer-
sity Press, New Haven, 1986.
[7] T. ElGamal, “A Public Key Cryptosystem and a Signa-
ture Scheme Based on Discrete Log-Arithmetic”, IEEE
Transactions on Information Theory, Vol. 31, No. 4, 1985,
pp. 469-472. doi:10.2307/2006975
[8] N. Koblitz, A. Menezes and S. Vanstone, “The State of
Elliptic Curve Cryptography”, Designs, Codes and Cryp-
tography, Vol. 19, No. 2-3, 2000, pp. 173-193.
doi:10.1023/A:1008354106356
[9] E. Gethner, S. Wagon and B. Wick, “A Stroll through the
Gaussian Primes”, American Mathematics Monthly, Vol.
105, No. 4, 1998, pp. 327-337. doi:10.2307/2589708
[10] B. Verkhovsky, “Double-Moduli Gaussian Encryption/De-
cryption with Primary Residues and Secret Controls”, In-
ternational Journal of Communications, Network and Sys-
tem Sciences, Vol. 4, No. 7, 2011, pp. 475-481.
doi:10.4236/ijcns.2011.47058
[11] A. Karatsuba and Yu. Ofman, “Multiplication of Multi-
Digit Numbers on Automata”, Soviet Physics Doklady,
Vol. 7, 1963, pp. 595-596.
[12] D. Knuth, “The Art of Computer Programming, Vol. 1:
Fundamental Algorithms”, 2nd Edition, Addison-Wesley,
Boston, 1973.
[13] B. Verkhovsky, “Hardness of Cry ptanalysis of Pu blic Keys
Crypto-Systems with Known Timing of Modular Expo-
nentiation”, Advances in Computer Cybernetics, Vol. 6,
1998, pp. 80-84.
[14] B. Verkhovsky, “Space Complexity of Algorithm for Mo-
dular Multiplicative Inverse”, International Journal of Com-
munications, Network and Syst em Sci ence s, Vol. 4, No. 6,
2011, pp. 357-363. doi:10.4236/ijcns.2011.46041
[15] R. D. Carmichael, “Note on a New Numbe r The ory Func-
tion”, Bulletin of American Mathematical Society, Vol. 16,
No. 5, 1910, pp. 232-238.
doi:10.1090/S0002-9904-1910-01892-9
[16] R. G. E. Pinch, “The Carmichael Numbers up to 1015”,
Mathematics of Computation, Vol. 61, 1993, pp. 381-391.
[17] H. Dubner, “A New Method for Producing Large Carmi-
chael Numbers”, Mathematics of Computation, Vol. 53,
1989, pp. 411-414.
doi:10.1090/S0025-5718-1989-0969484-8
[18] B. Verkhovsky and A. Mutovic, “Primality Testing Algo-
rithm Using Pythagorean Integers”, Proceedings of In-
ternational Computer Science and Information Systems
Conference, Athens, June 2005.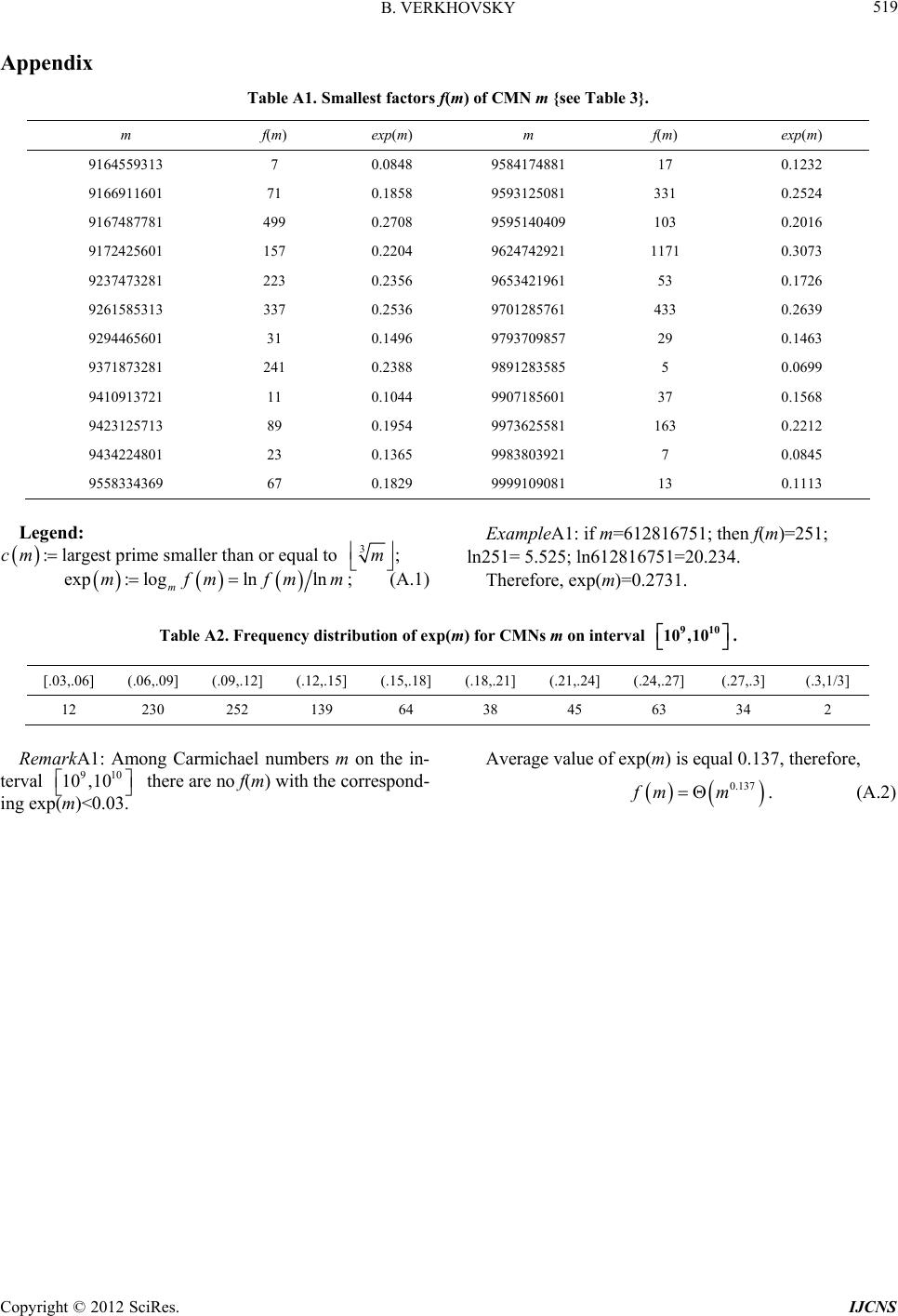

B. VERKHOVSKY 519
Appendix
Table A1. Smallest factors f(m) of CMN m {see Table 3}.
m f(m) exp(m) m f(m) exp(m)
9164559313 7 0.0848 9584174881 17 0.1232
9166911601 71 0.1858 9593125081 331 0.2524
9167487781 499 0.2708 9595140409 103 0.2016
9172425601 157 0.2204 9624742921 1171 0.3073
9237473281 223 0.2356 9653421961 53 0.1726
9261585313 337 0.2536 9701285761 433 0.2639
9294465601 31 0.1496 9793709857 29 0.1463
9371873281 241 0.2388 9891283585 5 0.0699
9410913721 11 0.1044 9907185601 37 0.1568
9423125713 89 0.1954 9973625581 163 0.2212
9434224801 23 0.1365 9983803921 7 0.0845
9558334369 67 0.1829 9999109081 13 0.1113
Legend:

3
:largest prime smaller than or equal to cm m




;
 
exp:logln
m
mfmlnfmm
910
10 ,10
; (A.1)
ExampleA1: if m=612816751; then f(m)=251;
ln251= 5.525; ln612816751=20.234.
Therefore, exp(m)=0.2731.


Table A2. Frequency distribution of exp(m) for CMNs m on interval .

[.03,.06] (.06,.09] (.09,.12] (.12,.15] (.15,.18] (.18,.21] (.21,.24] (.24,.27] (.27,.3] (.3,1/3]
12 230 252 139 64 38 45 63 34 2
RemarkA1: Among Carmichael numbers m on the in-
terval  there are no f(m) with the correspond-
ing exp(m)<0.03.
Average value of exp(m) is equal 0.137, therefore,
910
10 ,10




0.137
fm m . (A.2)