Received 7 August 2015; accepted 22 September 2015; published 25 September 2015

ABSTRACT

We try briefly the relationship between numbers and some aspects of physical reality. By means of a simple set of mathematical and physical tools what we wanted to find was dimensionless numbers that could fit with a particular symmetry. In this paper we describe a small sheaf of numerical results.

Keywords:

Universe, Numerology

1. Introduction

In his book “Philosophy of Physics” [1] Mario Bunge states that every physical hypothesis must be expressed mathematically. But mathematical form alone won’t tell us anything about the physical meaning of the formula. By itself mathematical theories are neutral with respect to any hypotheses about the actual world. Numerology can be defined as the juggling with dimensionless constants with a view to producing significant relations. Number games can occasionally lead to insights and even spark a theory proper.

Also it’s known that P.A. Dirac, inspired by Eddington, Milne and others suggested a reconsideration of Cosmology based on the large dimensionless numbers that could be constructed from the fundamental constants of nature. Namely, all very large numbers occurring in nature are interconnected [2] .

Besides, there is the issue of reality’s stuff: Is it continuous or discrete? We assume that spacetime is granu- lar.

2. Method

We’ll analyze relationship among physical constants using a simple tool-kit of mathematical and physical concepts described as defined below.

I. Symmetry (ng + mj) where n, m are natural numbers. And the ratio

II. Series 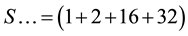including series having the same symmetry.

III. As for the subject of the discreteness of space-time, we’ll apply Avogadro’s number [3]

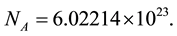
IV. An item called “sit”, associated with the topic III, representing a space-time size, arbitrarily very small.

Define

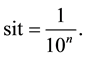
(By the way you can obtain a good approximation to the number p using properly topics I and II, as we described in a paper time ago).

3. Some Selected Results

Without further delay we will describe some examples of the matter at hand.

3.1. A Geometric Beginning

Start looking back on the topics I and II. Assign specific values to each

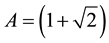(1)

(2)

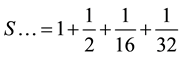(3)

will include two concepts more:

Euler’s number e = 2.7182818…

And Neutron-Proton mass ratio [4]

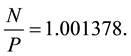
Obtaining the following equation of evolution

(4)

Resulting volume to define in paragraph 3. Now, it is easy to see that

(5)

This new volume is defined as follow

(6)

Therefore the evolution from the Torus 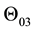to the Torus

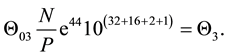(7)

3.2. Vacuum Expectation Value of the Higgs Field

The Higgs field has a nonzero expectation value

[5] .

The energy in electron volts of a photon after Planck equation [6] reads

(8)

[7] .

Assign a specific frequency

(9)

The resulting equation relates the volume of a particular Torus with the Higs vacuum value and the energy in eV of a photon at a specific frequency mode of vibration

(10)

Now it’s interesting to see the following numerical equivalence

(11)

Therefore rearranging the equation for the evolution described above

(12)

3.3. A Light Beam Travels Three Spatial Axes for a Specified Period of Time; the Resulting Spatial Volume Is Equal to the Volume of a Particular Torus

Volume inside a Torus

[8] .

Suppose:

refers to length dimension associated to Avogadro’s number.

Therefore the volume of this particular Torus is defined as follow

(13)

The distance light travels in one second in vacuum

[9] .

Write three spatial axes light will travel

Duration of travel in each of the axes

, and.

(It’s worth to say that according to the most recent data from the cosmic microwave background (CMB), the age of the universe is around 10¹⁷ seconds [10] ).

Consequently

Therefore polyhedron’s volume

(14)

A simple arithmetic operation shows that

(15)

The results of paragraphs 1, 2 and 3 lead us to write the schematic sequence of evolution

(16)

3.4. Relationship among and Proton Compton Wavelength

Proton Compton wavelength is equivalent to the wavelength of a photon whose energy is the same as the rest-mass energy of the particle.

The Compton wavelength of the proton

[11] .

Relationship between and Avogadro’s number reads

(17)

Now, consider a sphere whose radius is equal to

(18)

And the volumen inside a Torus defined in Equation (13)

Trying to abreviate symbols

(19)

Now will write the resulting formula

(20)

(it is assumed that the volume units are canceled on both sides of the equation).

3.5. Einstein’s Gravitational Constant

Einstein’s constant denoted K (kappa) is a coupling constant that appears in his field equations, whose value is given by

[12] .

Write the volume of a particular torus

(21)

will apply the atomic mass constant

[13] .

Consider a system whose mass is

(22)

and whose acceleration is equal to

(23)

Therefore the system acquires a force

(24)

It’s easy to check that Einstein’s gravitational constant units are given by

Apply an arbitrary value to the fourth method’s topic associated with the time dimension

(25)

Now, will arrange all the concepts in the following formula

(26)

3.6. Today Energy Density

The energy density of Cosmic microwave background (CMB) in the current epoch, at a temperature T₀ = 2.726 K

[14] .

Looking for a dimensionless number, write the following equation

(27)

h refers to Planck constant

[15] .

The letter e refers to the Euler’s number = 2.7182818…

As for Torus volume in Equation (27) let’s rewrite Equation (13)

The quantity 10⁹² could be written differently:

As for the CMB, the spectral radiance peaks at

[16]

in the microwave range of frequencies.

We should also mention the ratio between and Euler’s number

(28)

3.7. Black Hole Entropy

Starts with Bekensteing-Hawking equation [17] describing the entropy of a black hole

(29)

C refers to speed of light in vacuum (already referenced in paragraph 3).

Newtonian constant of gravitation

[18]

[19]

Write the surface’s area of a torus

[20] .

Define a certain dimension of length associated to Avogadro’s constant

which is equivalent to the Planck scale [21] .

Assign to the larger radius of the torus the value

refers to an Avogadro’s number “collapsed”. (This is intended to symbolize the collapse of a huge star into a black hole)

As for the smallest radius

Now write the area of this particular torus

(30)

Summarize the formula for entropy

(31)

Symbol (Greek capital letter theta with subscript 2) stands for torus surface as was described above. We found

(32)

which in other way reads

(33)

α is the fine-structure constant [22] , dimensionless value associated to electromagnetic interaction, equal to 0.007297353… (at zero energy).

4. Discussion

Since the aim of this paper is only to review some numerical approaches to the physical constants and the physical amounts that defines the universe and reality, nobody should have to wait a theory nor one set of predictions.

We found interesting review the numerical equivalence described by Equation (13) because the accuracy of significant digits between the constants involved in both volumes. Still more when proton Compton wavelength fits numerically (20).

The above considerations are also valid for the material developed under paragraph 5, while recognizing greater freedom (arbitrariness) in the use of the “sit”.

We think appropriate to briefly comment the numerical connection among Equations (13), (20) and (26). It allow us to note a numerical linkage between one parameter belonging to Quantum mechanics, i.e. proton Compton wavelength with another one parameter associated with General relativity as Einstein’s gravitational constant (k).

As for the items 1 and 2, considering the assumptions or theories about cosmic inflation and related matters, we have seen curious the sequence (16). Of course always from a numerical point of view.

Under the heading 6, we review two subjects. On one side is the number of photons in the Universe. Although it is still a speculative matter, estimations range around 10⁹⁰, hence we have seen interesting the value obtained in the Equation (27) related to the Avogadros number i.e.. On the other hand it should be noted that Euler’s number come on the scene spontaneously while we operated with other values.

Finally, the matter of black hole entropy shows high numerical accuracy. Although we have chosen arbitrarily the type of Surface and the value of the “sit”. As the values of speed of light and Planck constant are very accurate, we would have a more accurate value of G, the Newtonian constant of gravitation.

5. Conclusion

As for the numerology applied to Physics and Cosmology we have selected a little set of subjects. In our view they are numerically interesting. Maybe someone can see in it some kind of theoretical inspiration.

Acknowledgements

We want to thank Kelly Sang and Freya Zhang for helpful recommendations in the correct edition of this paper.

Cite this paper

AlbertoCoe, (2015) Some Numerical Curiosities about the Universe. Journal of Modern Physics,06,1671-1678. doi: 10.4236/jmp.2015.611169

References