Theoretical Economics Letters
Vol.2 No.2(2012), Article ID:19331,2 pages DOI:10.4236/tel.2012.22042
The Policy Role in the Stock Markets
Economics Department, University of the West Indies, St. Augustine, USA
Email: malghalith@gmail.com
Received April 5, 2012; revised April 20, 2012; accepted April 27, 2012
Keywords: Portfolio; Stock; Risk-Free Interest Rate; Policy
ABSTRACT
This note is an attempt to model the role of the policymaker in stabilizing the stock markets. In doing so, we present an elasticity formula that links the risk-free interest rate to the value of the stock index.
1. Introduction
The theoretical literature on portfolio selection is vast (see, for example, [1-3] among many others. However, the empirical applications of these models have not been extensive. Moreover, the policy role in the financial markets is neglected by the literature, given the extreme importance an the timeliness of the topic in a very volatile financial environment.
To our knowledge, this note is the first methodological and empirical attempt to model the role of policy (the Central Bank) in stabilizing the financial markets. More specifically, we introduce a novel method of measuring the preferences of investors. In doing so, we used historical observed data to compute the values of the unobserved preferences. The results of this estimation are immensely valuable to policy makers because they reveal to them important information about the financial markets. Most importantly, we develop an elasticity formula that links the risk-free interest rate to the value of the portfolio. This formula is very useful to policymakers, since they control the risk-free interest rate. That is, they can adjust this rate to offset a decline in the value of the stock index. This note is organized into two main sections: the development of the model and the empirical analysis using data for the Trinidad and Tobago stock market.
2. The Model and Method
We develop our model using the stochastic portfolio model (see, for example, [4] among many others). The dynamics of the risky asset price are given by
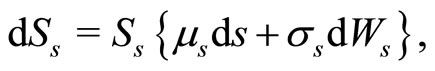 (1)
(1)
where the superscript ![]() denotes time,
denotes time, 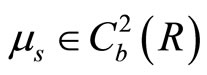 and
and 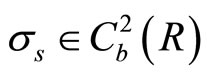 are the rate of return and the volatility, respectively.
are the rate of return and the volatility, respectively.
The wealth process is given by
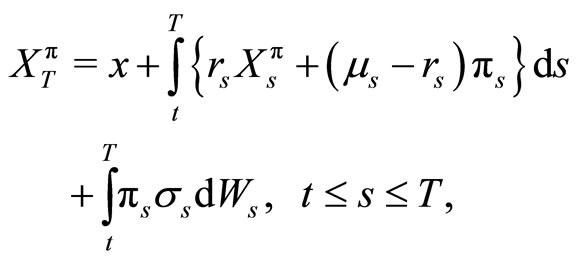 (2)
(2)
where ![]() is the initial wealth,
is the initial wealth, 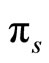 is the portfolio process, with
is the portfolio process, with 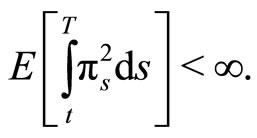 The portfolio
The portfolio 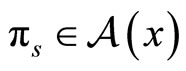 is admissible (i.e.
is admissible (i.e.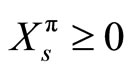 ) The dynamics of the wealth process are given by
) The dynamics of the wealth process are given by
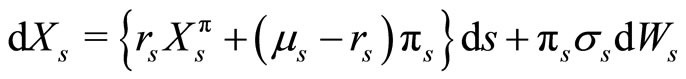
The investor maximizes the expected utility of the terminal wealth
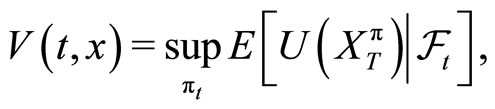 (3)
(3)
where 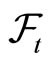 is the filtration of information,
is the filtration of information, 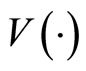 is the value function,
is the value function, 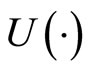 is a continuous and bounded utility function.
is a continuous and bounded utility function.
If the value function is smooth, it satisfies the HamiltonJacobi-Bellman partial differential equation
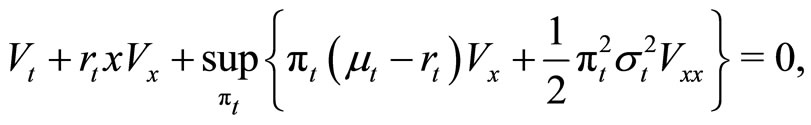 (4)
(4)
Hence, the optimal solution is
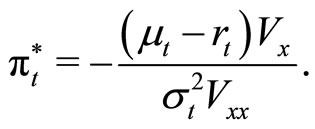 (5)
(5)
The crucial relationship for policymakers is the relationship between the optimal portfolio (index) and the Treasury Bill rate (the risk-free rate). This relationship is given by the following elasticity formula
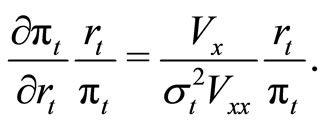 (6)
(6)
3. Empirical Results
However, we need to to generate a data series for 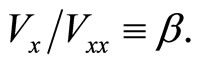 In particular, we used daily data (2005-2011) for the Trinidad and Tobago Composite Index
In particular, we used daily data (2005-2011) for the Trinidad and Tobago Composite Index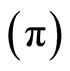 , the discount rate on the Trinidad and Tobago Treasury bills
, the discount rate on the Trinidad and Tobago Treasury bills 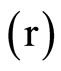 and the return on the Trinidad and Tobago Composite Index
and the return on the Trinidad and Tobago Composite Index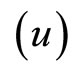 . We also generated data for the volatility of the index as follows
. We also generated data for the volatility of the index as follows
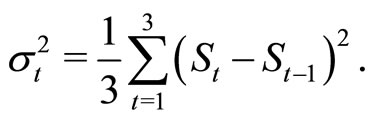
Using (5), we generate the following data series for 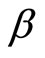 by direct calculations. Thus, we can calculate (6), using the average values of
by direct calculations. Thus, we can calculate (6), using the average values of 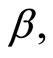
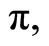
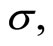 and
and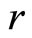 , as follows
, as follows
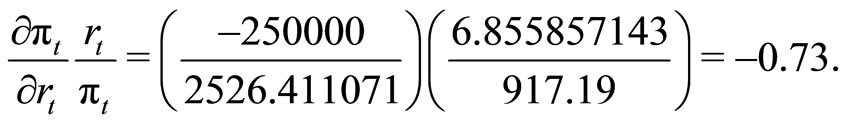
Thus a 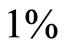 decrease in the Treasury bill rate will increase the portfolio by
decrease in the Treasury bill rate will increase the portfolio by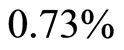 . This relationship enables the policymakers to offset swings in the portfolio and thus stabilize the stock market.
. This relationship enables the policymakers to offset swings in the portfolio and thus stabilize the stock market.
REFERENCES
- M. Alghalith, “General Closed-Form Solutions to the Dynamic Optimization Problem in Incomplete Markets,” Applied Mathematics, Vol. 2, No. 4, 2011, pp. 433-435. doi:10.4236/am.2011.24054
- S. E. Shreve and H. M. Soner, “Optimal Investment and Consumption with Transaction Costs,” The Annals of Applied Probability, Vol. 4, No. 3, 1994, pp. 609-692. doi:10.1214/aoap/1177004966
- G. Yin and X. Y. Zhou, “Mean Variance Portfolio Selection under Markov Regime: Discrete Time Models and Continuous Time Limits,” Proceedings of the 15th International Symposium on Mathematical Theory of Networks and Systems, Leuven, 5-9 July 2000, pp. 1-6.
- J. Cvitanic and F. Zapatero, “Introduction to the Economics and the Mathematics of Financial Markets,” MIT Press, Cambridge, 2004.

