Engineering, 2010, 2, 438-444
doi:10.4236/eng.2010.26057 Published Online June 2010 (http://www.SciRP.org/journal/eng)
Integrated Optimization of Mechanisms with Genetic
Algorithms
Jean-Luc Marcelin
Laboratoire G-SCOP, Université de Grenoble, Domaine universitaire, Grenoble, France
Received January 27, 2010; revised March 6, 2010; accepted March 9, 2010
Abstract
This paper offers an integrated optimization of mechanisms with genetic algorithm, the principle of which is
to use a neural network as a global calculation program and to couple the network with stochastic methods of
optimization. In other words, this paper deals with the integrated optimization of mechanisms with genetic
algorithms, and, in conclusion, the possible use of neural networks for complex mechanisms or processes.
Keywords: Optimization, Mechanisms, Genetic Algorithm
1. Introduction: The Need for an Integrated
Optimal Design Process
The search for the best compromise between economic,
mechanical and technological imperatives has always
been the primary aim of the mechanical engineer. The
methods used to achieve these excellence objectives have
considerably evolved over the last years. The author's
experience in optimization began in 1983. At this time,
the design stage was the main concern, and then came
the calculation and afterwards the optimization. In prac-
tice, and during shape optimization of mechanical struc-
tures, occurred between 1985 and 1990, many extreme
cases were encountered. In these cases, the optimization
was not necessary until damage occurred during service;
the author’s industrial partners realized, often too late,
that their designing left quite a bit to be desired. They
would then call for the author’s help in using optimiza-
tion programs to supply them with an improved shape.
These shapes were reached despite technological limita-
tions being very severe at this stage; so severe, in fact,
that engineers were powerless to resolve the problem.
Innumerable problems such as this were dealt with.
Such an approach to designing has become unthink-
able these days. The economic competition has increased,
the design and manufacture delays have been reduced
and therefore the numerous overlaps that this approach
involves have become prohibitive. That is, optimization
can no longer be distinct from designing. It is now ad-
mitted that, in an integrated design approach, optimiza-
tion has to begin from the design stage, taking into ac-
count the constraints both in terms of specification and
those induced by different materials. Optimization is
therefore facilitated because constraints or limitations
can be more easily varied, in agreement with all those
involved with the project.
This paper aims at showing that the integration of op-
timization from the design phase is possible thanks to the
new optimization techniques, according to the author.
Some optimization methods are popular for now, they
are known as probabilistic or stochastic. For example,
the simulated annealing method or genetic algorithms,
whose principle advantages are an assured convergence
without the use of derivatives and eventual functions
with discrete and non-derivable variables, even though
determinist methods of optimization (called gradient
methods) require a calculation resistant to these sensi-
tivities. Genetic algorithms rely on the natural laws of
selection which let a living organism adapt to a given
environment. From these principles, it seems judicious to
apply genetic algorithms to the optimization of mechanical
structures. Precise examples will show that genetic algo-
rithms will allow the adaption of the mechanical object
to its environment and to the specifications, from the
beginning of the design process.
State of the art
In [1], an integrated design optimization combining the
mechanism method with genetic algorithms is presented.
The former is currently one of the principal arch assess-
ment tools; the latter are powerful numerical function
optimization techniques. The method is proposed as a
design aid for structural engineers involved in the as-
sessment, maintenance and repair of existing bridges, or
the design of new arches. In [2], fully integrated design
optimization of plate structures is presented. First, to-

J. L. MARCELIN 439
pology optimization is introduced based on a hybrid al-
gorithm, then fitting optimization is applied. Finally, the
sizing optimization is described. In [3], the research tries
to define the class of perfectly flexible mechanism. It
proposes a generalized design methodology of perfectly
flexible mechanism, and attempts to explore the technique
of integrated mechanism for achieving the most optimal
design alternative. In [4], a novel optimization approach
to the design of mechanisms in morphing aircraft struc-
tures is presented. The layout of the mechanism and the
location and number of actuators and pivots are deter-
mined by an extended formulation of a material-based
topology optimization. The design problem is modeled
within a coupled fluid-structure analysis framework to
directly assess aerodynamic performance criteria while
optimizing the overall mechanized system. In [5], it is
said that the integrated design of missile weapon system is
quite complicated, which challenges the sharing and op-
timization of models and design parameters. The paper
first presents the conception of virtual collaborative de-
sign space on the basis of technology of virtual prototype
and computer supported cooperative work, and then
brings forward the architecture of virtual collaborative
studio for integrated missile design and optimization.
On one hand, after introducing the methods and tools
used (in part 2), this paper focuses on applications in the
field of mechanical technology, and then on the analysis
of mechanical systems (part 3). The examples of part 3
are to illustrate that the integrated optimization of me-
chanical structures has become a reality.
On the other hand, the conclusion explains why the
difficulties are more important in the case of an inte-
grated, optimal design process of mechanical systems,
because of the complexity of the problems. Nevertheless,
an integrated optimization can effectively be considered
with the use of neural networks. Therefore, the conclu-
sion provides a possible solution for the whole problem.
2. The Methods Used: Adaptation of
Optimization Tools to Mechanical
Technology
In addition to the above-mentioned elements, the author's
experience began with the shape optimization of me-
chanical structures (2-D and symmetrical), although this
was in the context of conventional design. See [6,7].
Mathematical optimization programs were quite diffi-
cult to use and not sufficiently versatile to adapt quickly
to new cases. According to author, the optimal integrated
design could not be achieved with normal mathematical
programming techniques, which require a formulation
heavily specific to each given problem. This paper aims
at showing that stochastic techniques are ideally suited to
integrated optimization and to mechanical technology
problems.
Note that the problems’ main features are the follow-
ing:
―the design variables are often a mixture of discrete
and continuous values;
―they are often highly constrained by strict techno-
logical constraints.
The problem consists in maximizing a function of n
variables. The principle of genetic algorithms is to make
a population of individuals evolve according to a replica
of Darwinian theories. The starting point is a population
of individuals, chosen randomly and coded by binary
numbers (as an example) called chromosomes. From this
point, the algorithm generates, more or less randomly,
new populations formed from individuals, increasingly
more adapted to a given, well-defined environment. Se-
lections and reproductions are made from the best per-
forming parents of the population from which they come.
They are stochastic or deterministic. These offsprings are
generated applying genetic operators (mutation, cross-
ing). It is always stochastic. The new replacement popu-
lation is created by the selection of the best performing
individuals, either among the offspring or its parents.
The substitution is either stochastic or deterministic. In
the books [8-11], additional information can be found,
and the convergence of the method is shown.
The main advantage of these methods is that they op-
erate simultaneously on a test space of the solutions. The
genetic method differs from the simulated annealing
method, because of the operators which are used to force
the evolution of the test population. In all cases, the con-
vergence is always assured towards an extreme. This
extreme is not necessarily the absolute extreme, but has
more chance of being so, than with the use of a tradi-
tional gradient method. This is shown in [8]. Actually, a
stochastic method explores a larger solution space. In
addition, another crucial advantage of these methods is
the small number of required assumptions for the objec-
tive function. Genetic algorithms are now well-known.
Neural networks
We are to study the possible use of neural networks in
the conclusion. The operation of artificial neural net-
works, as their name suggests, comes from that of bio-
logical neural networks, from which lots of terms have
been borrowed. To the author, this is as far as the simi-
larities go. More details on the theory, which will be
summarized later, can be found in [12]. The use of neural
networks for the simulation or modeling will be done in
two stages: one phase called apprenticeship, using finite
elements calculations―for example in mechanics of struc-
tures―and then a calculation or generalization phase. In
the present case, neural networks should be able to esti-
mate an objective function or a cost function of entry or
design variables. It should be noted here that the entry
variables will be the binary digits of the chromosomes―
when using a G.A.―or the real values of the design
variables―when using the simulated annealing method.

J. L. MARCELIN 440
The apprenticeship phase consists in optimizing or
adapting, through an apprenticeship rule and by modify-
ing the weights at each link. To do this, an apprentice-
ship sample is used, that is solutions which will be pre-
viously determined by finite element analysis, for exam-
ple in mechanics of structures. The principle criterion is
to have a minimal error for the evaluation of the function.
Local adaption rules (for which the weight optimization
is based on the states of the neurons connected to corre-
sponding links) are distinguished from other rules, which
are much more difficult to put into use. The best known
local rules, for which details can be found in [12], are the
ones called supervised or non-supervised, and the itera-
tive rules.
To summarize, a neural network works in two phases.
In the first place, the apprenticeship phase, during which
the adaption function is active. This allows the weight
values to be optimized from a set of entry values (the
design or conception variables) and from exit values (the
objective function(s) or cost function) called the appren-
ticeship set. Then, the values of the weights are fixed
during the second phase that is the calculation or genera-
tion mode. This allows the calculation by the neural
network of the exit values, as a function of the entry val-
ues.
The results obtained bring a lot of hope in applying
neural networks to modeling, especially for the simula-
tion of the calculations for mechanical structures. See [13]
and [14]. The continuation to modeling seems natural, as
the action of modeling a process or a behavior requires
knowing the principle characteristics of the process or
behavior. The network knows how to extract these char-
acteristics and can therefore be memorized easily.
3. Integrated Optimal Design of Particular
Mechanical Systems Optimization of
Gears
Gears are very complicated components. A large number
of dominating factors vary in every case: radius of cur-
vature, unitary loading, pressure, slip speeds, etc.... In
some cases, the design variables are huge and take very
discrete values (such as the module, the choice of mate-
rials). Often, several objectives work in competition:
balancing the energy transmission in bending and under
pressure, optimization of masses, balancing the slips, to
mention only a few. The idea consists of automatically
dimensioning a right-sided cylindrical gear or helical
gear, so as to find a good compromise between a mini-
mum weight, dynamic performance (energy transmission)
and geometric criteria such as balancing the slips. This
optimization problem is very difficult to solve by hand
and often leads to compromised solutions that are not
entirely satisfactory, therefore the idea of an automatic
optimization technique is most desirable for this complex
problem. The mathematical optimization methods de-
pend on the understanding of objective function gradi-
ents and are difficult to adapt to gears for three main
reasons:
1) first, some design variables are continuous while
others are discrete,
2) then, derived programming is quite delicate because
the optimizing functions often depend implicitly on the
design variables,
3) finally, the major flaw is that these methods become
blocked at a local extreme (often, the only way to pursue
the program is to rerun the calculation from a new start-
ing point). As all specialists must know, the optimization
of gears has numerous solutions and often it is better to
adapt them to given situations. Therefore, this leads to
the use of a genetic algorithm to solve the problem. The
problem of gear optimization is illustrated in Figure 1.
This problem presents two main difficulties. First of
all, coding the solution in the form of a simple and effi-
cient chromosome is complicated; so is finding a good
compromise according to different objectives between
the different criteria (weight, power differential, balanc-
ing slips).
The coded parameters are restrained so the field of
study is not too large, and therefore the chromosome is
not too long. In this way, we have not considered all of
the design parameters in gearing, but only six main pa-
rameters: k, z1, x1, x2, mn0, and the material; other pa-
rameters such as the helix angle are fixed during the op-
timization. In such a case, this choice can be modified
without any problems (Figure 1).
When selecting the objective function, we use a
multi-objective technique where the objective function
will actually be a balanced sum of the different functions
that we want to obtain, such as the minimum weight and
minimum difference between slips. In this case, we must
compare some objectives with others; the effective
choice can easily be reset, in the case of the same script
for different objectives (the shape under which they ap-
pear is chosen by the researcher in the field of optimiza
tion). Above all though, the difficulty consisted in
choosing the weighting of the coefficients, in respect to
a
n1
n2
Z1 ?x1 ?mn0 ?
x2 ? materials ?
b ?
Figure 1. Definition of optimizing gearing.

J. L. MARCELIN 441
their influence (that are of different natures). This can
only be done as a result of numeric experiments, where
the goal was to find the best possible compromise be-
tween various objectives.
In the first place, the coding of the variables that we
used in the genetic algorithm is the following: each of
the values: k, z1, x1, x2, mn0 and materials are encoded
in a binary numeration system. So, six strings are ob-
tained C1, C2, C3, C4, C5, C6, lengthing 4, 6, 6, 7, 4, 3
respectively.
An example of a genetic identity card (chromosome)
for a gearing system is given here.
Genetic identity coding (chromosome) for gearing:
1001 110101 101100 1010100 1001 010
C1 C2 C3 C4 C5 C6
C1: size coefficient of tooth ‘k’,
C2: number of teeth ‘Z1’,
C3: coefficient ‘x1’,
C4: coefficient ‘x2’,
C5: real shape module ‘mn0’,
C6: material chosen from a library of 8 different types.
This coding is limited to a thirty-gene-long chromo-
some, and the genes are arranged end to end (the order is
not important), so is the relative information of the gear-
ing. This coding restrains the admissible field of design
itself. There are only 24 = 16 possible width ‘k’ coeffi-
cients; only 26 = 64 possibilities for the number of teeth
‘z1’ (that can vary between 12 and 75 for example); x1
and x2 only vary between –0.5 and 0.5 with two signifi-
cant numbers; for mn0 there are 16 normalized numbers
possible; finally, the material is the same for the pinion
and for the gearwheel, and eight possible choices can be
selected from the library of materials. For example, the
code 001 corresponds to 30CND8, the code 110 to 16NC6,
and so on. It is thereafter possible to modify the structure
or the length of the chromosome without too much diffi-
culty.
In the second place, ‘multi-objective’ functions, in the
case of gearing, are rather complicated. According to u,
the following allows us to modify at will, according to
the results of diverse numerical experiments. The idea is
to build the function as if it were the sum of the weighted
representative terms, by coefficients that we can have
varied when we wish, more or less according to the im-
portance of such and such a criterion. The function that
we used for the following tests is illustrated below:
10 11 22s1 s2
max1 max
3r uptransprestrans
trans
Ibd
F10()() Igg
Rap bd
Rap
I[ Pc.PPc.P]
P
 

I1, I2 and I3: weighting coefficients,
gs1, gs2: maximum absolute slips,
Rap: ratio of quality against price of material,
b: width of material,
d1: primitive diameter of pinion.
The presence of the term 1010 is due to the fact that the
G.A. maximizes the functions. To calculate the functions
at a minimum, it is possible to look for the maximum of
the opposing function plus a very large term. The second
term affected by coefficient I1 is a term relating to the
minimization of gear size, in relation to a given maxi-
mum size. This term is penalized when it comes to the
quality/price ratio of a material. The third term, affected
by coefficient I2, expresses the equalizing of the absolute
slip (crucial in reducing wear). Finally, the fourth term,
affected by coefficient I3, is a term expressing the search
for balance between the transmissible powers under
pressure and under flexion, and that must also respect the
safety factor with relation to power transmitted. It is pos-
sible to add other criteria to this multi-objective function,
e.g., a term expressing maximization of driving relation,
or a term ensuring imposed distances between axes are
respected. After several numeric tests on a basic example,
the below values of weighting coefficients were chosen
for the following test case:
I
1 = 0.2
I2 = 0.1
I3 = 10
This test deals with a helical gear used in a fixed axis
gearbox.
The parameters of the G.A. are:
population size = 200
number of generations = 100
The results are compared to a reference solution, op-
timized using other methods.
The given factors are:
Ptrans = 400 KW
Nmax(input) = 1,485 rpm
transmission relationship u = 6
developing circle of teeth b = 8°33'
Quality factor Q = 6
Life H = 200,000 hours
operating with negligible shock.
The following is the best solution of the last generation:
Geometrical analysis :
mn0 Z1 x1 x2 k Material
reference solution 5 26 0.44 –0.45 32 16NC6
genetic algorithm 6 23 0.10 0.09 13 16NC6
reference solution genetic algorithm
width b (mm) 160 78
d1 (mm) 131.4 139.9
volume bd12 2.7E6 1.5E6
gs1 0.24 0.48
gs2 0.33 0.30
ee 1.63 1.85
Pflex (kW) 1100 760
Ppres (kW) 1000 740
The objectives have been achieved: that is, we ob-
tained a correct balance between absolute slips gs1 and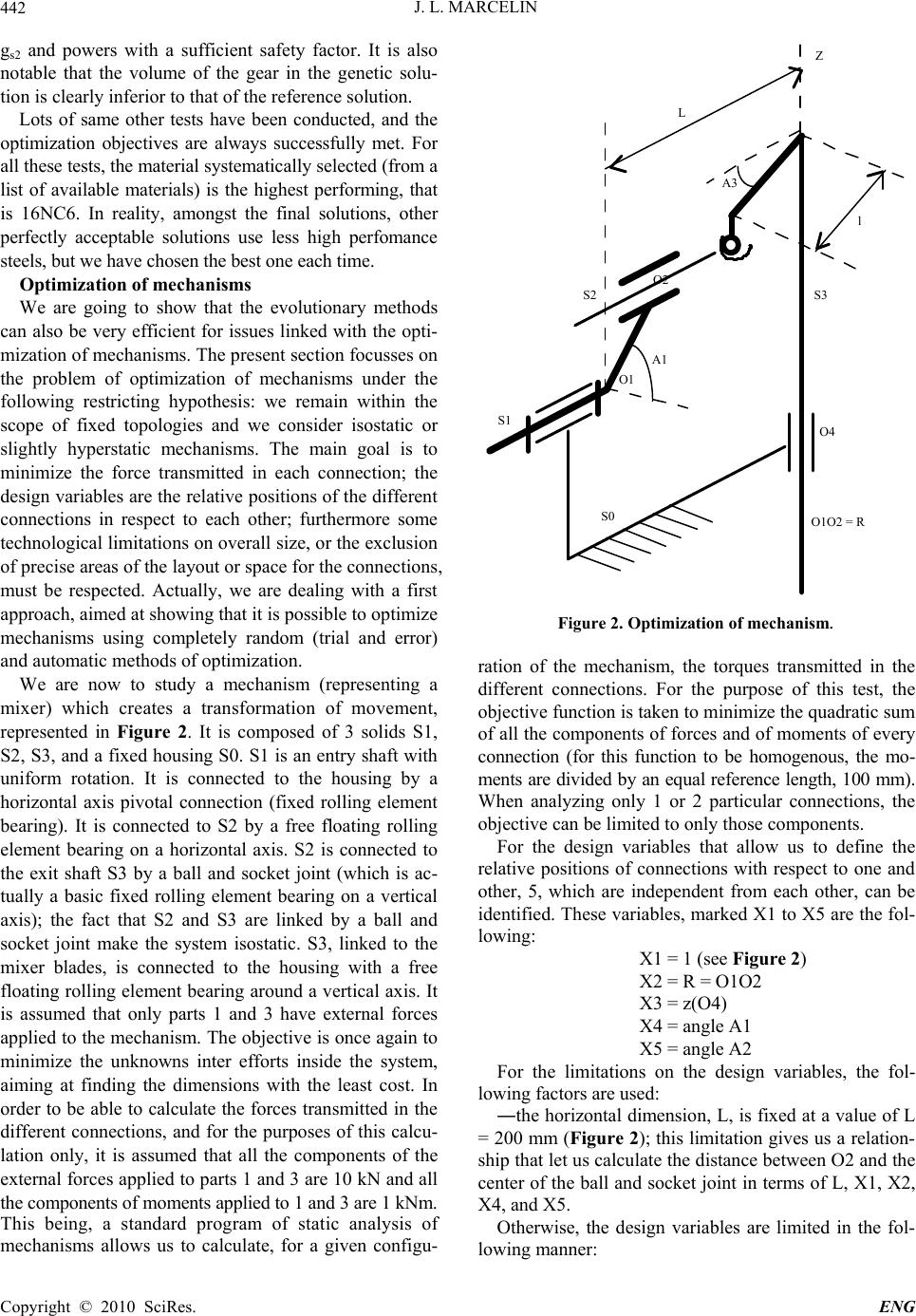

J. L. MARCELIN 442
gs2 and powers with a sufficient safety factor. It is also
notable that the volume of the gear in the genetic solu-
tion is clearly inferior to that of the reference solution.
Lots of same other tests have been conducted, and the
optimization objectives are always successfully met. For
all these tests, the material systematically selected (from a
list of available materials) is the highest performing, that
is 16NC6. In reality, amongst the final solutions, other
perfectly acceptable solutions use less high perfomance
steels, but we have chosen the best one each time.
Optimization of mechanisms
We are going to show that the evolutionary methods
can also be very efficient for issues linked with the opti-
mization of mechanisms. The present section focusses on
the problem of optimization of mechanisms under the
following restricting hypothesis: we remain within the
scope of fixed topologies and we consider isostatic or
slightly hyperstatic mechanisms. The main goal is to
minimize the force transmitted in each connection; the
design variables are the relative positions of the different
connections in respect to each other; furthermore some
technological limitations on overall size, or the exclusion
of precise areas of the layout or space for the connections,
must be respected. Actually, we are dealing with a first
approach, aimed at showing that it is possible to optimize
mechanisms using completely random (trial and error)
and automatic methods of optimization.
We are now to study a mechanism (representing a
mixer) which creates a transformation of movement,
represented in Figure 2. It is composed of 3 solids S1,
S2, S3, and a fixed housing S0. S1 is an entry shaft with
uniform rotation. It is connected to the housing by a
horizontal axis pivotal connection (fixed rolling element
bearing). It is connected to S2 by a free floating rolling
element bearing on a horizontal axis. S2 is connected to
the exit shaft S3 by a ball and socket joint (which is ac-
tually a basic fixed rolling element bearing on a vertical
axis); the fact that S2 and S3 are linked by a ball and
socket joint make the system isostatic. S3, linked to the
mixer blades, is connected to the housing with a free
floating rolling element bearing around a vertical axis. It
is assumed that only parts 1 and 3 have external forces
applied to the mechanism. The objective is once again to
minimize the unknowns inter efforts inside the system,
aiming at finding the dimensions with the least cost. In
order to be able to calculate the forces transmitted in the
different connections, and for the purposes of this calcu-
lation only, it is assumed that all the components of the
external forces applied to parts 1 and 3 are 10 kN and all
the components of moments applied to 1 and 3 are 1 kNm.
This being, a standard program of static analysis of
mechanisms allows us to calculate, for a given configu-
S0
S1
S2 S3
O1
O2
O1O2 = R
l
L
Z
O4
A1
A3
Figure 2. Optimization of mechanism.
ration of the mechanism, the torques transmitted in the
different connections. For the purpose of this test, the
objective function is taken to minimize the quadratic sum
of all the components of forces and of moments of every
connection (for this function to be homogenous, the mo-
ments are divided by an equal reference length, 100 mm).
When analyzing only 1 or 2 particular connections, the
objective can be limited to only those components.
For the design variables that allow us to define the
relative positions of connections with respect to one and
other, 5, which are independent from each other, can be
identified. These variables, marked X1 to X5 are the fol-
lowing:
X1 = 1 (see Figure 2)
X2 = R = O1O2
X3 = z(O4)
X4 = angle A1
X5 = angle A2
For the limitations on the design variables, the fol-
lowing factors are used:
―the horizontal dimension, L, is fixed at a value of L
= 200 mm (Figure 2); this limitation gives us a relation-
ship that let us calculate the distance between O2 and the
center of the ball and socket joint in terms of L, X1, X2,
X4, and X5.
Otherwise, the design variables are limited in the fol-
lowing manner:

J. L. MARCELIN 443
0 < X1 < 100
0 < X2 < 50
–100 < X3 < 0
0 < X4 < 90°
0 < X5 < 45°
For this test, we must make an initial optimization us-
ing a G.A. to roughly work out the problem. The more
precise optimization uses simulated annealing methods,
starting from an initial solution given by the G.A..
Therefore, the optimization by the G.A. will be effective
and, as it is only used for the first approximation, we
limit the coding of the five design variables to a binary
chromosome of 10 digits in total. The structure of this
binary chromosome is the following:
―the first 2 digits allow the coding of variable X1, the
following 2 digits the coding of X2, and so on;
―the 2 × 5 digits are then put side by side to form a
chromosome of 10 digits;
The coding is crude, but it is after an initial passage
that can be improved using a more precise coding. In our
case, the decoding will be done in the following manner:
variable X1: 00 --> 20
01 --> 50
10 --> 75
11 --> 100
variable X2: 00 --> 20
01 --> 30
10 --> 40
11 --> 50
variable X3: 00 --> –50
01 --> – 60
10 --> –80
11 --> –100
variable X4: 00 --> 0°
01 --> 20°
10 --> 50°
11 --> 90°
variable X5: 00 --> 0°
01 --> 10°
10 --> 25°
11 --> 40°
We can see that the limitations of the problem, in par-
ticular on the design variables are integrated in the cod-
ing. It is not necessary to penalize an objective function
that will be of type a-F (“a” being a very large constant)
because the G.A. maximizes the functions. For a popula-
tion of 30 individuals and 50 generations, the G.A. quickly
comes to the following solution:
X1 = 100;
X2 = 50;
X3 = –50;
X4 = 20°;
X5 = 0°;
which corresponds to the chromosome 111000100, and a
value of 1.1013E8 for F. This represents a gain of 30% in
comparison to an average solution, for example:
X1 = 20;
X2 = 20;
X3 = –100;
X4 = 90°;
X5 = 40°;
Chromosome = 0000111111;
F = 1.318E8;
We note that the solutions tend at taking X1 as large as
possible and small angles A1 and A2, as far as the tech-
nology will allow. For the components of forces and
moments, the results for the final solution and some
force characteristics are given in the table below. Values
for the average solution (chromosome 0000111111) are
given in brackets.
for connection 01: Y01 = 200. DaN (753.), M01 =
4974. mmDaN (8467.)
for connection 12: Y12 = 1. DaN (6.5), M12 = 5025.
mmDaN (18467.), N12 = 5028. mmDaN (120522.)
for connection 23: Y23 = 1. DaN (6.5)
for connection 03: Y03 = 0.1 DaN (553.), L03 =
13386. mmDaN (89601.), M03 = 6. mmDaN (8467.)
A very important reduction of the values of forces and
moments can be noted.
4. Conclusions: Towards an Optimal
Integrated Design for Mechanical Systems
As this paper showed, it is possible to aim at an optimal
integrated design for mechanical structures. For now, the
implementation of an optimal integrated design for me-
chanical systems, that is taking into account a maximum
of information from the beginning (know-how, ability,
optimization constraints), is difficult due to the fact that
the necessary specialist software, in most cases, work
independently from other programs. This can be illus-
trated by the example of a gear box. A program of me-
chanical analysis is used initially to ensure a sound struc-
ture from the start, afterwards, specialist software is used
for calculations of gears, bearings, shafts,... The same
applies for finite element calculations to control the shape
and strength of certain components. Currently, even if
each stage of the problem is presented in terms of opti-
mization as part 3 showed (dealing with gears); the prob-
lems remain most of the time bound to a specific order.
Research in integrated design is orientated towards the
use of common databases at different stages of the de-
sign.
This work aims at offering a fundamentally different
approach, allowing at once a both global and almost
automatic optimization. It should be made clear that the
point of view given here is that of a mathematician. The
principle of the offered method is to use a neural network
as a global calculation program, and to couple this net-
work with stochastic methods of optimization. It is nec-
essary to keep in mind that the new strategy proposed
consists of three stages: first, defining the parameters of

J. L. MARCELIN 444
the mechanism taking stock of all design variables, as
well as desired objectives and technological limitations;
secondly, the "learning" of the neural network with the
goal of having a "mega-program" of analysis and calcu-
lation (perfectly adapted to the task in hand), including
knowledge of all the programs which will be used in the
design process; finally, use of this "mega-program" for
totally automatic optimization, without the need for hu-
man intervention, thanks to stochastic methods; the me-
thod used here is that of G.A.. The expected result is a
play of optimal design variables. This strategy has been
developed in [15] for gear boxes, and in [16] for hot-
rolled complex beams.
5
. References
[1] D. M. Peng and C. A. Fairfield, “Optimal Design of Arch
Bridges by Integrating Genetic Algorithms and the Me-
chanism Method,” Engineering Structures, Vol. 21, No. 1,
1999, pp. 75-82.
[2] F. Belblidia and E. Hinton, “Fully Integrated Design Op-
timization of Plate Structures,” Finite Elements in Analysis
and Design, Vol. 38, No. 3, 2002, pp. 227-244.
[3] W. G. Shao, “Perfectly Flexible Mechanism and Inte-
grated Mechanism System Design,” Mechanism and Ma-
chine Theory, Vol. 39, No. 11, 2004, pp. 1155-1174.
[4] K. Maute and G. W. Reich, “Integrated Multidisciplinary
Topology Optimization Approach to Adaptive Wing De-
sign,” Journal of Aircraft, Vol. 43, No. 1, 2006, pp.
253-263.
[5] S. Mei, W. Zhao and W. Wang, “A Virtual Collaborative
Design Space for Integrated Missile Design,” Journal of
System Simulation, Vol. 16, No. 7, 2004, pp. 1509-1529.
[6] J. L. Marcelin and Ph. Trompette, “Optimal Shape De-
sign of Thin Axisymmetric Shells,” Engineering Optimi-
zation, Vol. 13, No. 2, 1988, pp. 109-117.
[7] V. Steffen and J. L. Marcelin, “On the Optimization of
Vibration Frequencies of Rotors,” The International Jour-
nal of Modal Analysis, Vol. 3, No. 3, 1988, pp. 77-80.
[8] D. E. Goldberg, “Genetic Algorithm in Search, Optimiza-
tion and Machine Learning,” Addison-Wesley, 1989.
[9] J. R. Koza, “Genetic Programming: On the Programming
of Computers by Means of Natural Evolution,” MIT Press,
Massachusetts, 1992.
[10] Z. Michalewicz, “Genetic Algorithms + Data Stuctures =
Evolution Programs,” 3rd Edition, Springer Verlag, New
York, 1996.
[11] D. E. Rumelhart and J. L. McClelland, “Parallel Distrib-
uted Processing,” MIT Press, Cambridge, Massachusetts,
1986.
[12] J. F. Joduin, “Les Réseaux Neuromimétiques,” Hermès,
1994.
[13] Z. Szewczyk and P. Hajela, “Neurocomputing Strategies
in Structural Design-Decomposition Based Optimization,”
Structural and Multidisciplinary Optimization, Vol. 8, No.
4, 1998, pp. 242-250.
[14] P. Hajela and Z. Szewczyk, “Neurocomputing Strategies
in Structural Design-On Analysing Weigths of Feedfor-
ward Neural Networks,” Structural and Multidisciplinary
Optimization, Vol. 8, No. 4, 1994, pp. 236-241.
[15] J. L. Marcelin, “A Metamodel Using Neural Networks
and Genetic Algorithms for Integrated Optimal Design of
Mechanisms,” International Journal of Advanced Manu-
facturing Technology, Vol. 24, No. 9-10, 2004, pp. 708-714.
[16] J. L. Marcelin, “Optimization of the Cooling Regime of
Hot-Rolled Complex Beams,” International Journal of
Advanced Manufacturing Technology, Vol. 32, No. 7-8,
2007, pp. 711-718.