Journal of Minerals & Materials Characterization & Engineering, Vol. 11, No.3, pp. 221-242, 2012
jmmce.org Printed i n the USA. All rights reserved
221
Revisiting Sphere Unf olding Relat ionships for the Stereological Analysis of
Segmented Digital M icr ost ru ct ur e Im ages
E. J. Payton*
Institute for Materials, Ruhr-Universität Bochum, 44780 Bochum, Germany
*Corresponding author: [e-mail]
ABSTRACT
Sphere unfolding relationships are revisited with a specific focus on the analysis of segmented
digital images of microstructures. Since the features of such images are most easily quantified by
counting pixels, the required equations are re-derived in terms of the histogram of areas (instead
of diameters or radii) as inputs and it is shown that a substitution can be made that simplifies the
calculation. A practical method is presented for utilizing negative number fraction bins (which
sometimes arise from erroneous assumptions and/or insufficient numbers of observations) for the
creation of error bars. The complete algorithm can be implemented in a spreadsheet. The
derived unfolding equations are explored using both linear and logarithmic binning schemes,
and the pros and cons of both binning schemes are illustrated using simulated data. The effects
of the binning schemes on the stereological results are demonstrated and discussed with
reference to their consequences for practical materials characterization situations, allowing for
the suggestion of guidelines for proper application of this, and other, distribution-free
stereological methods.
Keywords: stereology; image analysis; microstructure; electron microscopy; optical microscopy
1. INTRODUCTION
As digital imaging has become standard practice in metallography, so has the use of digital
imaging and image processing techniques for materials characterization. There are numerous
widely-available softwar e pack ages (b oth comm ercial and freewa re) th at a llo w for enhan cemen t,
segmentation, and measurement of image features . These software packages enable a ver y large

222 E. J. Payt on Vol.11, No.3
number of observations to be collected in a fraction of the time that would be required to produce
the same results manually.
Many phys ics-based models of microstructural evolution require 3D particle sizes as input [1-5].
While 3D serial sectioning methods exist and are becoming more accessible with focused ion
beam instruments, observations in planar cross-section remain the most efficient method of
micros tru ctu ral chara cter i z at io n for pract ical re asons . Th us , t he 3D part icl e si z e distribution must
be stereologically calculated from the 2D observation. In light of recent and continued interest in
computer-based segmentation of microstructural images [6-10] and the ongoing need for dat a for
the development, calibration, and improvement of microstructural models [5,11,12], it seems
appropriate to revisit some remaining issues with the common distribution-free stereological
method for ‘unfolding’ the 3D particle size distribution of a population of spheres from the
observation of their 2D cross-sections, as it would be of practical benefit to those materials
scientists who are using automated image processing techniques and those who are unfamiliar
with this procedure.
While lineal intercept techniques are often most convenient for quantifying features manually,
the observation of features on a digital ima ge is equivalent to a s ystematic point count [13]. The
standard solution for converting the 2D observations to 3D data, which is well-chronicled in
classical metallurgical stereology texts [14,15], involves the assumption of non-interacting
spherical particles observed in perfectly planar cross-section, in which the plane of polish may
intersect the particle at any point in that particle’s body, producing a range of possible cross-
section sizes.
For any shape more complex than either an elongated or flattened spheroid with bivariate axes,
there is no analytical solution to the stereological problem without imposing additional
assumptions, such as the requirement of a specific size distribution of particles [16-18]. Since
particle shapes in materials are neither necessarily uniform nor is the size distribution usually
known, the assumption of spherical particles (or at least globally-convex particles which have the
average shape of a sphere in rotation) remains common in materials science (e.g., [5,19-21]). In
the present work, the unfolding relationship for spheres is re-derived in ter ms of the histogram of
observation areas as inputs (rather than radii or diameters) and a practical method is presented
for utilizing the un-ph ysical results that propagate during the calculation for the creation of erro r
bars. The derived algorithms can be easily programmed into a spreadsheet for rapid
implementation, and are useful in situations where it is desirable to be able to examine the error
that is introduced by the histogramming procedure. The errors associated with histogramming
both on linear and logarithmic scales are then explored to shed light on the number of
observations that should be made for best practice in application of the stereological method.

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 223
2. STEREOLOGY OF PLANAR OBSERVATIONS IN TERMS OF AREAS
The dist ributions of possible cross-section sizes as well as the intrinsic size distribution of the 3D
particles in the material both contribute to the distribution of experimentally-observed cross-
section sizes. The central stereological problem is the deconvolution of these distributions. The
classical approach involves first assuming that the size class (in the histogram of experi ment all y-
observed cross-section sizes) that corresponds to the largest experimentally-observed cross-
section is generated by the intersection of a plane with the middle of the largest 3D particle in the
system, producing the largest possible cross-section for that particle size. Then, by assuming
spherical particles, the distribution of the sizes of the other possible cross-sections through that
particle is predi cted. Using the number frequency of this largest-particle size class, the
distribution of cross-sections that should come from an array of uniform spheres of this size is
then subtracted from the histogram of 2D cross-sections. To calculate a likely 3D distribution of
particle sizes, this process is repeated for each bin in the histogram, going from the bins
corresponding to the largest particles to those corresponding to the smallest, “stripping” away the
part of the histogram that comes from the largest-particle size class that still has a non-zero
number fraction, and “unfolding” the 3D particle size distribution. The assumptions described
above are most reasonable when the number of measurements is large and there are a large
number of bins, two interrelated values when it comes to producing a smoothly-varying
histogram.
Due to imaging biases, sampling statistics, and other practical problems, the classical approach
described above often results in bins with negative number fractions. The problem can be solved
numerically in a way that prevents these artifacts from occurring by, for example, using the
expectation -maximization (EM) algorithm [22]; however, this approach does not necessarily
produce a unique solution [23] and is not easily programmed into a spreadsheet. In addition to
being easier to implement, the classical approach also retains a benefit in that error bars can be
calculated from the artifacts. The error bars can in turn be used to gauge the quality of the
histogramming procedure, as will be demonstrated in the present paper.
The results of more adva nced numerical methods such as the EM algorithm are still affected b y
the quality of the histogram of the initial data because the binning itself introduces systematic
errors in to the stereol ogical resu lts. While it m ust be noted that there are also advanced methods
that can b e applied to the histogramming procedure, it remains of general interest to have rules-
of-thumb for the numbers of observations, numbers of bins, and the scaling of the bins that
should be used to produce a histogram that accurately represents the underlying distribution. Due
to the fact that feature size distributions are not necessarily normal or lognormal, “Scott’s rule”
[24] may not necessarily apply. These issues will be addressed in the latter part of this paper
using a simulation-based approach.

224 E. J. Payt on Vol.11, No.3
The historical development of the classical unfolding method was recorded by
Underwood [14,15], and the most useful derivations were contributed by Saltikov [14,15,25]. A
primary difference between several of the derivations is whether they use a linear binning
scheme, as one typically uses for making a histogram of measurement results, or a logarithmic
binning scheme, in which the width of the bins increases logarithmically as the particle size
represented by the bin increases, such that there is a higher density of bins corresponding to
smaller particles. The logarithmic binning scheme is useful in many materials characterization
applications due to sampling statistics, since fewer observations are often made of the largest
particl e siz es. Both methods require a fixed number of bins (co rresp ondin g t o siz e class es) in the
histogram for performing the calculation due to the usage of either look-up tables or a fixed
equation. The Johnson-Saltikov working table [15], for example, assumes that the relative area
occupied by cross-sections of each size class is constant relative to the maximum possible cross-
sectio n size cl ass, i.e. for 30 bins on a logarithmic (base 10) scale, t he perc entage of sections per
area occupied by the bin containing the largest areal cross sections is always 60.749%, the next
smaller bin is 16.833%, followed by 8.952%, and so on. In each step of the stripping of the
cross-section histogram to produce the 3D histogram, the working table becomes more
inaccurate because the percentages no longer sum to 100%.
It is no l onger necessar y to us e a working tabl e with fix ed section percentages be cause the en tire
histogram stripping process may be performed rapidly, for any number of bins, with simple
computer programs (see, for example, Heilbronner's StripStar code [26,27]). Furthermore, usage
of fix ed percentages can add to errors cau sed by th e biases of the i maging and image proces sing
techniques. It is therefore useful to develop relations that can be used universally for any number
of bins, with any scaling of the bin size axis, and with any functional form of imaging bias (a
topic that has been explored in greater detail by the present author in a separate paper [20]).
Figure 1: Geometry of intersection of a sphere of radius
R
and planes, producing circular
cross-sections of radius
r
separated by a distance
h
.

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 225
The in tersectio n between a sphere of radi us
R
and a plan e at a distan ce
x
from the center of the
sphere produces a circle of radius
r
, as shown in Figure 1. The radius of the intersection circle in
Figure 1 is given by simple geometry:
22
xRr
−= (1)
If there are an infinite number of spheres of uniform radius
R
arran ged rand o m l y in sp ac e, and a
plane is passed through the array of spheres, the spheres will be intersected at many different
values of
x
(both positive and negative in Figure 1, depending on whether the sphere resides
below or above the plane of intersection). In this case, a distribution of circle sizes will be
developed. For any array of uniformly-sized spheres, the distribution of sizes is invariant when
normalized by the sphere radius
R
. The sign of
x
is unimportant due to symmetry, so Eq. 1 can
be rewritten as
2
1







−= R
x
R
r
(2)
Analogous to the case of a hypothetical array of randomly-arranged uniformly-sized spheres, the
distribution of cross-sections observed in a metallographic section may have originated from
particles with centroids either above or below the plane of polish. Second phase particles are
likely to have a size distribution of their own, however, and it is generally not possible to
determine the 3D size of an individual particle that generates a given 2D cross-section in an
opaque specimen.
In the histogram of cross-sectional areas, the edges of the bins may come from any two
x
values. It is therefore necessary to have a relation that provides the probability of observing an
intersection circle between two predetermined values of
x
. In the case of true planar
inters ecti on s, th e di st ance bet ween two pa ral l el p lan es i nt ersect ing a sin gle s ph ere in si z e cl ass
j
may be easily obtained from Eq. 2 using the definitions of
R
,
r
, and
h
set forth in Figure 1:
2221 2
1, ijij
jii
rRrRh −−−=
−−
(3)
The index
i
has been introduced in Eq. 3 for numbering planes in order of their absolute distance
from
0=x
, because it is not clear from the value of
r
if a plane intersects at
x+
or
x−
in
material viewed in cross-section. In subsequent equations
j
will continue to be used as an index
for the bin in the histogram corresponding to the largest sections in the system.
With digital images, areas are the natural units of measurement because measurements may be
easily performed using pix el counting techniques. Eq. 3 ma y be rewritten in terms of areas using

226 E. J. Payt on Vol.11, No.3
2
jj RA
π =
and
2
i
j
i
ra π =
, wher e
j
A
corresponds to the maximum intersection area of a sphere of
size
R
j (which occurs at
0=x
in Figure 1), and
j
i
a
is the area of the circle created by the
intersection of plane
i
and the sphere of size class
j
:
( )
ijij
jii
aAaAh −−−=
−− 11,
1
π
(4)
The probability
p
of intercepting a sphere of radius
R
within the interval
h
is given by
Rh
.
Again using the equation for the area of a circle, it is found that
( )
ijij
j
jii
aAaA
A
p−−−=
−− 11,
1
(5)
In the correction of imaging biases (which may arise, for example, when using backscatter
imaging since the signal comes from an ill-defined volume within the specimen), a transfer
function between the correct cross-section
a
and the observed cross-section
a′
can be inserted
into Eq. 5 to obtain the bias-corrected probability of intersection [4,20].
The mean area of the cross sections between
j
i
a
1−
and
j
i
a
, assuming uniform probability of
inters ecting at an y height
x
, is given by dividing the v olume of a sli ce of a sphere b y th e height
h
of the sl ice, i.e.
jii j
ii
jii hVa 1,1,1, −−− =
. Th e volume of a sl ice of a sphere in terms of section areas
is [28]:
() ( )







++=
−
−
−
−
32
2
1,
1
1,
1,
jii
j
i
j
i
jii
j
ii
h
aa
h
V
π
(6)
The area taken up by each size group is generally given as the product of the average area and
the probability of intersection,
jii jii
pa
1,1, −−
; however, we note that
j
j
ii
j
jii
jii
j
ii
jii jii
R
V
R
h
h
V
pa
1,1,
1,
1,
1,1,
−−
−
−
−−
=⋅=
which allows us to write

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 227
() ( )







++==
−
−
−−
−−
3
2
2
1,
1
1,1,
1,1,
jii
j
i
j
i
j
jii
j
j
ii
jii jii
h
aa
A
h
R
V
pa
ππ
(7)
Now, substituting the definition
j
jii jii
Rhp
1,1, −−
=
into Eq. 7, we find that
jii jii pa 1,1,−−
can be writ ten
more simply as:
( )
( )







++=
−
−
−
−−
32
2
1,
1
1,
1,1,
jiij
j
i
j
i
jii
jii jii
pA
a a
p
pa
(8)
The above substitution allows for
jii jii
pa
1,1, −−
to be obtained in only two calculation steps, using
Eqs. 5 & 8.
The fraction of sections per unit area with cross-sectional areas between j
i
a1− and
j
i
a
that come
from an array of particles of size class
j
,
( )
j
ii A
N1, −
, may now be obtained using
( )
∑ −−
−−
−
=
j
i
jii jii
jii jii
j
ii
A
pa
pa
N
1,1,
1,1,
1,
(9)
The value of the fraction in the 3D distribution for the bin
j
is given by
( )
j
jj
A
j
D
j
DN
f
f
1,
2
3
−
=
(10)
where j
D
f
2
is the result of stripping away the influence of all bins greater than
j
from the area-
weighted histogram of observations,
j
A
f
. For all values
ji <
,
j
D
f2
is obtained by stripping the
distribution of cross-sections coming from
j
D
f
3
(Eq. 10) from the 2D distribution:
( )
∑
+= −
−= k
ji
j
ii
A
iD j
A
j
DNfff
11,
32
(11)
where
j
A
f
corresponds to the histogram of measured area fractions per feature size group. This
process is performed for all
j
starting from the bin corresponding to the largest particles
remaining in the histogram. The volume-weighted fractions can be converted to the number of
particles per unit volume by dividing each bin by the volume of the particles represented therein,

228 E. J. Payt on Vol.11, No.3
and can be converted to number fractions by dividing the number of particles per unit volume by
their sum.
3. ERROR IN 3D PARTICLE SIZE DISTRIBUTION CALCULATION
The histogram stripping process often produces negative bin values in the 3D distribution.
Negative number fractions do not have any physical meaning, and can only be produced by
errors in either the measurement process or poor assumptions in the 2D
→
3D conversion
calculation. Th e errors are propagated throu gh the calculation. Previ ous r es earchers have tra cked
the negative bin values that are propagated during the histogram subtraction [26,27], but to the
present author’s knowledge, a meaningful usage of the resultant negative values has not been
provided in the literature for practical application by researchers continuing to use the classical
unfolding methods. The best choice for dealing with the negative volume fractions is not
immediately obvious. If the negative frequencies are simply discarded, the volume fraction
resulting from the stereological calculation will not be equal to that of the measured area
fraction. Thus, the histogram must be re-normalized after the stereological calculation; however,
without error bars, the effect of the normalization on the final result will remain unclear and
potentially misleading. Despite problems associated with the spherical assumption (which will be
discussed later), the sphere-based methods remain in frequent use because of their relative
simplicity, so it would be useful to exploit the un-physical values in the production of error bars.
If it is assumed that the error producing the negative-frequency bin could come from any single
bin corresponding to larger particles than those contained in the bin with a negative number
fraction, then the required change in the number fraction of any bin
k
to produce a negative
frequency at bin
j
may be calculated (assuming that all of the error is concentrated at bin
k
)
using:
( )
k
jj
A
j
D
k
jN
f
1,
2
−
= ε
(12)
where
k
j
ε
is the change at bin
k
required to return the frequency at bin
j
to the physically-
reasonable value of zero. It must be noted that k
j
ε as calculated by Eq. 12 may exceed k
D
f3; in
this case, w e s et
k
D
k
j
f
3
−= ε
. It should be noted at this point that
k
j
ε
can be converted into volume
fractions, number fractions, or particles per unit area similar to j
D
f3 from Eq. 10.
We may provide the sample standard deviation of the possible physically-reasonable values of
k
D
f3 that do not produce negative frequencies at an y bins by summing the k
j
ε matrix values over

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 229
their index
k
for each bin
j
, dividing by the number of bins that could contribute to the error for
that bin, and taking the square roots:
( )
∑
>
=k
ji
k
ij j
s2
1
ε (13)
because
k
j
ε
is the difference between the expected value and the required value for a
nonnegative result at
j
. It is not known which bins
k
contribute to the erroneous result at
j
.
Realistically, there is a correlation between the errors because they propagate during the
calculation from bins corresponding to coarser particle sizes toward bins corresponding to finer
particle sizes; however, for many practical applications, it is probably sufficient to simply
provide descriptive error bars such that the reader can gauge the error introduced during the
process. If it is assumed that all bins
jk >
have an equal probability of producing the error at
j
,
then the standard error of these values is then given by
j
s
SE
j
j
=
(14)
This standard error value may be used to estimate a lower bound to the error produced during the
stereological unfolding procedure.
4. ILLUSTRATION OF RESULTS
The derivation presented in the previous section can be programmed efficiently in either a
spreadsheet or in modern computer languages in a few lines, as illustrated by the matlab/octave
source code provided in the appendix. After the 3D conversion, the x-ax is may be rescal ed from
areas to diameters. The mean spherical-equivalent particle diameter is then estimated as
∑
=
j
j
D
dfd
3
. The method derived in the previous section takes as input the area fraction of
particles of a given size class. In the case of 100% volume fraction, as in a grain size distribution,
the sum of the number fractions or volume fractions should be unit y. In the case of a distribution
of particles, the initial area fraction should be used. When corrections for observation biases are
not used, then the area fraction at the beginning of the calculation is identical to the volume
fraction after the stereological calculation. The number fraction of particles per size class in the
initial state may be obtained by dividing the area fraction t aken up b y particles of the given siz e
class by the area represented by that bin, then normalizing such that the sum of the number
fractions is unity.

230 E. J. Payt on Vol.11, No.3
To illustrate the results of the above-described procedure, the lognormal distribution was
randomly sampled to simulate a hypothetical distribution of sphere cross-sectional areas. The
number of samples, the shape parameter σ of the distribution, and the number of bins were varied
while holding the mean particle size constant. The lognormal distribution was chosen because it
is observed over a large range of materials that particle size cross-sections are often
approximately lognormally distributed.
It is probably worth noting at this point that the minimum bin size must not correspond to
particles below the resolution limit of the imaging technique; otherwise, excessively large error
bars will be computed by the method proposed in the previous section. Also, the choice of
binning scale is extremely important: A sufficient number of bins must be chosen such that the
average s iz e r etu rn ed by the hi st ogr am i s as clo se as po ss ib le t o t he m ean of the co ll e ct ed dat a. If
an excessive number of bins is chosen, then the fluctuations in the bin height will increase the
uncertainty in the stereologically-calculated result. Figure 2 shows the standard deviation of the
mean particle size represented by a linearly-binned histogram (a) and a logarithmically-binned
histogram (b), as determined by 5000 simulations of particle size observations with a mean
particle diameter of 1.2 microns and a lognormal shape parameter σ of 0.5. Isocontour lines of
constant standard deviation regions are shown, wi th the number of bins plott ed on the x-ax is an d
(a) (b)
Figure 2: The standard deviation of the apparent population mean resulting from histogram
binning, for 5000 simulations of particle size measurements given by randomly sampling a
lognormal distribution with a mean particle diameter of 1.2 microns and a lognormal shape
parameter of 0.5: (a) Linear binning; (b) Logarithmic binning. Linear binning produces the
most accurate results for low numbers of observations for this value of sigma, but the
difference between logarithmic and linear binning decreases significantly as the number of
observations increases.

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 231
the number of observations plotted on the y-axis. From the comparison of Figures 2 (a) and (b),
it is clear that linear binning produces more accurate results for low numbers of observations, but
the difference between logarithmic and linear binning decreases significantly as the number of
observations exceeds 500.
Figure 3 shows the variation in the standard deviation of the mean particle size with the shape
parameter σ of a lognormal distribution (with a mean value of 1.2 microns) represented by a
linearly-binned histogram (a) and a logarithmically-binned histogram (b). For each standard
deviation, 5000 simulations of 500 particle size observations with a mean particle diameter of 1.2
microns were performed. Isocontour lines of constant st andard deviation re gions are shown, with
the number of bins plotted on the x-axis and the shape parameter of the distribution plotted on
the y-axis. Comparing Figures 3 (a) and (b), it is seen that logarithmic binning generally provides
better performance for more skewed distributions. Linear binning is only better when the number
of bins is large and the shape parameter is small.
On initial examination of Figures 2 and 3, it appears that linear binning offers some distinct
benefits. For example, the mean particle size is more easily accurately reproduced for fewer
observations, as shown in Figure 2. A tradeoff exists, however, because a smoothly-varying
distribution is better for the purposes of our stereological calculation since it reduces the
(a) (b)
Figure 3: The standard deviation of the apparent population mean resulting from histogram
binning, for 5000 simulations of particle size measurements given by 500 random samples of
a lognormal distribution with a mean particle diameter of 1.2 microns: (a) Linear binning;
(b) Logarithmic binning. Logarithmic binning generally provides better performance at this
number of observations except when the number of bins is large and the shape parameter is
small.

232 E. J. Payt on Vol.11, No.3
likelihood of the negative number fraction artifacts. The production of a smoothly-varying
histogram is explored in Figures 4 and 5, in whic h a given number of observations are randomly
sampl ed from a lognormal distribution of known parameters under different binning schemes to
determine the deviation of the histograms from the known shape of the distributions. The
smoothness of the histograms was quantified using the mean absolute value of the deviation of
each bin height from the expected height of that b in (i.e., the height that would be observed if an
infinite number of measurements were made on a particle population of the given size
distribution). S o that t he deviat ion valu es for th e cases with different numbers of bins would fall
in comparable ranges, the distributions in all cases were normalized by the maximum height of
the smooth distribution of the same number of bins. Simulations were performed for distributions
with lognormal shape parameters ranging from 0.2 to 1.4, 6 to 36 bins on both linear and
logarithmic scales, and between 50 and 3000 observed particles. The mean diameter of the
simulated particles was 1.2 microns in all cases. The presented values are the mean v alues from
5000 repeated simulations.
(a) (b)
Figure 4: Smoothness of histograms with mean particle size of 1.2 microns, as characterized
by the 5000 repeat measurements of the deviation of the observed number fractions from the
expected number fractions for the input distribution: (a) Linear binning, 500 observed
particles; (b) Logarithmic binning, 500 observed particles. It can be seen that lognormal
binning provides more consistent smoothness over a wider range of shape parameter values.

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 233
Figures 4 (a) and (b) contain the results for the binning of the simulated observations of 500
particles of various lognormal distribution shapes in the linear and logarithmic binning cases,
respectively. The plots show isocontour lines of constant smoothness of the histograms; low
(a) (b)
(c) (d)
Figure 5: Smoothness of histograms of lognormal distributions with a mean particle diameter
of 1.2 microns, as characterized by the 5000 repeat measurements of the deviation of the
observed number fractions from the expected number fractions for the input distribution:
(a) Linear binning, σ=0.2; (b) Logarithmic binning, σ=0.2; (c) Linear binning, σ=1.4;
(d) Logarithmic binning, σ=1.4. While the performance of linear and lognormal binning are
comparable at low values of the shape parameter, the relative performance of lognormal
binning improves relative to linear binning as the skew of the distribution increases.

234 E. J. Payt on Vol.11, No.3
values represent smaller deviations from the expected values, and thus a more accurate
reproduction of the actual distribution shape. The variation in the lognormal shape parameter is
given on the y-axis; the differing numbers of bins used in the binning procedure are given on the
x-axis. While large numbers of bins improve the reproduction of the mean particle size of the
population (Figures 2 and 3), it is shown in both subfigures of Figure 4 that increasing the
number of bins reduces the smoothness of the distributions for a given distribution shape – which
will, in turn, increase the errors propagated through the stereological procedure. In Figure 4, it
can be observed that logarithmic binning (of a lognormal distribution of observation sizes)
provides more consistent smoothness over a wider range of shape parameter values than linear
binning, with much improved performance at higher numbers of observations.
Figures 5 (a) and (b) contain the results for binning different numbers of observed particles over
different numbers of bins, for linear and logarithmic binning schemes, respectively, of a
distribution with a shape parameter of 0.2; Figures 5 (c) and (d) show the results corresponding
to a shap e p aram eter of 1. 4. The plots again show isocontour lines of constant smoothness of t he
histograms, using the same procedure for quantifying the smoothness as was used in Figure 4.
The number of particles observed is plotted on the y-axis and the number of bins used is plotted
on the x-axis. All subfigures of Figure 5 show that increasing the number of bins (which was
observed to improve the reproduction of the mean particle size in Figures 2 and 3) generally
reduces the histogram smoothness fo r a given number of observations. As would be expected,
the smoothness improves as the number of observations is increased. Increasing the number of
simulated measurements (to something more than the 5000 used here) could be expected to
further smoothen the variations in the isocontours such that the sm oothness at a constant number
of observations continually degrades with increasing numbers of bins (the jaggedness is
particularly notable in Figure 5 (b)); however, the trend is more than sufficiently clear in the
present results. Figures 5 (a) and (b) show that the performance of linear and logarithmic binnin g
is comparable for narrow particle size distributions, while Figures 5 (c) and (d) illustrate that the
performance of logarithmic binning is superior to that of linear binning when the particle size
distribution is highly skewed. Lognormal binning provides more consistent smoothness over a
wider range of shape parameter values, with consistently improving smoothness as the number of
observations increases, as seen by comparison of Figures 5 (b) and (d).
The errors produced in the binning process are propagated to the stereology. Figure 6 shows the
results of binning with 12 and 36 bins on linear and logarithmic scales for 800 observations
simulated by random sampling of a lognormal distribution with a mean of 1.2 microns and a
shape parameter of 0.8. The set of observations produced a mean cross-sectional diameter of
1.23 m icrons. When too few linear bins are used, as in Figure 6 (a), the details of the distribution
are lost. A larger number of bins are required to more accurately represent the distribution under
a linear binning scheme, as shown in Figure 6 (b). The excess bins on the coarse side of the
distribution result in strong fluctuations in number fractions on this side of the distribution. A

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 235
reasonable number of bins in the linear scheme is often excessive under a logarithmic binning
scheme, as s een b y comparison of Figures 6 (b) an d (d). As suggested b y the results of Fi gures 2
through 5, the most appropriate binning scheme for this particular set of particles – at least in
terms of producing a smooth variation of number fractions and accurate reproduction of the
shape of the distribution – is logarithmic binning with a moderate number of bins, such as
Figure 6 (c).
(a) (b)
(c) (d)
Figure 6: Illustration of the stereological results of varying the number of bins for 800
simulated observations obtained from randomly sampling a logarithmic distribution with a
shape parameter of σ=0.8: (a) 12 linear bins; (b) 36 linear bins; (c) 12 logarithmic bins;
(d) 36 logarithmic bins.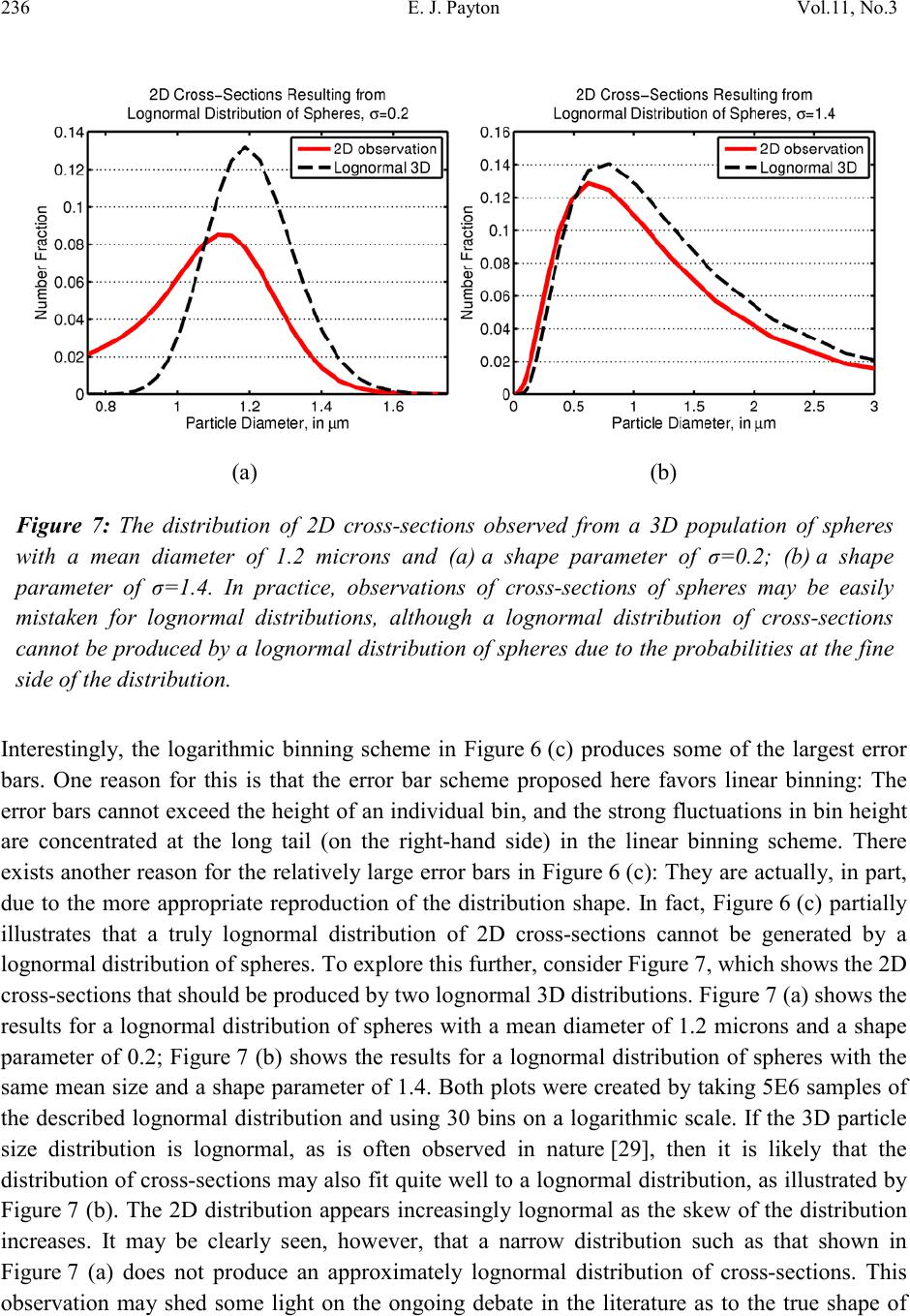

236 E. J. Payt on Vol.11, No.3
(a) (b)
Figure 7: The distribution of 2D cross-sections observed from a 3D population of spheres
with a mean diameter of 1.2 microns and (a) a shape parameter of σ=0.2; (b) a shape
parameter of σ=1.4. In practice, observations of cross-sections of spheres may be easily
mistaken for lognormal distributions, although a lognormal distribution of cross-sections
cannot be produced by a lognormal distribution of spheres due to the probabilities at the fine
side of the distribution.
Interestingly, the logarithmic binning scheme in Figure 6 (c) produces some of the largest error
bars. One reason for this is that the error bar scheme proposed here favors linear binning: The
error bars cannot exceed the height of an individual bin, and the strong fluctuations in bin height
are concentrated at the long tail (on the right-hand side) in the linear binning scheme. There
exis ts another reason fo r the relati vely large error bars in Figure 6 (c): They ar e actuall y, in part,
due to the more appropriate reproduction of the distribution shape. In fa ct, Figure 6 (c) partially
illustrates that a truly lognormal distribution of 2D cross-sections cannot be generated by a
lognormal distribution of spheres. To explore this further, consider Figure 7, which shows the 2D
cross-sections that should be produced by two lognormal 3D distributions. Figure 7 (a) shows the
results for a lognormal distribution of spheres with a mean diameter of 1.2 microns and a shape
parameter of 0.2; Figure 7 (b) shows the results for a lognormal distribution of spheres with the
same mean size and a shape param eter of 1.4. Bot h plots were created by taking 5E6 s amples of
the described lognormal distribution and using 30 bins on a logarithmic scale. If the 3D particle
size distribution is lognormal, as is often observed in nature [29], then it is likely that the
distribution of cross-sections may also fit quite well to a lognormal distribution, as illustrated by
Figure 7 (b). The 2D distribution appears increasingly lognormal as the skew of the distribution
increases. It may be clearly seen, however, that a narrow distribution such as that shown in
Figure 7 (a) does not produce an approximately lognormal distribution of cross-sections. This
observation may shed some light on the ongoing debate in the literature as to the true shape of

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 237
the distributions of grains and particle sizes observed in materials, though further work is
required to determine what distribution shape (Rayleigh, Weibull, or Lognormal) matches best to
the present 2D results, and whether the 3D distribution is indeed lognormal. Despite the
difference in the fine-side tail observed in Figure 7 (a), it is still likely that a distribution with
such a shape may still be mistaken for a lognormal distribution in practice, as re al measu remen ts
rarely produce a perfectly smooth histogram, and there are other sources of error – such as
imaging bias – that can affect the measurement.
5. DISCUSSION
It is clear when comparing Figures 6 (a) and (b) with Figures 6 (c) and (d) that logarithmic
binning more efficiently reproduces the distribution shape (i.e. uses fewer bins) under the
explored circumstances. The most accurate stereological results will be produced using a
histogram that simultaneously reproduces the correct mean size of the observed values (Figures 2
and 3) and the details of the shape of the true underlying distribution (Figures 4 and 5). Thus, a
tradeoff exists between the number of bins used, the binning scheme, the n umber of observations
made, and the quality of the stereological results. The mean values for bot h the input histograms
and the stereological results are given in the subfigures of Figure 6. There is significant variation
between the resulting 3D stereological means for the input 2D histograms. The true mean of the
population and the shape are best reproduced by Figure 6 (c); it must be assumed that this also
represents the best stereological result of the four binning options shown in this figure.
It comes as no surprise that logarithmic binning of a lognormal distribution of particle size
observations produces a more smoothly-varying distribution than linear binning; however,
Figures 2 through 5 of the present work should help clarify the situation in which logarithmic
binning is beneficial. The results shown in Figures 2 through 5 also emphasize the importance of
making a large number of individual particle measurements in stereological practice, as the
accurate reproduction of the mean particle size in a histogram depends significantly on the
number of measurements made when logarithmic binning is used. Binning on a logarithmic scale
is typically useful in metallurgical particle size measurements because it reduces the number of
measurements required to produce a smoothly-varying histogram for appro ximat ely-lognormally
skewed distributions, as shown in Figures 5 (c) and (d). In practice, producing a smoothly-
varying histogram for input into the stereological procedure may be more difficult than is
implied in the present cases, which were formed from randomly sampling a lognormal
distribution.
There are many additional aspects that should be considered when performing the stereology on
real particle populations. It is well-known that the variations in the shape of the particles
generating the cross-sections can have great consequences on the final results [16-18,30]. The
situation often arises, however, that particle shapes vary within a single specimen (such as, for

238 E. J. Payt on Vol.11, No.3
example, Ni-based superalloys exhibiting populations of both secondary and tertiary γ’ phase). In
this case, the spherical assumption is not easily avoided, and it becomes much more challenging
to produce 3D data for model inputs [22]. A trade-off exists between metallographic efficiency
and the ability to obtain accurate results. In terms of providing 3D data for use in physics-based
models, many microstructural models for which 3D data is needed also contain the spherical
assumption (e.g. [1,4,5,12]). In these situations, a sphere-based unfolding method may be
thought of as a necessary first step toward producing the required data, and refinement of both
the stereological method and the modeling parameters may be completed at a later stage as
necessary for producing realistic simulation results. Ultimately, it is important that metallurgists
continuing to use sphere unfolding relationships are aware that the assumption of spherical
particles can produce errors in the final results. The calculation of error bars presented in the
present paper is inten ded to h elp th e resear cher gau ge the d egree to which the assumptions in the
stereological method are weak for the specific set of data under investigation, but it should be
noted that the utility of the error bars is dependent upon a reasonable choice of binning
parameters for a given set of measured particle cross-sections.
6. SUMMARY AND CONCLUSIONS
In light of the rapidly increasing adoption of digital image segmentation methods in
metallography, and their potential for use in calibration and future development of physics-based
models of microstructure evolution, the sphere unfolding relationship has been re-derived in
terms of areas for practical usage by metallographers continuing to use these stereological
techniques and for materials scientists who may not be familiar with the technique. A practical
method has been presented for usin g the negative frequency bins that som etimes arise during the
calculation for the creation of error ba rs, and the method has b een demonstrated using simulated
measurements. The effect of binning on the smoothness of histograms for input into the
unfolding algorithm has been explored to gauge the errors introduced by the binning process, and
the unfolding results have been illustrated for some interesting cases. From the results of the
present study, the following conclusions may be drawn:
1. For increas ingly left-skewed particle size distributions, logarithmic binning more accurately
reproduces the population mean than linear binning (Figure 3) as long as a sufficient number
of observations is made (Figure 2). As a rule of thumb, at least 500 individual particle size
measurements should be used for a reasonable probability of accurately reproducin g the
mean particle size of a skewed population under a logarithmic binning scheme (Figure 2).
2. Logarithmic binning is often useful in metallurgical particle size measurements due to
sampling statistics: Fewer observations tend to be made of the largest cross-sections. Thus,
logarithmic binning consistently produces smoothly-varying histograms over a wider range
of left-sided distribution skews than linear binning (Figure 4). The smooth ness continuously
improves with an increasing number of observations (Figure 5).

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 239
3. Errors in binning are propagated to the stereology. If the binning method is unable to
reproduce the correct mean particle size, the error will be passed along to the stereological
result (Figure 6).
4. If the 3D particle size distribution that generates the observed cross-sections is
approximately lognormal, it is very likely that the distribution of observed cross-sections
will likely appear approximately lognormal, even though the cross-section distribution
cannot strictly be lognormal (Figure 7).
ACKNOWLEDGEMENTS
This work was initiated while the author was at The Ohio State University and completed at
Ruhr-Universität Bochum. The author wishes to gratefully acknowledge support from GE
Aviation for the portion of the work performed at Ohio State and Lehrstuhl
Werkstoffwissenschaft (G. Eggeler) for the portion of the work completed at Ruhr-Uni. The
author also wishes to express his gratitude to Dr. V. A. Yardley for reading the draft of this paper
and providing several helpful suggestions.
REFERENCES
[1] Abbruzzese G., 1985, “Computer simulated grain growth stagnation.” Acta Metall., Vol.
33, pp. 1329–1337.
[2] Dieter, G.E., 1986, Mechanical Metallurgy, 3rd ed., McGraw-Hill Series in Materials
Science and Engineering, McGraw-Hill, Boston, MA.
[3] Porter, D.A. and Easterling, K. E., 1992, Phase Transformations in Metals and Alloys, 2nd
ed., CRC press, Boca Raton, FL.
[4] Payton, E.J., 2009, Characterization and Modeling of Grain Coarsening in Powder
Metallurgical Nickel-based Superalloys, Ph.D. thesis, The Ohio State University,
Columbus, OH.
[5] Wang, G., Xu, D.S., Payton, E.J., Ma, N., Yang, R., Mills, M.J., and Wang, Y., 2011,
“Mean-field statistical simulation of grain coarsening in the presence of stable and unstable
pinning particles.” Acta Mater ., Vol. 59, pp. 4587-4594.
[6] Kahn, H., Mano, E.S., and Tassinari, M.M., 2002, “Image analysis coupled with a SEM-
EDS applied to the characterization of a Zn-Pb partially weathered ore.” J. Miner. Mat er.
Charact. Eng., Vol. 1, pp. 1-9.
[7] Gu, Y., 2003, “Automated scanning electron microscope based mineral liberation analysis:
An introduction to JKMRC/FEI mineral liberation analyzer.” J. Miner. Mater. Charact.
Eng., Vol. 2, pp. 33-41.
[8] Hagni, A.M., 2008, “Phase identification, phase quantification, and phase association
determinations utilizing automated mineralogy technology.” JOM, Vol. 60, pp. 33-37.

240 E. J. Payt on Vol.11, No.3
[9] Payton, E.J., Phillips, P.J., and Mills, M.J., 2010, “Semi-automated characterization of the
gamma prime phase in Ni-based superalloys via high-resolution backscatter imaging.”
Mater. Sci. Eng. A, Vol. 527, pp. 2684–2692.
[10] Schouwstra, R.P. and Smit, A.J ., 2011, “Developments in mineralogical techniques – What
about mineralogists?” Miner. Eng., Vol. 24, pp. 1224-1228.
[11] Payton, E.J., Wang, G., Wang, G., Ma, N., Wang, Y., Mills, M.J., Whitis, D.D., Mourer,
D.P., and Wei, D., 2008, “Integration of simulations and experiments for modeling
superalloy grain growth,” in: Superalloys 2008, pp. 975-985, The Minerals, Metals &
Materials Society, Warrendale, PA.
[12] Wang, G., Xu, D.S., Ma, N., Zhou, N., Payton, E.J., Yang, R., Mills, M.J., and Wang, Y.,
2009, “Simulation study of effects of initial particle size distribution on dissolution.” Acta
Mater., Vol. 57, pp. 316-325.
[13] Hilliard, J.E. and Cahn, J.W., 1961, “An evaluation of procedures in quantitative
metallography for volume-fraction analysis.” Trans. AIME, Vol. 221, pp. 344-352.
[14] Underwood, E.E., 1968, “Particle-size Distribution,” in: Quantitative Microscopy, pp. 149–
200, McGraw-Hill Book Company, New York, NY.
[15] Underwood, E.E., 1970, Quantitative Stereology, 2nd ed., Addison-Wesley Publishing
Company, Reading, MA.
[16] Cruz-Orive, L.M., 1976, “Particle size-shape distributions: the general spheroid
problem.” J. Microsc., Vol. 107, pp. 235–253.
[17] Cruz-Orive, L.M., 1978, “Particle size-shape distributions: the general spheroid problem:
II. Stochastic model and practical guide.” J. Microsc., Vol. 112, pp. 153–167.
[18] Cruz-Orive, L.M., 1983, “Distribution-free estimation of sphere size distributions from
slabs showing overprojection and truncation, with a review of previous methods.” J.
Micros c., Vol. 131, pp. 265–290.
[19] Takahashi, J. and Suito, H., 2003, “Evaluation of the accuracy of the three-dimensional
size distribution estimated from the Schwartz-Saltikov method.” Metall. Mater. Trans. A,
Vol. 34, pp. 171-181.
[20] Payton, E.J. and Mills, M. J., 2011, “Stereology of backscatter electron images of etched
surfaces for characterization of particle size distributions and volume fractions: Estimation
of imaging bias via Monte Carlo simulations.” Mater. Charact., Vol. 62, pp. 563-574.
[21] Jeppsson, J., Mannesson, K., Borgenstam, A., and Ågren, J., 2011, “Inverse Saltikov
analysis for particle-size distributions and their time evolution.” Acta Mater., Vol. 59, pp.
874-882.
[22] Ohser, J. and Mücklich, F., 2000, Statistical analysis of microstructures in materials
science, John Wiley & Sons, New York, NY.
[23] Ohser, J. and Mucklich, F., 1995, “Stereology for some classes of polyhedrons.” Adv. Appl.
Prob., Vol. 27, pp. 384-396.
[24] Scott, D.W., 1979, “On optimal and data-based hist ograms.” Biometrika, Vol. 66, pp. 605-
610.

Vol.11, No .3 Revisiting Sphere U nfolding Relationships 241
[25] Saltikov, S.A.: “The determination of the size distribution of particles in an opaque
material from a measurement of the size distribution of their sections,” in: Stereology:
Proceedings of the Second International Congress for Stereology, Chicago, 1967, pp. 163–
173.
[26] Heilbronner, R. and Bruhn D., 1998, “The influence of three-dimensional grain size
distributions on the rheology of polyphase rocks.” J. Struct. Geol., Vol. 20, pp. 695–705.
[27] Heilbronner, R., 2002, “How to derive size distributions of particles from size distributions
of sectional areas,” Conférence Universitaire de Suisse Occidentale, 3ème Cycle
Séminaire: “Analyse d’images et morphométrie d’objets géologiques,” Organisé à
Neuchâtel, Institut de Géologie, Université de Neuchâtel.
[28] Ford, W.B., 1922, A Brief Course in College Algebra, The Macmillan Company, New
York, NY.
[29] Limpert, E., Stahel, W.A., and Abbt, M., 2001, “Log-normal Distributions across the
Sciences: Keys and Clues.” BioScience, Vol. 51, pp. 341-352.
[30] Russ, J.C. and Dehoff, R.T., 2000, Practical Stereology, Kluwer Academic, New York,
NY.
APPENDIX: SOURCE CODE
The equations given in the present paper can be coded in a spreadsheet or rather efficiently in a
few lines of code in, for example, the Matlab/Octave programming languages, as demonstrated
in the following example where the number fractions in the histogram of o bservations are inputs
the array ‘f2d’, the edges of the areal binning array are input as ‘a’, the mean areas of the bins are
given as ‘ab’, the particle volumes represented by the bins are given by ‘V’, and the volume
fraction of particles is given as ‘vf’:
nb=length(a)-1; % Number of bins
p=zeros(1,nb);am=zeros(1,nb);ap=zeros(1,nb); % Preallocate variables
NA=zeros(nb);e=zeros(nb);am(1:end)=a(1:end-1);% "
fA=ab.*f2d;fA=vf*fA/sum(fA); % Convert to area-weighting
for j=nb:-1:1 % Loop through bins
p(1:j)=(sqrt(a(j+1)-am(1:j)) ...
-sqrt(a(j+1)-a(2:j+1)))/sqrt(a(j+1));% Eq. 5
ap(1:j)=0.5.*p(1:j).*(am(1:j) ...
+a(2:j+1)+(a(j+1).*p(1:j).^2)./3);% Eq. 8
NA(j,1:j)=ap(1:j)/sum(ap(1:j));% Eq. 9
f3d(j)=fA(j)/NA(j,j);% Eq. 10
if f3d(j)<0
e(j,j+1:nb)=fA(j)./NA(j+1:nb,j);f3d(j)=0.0; % Eq. 12
end;
fA(j)=0.0;fA=fA-f3d(j)*NA(j,:); % Eq. 11
end;clear p ap am NA j fA
e=max(-repmat(f3d,[nb 1]),e); % Limit error array values

242 E. J. Payt on Vol.11, No.3
f3d=vf.*f3d/sum(f3d); % Restore correct volume fraction
f3d=f3d./V;e=e./repmat(V,[nb 1]); % Number of particles per unit volume
e=e/sum(f3d);f3d=f3d/sum(f3d); % Number fractions
SE=-sqrt(sum(e.^2,1)./(1:nb))./sqrt(1:nb); % Eqs. 13 & 14
clear e nb