Received 22 August 2014; revised 19 September 2014; accepted 15 October 2014

ABSTRACT

A process model of quantum mechanics utilizes a combinatorial game to generate a discrete and finite causal space, which can be defined as a self-consistent quantum mechanics. An emergent space-time 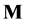and continuous wave function arise through a non-uniform interpolation process. Standard non-relativistic quantum mechanics emerges under the limit of infinite information (the causal space grows to infinity) and infinitesimal scale (the separation between points goes to zero). This model has the potential to address several paradoxes in quantum mechanics while remaining computationally powerful.

Keywords:

Process Theory, Quantum Foundations, Discrete Models, Emergent Models

1. Introduction

Questions concerning the completeness of quantum mechanics and the proper interpretation of the wave function date back to its earliest days and remain unresolved to this present day. Recent research into hidden variable theories [1] and quantum information [2] rather strongly suggest that quantum mechanics is a complete theory, at least in so far as its probabilistic and statistical structure is concerned. Debate into the nature of the wave function continues [3] [4] , with some authors continuing to view it in probabilistic terms [5] while others have mounted arguments for it being a physical entity [6] . This paper aims to contribute to these debates, presenting a decidedly unromantic (to quote Bell [7] ) model of quantum mechanics, grounded in process theory, in which wave functions correspond to real physical waves, in which space-time and physical entities are emergent, and which is discrete, finite, intuitive, causal, quasi-local and quasi-non-contextual, yet retaining the computational power of standard quantum mechanics.

There have been previous attempts to provide a realist, emergent, or process based quantum mechanics: Bohmian mechanics, quantum hydrodynamics, Wolfram’s cellular automata, continuous spontaneous localization (GRW), Finkelstein’s quantum relativity, Noyes’s bit-string physics, Bastin and Kilmister’s combinatorial physics, Hiley’s process physics [8] [9] . Most of these have not gained much purchase within the larger physics community, possibly because the path back to standard quantum mechanics is not straightforward. The necessity to consider discrete models arises from considerations in quantum gravity [10] , from the need to avoid divergences in quantum field theories, and from recent work by Gisin [11] , who constructed a Bell type inequality showing that either one must reject the principle of continuity or accept instantaneous information transfer between space-like separated entities (thus rejecting special relativity). In the model presented below, continuity is recovered via an interpolation procedure (based upon an idea of Kempf [12] ) and quantum mechanics (at least non-relativistic quantum mechanics) arises directly as an effective theory when a continuum idealization can be assumed.

The key idea, based on Whitehead’s Process Theory [13] assumes that the elements of physical reality do not simply exist, but rather are emergent upon a lower level of entities. Whitehead called these entities “actual occasions” but they shall be referred to as informons to reflect their fundamental informational character. These informons are generated moment to moment through the actions of processes, which interpret, transform and supplement the information of the current generation of informons and incorporate it into the next. Informons are postulated to be discrete, fuzzy, finite and organized into distinct generations. They are transient-arising, persisting briefly as their information is incorporated into the next generation of informons, then abating. Information passes causally from one generation to the next, never within a generation. As a consequence, special relativity is not violated [14] .

Space-time, and the physical entities that manifest in space-time, are all postulated to be emergent from informons which manifest at a scale that precludes any possibility of direct observation by the physical entities that emerge from them. Ironically, informons must be interpreted in reference to the entities they generate [15] . This is because observations of informons can only occur through an act of measurement, which is understood to involve an interaction between a system process and a dynamically specialized measurement apparatus process.

The passing of information from one generation to another induces a causal structure. Given two informons, n, n', write 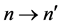(or) if n was in a earlier generation than n' and information was passed from n to n'. In addition they may be assigned a causal distance. Each informon n is assigned a tuple p_n of properties inherited from the process that generates it, the most important being the “strength” or “coupling effectiveness” of the generating process, , attributed to n. Finally, to each n there is associated an informational content G_n, which for convenience is simply referenced to the prior informons that contributed information to its generation. G_n will thus be a set of informons from previous generations of informons that forms either an acyclic directed or ordered set. Properties are intrinsic, whereas interpretations are extrinsic but provide the connection to theory.

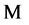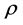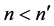Although informons are transient, it is useful to exploit the artifice of a history of their appearance, thus interpreting each informon n as a point x_n in a causal manifold with causal ordering and metric [16] . Given if then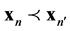. Sometimes one requires tha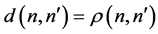t. Let 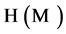denote the Hilbert space on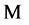. Each informon is also interpreted as providing a local 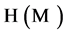-contribution 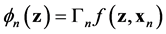to the wave function of some physical entity. In general f will be a translation of a single generating function g, that is. The global -interpretation forms an actual physical wave that approximates the wave function. The accuracy of the approximation depends upon f as determined by interpolation theory.

Formally, denote an informon by where.

Informons are understood to be generated by processes. Processes possess only algebraic properties: they generate space-time and so cannot be situated in space-time. A process may be active, in which case it acts in a series of rounds to generate informons, or inactive. Each process is described by several parameters: one or more tuples of properties, the number of informons generated during a round, the number of previous informons whose information is incorporated into a nascent informon, the number of rounds needed for a generation, the temporal and spatial scales of informons. The triple of current generation, process, and nascent generation, forms what philosophers term a compound present. A system unfolds as a succession of such present moments.

A primitive process is defined as generating a single informon during a single round. Intuitively, the action of a primitive process is to generate, one by one, a succession of informons, thus forming a generation. Although logically is prior to, it may be useful to think of each generation as forming a discrete version of space-time, which embeds into as a discrete sampling of a space-like hyper-surface. Since no information passes between informons within a generation they form a causal antichain. It is also useful, though technically incorrect, to view the informons as forming a discrete sampling of a wave function defined on that surface by. Collating all such generations yields a discrete version of and a discrete sampling of a global wave function on. Information from previous generations propagates as a discrete version of a dissipative wave interacting with its environment through various types of couplings. Standard quantum mechanics can be viewed as an idealization or as an effective theory of the in the limit of and. The conditions under which this is possible depend upon the form of the generating function g for the local Hilbert space contribution and the geometry of the embedding into, and can be derived from various interpolation theories [17] [18] .

The generation of an informon can trigger a coupling between processes or the activation or inactivation of processes, depending upon the compatibility of these informons [19] . Couplings between processes take many forms, providing the space of processes with a rich algebraic and combinatorial structure. Processes may act sequentially (denoted as sums) or concurrently (denoted as products). They may act independently of one another (independent) or their actions may be constrained, so that the action of one forces limitations on the actions of another (interactive). They may act on the same nascent informon (free or bosonic) or only on distinct informons (exclusive or fermionic). These considerations give rise to 6 relevant possibilities—1) Sequential sums: (exclusive, independent), (exclusive, interactive), 2) Concurrent products: (exclusive, independent), (free, independent), (exclusive, interactive), (free, interactive). The interactive case is actually shorthand for a set of possible interactions. Only exclusive sums are considered since the ontology of the process approach requires that superpositions only involve the generating processes and never the informons that they generate.

Primitive processes combine to generate multiple informons during a round. Complex processes are formed through algebraic combinations of simple processes. Although processes generate informons non-locally there is no actual non-local exchange of information. A superposition of simple processes takes the form, meaning that during a given round only one of the is active, generating a single informon, but this may change from round to round. More generally one has, where indicates a modification of certain attributes of by the factor, for example multiplying the wave function contribution by.

A product, (or) or an entanglement of primitive processes, (or) means that during a given round, all of the are concurrently generating single informons. Entanglement uses the interactive product because in interaction mode their actions are mutually constrained, and the resulting informons will be correlated. Note that no information passes among these informons. Each is generated by its own process using only causally local information propagating from current informons linked to that process. There is no “spooky action at a distance”. There is just the realization that the generating sub-processes are not independent of one another but rather are in an interactive mode.

The process viewpoint leads to the insight that the proper setting for quantum dynamics is not the Hilbert space but rather the space of generating processes. Dynamical information is lost when considering only the wave function. Beginning with some generation of informons, a primitive process, once activated, will generate a sequence of of informons. Due to the non-deterministic nature of the process action, reactivating the process on the same initial generation will, in all likelihood, result in a different sequence of informons, say. Each sequence results potentially in a different global - interpretation, ,. Collecting all such possible interpretations into a set, one obtains a set valued map given by. This holds for primitive processes but may be extended to more complicated processes by defining it on sums and products as

where for two sets of functions A, B the sum and

The initial causal tapestry is fixed above, so strictly one should write. The situation for interactive products is much more complicated and space does not permit its discussion here.

Interpolation theory shows that given certain choices of the interpolation function g, in the limit, , a singleton set.

The process covering map (PCM) provides a linkage between the space of processes, and the Hilbert space, and thus to NRQM. In general the PCM will depend upon the strategy used to implement the actions of the processes as well as the initial conditions. As will be made explicit in the example below, if the strength for some non-relativistic wave function which has energy and momenta bounded away from Planck energy and momentum, then, and if is not band-limited in this way, then this will still be true in the limit.

Conservation laws and symmetries applied to the properties of processes provide a set of algebraic constraints upon possible interactions among processes. These are inherited by the wave functions through the process covering map suggesting that processes are primary and wave functions secondary. Quantum mechanics may be best viewed as an effective theory, valid under certain asymptotic limits, but not necessarily the final theory.

Processes are considered to act non-deterministically, a term used in computation theory to mean that actions are described by set-valued maps without any intrinsic probability structure. Probabilities arise through two mechanisms: combinatorial proliferation, similar to the case for iterated function systems, and coupling of processes, in particular through couplings to measurement processes. One cannot do justice to this topic in a short note and the theory of interaction and measurement will be discussed in a separate letter.

2. A Model of NRQM

The simplest, heuristic representation of process is as a two player, co-operative, combinatorial game [20] , based on the forcing games used in mathematical logic to generate models [21] . Combinatorial games are intuitive and capture all of the essential algebraic structure of the process space. To play, it is customary to assign each player a strategy (a set of rules determining their moves). A basic strategy which provides an in-principle demonstration of the power of the method is that of the Bounded Radiative Uniform Sinc Kernel Strategy. Sinc interpolation has been widely studied, providing a nice intuitive interpretation as consisting of local dissipative waves, and non-uniform sinc interpolation has been shown to be as effective as uniform interpolation, though the latter is much easier to work with formally [22] . More realistic models require the use of non-uni- form strategies but the mathematical complications would obscure the basic ideas.

Let us consider a single primitive non-relativistic process interacting with a potential, which summarizes the effect of the environment so that the environment process may be ignored. Strictly speaking, there are at least three different types of interactions between a system process and an environment process. These are (non-interacting), (bound) and (scattering). A different kernel is required for each case. The following describes only the case. Set.

Player I propagates information forward to the nascent generation while Player II uses this to construct the new informons. Let be the current generation and the nascent generation. Let. Being bounded and uniform, the causal distance between, takes the form , for some r. Information propagates from j into a hypercube of diameter r. will embed into as a space-like lattice of the form.

Let denote a nascent informon. Then will lie at a compatible point on. is constructed by propagating information forward from to as a diminishing wave of the

form scattering off the potential at j. In the sinc strategy, the function is a

translated sinc function, with temporal and spatial wavelengths given by t_P and l_P respectively. Depending upon the exact model, t_P, l_P may be universal, for example the Planck time and length respectively, or they may depend upon the energy and momentum of the system. Note that the dynamics is defined using information from and and does not require the interpretations. Write

where and set.

Then

.

Parzen’s theorem (see [23] ) states that if is a function band limited to the N-dimensional rectangle, , so that its Fourier transform is such that

for, , and, then

Now, the kernel for the integral form of the Schrödinger equation [24] .

Let. Then the global wave function on the hypersurface is given by

which for very large r and N is approximately

which, if recursively, is approximately

which according to Parzen’s theorem and Feynman and Hibbs [23] implies that

in the case that has bounded energy and momenta (so t_P, l_P can be finite). If this is not the case then one must also take the limit as. In any case, the NRQM wave function emerges in the asymptotic limit.

The discrepancy between the global Hilbert space interpretation given above and the standard non-relativistic quantum mechanics wave function depends upon the accuracy of the approximation to the integral

, the deviations from uniformity of the causal embedding points, the number r of cur-

rent informons contributing information to any nascent informon as well as the values of t_P, l_P. This is a difficult problem to assess in general but results are available in special cases. For example, in one dimension, if the

wave function satisfies for, , the discrepancy

between each embedding point and its ideal lattice embedding point is less that, and the truncation number, then according to a theorem of Butzer (see Zayed), the error E satisfies

where

Hence, if l_P is the Planck length. In three dimensions,.

The appropriate strategies and interpolation methods are a matter for future study and comparison to empirical data. Most promising are radiative, action or kernel and non-uniform strategies.

3. Conclusion

In summary, the adoption of a process point of view results in a novel model of (non-relativistic) quantum mechanics which is discrete, finite and intuitive. The model is self contained, and NRQM appears as an idealization under certain limiting conditions. It involves the propagation of only causally local information, although the discontinuous action of process makes it quasi-local. Informons possess definite properties, but only those properties imparted to them by their generating processes, which can only be determined through an interaction with a measurement process. The model is locally non-contextual but globally contextual, hence quasi-non-contextual. Any type of computation involving the NRQM wave function may be carried out using the global -in- terpretation, so the model is as computationally powerful as NRQM. The model challenges the usual hidden variable arguments [25] and may open the door to a new generation of hidden variable models. More research is needed to determine whether the approach can be applied to quantum field theory.

Acknowledgements

Thanks are due to Irina Trofimova and Robert Mann for many fruitful discussions.

References