Paper Menu >>
Journal Menu >>
 J. Modern Physics, 2010, 1, 124-136 doi:10.4236/jmp.2010.12018 Published Online June 2010 (http://www.SciRP.org/journal/jmp) Copyright © 2010 SciRes. JMP Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at All Times Athanasios N. Petridis1, Lawrence P. Staunton1, Jon Vermedahl1, Marshall Luban2 1Department of Physics and Astronomy, Drake University, Des Moines, USA;2Ames Laboratory and Department of Physics and Astronomy, Iowa State University, Ames, USA. Email: athan.petridis@drake.edu Received March 2nd, 2010; revised April 7th, 2010; accepted April 30th, 2010. Abstract The departure at large times from exponential decay in the case of resonance wavefunctions is mathematically demonstrated. Then, exact, analytical solutions to the time-dependent Schrödinger equation in one dimension are developed for a time-independent potential consisting of an infinite wall and a repulsive delta function. The exact solutions are obtained b y means of a superposition of time-indep endent solutions spanning the given Hilbert space with appropriately chosen sp ectral functions for which the resultin g integrals can be evaluated exactly. Square-integrability and the boundary cond itio ns are sa tisfied . The simplest of the obta ined so lutio ns is presen ted and the pro bab ility fo r the particle to be found inside the potential well as a function of time is calculated. The system exhibits non-exponential decay for all times; the probability decreases at large times as 3 t . Other exact solutions found exhibit power law behavior at large times. The results are generalized to all normalizable solutions to this problem. Additionally, numerical solutions are obtained using the stagge red leap-fro g algorithm for select p otentia ls exhibiting the prevalence of non-exponential decay at short times. Keywords: Non-Exponential , Decay, Exact , Solutions 1. Introduction The law of exponential decay is typically discussed in association with atomic transitions or resonances in scattering amplitudes. Even though the approximations made in order to arrive at exponential decay of excited states or resonances are well understood the mistaken impression that this law is universal and exact often prevails. This perception is reinforced by experiments often done in student laboratories geared towards studying the half-lives of radioactive nuclei or unstable particles and, very importantly, by numerous research publications and data tables in which exponential decay is tacitly assumed. The fact that these experiments measure counting rates during only finite time intervals and are focused on decays of quasi-stationary states is usually not discussed, let alone studied in detail. The history of this particular problem is quite interes- ting. Early on Khalfin [1] used dispersion relations to show that even quasi-stationary states with spectral functions that have a lower bound in their energy spectrum must decay non-exponentially at large times. Winter [2] examined the infinite wall plus repulsive delta function potential and obtained a single implicit solution in the form of an integral for the special case in which the initial wavefunction is an eigenfunction of the infinite square well of the same width and as a result it is a near-resonance (quasi-stationary) state of the actual potential. His analytic approximation to the integral in the limit of low barrier transmittance (large strength of the delta function) proved that the survival probability exhibits exponential decay in the (intermediate) time interval-when the dominant quasi-stationary resonance prevails inside the well-while at very large times it decays following the power law 3 t. By means of numerical studies the same author found oscillations in the probability current at times before the power law sets  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 125 in if the initial state has a relatively wide energy spec- trum. The purpose of this article is to demonstrate explicitly the existence of systems that exhibit non-exponential decay at all times by developing exact, analytical, closed form solutions to the time-dependent Schrödinger equa- tion for a one-dimensional potential and non-quasis- tationary initial states as well as to illustrate non- exponential decay using numerical solutions to specific problems for which analytical solutions are not obtaina- ble. The clear advantage of the analytical approach without any approximations is that it yields an equation for the survival probability of the initial state that can be studied for any time interval and that is unequivocally non-exponential. The conclusions are easily generalized and the long-time behavior of the solutions is predicted and shown to follow an asymptotic power law. It is, thus, established that for a large class of systems, non-expo- nenential decay is the rule rather than the exception. This paper also elucidates and generalizes previous research work. Recently there has been increasing interest in the time dependent Schrödinger equation and, in particular, in the decay of physical systems. The equivalence of exponential decay of a perturbed energy eigenstate with Fermi's golden rule when the final density of states is energy-independent and with the Breit-Wigner resonance curve has been long known and presented in several papers [3] and textbooks [4]. Dullemond [5] has verified this behavior for a simple but exactly solvable model and found, however, that if final-state energy-dependence is introduced into this model a non-exponential decay pattern will dominate at large times. Oleinik and Arepjev [6] have shown that tunneling of electrons out of a finite potential well when a long-range electric field is suddenly switched on follows a 3 t probability decay law at large times. Specific systems that may exhibit non-exponential decay include systems with non-local interactions [7], certain closed many-body systems [8], quasi-particles in quantum dots [9], polarons [10], and non-extensive systems [11]. Petridis et al., [12] have studied numerically a variety of systems in which the initial wave function is mostly or entirely set in a finite potential well and have observed rich behavior, including non-exponential decay into the continuum. Non-exponential decay was experimentally observed for the first time by Wilkinson et al., [13] in the tunneling of ultra-cold sodium atoms initially trapped in an accelerating periodic optical potential created by a standing wave of light. Kelkar, Nowakowski, and Khem- chandani [14] have reported evidence for the non- exponential alpha decay of Be 8. Rothe, Hintschich, and Monkman [15] have clearly measured non-exponential time-dependence in the luminescence decay of dissolved organic materials after pulsed laser excitation. Time-dependent quantum mechanical problems are usually addressed using time-dependent perturbation theory, adiabatic or sudden approximations as well as several numerical techniques. Exact analytical solutions to certain problems are highly desirable, especially in cases when the approximate methods may be inadequate to describe all aspects of the solutions or when numerical treatments do not explicitly reveal their mathematical properties. Burrows and Cohen [16] have developed exact solutions for a double-well quasi-harmonic potential model with a time-dependent dipole field. Cavalcanti, Giacconi, and Soldati [17] have solved the problem of decay from a point-like potential well in the presence of a uniform field and have indicated that, due to an infinitely large number of resonances, there may be deviations from the naively expected exponential time- dependence of the survival probability. In this article a well established method for solving time-dependent quantum mechanics problems is used to develop exact, analytical, closed-form solutions to the infinite wall plus repulsive delta function potential. The large-time non-exponential decay for three solutions to this system is established and the asymptotic power law behavior is explicitly demonstrated to be 3 t for the first two and 4 t for the third. It is also proven that this result, (or a higher negative power of t), is valid for all square-integrable solutions to this system. Furthermore numerical solutions are developed for finite-range po- tentials and shown to exhibit a rich, non-exponential decay behavior, including oscillations. 2. The Exponential Decay Approximation The time-dependent wavefunction, ) , ( t x , can be expressed as a superposition of fixed energy states, )( x E , each evolving in time as iEt e, ,)()(=),( dEexEtx iEt E (1) where )( x E are fixed-energy (stationary) solu- tions to the Schrödinger equation for the given Hamil- tonian and )(E is an energy distribution or “spectral function”. It is important that this integral converge and the resulting wavefunction is square-integrable for the given boundary conditions (i.e., it belongs to the related Hilbert space). If the energy is non-negative and its distribution in the above integral has a dual-pole (resonance) structure in the complex plane, that is , )( 1 = ))(( 1 =)(22 0 * 00 EEEE E (2)  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 126 where iE00 = , and 0 <<<0 E, then )(E is strongly peaked at 0 E and essentially only )( 0 x E contributes, i.e., to a good approximation . )( )(=),( 22 0 0 0dE EE e xtx iEt E (3) With the substitution )/(= 0 EEu , the integral becomes . 1 )(=),( 2 / 0 0 0du u ee xtx tui E tiE E (4) Defining 0>= t for forward evolution and 0>/= 0E the above expression can be re-written as, ,),(),()(=),( 0 0 iSC e xtx tiE E (5) where . 1 )(sin =),(, 1 )(cos =),( 22 du u u Sdu u u C (6) With uu = ' the first integral is . 1)( )(cos = 1 )(cos 1 )(cos =),( ' 2' ' 22 du u u e du u u du u u C (7) Similarly the second integral is ' ' 22 '2 sin()sin( )sin() (,)== , 11()1 uu u Sdududu uu u (8) since the integrand in the first term is odd in u and vanishes as ||u. The wavefunction, therefore, becomes (dropping the primes on u) . 1 )(=),( 2 0 0 du u e e e xtx iu tiE E (9) At this stage the exponential-integral function dy y e zE y z =)( 1 (10) is useful. Clearly, .= )( 1 z e d z zdEz (11) Upon defining the function ,)()( 2 =),( 11 iuEeiuEe i uf (12) its derivative is calculated to be du iudE e du iudE e i du df )()( 2 =11 iuiu eiu 11 2 = . 1 =2u eiu (13) Therefore, .)()( 2 = |),(= 1 11 2 iEeiEe i ufdu u eiu (14) Using the well-known expansion, ,... 21 1=)(2 1 zzz e zEz (15) and keeping only the two first terms for large || i , the wavefunction becomes 1 )(),( 2 0 0 i tiE Eei e e xtx .)(=22 0 00 0 E e t i e e x tiE t tiE E (16) Thus, the probability density for times large relative to 1/222 0)( E is ])(sin 12 11 [|)(||),(| 0 22 0 2 22 0 2 2 2 2 2 0 2 tE E e t Et extx t t E (17) and it has a term decaying exponentially with constant 2Γ plus a 2 t term dominating at very large times as well as an “intermediate” decaying oscillatory term. In this example not only is the rise of exponential decay shown to emerge for a spectral function exhibiting a resonance (dual-pole) structure but the departure from this behavior at large times is clearly elucidated, having a power-law dependence. It is noteworthy that the non- exponential behavior is related to the cut-off in the energy interval. If the energy were to vary over the entire real axis then the residue theorem would yield exponen- tial decay. The short time behavior is very complicated as Equation (9) indicates and it is also not exactly exponential. 3. Infinite Wall and Delta-function Potential The method to be employed to address the problem of an infinite wall plus a delta-function potential is standard and consists of the following steps: a) The time- independent solutions to Schrödinger equation are found subject to the boundary conditions of the problem. These  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 127 are stationary solutions (energy eigenfunctions) that span the Hilbert space of the given Hamiltonian. b) Since any finite or infinite, discrete or continuous linear combina- tion of the stationary solutions (basis functions), as long as it is square-integrable, is also a solution belonging to the given Hilbert space, exact analytical solutions can be developed by a superposition of the eigenfunctions with energy-dependent spectral functions multiplied by the standard oscillatory time-dependence of the stationary states. It is, obviously, necessary that the superposition integral over the energy converge. Spectral functions for which the resulting integrals are tractable are chosen here. The convergence as well as the square-integrability (normalizability) of the resulting wave functions are verified. c) The survival probability, i.e., the probability for finding the particle inside the potential well is calculated and its properties are studied analytically. The problem is defined by the one-dimensional repulsive potential, ,<0)( 0< =)( 0xLxV x xV (18) with 0>L and 0> 0 V. The steps outlined above are followed. a) The solutions to the time-independent Schrödinger equation, ),(=)()( )( 2 1 2 2xExxV dx xd EE E (19) (with particle mass 1=m, 1=, and 0E for this potential) are, (0) ()=0,0("0"), Exx region (20) ),""(0),(sin=)( 1 )( IregionLxpxCx I E (21) ),""( ),(cos)(sin=)( 32 )( IIregionxL pxCpxCx II E (22) where Ep 2= and 1,2,3 C are constants in x. These functions obey the boundary conditions ),(=)( )()(LLII E I E (23) ),(2=)()( )( 0 )()(LVL dx d L dx dI E II E I E (24) while the boundary conditions at 0=x are automa- tically satisfied. The energy eigenfunctions, E , are not required to vanish at infinity since time-dependent func- tions, ),(tx , produced by Equation (1) for large x are acceptable solutions. Selecting C1 as the overall norma- lization constant, the boundary conditions at Lx = yield ,)(cos)(sin 2 1= 0 12 pLpL p V CC (25) ),( sin 2 =2 0 13 pL p V CC (26) rendering 2 C and 3 C functions of the energy. The choice of 2 C or 3 C as the normalization constant would introduce an energy-dependence in 1 C and would effectively amount to different choices of spectral functions. The linearly independent energy eigenfunctions obtained are orthogonal under the inner product ,)()( lim )()(=),( 2 * 1 )( 0 2 * 1 0 21 dxxxe dxxx Lx L L (27) with all wavefunctions in the defined Hilbert space identically vanishing for 0x. The orthogonality relation is ),()(=),( ' 'ppEw E E (28) where Ep2= , '' 2= Ep and 2 3 2 2|)(||)(| 2 =)(ECECEw .)(2sin2)(2cos22 2 |=| 0 2 0 2 0 2 2 2 1pLpVpLVVp p C (29) The Dirac -function representation used is . )( 1 lim =)(22' 0 ' pp pp (30) b) The solution to the time-dependent Schrödinger equation, ),,()( ),( 2 1 = ),( 2 2txxV x tx t tx i (31) can be written as the energy-convolution integral, ,)()(=),(0dEexEtx iEt E (32) with )(E a spectral function such that this integral is convergent for all x and all t and the resulting wavefunction is square-integrable. Note that square- integrability of ),( tx also requires E to be real. The overall normalization constant is, then, calculated from * 0(,) (,)=1.xtxtdx (33) The first choice of spectral function to be considered is  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 128 ,=)( 2 1 EK eE (34) with K a positive constant. This offers the advantage that the integrals above can be evaluated in closed form and the resulting wave function is square-integrable even without the presence of the convergence factor that appears in Equation (27). The time-dependent solution is, then, 0,=),( (0) tx (35) ,)( 2 =),( 3/22 ) 2 2( 2 1 )( itKexCtx itK x I (36) 3/22 2 2 2 2 2 1 )( )( 2 =),( itKeCtx itK xLxL II ,)()( 00 2 ) 2 2( 2 )2( 0 2 ) 2 2( 2 xitVVKeVitKe itK xL itK x (37) where 1/2 2 0 3/2 2 2 2 0 3/2 3 0 3/2 2 2 3 3/2 122 28 = K Ve K V K VLe K CK L K L (38) is the overall normalization factor obtained by means of Equation (33). c) The probability density ),(),(= * t x t x can be calculated for the interior (region I) and the exterior (region II) of the potential well. It is presented in Figure 1 at six times starting from 0=t, in increasing order. The initial wavefunction is not entirely localized inside the well. As time progresses the wavefunction spreads and tunnels through the potential barrier in both directions. The interference of the wave that propagates outwards through the barrier and the wave that is outside creates the observed ripples. Inside the well there are no ripples because the wavefunction is forced to be odd in x , having a node at 0=x. The centroid of the pro- bability density in region II at 0=t is always located at L2, regardless of the value of K . The survival probability is, then, defined to be .),(),(=)( * 0dxtxtxtPL in (39) This yields the closed-form result 22 3/2 42 2 1342342 2 ()= erf 88 KL Kt in KL KL Pt Ce KKt KKt (40) A plot of the survival probability versus time is given in Figure 2. (0) in P is controlled by K . It decreases as K increases, i.e., as the momentum spectrum becomes sharper. For example, if 3=L, (0) in P is 0.9615 for 0.1=K, 0.5 for 0.5=K, and 0.1468 for 1.2=K. A physical interpretation of this effect is that at 0=t some decays have already happened. On the other hand the decay becomes slower as K increases. The expansion of in P in inverse powers of time includes only odd terms with alternating signs. At large times the leading term, that has a positive sign, is proportional to 3 t, a clearly non-exponential behavior. 4. Corrections to the Exponential Decay Law The law governing the decay of physical systems is typically assumed to be a simple exponential time- dependence of the number )(tN of the systems that have not decayed until time t, i.e., ()= (0)NtN e( ) x pt , where is the decay constant. As mentioned earlier this simple law is consistent with the Breit-Wigner curve and Fermi's golden rule if the final density of states is energy independent. It refers to the survival probability of a given initial energy resonance (quasi-stationary state). For the choice of spectral function given by Equation (34) the initial state is not a resonance state. If a very large number of systems is assumed to be initially described by ,0)( x and a system is said to have decayed if the particle has exited the potential well, then the number of surviving systems is proportional to the probability in P, i.e., . (0) )( = (0) )( in in P tP N tN (41) The differential decay law is ,)()(= dttNtdN (42) where, is, in general, dependent on time. Substi- tution from Equation (41) gives ))].((l[= 1 =)( tPn dt d dt dP P tin in in (43) In the case studied, Equation (40) yields , )](e2)[( 4 =)( 2 24 3 2 zrfzetK tze tz z (44) where 24 /= tKKLz . This function is plotted versus time in Figure 3. The decay parameter peaks in time. Its maximal value, max , is smaller as K or L increases but does  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 129 Figure 1. The probability density for a potential consisting of an infinite wall and a repulsive delta function and using the spectral function given by Equation (34) at six times (from the upper panel in the left colume to the lower panel in the right column, = 0.0,0.3,0.6,0.9,1.2,1.5t). In this plot =3L, 0=1V and =1/2K not depend on 0 V . The peak and the small time interval around it correspond to an almost exponential decay. This, however, cannot be directly associated with the dominant (lowest energy) resonance that this potential accommodates. Resonances in the energy can be iden- tified as the maxima of the function [18] , )8(sin8)]8(cos[122 2 = |||| || =)( 0 2 0 2 3 2 2 2 1 ELEVELVE E CC C Eg (45) plotted in Figure 4 for 3=L and 1= 0 V. It can be 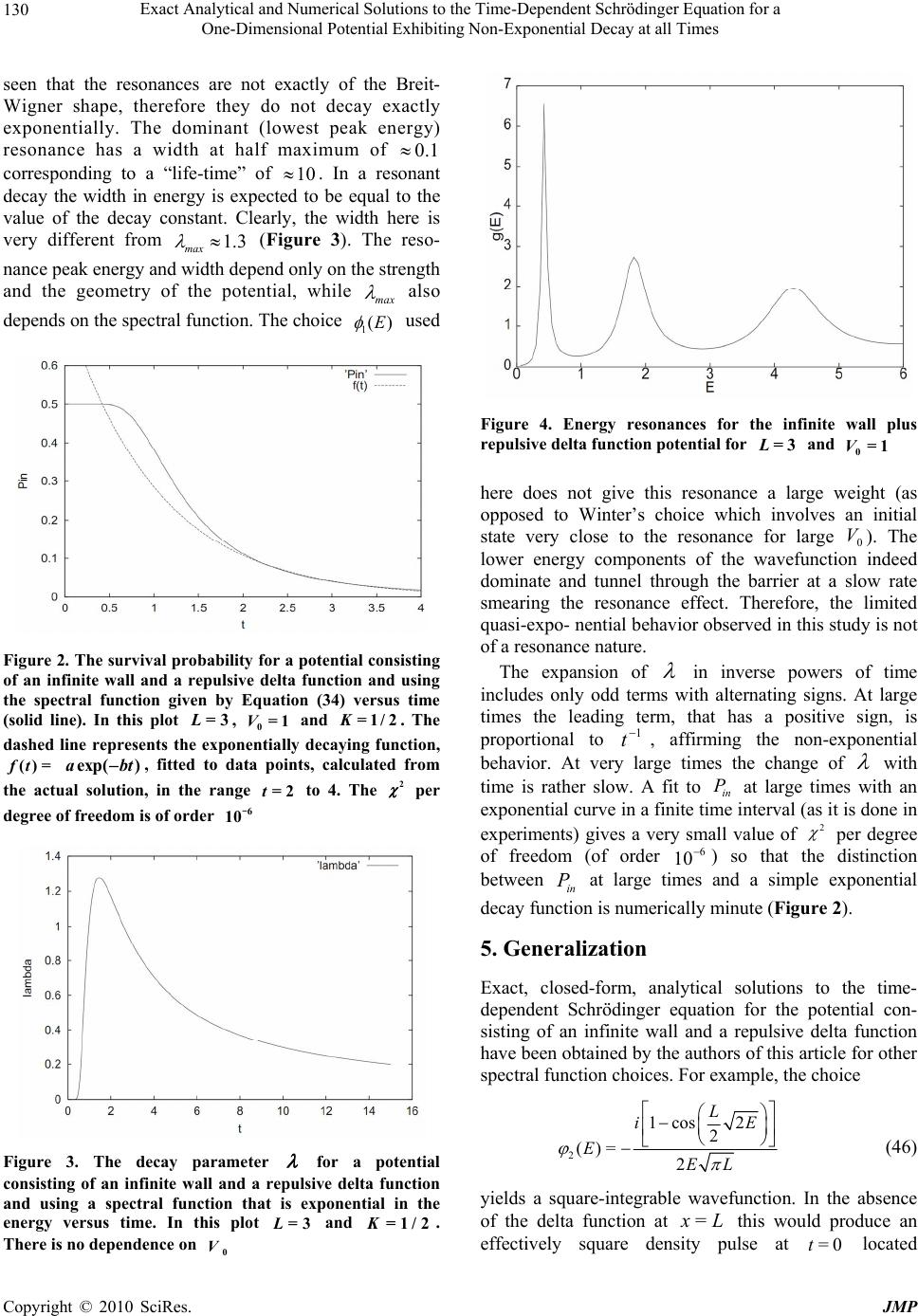 Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 130 seen that the resonances are not exactly of the Breit- Wigner shape, therefore they do not decay exactly exponentially. The dominant (lowest peak energy) resonance has a width at half maximum of 0.1 corresponding to a “life-time” of 10. In a resonant decay the width in energy is expected to be equal to the value of the decay constant. Clearly, the width here is very different from 1.3 max (Figure 3). The reso- nance peak energy and width depend only on the strength and the geometry of the potential, while max also depends on the spectral function. The choice )( 1E used Figure 2. The survival probability for a potential consisting of an infinite wall and a repulsive delta function and using the spectral function given by Equation (34) versus time (solid line). In this plot =3L, 0=1V and =1/2K. The dashed line represents the exponentially decaying function, ()= f t ex p ()abt, fitted to data points, calculated from the actual solution, in the range =2t to 4. The 2 per degree of freedom is of order 6 10- Figure 3. The decay parameter for a potential consisting of an infinite wall and a repulsive delta function and using a spectral function that is exponential in the energy versus time. In this plot =3L and =1/2K. There is no dependence on 0 V Figure 4. Energy resonances for the infinite wall plus repulsive delta function potential for =3L and 0=1V here does not give this resonance a large weight (as opposed to Winter’s choice which involves an initial state very close to the resonance for large 0 V ). The lower energy components of the wavefunction indeed dominate and tunnel through the barrier at a slow rate smearing the resonance effect. Therefore, the limited quasi-expo- nential behavior observed in this study is not of a resonance nature. The expansion of in inverse powers of time includes only odd terms with alternating signs. At large times the leading term, that has a positive sign, is proportional to 1 t, affirming the non-exponential behavior. At very large times the change of with time is rather slow. A fit to in P at large times with an exponential curve in a finite time interval (as it is done in experiments) gives a very small value of 2 per degree of freedom (of order 6 10) so that the distinction between in P at large times and a simple exponential decay function is numerically minute (Figure 2). 5. Generalization Exact, closed-form, analytical solutions to the time- dependent Schrödinger equation for the potential con- sisting of an infinite wall and a repulsive delta function have been obtained by the authors of this article for other spectral function choices. For example, the choice 2 1cos 2 2 ()=2 L iE EEL (46) yields a square-integrable wavefunction. In the absence of the delta function at Lx = this would produce an effectively square density pulse at 0=t located  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 131 between 0=x and /2=Lx . Due to the actual boundary conditions at Lx= this spectral function also produces a cusp centered at Lx 2= . The survival probability is readily expressible in terms of Fresnel sine and cosine integrals [19]. Its asymptotic large time behavior is 3 t. A question that naturally arises at this point is whether the asymptotic time behavior can be generalized to other possible solutions to this problem. This question was first addressed by Khalfin [1] specifically for the case of quasi-stationary initial states. Here a detailed answer is provided for non-resonance cases employing the general requirements of convergence and square-integrability. There is a one-to-one correspondence between spectral functions and square-integrable wavefunctions. This can be seen upon projecting the wavefunction at =0t on an energy eigenfunction and employing the orthogonality condition of Equation (28): .,0)()( )( 1 =)(* 0dxxx Ew EE (47) Given an initial wavefunction the corresponding spectral function can, in principle, be constructed. Schrödinger’s time-dependent equation then produces the wavefunction at any later (or earlier) time. Convergence of the energy superposition integral in region (II) requires that the spectral function be finite at 0E. In addition, in order for ),( tx to be square-integrable, )( E must vanish at large energies. This requirement can be made precise by inserting Equation (32) into Equation (33) and applying Equation (28) to obtain 1.=|)(|)( 2 0dEEEw (48) Inspection of the function )(Ew , given in Equation (29), leads to the conclusion that |)(| E must vanish for E faster than E1/ due to a constant term in )(Ew . Assuming that)(E satisfies the convergence condi- tions and has no resonance structure, its contribution to the energy superposition integral giving ),( )( tx I , in region (I), comes mostly from low energies. Again, this situation must be contrasted to the case studied by Winter [2]. Then at any x in region (I) the wave- function can be approximated as () () 10 (,)(0)2. Et max IiEt x tC ExedE (49) The upper limit of the integration is chosen as follows: the factor )(exp iEt oscillates more rapidly as a function of the energy as t increases. At very large times these oscillations eventually lead to a vanishing contribution to the integral. Therefore, the integral can be cut off at a point )(tEmax whose first order term in the expansion in powers of t1/ is tymax/, where max y is constant in t. At low energies )( E is replaced by its (finite and non-zero) value at 0=E and the function )2(sin Ex is replaced by its argument at a given x . Then, the variable change Ety= yields .2(0) 0 3/2 1 )(dyeytxC iy max y I (50) For small max y the integral is approximately 3/2 2 [(2/3)max y5/2 (2 / 5)] max iy. The wavefunction in region (I) is to the first non-vanishing order ,(0)),( 3/2 1 )( tMxCtx I (51) where M is a constant and the survival probability (Equation (39)) decreases with time as 3 t. Therefore, in order for the wavefunction to be square-integrable, the spectral function must be finite at 0E and decrease at large E faster than E1/ . Then, if 0(0) , necessarily, the survival probability asymptotically decreases as 3 t. This argument can be extended to any finite value of x including region (II) since the coefficients 2 C and 3 C are at most of (1)O for small E. Therefore, the integral of the probability density over any finite range of x is finite (even without the convergence factor present in Equation (27)) and it decreases asymptotically as 3 t. The constant M in Equation (51) can be exactly evaluated if )(E decreases at large E faster than E1/ . Then if )(E is analytic in the fourth quadrant of the complex E -plane the contour integral of ()sinE (2) x Ee( ) x piEt along a closed path, consisting of the positive real axis from R to 0, the negative imaginary axis from 0 to iR and a quarter-circle, , of radius R, is zero (Figure 5). The integral along is bounded by a constant times k R1/ with |=|ER and 1>k and, consequently, vanishes in the limit R. Then the integration over the real axis gives the same result as that over the imaginary axis. The variable change iyE = with y real, then, yields () 10 (,)=( )sin2. Iyt x tiCiy xiyedy (52) For large times only small values of y contribute to the integral. The spectral function is substantially 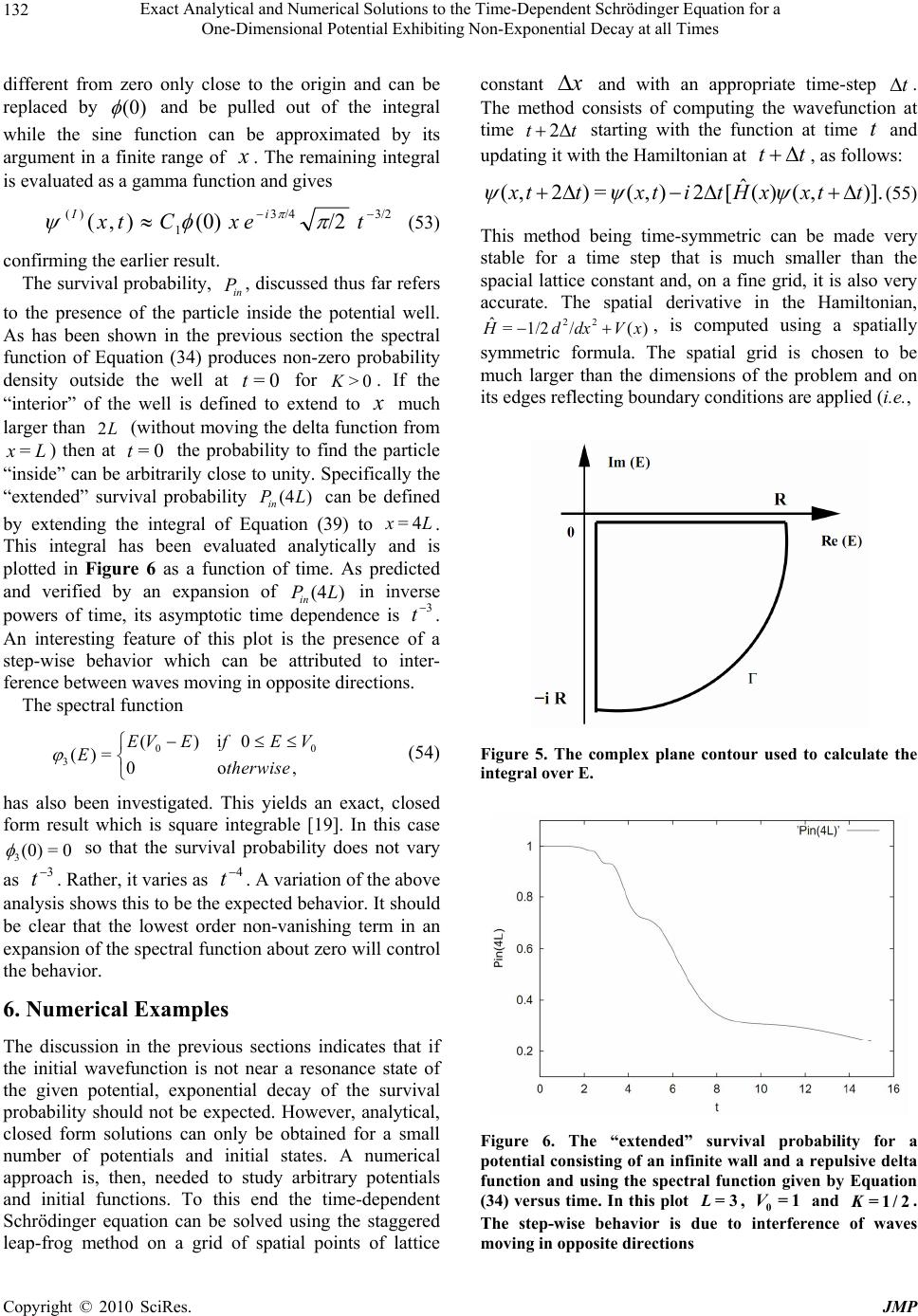 Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 132 different from zero only close to the origin and can be replaced by (0) and be pulled out of the integral while the sine function can be approximated by its argument in a finite range of x . The remaining integral is evaluated as a gamma function and gives 3/2/43 1 )( /2(0)),( texCtxiI (53) confirming the earlier result. The survival probability, in P, discussed thus far refers to the presence of the particle inside the potential well. As has been shown in the previous section the spectral function of Equation (34) produces non-zero probability density outside the well at 0=t for 0>K. If the “interior” of the well is defined to extend to x much larger than L 2 (without moving the delta function from Lx =) then at 0=t the probability to find the particle “inside” can be arbitrarily close to unity. Specifically the “extended” survival probability )(4 L P in can be defined by extending the integral of Equation (39) to Lx 4= . This integral has been evaluated analytically and is plotted in Figure 6 as a function of time. As predicted and verified by an expansion of )(4L P in in inverse powers of time, its asymptotic time dependence is 3 t . An interesting feature of this plot is the presence of a step-wise behavior which can be attributed to inter- ference between waves moving in opposite directions. The spectral function 00 3 ()i0 ()=0o, E VE fEV Etherwise (54) has also been investigated. This yields an exact, closed form result which is square integrable [19]. In this case 0=(0) 3 so that the survival probability does not vary as 3 t. Rather, it varies as 4 t. A variation of the above analysis shows this to be the expected behavior. It should be clear that the lowest order non-vanishing term in an expansion of the spectral function about zero will control the behavior. 6. Numerical Examples The discussion in the previous sections indicates that if the initial wavefunction is not near a resonance state of the given potential, exponential decay of the survival probability should not be expected. However, analytical, closed form solutions can only be obtained for a small number of potentials and initial states. A numerical approach is, then, needed to study arbitrary potentials and initial functions. To this end the time-dependent Schrödinger equation can be solved using the staggered leap-frog method on a grid of spatial points of lattice constant x and with an appropriate time-step t . The method consists of computing the wavefunction at time tt 2 starting with the function at time t and updating it with the Hamiltonian at tt , as follows: )].,()( ˆ [2),(=)2,( ttxxHtitxttx (55) This method being time-symmetric can be made very stable for a time step that is much smaller than the spacial lattice constant and, on a fine grid, it is also very accurate. The spatial derivative in the Hamiltonian, )(/1/2= ˆ22 xVdxdH , is computed using a spatially symmetric formula. The spatial grid is chosen to be much larger than the dimensions of the problem and on its edges reflecting boundary conditions are applied (i.e., Figure 5. The complex plane contour used to calculate the integral over E. Figure 6. The “extended” survival probability for a potential consisting of an infinite wall and a repulsive delta function and using the spectral function given by Equation (34) versus time. In this plot =3L, 0=1V and =1 / 2K. The step-wise behavior is due to interference of waves moving in opposite directions 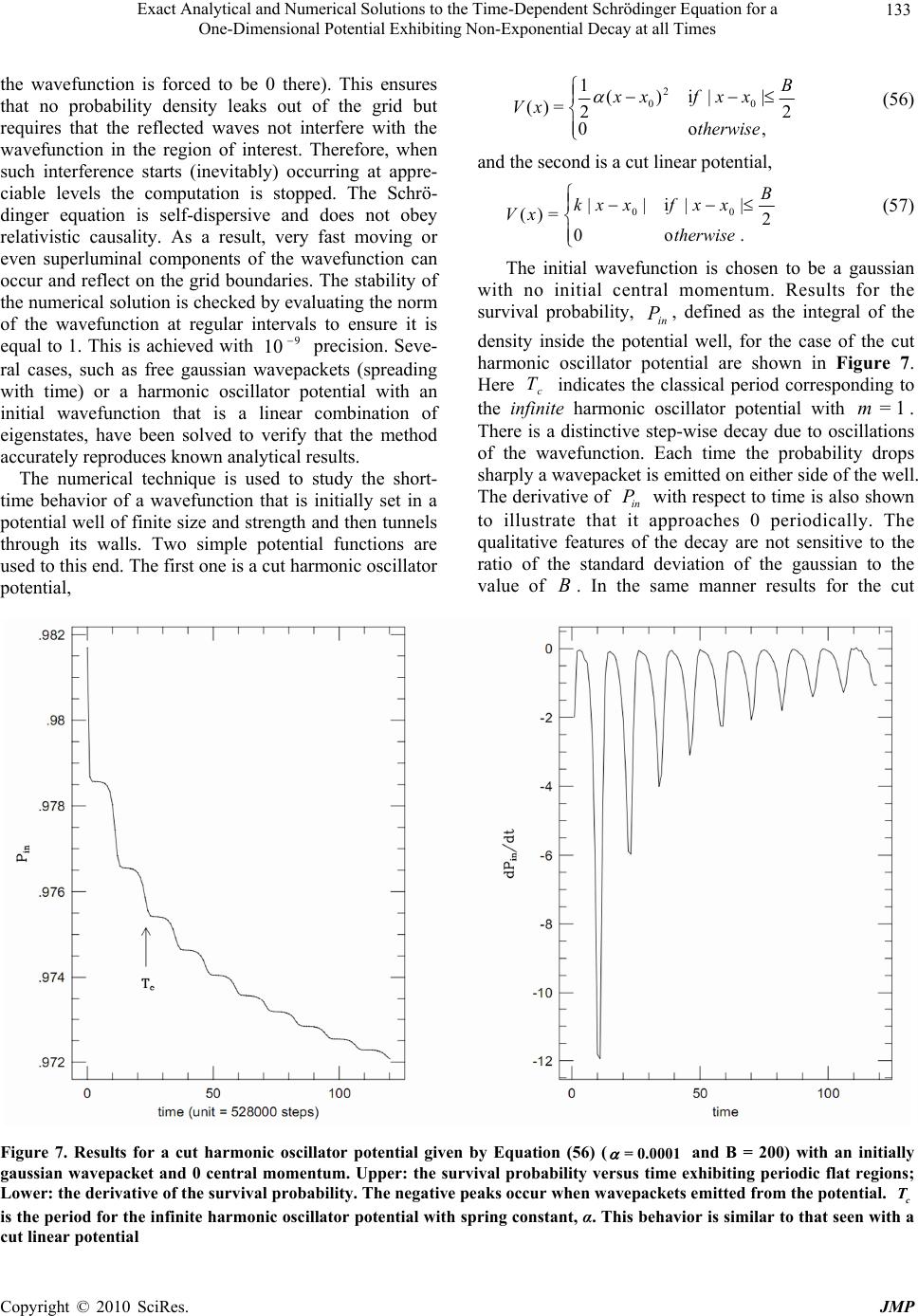 Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 133 the wavefunction is forced to be 0 there). This ensures that no probability density leaks out of the grid but requires that the reflected waves not interfere with the wavefunction in the region of interest. Therefore, when such interference starts (inevitably) occurring at appre- ciable levels the computation is stopped. The Schrö- dinger equation is self-dispersive and does not obey relativistic causality. As a result, very fast moving or even superluminal components of the wavefunction can occur and reflect on the grid boundaries. The stability of the numerical solution is checked by evaluating the norm of the wavefunction at regular intervals to ensure it is equal to 1. This is achieved with 9 10 precision. Seve- ral cases, such as free gaussian wavepackets (spreading with time) or a harmonic oscillator potential with an initial wavefunction that is a linear combination of eigenstates, have been solved to verify that the method accurately reproduces known analytical results. The numerical technique is used to study the short- time behavior of a wavefunction that is initially set in a potential well of finite size and strength and then tunnels through its walls. Two simple potential functions are used to this end. The first one is a cut harmonic oscillator potential, ,o0 2 ||i)( 2 1 =)( 0 2 0 therwise B xxfxx xV (56) and the second is a cut linear potential, .o0 2 ||i|| =)( 00 therwise B xxfxxk xV (57) The initial wavefunction is chosen to be a gaussian with no initial central momentum. Results for the survival probability, in P , defined as the integral of the density inside the potential well, for the case of the cut harmonic oscillator potential are shown in Figure 7. Here c T indicates the classical period corresponding to the infinite harmonic oscillator potential with 1=m. There is a distinctive step-wise decay due to oscillations of the wavefunction. Each time the probability drops sharply a wavepacket is emitted on either side of the well. The derivative of in P with respect to time is also shown to illustrate that it approaches 0 periodically. The qualitative features of the decay are not sensitive to the ratio of the standard deviation of the gaussian to the value of B . In the same manner results for the cut Figure 7. Results for a cut harmonic oscillator potential given by Equation (56) (=0.0001 and B = 200) with an initially gaussian wavepacket and 0 central momentum. Upper: the survival probability versus time exhibiting periodic flat regions; Lower: the derivative of the survival probability. The negative peaks occur when wavepackets emitted from the potential. c T is the period for the infinite harmonic oscillator potential with spring constant, α. This behavior is similar to that seen with a cut linear potential 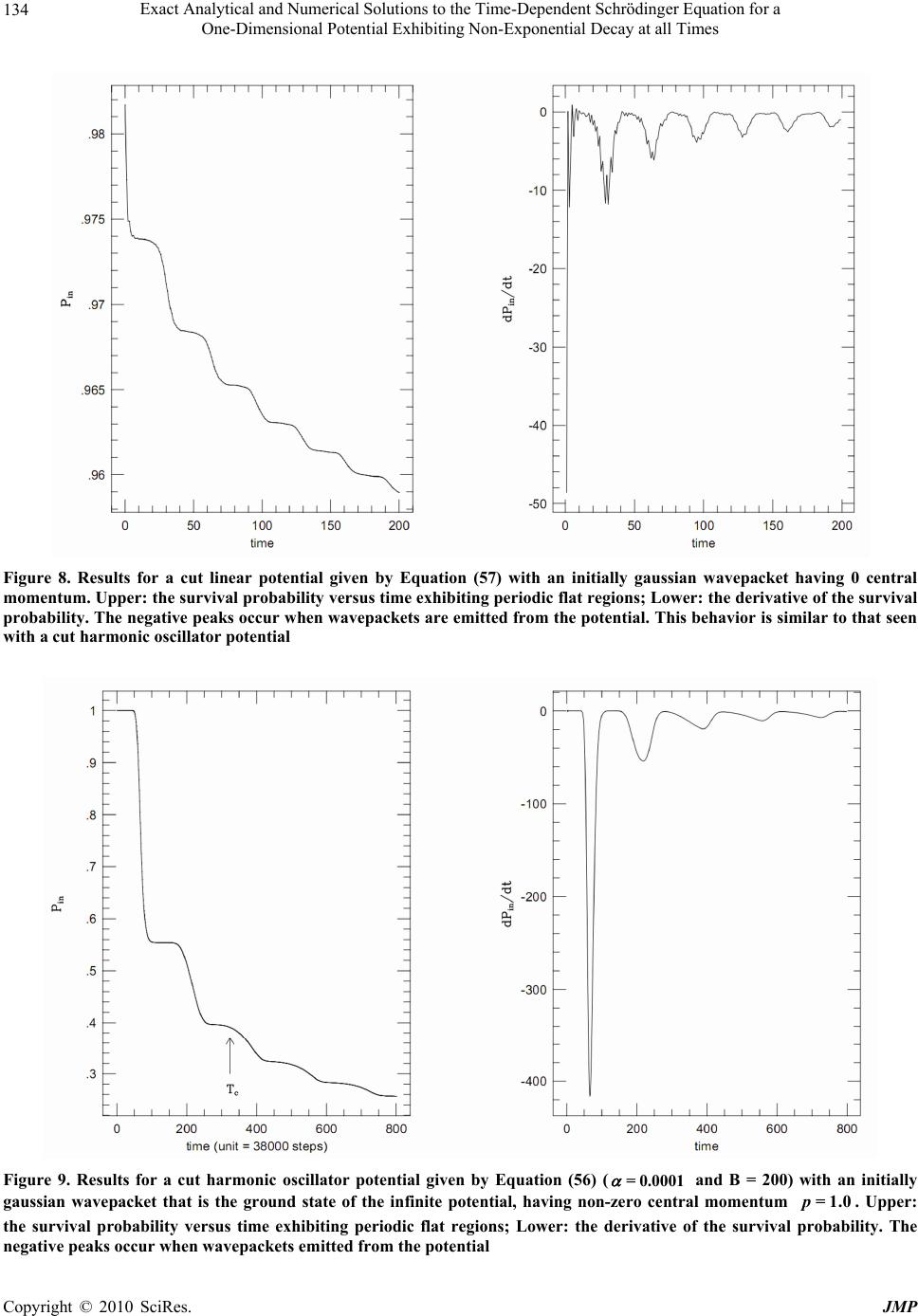 Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 134 Figure 8. Results for a cut linear potential given by Equation (57) with an initially gaussian wavepacket having 0 central momentum. Upper: the survival probability versus time exhibiting periodic flat regions; Lower: the derivative of the survival probability. The negative peaks occur when wavepackets are emitted from the potential. This behavior is similar to that seen with a cut harmonic oscillator potential Figure 9. Results for a cut harmonic oscillator potential given by Equation (56) (=0.0001 and B = 200) with an initially gaussian wavepacket that is the ground state of the infinite potential, having non-zero central momentum =1.0p. Upper: the survival probability versus time exhibiting periodic flat regions; Lower: the derivative of the survival probability. The negative peaks occur when wavepackets emitted from the potential  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 135 Figure 10. The probability density for a cut harmonic oscillator potential given by Equation (56) (=0.0001 and B = 200) with an initially gaussian wavepacket that is the ground state, 0 u, of the infinite potential, having non-zero central momentum, =1.0 p , captured at about 2.5 classical periods of the infinite potential. The classical amplitude of oscillations is =100 c A. All quantities are expressed in natural units. Wavepackets are periodically emitted from the non-zero potential region, propagate outwards and spread out. The first emitted packet is traveling to the right and at this time frame is centered at 3500x. The second emitted packet is traveling to the left and at this moment is centered at 900x. The interior wavefunction is hitting the left wall of the potential well at this moment linear potential are shown in Figure 8 with similar initial conditions. Again the decay is non-exponential with a step-wise behavior. To illustrate this result further an initial gaussian with non-zero central velocity, 0 v, is set in a cut harmonic oscillator potential. This is accom- plished by multiplying the initial gaussian by )(expipx, where 0 = p mv is the central momentum. The results are shown in Figure 9. In this case in P decays in larger steps. The emission of wavepackets is shown in Figure 10,where the probability density is plotted versus x at a particular time. 7. Conclusions Exponential time-dependence has been shown to be only an approximation to any real decay process even in the case of commonly encountered resonance states. For resonances, at large times a 2 tdependence emerges preceded by some oscillations. The time-dependent Schrödinger equation for non-resonance initial states has been solved utilizing the eigenfunctions for a given Hamiltonian. It has been applied to the case of a potential consisting of an infinite wall and a repulsive delta function. Exact, analytical, normalized solutions have been obtained in closed form. In the case specifically exhibited, i.e. , the choice spectral function )( 1 E (Equation (34)), the survival probability, which is exactly detailed in Equation (40), exhibits a non-exponential behavior at all times. At large times it decays as 3 t. To ensure square- integrability the spectral function must be finite at 0 E and decrease to 0 at large energies faster than E1/ . It was shown that this behavior pertains to all square-integrable wavefunctions that are solutions to this problem for which (0) 0 . Other spectral functions result in decays varying as t –n with n greater than 3. With the appropriate choice of spectral functions which, due to linear independence need not be the same for waves propagating in different directions, the method could be applied to a variety of potentials. Numerical studies of finite potential wells show that non-exponential decay prevails at short times and can exhibit an interesting step-wise behavior. In conclusion quantum mechanics predicts non-exponential decay for all systems studied. 8. Acknowledgements Ames Laboratory is operated for the U.S. Department of Energy by Iowa State University under Contract No. W-7405-Eng-82. REFERENCES [1] S. A. Khalfin, “Contribution to the Decay Theory of a Quasi-Stationary State,” Soviet Journal of Experimental and Theoretical Physics, Vol. 6, 1958, pp. 1053-1063. [2] R. Winter, “Evolution of a Quasi-Stationary State,” Phy- sical Review, Vol. 123, No. 4, 1961, pp. 1503-1507. [3] V. Weisskopf and E. Wigner, “Berechnung der natür- lichen Linienbreite auf Grund der Diracschen Lichtt- heorie,” Zeitschrift für Physik, Vol. 63, No. 1-2, 1930, pp. 54-73. [4] J. J. Sakurai, “Modern Quantum Mechanics,” The Benja- min-Cummings Publishing Company, 1985. [5] C. Dullemond, “Fermi’s ‘Golden Rule’ and Non-Expo- nential Decay,” arXiv:quant-ph/0202105, 2003. [6] V. P. Oleinik and J. D. Arepjev, “On the Tunneling of Electrons out of the Potential Well in an Electric Field,” Journal of Physics A, Vol. 17, No. 9, 1984, pp. 1817-1827.  Exact Analytical and Numerical Solutions to the Time-Dependent Schrödinger Equation for a One-Dimensional Potential Exhibiting Non-Exponential Decay at all Times Copyright © 2010 SciRes. JMP 136 [7] M. I. Shirokov, “Exponential Character of Decay Laws,” Soviet Journal of Nuclear Physics, Vol. 21, 1975, pp. 347-353. [8] V. V. Flambaum and F. M. Izrailev, Unconventional decay law for excited states in closed many-body systems. Physical Review E, Vol. 64, No. 2, 2001, pp. 026124- 026130. [9] P. G. Silvestrov, “Stretched Exponential Decay of a Quasiparticle in a Quantum Dot,” Physical Review B, Vol. 64, No. 11, 2001, pp. 113309-113313. [10] L. Accardi, S. V. Kozyrev and I. V. Volovich, “Non- Exponential Decay for Polaron Model,” Physics Letters A, Vol. 260, No. 1-2, 1999, pp. 31-38. [11] G. Wilk and Z. Wlodarczyk, “Nonexponential Decays and Nonextensivity,” Physics Letters A, Vol. 290, No. 1-2, 2001, pp. 55-58. [12] A. N. Petridis, L. P. Staunton, M. Luban and J. Vermedahl, Talk Given at the Fall Meeting of the Division of Nuclear Physics of the American Physical Society, Tucson, Arizona, Unpublished, 2003. [13] S. R.Wilkinson, et al., “Experimental Evidence for Non- Exponential Decay in Quantum Tunnelling,” Nature, Vol. 387, 1997, pp. 575-577. [14] N. G. Kelkar, M. Nowakowski and K. P. Khemchandani, “Hidden Evidence of Nonexponential Nuclear Decay,” Physical Review C, Vol. 70, No. 2, 2004, pp. 24601- 24605. [15] C. Rothe, S. I Hintschich and A. P. Monkman, “Violation of the Exponential-Decay Law at Long Times,” Physical Review Letters, Vol. 96, No. 16, 2006, pp. 163601- 163604. [16] B. L. Burrows and M. Cohen, “Exact Time-Dependent Solutions for a Double-Well Model,” Journal of Physics A, Vol. 36, No. 46, 2003, pp. 11643-11653. [17] R. M. Cavalcanti, P. Giacconi and R. Soldati, “Decay in a Uniform Field: An Exactly Solvable Model,” Journal of Physics A, Vol. 36, No. 48, 2003, pp. 12065-12080. [18] A. Messiah, “Quantum Mechanics,” Dover Publishers, Mineola, 1999. [19] The expressions for this wavefunction and the probability density are very long and complicated. They are available from the authors upon request. |

