Theoretical Economics Letters
Vol. 2 No. 1 (2012) , Article ID: 17388 , 4 pages DOI:10.4236/tel.2012.21020
The Effects of Income Inequality on Education Policy and Economic Growth
Graduate School of Economics, Kyoto University, Kyoto, Japan
Email: k.naito.71@gmail.com, k.nishida@ft7.ecs.kyoto-u.ac.jp
Received November 30, 2011; revised December 20, 2011; accepted December 28, 2011
Keywords: Income Inequality; Majority Voting; Human Capital Accumulation; Economic Growth
ABSTRACT
This paper presents a simple model to investigate the relationship among initial income inequality, education and economic growth. Public expenditure on education is determined through majority voting. Although preferences of individuals are not single-peaked, the individual with the median income becomes the decisive voter. Our model predicts that high initial inequality has a negative impact on education expenditure and therefore retards economic growth.
1. Introduction
The relationship between initial levels of income inequality and economic growth is a central question in growth and development literature. Many political economists have addressed this question by analyzing how income inequality affects the size of redistribution. Standard politico-economic theories predict that, under majority voting, high income inequality is associated with a large scale of redistribution policies as the poor majority favors it. Persson and Tabellini [1] argue that income redistribution creates adverse incentive for investments and therefore high income inequality is harmful for growth. However, redistribution policies may promote economic growth if they are practiced through the provision of public goods that can enhance future productivity. SaintPaul and Verdier [2] construct a model in which public education is the channel of redistribution. In their model, high income inequality implies strong support for public education, which facilitates human capital accumulation and economic growth. In contrast to these theories, the hypothesis that high inequality is associated with redistribution is not supported by data. For example, crosscountry regressions by Easterly [3,4] show that higher inequality leads to lower levels of public goods, education, per capita income and growth rates. This suggests the necessity for further investigations on how income inequality affects public policies and growth.
This paper proposes a simple model to reconcile the theory and evidence, and analyzes the relationship among income inequality, human capital accumulation and economic growth in a politico-economic framework. In the model, the heterogeneity of human capital across individuals is the only source of income inequality. We focus on two features of education. The first one is a fixed cost of education. We consider a situation in which individuals must pay tuition fees to have access to education services although they are provided by the government. This aspect of education is particularly relevant to post-compulsory education, such as high school and university education. The second feature is that the return from education is positively correlated with the level of human capital inherited from parents.1 These two features play a key role in the determination of the size of education services under majority voting.
The main result of this paper is that high initial levels of inequality cause less publicly provided education services, or lower tax rates. In our model, the individual with median income is the decisive voter although preferences for tax rates are not single-peaked. When inequality is high and the income of the median voter is low, he or she does not prefer a high tax rate to enhance education. This is because the median voter cannot cover the fixed cost of education or the private return from education is too low due to his or her low level of inherited human capital. High inequality is therefore harmful for human capital accumulation and growth, which is in contrast to the result of Saint-Paul and Verdier [2].
2. The Model
We consider an overlapping generations economy in which individuals live for two periods. They are heterogeneous only with respect to their human capital within each generation. Each individual has one parent and one child, and the size of each generation is normalized to one. In the first period, individuals make no economic and political decisions, but receive education if their parents decide to invest in human capital of their children. In the second period, individuals inelastically supply their human capital to a final good sector and decide whether to invest in education for their children. Using human capital, h, the final good sector produces according to a linear production function, y = h, where y is the output. The final good market is perfectly competitive, and therefore, the wage for one unit of human capital is one. Individuals derive utility from consumption in their second period and human capital of their children. The preference of individual i born in period t are represented by a linear utility function,
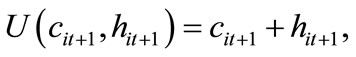 (1)
(1)
where 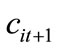 and
and 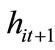 are consumption in the period t + 1 and human capital of his/her child, respectively.
are consumption in the period t + 1 and human capital of his/her child, respectively.
The investment in education requires one unit of the final good as a fixed cost. Individuals must self-finance the cost because human capital of their children is not valid collateral to lenders. The consumption of individual i born in period t is given by
 (2)
(2)
where  is the proportional labor income tax rate at period t+1. Remember that
is the proportional labor income tax rate at period t+1. Remember that  is the human capital of individual i born in period t, which is supplied to the final good sector at period t + 1.
is the human capital of individual i born in period t, which is supplied to the final good sector at period t + 1.
The government manages an education sector. By levying a labor income tax on parental individuals, the government finances public expenditure which raises the productivity of the education sector. Let the distribution of 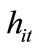 be denoted by
be denoted by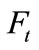 . The average human capital,
. The average human capital, 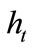 , is then given by
, is then given by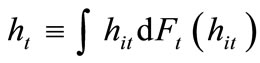 , and the tax revenue is
, and the tax revenue is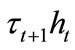 . Assuming that the government budget is balanced in each period, we obtain
. Assuming that the government budget is balanced in each period, we obtain
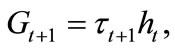 (3)
(3)
where 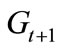 is the public expenditure on the education sector.
is the public expenditure on the education sector.
Individual i whose parent pays the fixed cost of education can have access to education services and accumulate human capital according to the following human capital production function:
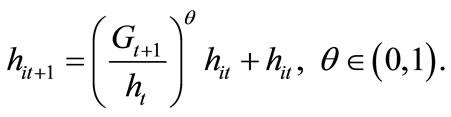 (4)
(4)
Notice that the human capital production function depends on the ratio of public education expenditure to average human capital. The interpretation is as follows. The government must hire teachers in the public education system. On the condition that the wage per teacher is equal to the average wage in the economy, the ratio  represents the number of teachers in the public education system. From (3) and (4), human capital of individual i born in period t+1 who receives education is given by
represents the number of teachers in the public education system. From (3) and (4), human capital of individual i born in period t+1 who receives education is given by
 (5)
(5)
In contrast, individuals just inherit their parental human capital if their parents do not invest in education:
 (6)
(6)
Individuals with 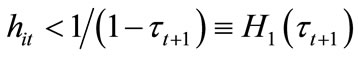 cannot afford to invest in education. The threshold H1 is increasing in
cannot afford to invest in education. The threshold H1 is increasing in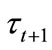 . A high level of
. A high level of  reduces disposable income of individuals and makes more individuals unable to invest in education. In contrast, individuals with
reduces disposable income of individuals and makes more individuals unable to invest in education. In contrast, individuals with 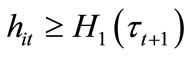 are able to invest in education.
are able to invest in education.
From (1), (2) and (5), the welfare of an individual with 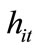 who chooses to have their children receive education is given by
who chooses to have their children receive education is given by
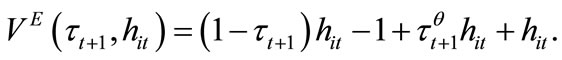 (7)
(7)
On the other hand, the welfare of an individual with  who chooses not to invest in education is given by
who chooses not to invest in education is given by
 (8)
(8)
The welfare function 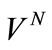 is decreasing in
is decreasing in 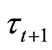 since higher tax rates reduce the consumption in the second period. It is easy to see that individuals with
since higher tax rates reduce the consumption in the second period. It is easy to see that individuals with 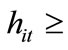
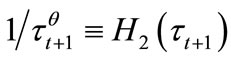 are willing to invest in education, while individuals with
are willing to invest in education, while individuals with 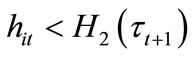 are not. Notice that the threshold H2 is decreasing in
are not. Notice that the threshold H2 is decreasing in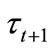 . An increase in
. An increase in 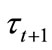 raises the return on education, and thus, makes more individuals willing to invest in education.
raises the return on education, and thus, makes more individuals willing to invest in education.
3. Preferred Tax Rates
We proceed to analyze the characteristics of a politicoeconomic equilibrium in which the level of labor income tax rate is determined under majority voting. Since schoolage individuals do not participate in voting in many countries, we assume that only individuals in the second period have voting rights. To characterize the politicoeconomic equilibrium, we need to identify the tax rate that each individual prefers the most. Let us define 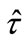 and
and 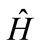 by
by 
First of all, for any 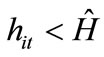 and
and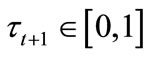 ,
,
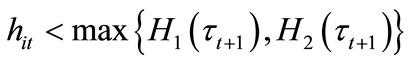 (see Figure 1). Any individuals with
(see Figure 1). Any individuals with 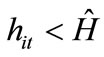 are unwilling or unable to have their children receive education and therefore prefer
are unwilling or unable to have their children receive education and therefore prefer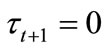 .
.
We then investigate preferences of individuals with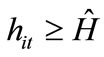 . It is useful to define
. It is useful to define  and
and 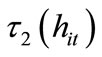 by
by

Figure 1. The features of H1 and H2.
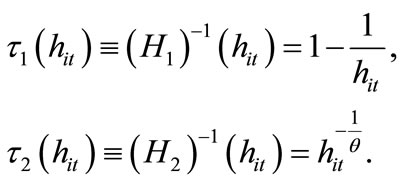
For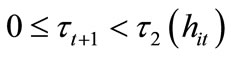 , an individual with
, an individual with  is unwilling to invest in education because the return from education is too low. For
is unwilling to invest in education because the return from education is too low. For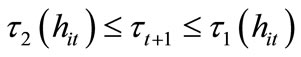 , the individual is willing and able to invest in education. For
, the individual is willing and able to invest in education. For , the individual cannot afford to invest in education because of the high labor income tax rate. The welfare of individual i with
, the individual cannot afford to invest in education because of the high labor income tax rate. The welfare of individual i with  is summarized as
is summarized as
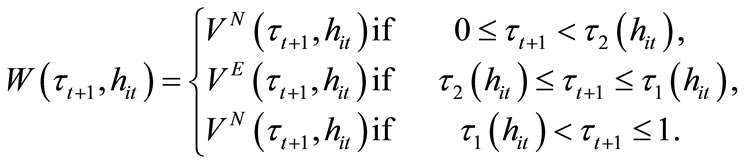 (9)
(9)
We define 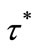 by
by
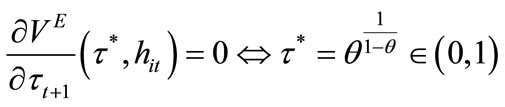
in order to fully describe the preferred tax rate of individual i with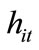 . It is clearly evident that
. It is clearly evident that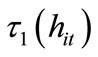 ,
,  and
and 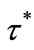 satisfy the following relations:
satisfy the following relations:
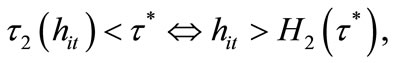
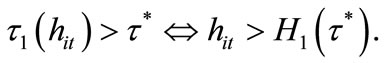
There are two cases that need to be considered: (i) 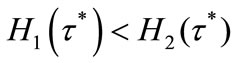 and (ii)
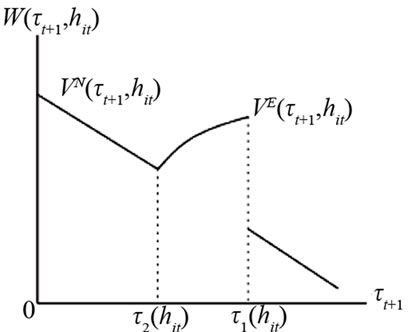
and (ii) . We start with case (i). Individuals with
. We start with case (i). Individuals with 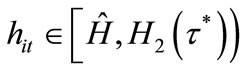 are unwilling to invest in education at
are unwilling to invest in education at 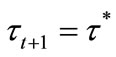 since
since . The welfare of such individuals is drawn in Figure 2(a). They prefer
. The welfare of such individuals is drawn in Figure 2(a). They prefer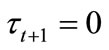 . Individuals with
. Individuals with 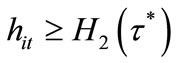 are willing to invest in education at
are willing to invest in education at 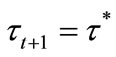 since
since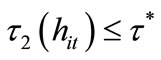 . The welfare of such individuals is depicted in Figure 2(b). Simple calculations show
. The welfare of such individuals is depicted in Figure 2(b). Simple calculations show
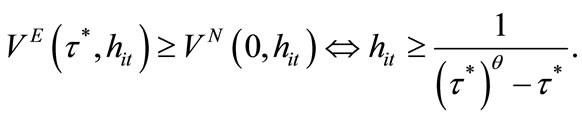
Hence, these individuals prefer 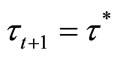 if
if
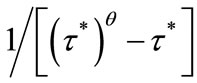
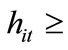 and prefer
and prefer 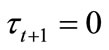 otherwise.
otherwise.
In case (ii), individuals with 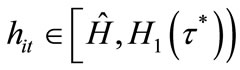 are not able to invest in education at
are not able to invest in education at 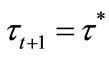 since
since 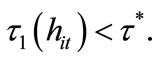
The welfare of these individuals is drawn in Figure 3(a). By simple calculations, we can see that
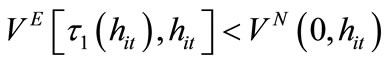 for any
for any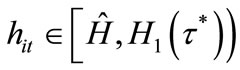 .
.
Hence, such individuals always prefer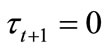 . Individuals with
. Individuals with 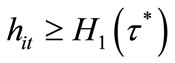 have their children receive education at
have their children receive education at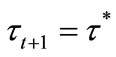 , and the welfare of such individuals are depicted in Figure 3(b). Similarly to case (i), these individuals prefer
, and the welfare of such individuals are depicted in Figure 3(b). Similarly to case (i), these individuals prefer 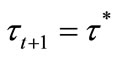 if
if 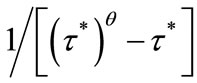
 and prefer
and prefer 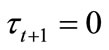 otherwise. We summarize the results of this section in Proposition 1.
otherwise. We summarize the results of this section in Proposition 1.
Proposition 1 Individual i with  prefers
prefers 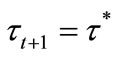
if , and prefers
, and prefers 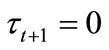 otherwise.
otherwise.
4. Majority Voting Equilibrium
This section shows that the individual with median income is the decisive voter although the welfare of individuals over tax rates is not single-peaked as shown in Figures 2 and 3. The logic shares similarity with that of Glomm and Ravikumar [6]. Let 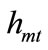 denote the human capital level of the individual with median income. If
denote the human capital level of the individual with median income. If
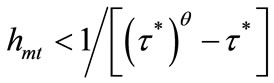 , then the individual with median income prefers
, then the individual with median income prefers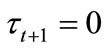 . Since individuals with
. Since individuals with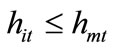 , who comprise of fifty percent of the total population,
, who comprise of fifty percent of the total population,
 (a)
(a) (b)
(b)
Figure 2. The welfare in case (i).
 (a)
(a)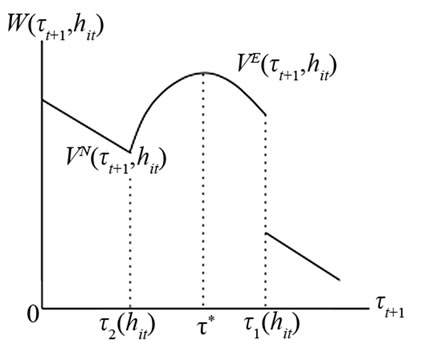 (b)
(b)
Figure 3. The welfare in case (ii).
also prefer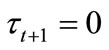 , there exists no tax rate that obtains more than fifty percent votes to beat
, there exists no tax rate that obtains more than fifty percent votes to beat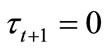 . If
. If
 , then the individual with median income prefers
, then the individual with median income prefers 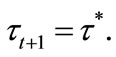 Since individuals with
Since individuals with , who constitute fifty percent of the total population, also prefer
, who constitute fifty percent of the total population, also prefer , no tax rate gains a majority vote to beat
, no tax rate gains a majority vote to beat . Hence, the individual with median income is the decisive voter.
. Hence, the individual with median income is the decisive voter.
Proposition 2 Under majority voting, 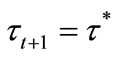 if
if 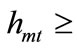
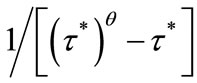 , and
, and  otherwise.
otherwise.
5. The Result
As described in Introduction, empirical evidence shows that high income inequality is associated with lower levels of education, public good provision and per capita income. In contrast to the results of Saint-Paul and Verdier [2], our model predicts that high inequality leads to less government expenditure on education. In the model, whether human capital is accumulated and the economy grows over time depends on the initial distribution of human capital, or income distribution. To understand this point, it should be noted that the child of the median voter is the median voter in the next period because human capital evolves according to (5) and (6).
If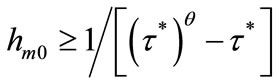 , then
, then 
for all 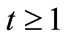 since human capital does not depreciate. Hence,
since human capital does not depreciate. Hence, 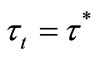 for all
for all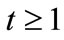 . All individuals in lineage i such that
. All individuals in lineage i such that 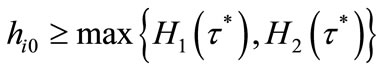 accumulate their human capital according to (5) with
accumulate their human capital according to (5) with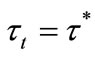 . In contrast, all individuals in lineage i such that
. In contrast, all individuals in lineage i such that
 just inherit their parental human capital in all periods, i.e.,
just inherit their parental human capital in all periods, i.e., 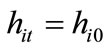 for all
for all .
.
If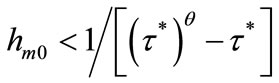 , then government expenditure on education is zero and no one can obtain education provided by the government. This situation continues and
, then government expenditure on education is zero and no one can obtain education provided by the government. This situation continues and  for all
for all 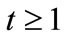 and i. Proposition 3 summarizes these results.
and i. Proposition 3 summarizes these results.
Proposition 3 If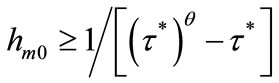 , then
, then 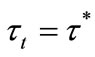
for all . All individuals in lineage i such that
. All individuals in lineage i such that
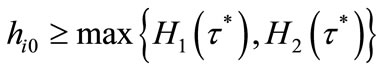 accumulate their human capital according to (5), while all individuals in lineage i such that
accumulate their human capital according to (5), while all individuals in lineage i such that 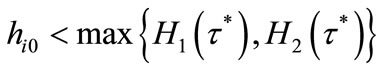 never enhance their inherited human capital. If
never enhance their inherited human capital. If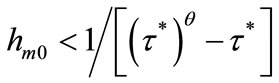 then
then 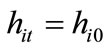 and
and 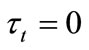 for all
for all 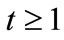 and i.
and i.
When , politically implemented public education accumulates the human capital of individuals in lineages whose initial human capital is greater than
, politically implemented public education accumulates the human capital of individuals in lineages whose initial human capital is greater than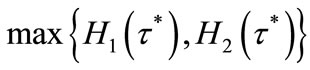 , and it stimulates economic growth. In contrast, when
, and it stimulates economic growth. In contrast, when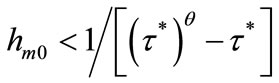 , public education is not implemented, and there is no human capital accumulation. These results imply that high initial inequality retards economic growth.
, public education is not implemented, and there is no human capital accumulation. These results imply that high initial inequality retards economic growth.
This paper has analyzed the relationship among income inequality, education and economic growth by focusing on two features of education, fixed costs and positive correlation between the return from education and the level of inherited human capital. Fixed costs of education are particularly relevant for post-compulsory education. The analysis on situations in which compulsory and post-compulsory education coexist would be a fruitful direction for further research.
REFERENCES
- T. Persson and G. Tabellini, “Is Inequality Harmful for Growth?” American Economic Review, Vol. 84, No. 3, 1994, pp. 600-621.
- G. Saint-Paul and T. Verdier, “Education, Democracy and Growth,” Journal of Development Economics, Vol. 42, No. 2, 1993, pp. 399-407. doi:10.1016/0304-3878(93)90027-K
- W. Easterly, “The Middle Class Consensus and Economic Development,” Journal of Economic Growth, Vol. 6, No. 4, 2001, pp. 317-335. doi:10.1023/A:1012786330095
- W. Easterly, “Inequality Does Cause Underdevelopment: Insights from a New Instrument,” Journal of Development Economics, Vol. 84, No. 2, 2007, pp. 755-776. doi:10.1016/j.jdeveco.2006.11.002
- E. Hanushek, “The Economics of Schooling: Production and Efficiency in Public Schools,” Journal of Economic Literature, Vol. 24, No. 3, 1986, pp. 1141-1177.
- G. Glomm and B. Ravikumar, “Opting out of Publicly Provided Services: A Majority Voting Result,” Social Choice and Welfare, Vol. 15, No. 4, 1998, pp. 187-199. doi:10.1007/s003550050099
NOTES
1Many empirical studies such as Hanushek [5] find a positive effect of parental human capital on the return from education.

